ET during the initial stage for annual crops is predominately in the form of evaporation. Therefore, accurate estimates for Kc ini must consider the frequency that the soil surface is wetted during the initial period. The initial period was defined in Chapter 6 for annual crops as the period between the planting date and the date of approximately 10% ground cover.
Chapter 6 presents background and figures for predicting Kc ini as a function of reference evapotranspiration (ETo), soil texture, and frequency and depth of wetting. Additional background and equations are given in Chapter 7. This annex provides further background on development of the Kc ini curves that are presented in Figures 29 and 30 of Chapter 6. Equations are presented here that can be used in place of Figures 29 and 30 when computers are used.
INTRODUCTION
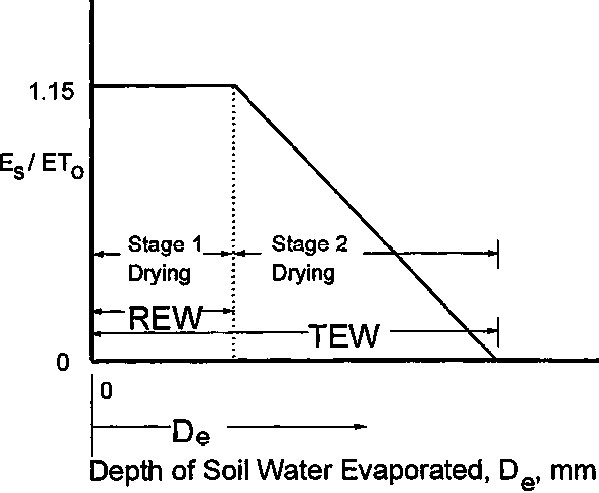
Evaporation from bare soil (Es) can be characterized as occurring in two distinct stages. The stage 1 is termed the "energy limited" stage. During this stage, moisture is transported to the soil surface at a rate sufficient to supply the potential rate of evaporation (Eso), which, in turn, is governed by energy availability at the soil surface. In this procedure, Eso is estimated from
Eso = 1.15 ETo (7-1)
where Eso is the potential rate of evaporation [mm d-1] and ETo is the the mean ETo during the initial period [mm d-1]. The value 1.15 represents increased evaporation potential due to low albedo of wet soil and the possibility of heat stored in the surface layer during previous dry periods.
Stage 2 is termed the "soil limited" stage, where hydraulic transport of subsurface water to the soil surface is unable to supply water at the potential evaporation rate. During stage 2, the soil surface appears partially dry and a portion of the evaporation occurs from below the soil surface. The energy required for subsurface evaporation is supplied by transport of heat from the soil surface into the soil profile. The evaporation rate during stage 2 drying decreases as soil water content decreases as shown in Figure 7.1 (see also Figure 38 of Chapter 7). The evaporation rate can therefore be expressed as being proportional to the water remaining in the evaporation layer relative to the maximum depth of water that can be evaporated from the same soil layer during stage 2 drying.
The maximum total depth of water that can be evaporated from the surface soil layer is termed "total evaporable water" or TEW. Equation 73 of Chapter 7 is used to predict TEW. In turn, the maximum total depth of water that can be evaporated during stage 1 is termed "readily evaporable water" or REW. Table 19 of Chapter 7 includes recommended values for REW.
If the evaporation rate during stage 2 drying is assumed to be linearly proportional to the equivalent depth of water remaining in the evaporation layer, as shown in Figure 7.1, then the average soil water evaporation rate during stage 2 can be estimated, similar to Equation 74 of Chapter 7:
(7-2)
for when De > REW, where Es is the actual evaporation rate [mm d-1] at any particular time when the depletion from the soil surface layer equals De. De is the depletion from the surface layer [mm] and REW is the readily evaporable water in the surface layer [mm]. The length of time required to complete stage 1 drying (t1) is equal to t1 = REW/Eso.
FIGURE 7.1. Two stage model for soil evaporation during the initial period
GENERAL EQUATION FOR Kc ini
Equation 7-2 can be integrated over the range REW to TEW, resulting in the basic equation for Kc ini during stage 2:
(7-3)
for tw > t1, where Kc ini = Es/ETo, tw is the mean interval between wetting events [days] and t1 is the time when stage 1 drying is completed (t1 = REW/Eso) [days]. The "exp" parameter represents the exponential of the value contained within the parenthesis following the parameter. The Kc ini calculated from Equation 7-3 is limited to Kc ini £ 1.15.
When tw < t1, i.e. the entire process resides within stage 1, so that:
(for tw < tl) (7-4)
Where furrow or trickle irrigation is practiced, and only a portion of the soil surface is wetted, the value calculated for Kc ini in Equations 7-3 and 7-4 should be reduced in proportion to the average fraction of surface wetted, fw [0,1]. Indicative values for fw are given in Table 20 of Chapter 7. Equation 60 of Chapter 6 is used to make the adjustment:
where fw is the fraction of surfaced wetted by irrigation or rain [0 - 1], and Kc ini (fw = 1) is the value for Kc ini for fw = 1 from Equation 7-3 or 7-4.
Accordingly, the value for the infiltration depth from irrigation (Iw) should be adjusted using Equation 61 of Chapter 6:
where Iw is the depth of irrigation water that is infiltrated over the part of the surface that is wetted [mm] and I is the depth of water infiltrated from irrigation, expressed as one-dimensional depth over the entire surface area [mm].
TOTAL EVAPORABLE WATER
The value for TEW is the maximum depth of water that can be evaporated from the soil following wetting. The value for TEW is governed by the depth of the soil profile contributing to soil water evaporation and by the soil water holding properties within the evaporating layer. In addition, the value for TEW is affected by the unsaturated hydraulic conductivity, by the presence of a hydraulically limiting layer beneath the evaporating layer, and by the conduction of sensible heat into the soil to supply energy for subsurface evaporation. An approximation for the maximum value of TEW for initial periods having ETo ³ 5 mm d-1 is:
TEW = 1000(q FC - 0.5 q WP) Ze (7-5)
where TEW has units of mm, q FC is soil water content at field capacity [m3 m-3], q WP is soil water content at wilting point [m3 m-3], and Ze is the depth of the soil surface soil layer that is subject to drying by way of evaporation [0.10 to 0.15 m]. If unknown, a value of Ze = 0.15 m is recommended. Typical values for q FC and q WP are given in Table 19 of Chapter 7.
During winter and other cool season months, less radiation energy is available to penetrate the soil surface and to evaporate water from within a drying soil, and TEW may be less. Therefore, when ETo < 5 mm d-1, TEW for use in Equation 7-3 is estimated as:
(7-6)
where ETo is reference ET in mm/day. Equation 7-6 is intended to correct TEW for use during the initial stage with mostly bare soil. It is not intended for use with the dual Kc procedure of Chapter 7. REW is limited so that REW £ TEW.
NUMBER OF WETTING EVENTS AND AVERAGE DEPTH
Estimating the number of wetting events and the corresponding time between wetting events during the initial period is described in Chapter 6. The number of wetting events (both from precipitation and irrigation) occurring during the initial period is determined by considering that two wetting events occurring on adjoining days can be counted as one event, and individual wetting events of less than 0.2 ETo can be ignored.
The average time between wetting events during the initial period (tw) is approximated as:
(7-7)
where tw is in days, Lini is the length of the initial period [days], and nw is the number of wetting events during the initial period.
The average depth of water added to the evaporating layer at each wetting event is determined by dividing the sum of the precipitation and irrigation infiltration occurring during all wetting events by the number of events, thus:
(7-8)
where Pmean is the average depth of infiltrated water per wetting event [mm], Pn is the depth of infiltrated precipitation occurring during the initial period, and Iw is the infiltrated irrigation depth for the part of the surface that is wetted [mm] (Equation 61). Each individual value of Pn and Iw must be limited in Equation 7-8 so that Pn £ TEW and Iw £ TEW where TEW is from Equation 7-5 or 7-6.
LIMITATIONS ON TEW AND REW
In the case of wetting depths (Pmean) that are smaller than the TEW, the evaporation process, including stage 1 drying, may terminate sooner than expected. The actual values for TEW and REW must be corrected according to Pmean. Therefore, TEW and REW are calculated according to the average total water available during each drying cycle:
(7-9)
and
(7-10)
where "min ()" is a function to select the minimum value of those in braces that are separated by the comma, and where TEW is from Equation 7-5 or 7-6. Wini is the equivalent depth of water [mm] in the evaporation layer (of thickness Ze) at the time of planting (beginning of the initial period). Wini has a maximum value of TEW when the initial soil water content of the evaporation layer is at field capacity. Values for TEWcor and REWcor from Equations 7-9 and 7-10 are used in place of TEW and REW in Equation 7-3.
EQUATIONS FOR FIGURES 29 AND 30 OF CHAPTER 6
Figures 29 and 30 of Chapter 6 can be reproduced numerically by applying Equation 7-3 under the following conditions. For all applications:
t1 = REWcor/Eso and Eso = 1.15 ETo (Equation 1).
If t1 < tw then Kc ini = 1.15 (Equation 4), and Equation 7-3 is not applied.
Otherwise, apply Equation 3 using the following parameters (TEWcor and REWcor are used in place of TEW and REW in Equation 3):
For Figure 29 (all soil textures having light infiltration depths (< 10 mm)):
TEWcor = 10 mm
REWcor = min(max(2.5, 6/(ETo)0.5), 7)
For Figure 30a (coarse soil textures having large infiltration depths (³ 40 mm)):
TEWcor = min(15, 7 (ET)0.5)
REWcor = min(6, TEWcor - 0.01)
For Figure 30b (medium and fine soil textures having large infiltration depths (³ 40 mm)):
TEWcor = min(28, 13 (ET)0.5)
REWcor = min(9, TEWcor - 0.01)
The max() and min() functions indicate the selection of the maximum or minimum value of the parameters that are separated by the comma. Most programming languages and spreadsheet programs include these functions.
The numerical application of Equation 7-3 using the parameters and constraints listed here will fully reproduce Figures 29 and 30a and b, with the exception that calculations made in the vicinity of ETo = 5 mm d-1 may deviate from the curves in Figures 30a and b, since curves in the vicinity of ETo = 5 mm d-1 were smoothed before plotting. The smoothing caused small, insignificant differences between the figures and the numerical procedure. The parameters listed above are reduced from equations 5 through 10 and using typical values for q FC and q WP.
In situations where wetting events are not equally spaced during the initial period, the dual Kc approach of Chapter 7, along with a daily soil water balance, can provide for more accurate results.
EXAMPLE 7-1. Application of Equation 7-3 to Example 25
|
As in Example 25 in Section B, small vegetables are cultivated in a dry area on a coarse textured soil and receive 20 mm of water twice a week by means of a sprinkler irrigation system. The average ETo during the initial stage is 5 mm/day. Estimate the crop evapotranspiration during that stage. |
|||
|
For: |
tw = 7/2 = |
3.5 |
day interval |
|
ETo = |
5 |
mm/day |
|
|
Eso = 1.15 ETo = 1.15 (5) = |
5.75 |
mm/day |
|
|
For Fig. 29: |
TEWcor = |
10 |
mm |
|
REWcor = min(max(2.5, 6/(50.5), 7) = |
2.7 |
mm |
|
|
t1 = REW/Eso = 2.7/5.75 = |
0.47 |
days |
|
|
since tw > t1, use Eq. 7-3: Kc ini (Fig 29) = (10 - (10 - 2.7) |
0.57 |
- |
|
|
exp[-(3.5 - 0.47)(5.75)(1 + 2.7/(10 - 2.7))/10])/(3.5(5)) = |
|
|
|
|
For Fig. 30.a: |
TEWcor = min(15,7(50.5)) = |
15 |
mm |
|
REWcor = min(6, 15 - 0.001) = |
6 |
mm |
|
|
t1 = REW/Eso = 6/5.75 = |
1.04 |
days |
|
|
since tw > t1, use Eq. 7-3: Kc ini (Fig. 30a) = (15 - (15 - 6) |
0.75 |
- |
|
|
exp[-(3.5 - 1.04)(5.75)(1 + 6/(15 - 6))/15])/(3.5(5)) = |
|
|
|
|
For: |
I = |
20 |
mm |
|
From Eq. 59: |
Kc ini = 0.57 + [(20 - 10)/(40 - 10)] (0.75-0.57) = 0.57 + 0.33(0.12) = |
0.63 |
- |
|
From Eq. 58: |
ETc = 0.63 (5) = |
3.2 |
mm/day |
|
The average crop evapotranspiration during the initial growth stage for the small vegetables is 3.2 mm/day. The values in this example agree relatively closely with those obtained from Example 25. |
|||