2.1.1. Introducción
2.1.2 Funciones
2.1.3 Potencias y logaritmos
2.1.4 Derivadas
2.1.5 Integrales
En el análisis de una pesquería y en la evaluación de las poblaciones, lo que interesa, principalmente, son los cambios que registran aquéllas. Puede haber cambios en el número de una población con el tiempo, cambios en el peso de los individuos con la edad, cambios en el rendimiento motivados por las variaciones en el esfuerzo pesquero, etc.
FIG. 2. Evolución de las características (número de individuos y pesos de una clase anual de peces durante la vida de éstos)
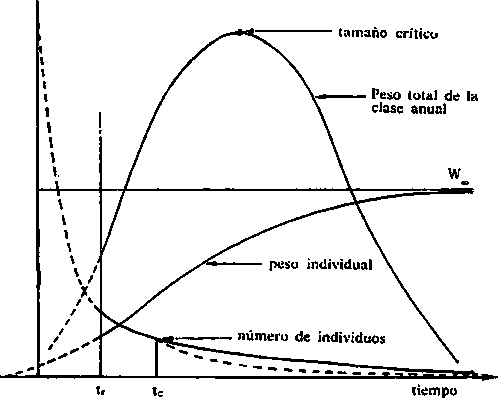
Los cambios en el tiempo se miden como tasas, es decir, el cambio en la magnitud de la cantidad considerada (peso, etc.) dividido por el período de tiempo durante el cual se produjo. Aun cuando el intervalo de tiempo no se especifique concretamente, por lo general, hay que suponer una unidad de tiempo (por ejemplo, un año), y por consiguiente, el cambio resulta implícitamente una tasa.
En términos matemáticos, si durante un período de tiempo
D t, una variable y cambia en la
cantidad D y, entonces la tasa media
el cambio durante este período es  .
Esta tasa es una tasa absoluta. Puede obtenerse una tasa relativa
dividiendo la tasa absoluta por el valor de la variable en algún punto
del período, por ejemplo, al principio, en que se convierte en
.
Esta tasa es una tasa absoluta. Puede obtenerse una tasa relativa
dividiendo la tasa absoluta por el valor de la variable en algún punto
del período, por ejemplo, al principio, en que se convierte en  .
Estos conceptos pueden generalizarse considerando t como una variable
cualquiera y no necesariamente como el tiempo.
.
Estos conceptos pueden generalizarse considerando t como una variable
cualquiera y no necesariamente como el tiempo.
Los modelos teóricos tienen la ventaja de permitir el análisis de la influencia de algunos factores mediante el estudio de las propiedades matemáticas de los modelos. Para mayor sencillez matemática, en estos modelos y en otras partes, se utilizan en muchos casos las tasas instantáneas.
Se pueden entender como tasas instantáneas el límite de las tasas medias cuando el período de tiempo, D t, tiende hacia cero. Matemáticamente, éste es el equivalente del concepto de derivada.
Las hipótesis formulables sobre las relaciones entre las tasas instantáneas y las variables pueden ser expresadas en forma de ecuaciones diferenciales. Los cálculos diferencial e integral son instrumentos matemáticos importantes para el análisis de la dinámica de las poblaciones y para otros sistemas. Algunas de estas hipótesis conducen a las funciones exponenciales, logarítmicas y potenciales.
Por las razones antes mencionadas, es importante una rápida reseña de las funciones potenciales, exponenciales y logarítmicas, así como de los cálculos diferencial e integral. De estas cuestiones tratan ampliamente Granville y Smith en su obra «Differential and Integral Calculus».
Supongamos que x e y representan dos variables. Si a cada valor de x corresponde un valor de y, entonces podemos decir que y es una función de x, o simbólicamente y = f (x). Gráficamente, si señalamos los valores de x en el eje de las abcisas (horizontal) y los valores correspondientes de y en el eje de las ordenadas (vertical), la curva que une los puntos P (x, y), con la abcisa x y la ordenada y, es una representación gráfica de la función y = f (x):
FIG. 2.1

Quizás la función más sencilla, y una de las más utilizadas, es la función lineal y = a + bx, en la que a y b son constantes. Su representación gráfica es una línea recta cuya intersección con el eje y es igual a a y su pendiente igual a b.
FIG. 2.2

Cuando a = 0, entonces y = x, lo que representa una línea recta que pasa por el origen. Esta relación indica que x e y son directamente proporcionales (fig. 2.3 (i)). Para el caso especial en que b = 1, la ecuación y = x es la bisectriz del cuadrante positivo (fig. 2.3 (ii)).
FIG. 2.3
(i)

(ii)

La figura que sigue indica la posición de la línea recta para diferentes valores de b.
FIG. 2.4

Otra forma de expresar la función lineal es: y - yc = b (x - x0), en la que (x0, y0) es un punto de la línea.
Esta forma es especialmente útil cuando se conocen dos puntos de la línea y se quiere formular la ecuación. Así, si un punto es (x0, y0) y el otro es (x1 y1), la línea pasará por ambos si b satisface la ecuación y1 - y0 = b (x1 - x0), es decir, b = (y1 - y0)/ (x1 - x0). En tal caso, la ecuación se puede escribir inmediatamente.
En una función lineal el valor medio absoluto de variación de y con x es constante e igual a la pendiente. Así, la tasa absoluta instantánea es también constante y su valor es la pendiente b.
Para otra función cualquiera, el valor medio absoluto entre dos valores x0 y x1 es la pendiente de la línea recta que pasa por los puntos (x0 y0) y (x1 y1).
FIG. 2.5

 pendiente = tasa absoluta
media
pendiente = tasa absoluta
media
Otra función muy útil es la parábola, llamada también polinomio de segundo grado, y = a + bx + cx2.
FIG. 2.6

La ecuación puede, a veces, expresarse en la forma siguiente:
y = A (x - x0)(x - x1), en la que x0 y x1 son las intersecciones sobre el eje de las abscisas, y el signo de la constante A determina si la concavidad es hacia arriba o hacia abajo.
FIG. 2.7
(A>0)

(A<0)

(A=0)

La función exponencial y = ax, en la que a es una constante positiva, tiene la siguiente representación gráfica:
FIG. 2.8
a) 
b) 
Una función exponencial corrientemente utilizada por su conveniencia matemática es aquella en la que a es igual a la constante matemática e (véase 2.1.2 Funciones).
Algunas curvas tienen una asíntota, es decir, una línea recta a la cual se acerca la curva cada vez más a medida que x se hace extraordinariamente grande (o extraordinariamente pequeño); en forma más precisa, son tangentes a la curva cuando x = ¥ (0 -¥). Por ejemplo: y =ax con a < 1 (véase fig. 2.8) tiene la asíntota y = 0; las curvas y = 1 - e-x e y = 1 - e-2x tienen ambas la asíntonta y = 1, aproximándose la segunda de ellas a esta asíntota bastante más rápidamente.
FIG. 2.9

La representación de la relación entre dos variables puede, con frecuencia, ser simplificada, transformando una de estas variables, es decir, utilizando alguna función de la variable en lugar de la variable misma.
Así, por ejemplo, si consideramos las relación:  ésta
puede ser transformada en una relación directamente proporcional utilizando
la variable
ésta
puede ser transformada en una relación directamente proporcional utilizando
la variable  , y entonces y
= Aw.
, y entonces y
= Aw.
Es siempre posible transformar una función matemática en una relación lineal mediante una adecuada transformación de las variables. Esto es con frecuencia útil cuando se trata de ajustar una curva teórica, y posiblemente complicada, a los datos observados; el ajuste de una línea recta, ya sea gráficamente a ojo, o mediante técnicas de regresión, es una operación sencilla. El ajuste de curvas más complejas, por ejemplo, las exponenciales, es más difícil, ya sea a ojo o por cálculo. Debe hacerse observar que la regresión de los mínimos cuadrados (o de otra curva ajustada) que utilizan la media aritmética de las variables transformadas no coincidirá probablemente con la media aritmética de las variables originales; así, por ejemplo, utilizando la transformación w = log x, la media aritmética de las w es la media geométrica de las x.
Como veremos más adelante (9. La curva simple de rendimiento), la curva que expresa el número de peces de una clase de edad vivos en el tiempo t puede expresarse por Nt = N0 e-zt y puede ser transformada en la línea recta y = a + bt, en la que a = loge N0 y b = - Z, utilizando la transformación logarítmica y = loge N.
FIG. 2.10


La relación funcional y = f (x) puede expresarse
también en la forma inversa, es decir, expresando x como una función
de y, o sea, x = g (y). Por ejemplo, la relación
lineal y = a + bx puede ser expresada en la forma inversa (también
lineal)  (a condición
de que b ¹ 0). Si la función
f (x) no es una función lineal simple, puede suceder que
más de un valor x dé el mismo valor de y; entonces,
la función inversa x = g (y) no será una función
simple con un solo valor. Por ejemplo, si y = x2,
entonces la función inversa es
(a condición
de que b ¹ 0). Si la función
f (x) no es una función lineal simple, puede suceder que
más de un valor x dé el mismo valor de y; entonces,
la función inversa x = g (y) no será una función
simple con un solo valor. Por ejemplo, si y = x2,
entonces la función inversa es  .
Gráficamente la representación de una función y de su inversa
son idénticas. Dada la representación gráfica de y =
f (x), ésta puede ser utilizada como una gráfica
de x = g (y) mediante un simple cambio de ejes.
.
Gráficamente la representación de una función y de su inversa
son idénticas. Dada la representación gráfica de y =
f (x), ésta puede ser utilizada como una gráfica
de x = g (y) mediante un simple cambio de ejes.
Una potencia se representa por dos números y se escribe simbólicamente
an, en la que el número a se llama base,
y el n, exponente. Cuando el exponente es un número entero positivo,
an se define como el producto de n factores iguales
a a; cuando el exponente es 0, entonces a0 se define
como igual a 1; cuando el exponente es una fracción, digamos por ejemplo
 , entonces, por definición
ap/q es igual a
, entonces, por definición
ap/q es igual a  ;
cuando el exponente es negativo, como por ejemplo - m, entonces por definición
;
cuando el exponente es negativo, como por ejemplo - m, entonces por definición .
.
Cuando la base es positiva, la potencia es positiva, pero cuando la base es negativa, la potencia es positiva si el exponente es par y negativa si el exponente es impar.
Es útil examinar el valor de una potencia cuando el exponente n aumenta ilimitadamente.
Si la base a es mayor que 1, entonces an aumenta también ilimitadamente.
Si la base a es igual a 1, entonces an es igual a 1 para todos los valores de n.
Si la base a es menor que 1 (y positivo), entonces an tiende hacia 0. Algunas reglas útiles para multiplicar o dividir potencias son las siguientes:
- Potencias con la misma base- Potencias con el mismo exponente
Para elevar una potencia a un exponente, la base se eleva al producto de los exponentes:
(an)m = anm
La función y = an puede ser considerada en dos formas, según que la base a o el exponente n se consideren como la variable de interés. En la forma y = xn (es decir, cuando la base es la variable) se llama una función de potencia; en la forma y = ax (es decir, cuando el exponente es la variable) se llama una función exponencial.
La función inversa de una potencia es una raíz y la función inversa de una función exponencial es una función logarítmica. Así si y = ax entonces x = loga y, o x es el logaritmo de y de base a.
Cuando la base es la constante e, los logaritmos se llaman naturales o Neperianos (o hiperbólicos).
De la definición anterior se ve que las propiedades de las potencias suponen propiedades correspondientes de los logaritmos, es decir,
loga (A · B) = loga A + loga B corresponde a la propiedad ax · ay = ax+y
loga (A/B) = loga A - loga B corresponde a la propiedad

loga (Am) = m loga A corresponde a la propiedad (ax)y = axy
Se pueden obtener también relaciones especiales tales como loga 1 = 0 y loga a = 1. La relación entre los logaritmos de un número de dos bases diferentes, a y b, es:
loga N = logb N · loga b
Las bases más utilizadas en los logaritmos son la base 10 y la base e (e » 2,72); la primera, porque 10 es la base del sistema utilizado normalmente y la segunda, porque da la forma más sencilla de varias relaciones matemáticas. De la relación antes indicada puede obtenerse el logaritmo de base e de un número multiplicando el logaritmo de base 10 de dicho número por loge 10 ~ 2,303. Esta es una expresión útil si no se dispone de una tabla de logaritmos naturales. Una de las ventajas de utilizar la base 10 es que cualquier número puede ser expresado como el producto de una potencia de 10 y un número entre 1 y 10, por ejemplo, 283,5 = 102 x 2,835; 0,0053 = 10-3 x 5,3. En esta forma el logaritmo decimal de cualquier número será la suma del logaritmo decimal de un número entre 1 y 10 (mantisa) más el logaritmo decimal de una potencia de 10, es decir, su exponente (característica).
Con los ejemplos anteriores se tendría log10 283,5 = 2 + log10 2,835; y log10 0,0053 = - 3 + log10 5,3. Los logaritmos de base 10 de los números comprendidos entre 1 y 10 se dan en las tablas correspondientes.
Existen, generalmente, tablas de logaritmos naturales de un alcance mayor (quizás desde 0,1 hasta 100), pero los logaritmos naturales se pueden obtener por un método semejante para cualquier alcance de las tablas de los logaritmos naturales de 1 a 10. Por ejemplo,
loge 283,5 = 2 loge 10 + loge 2,835 = 2 x 2,303 + 1,042 = 5,648 yloge 0,0053 = - 3 loge 10 + loge 5,3 = - 3 x 2,303 + 1,667 = - 5,242
Como ya se ha indicado anteriormente, el concepto de derivada es equivalente a la tasa instantánea absoluta y ésta es el limite de la tasa media absoluta durante un intervalo cuando la duración de éste tiende a cero.
Consideremos una función y = f (x). Si a x
se da un incremento D x, y tendrá
un incremento D y. El límite del
cociente de los incrementos  cuando D x tiende hacia cero será
la derivada de y respecto a x en el punto (x, y).
Esto puede representarse por los símbolos
cuando D x tiende hacia cero será
la derivada de y respecto a x en el punto (x, y).
Esto puede representarse por los símbolos  o y' o f (x).
o y' o f (x).
Gráficamente, la razón del incremento  es la pendiente de la secante a la curva que pasa por los puntos (x, y)
y (x + D x, y + D y)
y la derivada
es la pendiente de la secante a la curva que pasa por los puntos (x, y)
y (x + D x, y + D y)
y la derivada  es la
pendiente de la tangente a la curva en el punto (x, y) (la tangente es
el límite de la secante cuando D x
tiende hacia cero y x + D x tiende
hacia x).
es la
pendiente de la tangente a la curva en el punto (x, y) (la tangente es
el límite de la secante cuando D x
tiende hacia cero y x + D x tiende
hacia x).
FIG. 2.11


Así pues, derivada, tasa instantánea absoluta y pendiente de la tangente son conceptos equivalentes expresados desde distintos puntos de vista. Utilizando esta definición, podemos calcular la derivada de una función. Por ejemplo, para determinar la derivada de y = 3x2 podemos comenzar por calcular el incremento de y para un determinado incremento de x. Obtendremos el valor de la función en el punto x + D x y restaremos éste del valor de la función en el punto X:
en x y = 3x2en x + D x v + y = 3 (x + D x)2 = 3x2 + 6x D x + 3 D x2
y entonces
y = 6x D x + 3 D x2
La razón de incremento será  .
A medida que D x se hace muy pequeño
el segundo término de la derecha se hará también pequeño
y en el límite, a medida que D x
® 0, este segundo término tiende también
hacia cero, de modo que
.
A medida que D x se hace muy pequeño
el segundo término de la derecha se hará también pequeño
y en el límite, a medida que D x
® 0, este segundo término tiende también
hacia cero, de modo que  será
igual a 6x.
será
igual a 6x.
Se pueden obtener fácilmente las derivadas si deducimos, en esta forma, algunas reglas, por ejemplo:
La derivada de una constante c, es cero:
(obsérvese que la diferenciación se designa a menudo mediante el signo ').
La derivada de una variable x respecto a sí misma es:
La derivada del producto de una constante c y de una función u (x) es el producto de la constante por la derivada de la función:
(cu)' = cu' por ejemplo
La derivada de una suma de dos funciones, u (x) y v (x) es la suma de sus derivadas:
(u + v)' = u' + v' p. ej.:
La derivada de un producto de dos funciones, u (x} y v (x) viene dada por
(u · v)' = u'v + u · v' p. ej.:
La derivada de una potencia de una función u (x) viene dada por
(un)' = nun-1 u' p. ej.:
La derivada del cociente de dos funciones, u (x) y v (x), viene dada por
p. ej.:
Podemos obtener también mediante un análisis ulterior la derivada de funciones especiales utilizadas frecuentemente en los estudios de pesca, tales como
(ex)' = ex
(eu)' = eu u'
Es interesante observar que la derivada de la función ex es ex igualmente; es esta propiedad de la función exponencial de base e lo que hace a ésta tan importante desde el punto de vista teórico.
La derivada de la función y = eax es y' = eax a = ay; esto indica que la derivada, o la tasa instantánea, de y es proporcional a y, propiedad muy útil en muchos casos (por ejemplo, en los estudios de crecimiento, mortalidad, etc.).
Como ejemplo de cómo se pueden aplicar estas reglas procedamos a calcular la derivada de y = (3 + e2x) (1 - x2).
Aplicando la regla correspondiente al producto podemos escribir:
.
Para calcular la derivada del primer factor podemos aplicar la regla referente a la suma de dos funciones; entonces tendremos (3 + e2x)' = (3)' + (e2x)'. Vemos, pues, que (3)' = 0 y (e2x)' = w2x (2x)' = e2x · 2 y así (3 + e2x)' = 2e2x. Calculando la derivada del otro factor: (1 - x2)' = (1)'- (x2)' = 0 - 2x = 2 - 2a. Finalmente y' = 2e2x (1 - x2) - 2a (3 + e2x).
La derivada de una función de x es, en general, otra función de x. Esta función puede ser también diferenciada para dar otra función de x.
FIG. 2.12

Esta última se llama la segunda derivada de la función original. Generalmente se representa por los símbolos y" o d2y/dx2 y podría ser interpretada como la tasa absoluta de la tasa absoluta, que en física se llama aceleración. Se pueden, asimismo, definir las derivadas tercera, cuarta, etc.
Una aplicación de la primera derivada es el análisis del cambio de una función, y de la segunda derivada el análisis de la tasa a la cual este cambio se verifica. Para los puntos en que y' es positiva, y aumenta, y cuando y' es negativa, y disminuye. Si y' = 0, y es un punto fijo. Cuando y" es positiva, la pendiente de la curva aumenta y la gráfica de y es una curva cóncava hacia arriba; cuando y" es negativa, la pendiente de la curva disminuye y la curva es cóncava hacia abajo. Si y" = 0, y es un punto de inflexión (a menos que y' sea también 0). Del signo de y" podemos deducir si los puntos fijos son máximos o mínimos.
En la sección anterior vimos cómo, dada una función, podíamos obtener su derivada. El problema inverso sería obtener la función, conocida su derivada. Esta operación se llama integración, y la función así obtenida se denomina integral. Por ejemplo, ¿cuál es la integral de 3x2? Hemos visto que la derivada de 3x es 3x2; por tanto, una integral de 3x2? podría ser x3. Pero también lo es x3 + 4 o, en general, x3 + C, en la que C es una constante cualquiera, ya que la derivada de una constante es cero. Esto significa que la integración de una función no produce una función simple, sino una familia de funciones definidas por el aditivo, la constante arbitraria C.
La integral de f (x) está representada por  ó F (x) + C y se llama la integral indefinida.
Es indefinida a causa de la constante arbitraria C.
ó F (x) + C y se llama la integral indefinida.
Es indefinida a causa de la constante arbitraria C.
Las reglas de la integración pueden deducirse fácilmente de las reglas de la diferenciación, ya que son operaciones inversas. Así:
Expresiones útiles son
Una técnica muy útil para la integración es el cambio de la variable. Por ejemplo, para integrar e4x-3 podemos poner v = 4x - 3 y dv = (4x - 3)', dx ó dv = 4dx. Entonces:
Si se conoce un valor de la función integrada es posible determinar el valor correspondiente para la constante C. En términos generales podemos decir que si y = F (x) + C es la integral de una función, y sabiendo que (x0, y0) es un punto de la curva integral, entonces y0 = F (x0) + C, y C = y0 - F (x0); así, y - y0 = F (x0) da la curva que satisface las condiciones del problema.
Hemos visto la integración como la operación inversa de la diferenciación. Existe, sin embargo, otro concepto de la integral. Este concepto se puede comprender fácilmente mediante el cálculo de áreas, que es una de las aplicaciones más importantes de las integrales. Calculemos, por ejemplo, el área comprendida por la curva y = f (x), estando el eje de abscisas y de ordenadas en x = a y x = b.
FIG. 2.13

Una aproximación de este área viene dada por la suma de las áreas
de los rectángulos de base D xi
y de altura f (xi), esto es,  ,
en la que el intervalo de a a b se ha subdividido en n
pequeños intervalos D x1.
El límite de esta suma cuando el número de subdivisiones aumenta
indefinidamente y cada intervalo desciende hasta cero, puede dar el área
requerida. Este límite es entonces la integral definida. Esta
integral definida, g (x), es un valor posible de la integral
indefinida, ya que la tasa a la cual el área bajo la curva aumenta a
medida que aumenta x es igual a la altura de la curva, de modo que
,
en la que el intervalo de a a b se ha subdividido en n
pequeños intervalos D x1.
El límite de esta suma cuando el número de subdivisiones aumenta
indefinidamente y cada intervalo desciende hasta cero, puede dar el área
requerida. Este límite es entonces la integral definida. Esta
integral definida, g (x), es un valor posible de la integral
indefinida, ya que la tasa a la cual el área bajo la curva aumenta a
medida que aumenta x es igual a la altura de la curva, de modo que  .
El área comprendida por la curva entre x = a y x = b se
escribe
.
El área comprendida por la curva entre x = a y x = b se
escribe .
.
Para calcular la integral definida calculamos como antes la integral indefinida y restamos su valor para x = b y para x = a, esto es:
Como ejemplo, calculemos el área correspondiente a la función y = 3x2 + 5 entre x = 2 y x = X:
(Obsérvese que cuando se calculan áreas geométricas los valores de la función y de su integral deben considerarse como positivos.)
Otra aplicación muy importante de las integrales es en la solución de las ecuaciones diferenciales. Una ecuación diferencial es una ecuación con derivadas o diferenciales, por ejemplo, y' = 4x - 2, ó dy = (5 + 2x)dx.
Las ecuaciones diferenciales pueden ser muy difíciles de resolver, pero
algunos procesos elementales son aplicables a las ecuaciones fáciles.
Uno de estos procesos se llama la separación de variables. Por ejemplo,
integremos la ecuación dy = xydx. Mediante una simple operación
podemos obtener (separadas) todas las expresiones con la variable y en
un miembro de la ecuación y las expresiones con la variable x
en el otro: .Ahora, cada miembro
de la ecuación puede ser integrado se paradamente:
.Ahora, cada miembro
de la ecuación puede ser integrado se paradamente:
o
o, uniendo las constantes arbitrarias,
El mismo resultado podría presentarse en una forma ligeramente diferente, utilizando, en lugar de la constante C, un punto arbitrario (x0 y0), y así tendríamos:
ó
y
o bien,

Esta última expresión puede ser muy útil cuando se está interesado en señalar algún punto especial de la función.
Los estudios de las poblaciones de peces implican la medición y el análisis de muchas cantidades - como, por ejemplo, la composición por edades y las tasas de crecimiento -, pocas de las cuales pueden medirse directamente, sea por su variabilidad intrínseca o por la dificultad de su medición. Por consiguiente, es preciso utilizar la estadística hasta cierto punto, aunque sólo sea en forma tan simple como tomando la media de una serie de valores. Los métodos estadísticos básicos son los mismos, sea cualquiera el sujeto al que se aplican, y se describen en muchos libros de texto. Por consiguiente, estas notas sólo se ocuparán muy brevemente de los métodos básicos. Algunas de sus aplicaciones, como, por ejemplo, los análisis de correlación y regresión, se tratarán más adelante a medida que se presente la ocasión. En esta sección se dedicará más atención a los problemas del muestreo de las poblaciones de peces. (El aspecto estadístico se trata con más detalle en otro manual de esta serie, en el cual se describen tanto los métodos básicos como las aplicaciones especiales.)
En estadística nos interesa no tanto un valor individual como, por ejemplo, el tamaño de un determinado pez en el mercado pesquero, sino la frecuencia con que los varios valores (por ejemplo, tamaño del pez) se presentan. Estas distribuciones de frecuencia pueden representarse gráficamente, sea como histogramas, sea como polígonos de frecuencia. Gran parte de las distribuciones de frecuencia pueden describirse por dos cantidades: el valor medio (o la posición de la curva) y la dispersión. Las medidas más corrientes para el promedio son la media aritmética (o simplemente media), la mediana (o valor de medio recorrido) y la moda (o valor más frecuente). De éstos, la media es la que presenta mayores ventajas. La medida corriente de la dispersión es la varianza, que es el promedio del cuadrado de la desviación de la media; la raíz cuadrada de la varianza es la desviación típica. Un estudio más a fondo de estas medidas, junto con los métodos de su cálculo, etc., puede hallarse en la mayoría de los libros de texto, como, por ejemplo, los de YULE y KENDALL, capítulos 4, 5 y 6.
Las dócimas de significación constituyen otro grupo de instrumentos estadísticos de gran utilidad en la investigación pesquera, al igual que en casi todos los demás campos. Aunque la explicación de los procesos aritméticos que requiere una dócima determinada se dejarán para la sección correspondiente de los libros de texto, como, por ejemplo, YULE y KENDALL, capítulo 21, es conveniente poner de relieve aquí las bases en que se fundamentan las dócimas de significación. Es decir, presuponemos alguna hipótesis nula y sobre esta base calculamos la probabilidad de que se presenten los valores observados. Si esta probabilidad es suficientemente pequeña (generalmente uno en veinte, o uno en un centenar) rechazamos la hipótesis nula. Por ejemplo, usando la prueba t de STUDENT para la diferencia en las medias de dos muestras, la hipótesis nula es que las dos muestras proceden de la misma población. Si la probabilidad de un valor de t igual o mayor que el que se ha observado como presente es, pongamos por ejemplo, 0,01, esto significa que si las dos muestras hubieran procedido de la misma población se ha verificado un acontecimiento improbable (una posibilidad en un centenar) y, por consiguiente, creemos que las dos muestras no procedían de la misma población, es decir, que son estadísticamente diferentes. Tal prueba no proporciona ninguna información sobre la probabilidad de que las dos muestras provengan de distintas poblaciones, o sobre la significación práctica de la diferencia. Por ejemplo, dos muestras pequeñas y variables pueden diferir en una cantidad que estadísticamente no es importante, pero que en la realidad tendría gran importancia. Recíprocamente, en dos muestras grandes y homogéneas, la diferencia puede ser suficientemente grande para tener importancia estadísticamente, pero, sin embargo, ser tan pequeña que sea despreciable en la práctica.
2.3.1 Generalidades
2.3.2 Muestreo de los desembarques
2.3.3 Muestreo de la población
(Para más detalles véase la parte I del Manual de Métodos de Muestreo y Estadísticas para la Biología Pesquera.)
La mayoría de las cantidades utilizadas en los trabajos sobre poblaciones de peces no pueden ser obtenidas o medidas en la totalidad de la población; por ejemplo, es prácticamente imposible medir todos los peces capturados, y mucho menos todos los peces en el mar. Por ello se examina una sección, o muestra, de toda la población con respecto a los atributos que interesan - por ejemplo, porcentaje de peces maduros o talla media -. En el supuesto de que esta muestra sea representativa de toda la población, pueden estimarse los valores verdaderos de la población. Si el sistema de muestreo aplicado es bueno el valor estimado diferirá muy poco del valor real. Los méritos o inconvenientes de un sistema de muestreo pueden, por tanto, ser medidos por dos cantidades relacionadas con los valores estimados que se han obtenido (estas medidas no se refieren a ninguna estimación individual, sino al conjunto de estimaciones que pueden obtenerse por muestras repetidas); en primer lugar, la varianza, que, como se ha definido antes para cualquier distribución estadística, es la medida de la dispersión de los valores estimados alrededor de su valor medio; en segundo lugar, el sesgo, que es el grado de diferencia entre el valor medio de la serie de posibles valores y el valor verdadero. (El término sesgo se usa también para designar los procesos que conducen a esta diferencia.)
Debido a que, cuando existe un sesgo, éste existe en todas las muestras, y tiende a hacer las estimaciones siempre mayores (o menores) que el valor real, este sesgo no puede ser detectado valiéndose de la diferencia entre muestras repetidas; por esto, en general, el sesgo es muy difícil de descubrir y, por consiguiente, de eliminar, en subsiguientes análisis. Una varianza grande, por el contrario, aparece inmediatamente en las diferencias entre muestras. Por lo tanto, un sesgo grande es todavía menos deseable que una varianza grande, debido a que pueda hacer que lo que aparenta ser un conjunto de datos de garantía y coherentes dé resultados que sean coherentes sólo en el grado en que están errados.
La característica básica de cualquier buen sistema de muestreo es una muestra «aleatoria». La muestra aleatoria tiene como objeto asegurar que todos los miembros de la colección de objetos muestreados tengan la misma probabilidad de aparecer en la muestra. En la práctica puede prescindirse de esta condición y el muestreo puede no ser aleatorio mientras no exista una relación entre la probabilidad de que un objeto aparezca en la muestra y el valor del atributo que se mide. Por ejemplo, los primeros peces desembarcados por un arrastrero en el mercado son generalmente los últimos capturados, y quedarán colocados cerca del borde del montón, por lo que tendrán mayor posibilidad de aparecer en la muestra. Si sólo nos interesa muestrear para determinar el tamaño de los peces, esto puede no tener importancia porque hay muy poca relación entre el tamaño del pez y el momento de la captura, pero la muestra sería muy deficiente si nos interesara la condición o el grado de frescura del pez. El daño principal causado por el muestreo no aleatorio es la introducción de un sesgo (por ejemplo, la muestra tomada en la forma antes indicada estará sesgada en el sentido de tener demasiados peces frescos). El muestreo no aleatorio tiene otras desventajas, como, por ejemplo, que muchos de los métodos utilizados para estimar la varianza, etc., sólo son válidos para muestras aleatorias. Por consiguiente, lo que más interesa al tomar una muestra es asegurarse de que no existe ninguna forma de selección que pueda causar un sesgo. Una selección tal puede ser muy obvia y directa, como es la tendencia a tomar los mayores peces de un montón, dejando los pequeños para el final, pero puede ser también menos evidente; por ejemplo, en la temporada de la pesca de arenque en Inglaterra oriental puede parecer conveniente tomar muestras de aquél de los primeros barcos que lleguen cada mañana. Estos tendrán tendencia a proceder de las zonas más próximas, las que a su vez tienen peces de tamaños y edades que difieren poco. Por esto un muestreo no aleatorio en cuanto al momento de efectuarlo determina un sesgo en la estimación del tamaño medio del pescado desembarcado.
Las dificultades prácticas para tomar una muestra verdaderamente aleatoria de un conjunto grande y heterogéneo de objetos son considerables. Estas dificultades pueden superarse dividiendo el conjunto en secciones más pequeñas y compactas, en las cuales puede ser tomada con más facilidad una muestra aleatoria. Dos de estos métodos son el muestreo estratificado y el muestreo en dos etapas. En el primero, el conjunto total de objetos se divide en varias secciones o estratos, cada uno de los cuales es muestreado y analizado por separado; por ejemplo, los desembarques en diferentes puertos pueden considerarse como estratos. Este método es particularmente útil para reducir el sesgo y la varianza cuando hay una sensible diferencia entre los estratos.
El principal problema del muestreo en los estudios de poblaciones de peces, aparece cuando se trata de obtener índices de la abundancia de las distintas clases de edades y de tamaños de éstos, y particularmente al muestrear las capturas comerciales para obtener la composición por tallas y edades. Antes de entrar a considerar el procedimiento de muestreo deberá definirse el objetivo de éste, tanto en extensión como en el atributo que se mide, por ejemplo, tamaño de la solla desembarcada por los arrastreros ingleses del Mar del Norte. Siguiendo un esquema de muestreo estratificado, la población completa, que puede ser bastante heterogénea, podrá entonces ser dividida en estratos bastante uniformes. Para los desembarques ingleses de peces demersales se encontró que era conveniente tratar los desembarques en cada puerto y en cada mes separadamente, pero para los desembarques de arenque, que son más variables, se escogieron los desembarques efectuados en períodos de tres días. La primera medida en el procedimiento de muestreo es asegurarse de que la muestra que se tome no está sesgada. Al venderse la captura de un barco ésta puede ser distribuida entre diversos comerciantes, cada uno de los cuales preferirá seguramente cierto tamaño o calidad de pescado y, por lo tanto, cualquier muestra de las compras de un comerciante es casi seguro que estará sesgada. El muestreo de las capturas comerciales debe hacerse, por tanto, antes de que ésta sea dividida; en Inglaterra esto significa el llevar a cabo el muestreo por la mañana temprano, cuando la captura se expone en el mercado, antes de ser subastada.
La selección de los peces que se han de medir se hace convenientemente en dos etapas: primero se elige una muestra de uno o más barcos de toda la flota que desembarca pesca durante el período y después se toma una muestra de pescado del barco o barcos escogidos. La selección de los barcos que se han de muestrear es generalmente directa y no es probable que tengan importancia las pequeñas divergencias derivadas de tratarse de muestras no aleatorias, pero puede introducirse un sesgo cuando en el momento del desembarque o en la posición de los barcos en el muelle (que puede influir en su posibilidad de ser muestreados) influya la zona en que efectúan la pesca, y por lo tanto afecte a la composición de la captura. Esta dificultad puede superarse con una estratificación ulterior, muestreando y analizando las capturas de cada zona separadamente.
Al tomar una muestra de peces de la captura de un barco, una fuente importante de sesgo es la tendencia de la mayoría de las personas a tomar primero los peces mayores del montón y dejar los menores para el final. Esto se observa principalmente cuando se toman muestras de los peces en cubierta, como, por ejemplo, de la captura de un barco de investigaciones. En el mar, este sesgo sólo puede ser evitado usando la captura total, o por lo menos una parte determinada de ella (por ejemplo, un rincón) tomando todos los peces hasta el nivel de la cubierta. En el mercado, la mayoría de los peces se colocan en cajas a menudo poniendo los más grandes en la parte superior de éstas, y en ese caso el sesgo se evitará tomando como muestra una o más cajas completas. Si no hay una clasificación definida en dos o más categorías, son improbables las diferencias sistemáticas entre las cajas y, en tal caso, es justificable un método conveniente, aunque no sea aleatorio, de muestreo, por ejemplo, el tomar las cajas de uno de los extremos. En la elaboración de los datos obtenidos mediante un sistema de muestreo de este tipo, son importantes los factores de ampliación, es decir, la relación entre el peso muestreado y el peso total desembarcado, tanto para la totalidad de los desembarques como cada barco muestreado. El procedimiento es como sigue: suponiendo que lo que interesa es el número total de peces desembarcados de una talla (o edad, madurez, etc.), determinadas.
Sea m = número de barcos de los que se tomaron las muestras, y para un barco cualquiera de ellos, digamos el i-ésimo:
Wi = peso desembarcado
wi = peso muestreado
ni = número de peces del tamaño requerido en la muestra.
Tendremos  factor de ampliación
para el barco i-ésimo. Y por lo tanto,
factor de ampliación
para el barco i-ésimo. Y por lo tanto,  número de peces del tamaño requerido en el barco muestreado.
número de peces del tamaño requerido en el barco muestreado.
Sumando para todos los barcos muestreados:
número de peces del tamaño requerido que hay en todos ellos.
También, si
W = peso total desembarcado,
w = peso desembarcado por los barcos muestreados.
Entonces, R = factor de ampliación = 
y  número total de
peces desembarcados que tienen el tamaño requerido = N.
número total de
peces desembarcados que tienen el tamaño requerido = N.
Esto es,
Frecuentemente, los peces se clasifican en varias categorías de tamaños (las cuales pueden ser o no las mismas de un barco al siguiente); por lo tanto, es obvio que será necesario tomar una muestra de cada categoría en el barco que se examina. El número para todo el barco vendrá dado multiplicando la cantidad de cada categoría por el factor de ampliación apropiado. De aquí que, si suponemos que hay dos categorías, y usamos la notación anterior utilizando una o dos comas para distinguir las diferentes categorías, tendremos:
;
y el número de peces de un tamaño dado en el i-ésimo barco muestreado será:
por lo tanto, el número total desembarcado se puede estimar directamente como:
Otro procedimiento mejor será utilizar la clasificación en categorías como estratificación en todos los desembarques, y se podrán calcular y aplicar factores de ampliación para cada categoría. Entonces la estimación del número desembarcado será:
donde
Esta segunda estimación será más precisa (tendrá menor varianza) debido a que utiliza la información sobre la clasificación de todos los desembarques en categorías. Se puede aplicar mientras la clasificación sea constante, aunque no muy precisa, es decir, que el número y definición de las categorías sea constante, aunque la línea divisoria entre ellas sea variable.
En los estudios de poblaciones estamos interesados en varias características de los peces, como son la longitud, el peso, la edad, el estado de madurez, etc., muchas de las cuales están muy relacionadas entre sí. Algunas, como la longitud, son muy fáciles de determinar, tanto con rapidez, como con precisión, incluso en condiciones bastante adversas en el mar o en el mercado. Otras características, como la edad, que son mucho más trabajosas de determinar, se pueden obtener con más facilidad muestreando directamente para averiguar las tallas solamente, y utilizando muestras de edad relativamente pequeñas para establecer una relación que permita hacer la conversión de composición por tallas a composición por edades. Es decir, que el muestreo de tallas da el número de individuos en cada grupo de tallas y las muestras de edades dan la proporción de cada edad en cada grupo de tallas. El número de individuos de cada edad se obtiene con facilidad algebraicamente; si
Ni = número de individuos en el i-ésimo grupo de tallas;
Pij = proporción de peces de edad j en el i-ésimo grupo de tallas,en que Pij = nij/ni;ni = número de individuos de talla i examinados para determinar la edad;
nij = número de individuos de talla i examinados, que tenían edad j;
y entonces:
Ni Pij = número total de individuos de talla i y edad, j,
ynúmero total de peces de edad j.
Debe señalarse que estos cálculos no incluyen suposiciones acerca de la forma de crecimiento, aunque las ventajas del método en cuanto a aumento de la posibilidad de la precisión (reducción de la varianza y de sesgo) son máximas cuando el crecimiento es rápido y uniforme.
Los datos acerca de la composición de la captura son importantes por sí mismos, particularmente cuando se comparan y combinan los efectos de dos flotas distintas que explotan la misma población; o cuando se evalúan los efectos inmediatos de, digamos, un cambio en el tamaño de las mallas. Además, la captura, tanto de una flota comercial como de un barco de investigación, puede ser también considerada como una muestra de la población. Los métodos usuales de muestreo son aplicables directamente, por ejemplo el muestreo estratificado, mediante la división de la región en subáreas suficientemente uniformes, pero surgen problemas especiales cuando se trata de obtener estimaciones no sesgadas de la abundancia y de la composición de la población. El primero es un problema de relacionar la densidad de la población con la captura por unidad de esfuerzo; el segundo, un problema de selección en su sentido más amplio, es decir, incluyendo cualquier factor que haga que los peces de ciertos tamaños (o condiciones) tengan mayores posibilidades de ser capturados y retenidos por un arte, que los peces de otros tamaños. Un caso especial será la selectividad de la malla de la red de arrastre. Estos problemas serán discutidos más ampliamente en las secciones apropiadas de este manual.
1. Los valores de x, y los valores correspondientes de y vienen dados en la tabla:
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
10 |
25 |
32 |
38 |
41 |
Trazar una curva que pase por estos puntos. Determinar la tasa media absoluta del cambio de y durante el intervalo x = 1,5, x = 3,5. ¿Cuál es la tasa media relativa en el mismo intervalo? Dése el valor aproximado para la tasa instantánea absoluta con x = 1,5.
2. Calcular la ecuación de la recta que pasa por los puntos A (2, -5) y B (- 1, 3). Calcular los puntos en que corta al eje de las coordenadas. Escribir la ecuación de una paralela a esta recta.
3. Trazar una línea recta con pendiente negativa.
4. Calcular la línea recta que tiene como abscisa -2 y como ordenada 3. ¿Qué valor de y corresponde a x = 6? ¿A qué valor de x corresponde y = 3?
5. Calcular, sin utilizar tablas:
|
103 |
10-1 |
4° |
82/3 |
25-1/2 |
6. Calcular:
|
(a) |
log10 42,5 |
log10 0,018 |
log10 0,263 |
|
(b) |
loge 0,50 |
loge 2,52 |
loge 17,10 |
7. Determinar x en:
|
0,70 = e-x |
2,4 = 10x |
104 = ex |
8. Transformar (utilizando los logaritmos naturales):
y = 2x · e4+x y 
9. Calcular N teniendo:
loge N - loge Na = - Z (t - ta)
10. Calcular el producto:
log10 e x loge 10
11. Aplicar los logaritmos a las expresiones siguientes:
w = q · l3
x = (A + B) · C4

12. Calcular el valor de (1 + 1/n)n para n = 1; 2; 5; 10; 100, y 1.000. Comprobar que los resultados se aproximan al valor de e » 2,718 a medida que n aumenta.
13. Calcular  para las funciones
siguientes:
para las funciones
siguientes:
a) y = 3b) y = 4 - 6x
c) y = x5/2
d)

e) y = (1+4x)3
f) y = 4v2 con v = 5x2 - 2x
g) y = ex
h) y = e-4x e y = loge (5 + x)
i) y = (1 + e2x)(1 - e-2x)
14. Calcular la segunda derivada de:
|
y = 4x3 - 5x |
y = e4x |
y = loge (x + 2) |
15. Dada la función y = 2x (3 - x) calcular las derivadas primera y segunda y determinar el punto en que la tasa instantánea es cero; los intervalos en que y aumenta y en los que disminuye; la concavidad de la función. Trazar la función.
16. Utilizando la primera y segunda derivadas buscar los posibles puntos de máxima, mínima y de inflexión, los intervalos en los que las funciones aumentan y disminuyen y las concavidades para las funciones siguientes:
|
y = (x - 1)2 |
|
y = a (1 - e-bx)3 |
a > 0 y b > 0 |
17. ¿Cuál es la relación entre la tasa instantánea absoluta del loge y y la tasa instantánea relativa de y, siendo y una función de x?
18. Calcular la tasa instantánea relativa de aumento de N con respecto a t en:

19. Calcular la tasa instantánea absoluta de aumento de l con respecto a t en:

y expresarla en función de l.
20. Calcular la tasa instantánea relativa de aumento de l con respecto a t en:

y expresarla en función de la variable l.
21. Integrar las expresiones siguientes:
|
1/x |
4x |
7 |
ex |
4 - 2x |
(x - 1)(2 - 3x) |
22. Calcular:
|
|
|
|
|
|
|
|
|
23. Resolver las siguientes ecuaciones diferenciales:
|
dy = 3xdx |
con la condición que |
y = 2 |
para |
x = 1 | ||
|
|
» |
» |
» |
y = y0 |
» |
x = x0 |
|
|
» |
» |
» |
y - y0 |
» |
x - x0 |
|
|
» |
» |
» |
N = R |
» |
t = t0 |
|
|
» |
» |
» |
1 = 0 |
» |
t = t0 |
24. Calcular el área limitada por la curva y = 5x (4 - x) y los ejes de x entre x = 1 y x = 3.
25. Supongamos que y = f (x) sea una función tal que la tasa instantánea relativa es constante e igual a - a. Si (x0, y0) es un punto de la función, obténgase la expresión de ésta.
1. Dadas las dos distribuciones de frecuencia de talla:
|
Talla (cm.) |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Frecuencia |
1 |
3 |
8 |
16 |
18 |
17 |
12 |
6 |
2 |
1 |
0 |
y
|
Talla (cm.) |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
|
Frecuencia |
0 |
0 |
4 |
12 |
14 |
10 |
9 |
8 |
4 |
3 |
1 |
1 |
0 |
determinar lo siguiente:
a) la media,
b) la moda,
c) la mediana,
d) la varianza,
e) la desviación típica,
f) el error típico de cada media.
Utilizando estos resultados determinar si las diferencias entre las medias superan el doble (nivel del 5 por 100) o el triple (nivel del 1 por 100) de la desviación típica. (Obsérvese que la moda es más fácil de determinar gráficamente y que los otros parámetros lo son mediante el cálculo.)
2. Repetir (1) para las dos distribuciones:
a) 15, 17, 20, 23, 24, 27, 29, 31, 33, 35, 36, 36, 38, 40, 42, 42, 46, 49, 52, 53, 54, 58, 60, 65, 71b) 19, 26, 23, 29, 30, 32, 34, 37, 38, 40, 42, 42, 44, 45, 46, 48, 51, 54, 56, 59, 60, 65, 68, 75
3. Se muestreó una caja de 10 stones (1 stone = 6,35 kg.) de cada una de las categorías de merluza grande, media y pequeña en cada uno de los arrastreros. El número de individuos registrado en cada grupo de 10 cm. y los pesos desembarcados fueron:
|
Grupo de talla |
40- |
50- |
60- |
70- |
80- |
90- |
100- |
Total |
Peso desembarcado |
|
|
Barco A |
Grande |
|
|
|
|
7 |
7 |
|
14 |
2 |
|
Mediana |
|
|
8 |
15 |
3 |
|
|
26 |
10 |
|
|
Pequeña |
2 |
32 |
19 |
1 |
|
|
|
54 |
14 |
|
|
Barco B |
Grande |
|
|
|
|
5 |
4 |
3 |
12 |
23 |
|
Mediana |
|
|
4 |
17 |
6 |
1 |
|
28 |
53 |
|
|
Pequeña |
1 |
13 |
27 |
4 |
|
|
|
45 |
40 |
|
El número de cajas desembarcado por todos los barcos fue: grande 350; mediana 720; pequeña 1.056. Calcular el número y la distribución por tallas de la merluza desembarcada por los barcos muestreados, y el total para todos los barcos.
4. El número estimado de sollas macho desembarcadas en 1955 en Lowestoft en cada grupo de 5 cm. fue:
|
25-29 |
30-34 |
35-39 |
40-44 |
45-49 |
|
3.991.984 |
4.155.009 |
1.232.174 |
274.972 |
15.346 |
El número de machos cuyos otolitos fueron extraídos y sus edades estimadas, fue:
|
Edad |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Total |
|
Talla |
33 |
82 |
30 |
13 |
8 |
1 |
|
|
|
167 |
|
» |
8 |
48 |
53 |
24 |
34 |
12 |
5 |
1 |
1 |
186 |
|
» |
1 |
14 |
26 |
33 |
42 |
19 |
11 |
10 |
6 |
162 |
|
» |
|
1 |
8 |
2 |
12 |
5 |
5 |
- |
3 |
36 |
|
» |
|
|
|
|
|
1 |
4 |
- |
4 |
9 |
Estimar el número total de peces de seis años desembarcados.
5. Discutir los problemas y métodos de muestreo que se presentan en las pesquerías con las que se está familiarizado.