In order to perform estimations and predictions of the bioeconomic impact derived from different management strategies, a dynamic modelling approach of the resource and the fishery as a whole is needed. In this Secetion we develop : (1) the static and dynamic versions of the Gordon-Schaefer (Gordon, 1953, 1954) model; (2) a distributed-delays fleet dynamics model based on Smith's (1969) model; (3) yield-mortality models; and (4) age-structured dynamic models (Seijo & Defeo, 1994a).
The logistic equation (Verhulst, 1838) describes population growth based on the following mathematical expression (Graham, 1935):

Where r is the intrinsic rate of population growth, B(t) is population biomass in time t and K is the carrying capacity of the environment. Population behavior through time is described as a sigmoid curve, where the unexploited biomass increases unitl a maximum lievel B∞, constrained by K (Fig.2.1: see pella & Tomlinson, 1969; Schaefer, 1954 for details).
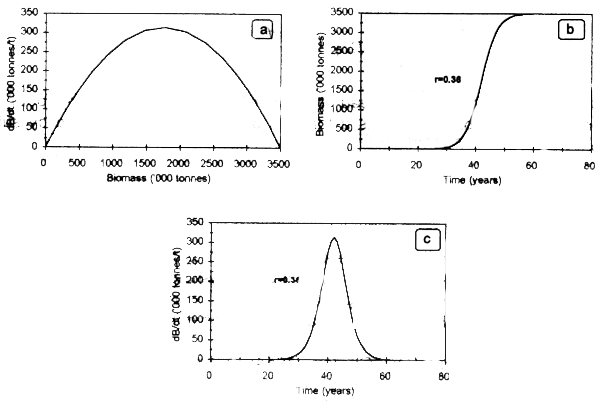
Figure 2.1. Population logistic growth model for K=3.5 million tonnes and r=0.36.
Under exploitation, Schaefer (1954) introduced the catch rate Y(t) as:
| Y(t)=qf(t)B(t) | (2.2) |
Where f(t) is the fishing effort and q is the catchability coefficient, defined as the fraction of the population fished by an effort unit (Gulland, 1983). Biomass changes through time can be expressed as:

When the population is at equilibrium, i.e., dB/dt=0, and thus losses by natural and fishing mortalities are compensated by the population increase due to individual growth and recruitment. Equilibrium yield can be defined as:

Thus, the equilibrium biomass (Beq) as a function of fishing effort can be defined as:

A given amount of fishing effort will lead to a specific level of Beq, being both variables inversely correlated. Equilibrium yield as a function of effort can be obtained by substituting (2.7) in (2.2):

Equation (2.8) gives a parabola that represents the long-term production function of the fishery, where the corresponding yield (Y) for a given level of fishing effort (f) in a population at equilibrium is called sustainable yield. Equilibrium yield will increase with f up to the point of Maximum Sustainable Yield (MSY), falling onwards as fishing effort increases.
The economic model developed by Gordon (1954) is based on Schaefer's model, and introduced the concept of economic overfishing in open access fisheries. The model establishes that the net revenues π derived from fishing are a function of total sustainable revenues (TSR) and total costs (TC):
| π=TSR-TC | (2.9) |
or, alternatively:
| π=pY-cf | (2.10) |
where p is the (constant) price of the species and c the (constant) costs per unit of effort. The latter includes fixed costs, variable costs and opportunity costs of labor and capital. Fixed costs are independent of fishing operations (depreciation, administration and insurance costs), whereas variable costs are incurred when fishers go fishing (fuel, bait, food and beverages, etc.). Opportunity costs are the net benefits that could have been achieved in the next best economic activity, i.e., other regional fisheries, capital investment or alternative employment, and thus must be integrated in cost estimations.
Substituting (2.2) in (2.10), π can be defined as a function of effort:
| π=[pqB-c]f | (2.11) |
As in the biological model, Gordon (1954) assumes equilibrium to obtain the long-term production function of the fishery. The open-access equilibrium yield occurs when TSR equals TC and thus π(t) = 0, and there will be no stimulus for entry or exit to the fishery. If, additionally, biomass is assumed a: equilibrium, the yield thus established will provide a simultaneous equilibrium in both an economic and a biological sense, leading to bioeconomic equilibrium (BE). Biomass at bioeconomic equilibrium (BBE) can be defined by solving equation (2.11) for B:

B(t) will be always greater than 0, because fishing effort will be reduced or even ceased at TC ≥TSR. Thus, the model predicts:(1) overexploitation, if the TC curve intersects the TSR curve at higher effort levels than those required to operate at MSY; and (2) non-extinction of the resource, because at effort levels above BE there will be no stimulus to entry to the fishery. The non-extinction prediction will depend on the rate of growth of the stock and the form of the function defined by equation 2.2 (Clark, 1985; Anderson, 1986). It will be correct if and only if the resulting biomass at BE exceeds a threshold biomass level required for a population to be viable.
TSR at equilibrium can be obtained by multiplying (2.4) by the unit price p:

The TSR curve as a function of effort will have the same form as the sustainable yield curve, but in monetary terms (Fig. 2. 1c). TC is obtained from equation (2.2), as a function of fishing effort:

The long-term function of TC is calculated by solving for f and multiplying by c:

Hence, the long-run sustainable biomass and production functions of the fishery can be built by specifying the corresponding levels of fishing effort at Maximum Economic Yield (fMEY), Maximum Sustainable Yield (fMSY) and bioeconomic equilibrium (fBE) (Fig. 2.2).

Figure 2.2. Gordon-Schaefer static model. Sustainable (a) biomass, (b) yield, and (c) total sustainable revenues (TSR) and costs (TC).
Under unrestricted access, the net benefit or economic rent of the fishery is positive when f< fBE and zero when TC equals TSR (Fig. 2.2c). The area under the TSR curve and above TC corresponds to the economic rent, which is maximized at MEY and the corresponding fMEY, where the difference between TC and TSR is highest. The position of the TC curve will determine changes in MEY and BE levels. It is assumed that additional effort is produced by the entry of additional fishing units, instead of effort expansion by the already existing vessels (Anderson, 1986). Gordon (1954) predicts that fBE will be twice fMEY (see below).
Both average (AY) and marginal (MY) yields correspond to the application of an additional unit of effort, and will be sustainable per unit of time. The former continuously falls as effort increases (Fig. 2.3a), until reaching 0 when the resource is exhausted. MY decreases more sharply than AY and reaches 0 at MSY, beyond which it takes negative values, i.e., the yield obtained by an additional effort unit is progressively lower than the preceding one. This happens because each fisher operates according to variations in his AY, and does not take into account the external effects caused to other users and to the fishery as a whole.

Figure 2.3. Open access regime. (a) Sustainable average and marginal yields; (b) average and marginal costs, and revenues, as a function of effort under open access conditions.
One biological goal is to set effort and yield levels at MSY through time. For this end, we can take the first derivative of the yield function in (2.8):

So:

Operating at fMEY maximizes the economic rent, because the difference between TSR and TC must be maximized. This also happens when the marginal value of the fishing effort (MVE) equals the costs per unit of effort, i.e. MVE = c(Fig. 2.3b). Considering equation (2.2), the biomass expressed as a function of fishing effort is given by:

Multiplying (2.22) by the average price of the species and dividing by f, the average value of the fishing effort (AVE) is obtained:

The marginal value of fishing effort (MVE) is obtained by multiplying (2.23) by the average price of the species (p):

Fishing effort at MEY (fMEY) is obtained by equaling (2.24) to the unit cost of fishing effort (c), and solving for f.

The bioeconomic equilibrium is reached when AVE equals the costs per unit of effort AVE = c: Fig. 2.3b). The latter can be estimated by equaling (2.23) to costs (c) and solving for f. It will be noted that fBE=2fMEY, i.e., fBE is twice fMEY.
The economic model developed by Gordon also takes into account the assumptions considered by Schaefer (1954) for the biological model:
The population is at equilibrium (see above). Thus, it behaves in a more or less regular fashion such that changes in the trajectory of catch and effort could be used to reflect assertions about the future behavior of the system (Caddy, 1996).
Under equilibrium, fishing mortality (F) is proportional to effort (f), being the catchability coefficient (q) the constant of proportionality, i.e.:
F=qf (2.26)
The catch per unit of effort (CPUE) is a relative index of population abundance:

The stock is constrained by a constant carrying capacity of the environment.
The stock will respond immediately to variations in the magnitude of effort exerted.
Fishing technology is constant.
Prices and marginal/average costs are constant and independent of the level of effort exerted.
TC are proportional to effort, and thus a change in the slope of the TC curve will determine changes in BE and MEY levels.
All processes affecting stock productivity (e.g., growth, mortality, and recruitment) are subsumed in the effective relationship between effort and catch.
The catchability coefficient q is not always constant, and may differ due to e.g, different aggregation behavior of pelagic and sedentary resources. Factors related to differential gear selectivity by age/lengths are not taken into account.
CPUE is not always an unbiased index of abundance. This is especially relevant for sedentary resources with patchy distribution and without the capacity of redistribution in the fishing ground once fishing effort is exerted. Sequential depletion of patches also determines a patchy distribution of resource users, precluding model applicability (see Caddy, 1975, 1989a, b; Conan, 1984; Orensanz et al.,1991).
Variations in the spatial distribution of the stock are usually ignored, as well as the biological processes that generate biomass, the intra/interspecific interactions, and stochastic fluctuations in the environment and in population abundance.
Ecological and technological interdependencies (see Chapter 3) and differential allocation of fishing effort in the short term (see Chapter 6) are not usually taken into account.
Improvement in technology and fishing power determines that q often varies through time.
It becomes difficult to distinguish whether population fluctuations are due to fishing pressure or natural processes. In some fisheries, fishing effort could be exerted at levels greater than twice the optimum (Clark, 1985).
Smith (1969) assumes that long-run fishing levels are proportional to profits:


If π(t)≥ O, vessels will enter the fishery; exit expected to occur ifπ(t)≤O. Parameter φ can be empirically estimated according to variations in π(t), turn will have a close relation with the incurred costs for different effort levels (Seijo et al., 1994b).
Variations in fishing effort might not be reflected immediatly in stock abundance and perceived yields. For this reason, Seijo (1987) improved Smith's model by incorporating the delay process between the moment fishers face positive or negative net revenues and the moment which entry or exit takes place. This is expressed by a distributed–delay parameter DEL) represented by an Erlang probability density function (Manetsch, 1976), which describes the average time lag of vessel entry/exit to the fishery once the effect of changes in the net revenues is manifested (see also Chapter 6). Hence, the long-run dynamics of vessel type m (Vm(t)) can be described by a distributed delay function of order g by the following set of differential equations:

where Vm is the input to the delay process (number of vessels which will allocate their fishing effort to target species); γtg(t) is the output of the delay process (number of vessels entering the fishery); γ1(t), γ2(t),…, γg-1(t) are intermediate rates of the delay; DELm is the expected time of entry of vessels to the fishery; and g is the order of the delay. The parameter g specifies the member of the Gamma family of probability density functions.
Example 2.1. Dynamic bioeconomic model
Consider a pelagic fishery with parameters defined in Table 2.1.
| Parameter/Variable | Value |
|---|---|
| Intrinsic growth rate | 0.36 |
| Catchability coefficient | 0.0004 |
| Carrying capacity of the system | 3500000 tonnes |
| Price of the target species | 60 US$/tonne |
| Unit cost of fishing effort | 30000US$/yr |
| Initial population biomass | 3500000 tonnes |
| Fleet dynamics parameter | 0.000005 |
Fig. 2.4 shows variations in biomass, yield, costs and revenues resulting from the application of the dynamic and static version of the Gordon-Schaefer model, as a function of different effort levels. fBE is reached at 578 vessels and fMEY at 289 vessels.

Figure 2.4. Static (equilibrium) and dynamic trajectories of biomass (a), yield (b) and cost-revenues (c) resulting from the application of different fishing effort levels.
Fig. 2.5 shows temporal fluctuations in performance variables of the fishery. Yield and net revenues decrease at fishing effort levels higher than 630 vessels, followed by a dynamic entry/exit of vessels to the fishery, as the economic rent becomes positive or negative, respectively. Bioeconomic equilibrium (π=0) is reached at 1200 tonnes, after 50 years of fishing operations.

Figure 2.5. Dynamic trajectories of (a) biomass, (b) yield, (c) economic rent, and (d) fishing effort.
Yield-mortality models link two main outputs of the fishery system: yield Y (dependent variable) and the instantaneous total mortality coefficient Z. Fitting Y against Z generates a Biological Production curve, which includes natural deaths plus harvested yield for the population as a whole (Figure 2.6). Y-Z models provide alternative benchmarks to MSY, based on the Maximum Biological Production (MBP) concept (Caddy and Csirke, 1983), such as the yield at maximum biological production (YMBP) and the corresponding mortality rates at which the total biological production of the system is maximised (ZBMBP and FMBP). Theory and approaches to fitting the models have been fully described (Caddy & Csirke, 1983; Csirke & Caddy, 1983; Caddy & Defeo, 1996) and thus will not be considered in detail here.
Csirke & Caddy (1983) expressed the equilibrium yield equation of Graham (1935) in terms of the equilibrium value of annual mortality rate (see p. 45 and also Caddy, 1986), thus reducing equation (2.1) to a quadratic form:
Yi = aZ2i + bZi + c (2.32)
Where Yi and Zi are the yield and the mean total mortality coefficient for year i, respectively.
Under logistic assumptions, equation (2.32) gives a parabola passing through the abscissa to the right of the origin. Using multiple regression, Where Zi and Zi2 are treated as two independent variables, the “convex-downwards” curve that relates annual values of yield and total mortality can be drawn. An estimate of the natural mortality coefficient M can be obtained by solving this equation for Z = M (Yi and F = 0). See Csirke & Caddy (1983) and Caddy & Defeo (1996) for the calculation of this and the other parameters related to the Biological Production curve (Fig.2.5).
Csirke & Caddy (1983) suggested an alternative approach to fitting the logistic model, based on the abundance index:

The above equation was preferred owing to theoretical objections to the direct fitting procedure (Hoenig & Hoenig, 1986; Caddy & Defeo, 1996). This model is fitted by using different trial values of M, in which the best value selected is that which maximize a goodness of fit criterion (Caddy, 1986). Parameters of this logistic model can be obtained as in Caddy & Defeo (1996).
Caddy & Defeo (1996) extended the theory of production modelling with mortality estimates to include the exponential model of Fox (1970). Linear and non-linear approaches were used to fit this model. The exponential model for yield and mortality data can be summarized as:

Where B∞ and b' can be estimated by nonlinear regression techniques. As in the case of the alternative logistic approach, the model is fitted for different trial values of M, selecting those that maximize a goodness of fit criterion. The estimation procedure for the remaining parameters is fully explained in Caddy & Defeo (1996). A linearised approach of the above equation can be easily derived as:

using In(Yi/Zi-M) and Zi as dependent and independent variables, respectively. Parameter estimation follows the same reasoning as in the previous approach, using trial values of M.
In order to obtain bioeconomic reference points (RPs) for precautionary fishery management (Caddy & Mahon, 1995), Defeo & Seijo (in press) developed an expression for the economic rent (π) of a stock from the exponential version of the yield-mortality model in its linearised form:

Where p is the average price of the target species and c is the unitary cost of the fishing effort.
Differentiating the above equation, and expression that yields the marginal rent (πm) with changes in F is obtained:

Solving for F, an expression that provides the fishing mortality rate at MEY (FMEY) is estimated as:

By doing a= e1/(pBq)c, a special function of MathCad®1 called W[a]can be built as follows:

1 Mathcad 5.0 for Windows. 1994. Mathsoft, Inc.

Example 2.2. Bioeconomic yield-mortality model
The example to be given below (Defeo & Seijo, in press) is based on a hypothetical data set used by Caddy (1986: p. 387), which is adapted to the methodology proposed (Table 2.2). Bioeconomic information that would allow the calculations reported here on a real data set is not available, so that the results (and the estimates of mortlity used) are only intended to illustrate the bioeconomic model developed and the proposed methodology of fitting the data. Input data chosen to run the model was p=$3000, q=0.0001, and c=$25. The M value used as input for the model was found by iterating equation (2.35) and maximizing the goodness-of-fit-criteria. The highest R2 corresponded to M=0.13/yr.
| Year | Yield (tonnes) | Z(1/yr) |
|---|---|---|
| 1 | 7.5 | 0.175 |
| 2 | 12.5 | 0.170 |
| 3 | 19.0 | 0.250 |
| 4 | 35.0 | 0.440 |
| 5 | 40.5 | 0.610 |
| 6 | 39.5 | 0.795 |
| 7 | 30.5 | 1.080 |
| 8 | 20.0 | 1.170 |
| 9 | 26.0 | 0.900 |
| 10 | 29.5 | 0.790 |
| 11 | 27.5 | 0.710 |
| 12 | 29.0 | 0.470 |
Fig. 2.6 shows the relationship between Y and Z, fitted by the linearised exponential model. The three main RPs: MSY, yMEY and YMBP, are illustrated for an optimized M of 0.13/yr. Table 2.3 shows estimates of the mean values of the parameters, together with the 95% confidence intervals obtained by bootstrap simulations (see Chapter 7). With the artificial data set provided, the bioeconomic RP fell below the other two ones, in the following order: YMEY≤YMBP ≤MSY. The same trend mentioned above remains valid for the remaining management parameters (Table 2.3), and thus the bioeconomic RPs were more conservative than the “maximum sustainable” ones, considering both the overall mean and the confidence intervals generated by bootstrap runs. It is worthy of note that YMPB as well as the corresponding mortality.
rates (FMBP and ZMBP) were consistently below those corresponding to MSY and thus could be considered precautionary RPs (Fig. 2.6).

Figure 2.6 Bioeconomic Y-Z model: yield and biological production curves fitted to hypothetical data. The position of MSY, Y MEY, MBP is shown. A M value of 0.13/yr that maximized the goodness-of-fit criterion in equation (2.35) was used as input for running the model (adapted from Defeo & Seijo, in press).
Simulations involving changes in the unit cost of fishing effort (c) resulted, as expected, in variations in the bioeconomic RPs derived from the Y-Z derived from the Y-Z model (Table 2.3). For instance, a reduction in c of 40% (from $25 to $15 per unit of effort) determined a concomitant increase in the mean bootstrap estimates of bioeconomic RPs of the order of 14% for YMEY, 38% for FMEY and fMEY, and 22% for ZMEY. Empirical distributions of YMEY and MSY obtained by bootstrapping under the two selected input values of c showed that YMEY fell below MSY, but got closer each other under a lower cost scenario. The same was valid for the remaining bioeconomic RPs when compared with the biological ones (Defeo & Seijo, in press). The reader is referred to Chapter 7 for a detailed discussion and application of bootstrapping to assess uncertainty.
The bioeconomic approach for fitting yield-mortality models developed by Defeo & Seijo (in press) unambiguously showed that mean and confidence intervals of bioeconomic RPs tended to fall in the lower bound of those corresponding to the biological model, clearly suggesting that they constitute relatively cautious RPs for management. The RPs derived from the Biological Production curve, such as the YMBP and the corresponding mortality rates (Caddy & Csirke, 1983), also constitute important benchmarks to be considered in future research on the subject, especially if it is considered that ZMBP was found to be a safer target that ZMSY.
Sensitivity analysis on the model to variations in unit costs resulted in changes in the bioeconomic RPs. As expected, they systematically increased with decreasing costs and approached the “maximum sustainable”RPs. This could be important in many artisanal coastal fisheries with relatively low total costs and high unit value of harvested stocks, such as shellfisheries, where the bioeconomic equilibrium is often reached at high levels of fishing effort (Seijo & Defeo, 1994b) and the corresponding FMEY approaches FMSY. Therefore, at very low levels of unit cost of effort, FMBP could become a more precautionary RP than FMEY. The biomass-rent trade-off can be estimated to reflect the societal cost of adopting a highly risk averse management option which departs from the rent maximizing paradigm.
| Parameter | c=$15 | c=$25 | ||||
|---|---|---|---|---|---|---|
| Mean | 2.5 Cl | 97.5 Cl | Mean | 2.5 Cl | 97.5 Cl | |
| B∞ | 225 | 160 | 291 | 228 | 185 | 296 |
| MSY | 36 | 31 | 41 | 36 | 32 | 41 |
| FMSY | 0.440 | 0.348 | 0.531 | 0.435 | 0.363 | 0.511 |
| ZMSY | 0.570 | 0.478 | 0.661 | 0.565 | 0.493 | 0.641 |
| YMEY | 32 | 26 | 38 | 28 | 22 | 34 |
| FMEY | 0.258 | 0.234 | 0.283 | 0.187 | 0.168 | 0.203 |
| ZMEY | 0.388 | 0.364 | 0.413 | 0.317 | 0.298 | 0.333 |
| MBP | 48 | 40 | 56 | 49 | 42 | 57 |
| YMBP | 35 | 31 | 40 | 35 | 32 | 40 |
| FMBP | 0.375 | 0.283 | 0.466 | 0.352 | 0.281 | 0.429 |
| ZMBP | 0.505 | 0.413 | 0.596 | 0.482 | 0.493 | 0.559 |
| fMSY | 4,395 | 3,476 | 5,314 | 4,349 | 3,527 | 5,171 |
| fMEY | 2,584 | 2,339 | 2,828 | 1,867 | 1,690 | 2,044 |
A simple approach to formulation of risk-averse management strategies was explored by Defeo and Seijo (in press), using decision theory (Schmid, 1989: see Chapter 7) jointly with the bioeconomic Y-Z approach developed here. For this purpose, the concepts of Maximax. Maximin and Minimax were recognised as powerful tools for choice under uncertainty, because they seem to be well adapted for formulation of risk-averse management strategies and precautionary fisheries management (FAO, 1995a, Pérez & Defeo, 1996). An alternative risk analysis could be carried out by using the probability density functions of YMEY and MSY generated by bootstrapping against the corresponding mortality rates used as control variables, in the way described by Caddy & Defeo (1996).
In our view, yield-mortality models have some advantages over the classic catch-effort models because (see also Caddy & Defeo, 1996; Caddy, 1996):
They can be considered as “output-output”, i.e., both Y and Z constitute outputs of the biologic and economic subsystems. Thus, errors due to poor calibration of fishing effort (input variable) in standard catch-effort models, as well as unperceived effects of changes in q with fishing intensity and biomass, might be reduced using this approach.
Values calculated from the logistic model for the total mortality rate at maximum biological production ZMBP tend to fall in the low percentiles of the ZMSY cumulative distribution, thus constituting a relatively cautious reference point for management. Depending on the unit cost of effort, ZMBP is even more cautious than ZMEY
Unless there have been very considerable annual changes in fishing effort, the successive annual points in a Y-Z plot would not show the sharp jumps from left to right hand sides of the yield curve, characteristic of catch-effort production models with wide departures from equilibrium.
The bioeconomic model shown here assumes “pseudo-equilibrium conditions” (sensu Caddy, 1996: p. 219). Nevertheless, Z values derived from catch curves and multi-age group analysis more closely represent past and present impacts of fishing on all harvested year classes than do annual values of fishing effort, thus providing robustness with respect to departures from equilibrium.
A stochastic dynamic model following the systems science approach could be alternatively formulated to compare the performance of both dynamic and static approaches and to evaluate, under the light of model assumptions, which of them will prove most effective and useful for management advice. A multiple criterion optimization approach could also be developed for one or more sets of policy goals and management targets, in order to reflect the willingness of the decision maker to allow for tradeoffs among performance variables (Diaz de León & Seijo, 1992; Seijo et al., 1994c: see Chapter 5).
Age structured models consider factors affecting biomass through time, such as growth, recruitment and mortality, in a population homogeneously distributed in space and time. These models are based on the static model of Beverton & Holt (1957), and explicitly include the age structure of the population. The Beverton & Holt model and subsequent variations, assume that recruitment is independent of stock size and that it is not affected by variations in fishing intensity. Moreover, it relies on the “Dynamic Pool Assumption”, which allows a unit stock to be treated as perfectly mixed age groups with homogenous distribution and equal probability of capture within the distribution area, before and after applying fishing effort. Growth and mortality parameters are the same for the entire area, and constant for the entire life span of the species (see Hancock, 1973 and Seijo et al., 1994b for details).
An alternative approach to static models considers variations in population structure through time, based on the dynamic accounting of inflows and outflows of individuals to each age of the population structure. The incorporation of recruits is dynamic, allowing for a seasonal analysis of recruitment and its distribution (Seijo, 1986; Seijo & Defeo, 1994b). In the dynamic model, changes in the number of individuals through time can be defined as:

Where Si denotes the survival rate of organisms of age i and Ai correspond to the total mortality rate (Gulland, 1983). Therefore, Sl-1(t) can be expressed as:
St-1(t)=1-[MRt-1(t)+FRT-1(T)] (2.47)
where MR(t) and FR(t) are the finite natural and fishing mortality rates, respectively, derived from previous estimations of the corresponding instantaneous rates of natural and fishing mortality.
Rearranging:

Thus, the number of individuals in each cohort (Ni) can be obtained by integrating in the interval [t, t+DT], the number of individuals of age i-1 that survive and grow into a cohort in time t, minus the total mortality rate (Ai) minus the rate at which organisms surviving cohort i (Si) are incorporated into cohort i+1 in time t (Seijo & Defeo, 1994b). Using Euler numerical integration (Chenney & Kincaid, 1985), the dynamic population structure cna be expressed as:

Bi(t + DT) = Ni((t)+DT[Si-1Ni-1(t)-Ni(t)] 2.50
In this case, the von Bertalanffy growth equation and a length-weight relationship (W=a.lb) are used to estimate the biomass for each age class:
Bi(t + DT) = Ni((t + DT)Wi (2.51)

Fishing mortality (Fi) and yield Yi(t) by age class are obtained as in (2.26) y (2.2) respectively, but in this case both B and q are given by age class:

Total revenues TR are obtained by multiplying the unit price (pi) by the yield estimated for each age:
Yi(t) = qi Bi(t) f (t) (2.54)

Total costs (TC (t) and net revenues π(t) are obtained as in the Gordon-Schaefer model.
Example 2.3. Age-structured dynamic bioeconomic model
In the following example, the dynamic behaviour of population biomass, yield, effort and revenues is analyzed for a hypothetical trawl fishery with parameters defined in Table 2.4. Simulations involve variations in the age at first capture (tc) and in the amount of fishing effort f.
| Parameter/Variable | Value |
|---|---|
| Maximum observed age | 10 years |
| Age at first maturity | 2 years |
| Average fecundity | 5000 eggs |
| Age at first capture | 2 years |
| Sex proportion | 0.5 |
| Natural mortality coefficient | 0.2/mo |
| Curvature parameter of von Bertalanffy equation | 0.5/yr |
| ι0 of von Bertalanffy equation | 0.0 |
| Asymptotic length L∞ | 100 mm |
| Asymptotic weight W∞ | 200 g |
| Selectivity parameters | L50=20 mm |
| L75=30 mm | |
| Area swept per day | 0.1 Km2 |
| Total distribution area of the stock | 10 Km2 |
| Maximum observed recruitment | 20000000 |
| Average price | 10000 US$/tonne |
| Unit cost of fishing effort | 75000 US$/vessel/d |
| Fleet dynamics parameter | 0.00005 |
The dynamic trajectories of fishery performance varibles under different tc values are observed in Fig. 2.7. Biomass decreases to a minimum concurrently with highest yields, 20 years after the beginning of the fishery. Decrements in biomass are more noticeable with low tc values, which in turn determines the lowest values of yields and economic rent. A long-term equilibrium is reached after 45 years (Fig. 2.7a to d). Maximum fishing effort is about 200 vessels for a tc comprised between 2 and 3 yr at ca. 20 years and diminishes onwards as a result of negative economic rent (Fig.2.7c). The number of vessels at tc values varying from 1 to 4 yr under bioeconomic equilbrium, are, respectively, 67, 90, 115 142 (Fig. 2.7d); i.e., a relatively high tc (e.g., 4 yr) allows the fishery to support a greater number of vessels. However, an indiscriminate increase in tc (e.g., greater than 4 years) could not justify vessels operating in the fishery. Yields and economic rent are highest with tc = 2 years. Certainly, the resulting dynamic biomass for high tc values are higher and with low variations through time. Fishing effort tends to increase proportionally to the rent generated by the fishery under different tc scenarios (Fig. 2.7d). In the long run, under open access conditions and with tc = 4, the fishery is able to support more than twice the number of vessels than with tc = 1 yr. The yield at bioeconomic equilibrium increases from 158 tonnes with tc = 1 yr to 272 tonnes with a tc =4 yr (Fig.2.7b).

Figure 2.7. Age-structured bioeconomic model: dynamic effect of different tc in (a) biomass; (b) yield; (c) economic rent; and (d) fishing effort.
As can be observed from the above example, the dynamic age-structured model allows one to explore the impact of several sizes/ages at first capture. When the selectivity by size is variable, this important control variable becomes a management instrument that the global models such as the Gordon-Schaefer cannot handle.
Two key predictions were derived from the classical static bioeconomic model: 1) an open access regime leads to stock overexploitation and dissipation of the economic rent; and 2) MEY will occur at a lower exploitation rate than MSY. However, this model ignores the time dimension in the estimation of optimal yield and effort levels. In this section we introduce the price of time to explain the bioeconomic dynamic behaviour of a fishery. We also show that the optimal exploitation rate of a fish stock could be greater or lower than MEY or MSY, depending on the intertemporal preferences of society concerning resource use.
Fishing effort investment decisions are related to the expectation that the fishing unit (i.e. vessel + gears) assures positive net revenues throughout its lifetime. An approach to the incorporating problem of the dimension and importance of time as a key factor in investment and development of fisheries, is to consider the preferences in the consumption of a certain good in different periods.
For example, consider an individual that has the alternative of consuming goods in the present or in subsequent years. This person will not necessarily be indifferent to the choice of spending now or in the future, even if prices remain constant. Indeed, consumption in a period constitutes a different good to consume in another period. Each society member has temporal preferences concerning the consumption of a good in different time periods. This is measured by the marginal time preference rate (MTPR). If an individual is indifferent between consuming an additional 1 US$ in a year or 1.10 US$ in the following, he has a MTPR of 10% per year. The termmarginal is used because a MTPR measures the individual preference between small increments in consumption through time. This presupposes that the individual has dissimilar expectations about the amount of a good that will consume in different periods (see Sudgen & Williams, 1978 for a detailed discussion on the subject).
Preference analysis in the use of a fishery resource could not be static, for two reasons: 1) its renewable nature implies variability in availability and uncertainty in its magnitude through time; 2) a different temporal marginal preference of resource use will exist according to the type of fishery considered. For example, open access fisheries are generally characterized by a high MTPR, because of the inherent characteristics of fish stocks developed in Chapter 1. Thus, there will be incentives to increase fishing effort levels (and thus yields and profits) in the short- run, having little or no concern for the future. In mechanized fisheries, the investment carried out in planning and developing fishing activities is not immediately paid. The lifetime of the fishing unit should be taken into account to evaluate the investment magnitude, as well as present and future costs, and the probable revenues derived from fishing. In these cases, it is probable that, under precautionary management schemes (e.g. limited entry), a low MTPR occurs, in order to favor investments and to sustain the resource in the long run.
Consider a fisher A who has to decide on how to distribute his consumption activities in two time periods t1 and t2 (Randall, 1981). Total consumption in each period (ψt) could be defined as a budget in each period, that is, ψt1 in t1 and ψt2 in t2. Assume that the fisher receives an income Q1 in t1 and Q2 in t2, being Q1=Q2. Figure 2.8 shows the indifference curve la for fisher A, which defines his time preferences in resource use in two successive time periods. WW is the intertemporal budget line, where W=Q1+Q2. WW has a negative slope = -1, and thus the income could be transferred for one period to another on a one to one basis. The indifference curve passes through a common point represented by Q1 and Q2. Fisher A has a neutral time preference if he prefers the same consumption in t1 as in t2(with ψt1=ψt2and Q1=Q2).

Figure 2.8. Intertemporal neutral preference (adapted from Randall, 1981).
Now consider a fisher B and his respective utility function (indifference curve lb) in two-time periods t1 and t2 (Fig. 2.9). If consumption could be reallocated between periods (e.g. if it is possible to transfer incomes), fisher B could transfer part of his consumption from t2 to t1, and his total consumption would be Q*1b + Q*2b. Fisher B has a positive time preference or a high MTPR, since he prefers to consume immediately, rather than in subsequent periods, i.e., he would sacrifice a relatively high amount of a good to be consumed in the future in exchange for an increment in the current consumption.

Figure 2.9. Intertemporal positive preference (adapted from Randall, 1981).
Fisher C (Fig. 2.10) has a negative time preference or a low MTPR. He will transfer part of his consumption in the current period to the subsequent one, in such a way that his consumption will be Q*1c + Q*2c. Thus, his optimal intertemporal consumption is achieved at the tangent between WW and the indifference curve l*c.

Figure 2.10. Intertemporal negative preference (adapted from Randall, 1981).
The present value of flow of future revenues allows for comparisons of money during different time periods. The discount rate (d) is used for this purpose. Individuals with different time preferences adjust their intertemporal consumption profile so as to be indifferent between now and later. For example, suppose that an individual has a MTPR of d per time period, i.e., he is indifferent between an extra consumption of 1 unit in period 0 and 1 + d units in period 1. Analogously, he would be indifferent to the alternative of consuming (1 + d)2 extra units in period 2. Thus, an extra unit consumed in period 1 has a present value of (1/1+d) units in period 0, and an extra unit consumed in period 2 has a present value of 1/(1+d)2 units in period 0, and so on for t periods (1/ (1+ d)t). The d rate to which future revenues are discounted at present values is the discount rate. A higher discount rate would lead to a lower present value, and vice versa. The discount rate differs from MTPR in that it does not imply an interpretation of the rate to which it refers, but rather it is simply a number, generally constant, used in arithmetic manipulations.
Related concepts, such as the discount and compensation factors, could be used for calculations. The discount factor v td is the present value of an accumulated unit in the period t1 when the discount rate is d. The discount factor can be described as a geometric regular pattern of the form:

The compensation factor ad is the present value of a flow of revenues based on the accumulation of one unit in each of the t periods, at a discount rate d:

where: t=1,2,...,n. In terms of the discount factor:

The compensation factor is useful when the flow of costs and benefits through time is the same. This is rarely the case in fisheries.
Although the equilibrium estimators MSY,MEY and BE are useful benchmarks as RPs in the bioeconomic analysis of fisheries, their static nature diminish their reliability as appropriate management tools. Considering it extremely unlikely that the fishery system reflects equilibrium states, the dynamic fitting of the Schaefer-Gordon model should be preferred to its static counterpart, as it takes into account the intertemporal flow of costs and benefits from different fishing effort levels and dynamic biomass fluctuations. Thus, a fishery should be managed by maximizing a dynamic exploitation pattern more than by setting a specific (static) sustainable yield level. Indeed, a fishery will be economically efficient if it maximizes the net present value of catches. Since these are autocorrelated in time, the bioeconomic static analysis loses significance as an appropriate fisheries management tool.
The net present value of a flow of benefits and costs through time could be expressed as:

where PVπ is the present value of the net revenues π(t).
Clark (1985) develops a bioeconomic dynamic model based on the concept of a sole owner attemoting to maximize his profits from a fishery. This concept does not mean a monoply, in which prices could be fixed as a result of market control. Indeed, the dynamic Gordan-Schaefer model developed by clark assumes thar the industry is a price taker (i.e.,prices are constant through time). The model considers the discount rate d in its continuos form. The discount factor defined in (2.56) is expressed in its exponential form as:

In this expression,δ is the annual continous discount rate (Clark, 1985). According to (2.60), δ is related with d in the following form:
δ=ln(1+d) (2.61)
The present value of the revenues π(ι) in a time interval (O,T) will be:

In the long run (Τ = + ∞), a single fishery owner will tend to maximize the present value of π(t). Thus, substituting π(t) in (2.62):

The above is subjected to the differential equation that defines the classic surplus production model:

where f(ι)>0 and that the initial biomass Bo is known. Solving for f(ι) in (2.64), substituting in (2.63) and integrating by parts, Clark (1985) showed that the optimum biomass level (Bopt for a given discount rate is given by:

where BBE is defined as c/pq (see eq. 2.12). Optimum biomass BOPT decreases as δ increases, and consequently will approach the biomass at bioeconomic equilibrium BBE for δ → +∞ (Clark, 1985).
The optimal sustainable yield (OSY) and optimal effort (foptlevels for a given price of time δ are obtained by:

Sustainable exploitation of a fishery resource requires that the sum of the present value of net revenues be maximized. Setting sustainable yield levels for this purpose will depend on: (a) the biological balance between recruitment, somatic growth and mortality rates; (b) dynamic fluctuations in costs and prices in a regional and international context, probably reflected in the interest rate; and (c) socio-economic and political conditions. Expectation of changes in costs, prices and stock magnitude, should be included in the bioeconomic analysis of a fishery through a weighed analysis of the probability distribution of alternative management actions, based on a dynamic stochastic approach. In this context, the selection of a specific discount rate value will be critical in setting an adequate exploitation strategy, and will depend on the expected variability in the bio-socio-economic variables above mentioned.
A high rate of discounting (δ → +α) will threaten the viability of the resource. In this case, the dynamic MEY will tend to BE. On the contrary, when resource characteristics support a long-term exploitation strategy, there is a certain stability in prices and costs, socio-economic conditions encourage investments, and the future is not discounted. Thus as δ → 0, the dynamic and static MEY's will coincide. In general, the dynamic MEY will fluctuate between these two extreme situations (Anderson, 1986).
According to clark (1973; 1985), high δ values increase the risk of stock overexploitation. Hannesson (1986; 1987) expresses that this view ignores the implications derived from a high interest rate in the cost of capital, an effect previously established by Farzin (1984) for non-renewable resources. According to Hannesson, a high d value will increase harvesting costs, since sudden exploitation will require short-term investments in gear, equipment, etc.
Hannesson (1986) discusses the ambiguity of δ: on the one hand, it expresses the return rate required for achieving short-term profits, in such a way that high d values will imply high exploitation rates and a decrease in stock availability through time. On the other hand, δ expresses the opportunity cost of capital to be invested in the fishing unit (e.g. vessel, gears); thus a high δ value will imply high operation costs and therefore optimal exploitation rates at lower levels than in the previous case, promoting an increase in stock availability.