Exercise 2.1 Mean value and variance
Worksheet 2.1
|
j |
L(j) - L(j) + dL |
F(j) |
|
|
|
|
|
1 |
23.0-23.5 |
1 |
23.25 |
23.25 |
-2.968 |
8.809 |
|
2 |
23.5-24.0 |
1 |
23.75 |
23.75 |
-2.468 |
6.091 |
|
3 |
24.0-24.5 |
1 |
24.25 |
24.25 |
-1.968 |
3.873 |
|
4 |
24.5-25.0 |
2 |
24.75 |
49.50 |
-1.468 |
4.310 |
|
5 |
25.0-25.5 |
2 |
25.25 |
50.50 |
-0.968 |
1.874 |
|
6 |
25.5-26.0 |
6 |
25.75 |
154.50 |
-0.468 |
1.314 |
|
7 |
26.0-26.5 |
5 |
26.25 |
131.25 |
0.032 |
0.005 |
|
8 |
26.5-27.0 |
6 |
26.75 |
160.50 |
0.532 |
1.698 |
|
9 |
27.0-27.5 |
2 |
27.25 |
54.50 |
1.032 |
2.130 |
|
10 |
27.5-28.0 |
2 |
27.75 |
55.50 |
1.532 |
4.694 |
|
11 |
28.5-29.0 |
2 |
28.25 |
56.50 |
2.032 |
8.258 |
|
12 |
28.5-29.0 |
1 |
28.75 |
28.75 |
2.532 |
6.411 |
|
sums |
|
31 |
|
812.75 |
|
49.467 |
|
|
s2 = 1.6489 |
s = 1.2841 | ||||
Exercise 2.2 The normal distribution
Worksheet 2.2
|
x |
Fc(x) |
x |
Fc(x) |
|
22.0 |
0.02 |
26.0 |
4.75 |
|
22.5 |
0.07 |
26.5 |
4.70 |
|
23.0 |
0.21 |
27.0 |
4.00 |
|
23.5 |
0.51 |
27.5 |
2.93 |
|
24.0 |
1.08 |
28.0 |
1.84 |
|
24.5 |
1.97 |
28.5 |
0.99 |
|
25.0 |
3.07 |
29.0 |
0.46 |
|
25.5 |
4.12 |
29.5 |
0.18 |
Fig. 18.2.2 Bell-shaped curve determined for length-frequency sample of Fig. 17.2.1

Fig. 18.2.4 Ordinary regression analysis, regression line and scatter diagram (see Worksheet 2.4)
Exercise 2.3 Confidence limits
L - t30 * s/Ö n = 26.22 - 2.04 * 1. 284/Ö 31 = 25.75
L + t30 * s/Ö n = 26.22 - 2.04 * 1. 284/Ö 31 = 26.69
Exercise 2.4 Ordinary linear regression analysis
Worksheet 2.4
|
year
|
i
|
number of boats |
|
catch per boat per year |
|
|
|
x(i) |
x(i)2 |
y(i) |
y(i)2 |
x(i) * y(i) |
||
|
1971 |
1 |
456 |
207936 |
43.5 |
1892.25 |
19836.0 |
|
1972 |
2 |
536 |
287296 |
44.6 |
1989.16 |
23905.6 |
|
1973 |
3 |
554 |
306916 |
38.4 |
1474.56 |
21273.6 |
|
1974 |
4 |
675 |
455625 |
23.8 |
566.44 |
16065.0 |
|
1975 |
5 |
702 |
492804 |
25.2 |
635.04 |
17690.4 |
|
1976 |
6 |
730 |
532900 |
30.5 |
930.25 |
22265.0 |
|
1977 |
7 |
750 |
562500 |
27.4 |
750.76 |
20550.0 |
|
1978 |
8 |
918 |
842724 |
21.1 |
445.21 |
19369.8 |
|
1979 |
9 |
928 |
861184 |
26.1 |
681.21 |
24220.8 |
|
1980 |
10 |
897 |
804609 |
28.9 |
835.21 |
25923.3 |
|
Total |
|
7146 |
5354494 |
309.5 |
10200.09 |
211099.5 |
|
|
|
|||||
|
|
|
|||||
|
|
|
|||||
|
|
||||||
|
|
sx = 165.99 |
|||||
|
|
sy = 8.307 |
|||||
|
|
||||||
|
|
|
|||||
|
variance of b: |
||||||
|
|
sb = 0.01034 |
|||||
|
variance of a: |
||||||
|
|
sa = 7.568 |
|||||
|
Student's distribution: tn-2 = 2.31 |
||||||
|
confidence limits: |
||||||
|
b - sb * tn-2, b + sb * tn-2 = [-0.0645, -0-0167] |
||||||
|
a - sa * tn-2, a + sa * tn-2 = [42.5,77.4] |
||||||
Exercise 2.5 The correlation coefficient
In principle the number of boats can be measured with any accuracy, so this is the natural independent variable. The correlation coefficient is not considered useful in the present context. Nevertheless, as an exercise we calculate the confidence limits, using Eqs. 2.5.3 in sections called A and B:
A = 0.5 * ln[(1 + r)/(1 - r)] = 0.5 * ln[(1 - 0.811)/(1 + 0.811)] = -1.130

r1 = tanh(A - B) = -0.95
r2 = tanh(A + B) = -0.37
Exercise 2.6a Linear transformations, the Bhattacharya plot Worksheet 2.6a
|
x |
F(x) |
ln F(x) |
D ln F(z) |
x + dL/2 |
remarks |
|
|
|
|
(y) |
(z) |
|
|
4.5 |
2 |
0.693 |
|
|
not used |
|
|
|
|
0.916 |
5 |
|
|
5.5 |
5 |
1.609 |
|
|
|
|
|
|
|
0.875 |
6 |
|
|
6.5 |
12 |
2.485 |
|
|
|
|
|
|
|
0.693 |
7 |
|
|
7.5 |
24 |
3.178 |
|
|
|
|
|
|
|
0.377 |
8 |
|
|
8.5 |
35 |
3.555 |
|
|
|
|
|
|
|
0.182 |
9 |
|
|
9.5 |
42 |
3.737 |
|
|
not used contaminated |
|
|
|
|
0.000 |
10 |
|
|
10.5 |
42 |
3.737 |
|
|
|
|
|
|
|
0.091 |
11 |
|
|
11.5 |
46 |
3.829 |
|
|
|
|
|
|
|
0.197 |
12 |
|
|
12.5 |
56 |
4.025 |
|
|
|
|
|
|
|
0.035 |
13 |
|
|
13.5 |
58 |
4.060 |
|
|
not used |
|
|
|
|
-0.254 |
14 |
|
|
14.5 |
45 |
3.807 |
|
|
|
|
|
|
|
-0.716 |
15 |
|
|
15.5 |
22 |
3.091 |
|
|
|
|
|
|
|
-1.145 |
16 |
|
|
16.5 |
7 |
1.946 |
|
|
|
|
|
|
|
-1.253 |
17 |
|
|
17.5 |
2 |
0.693 |
|
|
|
|
|
First component |
Second component |
|
intercept (a) |
2.328 |
5.978 |
|
slope (b) |
-0.240 |
-0.446 |
|
|
9.7 |
13.4 |
|
s2 = - 1/b |
4.18 |
2.24 |
|
s |
2.04 |
1.50 |
Worksheet 2.6b
|
First component |
Second component |
|
|
|
|
B = -1/(2 * 2.042) = -0.120 |
B = -1/(2 * 1.502) = -0.222 |
|
|
|

|
x |
Fc(x) |
Fc(x) |
x |
Fc(x) |
Fc(x) |
|
1.5 |
0.0 |
|
11.5 |
26.4 |
23.7 |
|
2.5 |
0.1 |
|
12.5 |
15.2 |
44.2 |
|
3.5 |
0.4 |
|
13.5 |
6.9 |
52.8 |
|
4.5 |
1.5 |
|
14.5 |
2.4 |
40.4 |
|
5.5 |
4.7 |
|
15.5 |
0.7 |
19.9 |
|
6.5 |
11.4 |
|
16.5 |
0.2 |
6.3 |
|
7.5 |
21.8 |
0.0 |
17.5 |
0.0 |
1.3 |
|
8.5 |
32.7 |
0.3 |
18.5 |
|
0.2 |
|
9.5 |
38.7 |
1.8 |
19.5 |
|
0.0 |
|
10.5 |
36.0 |
8.2 |
20.5 |
|
|
Fig. 18.2.6A Bhattacharya plots (linear transformations) (see Worksheet 2.6a)

Exercise 3.1 The von Bertalanffy growth equation Worksheet 3.1
|
age |
standard length |
total length |
body weight |
|
0.5 |
1.0 |
1.4 |
0.04 |
|
1.0 |
6.6 |
8.0 |
9 |
|
1.5 |
11.8 |
14.1 |
45 |
|
2 |
16.5 |
19.7 |
118 |
|
3 |
24.9 |
29.6 |
380 |
|
4 |
32.0 |
37.9 |
775 |
|
5 |
38.0 |
45.0 |
1262 |
|
6 |
43.0 |
51.0 |
1802 |
|
7 |
47.3 |
56.0 |
2359 |
|
8 |
50.9 |
60.3 |
2909 |
|
9 |
54.0 |
63.9 |
3434 |
|
10 |
56.6 |
67.0 |
3922 |
|
12 |
60.6 |
71.7 |
4770 |
|
14 |
63.5 |
75.1 |
5444 |
|
16 |
65.5 |
77.5 |
5961 |
|
20 |
68.1 |
80.5 |
6637 |
|
50 |
70.7 |
83.6 |
7388 |
Fig. 18.3.1 Growth curves based on von Bertalanffy growth equations

Exercise 3.1.2 The weight-based von Bertalanffy growth equation Worksheet 3.1.2
|
age |
length |
weight |
age |
length |
weight |
|
0 |
2.54 |
0.38 |
0.9 |
9.34 |
19.00 |
|
0.1 |
3.63 |
1.11 |
1.0 |
9.78 |
21.83 |
|
0.2 |
4.62 |
2.29 |
1.2 |
10.55 |
27.36 |
|
0.3 |
5.51 |
3.90 |
1.4 |
11.17 |
32.53 |
|
0.4 |
6.32 |
5.88 |
1.6 |
11.69 |
37.21 |
|
0.5 |
7.05 |
8.16 |
1.8 |
12.11 |
41.37 |
|
0.6 |
7.71 |
10.69 |
2.0 |
12.45 |
44.99 |
|
0.7 |
8.31 |
13.37 |
2.5 |
13.06 |
51.93 |
|
0.8 |
8.85 |
16.16 |
3.0 |
13.43 |
56.47 |
Fig. 18.3.1.2 Growth curves for ponyfish

Exercise 3.2.1 Data from age readings and length compositions (age/length key) Worksheet 3.2.1
|
cohort |
1982 |
1981 |
1981 |
1980 |
number in length sample |
1982 |
1981 |
1981 |
1980 |
|
length interval |
key |
|
numbers per cohort | ||||||
|
35-36 |
0.800 |
0.200 |
0 |
0 |
53 |
42.4 |
10.6 |
0 |
0 |
|
36-37 |
0.636 |
0.273 |
0.091 |
0 |
61 |
38.8 |
16.7 |
5.6 |
0 |
|
37-38 |
0.600 |
0.300 |
0.100 |
0 |
49 |
29.4 |
14.7 |
4.9 |
0 |
|
38-39 |
0.500 |
0.400 |
0.100 |
0 |
52 |
26.0 |
20.8 |
5.2 |
0 |
|
39-40 |
0.364 |
0.364 |
0.182 |
0.091 |
70 |
25.5 |
25.5 |
12.7 |
6.4 |
|
40-41 |
0.273 |
0.455 |
0.182 |
0.091 |
52 |
14.2 |
23.7 |
9.5 |
4.7 |
|
41-42 |
0.222 |
0.444 |
0.222 |
0.111 |
49 |
10.9 |
21.8 |
10.0 |
5.4 |
|
|
|
|
|
total |
386 |
187.2 |
133.8 |
48.8 |
16.5 |
Exercise 3.3.1 The Gulland and Holt plot
Worksheet 3.3.1
|
A |
B |
C |
D |
E |
F |
|
fish |
L(t) |
L(t + D t) |
D t |
|
|
|
1 |
9.7 |
10.2 |
53 |
3.44 |
9.95 |
|
2 |
10.5 |
10.9 |
33 |
4.42 |
10.70 |
|
3 |
10.9 |
11.8 |
108 |
3.04 |
11.35 |
|
4 |
11.1 |
12.0 |
102 |
3.22 |
11.55 |
|
5 |
12.4 |
15.5 |
272 |
4.16 |
13.95 |
|
6 |
12.8 |
13.6 |
48 |
6.08 |
13.20 |
|
7 |
14.0 |
14.3 |
53 |
2.07 |
14.15 |
|
8 |
16.1 |
16.4 |
73 |
1.50 |
16.25 |
|
9 |
16.3 |
16.5 |
63 |
1.16 |
16.40 |
|
10 |
17.0 |
17.2 |
106 |
0.69 |
17.10 |
|
11 |
17.7 |
18.0 |
111 |
0.99 |
17.85 |
|
a (intercept) = 8.77 |
b (slope) = -0.431 | ||||
|
K = -b = 0.43 per year |
L¥ = -a/b = 20.3 cm | ||||
|
| |||||
|
sb = 0.145 |
t9 = 2.26 | ||||
|
confidence interval of K = [0.10, 0.76] | |||||
Fig. 18.3.3.1 Gulland and Holt plot (see Worksheet 3.3.1)

Exercise 3.3.2 The Ford-Walford plot and Chapman's method
Worksheet 3.3.2
|
Plot |
FORD-WALFORD |
CHAPMAN | ||
|
t |
L(t) |
L(t + D t) |
L(t) |
L(t + D t) - L(t) |
|
1 |
35 |
55 |
35 |
20 |
|
2 |
55 |
75 |
55 |
20 |
|
3 |
75 |
90 |
75 |
15 |
|
4 |
90 |
105 |
90 |
15 |
|
5 |
105 |
115 |
105 |
10 |
|
a (intercept) |
26.2 |
26.2 | ||
|
b (slope) |
0.86 |
-0.14 | ||
|
|
0.0009268 |
0.0009271 | ||
|
|
0.030 |
0.030 | ||
|
tn-2 |
3.18 |
3.18 | ||
|
confidence limits of b |
[0.76, 0.96] |
[-0.24, -0.04] | ||
|
K |
- ln b/D t = 0.15 |
-(1/1) * ln (1 + b) = 0.15 | ||
|
L¥ |
1/(1 - b) = 185 cm |
-a/b = 185 cm | ||
Fig. 18.3.3.2 Ford-Walford and Chapman plots for yellowfin tuna off Senegal. Data source: Postel, 1955, (see Worksheet 3.3.2)
Ford-Walford plot
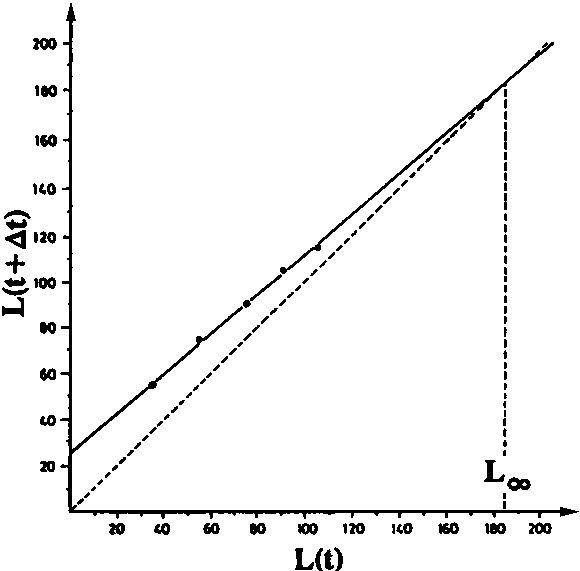
Chapman's method

Exercise 3.3.3 The von Bertalanffy plot
We choose 11 inches as estimate for L¥ , because very few (1.5%) of the seabreams are longer than 11 inches.
We assign the arbitrary ages of 1,2,3 and 4 years to the four age groups.
|
age |
L |
-ln (1 - L/L¥ ) |
|
1 |
3.22 |
0.35 |
|
2 |
5.33 |
0.66 |
|
3 |
7.62 |
1.18 |
|
4 |
9.74 |
2.17 |
b (slope) = K = 0.60 per year
At least, K has now got the correct sign.
sb2 = 0.0119, sb = 0.109, t2 = 4.3
confidence interval of K= [0.13, 1.07]
t0 cannot be estimated because the absolute age is not known.
Fig. 18.3.3.3 Von Bertalanffy and Gulland and Holt plots for sea breams. Data source: Cassie, 1954
von Bertalanffy plot

Gulland and Holt plot

Exercise 3.4.1 Bhattacharya's method
There is no "correct" solution to this exercise. The following is a "suggestion for a solution". It is not the same result as the one obtained by Weber and Jothy (1977) by using the Cassie method.
Fig. 18.3.4.1A Bhattacharya plots for threadfin bream. (See Worksheets 3.4.1a, b and c)
Worksheet 3.4.1a
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
|
length interval |
N1+ |
ln N1+ |
D ln N1+ |
L |
D ln N1 |
ln N1 |
N1 |
N2+ |
|
5.75-6.75 |
1 |
0 |
- |
- |
- |
- |
1 |
0 |
|
6.75-7.75 |
26 |
3.258 |
(3.258) |
6.75 |
1.262 |
- |
26 |
0 |
|
7.75-8.75 |
42# |
3.738# |
0.480 |
7.75 |
0.354 |
3.738# |
42# |
0 |
|
8.75-9.75 |
19 |
2.944 |
-0.793 |
8.75 |
-0.554 |
3.183 |
19 |
0 |
|
9.75-10.75 |
5 |
1.609 |
-1.335* |
9.75 |
-1.462 |
1.722 |
5 |
0 |
|
10.75-11.75 |
15 |
2.708 |
1.099 |
10.75 |
- |
-0.648 |
0.5 |
14.5 |
|
11.75-12.75 |
41 |
3.714 |
1.006 |
11.75 |
2.370 |
-3.926 |
0.0 |
41.0 |
|
12.75-13.75 |
125 |
4.828 |
1.115 |
12.75 |
-3.278 |
- |
- |
125 |
|
13.75-14.75 |
135 |
4.905 |
0.077 |
13.75 |
- |
- |
- |
135 |
|
.......... |
.......... |
.......... |
|
|
- |
|
|
|
|
Total |
1069 |
|
|
|
|
|
93.5 |
|
|
a (intercept) = 7.391 |
b (slope) = -0.908 | |||||||
|
|
| |||||||
|
*) points used in the regression analysis | ||||||||
Worksheet 3.4.1b
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
|
interval |
N2+ |
ln N2+ |
D ln N2+ |
L |
D ln N2 |
ln N2 |
N2 |
N3+ |
|
...... |
..... |
|
|
|
|
|
|
|
|
10.75-11.75 |
14.5 |
2.674 |
- |
10.75 |
- |
- |
14.5 |
0 |
|
11.75-12.75 |
41 |
3.714 |
1.039* |
11.75 |
- |
- |
41 |
0 |
|
12.75-13.75 |
125# |
4.828# |
1.115* |
12.75 |
- |
4.828# |
125# |
0 |
|
13.75-14.75 |
135 |
4.905 |
0.077* |
13.75 |
0.238 |
5.066 |
135 |
0 |
|
14.75-15.75 |
102 |
4.625 |
-0.280* |
14.75 |
-0.262 |
4.806 |
102 |
0 |
|
15.75-16.75 |
131 |
4.875 |
0.250 |
15.75 |
-0.761 |
4.843 |
57.0 |
74.0 |
|
16.75-17.75 |
106 |
4.663 |
-0.212 |
16.75 |
-1.261 |
4.043 |
16.2 |
89.8 |
|
17.75-18.75 |
86 |
4.454 |
-0.209 |
17.75 |
-1.760 |
2.782 |
2.8 |
83.2 |
|
18.75-19.75 |
59 |
4.078 |
-0.377 |
18.75 |
-2.260 |
1.022 |
0.3 |
58.7 |
|
19.75-20.75 |
43 |
3.761 |
-0.316 |
19.75 |
-2.759 |
-1.038 |
0.0 |
43 |
|
20.75-21.75 |
45 |
3.807 |
0.045 |
20.75 |
- |
-3.997 |
- |
45 |
|
21.75-22.75 |
56 |
4.025 |
0,219 |
21.75 |
- |
- |
- |
56 |
|
...... |
..... |
|
|
|
|
|
|
|
|
Total |
|
|
|
|
|
|
493.8 |
|
|
a (intercept) = 7.11 |
b (slope) = -0.500 | |||||||
|
|
| |||||||
Worksheet 3.4. 1c
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
|
interval |
N3+ |
ln N3+ |
D ln N3+ |
L |
D ln N3 |
ln N3 |
N3 |
N4+ |
|
...... |
..... |
|
|
|
|
|
|
|
|
15.75-16.75 |
74.0 |
- |
- |
15.75 |
- |
- |
74 |
0 |
|
16.75-17.75 |
89.8 |
4.498 |
0.194* |
16.75 |
- |
- |
89.9 |
0 |
|
17.75-18.75 |
83.2# |
4.421# |
-0.076* |
17.75 |
- |
4.421# |
83.2# |
0 |
|
18.75-19.75 |
58.7 |
4.072 |
-0.348* |
18.75 |
-0.225 |
4.196 |
58.7 |
0 |
|
19.75-20.75 |
43 |
3.761 |
-0.312* |
19.75 |
-0.404 |
3.792 |
43.0 |
0 |
|
20.75-21.75 |
45 |
3.807 |
0.046 |
20.75 |
-0.583 |
3.209 |
24.8 |
20.2 |
|
21.75-22.75 |
56 |
4.025 |
0.219 |
21.75 |
-0.762 |
2.447 |
11.6 |
44.4 |
|
22.75-23.75 |
20 |
2.996 |
-1.030 |
22.75 |
-0.941 |
1.506 |
4.5 |
15.5 |
|
23.75-24.75 |
8 |
2.079 |
-0.916 |
23.75 |
-1.120 |
0.386 |
1.5 |
6.5 |
|
24.75-25.75 |
3 |
1.099 |
-0.981 |
24.75 |
-1.299 |
-0.913 |
0.4 |
2.6 |
|
25.75-26.75 |
1 |
0 |
-1.099 |
25.75 |
- |
- |
- |
1 |
|
Total |
|
|
|
|
|
|
391.5 |
|
|
a (intercept) = 3.13 |
b (slope) = -0.179 | |||||||
|
|
| |||||||
Worksheet 3.4.1d
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
|
interval |
N2+ |
ln N2+ |
D ln N2+ |
L |
D ln N2 |
ln N2 |
N2 |
N3+ |
|
...... |
..... |
|
|
|
|
| ||
|
20.75-21.75 |
20.2 |
3.006 |
- |
20.75 |
? |
too few observations | ||
|
21.75-22.75 |
44.4 |
3.793 |
0.787 |
21.75 |
? |
| ||
|
22.75-23.75 |
15.5 |
2.741 |
-1.052 |
22.75 |
? |
| ||
|
23.75-24.75 |
6.5 |
1.892 |
-0.869 |
23.75 |
? |
| ||
|
24.75-25.75 |
2.6 |
0.956 |
-0.916 |
24.75 |
? |
| ||
|
25.75-26.75 |
1 |
0 |
-0.956 |
25.75 |
? |
| ||
Gulland and Holt plot:
|
age |
|
D L/D t |
L |
|
1 |
8.1 |
|
|
|
|
|
6.1 |
11.15 |
|
2 |
14.2 |
|
|
|
|
|
3.3 |
15.85 |
|
3 |
17.5 |
|
|
a (intercept) = 12.7
K = -b = 0.60 per year
b (slope) = -0.60
L¥ = -a/b = 21.4 cm
Fig. 18.3.4.1B Gulland and Holt plot of mean lengths of cohorts obtained by the Bhattacharya method (see Worksheets 3.4.1a, b, and c and Fig. 18.3.4.1A)

Exercise 3.4.2 Modal progression analysis
A. Leiognathus splendens:
Worksheet 3.4.2
|
|
|
GULLAND AND HOLT PLOT |
VON BERTALANFFY PLOT | ||
|
time of sampling |
L (t) |
D L/D t |
L |
t |
-ln (1 - L/L¥ ) |
|
1 June |
2.8 |
|
|
0.42 |
0.325 |
|
|
|
6.8 |
3.65 |
|
|
|
1 Sep. |
4.5 |
|
|
0.67 |
0.590 |
|
|
|
5.2 |
5.15 |
|
|
|
1 Dec. |
5.8 |
|
|
0.92 |
0.854 |
|
|
|
4.0 |
6.30 |
|
|
|
1 March |
6.8 |
|
|
1.17 |
1.119 |
|
a (intercept) |
10.65 |
-0.12 | |||
|
b (slope, -K or K) |
-1.06 |
1.06 | |||
|
-a/b |
L¥ = 10.1 |
t0 = 0.11 | |||
|
L (t) = 10.1 * [1 - exp(-1.1 * (t - 0.11))] | |||||
Fig. 18.3.4.2A Modal progression in time series of length-frequencies of ponyfish. (See Worksheet 3.4.2)

B. Rastrelliger kanagurta:
|
|
|
GULLAND AND HOLT PLOT |
VON BERTALANFFY PLOT |
||
|
time of sampling |
L (t) |
D L/D t |
L |
t |
-ln (1 - L/L¥ ) |
|
1 Feb
|
13.3 |
|
|
0.08 |
0.648 |
|
|
21.6 |
14.20 |
|
|
|
|
1 March
|
15.1 |
|
|
0.17 |
0.779 |
|
|
17.4 |
16.55 |
|
|
|
|
1 May
|
18.0 |
|
|
0.33 |
1.036 |
|
|
16.8 |
18.70 |
|
|
|
|
1 June
|
19.4 |
|
|
0.42 |
1.189 |
|
|
13.2 |
19.95 |
|
|
|
|
1 July
|
20.5 |
|
|
0.50 |
1.327 |
|
|
9.6 |
20.9 |
|
|
|
|
1 August |
21.3 |
|
|
0.58 |
1.442 |
|
a (intercept) |
44.57 |
0.512 |
|||
|
b (slope, -K or K) |
-1.60 |
1.61 |
|||
|
-a/b |
L¥ = 27.9 |
t0 = -0.32 |
|||
|
L(t) = 27.9 * [1 - exp(-1.6 * (t + 0.32))] |
|||||
Fig. 18.3.4.2B Modal progression in time series of length-frequencies of Indian mackerel. (See Worksheet 3.4.2)

Exercise 3.5.1 ELEFAN I
Worksheet 3.5.1
|
RESTRUCTURING OF LENGTH FREQUENCY SAMPLE | ||||||||
|
|
|
STEP |
STEP |
STEP |
STEP |
STEP |
STEP |
STEP |
|
mid-length |
orig. freq. |
MA(L) |
FRQ/MA |
|
zeroes |
deemphasized |
points |
highest positive points |
|
5 |
4 |
4.6 |
0.870 |
-0.197 |
2 |
-0.197 |
-0.109 |
|
|
10 |
13 |
4.6 |
2.826 |
1.610 |
2 |
0.966 |
0.966 |
0.966 |
|
15 |
6 |
4.8 |
1.250 |
0.154 |
1 |
0.123 |
0.123 |
|
|
20 |
0 |
4.0 |
0 |
-1.000 |
1 |
-1.000 |
0 |
|
|
25 |
1 |
1.4 |
0.714 |
-0.341 |
3 |
-0.340 |
-0.188 |
|
|
30 |
0 |
0.4 |
0 |
-1.000 |
2 |
-1.000 |
0 |
|
|
35 |
0 |
1.0 |
0 |
-1.000 |
1 |
-1.000 |
0 |
|
|
40 |
1 |
1.0 |
1.000 |
-0.077 |
2 |
-0.077 |
-0.043 |
|
|
45 |
3 |
1.0 |
3.000 |
1.770 |
2 |
1.062 |
1.062 |
1.062 |
|
50 |
1 |
1.2 |
0.833 |
-0.231 |
1 |
-0.230 |
-0.127 |
|
|
55 |
0 |
1.0 |
0 |
-1.000 |
1 |
-1.000 |
0 |
|
|
60 |
1 |
0.4 |
2.500 |
1.308 |
3 |
0.523 |
0.523 |
0.523 |
|
S = 12.993 |
SP = 2.674 |
| ||||||
|
(S /12) = M = 1.083 |
SN = -4.845 |
ASP = 2.551 | ||||||
|
|
-SP/SN = R = 0.552 |
| ||||||
Fig. 18.3.5.1 ELEFAN I, restructured data and highest positive points (see Worksheet 3.5.1, step 5)
Exercise 3.5.1a ELEFAN I, continued
Worksheet 3.5.1a
|
RESTRUCTURING OF LENGTH FREQUENCY SAMPLE | ||||||||
|
|
|
STEP |
STEP |
STEP |
STEP |
STEP |
STEP |
STEP |
|
mid-length |
orig. freq. |
MA(L) |
FRQ/MA |
|
zeroes |
deemphasized |
points |
highest positive points |
|
20 |
14 |
18.2 |
0.769 |
-0.194 |
2 |
-0.194 |
-0.159 |
|
|
24 |
32 |
40.0 |
0.800 |
-0.162 |
1 |
-0.162 |
-0.133 |
|
|
28 |
45 |
63.0 |
0.714 |
-0.252 |
0 |
-0.252 |
-0.206 |
|
|
32 |
109 |
75.8 |
1.438 |
0.506 |
0 |
0.506 |
0.506 |
|
|
36 |
115 |
78.4 |
1.467 |
0.537 |
0 |
0.537 |
0.537 |
0.537 |
|
40 |
78 |
75.2 |
1.037 |
0.086 |
0 |
0.086 |
0.086 |
|
|
44 |
45 |
58.0 |
0.776 |
-0.187 |
0 |
-0.187 |
-0.153 |
|
|
48 |
29 |
37.2 |
0.780 |
-0.183 |
0 |
-0.183 |
-0.150 |
|
|
52 |
23 |
24.0 |
0.958 |
0.003 |
0 |
0.003 |
0.003 |
0.003 |
|
56 |
11 |
16.0 |
0.688 |
-0.279 |
0 |
-0.279 |
-0.228 |
|
|
60 |
12 |
10.6 |
1.132 |
0.186 |
0 |
0.186 |
0.186 |
0.186 |
|
64 |
5 |
6.2 |
0.806 |
-0.156 |
0 |
-0.156 |
-0.128 |
|
|
68 |
2 |
4.4 |
0.455 |
-0.523 |
0 |
-0.523 |
-0.428 |
|
|
72 |
1 |
2.0 |
0.500 |
-0.476 |
1 |
-0.476 |
-0.390 |
|
|
76 |
2 |
1.0 |
2.000 |
1.095 |
2 |
0.657 |
0.657 |
0.657 |
|
S = 14.320 |
SP = 1.975 |
| ||||||
|
(S /15) = M = 0.9547 |
SN = -2.413 |
ASP = 1.383 | ||||||
|
|
-SP/SN = R = 0.818 |
| ||||||
Fig 18.3.5.1A Regrouped length-frequency data of 523 pike (4 cm length intervals), ELEFAN I restructured data and highest positive points and mean lengths as determined from age reading (low arrow). (See Worksheet 3.5.1a, cf. Fig 17.3.5.1C)

Exercise 4.2 The dynamics of a cohort (exponential decay model with variable Z)
Worksheet 4.2
|
age group |
M |
F |
Z |
e-0.5z |
N(t1) |
N(t2) |
N(t1) - N(t2) |
F/Z |
C(t1, t2) |
|
0.0-0.5 |
2.0 |
0.0 |
2.0 |
0.3679 |
10000 |
3679 |
6321 |
0 |
0 |
|
0.5-1.0 |
1.5 |
0.0 |
1.5 |
0.4724 |
3679 |
1738 |
1941 |
0 |
0 |
|
1.0-1.5 |
0.5 |
0.2 |
0.7 |
0.7047 |
1738 |
1225 |
513 |
0.286 |
147 |
|
1.5-2.0 |
0.3 |
0.4 |
0.7 |
0.7047 |
1225 |
863 |
362 |
0.571 |
207 |
|
2.0-2.5 |
0.3 |
0.6 |
0.9 |
0.6376 |
863 |
550 |
313 |
0.667 |
209 |
|
2.5-3.0 |
0.3 |
0.6 |
0.9 |
0.6376 |
550 |
351 |
199 |
0.667 |
133 |
|
3.0-3.5 |
0.3 |
0.6 |
0.9 |
0.6376 |
351 |
224 |
127 |
0.667 |
85 |
|
3.5-4.0 |
0.3 |
0.6 |
0.9 |
0.6376 |
224 |
143 |
81 |
0.667 |
54 |
|
4.0-4.5 |
0.3 |
0.6 |
0.9 |
0.6376 |
143 |
91 |
52 |
0.667 |
35 |
|
4.5-5.0 |
0.3 |
0.6 |
0.9 |
0.6376 |
91 |
58 |
33 |
0.667 |
22 |
Fig. 18.4.2 Exponential decay of a cohort with variable Z
Exercise 4.2a The dynamics of a cohort (the formula for average number of survivors, Eq. 4.2.9)
The formula for average number of survivors (Eq. 4.2.9).
Exact value:

Approximation:

Exercise 4.3 Estimation of Z from CPUE data
Worksheet 4.3
|
|
|
cohort |
1982 A |
1982 S |
1981 A |
1981 S |
1980 A |
|
age |
1.14 |
1.64 |
2.14 |
2.64 |
3.14 |
||
|
CPUE |
111 |
67 |
40 |
24 |
15 |
||
|
cohort |
age |
CPUE |
|
|
|
|
|
|
1983 S |
0.64 |
182 |
0.99 |
1.00 |
1.01 |
1.01 |
1.00 |
|
1982 A |
1.14 |
111 |
------ |
1.03 |
1.02 |
1.02 |
1.00 |
|
1982 S |
1.64 |
67 |
------ |
------ |
1.03 |
1.03 |
1.00 |
|
1981 A |
2.14 |
40 |
------ |
------ |
------ |
1.02 |
0.98 |
|
1981 S |
2.64 |
24 |
------ |
------ |
------ |
------ |
0.94 |
Exercise 4.4.3 The linearized catch curve based on age composition data
Worksheet 4.4.3
|
age |
year |
C(y, t, t + 1) |
ln C(y, t, t + 1) |
remarks |
|
0 |
1974 |
599 |
6.395 |
not used |
|
1 |
1975 |
860 |
6.757 |
|
|
2 |
1976 |
1071 |
6.976 |
|
|
3 |
1977 |
269 |
5.596 |
used in the analysis |
|
4 |
1978 |
69 |
4.234 |
|
|
5 |
1979 |
25 |
3.219 |
|
|
6 |
1980 |
8 |
2.079 |
|
|
7 |
1981 |
- |
- |
|
|
slope: b = -1.16 |
sb2 = [(sy/sx)2 - b2]/(n - 2) = 0.002330 | |||
|
sb = 0.0483 |
sb * tn-2 = 0.0483 * 4.30 = 0.21 Z = 1.16 ± 0.21 | |||
Fig. 18.4.4.3 The linearized catch curve based on age composition data (see Worksheet 4.4.3)

Exercise 4.4.5 The linearized catch curve based on length composition data Worksheet 4.4.5
|
L1 - L2 |
C(L1, L2) |
t(L1) |
D t |
|
|
z |
remarks |
|
7-8 |
11 |
0.452 |
0.0759 |
0.489 |
4.976 |
- |
not used |
|
8-9 |
69 |
0.527 |
0.0796 |
0.567 |
6.765 |
- |
|
|
9-10 |
187 |
0.607 |
0.0836 |
0.648 |
7.712 |
- |
|
|
10-11 |
133 |
0.691 |
0.0881 |
0.734 |
7.319 |
- |
|
|
11-12 |
114 |
0.779 |
0.0931 |
0.825 |
7.110 |
- |
|
|
12-13 |
261 |
0.872 |
0.0987 |
0.921 |
7.880 |
- |
|
|
13-14 |
386 |
0.971 |
0.1050 |
1.022 |
8.210 |
- |
|
|
14-15 |
445 |
1.076 |
0.112 |
1.13 |
8.286 |
- |
|
|
15-16 |
535 |
1.188 |
0.120 |
1.25 |
8.400 |
- |
used in analysis |
|
16-17 |
407 |
0.308 |
0.130 |
1.37 |
8.051 |
- |
|
|
17-18 |
428 |
1.438 |
0.141 |
1.51 |
8.019 |
1.43 |
|
|
18-19 |
338 |
1.579 |
0.154 |
1.65 |
7.693 |
1.60 |
|
|
19-20 |
184 |
1.733 |
0.170 |
1.82 |
6.987 |
2.27 |
|
|
20-21 |
73 |
1.903 |
0.190 |
2.00 |
5.953 |
3.07 |
|
|
21-22 |
37 |
2.092 |
0.214 |
2.20 |
5.152 |
3.45 |
|
|
22-23 |
21 |
2.307 |
0.246 |
2.43 |
4.446 |
3.54 |
|
|
23-24 |
19 |
2.553 |
0.290 |
2.69 |
4.183 |
3.30 |
|
|
24-25 |
8 |
2.843 |
0.352 |
3.01 |
3.124 |
3.20 |
|
|
25-26 |
7 |
3.195 |
0.448 |
3.40 |
2.749 |
- |
too close to L¥ |
|
26-27 |
2 |
3.643 |
0.617 |
3.92 |
1.176 |
- |
|
Details of the regression analyses:
|
length group |
slope |
number of observations |
Student's distrib. |
variance of slope |
stand. dev. of slope |
confidence limits of Z |
|
L1 - L2 |
Z |
n |
tn-2 |
sb2 |
sb |
Z ± tn-2 * sb |
|
15-16 |
- |
1 |
- |
- |
- |
- |
|
16-17 |
- |
2 |
- |
- |
- |
- |
|
17-18 |
1.43 |
3 |
12.70 |
0.59 |
0.7681 |
1.43 ± 9.75 |
|
18-19 |
1.60 |
4 |
4.30 |
0.12 |
0.3464 |
1.60 ± 1.49 |
|
19-20 |
2.27 |
5 |
3.18 |
0.156 |
0.3950 |
2.27 ± 1.26 |
|
20-21 |
3.07 |
6 |
2.78 |
0.228 |
0.4475 |
3.07 ± 1.33 |
|
21-22 |
3.45 |
7 |
2.57 |
0.140 |
0.3742 |
3.45 ± 0.96 |
|
22-23 |
3.54 |
8 |
2.45 |
0.071 |
0.2665 |
3.54 ± 0.65 |
|
23-24 |
3.30 |
9 |
2.37 |
0.051 |
0.2258 |
3.30 ± 0.54 |
|
24-25 |
3.20 |
10 |
2.31 |
0.030 |
0.1732 |
3.20 ± 0.40 |
Fig. 18.4.4.5 The linearized catch curve based on length composition data (see Worksheet 4.4.5)

Fig. 18.4.4.6 The cumulated catch curve based on length composition data (Jones and van Zalinge method) (see Worksheet 4.4.6)

Exercise 4.4.6 The cumulated catch curve based on length composition data (the Jones and van Zalinge method)
Worksheet 4.4.6
|
L1 - L2 |
C(L1, L2) |
S C (L1, L¥ ) cumulated |
ln S C (L1, L¥ ) |
ln (L¥ - L1) |
Z/K |
remarks |
|
7-8 |
11 |
3665 |
8.207 |
3.100 |
- |
not used, not under full exploitation |
|
8-9 |
69 |
3654 |
8.204 |
3.054 |
- |
|
|
9-10 |
187 |
3585 |
8.185 |
3.006 |
- |
|
|
10-11 |
133 |
3398 |
8.131 |
2.955 |
- |
|
|
11-12 |
114 |
3265 |
8.091 |
2.901 |
- |
|
|
12-13 |
261 |
3151 |
8.055 |
2.845 |
- |
|
|
13-14 |
386 |
2890 |
7.969 |
2.785 |
- |
|
|
14-15 |
445 |
2504 |
7.825 |
2.721 |
- |
|
|
15-16 |
535 |
2059 |
7.630 |
2.653 |
- |
used in analysis |
|
16-17 |
407 |
1524 |
7.329 |
2.580 |
- |
|
|
17-18 |
428 |
1117 |
7.018 |
2.501 |
4.03 |
|
|
18-19 |
338 |
689 |
6.565 |
2.416 |
4.56 |
|
|
19-20 |
184 |
351 |
5.861 |
2.322 |
5.28 |
|
|
20-21 |
73 |
167 |
5.118 |
2.219 |
5.81 |
|
|
21-22 |
37 |
94 |
4.543 |
2.104 |
5.86 |
|
|
22-23 |
21 |
57 |
4.043 |
1.974 |
5.62 |
|
|
23-24 |
19 |
36 |
3.584 |
1.825 |
5.25 |
|
|
24-25 |
8 |
17 |
2.833 |
1.649 |
5.00 |
|
|
25-26 |
7 |
9 |
2.197 |
1.435 |
- |
too close to L¥ |
|
26-27 |
2 |
2 |
0.693 |
1.163 |
- |
|
Details of the regression analyses:
|
length group |
slope |
number of obs. |
Student's distrib. |
variance of slope |
stand. dev. of slope |
confidence limits of Z |
|
L1 - L2 |
Z |
n |
tn-2 |
sb2 |
sb |
Z ± K * tn-2 * sb |
|
15-16 |
- |
1 |
- |
- |
- |
- |
|
16-17 |
- |
2 |
- |
- |
- |
- |
|
17-18 |
2.44 |
3 |
12.70 |
0.00289 |
0.05376 |
2.44 ± 0.41 |
|
18-19 |
2.77 |
4 |
4.30 |
0.858 |
0.2929 |
2.77 ± 0 76 |
|
19-20 |
3.20 |
5 |
3.18 |
0.169 |
0.4111 |
3.20 ± 0.79 |
|
20-21 |
3.52 |
6 |
2.78 |
0.141 |
0.3755 |
3.52 ± 0.63 |
|
21-22 |
3.55 |
7 |
2.57 |
0.064 |
0.2530 |
3.55 ± 0.39 |
|
22-23 |
3.41 |
8 |
2.45 |
0.045 |
0.2121 |
3.41 ± 0.32 |
|
23-24 |
3.20 |
9 |
2.37 |
0.056 |
0.2366 |
3.20 ± 0.34 |
|
24-25 |
3.03 |
10 |
2.31 |
0.045 |
0.2121 |
3.03 ± 0.30 |
Exercise 4.4.6a The Jones and van Zalinge method applied to shrimp
Worksheet 4.4.6a
|
carapace length mm |
numbers landed/year |
cumulated numbers/year |
|
|
|
remarks |
|
L1 - L2 |
C (L1, L2) |
S C (L1, L¥ ) |
ln S C (L1, L¥ ) |
ln (L¥ - L1) |
Z/K |
|
|
11.18-18.55 |
2.81 |
18.16 |
2.899 |
3.592 |
- |
not used |
|
18.55-22.15 |
1.30 |
15.35 |
2.731 |
3.366 |
- |
|
|
22.15-25.27 |
2.96 |
14.05 |
2.643 |
3.233 |
- |
|
|
25.27-27.58 |
3.18 |
11.09 |
2.406 |
3.101 |
- |
used in analysis |
|
27.58-29.06 |
2.00 |
7.91 |
2.068 |
2.992 |
- |
|
|
29.06-30.87 |
1.89 |
5.91 |
1.777 |
2.915 |
3.36 |
|
|
30.87-33.16 |
1.78 |
4.02 |
1.391 |
2.811 |
3.52 |
|
|
33.16-36.19 |
0.98 |
2.24 |
0.806 |
2.663 |
3.68 |
|
|
36.19-40.50 |
0.63 |
1.26 |
0.231 |
2.426 |
3.32 |
|
|
40.50-47.50 |
0.63 |
0.63 |
-0.462 |
1.946 |
too close to L¥ | |
Details of the regression analysis:
|
lower length |
slope |
number of obs. |
Student's distrib. |
variance of slope |
stand. dev. of slope |
confidence limits of slope |
|
L1 |
Z/K |
n |
tn-2 |
sb2 |
sb |
Z/K ± tn-2 * sb |
|
29.06 |
3.36 |
3 |
12.70 |
0.0354 |
0.1882 |
3.36 ± 2.39 |
|
30.87 |
3.52 |
4 |
4.30 |
0.0143 |
0.1196 |
3.52 ± 0.51 |
|
33.16 |
3.68 |
5 |
3.18 |
0.0096 |
0.0980 |
3.68 ± 0.31 |
|
36.19 |
3.32 |
6 |
2.78 |
0.0224 |
0.1497 |
3.32 ± 0.42 |
Fig. 18.4.4.6A Cumulated catch curve based on industrial shrimp fisheries in Kuwait. Data source: Jones and van Zalinge, 1981 (see Worksheet 4.4.6a)

Exercise 4.5.1 Beverton and Holt's Z-equation based on length data (applied to shrimp)
Worksheet 4.5.1
|
A |
B |
C |
D |
E |
F |
G |
H |
|
|
carapace length group |
numbers landed/year |
cumulated catch |
mid-length |
*) |
*) |
*) |
*) |
remarks |
|
L' (L1) - L2 |
C (L1, L2) |
S C (L1, L¥ ) |
|
|
|
|
Z/K |
|
|
11.18-18.55 |
2.81 |
18.16 |
14.87 |
41.77 |
478.56 |
26.35 |
1.39 |
not used |
|
18.55-22.15 |
1.30 |
15.35 |
20.35 |
26.46 |
436.79 |
28.46 |
1.92 |
|
|
22.15-25.27 |
2.96 |
14.05 |
23.71 |
70.18 |
410.33 |
29.21 |
2.59 |
|
|
25.27-27.58 |
3.18 |
11.09 |
26.43 |
84.03 |
340.15 |
30.67 |
3.12 |
|
|
27.58-29.06 |
2.00 |
7.91 |
28.32 |
56.64 |
256.12 |
32.38 |
3.15 |
|
|
29.06-30.87 |
1.89 |
5.91 |
29.97 |
56.63 |
199.48 |
33.75 |
2.93 |
|
|
30.87-33.16 |
1.78 |
4.02 |
32.02 |
56.99 |
142.85 |
35.53 |
2.57 |
|
|
33.16-36.19 |
0.98 |
2.24 |
34.68 |
33.98 |
85.86 |
38.33 |
1.77 | |
|
36.19-40.50 |
0.63 |
1.26 |
38.35 |
24.16 |
51.88 |
41.17 |
1.27 |
numbers too low |
|
40.50-47.50 |
0.63 |
0.63 |
44.00 |
27.72 |
27.72 |
44.00 |
1.00 |
|
Exercise 4.5.4 The Powell-Wetherall method
Worksheet 4.5.4
|
A |
B |
C |
D *) |
E *) |
F *) |
G *) |
H *) |
|
L' (L1) - L2 |
C (L1, L2) (% catch) |
|
S C(L',¥) |
|
|
|
|
|
(x) |
|
|
|
|
|
|
(y) |
|
14-15 |
1.8 |
14.5 |
100.1 |
26.10 |
2086.95 |
20.849 |
6.849 |
|
15-16 |
3.4 |
15.5 |
98.3 |
52.70 |
2060.85 |
20.965 |
5.965 |
|
16-17 |
5.8 |
16.5 |
94.9 |
95.70 |
2008.15 |
21.161 |
5.161 |
|
17-18 |
8.4 |
17.5 |
89.1 |
147.00 |
1912.45 |
21.646 |
4.464 |
|
18-19 |
9.1 |
18.5 |
80.7 |
168.35 |
1765.45 |
21.877 |
3.877 |
|
19-20 |
10.2 |
19.5 |
71.6 |
198.90 |
1597.10 |
22.306 |
3.306 |
|
20-21 *) |
14.3 |
20.5 |
61.4 |
293.15 |
1398.20 |
22.772 |
2.772 |
|
21-22 *) |
13.7 |
21.5 |
47.1 |
294.55 |
1105.10 |
23.463 |
2.463 |
|
22-23 *) |
10.0 |
22.5 |
33.4 |
225.00 |
810.50 |
24.266 |
2.266 |
|
23-24 *) |
6.3 |
23.5 |
23.4 |
148.05 |
585.50 |
25.021 |
2.021 |
|
24-25 *) |
6.4 |
24.5 |
17.1 |
156.80 |
437.45 |
25.582 |
1.582 |
|
25-26 *) |
5.3 |
25.5 |
10.7 |
135.15 |
280.65 |
26.229 |
1.229 |
|
26-27 *) |
3.3 |
26.5 |
5.4 |
87.45 |
145.5 |
26.944 |
0.944 |
|
27-28 *) |
1.8 |
27.5 |
2.1 |
49.50 |
58.05 |
27.643 |
0.643 |
|
28-29 *) |
0.3 |
28.5 |
0.3 |
8.55 |
8.55 |
28.500 |
0.500 |
|
b (slope) = -0.2997 |
a (intercept) = 8.795 | ||||||
|
Z/K = -(1 +b)/b = 2.337 |
L¥ = -a/b = 29.35 | ||||||
|
*) Considered fully recruited (n = 9) | |||||||
Comment:
Back in 1974, when Munro (1983) reported on the grunts, it was not easy to estimate L¥ (ELEFAN etc. was not available). The Ford-Walford plot resulted in almost parallel lines for all species and, consequently, could not produce reliable estimates of their L¥ . Based on modal progression analysis, Munro instead, obtained by trial-and-error, the value of L¥ which seemed to produce a straight line in the von Bertalanffy plot. The result was L¥ = 40 cm producing K = 0.26 per year. Using L' = 20 cm he then obtained Z/K = (40 - 22.772)/2.772 = 6.2 from Beverton and Holt's formula. (This estimate represents the straight line on the plot that connects the L' = 20 cm point with an x-intercept of L¥ = 40 cm, i.e. a line with slope b = -(1 + Z/K)-1 = -0.14.) Thus, Munro obtained Z = 6.2 * 0.26 = 1.6 per year. However, a L¥ » 30 cm changes Munro's MPA somewhat and using his procedure one cannot reject L¥ » 30 cm and K » 0.5 per year. Using our results we then obtain Z = 2.34 * 0.5 = 1.17 per year.
Exercise 4.6 Plot of Z on effort (estimation of M and q)
Worksheet 4.6
|
year |
effort |
mean length |
|
|
|
*) |
|
|
|
1966 |
2.08 |
15.7 |
1.97 |
|
1967 |
2.80 |
15.5 |
2.05 |
|
1968 |
3.50 |
16.1 |
1.82 |
|
1969 |
3.60 |
14.9 |
2.32 |
|
1970 |
3.80 |
14.4 |
2.58 |
|
1071 |
no data | ||
|
1972 |
no data | ||
|
1973 |
9.94 |
12.8 |
3.74 |
|
1974 |
6.06 |
12.8 |
3.74 |
|
*) in millions of trawling hours | |||
L¥ = 29.0 cm
K = 1.2 per year
Lc = 7.6 cm
a) Based on data for the years 1966-1970:
slope: q = 0.23 ± 0.66
sq2 = 0.0424
sq = 0.206
t3 * sq = 3.18 * 0.206 = 0.66intercept: M = 1.41 ± 2.11
sM2 = 0.439
sM = 0.663
t3 * sM = 3.18 * 0.663 = 2.11
Both confidence intervals contain 0 and negative values which makes no biological sense. The variation in effort is too small to support a dependable regression analysis.
b) Based on data for the years 1966-1974:
slope: q = 0.27 ± 0.17
sq2 = 0.00429
sq = 0.0655
t5 * sq = 2.57 * 0.0655 = 0.17intercept: M = 1.39 ± 0.87
sM2 = 0.115
sM = 0.339
t5 * sM = 2.57 * 0.339 = 0.87
Fig. 18.4.6 Plot of Z on effort, to estimate M and q of Priacanthus sp. Data source: Boonyubol and Hongskul, 1978 (see Worksheet 4.6)

Exercise 5.2 Age-based cohort analysis (Pope's cohort analysis)
a) terminal
F = F6 = 1.0
C6 = 8

|
C5 = 25 |
N5 = 44.4 |
F5 = 0.97 |
|
C4 = 69 |
N4 = 130.4 |
F4 = 0.88 |
|
C3 = 269 |
N3 = 456.6 |
F3 = 1.05 |
|
C2 = 1071 |
N2 = 1741.3 |
F2 = 1.14 |
|
C1 = 860 |
N1 = 3077.3 |
F1 = 0.37 |
|
C0 = 599 |
N0 = 4420.7 |
F0 = 0.16 |
b) terminal
F = F6 = 2.0
C6 = 8

|
C5 = 25 |
N5 = 39.7 |
F5 = 1.18 |
|
C4 = 69 |
N4 = 124.8 |
F4 = 0.94 |
|
C3 = 269 |
N3 = 449.7 |
F3 = 1.08 |
|
C2 = 1071 |
N2 = 1732.9 |
F2 = 1.15 |
|
C1 = 860 |
N1 = 3067.3 |
F1 = 0.37 |
|
C0 = 599 |
N0 = 4408.0 |
F0 = 0.16 |
Fig. 18.5.2 Pope's (age-based) cohort analysis of whiting, with different values of terminal F, to demonstrate VPA convergence. Data source: ICES, 1981

Exercise 5.3 Jones' length-based cohort analysis
Worksheet 5.3
|
length group |
natural mortality factor |
number caught (mill.) |
number of survivors |
exploitation rate |
fishing mortality |
total mortality |
|
L1 - L2 |
H(L1, L2) |
C(L1, L2) |
N(L1) |
F/Z |
F |
Z |
|
11.18-18.55 |
1.1854 |
2.81 |
119.82 |
0.08 |
0.32 |
4.22 |
|
18.55-22.15 |
1.1047 |
1.30 |
82.90 |
0.08 |
0.34 |
4.24 |
|
22.15-25.27 |
1.1035 |
2.96 |
66.75 |
0.20 |
0.99 |
4.89 |
|
25.27-27.58 |
1.0858 |
3.18 |
52.13 |
0.29 |
1.62 |
5.52 |
|
27.58-29.06 |
1.0596 |
2.00 |
41.29 |
0.31 |
1.77 |
5.67 |
|
29.06-30.87 |
1.0806 |
1.89 |
34.89 |
0.28 |
1.51 |
5.41 |
|
30.87-33.16 |
1.1175 |
1.78 |
28.13 |
0.25 |
1.28 |
5.18 |
|
33.16-36.19 |
1.1949 |
0.98 |
20.93 |
0.14 |
0.63 |
4.53 |
|
36.19-40.50 |
1.4331 |
0.63 |
13.84 |
0.08 |
0.36 |
4.26 |
|
40.50-47.50 |
- |
0.63 |
6.30 |
0.10 |
0.43 *) |
4.33 |
|
*) F (40.50 - 47.50) = 3.9 * 0.1/(1 - 0.1) = 0.43 | ||||||
The cumulated catch curve (Exercise 4.4.6a) gave a Z/K value of about 3.
From this we have Z = 3 * 2.6 = 7.8; F = Z-M = 7.8-3.9 = 3.9; exploitation rate, F/Z = 3.9/7.8 = 0.5
Exercise 6.1 A mathematical model for the selection ogive
L50% = 13.6 cm
S1 = 13.6 * ln (3)/(14.6 - 13.6) = 14.941
L75% = 14.6 cm
S2 = ln (3)/(14.6 - 13.6) = 1.0986
S (L) = 1/[1 + exp(14.941 - 1.0986 * L)]
|
L |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
S(L) |
0.05 |
0.15 |
0.34 |
0.61 |
0.82 |
0.93 |
0.98 |
0.99 |
Fig. 18.6.1 Length-based selection ogive

Exercise 6.5 Estimation of the selection ogive from a catch curve
Worksheet 6.5
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
|
length group |
t |
D t |
C(L1, L2) |
ln (C/D t) |
St obs. |
ln (1/S - 1) |
est. |
remarks |
|
|
(x) |
|
|
|
|
(y) |
|
|
|
6-7 |
0.56 |
0.102 |
3 |
3.38 |
0.0001 |
9.07 |
- |
not used |
|
7-8 |
0.67 |
0.109 |
143 |
7.18 |
0.0081 |
4.81 |
0.02 |
used to estimate St |
|
8-9 |
0.78 |
0.116 |
271 |
7.76 |
0.0229 |
3.75 |
0.02 |
|
|
9-10 |
0.90 |
0.125 |
318 |
7.86 |
0.041 |
3.15 |
0.04 |
|
|
10-11 |
1.03 |
0.134 |
416 |
8.04 |
0.087 |
2.58 |
0.08 |
|
|
11-12 |
1.17 |
0.146 |
488 |
8.11 |
0.168 |
1.60 |
0.17 |
|
|
12-13 |
1.32 |
0.160 |
614 |
8.25 |
0.362 |
0.67 |
0.34 |
|
|
13-14 |
1.49 |
0.177 |
613 |
8.15 |
0.666 |
-0.69 |
0.59 |
used to estimate Z (see Table 4.4.5.1) |
|
14-15 |
1.67 |
0.197 |
493 |
7.83 |
1.020 |
- |
0.81 |
|
|
15-16 |
1.88 |
0.223 |
278 |
7.13 |
- |
- |
0.94 |
|
|
16-17 |
2.12 |
0.257 |
93 |
5.89 |
- |
- |
0.99 |
|
|
17-18 |
2.40 |
0.303 |
73 |
5.48 |
- |
- |
1.00 |
|
|
18-19 |
2.74 |
0.370 |
7 |
2.94 |
- |
- |
1.00 |
|
|
19-20 |
3.15 |
0.473 |
2 |
1.44 |
- |
- |
1.00 |
|
|
20-21 |
3.70 |
0.659 |
2 |
1.11 |
- |
- |
1.00 |
not used too close to L¥ |
|
21-22 |
4.53 |
1.094 |
0 |
- |
- |
- |
1.00 |
|
|
22-23 |
6.19 |
4.094 |
1 |
-1.40 |
- |
- |
1.00 |
|
|
23-24 |
- |
- |
1 |
- |
- |
- |
1.00 |
|
|
K = 0.59 per year, Selection regression: a = T1 = 8.7111 | ||||||||
Exercise 6.7 Using a selection curve to adjust catch samples
L50% = 13.6 cm
S1 = 13.6 * ln (3)/(14.6 - 13.6) = 14.941
L75% = 14.6 cm
S2 = ln (3)/(14.6 - 13.6) = 1.0986
SL = 1/[1 + exp (14.941 - 1.0986 * L)]
Worksheet 6.7
|
length group |
mid point |
observed biased sample |
selection ogive |
estimated unbiased sample |
|
6-7 |
6.5 |
3 |
0.00041 |
7326a) |
|
7-8 |
7.5 |
143 |
0.00123 |
116491 |
|
8-9 |
8.5 |
271 |
0.00367 |
73769 |
|
9-10 |
9.5 |
318 |
0.01094 |
29067 |
|
10-11 |
10.5 |
416 |
0.03212 |
12952 |
|
11-12 |
11.5 |
488 |
0.09054 |
5390 |
|
12-13 |
12.5 |
614 |
0.2300 |
2670 |
|
13-14 |
13.5 |
613 |
0.4726 |
1297 |
|
14-15 |
14.5 |
493 |
0.7288 |
676 |
|
15-16 |
15.5 |
278 |
0.890 |
312 |
|
16-17 |
16.5 |
93 |
0.960 |
97 |
|
17-18 |
17.5 |
73 |
0.986 |
74 |
|
18-19 |
18.5 |
7 |
0.995 |
7 |
|
19-20 |
19.5 |
2 |
0.998 |
2 |
|
20-21 |
20.5 |
2 |
0.999 |
2 |
|
21-22 |
21.5 |
0 |
1.000 |
0 |
|
22-23 |
22.5 |
1 |
1.000 |
1 |
|
23-24 |
23.5 |
1 |
1.000 |
1 |
|
a) 3/0.00041 = 7326 | ||||
Fig. 18.6.7 Biased sample of goatfish and estimated unbiased sample, corrected for selectivity. Data source: Ziegler, 1979. (see Worksheet 6.7)

Exercise 7.2 Stratified random sampling versus simple random sampling and proportional sampling
Worksheet 7.2
|
stratum |
s (j) |
s (j)2 |
N (j) |
|
|
|
1 large |
28.906 |
835.57 |
10 |
25413 |
423 |
|
2 medium |
8.569 |
73.43 |
30 |
9091 |
457 |
|
3 small |
2.809 |
7.89 |
60 |
1524 |
252 |
|
total |
|
|
100 |
36028 |
1132 |
|
| |||||
|
a) Simple random sampling
b) Proportional sampling
| |||||
c) Optimum stratified sampling
|
stratum |
s(j) * N(j) |
|
|
|
1 large |
289.06 |
0.40 |
8 |
|
2 medium |
257.07 |
0.36 |
7 |
|
3 small |
168.55 |
0.24 |
5 |
|
Total |
714.68 |
1.00 |
n = 20 |
|
| |||
|
Comparison of results | |||
|
|
random |
proportional |
optimum |
|
|
3.06 |
2.10 |
1.20 |
|
allocation per stratum |
|
|
|
|
1 large |
? |
2 |
8 |
|
2 medium |
? |
6 |
7 |
|
3 small |
? |
12 |
5 |
Exercise 8.3 The yield per recruit model of Beverton and Holt (yield per recruit, biomass per recruit as a function of F)
Worksheet 8.3
|
|
Tc = Tr = 0.2 |
Tc = 0.3 |
Tc = 1.0 | |||
|
F |
Y/R |
B/R |
Y/R |
B/R |
Y/R |
B/R |
|
0.0 |
0.00 |
8.28 |
0.00 |
8.00 |
0.00 |
4.53 |
|
0.2 |
1.36 |
6.81 |
1.33 |
6.67 |
0.79 |
3.96 |
|
0.4 |
2.28 |
5.71 |
2.26 |
5.65 |
1.41 |
3.51 |
|
0.6 |
2.91 |
4.85 |
2.92 |
4.86 |
1.89 |
3.15 |
|
0.8 |
3.34 |
4.18 |
3.39 |
4.24 |
2.28 |
2.85 |
|
1.0 |
3.64 |
3.64 |
3.73 |
3.73 |
2.60 |
2.60 |
|
1.2 |
3.84 |
3.20 |
3.98 |
3.31 |
2.86 |
2.39 |
|
1.4 |
3.97 |
2.84 |
4.15 |
2.97 |
3.08 |
2.20 |
|
1.6 |
4.06 |
2.54 |
4.28 |
2.68 |
3.27 |
2.05 |
|
1.8 |
4.11 |
2.28 |
4.38 |
2.43 |
3.43 |
1.91 |
|
2.0 |
4.14 |
2.07 |
4.44 |
2.22 |
3.57 |
1.79 |
|
2.2 |
4.15 * |
1.88 |
4.49 |
2.04 |
3.69 |
1.68 |
|
2.4 |
4.14 |
1..73 |
4.51 |
1.88 |
3.80 |
1.58 |
|
2.6 |
4.13 |
1.59 |
4.53 |
1.74 |
3.89 |
1.50 |
|
2.8 |
4.10 |
1.47 |
4.54 |
1.62 |
3.98 |
1.42 |
|
3.0 |
4.08 |
1.36 |
4.54 * |
1.51 |
4.05 |
1.35 |
|
3.5 |
4.00 |
1.14 |
4.52 |
1.29 |
4.21 |
1.20 |
|
4.0 |
3.91 |
0.98 |
4.48 |
1.12 |
4.33 |
1.08 |
|
4.5 |
3.82 |
0.85 |
4.44 |
0.99 |
4.42 |
0.98 |
|
5.0 |
3.74 |
0.75 |
4.39 |
0.88 |
4.50 |
0.90 |
|
100.0 |
2.39 |
0.02 |
3.35 |
0.03 |
5.15 * |
0.05 |
|
*) MSY/R | ||||||
MSY increases when Tc increases, because more fish survive to a large size before they are caught. From age 0.2 years to age 1.0 years the biomass production caused by individual growth exceeds the loss caused by the death process. This, of course, is not true for any high value of Tc. If, for example, Tc would be larger than the lifespan of the species in question, no fish would be caught.
curve A: (Tc = 0.2) MSY/R = 4.15 (indicated by "*" in the Table)
curve B: (Tc = 0.3) MSY/R = 4.54
curve C: (Tc = 1.0) MSY/R = 5.15
For F = 1 the Y/R is 3.64 (curve A), 3.73 (curve B) or 2.60 (curve C).
Thus, irrespective of the actual mesh size in use an increased yield is expected for an increase of effort (F).
The smaller the actual mesh size the smaller the gain in yield from an effort increment.
Exercise 8.4 Beverton and Holt's relative yield per recruit concept
Worksheet 8.4
|
|
Lc = 118 cm |
Lc = 150 cm |
|
|
E |
(Y/R)' |
(Y/R)' |
(F) |
|
0 |
0 |
0 |
0 |
|
0.1 |
0.019 |
0.022 |
0.020 |
|
0.2 |
0.035 |
0.043 |
0.045 |
|
0.3 |
0.048 |
0.062 |
0.077 |
|
0.4 |
0.059 |
0.079 |
0.120 |
|
0.5 |
0.067 |
0.093 |
0.180 = M |
|
0.6 |
0.071 |
0.105 |
0.270 |
|
0.7 |
0.071 *) |
0.112 |
0.42 |
|
0.8 |
0.068 |
0.116 |
0.72 |
|
0.9 |
0.063 |
0.117 *) |
1.62 |
|
1.0 |
0.056 |
0.114 |
¥ |
|
*) relative MSY/R | |||
Fig. 18.8.3 Yield per recruit and biomass per recruit curves as a function of F at different ages of first capture of ponyfish. Data source: Pauly, 1980

Fig. 18.8.4 Relative yield per recruit curves a a function of exploitation rate (E) for two different values of 50% retention length of swordfish. Data source: Berkeley and Houde, 1980

Exercise 8.6 A predictive age-based model (Thompson and Bell analysis)
Worksheet 8.6
a. No change in fishing effort:
|
age group |
mean weight (g) |
beach seine mortality |
gill net mortality |
natural mortality |
total mortality |
stock number |
beach seine catch |
gill net catch |
beach seine yield |
gill net yield |
total yield |
|
t |
|
FB |
FG |
M |
Z |
'000 |
CB |
CG |
YB |
YG |
YB + YG |
|
0 |
8 |
0.05 |
0.00 |
2.00 |
2.05 |
1000 |
21.3 |
0 |
170 |
0 |
170 |
|
1 |
283 |
0.40 |
0.00 |
0.80 |
1.20 |
129 |
30.0 |
0 |
8486 |
0 |
8486 |
|
2 |
1155 |
0.10 |
0.19 |
0.30 |
0.59 |
39 |
2.9 |
5.7 |
3383 |
6428 |
9810 |
|
3 |
2406 |
0.01 |
0.59 |
0.20 |
0.80 |
21 |
0.15 |
8.7 |
356 |
21002 |
21358 |
|
4 |
3764 |
0.00 |
0.33 |
0.20 |
0.53 |
9.7 |
0 |
2.5 |
0 |
9312 |
9312 |
|
5 |
5046 |
0.00 |
0.09 |
0.20 |
0.29 |
5.7 |
0 |
0.44 |
0 |
2241 |
2241 |
|
6 |
6164 |
0.00 |
0.02 |
0.20 |
0.22 |
4.3 |
0 |
0.08 |
0 |
471 |
471 |
|
7 |
7090 |
0.00 |
0.00 |
0.20 |
0.20 |
3.4 |
0 |
0 |
0 |
0 |
0 |
|
total |
54.35 |
17.42 |
12395 |
39454 |
51848 | ||||||
b. Closure of the beach seine fishery:
|
age group |
mean weight (g) |
beach seine mortality |
gill net mortality |
natural mortality |
total mortality |
stock number |
beach seine catch |
gill net catch |
beach seine yield |
gill net yield |
total yield |
|
t |
|
FB |
FG |
M |
Z |
'000 |
CB |
CG |
YB |
YG |
YB + YG |
|
0 |
8 |
0.00 |
0.00 |
2.00 |
2.00 |
1000 |
0 |
0 |
0 |
0 |
0 |
|
1 |
283 |
0.00 |
0.00 |
0.80 |
0.80 |
135 |
0 |
0 |
0 |
0 |
0 |
|
2 |
1155 |
0.00 |
0.19 |
0.30 |
0.49 |
61 |
0 |
6.9 |
0 |
10550 |
10550 |
|
3 |
2406 |
0.00 |
0.59 |
0.20 |
0.79 |
39 |
0 |
16.0 |
0 |
36560 |
36560 |
|
4 |
3764 |
0.00 |
0.33 |
0.20 |
0.53 |
17.8 |
0 |
4.6 |
0 |
16301 |
16301 |
|
5 |
5046 |
0.00 |
0.09 |
0.20 |
0.29 |
10.5 |
0 |
0.8 |
0 |
3923 |
3923 |
|
6 |
6164 |
0.00 |
0.02 |
0.20 |
0.22 |
7.8 |
0 |
0.14 |
0 |
824 |
824 |
|
7 |
7090 |
0.00 |
0.00 |
0.20 |
0.20 |
6.3 |
0 |
0 |
0 |
0 |
0 |
|
total |
0 |
28.44 |
0 |
68158 |
68158 | ||||||
Although total yield increased in the case of closure of the beach seine fishery, a closure of this fishery without considering the socio-economic aspects is not recommended.
Exercise 8.7 A predictive length-based model (Thompson and Bell analysis)
Worksheet 8.7
|
length class |
|
|
mean biomass |
catch |
yield |
value |
|
L1 - L2 |
F(L1, L2) |
N(L1) |
* D t |
C(L1, L2) |
(L1, L2) |
(L1, L2) |
|
10-15 |
0.03 |
1000 |
6.47 |
9.94 |
0.19 |
0.19 |
|
15-20 |
0.20 |
890.56 |
17.02 |
63.54 |
3.40 |
3.40 |
|
20-25 |
0.40 |
731.70 |
31.97 |
112.28 |
12.79 |
19.18 |
|
25-30 |
0.70 |
535.20 |
45.18 |
152.08 |
31.62 |
47.44 |
|
30-35 |
0.70 |
317.95 |
50.39 |
102.75 |
35.27 |
70.55 |
|
35-40 |
0.70 |
171.15 |
48.27 |
64.08 |
33.79 |
67.59 |
|
40 - L¥ |
0.70 |
79.60 |
61.10 |
55.72 |
42.77 |
85.55 |
|
Totals |
|
|
260.44 |
560.39 |
159.86 |
293.91 |
Exercise 8.7a A predictive length-based model (Yield curve, Thompson and Bell analysis)
Worksheet 8.7a
|
length class |
|
|
mean biomass |
catch |
yield |
value |
|
L1 - L2 |
F(L1, L2) |
N(L1) |
* D t |
C(L1, L2) |
(L1, L2) |
(L1, L2) |
|
10-15 |
0.06 |
1000 |
6.44 |
19.79 |
0.38 |
0.38 |
|
15-20 |
0.40 |
881.22 |
16.25 |
121.30 |
6.50 |
6.50 |
|
20-25 |
0.80 |
668.94 |
27.08 |
190.22 |
21.66 |
32.50 |
|
25-30 |
1.40 |
407.39 |
29.97 |
201.75 |
41.95 |
62.93 |
|
30-35 |
1.40 |
162.40 |
22.02 |
89.80 |
30.82 |
61.65 |
|
35-40 |
1.40 |
53.36 |
12.56 |
33.36 |
17.59 |
35.19 |
|
40 - L¥ |
1.40 |
12.84 |
5.80 |
10.57 |
8.12 |
16.24 |
|
Totals |
|
|
120.13 |
666.79 |
127.05 |
215.41 |
Fig. 18.8.7A Thompson and Bell analysis, prediction of mean biomass, yield and value (values for X = 1 and X = 2 correspond to those calculated on Worksheets 8.7 and 8.7a respectively)

Exercise 9.1 The Schaefer model and the Fox model *)
Worksheet 9.1
|
year |
yield (tonnes) headless |
effort |
Schaefer |
Fox |
|
i |
Y(i) |
f(i) |
Y/f |
ln (Y/f) |
|
1969 |
546.7 |
1224 |
447 |
6.103 |
|
1970 |
812.4 |
2202 |
369 |
5.911 |
|
1971 |
2493.3 |
6684 |
373 |
5.922 |
|
1972 |
4358.6 |
12418 |
351 |
5.861 |
|
1973 |
6891.5 |
16019 |
430 |
6.064 |
|
1974 |
6532.0 |
21552 |
303 |
5.714 |
|
1975 |
4737.1 |
24570 |
193 |
5.263 |
|
1976 |
5567.4 |
29441 |
189 |
5.242 |
|
1977 |
5687.7 |
28575 |
199 |
5.293 |
|
1978 |
5984.0 |
30172 |
198 |
5.288 |
|
mean value |
17286 |
305.2 |
5.666 | |
|
standard deviation |
11233 |
102.9 |
0.3558 | |
|
intercept (Schaefer: a, Fox: c) |
444.6 |
6.1508 | ||
|
slope (Schaefer: b, Fox: d) |
-0.008065 |
-0.000028043 | ||
|
variance of slope: |
2.361 * 10-6 |
2.7113 * 10-11 | ||
|
standard deviation of slope, sb |
0.0015364 |
0.000005207 | ||
|
Student's distribution t10-2 |
2.31 |
2.31 | ||
|
confidence limits of slope: |
|
| ||
|
b + tn-2 * sb |
upper |
-0.0045 |
-0.00001601 | |
|
b - tn-2 * sb |
lower |
-0.0116 |
-0.00004007 | |
|
variance of intercept: |
973.4 |
0.01152 | ||
|
standard deviation of intercept |
31.20 |
0.1073 | ||
|
confidence limits of intercept: |
|
| ||
|
a + tn-2 * sa |
upper |
517 |
6.40 | |
|
a - tn-2 * sa |
lower |
372 |
5.90 | |
|
MSY Schaefer: -a2/(4b) |
6128 tonnes |
| ||
|
MSY Fox: -(1/d) * exp (c - 1) |
|
6154 tonnes | ||
|
fMSY Schaefer: -a/(2b) |
27565 boat days |
| ||
|
fMSY FOX: -1/d |
|
35660 boat days | ||
|
*) a, b replaced by c, d for the Fox-model | ||||
Worksheet 9.1a
|
f |
Schaefer |
Fox |
|
5000 |
2021 |
2039 |
|
10000 |
3640 |
3544 |
|
15000 |
4854 |
4620 |
|
20000 |
5666 |
5354 |
|
25000 |
6074 |
5817 |
|
fMSY |
6128 = MSY |
|
|
30000 |
6080 |
6068 |
|
35000 |
5681 |
6153 |
|
fMSY |
|
6154 = MSY |
|
40000 |
4880 |
6112 |
|
45000 |
3675 |
5976 |
Exercise 13.8 The swept area method, precision of the estimate of biomass, estimation of MSY and optimal allocation of hauls
Worksheet 13.8
STRATUM 1:
|
|
CPUE |
VESSEL |
TRAWL |
CURRENT |
DIST |
AREA |
CPUA | ||
|
haul no. |
Cw/t |
speed |
course |
w. spr. |
speed |
dir. deg. |
nm. |
swept |
Cw/a = Ca |
|
i |
|
VS |
dir V |
h * X2 |
CS |
dir C |
D |
a |
|
|
1 |
7.0 |
2.8 |
220 |
18 |
0.5 |
90 |
2.508 |
.02438 |
287.2 |
|
2 |
7.0 |
3.0 |
210 |
16 |
0.5 |
180 |
3.442 |
.02974 |
235.4 |
|
3 |
5.0 |
3.0 |
200 |
17 |
0.3 |
135 |
3.139 |
.02881 |
173.6 |
|
4 |
4.0 |
3.0 |
180 |
18 |
0.4 |
230 |
3.271 |
.03180 |
125.8 |
|
5 |
1.0 |
3.0 |
90 |
17 |
0.5 |
270 |
2.500 |
.02295 |
43.6 |
|
6 |
4.0 |
3.0 |
45 |
18 |
0.4 |
160 |
2.854 |
.02774 |
144.2 |
|
7 |
9.0 |
3.5 |
25 |
18 |
0.4 |
200 |
3.102 |
.03015 |
298.5 |
|
8 |
0.0 |
3.0 |
210 |
18 |
0.3 |
300 |
3.015 |
.02930 |
0.0 |
|
9 |
0.0 |
3.5 |
0 |
18 |
0.4 |
0 |
3.900 |
.03790 |
0.0 |
|
10 |
14.0 |
2.8 |
45 |
18 |
0.6 |
0 |
3.252 |
.03161 |
442.9 |
|
11 |
8.0 |
3.0 |
120 |
18 |
0.3 |
300 |
2.700 |
.02624 |
304.9 |
|
| |||||||||
STRATUM 2:
|
|
CPUE |
VESSEL |
TRAWL |
CURRENT |
DIST |
AREA |
CPUA | ||
|
haul no. |
Cw/t |
speed |
course |
w. spr. |
speed |
dir. deg. |
nm. |
swept |
Cw/a = Ca |
|
i |
|
VS |
dir V |
h * X2 |
CS |
dir C |
D |
a |
|
|
12 |
42.0 |
4.0 |
30 |
17 |
0.5 |
160 |
3.698 |
.03395 |
1237.1 |
|
13 |
98.0 |
3.3 |
215 |
17 |
0.4 |
90 |
3.088 |
.02835 |
3457.3 |
|
14 |
223.0 |
3.9 |
30 |
17 |
0.0 |
0 |
3.900 |
.03580 |
6229.2 |
|
15 |
59.0 |
3.8 |
35 |
17 |
0.3 |
180 |
3.558 |
.03266 |
1806.3 |
|
16 |
32.0 |
3.5 |
210 |
17 |
0.5 |
270 |
3.775 |
.03465 |
923.5 |
|
17 |
6.0 |
2.8 |
210 |
17 |
0.5 |
330 |
2.587 |
.02374 |
252.7 |
|
18 |
66.0 |
3.8 |
45 |
17 |
0.5 |
30 |
4.285 |
.03933 |
1678.0 |
|
19 |
60.0 |
4.0 |
30 |
18 |
0.5 |
180 |
3.576 |
.03475 |
1726.5 |
|
20 |
48.0 |
4.0 |
210 |
18 |
0.5 |
180 |
4.440 |
.04315 |
1112.3 |
|
21 |
52.0 |
3.8 |
20 |
18 |
0.4 |
180 |
3.427 |
.03331 |
1561.3 |
|
22 |
48.0 |
4.0 |
30 |
18 |
0.5 |
190 |
3.534 |
.03435 |
1397.4 |
|
23 |
18.0 |
3.0 |
210 |
18 |
0.3 |
190 |
3.284 |
.03192 |
563.9 |
|
| |||||||||
|
confidence limits of | ||||||
|
stratum |
number of hauls |
|
s |
s/Ö n |
Student's distr. |
confidence limits for |
|
1 |
11 |
186.9 |
141.6 |
42.7 |
2.23 |
[92, 282] |
|
2 |
12 |
1828.8 |
1597.5 |
461.2 |
2.20 |
[814, 2843] |
Mean biomass for total area:
Area of stratum 1 and 2 combined: A = A1 + A2 = 24 + 53 = 77 sq.nm.

Total biomass of whole area: B(A) = 1317.0 * 77/0.5 = 202818 kg, say 203 tons
From Eq. 9.3.1: MSY = 0.5 * 0.6 * 203 = 61 tons/year.
Worksheet 13.8a (for plotting graph maximum relative error)
|
number of hauls |
tn-1 |
stratum 1 |
stratum 2 |
|
n |
|
e a) |
e b) |
|
5 |
2.78 |
0.94 |
1.09 |
|
10 |
2.26 |
0.54 |
0.62 |
|
20 |
2.09 |
0.36 |
0.41 |
|
50 |
2.01 |
0.22 |
0.25 |
|
100 |
1.98 |
0.15 |
0.17 |
|
200 |
1.97 |
0.11 |
0.12 |
Worksheet 13.8b (optimum allocation)
|
|
|
|
|
|
|
|
stratum |
s |
A |
A * s |
A * s/S A * s |
200*A*s\S A*s |
|
1 |
141.6 |
24 |
3398 |
0.039 |
8 hauls |
|
2 |
1597.5 |
53 |
84670 |
0.961 |
192 hauls |
|
Total |
|
|
88068 |
|
200 hauls |
In Part 1: Manual, a selection of methods for fish stock assessment are described in detail, with examples of calculations. Special emphasis is placed on methods based on the analysis of length frequencies. After a short introduction to statistics, the manual covers the estimation of growth parameters and mortality rates; virtual population methods, including age-based and length-based cohort analysis; gear selectivity; sampling; prediction models, including Beverton and Holt's yield-per-recruit model and Thompson and Bell's model; surplus production models; multispecies and multifleet problems; the assessment of migratory stocks; plus a discussion on stock/recruitment relationships and demersal trawl surveys, including the swept-area method. The manual ends with a review of stock assessment, giving an indication of methods to be applied at different levels of availability of input data, a review of relevant computer programs produced by or in cooperation with FAO, and a list of references. In Part 2: Exercises, a number of exercises are given with solutions. These exercises are directly related to the various chapters and sections of the manual.