APPENDIX II: FITTING A MATHEMATICAL MODEL TO THE ACOUSTIC DATA OF LAKE TANGANYIKA¹

¹ Bazigos, G.P. (1975), The statistical efficiency of echo-surveys with special reference to Lake Tanganiyka, FAO Fish.Tech.Pap., (139):52 p.

The main objective of this analysis was to attempt to fit a mathematical model to the empirical data of the conducted acoustic survey in Lake Tanganyika in order to explain the spatial distribution of the fish stocks, and to obtain a suitable transformation to normalize the frequency distribution of the data in order to perform further statistical analysis such as regression and analysis of variance.

Methodology

For this analysis Stratum 2, the largest stratum of the survey area was selected (see map, p. 135). The basic variable considered was y = integrator reading. Also, it was recognized that the fish move in schools in daytime and in layers at night. Hence, daytime and night-time data were treated separately.

Night data

Firstly, the night data were arranged in a frequency distribution table. The sample mean (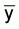) and variance (s²) were then computed. The purpose was to compare the magnitudes of the two statistics 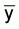and s², to indicate which theoretical distribution might be a suitable model. Now for this type of population, three mathematical distributions are possible models, namely Positive Binomial (s² < m), Poisson (s² = m), and Negative Binomial (s² > m), where m, s² are population mean and variance respectively; 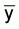was found to be 170.90, whilst s² was 141896.61. As 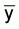and s² are unbiased estimates of the population mean (m) and variance (s²) and s² > 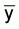, there is a strong indication that the Negative Binomial Distribution is the most probable model. The chi-squared “goodness-of-fit” test was applied to ascertain the adequacy of the model. The model was found to be adequate, the spatial dispersion of the population could be described as a contagious distribution or clumped distribution, (see Appendix I). The estimated value of the clumping coefficient was .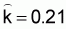

Logarithmic transformation

The next step was to find a suitable transformation to normalize the frequency distribution. Now for a Negative Binomial Distribution with k less than two, the usual transformation is the logarithmic transformation. In particular the zero counts in the data suggested the transformation z = log_e(y + 1) as the appropriate transformation for normality. To test the validity of this transformation the chi-squared “goodness-of-fit” test was applied. The transformed data were assumed to follow the normal distribution whose mean and variance were estimated by the corresponding sample values. The expected frequencies (f!) were obtained by considering the cumulative distribution tables of the normal distribution. The chi-squared statistic,

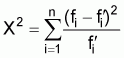
was then computed to be 28.11, where f_i = observed frequencies, and n = number of frequency classes. Now, under the hypothesis of normality the above statistic follows a chi-squared distribution with n-3 degrees of freedom (df). Now n = 32, therefore df = 29. But the tabulated value for 95 percent level of X²₍₂₉₎= 42.56. Hence, it is concluded that at 95 percent confidence level the normal distribution fits our empirical data adequately. Hence the recommended transformation is z = log_e(y + 1). The analysis was repeated for the daytime data and the Negative Binomial Distribution was again found to be the appropriate mathematical model. Again the transformation log(y + 1) was found to normalize the data. Except for two points out of 41 which could be treated as outliers all the remaining 39 points in the frequency distribution table satisfied the chi-squared criterion.

STRATUM 2 - NIGHT DATA

Mean

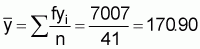
Sample variance

= negative binomial model

ACOUSTIC SURVEY - LAKE TANGANYIKA
STRATUM 2 - NIGHT DATA

f	y	y2	fy	fy2	z = loge(y+1)	z2f	zf
1	0	0	0	0	0.00	0.00	0.00
2	2	4	4	8	1.10	2.42	2.20
2	4	16	8	32	1.61	5. 18	3.22
1	5	25	5	25	1.79	3.20	1.79
1	6	36	6	36	1.95	3.80	1.95
2	7	49	14	98	2.08	8.33	4.16
2	10	100	20	200	2.40	11.52	4.80
1	11	121	11	121	2.48	6. 15	2.48
1	14	144	12	144	2.56	6.55	2.56
1	16	256	16	256	2.83	8.01	.2.83
1	20	400	20	400	3.04	9.24	3.04
2	28	784	56	1568	3.37	22.71	6.74
1	29	841	29	841	3.40	11.56	3.40
1	30	900	30	900	3.43	1 1.76	3.43
1	36	1296	36	1296	3.61	13.03	3.61
2	38	1444	76	2888	3.66	26.79	7.32
2	42	1764	84	3528	3.76	28. 14	7.52
2	48	2304	96	4608	3.89	30.13	7.78
1	52	2704	52	2704	3.97	15.76	3.97
1	55	3025	55	3025	4.03	16.24	4.03
1	71	5041	71	5041	4.28	18.32	4.28
1	72	5184	72	5184	4.29	18.33	4.29
1	94	8836	94	8836	4.55	20.70	4.55
2	105	11025	210	22050	4.66	43.42	9.32
1	304	92416	304	92416	5.72	32.72	5.72
1	310	96100	310	96100	5.74	32.95	5.74
1	366	133956	366	133956	5.91	34.93	5.91
1	450	202500	450	202500	6.11	37.33	6.11
1	470	220900	470	220900	6.15	37.82	6.15
1	880	774400	880	774400	6.78	45.97	6.78
1	1170	1368900	1170	1368900	7.06	49.34	7.06
1	1980	3920400	1980	3920400	8.44	71.23	8.44
Total n = 41						688.08	153.18

Log transformation: z = log_e(y+l)

ACOUSTIC SURVEY - LAKE TANGANYIKA
STRATUM 2 - NIGHT DATA

yi	fi	x	Fi(x)	nFi(x)			X2
0	1	-1.90	0.03	1.23	1.23	0.05	0.04
2	2	-1.31	0.10	4.10	2.87	0.76	0.26
4	2	-1.04	0.15	6.15	2.05	0.0025	0.00
5	1	-0.95	0.17	6.97	0.82	0.03	0.04
6	1	-0.86	0.19	7.79	0.82	0.03	0.04
7	2	-0.79	0.21	8.61	0.82	1.39	1.70
10	2	-0.62	0.27	11.07	2.46	0.2!	0.09
11	1	-0.58	0.28	11.48	0.41	0.35	0.85
12	1	-0.54	0.29	11.89	0.41	0.35	0.85
16	1	-0.39	0.35	14.35	2.46	2.13	0.87
20	1	-0.28	0.39	15.99	1.64	0.41	0.25
28	2	-0.1063	0.45	18.45	2.87	0.76	0.26
29	1	-0.0904	0.46	18.86	0.41	0.35	0.85
30	1	-0.07	0.47	19.27	0.41	0.35	0.85
36	1	0.02	0.51	20.91	1.64	0.41	0.25
38	2	0.05	0.52	21.32	0.41	2.53	6.17
42	2	0. 10	0.54	22. 14	0.82	1.39	1.70
48	2	0.17	0.57	23.37	1.23	0.59	0.48
52	1	0.21	0.58	23.78	0.41	0.35	0.85
55	1	0.25	0.60	24.60	0.82	0.03	0.04
71	1	0.3776	0.64	26.24	2.05	1.10	0.54
72	1	0.3829	0.65	26.65	0.41	0.35	0.85
94	1	0.5212	0.70	28.70	2.05	1.10	0.54
105	2	0.58	0.72	29.52	0.82	1.39	1.70
304	1	1.14	0.87	35.67	6. 15	26.52	4.31
310	1	1.1542	0.88	36.08	0.41	0.35	0.85
366	1	1.24	0.89	36.49	0.41	0.35	0.85
450	1	1.35	0.91	37.31	0.82	0.03	0.04
470	1	1.3723	0.92	37.72	0.41	0.35	0.85
880	1	1.71	0.96	39.36	1.64	0.41	0.25
1170	1	.86	0.97	39.77	0.41	0.35	0.85
1980	1	2.59	1.00	41.00	1.23	0.05	0.04

z = loge(y+1)

X2 = 28.11

No. of frequency classes - 32

No. of parameters estimated from N(m, s²) = 2

Therefore, d.f. = 32-2-1 = 29

Tabulated value of X²₍₂₉₎ at 95 percent level = 42.56

Hence normal distributions fit adequately at 95 percent confidence level

MATHEMATICAL MODEL FOR ACOUSTIC SURVEY OF LAKE TANGANYIKA
STRATUM 2 - DAY DATA

Frequency distribution of integrator value (y)

f	19	18	5	6	2	2	1	2	3	1	1	4	2
y	0	1	2	3	4	5	6	7	a	9	11	12	13

f	1	2	2	3	3	1	1	1	2	1	3	1	1
y	14	17	18	22	24	26	30	31	32	36	42	45	46

f	2	1	2		1	1	1	1	1	1		1
y	50	54	56		105	125	133	152	170	210		360

n = 102

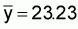
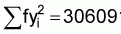
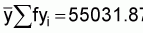
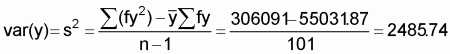
i.e. 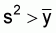= Negative binomial model

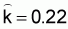Required transformation y + log(y+1)

ACOUSTIC SURVEY - LAKE TANGANYIKA
STRATUM 2 - DAY DATA

yi	fi	x	Fi(x)	nFi(xi)			X2
0	19	-1.26	0.10	10.20	10.20	77.44	7.59*
1	18	-0.82	0.20	20.40	10.20	60.84	5.96
2	5	-0.55	0.29	29.58	9.18	17.47	1.90
3	6	-0.37	0.36	36.72	7.14	1.30	0.18
4	2	-0.23	0.41	41.82	5.10	9.61	1.88
5	2	-0.11	0.46	46.92	5.10	9.61	1.88
6	1	-0.01	0.50	51.00	4.08	9.49	2.33
7	2	0.08	0.53	54.06	3.06	1.12	0.37
8	5	0.15	0.55	56.10	2.04	4.24	2.08
9	I	0.22	0.59	60.18	4.08	9.49	2.33
11	1	0.34	0.63	64.26	4.08	9.49	2.33
12	4	0.39	0.65	66.30	2.04	3.84	1.88
13	. 2	0.44	0.67	68.34	2.04	0.00	0.00
14	1	0.48	0.68	69.36	1.02	0.00	0.00
17	2	0.60	0.73	74.46	5.10	9.61	1.88
18	2	0.6322	0.74	75.48	1.02	0.96	0.94
22	3	0.76	0.78	79.56	4.08	1.17	0.29
24	3	0.86	0.79	80.58	1.02	3.92	3.84
26	1	0.81	0.81	82.62	2.04	1.08	0.53
30	1	0.95	0.82	83.64	1.02	0.00	0.00
31	1	0.9741	0.83	84.66	1.02	0.00	0.00
32	2	0.99	0.84	85.68	1.02	0.96	0.94
36	1	1.06	0.86	87.72	2.04	1.08	0.53
42	3	1.1612	0.87	88.74	1.04	3.84	3.69
45	1	1.2064	0.88	89.76	1.02	0.00	0.00
46	1	1.2193	0.89	90.78	1.02	0.00	0.00
50	2	1.27	0.90	91.80	1.02	0.96	0.94
54	1	1.3225	0.9066	92.47	1.02	0.00	0.00
56	2	1.3419	0.9099	92.81	0.34	2.76	8.11*
105	1	1.74	0.9591	97.83	5.02	16.16	3.22
125	1	1.8580	0.9686	98.80	1.02	0.00	0.00
133	1	1.8967	0.9713	99.07	0.27	0.53	1.96
152	1	1.98	0.9761	99.56	0.49	0.26	0.53
170	1	2.0516	0.9798	99.94	0.38	0.38	1.00
210	1	2.19	0.9857	100.54	0.60	0.16	0.27
360	1	2.54	0.9945	101.44	0.90	0.01	0.01

z = log_e(y+1)

n = 102

X² = 59.48
X² = 43.78**

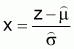
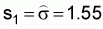
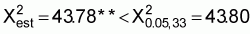
** Estimated x² without the two values indicated by asterisk