Introduction
Stock assessment in the tropics is generally more difficult than in temperate waters. There are a large number of reasons for this, and two of them may be listed here:
- Tropical fisheries - especially demersal fisheries - often exploit a large number of species simultaneously, with the result that neither the commercial fishery nor the artisanal fisheries - even when relatively well monitored - can be expected to provide detailed catch and catch/effort statistics on a per species basis. For this reason, it is common in tropical fisheries to treat whole species assemblages as if they were single species.
- Tropical countries generally have a relatively limited research capability - as far as fisheries research is concerned - which often leaves most of the stocks sustaining their fishery completely univestigated.
Despite these and other problems, the fishery biologists working in tropical countries have been traditionally expected to provide (fast) answers to pressing questions such as
- How much fish there is in a given area.
- How much should be taken annually.
- What gears should be used.
- How to accommodate various groups (e.g., of fishermen) with diverging, or even conflicting interests.
- How to manage a fishery (what specific regulatory measures, how to enforce these, etc.).
In answer to some of these needs, several models and techniques have been developed which give (at least rough) answers to these questions. This chapter aims at briefly presenting a few of the concepts involved, and to introduce some of the literature available on the subject.
Estimating Stock Sizes
Methods for estimating the stock sizes of pelagic fishes
Stock sizes of small pelagic fishes are generally estimated by means of acoustic surveys. The methodology of such surveys is outlined in more or less detailed fashion in the following texts: Forbes and Nakken (1972), Cushing (1973), Saville (1977). Results of pelagic acoustic surveys conducted in the Western Indian Ocean, south of the equator, have been reviewed in Gulland (1979, pages 5–6).
Estimating the standing stock size of large pelagic fishes such as tuna and other large scombroids is generally very difficult and the results obtained are often highly controversial (see Sharp, 1978, 1979). Earlier surveys conducted in the Western Indian Ocean have generally concentrated on relative abundance (rather than absolute stock sizes) as indicated by the spatial distribution of the catch/effort of a standard gear (Williams, 1967).
Methods for estimating the stock size of reef fishes
Strangely enough, there is at present no generally accepted standard method for estimating the standing stock sizes of reef fishes and the wide variety of methods used (involving poisoning and SCUBA divers' direct counts methods) as well as the different concepts of what actually belongs to a “reef” have led to widely differing standing stock estimates (see Russel et al., 1978). This leads to the suggestion that estimates of yield per area (see below) be used, together with estimates of fishing mortality to estimate standing stock indirectly.
Thus, since we have
Y = F · B | (38) |
which expresses the basic interrelationship between annual catch in weight or yield (Y), mean standing stock size (B) and fishing mortality (F), we also have

which can be used to estimate standing stock sizes given reliable estimates of Y and F, the latter being obtained, for example from the average of several single values of F from different species, as obtained from the mean length in the catch and an independent estimate of M.
Papers which may be consulted for obtaining more or less direct estimates of standing stock sizes in reefs are Bardach (1959) or Goeden (1978). The best reviews available to date of methods for use in coral reef fish studies are those of Russel et al. (1978) and the series of papers by Munro and co-authors (1973–1978) on the biology of Jamaican reef fishes and on the fishery based on these fishes.
Estimating the Biomass of Demersal Stocks
In areas where the sea bottom is smooth enough for trawling, standing stock sizes can be obtained from the relationship

where  is the mean catch per effort obtained during the survey (or for a given stratum),
A the total survey area (or the area of the stratum in question) and “a” the area “swept”
by the net during one unit of effort (e.g., one hour), x1 being the proportion of the fish in
the path of the gear that are actually retained by the net.
is the mean catch per effort obtained during the survey (or for a given stratum),
A the total survey area (or the area of the stratum in question) and “a” the area “swept”
by the net during one unit of effort (e.g., one hour), x1 being the proportion of the fish in
the path of the gear that are actually retained by the net.
In Southeast Asian waters, a value of x1 = 0.5 is commonly used (Isarankura, 1971; Saeger et al., 1976; SCSP, 1978) and there is some evidence that this value might in fact be very realistic (Pauly, 1979a).
For the Western Indian Ocean south of the equator, it has been suggested, on the other hand, that all fish in the path of the trawl might be caught, which corresponds to x1 = 1 (see Gulland, 1979, page 3).
The surface swept by the gear during one unit of effort is computed from the expression
a = t · v · h · x2 | (41) |
Where v is the velocity of the trawler over ground when trawling, h is the length of the trawl's head rope, t is the time spent trawling, and x2 is a fraction expressing the width of the area swept by the net divided by the length of the head rope. In Southeast Asian waters, values for x2 ranging between 0.4 (SCSP, 1978) and 0.66 (Shindo, 1973) have been used, with 0.5 possibly being the best compromise (see Pauly, 1979a).
Equations 40 and 41, incidentally can be used to obtain standing stock estimates from commercial trawlers, provided their catch per effort, head rope length and trawling speed are known.
The “swept area” method, as the method presented above is called, has been adapted- using certain assumptions as to the behaviour of fish - to line fishing over reefs (Wheeler and Ommaney, 1953), and this paper, along with the comments of Gulland (1979, page 4) should be consulted for details.
Estimating Maximum Sustainable Yield (MSY)
There are two basic models for estimating MSYs from fish stocks, namely the “yield-per recruit” model of Beverton and Holt (1957) and its variants and the “surplus yield” model of Schaefer (1954) and its variants.
When suitable growth and mortality parameters are available, the model of Beverton and Holt (1957) or one of its simplified versions (e.g., Beverton and Holt, 1966) may be used to estimate yield-per-recruit, and if recruitment is known or assumed to be constant, to identify an optimal fishing strategy (but see Chapter 7 on overfishing). This model, however, will not be reviewed here, both because its complexity would lead us astray and because it tells us surprisingly little about how to manage a tropical multispecies fishery.
The Schaefer model-in its simplest version at least-is quite easy to handle. Here is a stepwise approach to estimating MSY by means of this model:
| Step 1 | Tabulate the catch and effort data and compute catch-per-effort figures (see Table 11). |
| Step 2 | Plot the catch-per-effort values against their corresponding value of effort, and estimate the intercept (a) and the slope (b) by the linear regression technique. Change the sign of b from minus to plus. |
| Step 3 | Compute MSY = a²/4b optimum effort = a/2b yield for a given effort = af - bf² |
Steps 1–3 are illustrated in Figure 15, which is based on the data of Table 11.
| Year | Catch2 |  3 3 | f4 |
|---|---|---|---|
| 1969 | 50 | 0.080 | 623 |
| 1970 | 49 | 0.078 | 628 |
| 1971 | 47.5 | 0.091 | 520 |
| 1972 | 45 | 0.088 | 513 |
| 1973 | 51 | 0.077 | 661 |
| 1974 | 56 | 0.061 | 919 |
| 1975 | 66 | 0.057 | 1 158 |
| 1976 | 58 | 0.032 | 1 970 |
| 1977 | 52 | 0.039 | 1 317 |
1 From Dwippongo (1979)
2 In tons · 103
3 In tons · 103 per standard vessel
4 Number of standard vessels
There is, finally, a third method for estimating maximum sustainable yields for a given fishery, and this is the comparative method.
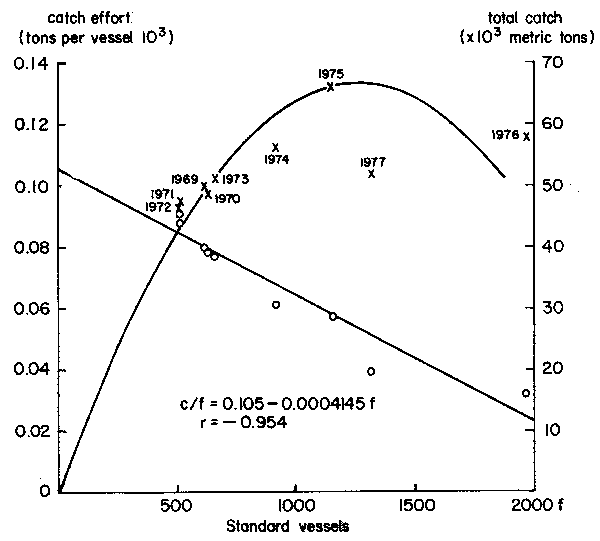
Figure 15 Trends of catch and catch-per-effort on effort, off the north Java coast. Based on data of Table 11. For fitting of “Schaefer Model” (see text)
Certain ecosystems are extremely productive (e.g., upwelling areas) or quite unproductive (such as the deep oceans). As far as tropical, shallow water systems are concerned, however, a remarkable consistency of yields (when expressed on a per area basis) can be noticed, with yield ranging between 4 and 8 t/km² (all fish) in inshore areas (including reefs) with values in exces of 10 t/km², where estuarine conditions boost productivity (Table 12). These figures may thus be used to assess certain stocks and fisheries, e.g., to assess if a certain stock is “underfished”, or “optimally exploited”.
| Exercises: | (1) | Use the data of Table 13 to estimate MSY (per km²) in the reefs of the Western Indian Ocean south of the equator. |
| (2) | Discuss the state of the stock and of the fisheries (in the midseventies) at Mahe (Seychelles), and in Mauritius and propose regulatory measures. |
| Type of ecosystem | Location | MSY (t/km²) | Source |
|---|---|---|---|
| Coral reef | Jamaica, Caribbean | 4 (all fish) | Munro (1975) |
| Western Indian Ocean | 5 (all fish) | Gulland (1979) | |
| Shelf | Gulf of Thailand | 3.6 (demersal only) | SCSP (1978) |
| (down to 50 m) | |||
| Estuaries | San Miguel Bay | 15 (all fish) | Pauly and |
| and lagoons | (down to 15 m) | Mines (MS) | |
| (The Philippines) | |||
| Shallow lagoons | Gulf of Mexico (Texas) | 12 (all fish) | Saila (1975)1 |
| (estuarine conditions) | Sakumo Lagoon (Ghana) | 15 (all fish) | Pauly (1976) |
1 Saila (1975) presents a compilation of data similar to those presented here, covering awide variety of ecosystems ranging from the North Sea to tropical ponds
Area | Current catch (t/km²) | Catch/effort (kg/trap set) | Fishing Intensity (trap sets/km²/year) |
|---|---|---|---|
Mauritius | 3.5 | 1.25 | 2 800 |
Tanzania (north) | 4.7 | 3.45 | 1 400 |
Mahé (east coast) | 1.37 | 5.37 | 260 |
Mahé (west coast) | 3.12 | 5.07 | 620 |
1 From Gulland (1979, page 9)