

0902-B4
M.B.Shrivastava and R.A.Singh 1
The paper describes the statistical procedure in a case study of Silver fir (Abies pindrow. Spach) forests of Western Himalayas in India to assess the breast height diameter and crown diameter of trees from stump diameter with the help of regression and correlation analysis. A series of regression equations have been developed using the stump diameter (DSH) as independent variable while crown diameter (CD) and breast height diameter (DBH) as dependent variables. With the incorporation of DSH in the equation, the DBH and CD of the felled and removed trees can be accurately predicted. The method is simple and easily applicable. The results will provide clues to detect the undersize recordings and excessive felling of trees. For each diameter class the crown area, number of trees per ha and the number of trees per ha after thinning can be calculated and a table constructed. This will provide an aid in thinning of even-aged crop and thinning can be done for any stage of the crop quantitatively, using this table.
Often the foresters are confronted with the problem of ascertaining and confirming the diameter (DBH) of felled trees, especially in the case of illicit felling and intentional oversize markings and undersize recordings by the field staff in connivance with the contractors and beneficiaries. Also excessive felling over and above the actual requirements are not uncommon, especially in ropeway alignments. The stumps are the only clue left to detect the offence and to arrive at a conclusion.
There is an urgent need to evolve an indirect method of predicting breast height diameter (DBH) and crown diameter (CD) of trees from stumps, which should be accurate and easily applicable. This will help in detecting the oversize markings and undersize recordings of trees and also excessive felling than actual requirements. This is possible by regression and correlation studies between stump parameters as independent variables and DBH and crown attributes as dependent variables.
Significant correlation's between bole diameter, cubical content of tree, total height, crown diameter and crown projection area have been established for a number of tropical and temperate tree species (Dilworth, 1959; Dawkins, 1963; Suri, 1970; Joshi, 1973; Rugmini and Jayaraman, 1995; Shrivastava, 1996, 1997). The present work aims at such studies covering Silver fir forests of Western Himalayas in India. The results will serve as a tool in ascertaining the DBH and crown diameter (CD) of felled trees, in unearthing the oversize and excessive markings, and also as an aid in thinning.
The study was confined to Silver fir (Abies pindrow Spach.) forests occupying an area of 319.55 ha on very steep slopes between 2,600 to 3,400 m elevations in Haban and Rajgarh Ranges of Rajgarh Forest Division in Himachal Pradesh, India. Shrivastava (1993) has described the area, locality factors, floristic, etc. in detail. The stand is nearly pure Silver fir occurring gregariously. The canopy is moderate to dense. The boles are cylindrical and straight. Trees are tall: a height of > 40 m is not uncommon. It is a typical selection forest. Young trees are markedly deficient and natural regeneration is a problem. Illicit felling of trees and illegal export of timber are not unusual.
In total 65 Silver fir trees from the whole area covering the entire spectrum of diameter were selected randomly. Stump and breast height diameters at 15 cm and 1.3 m above the ground level were measured in cm and recorded as DSH and DBH, respectively. The crown diameter, (CD) was recorded by fixing the ground points on either side of the trunk perpendicular to the tips of the longest branch and measuring the distance in meter.
In order to establish the relationships between measured tree parameters DSH, DBH and CD, linearity test by simple regression analysis was carried out using REGRESS Computer programme (Ryan et al., 1991). It uses least squares to fit a model to one or more predictors to predict future observations. It can do transformations and fit polynomials. REGRESS fits the model Y = Bo + Bi X + e, where Y is the response, X is the predictor, Bo and Bi are the regression coefficients, and e is an error term with a normal distribution with mean = 0 and standard deviation = o. It estimates Bo by bo, Bi by bi and o by s. The fitted equation is then Y = bo + bi X; Y is called the predicted or fitted value. The programme provides the Table of Coefficients, bo and bi along with their standard deviations, t-test for testing if the coefficient is 0, and the probability value of this test. It also provides the estimated standard deviation about the regression line (s), correlation's coefficient (r/R) and coefficient of determination (R-sq.) in percent.
The measured parameters along with their range, average and number of observations are presented in table I while the distribution of sample trees in 10-cm diameter classes is given in Table 2.
Table 1: Range, mean and sampling number of measured parameters.
Parameters |
Range |
Mean (X) |
N |
DSH |
11.0 - 99.5 cm |
53.5 cm |
65 |
DBH |
9.0 - 94.0 cm |
44.1 cm |
65 |
CD |
3.2 - 18.20 m |
10.94 m |
65 |
Table 2: Diameter class (cm) and distribution of sample trees.
Diameter Class (cm) |
, DSH |
DBH Trees (No.) Cumulative | ||
Trees (No.) |
Cumulative %, | |||
10 |
2 |
3.08 | ||
10 - 20 |
10 |
15.38 |
15 |
26.15 |
20 - 30 |
8 |
27.69 |
6 |
35.38 |
30-40 |
6 |
36.92 |
7 |
46.15 |
40 - 50 |
6 |
46.15 |
7 |
56.92 |
50 - 60 |
7 |
56.92 |
9 |
70.77 |
60 - 70 |
8 |
69.23 |
5 |
78.46 |
70 - 80 |
6 |
78.46 |
7 |
89.23 |
80-90 |
7 |
89.23 |
6 |
98.46 |
90 - 100 |
7 |
100.00 |
1 |
100.00 |
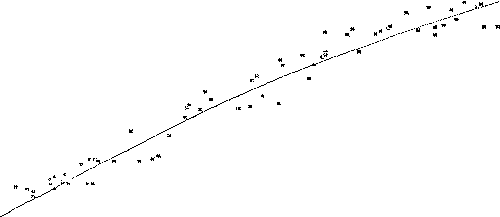
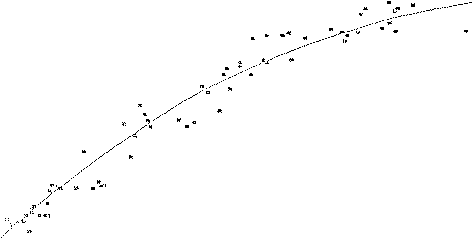
Regression analysis provided strong linear relationships between the measured parameters. No improvement was found in correlation coefficient by quadratic or cubic regressions between DBH and DSH. Quadratic regressions increased the strength of relationships with CD as dependent variable. The DBH and CD were found highly correlated with DSH. As an aid in thinning operations, relationships between CD and DBH were also studied. The study resulted in the development of a series of regression equations. Table 3 contains the abridged statistical analysis and regression equations while Figures 1, 2, and 3 exhibit the plotting and regression lines.
Table 3: Relationships between breast height diameter (DBH), crown diameter (CD) and stump diameter (DSH) of Silver fir trees.
Regression Equations |
s |
F |
r/R |
R-sq. (%) | |
(1) |
DBH = - 4.13 + 0.902 DSH |
2.75 |
5065*** |
0.994*** |
98.8 |
(2) |
CD = 1.40 + 0.178 DSH |
1.126 |
1179*** |
0.974*** |
94.9 |
(3) |
CD = - 0.362 + 0.265 DSH |
||||
-0.000795 DSH2 |
1.023 |
721*** |
0.979*** |
95.9 | |
(4) |
CD = 2.32 + 0.195 DBH |
1.246 |
953*** |
0.969*** |
93.8 |
(5) |
CD =-0.169+0344 DBH |
||||
-0.00160 DBH2 |
0.948 |
845*** |
0.982*** |
96.5 | |
| Significance limits: * = 5%; ** = 1%; *** = 0.1% |
The best prediction of DBH is expressed by the linear regression equation 1, in which DSH explains 98.8% (r = 0.994) of total variation in DBH with + 2.75 cm standard error of estimate, which is 6.24% with 44.1 cm mean DBH.
Crown diameter prediction with DSH is better explained in quadratic equation 3. It accounts for 95.9% (R 0.979) of the total variation in tree crown diameter with standard error of estimate of 10.29% (± 1.023 m) with mean CD 10.94 meter.
The regression equation 5 accounts for 96.5% (R = 0.982) of the variability in the CD, showing thereby that the correlation between DBH and CD is highly significant. The standard error of estimate is + 0.948 m (8.67 % with mean CD 10.94 m). Using this equation, the crown diameter for different DBH have been calculated and the crown projection area (3.1428 x CD2 x '/4) in m2 computed. The number of trees per hectare (100 m x 100 m) for 100% canopy cover for different DBH have been calculated by dividing the area (10000 m) with crown projection area of that DBH for thinning operations (Table 4). The tree numbers have further been corrected by multiplying with the factor 1.3 for steepness of the area (slope 30° to 40°); increase in the slope gradient increases the area and thereby the number of trees.
Table 4: Diameters, crown projection area (m) and number of trees per ha for an even aged normal forests of Silver fir (Abies pindrow Spach.).
Mean DBH (cm) |
CD (m) |
Crown area (m2) |
Tree No. per ha. |
Corrected Tree no. per ha. |
Trees/ha after thinning for 5 cm diameter growth. |
10 |
3.111 |
7.6 |
1,316 |
1,711 |
772 |
15 |
4.631 |
16.84 |
594 |
772 |
449 |
20 |
6.071 |
28.95 |
345 |
449 |
300 |
25 |
7.431 |
43.37 |
231 |
300 |
218 |
30 |
8.711 |
59.60 |
168 |
218 |
169 |
35 |
9.911 |
77.15 |
130 |
169 |
137 |
40 |
11.031 |
95.57 |
105 |
137 |
113 |
45 |
12.071 |
114.44 |
87 |
113 |
98 |
50 |
13.031 |
133.37 |
75 |
98 |
88 |
55 |
13.911 |
151.99 |
66 |
88 |
77 |
60 |
14.711 |
169.97 |
59 |
77 |
Column 5 contains the maximum number of trees per ha for the respective DBH crop when the crowns of trees cover all the available space and crowns are touching each other. Once the stocking (number) per ha in a fully stocked crop is known, the thinning can be done and the growing space provided by setting some realistic rate of DBH growth as a goal. Column 6 has been constructed from the figures of column 5; it provides the number of trees per ha to be retained after thinning for a DBH growth of 5 cm. For example, a crop of 20-cm diameter is to be thinned and a diameter of 25 cm is to be. expected at the end of thinning cycle without causing drastic openings, or permanent gaps, 300 trees per ha will be left just after thinning has been completed. Similarly, thinning can be done for any stage of the crop quantitatively, using this table.
The regression equation developed between DBH and DSH allows the determination of breast height diameter (DBH) of silver fir from stump diameter. The `r' (0.994) close to unity indicates that there is a strong relationship and that the regression equation will give relatively accurate predictions of the DBH values. High value of F.,1 (5,065) over the tabulated value (11.97) at probability 0.001 confirms that the DBH is highly related with DSH. The standard deviation of the actual DBH around the regression line signifies that the estimated values are within the error limit of < + 6.24% and over 2/3`d (68%) of the observed DBH lie within + 2.75 cm of the regression equation's predicted values. Thus the stump diameter can be used in the equation to ascertain the DBH of felled, removed and lost trees. It will be within the range of ± 2.75 cm of the predicted value. The statement concerning estimated values and error limits is true only at the mean value of DBH. The comparison between predicted and recorded DBH will allow drawing inference about oversize markings and undersize recordings. In case the recorded DBH lie within the range of predicted DBH + 2.75 cm, it will not be a case of oversize marking and undersize recording.
The crown diameter of silver fir can be predicted from stump diameter (Equation 3) with relatively high accuracy (R=0.979* * *), which will lie within the range of ± 1.023 m from the predicted value. Crown diameter is a measure of canopy crown. The crowns overlap each other if the distances between two trees are less than the sum of their crown radii. In such cases the removal of both the
s becomes essential when their crowns come in ropeways alignment. Such removals are out of ; ,purview of excessive markings.
The tree numbers per ha after thinning for 5-cm diameter growth worked out (Table 4) represent the number of trees in the uppermost canopy. Suppressed trees may be left to cover the soil, but these are quite additional to the main crop. For example 218 stems should be left per ha when average diameter of silver fir crop is 25 cm. This means that there is growing space in the uppermost canopy for 218 stems each of 25 cm DBH. That another about 200 suppressed or dominated trees may be left below this top storey does not affect the growing space of these 218 trees, and these extra 200 trees may be left or removed from quite other reasons.
The statistical relations (regression equations) developed are valid only for the collective they are representing, and applicable only for the area under study. It is therefore essential o develop fresh statistical relations for different forests on local or regional basis.
Relatively accurate determinations of breast height diameter and crown diameter of trees are possible through statistical studies. Regression and correlation studies disclose the relationships between dependent and independent variables and a number of equations can be developed. The bole and crown diameters of trees can be determined from stump measurements using such equations. Thus indirectly such dimensions of felled, removed or lost trees can be ascertained simply with the help of stumps remain in situ. It is a simple and practical method and easy to apply. The formulae are valid for the entity they represent and applicable to the areas under study. Therefore, it is worthwhile to develop equations on local or regional levels.
Dawkins, H.C. 1963. Crown diameters, their relation to bole diameters in tropical forest trees. Empirical Forestry Review 42 (4) No. 114, 318-33.
Dilworth, J.R.1959. Aerial photo-mensuration tables. Research Note No. 2, Forest Research Division, Oregon State College, Agriculture Experiment Station.
Joshi, S.C. 1973. Optimum scale of black and white aerial photography for growing stock assessments. Thesis, Indian Photointerpretation Institute, Dehradun, India. Rugmini, P. and Jayaraman, K. 1995. Estimation of tree volume from girth measurements below breast-height. Journal of Tropical Forestry 11 (1), 16-22.
Ryan, B.F., Joiner, B.L. and Ryan, A.R. 1991. Minitab Handbook. Duxbury Press, Boston. Shrivastava, M.B. 1993. Revised Working Plan for the Forests of Rajgarh Forest Division, Himachal Pradesh for the period 1991 to 2006. Vol I. H.P.Government, Dept. of Forest Farming and Conservation, H.P.F.D. Kalaghat, Solan (H.P.), India. Shrivastava, M.B. 1996. Predicting canopy and breast height diameters of chirpine (Pinus roxburghii) from stumps. Annals of Forestry 4(2), 1634-169.
Shrivastava, M.B. 1996. Method of assessing breast height and crown diameters of felled and lost trees. Research Nius, VI(2), 4-8. The Papua New Guinea University of Technology, Lae, PNG.
Shrivastava, M.B.1997. Determination of crown and breast height diameters of Cedar trees (Cedrus deodara) from stump diameter. Science in New Guinea 22 (3), 107-113. Suri, S.K. 1970. Some studies on correlation of crown projection area and bole diameter in Sal (Shorea robusta) as an aid in thinning. Indian Forester 96, 288-92.
IP I c - 1 : ER le 'I <-D -t-- 1 C) r-I s1--l I Lp ID E--- -t w C--- €r-I D)313 ar-I (-I ID S H ( s 1 1 z e~ af f I if ) -
![]()
![]()


![]()
0 20
40
a
60 80 100
DSH (cm)
I <J - 2 : 1-~ <-- I- za -t-- I (:) r-i :EH5 I-i I Lp be: -t w C-,- <E~ ri CID
Cl ID ---> 1-1
20 18 16 14 12 10
8
el
4I
2 -
20
40
Go
so
DSH (cm)
17 !a - 5 : R c--- -1 za -t i c:> ri fE5 1--i i LD
aria DSH
I-D at: w c-- c:Et ri C-- ID
![]()

i
20
40 60
Doil (cm)
80 100
1 Himachal Pradesh Forest Department, Talland, Shimla-171001 (India)