
EPR/81/5
August 1981


 | FOOD AND AGRICULTURE ORGANIZATION OF THE UNITED NATIONS | ESN: FAO/WHO/UNU EPR/81/5 August 1981 |
 | WORLD HEALTH ORGANIZATION | |
 | THE UNITED NATIONS UNIVERSITY |
Provisional Agenda Item 2.2.1
Joint FAO/WHO/UNU Expert Consultation on
Energy and Protein Requirements
Rome, 5 to 17 October 1981
BASAL METABOLIC RATE IN MAN
by
J.V.G.A. Durnin
University of Glasgow
Glasgow
Scotland
Mitchell (1962) has defined the Basal Metabolic Rate (BMR) in terms which, when considered precisely, would meet with general acceptance, but which have implications that are not often adjudged fully. “The basal metabolism of an animal is the minimal rate of energy expenditure compatible with life.” His definition represents the common view that basal metabolism reflects a fundamental biological property of the individual or the species and that if we can measure it accurately we are in possession of information of some importance. Since basal metabolism may well indicate an intrinsic property of the organism this is a theoretically justifiable opinion. Whether information on BMR is of practical value in the context of calculating energy requirements either of an individual or of a population is a complex question and the purpose of this article is to examine critically the various aspects of this problem.
One factor which may have considerable consequence is the variability between apparently similar individuals who might be expected to have uniform metabolic rates. If this variability is markedly inconsistent there may be great difficulty in utilizing BMR as a reference point for an individual unless that individual is separately measured; this is not normally desirable, since the purpose of a set of reference tables is to make any measurement unnecessary. Also if measurement of BMR is attempted, there are considerable technical difficulties attached to it.
As far as groups of individuals are concerned, while individual variability is not of import by itself in assessing the mean BMR of the population, it forms part of the error attached to previously published data, and, together with other sources of error, assumes significance. The dilemma was well expressed by Mitchell: a critical discussion of available knowledge inevitably involves evaluation of methods as well as the results of research. This difficulty can be resolved either by disregarding investigations of doubtful scientific accuracy or merit, or by discussing such investigations with appropriate reservations. The literature in the field of basal metabolism is in a state of knowledge which is only partially unambiguous and while many published studies on this topic can be accepted with little or no reservations, they are not sufficient in scope to allow unqualified conclusions to be drawn. Therefore data must be drawn upon about which a reviewer might have some reservations and it is necessary to perform the painful duty of pointing out specific items in a published work with respect to which an investigation is vulnerable, such as improper controls, inadequate calibration of equipment, failure to assess the magnitude of experimental error, and inexact use of statistical analyses. However, even correct statistical analyses will not compensate for incorrect experimentation. It is pertinent in much nutritional research on large populations to remember the dictum of the distinguished statistician R.A. Fisher - “a clean grasp of simple and standardized statistical procedures (is) only the means to a more important end …… to satisfy the requirements of sound and intelligible experimental design, and to supply the machinery for unambiguous interpretation.”
The theoretical basal metabolism may be properly regarded as a fundamental biological phenomenon. However, the real-life conditions under which BMR is measured result in a ‘resting rate’ which is not a fixed minimum metabolism on which life depends. The minimum rate of energy expenditure at any given time in an animal is not always the same and depends upon such things as the previous nutritional state, absence of disease or infection, the body temperature, the phase of the menstrual cycle in the female, and the degree of wakefulness. The influence of these variables may seriously affect the apparent standardization which is thought to be attained by carefully controlling the other well-known factors of food, muscular activity, environment, etc. The implications are as follows:-
The conditions which must be imposed (mostly as taken from Benedict, 1938) in order to measure ‘ideal’ basal metabolism in man are
absence of gross muscular activity - or, hopefully, obtaining complete muscular relaxation. It is well-known to workers in this field of research that ensuring this state in an individual unaccustomed to such a measurement is not easy and its success is difficult to quantify without measurements on repeated occasions, as the classical account of Pickworth (1927) and the more recent attempts over many years in our own laboratory amply demonstrate. Muscular activity prior to BMR determination should also be kept to a minimum. A rest period of at least 20–30 min. needs to be imposed immediately before the measurement is made.
The postabsorptive state is necessary, which is usually interpreted as 12 h or so after the last meal.
Thermal neutrality is another factor, which will depend upon the accustomed climatic temperature and clothing as well as the absolute laboratory temperature. In hot climates, the fact that some laboratories are air-conditioned whereas this may well not be the normal habitat of the person being measured might also affect the results.
Emotional disturbance must be minimal. While several classical studies have shown clearly that there is no significant rise or, at most, only a very small increase in metabolic rate when a resting, relaxed subject is asked to perform complicated mental tasks (Benedict & Benedict, 1933; Benedict & Carpenter, 1909; Chlopin, Jakowenko & Wolschinsky, 1927; Rosenblum, 1932), there is some evidence to show that emotional upset, particularly apprehension, may result in rises in BMR of from 15–40% (Young & Donaldson, 1946).
The degree of wakefulness may exercise a variable effect on BMR, often difficult to assess. Any conscious state implies a certain degree of muscular tension which will be, to some extent, an individual characteristic although Du Bois (1930–31) has suggested that certain races may be able to relax easier than others.
Sleep will depress the BMR, again to a variable amount in different individuals but probably averaging about minus 10%. This seems to be true even in Asians, who are supposed to have lower metabolic rates than those of Western races (Mason & Benedict, 1934). However, although the BMR seems to be reduced by sleep, the average metabolic rate during sleep will not necessarily be below the BMR. This apparent paradox occurs because the metabolic rate during the first few hours of sleep may be a little higher than the BMR because of the influence of the previous meal and other factors, and the fall below the BMR which happens later probably results in an average during the whole sleep period of a metabolic rate which, overall, is about that of the BMR.
The phase of the female sexual cycle seems to result in the BMR being at its lowest during menstruation and highest immediately prior to menstruation (Mitchell, 1962). These periods should therefore be avoided in the measurement of the BMR.
Purpose of imposing standardized experimental conditions. The stipulated experimental conditions outlined above are required not so much to secure minimal levels of metabolism but more to ensure that measurements of BMR made in different laboratories are comparable. These definable and comparable conditions allow, in theory at least, the ability to assess as independent factors such variables as sex, age, body composition, ethnic group, climate, etc. In practice, there are difficulties in being able to do this with complete confidence. This is primarily a reflection of the various types of individuals who may have been measured, and the way in which the measurements have been done. It depends upon the numbers, ages and sexes of people studied, their homogeneity and both inter- and intra-individual variability, and the particular methodology used (Benedict-Roth spirometer, Douglas Bag, mask or mouth-piece, continuous flow system, method of gas analysis, etc.). The quantitative results of all of these effects will be mentioned at various stages of this article, but a short description and discussion of the different aspects of the methodology may be worth noting here.
Apparatus for BMR measurements. There have been no radical improvements since Carpenter described this technique in 1915 (c.f. Durnin & Passmore, 1967). The basis of the measurement of BMR remains the indirect calorimetric measurement of oxygen consumption and its conversion into energy units usually expressed as kJ (previously kcal) per unit of body size. A short description of the principles underlying the measurement of metabolic rate and the advantages and disadvantages of various items of the necessary apparatus may be useful in perhaps clarifying some of the problems in adequately assessing the validity and the variability of experimental data.
Calorimetry in man, as its name implies, is the measurement of the heat emitted from the human body. Although a portion of the total energy which is produced in the body by chemical oxidation of organic nutrients, is utilized for mechanical work (a small quantity in basal conditions for the work of the heart, respiratory muscles, etc. and a much larger amount in physical activity for the contraction of skeletal muscles) all of this energy is eventually emitted as heat. This can be measured 1) directly by putting the individual inside a specially constructed calorimeter, and much of the classical and fundamental work on energy metabolism was done in this way, in particular the excellent and distinguished studies of Atwater & Benedict (1899). The use of this technique with a properly constructed calorimeter incurred no appreciable error in the actual measurement, but there are considerable disadvantages. Firstly, construction and operation of the apparatus is time-consuming and costly and very few of these instruments were ever made; secondly, the measurement must be made during a period of several hours, because of the large volume of the apparatus and the time-lag between alterations in the heat content inside the calorimeter chamber caused by the presence of the human being and their measurement. Obviously, even at the best, this is not a method for measuring large numbers of individuals.
In the more recent past, some of these disadvantages have been removed by the use of gradient layer calorimeters (Benzinger, Huebscher, Minard & Kitzinger, 1958; Jequier, Pittet & Gygax, 1978). These calorimeters are supposed to have a short period for thermal inertia and a rapid response time but, in practice, often much more than one hour is needed to attain thermal equilibrium and the basic drawbacks of large cost and maintenance and unsuitability for use on large numbers of individuals remain.
2) The commonly used method of estimating BMR continues to be the so-called indirect calorimetric measurement of the oxygen consumption of an individual, usually during a period varying from 10 to 30 min. The justification for this technique still rests largely with the results obtained by Atwater and his colleagues in the large respiration calorimeter. This chamber was commodious enough to allow a man to remain in it for several days during which the heat output and the oxygen and carbon dioxide exchange were simultaneously measured. In experiments described by Atwater & Benedict (1899) lasting 40 days on 3 men eating mixed diets the average energy expenditure calculated by the direct method was 11.37 MJ (2717 kcal) and by indirect calorimetry it was 11.39 MJ (2723 kcal), that is a difference of 0.2 percent. (An excellent critique of the theoretical bases for direct and indirect calorimetry is given by Blaxter, 1971).
However, to measure rates of oxygen consumption it is not necessary to put the individual person inside a respiration chamber. By making him breathe in and out through inspiratory and expiratory valves and measuring the volume and composition of the inspired and expired air, then the oxygen uptake and the carbon dioxide output of the body can be calculated. The only theoretically basic difference between the measurement of this respiratory exchange and that of the total oxygen and carbon dioxide exchange of the body relates to oxygen uptake and carbon dioxide excretion through the skin, which would obviously not be monitored by analysing inspired and expired air. It is well known that these gases are able to pass through the skin barrier, but it seems clear from a comprehensive review (Fitzgerald, 1957) that, to quote the author, “the quantity of the total respiration that occurs through the skin surface is negligible in normal individuals.”
To calculate oxygen consumption and carbon dioxide production in an individual it is not essential to analyse actually the inspired air. Since the oxygen and carbon dioxide content of the inspired air remain constant in a wide variety of environments and are known to sufficiently high levels of accuracy, all that is required to calculate oxygen consumption and carbon dioxide production is to meter the volume of the expired air and to analyse its gas content.
Methods for collecting, metering and analysing expired air have been established for more than 60 years. They still form one of the elementary techniques in almost all laboratories of human physiology. They are, nevertheless, not simple and they require constant supervision and much calibration of equipment. Gases readily leak from apparatus that is not well maintained. Valves, taps and all connections have to be regularly tested to ensure that they are air-tight. Gas meters require calibration at regular intervals and, in our experience, the calibration factors supplied by manufacturers for new instruments are often inaccurate.
Although it is perhaps not an entirely justified blanket condemnation, it seems from the ‘Methods’ section in some published work that the care with which instruments are treated in nutritional laboratories engaged in measurements of human energy expenditure is not always of the relatively high calibre which would be expected in most physiological or biochemical laboratories. This adds to the difficulty of assessing the validity of some data and in the overall conclusions which can be drawn about basal metabolic rates.
A description of the principles on which the derivation of heat output (in kJ per unit time - or kcal) can be determined from oxygen consumption is not required here. A short simple explanation is given in Durnin & Passmore (1967). It is sufficient to note that while, for many years, it used to be considered necessary to measure both oxygen consumption and carbon dioxide production in order to obtain the respiratory quotient (R.Q.), since the theoretical paper published by Weir (1949) it has become common-place to measure the total volume of expired air and its oxygen content only instead of measuring also the carbon dioxide content. The R.Q., which is the ratio of the volume of carbon dioxide excreted to the volume of oxygen consumed, was necessary because each litre of oxygen consumed by the body represented a slightly different quantity of energy depending on the value of the R.Q. - varying from 21.12 kJ (5.047 kcal) at an R.Q. of 1.000 when only carbohydrate would be combusted, to 19.61 kJ (4.686 kcal) at an R.Q. of 0.707 when only fat would be oxidised as a source of energy to the body. Weir showed that the R.Q. seemed an unnecessary piece of information. However, the measurement of oxygen consumption during short periods of only 10–15 min. or so - which is probably the usual practice - has not been validated against direct measurements of heat output. Some incomplete experiments are mentioned by Durnin (1978a) where these comparisons have been made in a gradient layer calorimeter, and differences of 14% were found on several occasions between the two sets of measurements. Also, one of the sources of error in calculating energy expenditure from oxygen consumption may exist in the use of both the classical R.Q. method of Zuntz & Schumburg (1901) or the method of Weir (1949). In both of these methods of calculation, if hyperventilation has occurred - which may not be uncommon in brief measurements of oxygen consumption on untrained subjects - and the R.Q. is greater than 1.00 an overestimate of energy expenditure of at least 7% may be the result. Indeed, both methods of calculation require that the R.Q., when measured, actually represents the relative production and consumption of carbon dioxide and oxygen in the tissues at the time of measurement. Anyone with a wide experience of these experimental measurements on a variety of human subjects must be well aware of the uncertainty attached to any R.Q. measured over 10 or 15 min. Even when the R.Q. appears well within the normal range - perhaps around 0.80 or 0.85 - it may still not represent the actual R.Q. in the tissues and, of course, if Weir's method is being employed and only the oxygen content of the expired air is measured, there will be no information at all on R.Q. so the possible error will be completely unknown.
Problems associated with equipment: Many of the published data on BMR have been obtained using the Benedict-Roth spirometer, a closed circuit method. Although there are no problems with the theory of this method, which depends upon having a spirometer containing a known volume of oxygen which then gradually diminished as it is breathed by the subject, yet some departures from normality may result from the procedure. This may happen because dry oxygen is being breathed and it is known that this sometimes has an effect on the normal respiratory pattern, and thus on the metabolism.
Of the open-circuit methods, the oldest and still probably the commonest is with the use of the Douglas Bag. This is now a plastic bag of variable size (a 100 litre or 150 litre is usually the most convenient for BMR determinations) which, by means of inspiratory and expiratory valves, collects all the air breathed out by the individual during the timed experimental period. Breathing into the Bag involves the use of either a light-weight mouthpiece or a mask fitted with inspiratory and expiratory valves. Either technique may again interfere with normal respiration in an individual unaccustomed to the procedure and can easily cause marked hyperventilation with a resultant increase in metabolic rate. It should always be routine practice to examine the level of pulmonary ventilation carefully to ensure that no obvious hyperventilation has been going on: a rough approximation would be maximum values of about 5 litres/min for a small woman and 10 litres/min for a large man, and more than these levels would make it a likelihood that the final calculation of the BMR may be too high. Needless to say, mouthpieces and masks should fit correctly with no leakage - not always a simple straightforward matter!
Analysis of the expired air for the oxygen and carbon dioxide content can be done by chemical means, using a ‘micro’-Scholander or a Lloyd-Haldane or other apparatus, or by more rapid and modern methods which depend upon certain physical characteristics of the gases. The former are slower and more tedious to use (and so less popular in nutritional as opposed to physiological laboratories) but are more reliable and are certainly very advantageous at least for the calibration of the more complex physical methods.
Other types of apparatus using a continuous flow and monitoring of the composition of air passing inside a hood across the face of the subject can also be employed with no necessity for the use of either a mouthpiece or a mask. If this equipment is calibrated frequently and used carefully, it is probably best of all for BMR determinations.
In summary, several factors may contribute to the variability in BMR, as recorded in published data, within any one individual and between roughly similar individuals. Some of these reflect methodological difficulties (e.g. the influence on normal respiration due to the use of masks or mouthpieces, etc.), some may be actual methodological errors (leaks in the apparatus, inadequate calibration of volumetric meters and gas-analysis equipment, errors in calculating metabolic rate because of hyperventilation and an incorrect R.Q., etc.), and some reflect the normal biological variability (e.g. Rutter, Brown & Hull, 1978), using apparently acceptable experimental techniques, found a S.D. of ± 15% in the resting oxygen consumption of small babies which was inexplicable on grounds of age, size, nutritional state, etc.; Bailey, Harry, Johnson & Kupprat (1973), in studies on 6 men and 4 women, whose BMR's were measured every 15 min. for 6 hours, found evidence of both diurnal and cyclic (about 2 hourly) variations with an amplitude of 7–20% of the mean).
Additional to these methodological influences, the selection of the value for the BMR, as it was actually measured, varies with different investigations. Much was written in the classical literature about which value should be reported as the BMR of an individual - e.g. the average of 2 or 3 readings made in duplicate on different days, the lowest reading, whether or not single readings were acceptable, etc. Probably, most investigations or reviews would not be in sympathy with the use of only the lowest measured value of the BMR (as in the study reported by Robertson & Reid, 1952), which has overriding physiological, philosophical and technical objections.
Variations from the highest to the lowest result, as investigated by Florentino & Guzman (1963) on 30 young adult women with duplicate measurements on 3 successive days, had a maximum value of 420 kJ (100 kcal) per day. Fulton (1972), in studies on 60 adult women, found that only 30% produced the highest result on the first test, and indeed 30% of these women had the lowest result on the first occasion they were measured. In fact, Sargent (1961) in a detailed review of this whole problem concludes that, with the exception of selecting the lowest BMR result, no significant effect is produced by the method of selection or computing of the basal metabolic data.
However the sum total of all the experimental and biological variations, even with maximal care to produce well-controlled situations, is not negligible, and it does not seem very sensible or logical to resort to manipulations concerned solely with producing minor improvements in standardization of data which has such a large variability.
Body weight or surface area: BMR is expressed as energy per unit of body size per unit of time. In the past, these units have frequently been kcal/sq.m. of surface area/hour. Whether or not these are the most appropriate units is a matter for considerable controversy (except that the energy unit is now preferentially the kJ instead of the kcal). It should be noted immediately that there is no unanimity on the proper unit for body size and that the decision may depend upon whether only man is being considered or whether a variety of animals covering a large range of body size is being examined. The classic table of Voit (1901) giving the heat production of resting animals of varying sizes in a thermoneutral environment shows clearly that the energy expenditure ranges from 212 kcal/kg/day for a mouse to 11 kcal/ kg/day for a horse - a 20-fold difference - whereas expressed per sq.m. of surface area the range is from 1200 kcal/day for the mouse to 950 kcal/day for the horse, and values for the other animals are within about ±20% of the mean for the group.
From this sort of information, it was concluded that animals of different body size must produce heat at approximately the same rate per sq.m. of body surface in order to maintain a constant body temperature. A further deduction is that basal metabolism is determined by the rate of loss of heat from the body.
The so-called ‘surface area law’ about the ‘constant’ relationship between basal metabolic rate and surface area had been the subject of experimentation and discussion by such great names as Rubner (1883), Richet (1889), and Krogh (1916), and it acquired and has retained for almost 100 years an aura of almost absolute validity. Almost all standards of BMR have been expressed in terms of energy per sq.m. of surface area per hour.
Much has been written on the ‘surface area law’, not all of it in favour and Brody (Brody & Elting, 1926) and Kleiber (1947) are two of the distinguished animal nutritionists who have disagreed with its use. However, the arguments in the past have mostly been oriented towards finding a formula which would be applicable in a reasonably uniform way to animals with a considerable range of body sizes. Although there may be applications from such data to man which require a universal formula, on the whole a less all-embracing approach is probably adequate, with the emphasis on an expression of the relationship between BMR and body size which encompasses the range, still quite wide, from young infants to the moderately obese adult (3 to 100 kg).
With this attitude in mind there are two theoretical considerations which somewhat inhibit the acceptance of surface area as the unit of size. Firstly, as mentioned above, if surface area determines the heat loss from the body, the level of basal metabolism must depend upon the surface area, whereas, in fact, basal metabolism is a function of the metabolic activity (or oxygen consumption) of all the separate active tissues of the body and is dependent on the relative mass of these tissues. The ratio of the mass of the different tissues in individuals of varying body size will not always be the same: e.g. in adults, relative masses of muscle, skeleton and adipose tissue may vary considerably and there are basic differences in many tissues between infants and adults. However, a fundamental premise might well be that the mass of the body tissues must be more important than the surface area of the body, although the metabolic rate of the same mass of tissue might differ as a function of age, and the relative masses of the several tissues within the whole body may also vary. Secondly, surface area is not a reference which is measured. It is calculated from height and weight, probably using the formula of Du Bois & Du Bois (1916), and has an unknown error attached to its use for any given individual: Mitchell, Strydom, van Graan & vander Walt (1971) found that the Du Bois formula consistently underestimated the surface area of 237 young adult males relative to the true area as measured by a photometric technique. Body weight, on the other hand, if it can be shown to be an acceptable reference, is one of the easiest and most accurate of all biological measurements.
It might be helpful to examine some illustrations of the supposed usefulness of surface area contrasted to gross body weight as the reference unit. Durnin (1959) has shown that in a range of different situations from sitting and standing to various types and severities of exercise, there is no difference in correlation coefficients when metabolic rate is related to either gross body weight or to surface area.
Keys, Taylor & Grande (1973) analysed relationships between BMR and weight (W), height (H), surface area (SA), and H and W in 296 men. They found that BMR was least correlated with H and most correlated with the combination of H and W, but there were no significant differences between the correlation coefficients and all values were low (r = +0.47 was the highest value). In this series, it was clear that the vast proportion of the variance was unrelated to any of these measurements of body size.
The BMR data of the women studied by Harris and Benedict (1919), when plotted against W (Fig. 1) and SA (Fig. 2), show the same variability:
FIGURE 1: BMR and body weight in women
(Harris & Benedict, 1919)
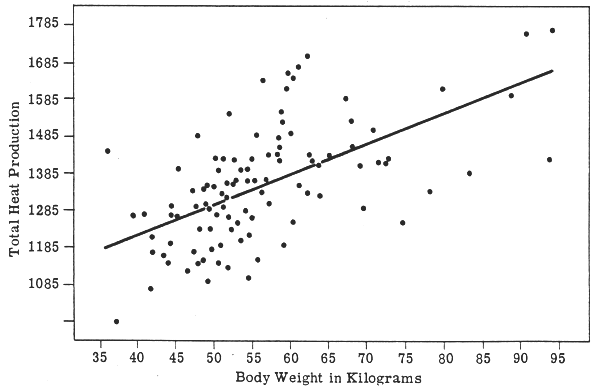
FIGURE 2: BMR and surface area in women
(Harris & Benedict, 1919)
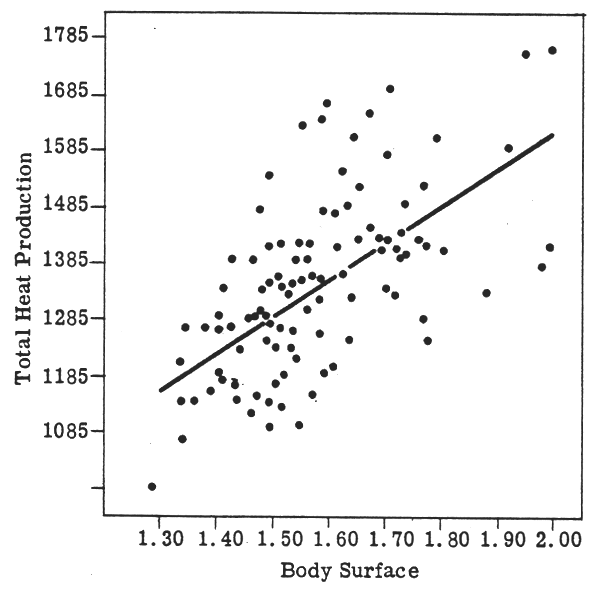
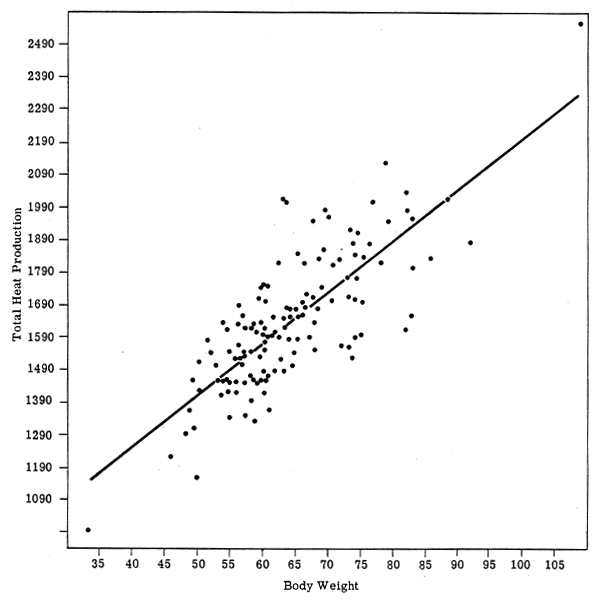
BMR and W for men (Fig. 3) shows perhaps a smaller degree of scatter, probably indicating a more homogeneous group. (It should be noted that these scatter diagrams are transposed directly from the original publication by Harris & Benedict and that the linear regression lines are also the originals: it may well be that the relationships are not best represented by these straight lines.) The use of SA as the reference provides no particular advantage (as the authors themselves pointed out). The correlation coefficients also demonstrate the similar effect of either W or SA, the slight differences between the sexes, and the relatively low influence of either W or SA on the variance. Table 1 gives these correlation coefficients for the re-analysed data of Harris and Benedict (1919) and also for the data of Boothby and Sandiford (1922) (with, in the latter case, the sex difference having the opposite tendency). The paper by Berkson & Boothby (1936) also confirms the lack of useful benefit in using SA as the reference rather than W, although that was not the intention of the authors. Indeed, the examination of a simple scatter diagram of W against BMR compared with one of SA against BMR for any set of published data on man will show clearly the complete absence of any important reduction in the variability of the data when SA is the reference.
FIGURE 3: BMR and body weight in men (Harris & Benedict, 1919)
| Men | Women | |
| W v BMR | +.795 | +.603 |
| SA v BMR | +.799 | +.611 |
| (re-analysed data of Harris & Benedict, 1919). | ||
| W v BMR | +.571 | +.816 |
| SA v BMR | +.626 | +.830 |
| (re-analysed data of Boothby & Sandiford, 1922). | ||
Perhaps one of the principal reasons why SA has remained for so long as the preferred unit has depended on the purpose for which BMR determinations were made. Until very recently, apart from an academic interest in comparative species or ethnic differences, by far the most prevalent use of the BMR was in the assessment of thyroid function and in the diagnosis of hyper- and hypothyroidism. For both the academic and the clinical objectives, the differences being assessed were often difficult to interpret because of the ‘blurred’ area in-between; that is, if the BMR of Chinses people was being compared to that of Mexicans, the variability of both peoples was such that there could clearly be a very considerable overlap, even if there happened to be basic dissimilarities between them, and similarly the range of the normal BMR was such that the diagnosis of hyper- or hypo-thyroidism was often a difficult problem. Therefore, great effort and much manipulation of parameters took place to try and reduce, by any means, the extent of this diversity and to make the BMR appear to be a more uniform biological variable.
Nowadays, BMR in the diagnosis of thyroid disease has been superseded by better and more specific techniques. The attainment of spurious homogeneity is less relevant and perhaps a more dispassionate and scientific attitude may now be adopted.
Nevertheless, the fact that variability of a moderate degree exists among individuals who appear comparable in body size and in other respects should be sufficient stimulus by itself for the continued search for an explanation and a better analysis of the relevant factors. One such clue might reside in differing body composition with variable amounts of ‘active’ tissue enclosed in the same total mass of the body. This concept, suggested by Benedict in 1915 (Benedict, 1915a), that the active protoplasmic mass as distinct from ‘metabolically inert fatty tissue’ was the most important governing factor in relation to BMR, has been more recently connected with the so-called ‘lean body mass’ or, more correctly, the fat-free mass. Within the past 30 years or so several methods have been described for measuring the fat mass and the fat-free mass of the human body, and a renewed quest has been instigated for the ideal reference to which can be related BMR, total haemoglobin, resting cardiac output, and many of the other variables which look as if they ought to be closely connected to some aspect of body size. The ‘active cell mass’ or the ‘lean body mass’ or a similarly named entity seemed to fulfil the purpose.
However the concept is biologically naïve. Firstly, the adipose tissue mass is not metabolically inactive. It has been known histologically for a long time that adipose tissue has a fairly profuse blood supply and, in the more recent past, it has been shown biochemically that adipose tissue may be active in energy transformations. Secondly, although ‘active tissue mass’ represents the sum of bodily tissues which participate more actively in the resting energy metabolism of the body, it is not, as Brozek and Grande (1955) discuss, an homogenous mass of tissues all having similar metabolic rates. Because of the wide range both of metabolic rates for different tissues and of relative masses of these tissues in different individuals, the BMR of apparently similar individuals will often vary markedly. Both from the theoretical point of view and from the practical experience demonstrated in the thousands of published results of BMR determinations, it is to be expected that no prediction of BMR, no matter what the reference unit, is possible without appreciable error being attached to it. The extent of this error has usually either not been well understood and appreciated or has been ignored, and this largely invalidates many previous reviews, such as the otherwise excellent one by Mitchell (1962) on ‘body size and basal metabolism’.
Nonetheless, on average, there may be small decrements in BMR due to a larger mass of adipose tissue and this may also exert an effect within the context of apparent differences between the sexes and progressive changes in metabolic rate with ageing, which will be discussed further in the subsequent section.
Basal metabolism and sex, age, race and climate, and nutritional state.
Sex: From the published data, which is mostly expressed as metabolic rate per unit of surface area, there seems to be a well-established difference in BMR values for males and females, (females having a lower rate), which appears after the first few years of life, reaches a maximum of about 10% at around puberty, and then gradually falls to 5% or so from early adult life onwards. The difference may be due to the larger adipose tissue mass in women. However, it has already been mentioned that in the days immediately prior to menstruation in the female cycle there may be a 2–5% increase in metabolic rate, so that for at least part of the normal menstrual cycle there will be insignificant differences between men and women. Sex differences will be discussed further in the section on practical applications.
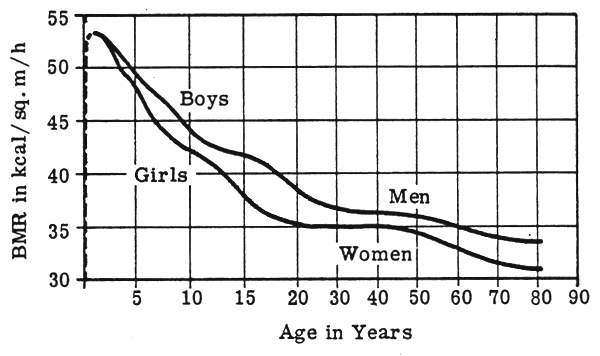
Age: Any table of BMR standards shows striking effects of age on BMR values, expressed as energy per unit body size. A typical example would be the data compiled by Fleisch (1951) based on several thousand observations from 24 sets of measurements and covering the age span from one year up to age 80. The maximum value is reached during the first year of life from which there is a fall of about 20% by age 10 y., a slight decrease in the rate of fall during puberty, then a further decline until about age 20 y. by which time BMR is only 70% of its rate (per unit of body surface area) at 1 year of age. Another 10% decrease then occurs by the age of 60 y. (Fig. 4). Per unit of body weight the BMR at age 20 is only just over 30% of its value in the first year of life.
FIGURE 4: Change in BMR with age (from Mitchell, 1962)
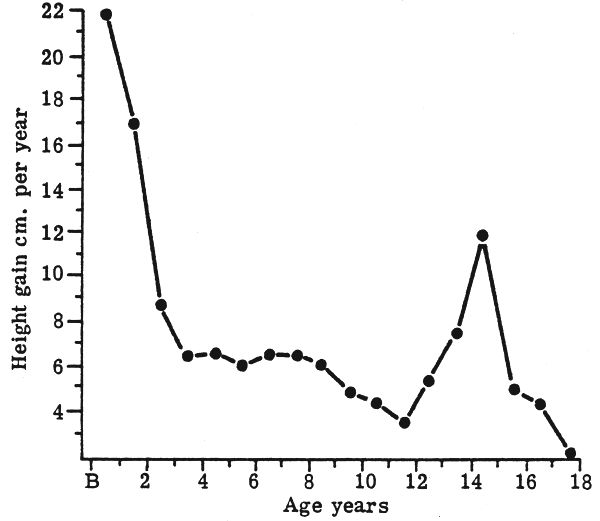
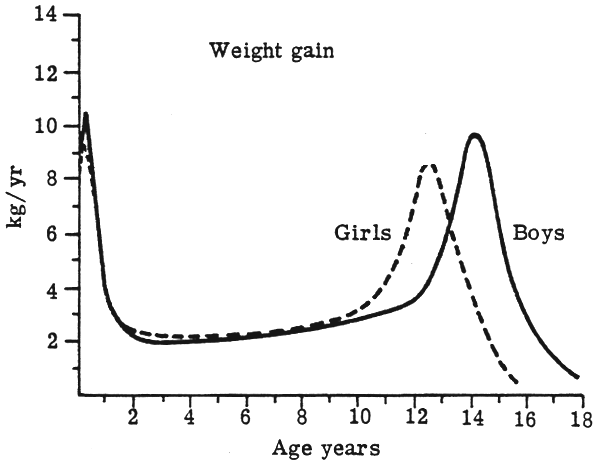
These considerable reductions in relative BMR are difficult to comprehend in relation to the ‘growth’ pattern during the first 20 years of life. First of all, they do not fit in very well with the velocity of growth which, for height (Fig. 5), can be seen to have minor spurts between age 4 to 7 y. but a major spurt at adolescence. The comparable velocity curve for weight (Fig. 6) shows a slow gradual rise throughout most of childhood and then the major spurt at adolescence. Therefore, not only is the overall mass of the tissues and organs in the body increasing during the period from birth to maturity, but for several years the actual rate of increase is accelerating. It seems at first astonishing that the BMR should be falling, proportionate to body size, during this time.
FIGURE 5: Height velocity curve (Tanner, 1962)
There are some partial explanations. Body mass increases by a factor of about ×20 from birth to maturity (from about 3 kg. to about 60 kg.). However, there are wide differences in the relative increase of the important organs (Sinclair, 1973). The brain, which has a fairly high metabolic rate, increases its mass by only a factor of ×5; the liver, heart and kidneys (with even higher relative metabolic rates) increase mass by a factor of about ×10 to ×12; whereas skeletal muscle, which has a low metabolic rate at rest, multiplies its mass from birth to maturity by about ×40. The effect of the increased relative proportion of muscle in the total body mass during growth, together with the effect of the low metabolic rate of the growing skeleton, results in the comparative lowering of BMR during even this period of life.
Table 2 gives some approximate values for the weights and metabolic rates of the liver, brain, heart, kidneys and skeletal muscles, which together account for about 80% of the energy expended in basal conditions by the whole adult body. These values are given for an average 70 kg. adult man and for a 3.5 kg. newborn baby. The metabolic rates for the neonate are calculated by multiplying the weight of the appropriate organ by the metabolic rate of that organ in adult tissue and, although the total metabolic rate for the organs and tissues approximates to the value given by Benedict & Talbot (1921) (750 kJ or 180 kcal), they may be an underestimate of the real values. Nevertheless the table gives a useful indication of the actual amount of energy required by these different organs in their ‘resting’ state in the adult, and also shows the proportionate alterations that have occurred between birth and maturity.
FIGURE 6: Weight velocity curves (Tanner, 1962)
| Adult | Neonate | |||||||
| Wt (kg) | MR (m102/min) | MR/day kJ(kcal) | MR/kg/day kJ(kcal) | % total MR | Wt (kg) | MR/day kJ(kcal) | % total MR | |
| Organ | ||||||||
| Liver | 1.6 | 67 | 2018 (482) | 1261 (301) | 27 | 0.14 | 177 (42) | 20 |
| Brain | 1.4 | 47 | 1414 (338) | 1010 (241) | 19 | 0.35 | 354 (84) | 44 |
| Heart | 0.32 | 17 | 512 (122) | 1600 (382) | 7 | 0.02 | 32 (8) | 4 |
| Kidneys | 0.29 | 26 | 783 (187) | 2700 (645) | 10 | 0.024 | 65 (15) | 7 |
| Muscle | 30.00 | 45 | 1356 (324) | 45 (11) | 18 | 0.8 | 37 (9) | 5 |
| Misc. | constitutes remainder | |||||||
| Total | 70.00 | 250 | 7530 (1800) | 108 (26) | 3.5 | 750 (180) | ||
Organ weights taken from Boyd (1962)
Another problem in estimating BMR from previously published tables, for ages covering the growth period, is caused by the so-called secular increase in growth which has taken place during the last several decades. The effect of this secular increase is that in most of the developed countries children aged say 8 y. old now would be the equivalent in height and probably also in weight to a child of 10 or 11 y. 40 years ago. The actual difference will vary, depending on the general state of the developing or the developed country and also on the social group of the child: in some countries, e.g. Sweden, parts of the United States, and in the south of England, it appears as if this effect has now reached a maximum and little detectable increase has occurred in children of any age during the past few years. In the more economically favoured social groups, this increase took place some decades ago, whereas in many developing countries the process has either not started in any general way or it is very far from reaching its final stages. Much useful information on growth of many populations in the world is presented in Eveleth & Tanner (1976).
Since much of the data on BMR was accumulated 40 years ago or more, its relevance at the present day will vary subject to the particular population in any given country: guide lines need to be clearly provided for the effective and appropriate practical use of these tables for estimating the BMR of children - something which has not happened in the past but which is attempted in the final section of this article.
During adult life, from age about 20 y. up to between 60 and 70 y., there is conflicting evidence. In the traditional tables, epitomised by those in the excellent review by Fleisch (1951), there is a steady fall in BMR per sq.m. of surface area with ageing. However, certain evidence suggests that this may be not so much age-related as caused by changes in body composition. Keys et al (1973) measured the BMR of 63 men at age 22 y. and again after 19 y. The BMR had decreased by 9% but there had been a gain in weight of 10.6 kg, which the authors suggested might have had some influence. Another group of 115 men aged 44–56 y. were measured for BMR 5 times during a 17 y. period. The change in body weight of these men was a gain of only 1 kg. and no reduction in BMR occurred. Most ‘ageing’ data is of a cross-sectional nature and, on the basis of their longitudinal studies, Keys and his colleagues suggest an ageing decline in BMR of their population of only 1–2% per decade between 20 and 70 years of age. Tzankoff & Norris (1977, 1978), from measurements on 959 men aged 20–97 y., thought that reductions in muscle mass (estimated by creatinine excretion) might be largely responsible for the fall in BMR with ageing. This conclusion was re-inforced by a longitudinal study during 10-plus years on 355 men. Some of the data of Shock & Yiengst (1955) also seem to support this. BMR on a small group of old men, obtained by Benedict, Emmes, Roth & Smith (1914), with one exception, also fit into this category.
The probability is that, when BMR is expressed as energy per unit of body weight, there will be a comparatively small reduction between young adulthood and age about 60 y. which may well reflect an increasing mass of adipose tissue and a decreasing mass of muscle, although beyond 60 y. the decline will be more marked. The actual allowance to be made for ageing will depend upon the type of population, being greater in people whose body weight tends to increase by more than a few kg throughout the span of young adult to middle age.
The inter-related topics of alterations in body mass, body composition, and ageing require much further investigation.
The influence of obesity on BMR is not clear. BMR values obtained by Boothby & Sandiford (1922) on 61 obese women (W = 96 kg) and 12 obese men (W = 105 kg) were within -4% to +1.5% of the Harris & Benedict (1919) standards. James, Bailes, Davies & Dauncey (1978) state that they found an elevated BMR in a group of 69 obese men and women but their data appears to show only that the total BMR on average, as total energy per day, was elevated relative to the total BMR in a group of normal subjects of the same age, sex and height, but relative to weight or surface area 64 out of the 69 individuals were between 80–100% of the standard (Fleisch, 1951).
Race, Climate and Season: The effect, if any, of these variables is still a matter of some differences in interpretation and it is made more difficult by reason of the possible interaction between race and climate. A large series of studies on people of different races was instigated mostly between 1925 and 1937 by the Nutrition Laboratory in Boston where the techniques were always similar and all the investigators had either received their training in the Nutrition Laboratory or been trained by research workers from that Laboratory. These studies and others were reviewed by Wilson (1945). Very considerable variations were reported showing differences from the ‘normal standard’ of from -17% to +15% for groups of individuals: low values were, in general, found on Asian populations whereas certain Central and South American populations had high values. However Wilson states that “from this survey it is apparent that so many different factors may play concurrent roles in affecting basal metabolism that it is impossible at the present time to say whether the different levels of basal metabolism noted with the various races thus far studied are reflections of a racial characteristic alone or are the results of a combination of some or all the factors (technique, functional normality, climate, diet, social milieu, degree of physical activity and muscular relaxation, anthropometric measurements, anthropological and constitutional types), or even of factors thus far unsuspected”.
Much new data has been collected since Wilson's review and perhaps the consensus is clearer now that ethnic differences, by themselves, have probably no effect on BMR and even climate has a limited importance. The BMR of Egyptians (Talaat, Habib & El-Khanagry, 1953), Burmese (Chitre, Mobsby, Thein & Hla Pe, 1959), Thais (Hori, Ohnaka, Shiraki, Tsujita, Yoshimura, Saito & Panata, 1977), Filipinos (de Guzman & Florentino, 1968), Japanese (Hori et al, 1977; Suzuki, 1959), Koreans (Kim, Kim, Ro & Choi, 1966), and several groups of Indians - children and adult men and women, including pregnant and lactating women (Banerjee & Bhattacharya, 1964; Dakshayani & Ramanamurthy, 1964; Mason, Jacob & Balakrishnan, 1964; Mason & Jacob, 1972; Khan & Belavady, 1973) have all been shown to be compatible with accepted standards for North American or European populations.
In studies on 73 Eskimo, a race which had previously seemed to have a relatively high BMR, Rodahl (1952) suggested that these results had been “due to apprehension and a high protein diet” and quoted his own BMR measurements as being the same as in ‘White controls’.
Reviews by Quenouille, Boyne, Fisher & Leitch (1951) and Wilson (1956a) give more detailed information and discussion of some of the published work.
The possibility that BMR may alter at different months or seasons of the year has been further investigated by Wilson (1956b) who measured 15 men monthly for two 6-month periods in a 2 year stay in the Antarctic. He found a seasonal trend but it was very small and he considered that factors (e.g. diet, activity, etc) other than the period of the year were responsible. No difference in the BMR of 4 Arctic Indians was found when they were measured in September (‘fall’) and April (‘spring’) in the Yukon: the environmental temperature in the room on both occasions was kept the same (Elsnet, Andersen & Hermansen, 1960). On the other hand, Gold, Zornitzer & Samueloff (1969), also in studies where the temperature (and also the humidity) was kept the same when BMR determinations were done during summer and again in winter in Israel, found that the mean value in winter was about 14% higher in a group of 17 men. Malhotra, Ramaswamy & Ray (1960) did not find any significant effect of season when 7 men were measured on 7 occasions between May and March of the following year with an outdoor environmental temperature range from 8°C to 39°C.
From the strictly physiological and biochemical point of view, if we consider the organs and tissues which contribute about 80% of BMR - i.e. brain, liver, heart, kidneys, and muscle - there is neither evidence nor likelihood that the metabolic rate of the brain, liver, heart, or kidneys would show any racial differences and the sole possibility might be related to either varying racial abilities in producing differing degrees of muscular relaxation or, perhaps more importantly, that minor degrees of muscular relaxation or, perhaps more importantly, that minor degrees of muscular activity may be induced by environmental temperatures which may still appear to be ‘comfortable’. Indeed, in a more basic sense, it may produce a very artificial situation to measure BMR in a ‘thermo-neutral’ environment on people living in the so-called temperate or in the cold regions of the world, if this ‘thermo-neutrality’ is significantly different from their normal environmental temperature. Since BMR is being analysed in the present context as a means towards calculating total energy requirements, there is little point in being concerned, other than peripherally, with the academic comparison of peoples living in various regions of the world when the measurements are made in artificially standardized conditions. Some allowance may need to be made for climatic factors. The extent of this allowance relative to the climate will need further investigation, which may be extensive and, in contrast to much of the earlier work, may put the emphasis on populations living in so-called temperate climates. As examples of apparently contradictory findings which need resolution, Du Bois, Ebaugh & Hardy (1952) measured relatively small differences in BMR of 13 women exposed to varying environmental temperatures covering a moderately wide zone whereas Wilkerson, Raven & Horvath (1972) showed that the BMR increased progressively in men exposed to ambient temperatures lower than those compatible with the lower critical temperature (about 25°C for unacclimatized Caucasians).
If a ‘climatic’ allowance is justified the result may be an addition to the BMR for people exposed to environmental temperatures lower than thermoneutrality (which will clearly be influenced by season or the time of the year). Such allowances will depend upon measurements of BMR on people in a thermal environment appropriate for the particular individuals being investigated. Since this experimental situation is not normally the case - and is actually contrary to the usual stipulations of a proper BMR determination - it makes the practical use of previously published BMR values, in the assessment of energy requirements, of even more complexity. It also further heightens the difficulty of justifying the use of involved and ultra-correct formulae designed to allow calculation of BMR from equations with powers for height, weight, sex, age, body composition, even temperature and humidity. As an example of the impracticability of such manoeuvres, body composition, from the aspect of the amount and distribution of adipose tissue, may well have an interactive effect with environmental temperature on metabolic rate, but it is not possible to take it into account in any realistic fashion. Yoshimura, Yukiyoshi, Yoshioka & Takeda (1966) in a comparison of American investigations showing no seasonal change in BMR and Japanese data demonstrating some seasonal effects (although only to the extent of about ±8%), speculated that the difference between the respective results might be due to the combination of a normal thermo-neutral environment of the American way of life, with central heating and air conditioning, coupled with a dietary intake and body composition, all different from the Japanese. With present knowledge useful predictive formulae will have to be simple formulae which concentrate on the most important variables - body weight, probably age to some extent, and sex.
Nutritional state: a point of some practical and also philosophical importance relates to the effect on the BMR of the nutritional state. In well-fed populations, this relationship is of no import unless a state of overnutrition has arisen acutely within the previous days or weeks with, as yet, little influence on the amount of adipose tissue in the body but with possibly a significant stimulatory effect on BMR. BMR values, and any extrapolations from them might then be too high. Excluding this unusual situation, chronic overnutrition will cause obesity and will probably not radically alter the BMR from the normal range (Means, 1916; Boothby & Sandiford, (1922) James, Bailes, Davies & Dauncey, 1978; Durnin, 1978b).
In people on a low plane of nutrition, the circumstances are both important and complex. They are important because it has been well-documented that BMR is reduced by undernutrition. There is little need to quote more than the classical experiments of (1) Benedict (1915b) which showed measureable falls in BMR after a few days of total fasting reaching a plateau level of about a 25% decrease after 20 days or so, (2) Benedict, Miles, Roth & Smith (1919) which also showed a considerable fall in BMR (16%) in 12 young men on an energy-restricted diet for 4 months, and (3) the exceptionally extensive studies of Keys and his colleagues (Keys, Brozek, Henschel, Mickelsen & Taylor, 1950). These last investigations were carried out on 32 young men who lived for 6 months on a ‘European war-time famine diet’ which resulted in a mean loss of body weight in the group of 24% of the original weight. BMR fell to a value only about 70% of the initial rate but the reduction had almost ceased towards the end of the experiment. These declines in both body weight and BMR were interpreted by Taylor & Keys (1950) as part of the process of adaptation to the nutritional stress. Presumably they would be expected also to be present in people chronically exposed to nutritional intakes which are lower than desirable. Therefore, measurements of BMR on some populations in developing countries might show lower values than those of European or North American peoples, not because of any racial or climatic factor but because of the nutritional state. Calculations based on current BMR values on such populations might therefore be used to estimate energy requirements of these groups but would not necessarily evaluate desirable levels of intake. Care would need to be exerted in utilising certain data in the literature because of this possibility.
It is also possible that specific nutrient deficiencies might affect the basal metabolism. No uncomplicated studies seem to have been carried out on man but numerous animal experiments, cited by Kleiber (1945) and Mitchell (1962), appear to indicate that dietary deficiencies of potassium, magnesium, and calcium quite definitely though not always substantially increase the BMR. Vitamin deficiencies have not been shown to affect the BMR.
State of physical fitness: populations differ markedly with regard to their state of physical training or fitness - for example, a group of agricultural labourers or military recruits compared to a sedentary group of office workers. If physical fitness had an influence on BMR this would need to be taken into consideration. The possibility has been intensively investigated in the past and any response when it occurred was so small as to have no significance for present purposes (Benedict & Smith, 1915; Harris & Benedict, 1919; Steinhaus, 1928; Schneider & Foster, 1931; Robinson & Harman, 1941; Knehr, Dill & Neufeld, 1942; Karpovich, 1953).
Altitude: there is a great deal of published data on the effect of altitude on BMR, most of it of little relevance in the present context since it concerns adaptations in BMR to relatively short sojourns at altitude. The results are often contradictory. Hannon & Sudman (1973) summarise some of the literature briefly and their conclusion, together with their own results, seems to show that BMR in acclimatized altitude dwellers falls within the normal range. It might be expected that BMR in permanent dwellers at altitude, e.g. on the Peruvian plateau, would be slightly raised because of the increased cardiac output at rest, increased respiratory movements, and even increased renal work required in the excretion of base, but these would all be comparatively small in extent and possibly still allow BMR to be near the normal range.
Practical Applications
Since the original FAO Committee on Calorie Requirements produced its report in 1950, which utilised BMR as part of its ‘factorial’ method of calculating energy requirements, neither of the subsequent Committees (FAO 1957; FAO/WHO 1973) nor other similarly commissioned bodies (e.g. Department of Health and Social Security, 1979; National Research Council, 1980) have used this approach. It is not the purpose of this article to elaborate on the usefulness or otherwise of the estimation of BMR as the first step in the calculation of energy requirements but, as its name implies, it has at least the potential of forming the base on which can be built the total energy needs of an individual or a group. BMR has not been used very sensibly in the past, and has indeed frequently been misused, but it may, in the future, be the key factor in a more flexible assessment of energy requirements for populations.
However, the first essential is to be fully aware of the limitations of the data on BMR. A brief re-capitulation of points to bear in mind might be useful.
The ideal situation - completely impracticable - is to have an actual BMR measurement on every individual whose total daily level of basal metabolism is required. Nevertheless, even if this were possible, because of 1) methodological problems in the measurement, 2) whether or not more than one measurement had been made, 3) the influence of various factors on the individual (anxiety, discomfort, nutritional state, sexual cycle in females, etc.), and 4) ‘normal’ biological variability, the validity even of a measured BMR on an individual would be open to some latitude in interpretation.
The next best information to have available would be data on the BMR of a similar population to the one being assessed, e.g. 10–15 year old children living in rural areas of N-E India or 20–40 y. men and women in Indonesia. Even when some data is available (and there is comparatively a considerable quantity on Indian children), at this stage the probability becomes greater of having to indulge in further ‘knowledgeable guesstimates’. In most situations of assessing BMR on populations there will almost certainly be a great dearth of up-to-date measurements available on comparable groups. For children, because of variable growth rates and secular increases in height and weight, it would appear to be even more difficult.
Finally, there are many so-far unresolved influences having a greater or lesser effect on BMR which are impossible to take into account - body composition, environmental temperature and climate, clothing insulation, are some of the more important.
The conclusion must surely be that, at the present time, there are no means available to us to be precise in our estimate of BMR, other than in a completely spurious manner. It is quite astonishing to consider the probably futile efforts which have been exerted in the examination, of the data on man, of weight, weight to the power 0.7, 0.73 or 0.75, and surface area, as the unit of preference when there is clearly almost no difference between any of them, all of them are useful only in a very imperfect fashion, and one of them - weight - is easy, accurate and simple to measure and to utilize. It is equally surprising to examine closely the tables produced by Quenouille et al (1951) and those in the FAO/WHO Report (1973). The former appear very useful tables of metabolic rate for boys and girls and men and women of a range of body weights with separate columns for each of a range of heights. A table is given for “U.S. - N. European Men” and another for “Asian Men” and there is the same arrangement for the women (no similar separate tables are given for the children). At least in the case of the men, this distinction seems quite unnecessary because the differences at any given weight and height are small enough to be without any importance; for example, in a random sample from the tables of 42 different weights and heights, the difference in total daily BMR between the U.S. - N. European and the Asian men averaged 160 kJ (38 kcal) and all of the large differences occurred in very tall men (more than 190 cm) who were also light in weight. In the case of the women, although the differences were still not large (175 kJ or 42 kcal) they were more consistently present and a minimal error would be made by subtracting this quantity from the U.S. - N. European values.
Similarly, in the FAO/WHO table (quoting Talbot's, 1938, data), although the data have been assembled from the original measurements in a manner not strictly valid, yet the difference between the values quoted for boys and those for girls, with body weights from 3 up to 30 kg, averaged about ±38 kJ (9 kcal) per day! With the available information such discrimination is without biological justification and fulfils no useful practical purpose.
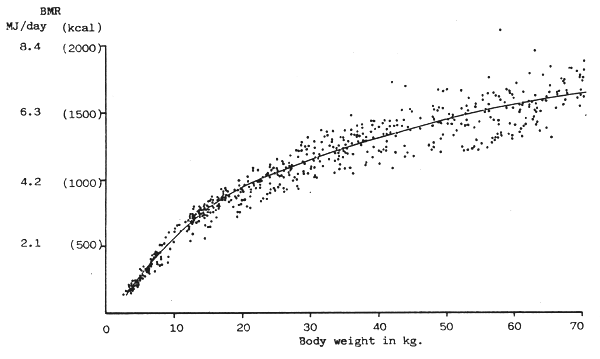
The philosophy developed thoughout the preceding sections of this assessment of basal metabolic rate has necessitated the production of a simple table to allow calculation of BMR with a degree of precision compatible with the validity of the data. With this objective, previously published data has been plotted with total daily basal energy and gross body weight as the ordinates, and various groups have been examined.
Fig. 7, and Figs. 8–13, have been constructed from BMR measurements on over 1200 infants, children and adolescents, the sources of which are given on the figures. The data represent U.S., Swedish, Danish, Dutch, Japanese and Indian populations, all of them apparently having the same general distribution. Figs. 16 and 17 are derived from data on men and women respectively, each of them covering many hundreds of individuals including U.S., Chinese, Burmese, Indian, Japanese and Swedes and also, for the women, some Filipinos. Again, in these adult data, there is no evidence that any of the groups differs significantly from the remainder.
Infants and children: some perhaps surprising implications arise from an examination of the relationships between body weight and basal metabolic rate in infants and children. First of all, in the range of body weights from about 3 kg up to about 30 kg, neither sex nor chronological age assume importance. (See also Garn & Clark, 1953 and Sargent, 1961). Body weight is the chief variable and differentiating the data between males and females and making allowances for age are unnecessary in any useful practical sense. A body weight of 30 kg corresponds on growth curves for weight (e.g. Tanner, Whitehouse and Takaishi, 1966, on British children) to an age of 10 y. or so but, although this age will obviously vary with the population, the actual age has little practical relevance. Below that weight, the growth curves at the 50th centile for boys and girls are almost identical; indeed the only slight difference between the sexes for any of the centiles is at the 90th centile which is marginally higher for girls during the last 2 or 3 years of this period.
FIGURE 7: BMR plotted against body weight for 1200 infants children and adolescents of both sexes
(Sources of data: Banerjee & Bhattacharya, 1964; Benedict & Talbot, 1921 Dakshayani & Ramana, 1964; Khan & Belavady, 1973 Lamb & Michie, 1954; Lewis, Kinsman & Iliff, 1937 Quenouille, Boyne, Fisher & Leitch, 1951 Talbot, Wilson & Worcester, 1937)
Therefore, for children weighing 30 kg or less, an estimate of their basal metabolic rate in energy units per day may reasonably be made from their body weight alone, with sex and age having no important influence on the calculated value.
Beyond a body weight of about 30 kg there is some increase in the scatter of the data. This part of the diagram would include the pubertal growth spurt which will often result in a marked sex difference in weight gain, and superimposed on this within each sex, there may be large variations in the rate of weight gain, i.e. the individual child may follow the 50th centile, or be somewhere nearer the lower or higher centile levels.
Accordingly, for both boys and girls of ages 10 y. up to 18 y., the data was plotted separately for each sex and further subdivided into 3 sub-groups in each case, a) those boys and girls between the 3rd and 25th centile, b) those between the 25th and 75th centile, and c) those between the 75th and 97th centile. That is, for both boys and girls, all of the separate BMR values from the sources quoted on the figures was plotted, depending on which was the appropriate centile range for the individual's weight relative to his or her age. The relevant centile ranges are given on the respective figures.
Figs. 8–10 show the data for the 3 centile ranges for the boys. The distribution of points differs, with, as would be expected, more of the boys in the 3–25 centile having body weights and BMRs at the lower end of the range compared to those in the 25–75 and 75–97 centiles. It would be helpful to have more information in the 75–97 centile but, assuming the data presented here does not give a distorted picture, it is interesting to note that the 3 sets of data can be superimposed on each other with an almost perfect fit of the regression lines. In other words, a single regression line can be drawn to fit all the data for these boys, aged 10 y. to 18 y. and with body weights ranging from 20 to over 70 kg. There is a considerable scatter of points around the line but this variance is of a similar order to all the BMR data in the literature.
FIGURE 8: BMR plotted against body weight for boys between 3 and 25
centile of Tanner, Whitehouse & Takaishi (1966) growth chart
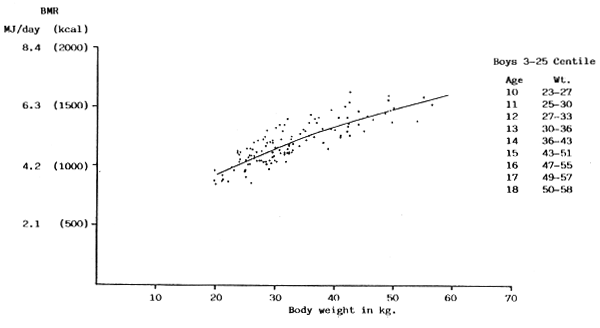
(Sources of data: Benedict & Talbot, 1921; de Bruin, 1939; Lewis, Kinsman & Iliff, 1937; Nakagawa, 1937; Olmstead, Barr & Du Bois, 1918; Stark, 1935; Topper & Mulier, 1932; Wang, 1939; Wang, Kern, Frank & Hays, 1926; Wilson & Roy, 1938)
FIGURE 9: BMR plotted against body weight for boys between 25 and 75
centile of Tanner, Whitehouse & Takaishi (1966) growth chart.
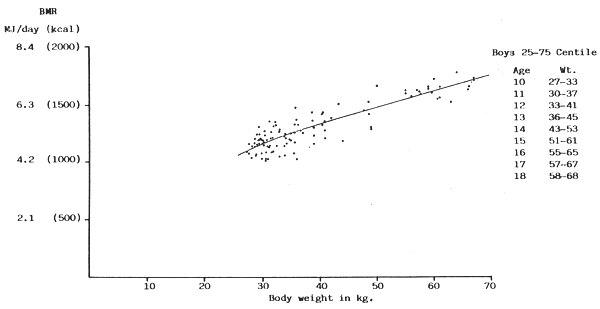
(Sources of data: de Bruin, 1939; Benedict & Talbot, 1921; Lewis, Kinsman & Iliff, 1937; Nakagawa, 1934; Nakagawa, 1937; Olmstead, Barr & Du Bois, 1918; Stark, 1935; Topper & Mulier, 1932; Wang, Kern, Frank & Hays, 1926)
FIGURE 10: BMR plotted against body weight for boys between 75 and
97 centile of Tanner, Whitehouse & Takaishi (1966) growth
chart
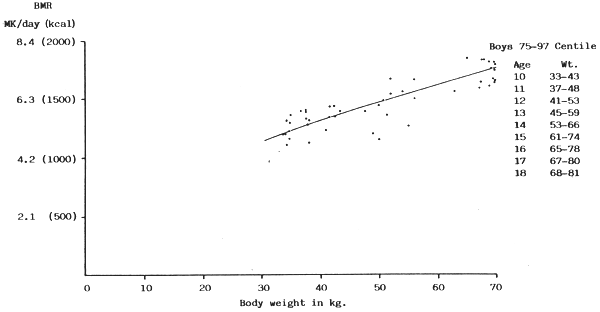
(Sources of data: Benedict & Talbot, 1921; de Bruin, 1939; Lewis, Kinsman & Iliff, 1937; Stark, 1935; Topper & Mulier, 1932)
FIGURE 11: Composite data for all boys between 3 and 97 centile
of Tanner, Whitehouse & Takaishi (1966) growth chart
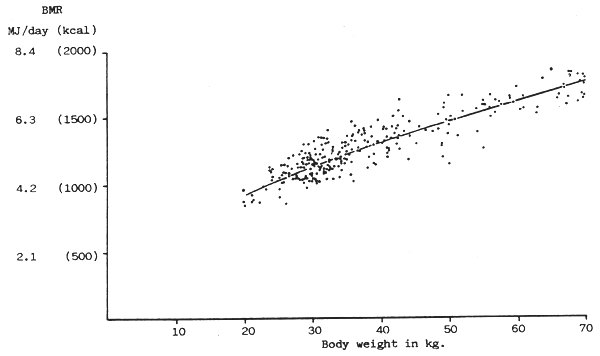
It seems clear therefore that in this age group also there is no specifically age-related effect of any importance. Also, since some Japanese and Indian boys were included (some of the latter being 40 Calcutta boys in the 3–25 centile from a low socio-economic group, who fitted well into the rest of the data in Fig. 8 the likelihood of a racial effect exerting a significant influence may not be high, although clearly the factors of climate and body composition in the heavier boys needs much further investigation.
The published data available for girls (Figs. 12–14) shows a similar picture to those of the boys, and again when the scatter diagrams are superimposed the same resultant single regression line fits the data adequately (Fig. 15).
With both boys and girls, the relationship is curvelinear, those with the heavier body weights having a lower BMR/kg body weight than those of lighter build. This may be a reflection of the fact both that the heavier weight represents an older individual and that it may also characterize a different body composition.
There are differences between the sexes in the weight range from about 30 kg upwards, the amount varying from a value for the boys of about 6% higher than the girls at weights 30–45 kg, 8% higher at 50 kg, 10% at 60 kg and 13% at 70 kg (values are given in Table 3). These differences, above body weights of 50 kg, are similar to those found between adult men and women and are presumably due partly to basic sexual differences which might be related both to metabolic rate of the same tissue (e.g. the same mass of muscle might conceivably have a higher metabolic rate in males than in females) and to differing relative masses of tissues (e.g. muscle and adipose tissue) in males and females. However, these are largely still suppositions and further research is needed in this field.
FIGURE 12: BMR plotted against body weight for girls between 3 and 25
centile of Tanner, Whitehouse & Takaishi (1966) growth chart
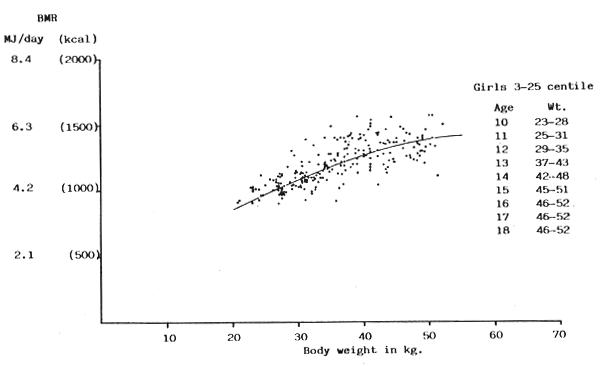
(Sources of data: Benedict & Talbot, 1921; Blunt, Tilt, McLaughlin & Gunn, 1926; de Bruin, 1939; Lewis, Kinsman & Iliff, 1937; Nakagawa, 1934; Nakagawa, 1937; Nylin, 1935; Topper & Mulier, 1932; Vogelius, 1945; Wang, 1939; Wang, Kern, Frank & Hays, 1926; Wang, Kaucher & Wing, 1936)
FIGURE 13: BMR plotted against body weight for girls between 25 and 75
centile of Tanner, Whitehouse & Takaishi (1966) growth chart
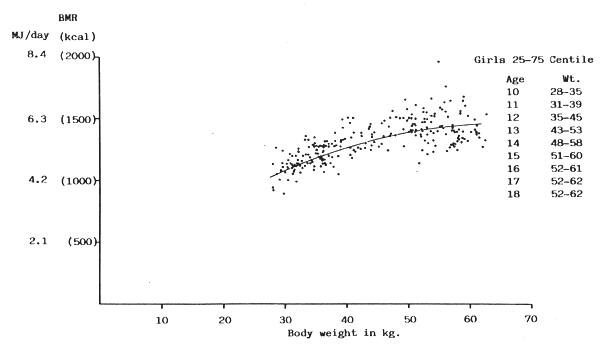
(Sources of data: Benedict & Talbot, 1921; Blunt, McLaughlin & Gunn, 1926; de Bruin, 1939; Lewis, Kinsman & Iliff, 1937; Nakagawa, 1934; Nakagawa, 1937; Nyling, 1935; Topper & Mulier, 1932; Vogelius, 1945; Wang, 1939; Wang, Kern, Frank & Hays, 1926; Wang, Kaucher & Wing, 1936)
FIGURE 14: BMR plotted against body weight for girls between 75 and 97
centile of Tanner, Whitehouse & Takaishi (1966) growth chart
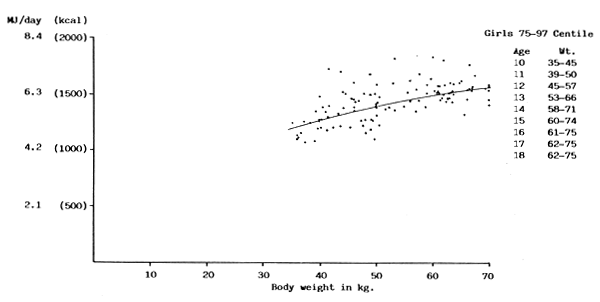
(Sources of data: Benedict & Talbot, 1921; Blunt, Tilt, McLaughlin & Gunn, 1926; de Bruin, 1939; Lewis, Kinsman & Iliff, 1937; Topper & Mulier, 1932, Vogelius, 1945; Wang, Kaucher & Wing, 1936)
FIGURE 15: Composite data for all girls between 3 and 97 centile of
Tanner, Whitehouse & Takaishi (1966) growth chart

| Infants & children | Ages 10–18 y. and over 30 kg | Adults | ||||||||||
| Column 1 | Column 2 | Column 3 | Column 4 | Column 5 | ||||||||
| Wt (kg) | MJ | (kcal) | Wt (kg) | Boys | Girls | Wt (kg) | Men | Women | ||||
| MJ | (kcal) | MJ | (kcal) | MJ | (kcal) | MJ | (kcal) | |||||
| 3 | .63 | 150 | 32 | 5.02 | 1200 | 4.69 | 1120 | 36 | - | - | 4.20 | 1005 |
| 4 | .84 | 200 | 34 | 5.17 | 1235 | 4.85 | 1160 | 38 | 4.85 | 1160 | 4.37 | 1045 |
| 5 | 1.09 | 260 | 36 | 5.31 | 1270 | 5.02 | 1200 | 40 | 5.04 | 1205 | 4.54 | 1085 |
| 6 | 1.34 | 320 | 38 | 5.46 | 1305 | 5.17 | 1235 | 42 | 5.21 | 1245 | 4.73 | 1130 |
| 7 | 1.55 | 370 | 40 | 5.61 | 1340 | 5.31 | 1270 | 44 | 5.36 | 1280 | 4.90 | 1170 |
| 8 | 1.88 | 450 | 42 | 5.73 | 1370 | 5.44 | 1300 | 46 | 5.52 | 1320 | 5.06 | 1210 |
| 9 | 2.13 | 510 | 44 | 5.84 | 1395 | 5.56 | 1330 | 48 | 5.67 | 1355 | 5.23 | 1250 |
| 10 | 2.34 | 560 | 46 | 5.94 | 1420 | 5.67 | 1355 | 50 | 5.82 | 1390 | 5.40 | 1290 |
| 11 | 2.55 | 610 | 48 | 6.07 | 1450 | 5.75 | 1375 | 52 | 5.98 | 1430 | 5.52 | 1320 |
| 12 | 2.76 | 660 | 50 | 6.19 | 1480 | 5.84 | 1395 | 54 | 6.13 | 1465 | 5.65 | 1350 |
| 13 | 2.93 | 700 | 52 | 6.32 | 1510 | 5.90 | 1410 | 56 | 6.28 | 1500 | 5.75 | 1375 |
| 14 | 3.14 | 750 | 54 | 6.44 | 1540 | 5.98 | 1430 | 58 | 6.42 | 1535 | 5.86 | 1400 |
| 15 | 3.31 | 790 | 56 | 6.57 | 1570 | 6.05 | 1445 | 60 | 6.57 | 1570 | 5.96 | 1425 |
| 16 | 3.43 | 820 | 58 | 6.69 | 1600 | 6.09 | 1455 | 62 | 6.69 | 1600 | 6.05 | 1445 |
| 17 | 3.56 | 850 | 60 | 6.80 | 1625 | 6.13 | 1465 | 64 | 6.84 | 1635 | 6.15 | 1470 |
| 18 | 3.68 | 880 | 62 | 6.92 | 1655 | 6.23 | 1490 | 66 | 6.97 | 1665 | 6.23 | 1490 |
| 19 | 3.81 | 910 | 64 | 7.05 | 1685 | 6.32 | 1510 | 68 | 7.07 | 1690 | 6.32 | 1510 |
| 20 | 3.93 | 940 | 66 | 7.15 | 1710 | 6.40 | 1530 | 70 | 7.18 | 1715 | 6.40 | 1530 |
| 22 | 4.14 | 990 | 68 | 7.28 | 1740 | 6.46 | 1545 | 72 | 7.26 | 1735 | 6.49 | 1550 |
| 24 | 4.35 | 1040 | 70 | 7.41 | 1770 | 6.52 | 1560 | 74 | 7.34 | 1755 | 6.55 | 1565 |
| 26 | 4.52 | 1080 | 76 | 7.43 | 1775 | 6.61 | 1580 | |||||
| 28 | 4.67 | 1115 | 78 | 7.49 | 1790 | 6.67 | 1595 | |||||
| 30 | 4.81 | 1150 | 80 | 7.55 | 1805 | 6.74 | 1610 | |||||
| 82 | 7.59 | 1815 | 6.80 | 1625 | ||||||||
| 84 | 7.66 | 1830 | 6.86 | 1640 | ||||||||
| 86 | 7.70 | 1840 | 6.90 | 1650 | ||||||||
| 88 | 7.74 | 1850 | 6.97 | 1665 | ||||||||
| 90 | 7.78 | 1860 | 7.03 | 1680 | ||||||||
| 92 | 7.82 | 1870 | 7.09 | 1695 | ||||||||
In this whole range of BMRs at different body weights throughout the age span of infancy up to 18 y., the values suggested are often similar to those quoted in FAO/WHO (1973) purporting to be the data of Talbot (1938) but, above a weight of about 20 kg, are higher than those of Quenouille et al (1951) (c.f. Table 4).
In practice, the use of the values for BMR suggested in Table 3 for infants, children and adolescents requires the use of separate columns depending on the age of the individual or group and on the sex. Below the age of 10 or below a weight of 30 kg column 1 should be used; between the ages of 10 y. and 18 y. and for body weights over 30 kg column 2 should be used for boys and column 3 for girls. For adults, i.e. those of 19 y. or older, columns 4 and 5 should be used for men and women respectively (c.f. also Fig. 16 and Fig. 17).
Certain qualifications need to be stated about the practical use of this table. These almost certainly do not apply to column 1 on infants and young children where the predicted BMRs are close enough to those of other authors (c.f. Table 4) to make their validity highly probable.
Columns 2 and 3 apply to the growth period when differences appear between the sexes. This is a difficult period to assess with any great precision as far as individual BMRs are concerned. There is so much variation in growth rates and in body weights, representing very different states of metabolic stimulus for the individual, that even though the general picture for each sex seems reasonably consistent yet there are considerable anomalies. These can only be properly resolved by discovering firstly how great a problem they raise in practice and secondly by the analysis of more up-to-date data. In the present table, while there is a reasonable progression from the predicted BMRs for the ‘under 30 kg’ column to the ‘10–18 y. over 30 kg’ columns for males and females, the integration of the latter values with those for adults in columns 4 and 5 presents some difficulties at the lower weight levels, between 36 and 44 kg particularly. There are differences of 10–15% between the BMRs for the same body weights in the ‘children’ columns and in the ‘adult’ columns. Part of this will be a spurious difference because a 40 kg girl, for example, may grow into a 55 kg woman with relatively little difficulty in the reconciliation of the BMRs between the ‘children’ and the ‘adult’ predictions. Other factors, such as changing body composition and the growth stimulus to metabolism may also have small additive effects. Nevertheless, the data do not fit together too well for these columns representing different periods of life and it remains to be seen how great a handicap this is.
FIGURE 16: BMR plotted against body weight for adult men
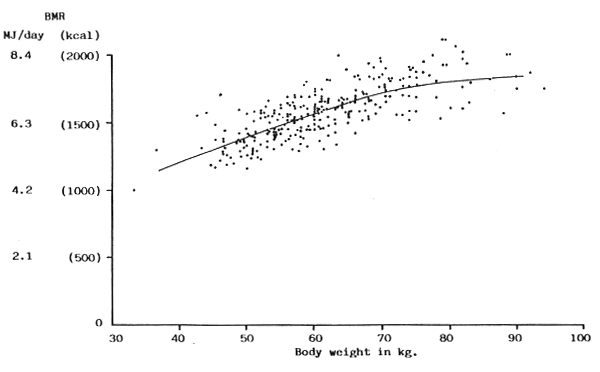
(Sources of data: Aub & Du Bois, 1917; Benedict, Emmes, Roth & Smith, 1914; Benedict & Garven, 1936; Boothby & Sandiford, 1922; Chitre, Mobsby, Thein & Hla Pe, 1959; Hamberger & Lundgren, 1965; Harris & Benedict, 1919; Hori, Ohnaka, Shiraki, Tsujita, Yoshimura, Saito & Panata, 1977; Keys, Taylor & Grande, 1973; Krishnan & Vareed, 1932)
FIGURE 17: BMR plotted against body weight for adult women
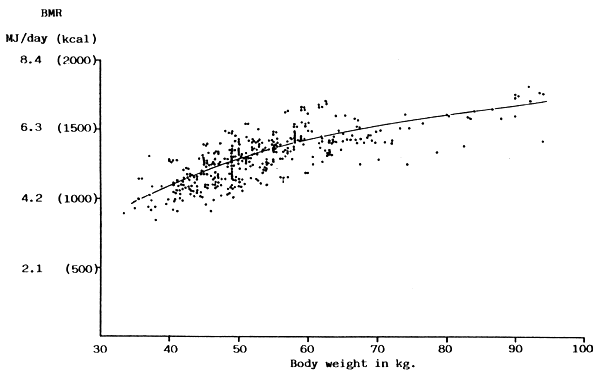
(Sources of data: Benedict, Emmes, Roth & Smith, 1914; Boothby & Sandiford, 1922; Dakshayani & Ramana Murthy, 1964; de Guzman & Florentino, 1968; Hamberger & Lundgren, 1965; Harris & Benedict, 1919; Khan & Belavady, 1973; Krishnan & Vareed, 1932; Mason & Benedict, 1931)
TABLE 4: Comparison of 3 sets of predicted BMR (in kcal/day).
| Wt | Present data | Quenouille et al | FAO/WHO | |||||
| Column 1 | ||||||||
| 10 | 560 | - | 540 | |||||
| 15 | 790 | 780 | 720 | |||||
| 20 | 940 | 905 | 860 | |||||
| 25 | 1060 | 960 | 1025 | |||||
| 30 | 1150 | 1080 | 1140 | |||||
| Column 2 | Column 3 | |||||||
| Males | Females | Males | Females | Males | Females | |||
| 35 | 1250 | 1180 | 1170 | 1050 | 1250 | 1160 | ||
| 40 | 1340 | 1270 | 1240 | 1125 | 1340 | 1240 | ||
| 45 | 1405 | Column 4 | 1340 | Column 5 | 1330 | 1160 | 1415 | 1320 |
| 50 | 1480 | (1390) | 1395 | (1290) | 1400 | 1240 | 1485 | 1400 |
| 55 | 1555 | (1485) | 1440 | (1360) | 1450 | 1290 | 1570 | 1490 |
| 60 | 1625 | (1570) | 1465 | (1425) | 1520 | 1350 | 1630 | 1545 |
| 65 | 1650 | 1480 | 1580 | 1390 | ||||
| 70 | 1715 | 1530 | 1630 | 1440 | ||||
| 75 | 1765 | 1575 | 1700 | 1480 | ||||
| 80 | 1805 | 1610 | 1750 | 1540 | ||||
| 85 | 1835 | 1645 | 1800 | 1590 | ||||
| 90 | 1860 | 1680 | 1850 | 1630 | ||||
The values given for adults agree within 4–6% within those suggested by Quenouille et al.
An ageing factor for most populations should probably be introduced, although this may well mostly reflect changes in body composition and might therefore need to be reduced in populations or individuals where little change seems to occur, or perhaps increased when these changes are more marked. Between the ages of 20 y. and 60 y., a decrement of 5% per 20 y. span is suggested as the standard. Between 60 and 75 y. another 10% reduction should be made. Beyond that age, because of several factors (relatively small numbers of such populations, relatively smaller quantities of adipose tissue, possible dangers of very low levels of energy intake, etc.), it is perhaps safer to make no further reduction.
Pregnancy and lactation increase BMR but not excessively out of proportion to the altered body weight of the mother and probably no special adjustment of BMR is needed.
Conclusion: A table has been formulated to allow prediction of BMR in individuals of any age or of a range of body weights. Body weight is the most important factor in modifying BMR but its effect will vary with the age group of the individual. The use of this table is certainly open to some error but the variability of the published data is such that it is unlikely that more complex methods of calculating BMR offer any increased accuracy and the present table has the great advantage of being very easy to apply.
No allowance has been made for climate, race or for seasonal influences, although further research may show that this is necessary.
If use is being made of BMR measurements - as opposed to predictions - on populations suspected of being undernourished, an increase in the calculation should be made to allow for this. Similarly, an addition to the body weight of such populations may be needed to produce ‘desirable’ BMR values. The implications of such manipulations are complex and both care and considerable knowledge are required to make valid re-assessments in such situations.
Throughout this article it has been pointed out that various areas of information are deficient and these particularly involve 1) alterations in BMR between late adolescence and young adulthood - e.g. studies on males and females of comparable body weight and composition between 15 and 25 years of age, 2) the effects of variable states of body composition, 3) the effects of climate, both temperate and hot, on BMR in the normal climatic environment.
References
ATWATER, W.O. & BENEDICT, F.G. (1899). Metabolism of matter and energy in the human body. U.S. Dept. Agric. Bull. No 69.
AUB, J.C. & Du BOIS, E.F. (1917). The basal metabolism of old men. Arch. int. Med. 19, 823–831.
BAILEY, D., HARRY, D., JOHNSON, R.E. & KUPPRAT, I. (1973). Oscillations in oxygen consumption of man at rest. J. appl. Physiol. 34, 467–470.
BANERJEE, S. & BHATTACHARYA, A.K. (1964). Basal metabolic rates of boys and young adults of Rajasthan. Ind. J. med. Res. 52, 1167–1172.
BENEDICT, F.G. (1915a). Factors affecting basal metabolism. J. biol Chem. 20, 263–299.
BENEDICT, F.G. (1915b). A study of prolonged fasting. Carnegie Inst. Wash. Publ. No 203. pp 416.
BENEDICT, F.G. (1938). Vital energetics. A study in comparative basal metabolism. Carnegie Inst. Wash. Publ. No 503.
BENEDICT, F.G. & BENEDICT, C.G. (1933). Mental effort in relation to gaseous exchanges, heart rate and mechanics of respiration. Carnegie Inst. Wash. Publ. No 446.
BENEDICT, F.G. & CARPENTER, T.M. (1909). The influence of muscular and mental work on metabolism and the efficiency of the human body as a machine. U.S. Dept. Agric. Off. Exper. Sta. Bull. No 208
BENEDICT, F.G., EMMES, L.E., ROTH, P. & SMITH, H.M. (1914). The basal, gaseous metabolism of normal men and women. J. biol. Chem. 18, 139–155.
BENEDICT, F.G. & GARVEN, H.S.D. (1936). The basal metabolism of male Chinese in Manchuria. Chinese J. Physiol. 10, 141–148.
BENEDICT, F.G. & SMITH, H.M. (1915). The metabolism of athletes as compared with normal individuals of similar height and weight. J. biol. Chem. 20, 243–252.
BENEDICT, F.G., MILES, W.R., ROTH, P. & SMITH, H.M. (1919). Human vitality and efficiency under prolonged restricted diet. Carnegie Inst. Wash. Publ. No 280. pp 701.
BENEDICT, F.G. & TALBOT, F.B. (1921). Metabolism and growth from birth to puberty. Carnegie Inst. Wash. Publ. No 302.
BENZINGER, T.H., HUEBSCHER, R.G., MINARD, D. & KITZINGER, C. (1958). Human calorimetry by means of the gradient principle. J. appl. Physiol. 12, Supp. 1. 1–28.
BERKSON, J. & BOOTHBY, W.M. (1936). Studies of the energy of metabolism of normal individuals. A comparison of the estimation of basal metabolism from (1) a linear formula and (2) “surface area”. Am. J. Physiol. 116, 485–494.
BLAXTER, K.L. (1971). Methods of measuring the energy metabolism of animals and interpretation of results obtained. Federation Proc. 30, 1436–1443.
BLUNT, K., TILT, J., MCLAUGHLIN, L. & GUNN, K.B. (1926). The basal metabolism of girls. J. biol. Chem. 67, 491–503.
BOOTHBY, W.M. & SANDIFORD, I. (1922). Summary of the basal metabolism data on 8614 subjects with especial reference to the normal standards for the estimation of the basal metabolic rate. J. biol. Chem. 54, 783–803.
BOOTHBY, W.M. & SANDIFORD, I. (1929). Normal values of basal or standard metabolism. A modification of the Du Bois standards. Am. J. Physiol. 90, 290–291.
BOOTHBY, W.M., BERKSON, J. & DUNN, H.L. (1936). Studies of the energy of metabolism of normal individuals: a standard for basal metabolism, with a nomogram for clinical application. Am. J. Physiol. 116, 468–484.
BOYD, E. (1962). in Growth, Including Reproduction and Morphological Development. (ed. Altman & Dittmer) pp 346–348. Washington: Biological Handbooks, Federation of American Societies for Experimental Biology.
BRODY, S. & ELTING, E.C. (1926). A new method of measuring surface area and its utilization to determine the relation between growth in surface area and growth in weight and skeletal growth in dairy cattle. Missouri. Agr. Expt. Sta. Res. Bull. No 89. pp 18.
BROZEK, J. & GRANDE, F. (1955). Body composition and basal metabolism in man: correlation analysis versus physiological approach. Human Biol. 27, 22–31. de BRUIN, M. (1939). Basal metabolic rate in children with abnormal bodily dimensions. Am. J. Dis. Child. 57, 29–51.
CARPENTER, T.M. (1915). A comparison of methods for determining the respiratory exchange of man. Carnegie Inst. Wash. Publ. No 216. pp 265.
CHITRE, R.G., MOBSBY, A.M., THEIN, K. & HLA PE, U. (1959). Studies on basal metabolism of Burmese people. J. Postgrad. Med. (Bombay) 5, 129–137.
CHLOPIN, G.W., JAKOWENKO, W. & WOLSCHINSKY, W. (1927). Weitere Untersuchungen über Einfluss der geistigen Tätigkeit auf den respiratorischen Gaswechsel und auf den Energieumsatz. Arch. Hyg. 98, 158–175.
DAKSHAYANI, R. & RAMANA MURTHY, P.S.V. (1964). Basal metabolism and creatinine excretion in different physiological groups. Ind. J. med. Res. 52, 1159–1166.
Department of Health and Social Security (1979). Recommended daily amounts of food energy and nutrients for groups of people in the U.K. Report on Health and Social Subjects 15. London: HMSO.
Du BOIS, E.F. (1930–31). Recent advances in the study of basal metabolism. Part I. Part II. J. Nutr. 3, 217–228, 331–343.
Du BOIS, D. & Du BOIS, E.F. (1916). Clinical calorimetry. Tenth paper. A formula to estimate the approximate surface area if height and weight be known. Arch. int. Med. 17, 863–872.
Du BOIS, E.F., EBAUGH, F.G. & HARDY, J.D. (1952). Basal heat production and elimination of 13 normal women at temperatures from 22°C to 35°C. J. Nutr. 48, 257–293.
DURNIN, J.V.G.A. (1959). The use of surface area and of body-weight as standards of reference in studies on human energy expenditure. Br. J. Nutr. 13, 68–71.
DURNIN, J.V.G.A. (1978a). Indirect calorimetry in man: a critique of practical problems. Proc. Nutr. Soc. 37, 5–12.
DURNIN, J.V.G.A. (1978b). Possible interaction between physical activity, body composition and obesity in man. In Recent Advances in Obesity Research (ed. Bray, G.A.) London: Newman Publishing.
DURNIN, J.V.G.A. & PASSMORE, R. (1967). Energy Work and Leisure. London: Heinemann Educational Books.
ELSNER, R.W., ANDERSEN, K.L. & HERMANSEN, L. (1960). Thermal and metabolic responses of Arctic Indians to moderate cold exposure at the end of winter. J. appl. Physiol. 15, 659–661.
EVELETH, P.B. & TANNER, J.M. (1976). Worldwide variation in human growth. Cambridge: Cambridge University Press.
FITZGERALD, L.R. (1957). Cutaneous respiration in man. Physiol. Rev. 37, 325–336.
FLEISCH, A. (1951). Le métabolisme basal standard et sa détermination au moyen du “Métabo calculator”. Helv. med. Acta. 18, 23–44.
FLORENTINO, R. & GUZMAN, P. de (1963). The selection of data for basal metabolic rate standards. Philippine J. Sc. 93, 307–318.
FAO (1950). Calorie requirements. FAO Nutritional Studies No 5. Washington: FAO.
FAO (1957). Calorie requirements. FAO Nutritional Studies No 15. Rome: FAO.
FAO/WHO (1973). Energy and protein requirements. WHO Tech. Rep. Ser. No 522. Geneva: WHO.
FULTON, D.E. (1972). Basal metabolic rate of women. J. Am. diet. Ass. 61, 516–520.
GARN, S.M. & CLARK, L.C. (1953). The sex difference in the basal metabolic rate. Child Development, 24, 215–224.
GOLD, A.J., ZORNITZER, A. & SAMUELOFF, S. (1969). Influence of season and heat on energy expenditure during rest and exercise. J. appl. Physiol. 27, 9–12.
de GUZMAN, P.E. & FLORENTINO, R.F. (1968). Basal metabolic data of 21 to 35 years old Filipino adults. Philippine J. Sci. 97, 229–239.
HAMBERGER, L. & LUNDGREN, O. (1965). Basal metabolic rate in a group of young medical students with a note on body surface formulas. Scand J. clin. Lab. Invest. 17, 281–286.
HANNON, J.P. & SUDMAN, D.M. (1973). Basal metabolic and cardiovascular function of women during altitude acclimatization. J. appl. Physiol. 34, 471–477.
HARRIS, J.A. & BENEDICT, F.G. (1919). A biometric study of basal metabolism in man. Carnegie Inst. Wash. Publ. No 279.
HOLLIDAY, M.A. (1978). Body composition and energy needs during growth. In Human Growth, vol. 2 pp 117–138. Ed. Falkner, F. & Tanner, J.M. New York: Plenum Press.
HORI, S., OHNAKA, M., SHIRAKI, K., TSUJITA, J., YOSHIMURA, H., SAITO, N. & PANATA, M. (1977). Comparison of physical characteristics, body temperature and basal metabolism between Thai and Japanese in a neutral temperature zone. Jap. J. Physiol. 27, 525–538.
ILIFF, A., LEE, V.A. & LEWIS, R.C. (1951). Interpretation of basal metabolic rate of children of unusual body build. Pediatrics, 8, 616–627.
JAMES, W.P.T., BAILES, J., DAVIES, H.L. & DAUNCEY, M.J. (1978). Elevated metabolic rates in obesity. Lancet, 1, 1122–1125.
JEQUIER, E., PITTET, Ph., & GYGAX, P-H. (1978). Thermic effect of glucose and thermal body insulation in lean and obese subjects: a calorimetric approach. Proc. Nutr. Soc. 37, 45–53.
KARPOVICH, P.V. (1953). Physiology of Muscular Activity. Philadelphia: Saunders.
KEYS, A., BROZEK, J., HENSCHEL, A., MICKELSEN, O. & TAYLOR, H.L. (1950). The Biology of Human Starvation. Minneapolis, Minnesota: Univ. of Minnesota Press. Vol. I & II.
KEYS, A., TAYLOR, H.L. & GRANDE, F. (1973). Basal metabolism and age of adult man. Metabolism, 22, 579–587.
KHAN, L. & BELAVADY, B. (1973). Basal metabolism in pregnant and nursing women and children. Ind. J. med. Res. 61, 1853–1860.
KIM, D.J., KIM, K.J., RO, K.S. & CHOI, K.H. (1966). Studies of basal metabolism and energy expenditure of Koreans in daily life. Tokyo: Proc. 11th Pacific Sc. Cong. pp 231–241.
KLEIBER, M. (1945). Dietary deficiencies and energy metabolism. Nutr. Abst. Rev. 15, 207–222.
KLEIBER, M. (1947). Body size and metabolic rate. Physiol. Rev. 27, 511–541.
KNEHR, C.A., DILL, D.B. & NEUFELD, W. (1942). Training and its effects on man at rest and at work. Am. J. Physiol. 136, 148–156.
KRISHNAN, B.T. & VAREED, C. (1932). Basal metabolism of young college students, men and women, in Madras. Ind. J. med. Res. 19, 831–858.
KROGH, A. (1916). The Respiratory Exchange of Animals and Man. London: Longmans, Green. pp 173.
LAMB, M.W. & MICHIE, J. McC. (1954). Basal metabolism of 19 children from 2 to 10 years old. J. Nutr. 53, 93–104.
LEWIS, R.C., KINSMAN, G.M. & ILIFF, A. (1937). The basal metabolism of normal boys and girls from 2 to 12 years old, inclusive. Am. J. Dis. Child. 53, 348–428.
MALHOTRA, M.S., RAMASWAMY, S.S. & RAY, S.N. (1960). Effect of environmental temperature on work and resting metabolism. J. appl. Physiol. 15, 769–770.
MASON, E.D. & BENEDICT, F.G. (1931). The basal metabolism of South Indian women. Ind. J. med. Res. 19, 75–98.
MASON, E.D. & BENEDICT, F.G. (1934). The effect of sleep on human basal metabolism with particular reference to South Indian women. Am. J. Physiol. 108, 377–383.
MASON, E.D., JACOB, M. & BALAKRISHNAN, V. (1964). Racial group differences in the basal metabolism and body composition of Indian and European women in Bombay. Human.Biol. 36, 374–396.
MASON, E.D. & JACOB, M. (1972). Variations in basal metabolic rate responses to changes between tropical and temperate climates. Human Biol. 44, 141–172.
MEANS, J.S. (1916). The basal metabolism in obesity. Arch. int. Med. 17, 704–710.
MITCHELL, H.H. (1962). Comparative Nutrition of Man and Domestic Animals. Vol. 1. pp 3–90. New York: Academic Press.
MITCHELL, D., STRYDOM, N.B., van GRAAN, C.H. & van der WALT, W.H. (1971). Human surface area: comparison of the Du Bois formula with direct photometric measurement. Pflügers Arch. 325, 188–190.
NAKAGAWA, I. (1934). Growth and basal metabolism. 11. Basal metabolism of elementary school children. Am. J. Dis. Child. 48, 35–38.
NAKAGAWA, I. (1937). Growth and basal metabolism v. Basal metabolism of high school children. Am. J. Dis. Child. 53, 985–990.
National Research Council (1980). Recommended dietary allowances. Committee on Dietary Allowances: Food and Nutrition Board. Washington: National Academy of Sciences.
NYLIN, G. (1935). The physiology of the circulation during puberty. Acta med. Scand. supp. 69.
OLMSTEAD, W.H., BARR, D.P. & Du BOIS, E.F. (1918). Metabolism of boys 12 and 14 years old. Arch. int. Med. 21, 621–626.
PICKWORTH, F.A. (1927). Basal metabolism as determined by the respiratory exchange. Part 1. Proc. roy. Soc. Lond. B. 101, 174–186.
QUENOUILLE, M.H., BOYNE, A.W., FISHER, W.B. & LEITCH, I. (1951). Statistical studies of recorded energy expenditure of man. Part 1. Basal metabolism related to sex, stature, age, climate and race. BUCKSBURN, ABERDEEN: Commonwealth Bureau of Animal Nutrition Tech. Comm. No 17.
RICHET, C. (1889). La Chaleur Animale. Paris: F. Alcan. pp 307.
ROBERTSON, J.D. & REID, D.D. (1952). Standards for the basal metabolism of normal people in Britain. Lancet, 1, 940–949.
ROBINSON, S. & HARMON, P.M. (1941). The effects of training and of gelatin upon certain factors which limit muscular work. Am. J. Physiol. 133, 161–169.
RODAHL, K. (1952). Basal metabolism of the Eskimo. J. Nutr. 48, 359–368.
ROSENBLUM, D.E. (1932). Untersuchungen über den respiratorischen Gastoffwechsel und Energieverbrauch bei geistiger Arbeit. Arbeitsphysiologie, 6, 214–234.
RUBNER, M. (1883). Ueber den Einfluss der Körpergrösse auf Stoff- und Kraftwechsel. Z. Biol. 19, 535–562.
RUTTER, N., BROWN, S.M. & HULL, D. (1978). Variations in the resting oxygen consumption of small babies. Arch. Dis. Childh. 53, 850–854.
SARGENT, D.W. (1961). An evaluation of basal metabolic data for children and youth in the United States. Home Economics Research Report No 14. Washington: U.S. Dept. Agri. Hum. Nutr. Res. Div.
SCHNEIDER, E.C. & FOSTER, A.O. (1931). The influence of physical training on the basal metabolic rate of man. Am. J. Physiol. 98, 595–601.
SHOCK, N.W. & YIENGST, M.J. (1955). Age changes in basal respiratory measurements and metabolism in males. J. Geront. 10, 31–40.
SINCLAIR, D. (1973). Human Growth after Birth. London: Oxford University Press.
SOKHEY, S.S. & MALANDKAR, M.A. (1939). Basal metabolism of Indians. A study based on the examination of 60 normal Indian men. Ind. J. med. Res. 27, 501–529.
STARK, M.E. (1935). Standards for predicting basal metabolism in the immediate pre-adult years. Am. J. Physiol. 111, 630–640.
STEINHAUS, A.H. (1928). Studies in the physiology of exercise. I. Exercise and basal metabolism in dogs. Am. J. Physiol. 83, 658–677.
SUZUKI, S. (1959). Basal metabolism in the Japanese population. Wld. Rev. Nutr. Diet. 1, 107–124.
TALAAT, M., HABIB, Y.A. & EL-KHANAGRY, H. (1953). Studies on the basal metabolic rate of normal Egyptians. Acta med. Scand. 147, 221–226.
TALBOT, F.B., WILSON, E.B. & WORCESTER, J. (1937). Basal metabolism of girls. Am. J. Dis. Child. 53, 273–347.
TANNER, J.M. (1962). Growth at Adolescence. 2nd. ed. Oxford: Blackwell Scientific Publications Ltd.
TANNER, J.M., WHITEHOUSE, R.H. & TAKAISHI, M. (1966). Standards from birth to maturity for height, weight, height velocity, and weight velocity: British children, 1965. Arch. Dis. Childh. 41. 454–471.
TAYLOR, H.L. & KEYS, A. (1950). Adaptation to calorie restriction. Science, 112, 215–218.
TOPPER, A. & MULIER, H. (1932). Basal metabolism of normal children. Am. J. Dis. Child. 43, 327–336.
TZANKOFF, S.P. & NORRIS, A.H. (1977). Effect of muscle mass decrease on age-related BMR changes. J. appl. Physiol. 43, 1001–1006.
TZANKOFF, S.P. & NORRIS, A.H. (1978). Longitudinal changes in basal metabolism in man. J. appl. Physiol. 45, 536–539.
VOGELIUS, H. (1945). Basal metabolism of girls. Acta med. Scand. Supp. 165.
VOIT, E. (1901). Uber die Grosse des Energiebedarfes der Tiere im Hungerzustande. Z. Biol. 41, 113–154.
WANG, C.C. (1939). Basal metabolism and preformed and total creatinine in urine of 70 children. Am. J. Dis. Child. 57, 838–850.
WANG, C.C., KERN, R., FRANK, M. & HAYS, B.B. (1926). Metabolism of undernourished children. 11. Basal metabolism. Am. J. Dis. Child. 32, 350–359.
WANG, C.C., KAUCHER, M. & WING, M. (1936). Metabolism of adolescent girls. 1. Basal metabolism and energy exchange. Am. J. Dis. Child. 51, 801–815.
WEIR, J.B. de V. (1949). New methods for calculating metabolic rate with special reference to protein metabolism. J. Physiol. 109, 1–9.
WILKERSON, J.E., RAVEN, P.B. & HORVATH, S.M. (1972). Critical temperature of unacclimatized male Caucasians. J. appl. Physiol. 33, 451–455.
WILSON, E.A. (1945). Basal metabolism from the standpoint of racial anthropology. Am. J. phys. Anthropol. 3, 1–19.
WILSON, O. (1956a). Adaptation of the basal metabolic rate of man to climate - a review. Metabolism, 5, 531–542.
WILSON, O. (1956b). Basal metabolic rate in the Antartic. Metabolism, 5, 543–554.
WILSON, H.E.C. & ROY, N.C. (1938). Observations on the basal metabolism of Indian boys in Calcutta. Ind. J. med. Res. 25, 901–910.
YOSHIMURA, M., YUKIYOSHI, K., YOSHIOKA, T. & TAKEDA, H. (1966). Climatic adaptation of basal metabolism. Fed. Proc. 25, 1169–1174.
YOUNG, C.M. & DONALDSON, E.G. (1946). Activity as it affects the basal metabolism of college women. J. Am. dietet. Ass. 22, 303–306.
ZUNTZ, N. & SCHUMBURG, W.A.E.F. (1901). Studien zu einer Physiologie des Marsches. Berlin: Hirschwald.