En el Capitulo 2 se desarrolló el modelo bioeconómico clásico estático, del cual se derivaron fundamentalmente dos predicciones claves: 1) el libre acceso a los recursos pesqueros ocasionará la sobreexplotación del recurso y disipación de los excedentes generados por una pesqueria; y 2) el máximo rendimiento económico (MRE) ocurrirá a una tasa de explotación menor a la del máximo rendimiento sostenible (MRS). Sin embargo, este modelo ignora la dimensión del tiempo en la estimación de los niveles óptimos de captura γ esfuerzo. En este Capitulo se describe el modelo bioeconómico dinámico, a través del cual se demuestra que la tasa óptima de explotación de un recurso pesquero puede ser mayor o menor al MREó al MRS, dependiendo de las preferencias intertemporales en el uso del recurso por parte del la sociedad.
A efectos de lograr una visión más profunda sobre la importancia del tiempo en la toma de decisiones, este Capitulo desarrolla en su primera sección conceptos clásicos relacionados con la preferencia intertemporal en el uso de un bien. La segunda sección considera conceptos claves en la evaluación de aquellos proyectos pesqueros, fundamentalmente financiados por el sector público, en los cuales el factor tiempo adquiere una dimensión relevante. La tercera analiza los criterios de decisión fundamentales para la inversión pública, en el contexto del análisis beneficio-costo. La cuarta sección comprende el estudio de aspectos relacionados con las preferencias intertemporales e impactos distribucionales en la sociedad derivados de la ejecución de un proyecto pesquero. La quinta sección se aboca exclusivamente al desarrollo del modelo bioeconómico dinámico en pesquerias, integrando el cuerpo teórico de conocimiento de las secciones precedentes. En el transcurso del Capitulo se intercalan ejemplos relacionados a pesquerias, a fin de discutir aplicaciones particulares de los principios básicos del análisis beneficio-costo y del modelo bioeconómico dinámico.
Las decisiones sobre inversión en esfuerzo pesquero están relacionadas con la promesa que éste asegure ingresos netos positivos durante la vida útil de una unidad de pesca (e.g. embarcación, artes y equipos que la componen). Una aproximación al problema de la dimensión e importancia del tiempo como factor clave en la inversión y desarrollo de actividades pesqueras, es considerar las preferencias en el consumo de un cierto bien en diferentes períodos.
A modo de ejemplo, considérese a un individuo en un cierto momento que tiene la alternativa de consumir bienes en el presente año y en los subsecuentes. La persona no necesariamente será indiferente a la elección de gastar ahora o en el futuro, aún si los precios de los bienes permanecen constantes. En efecto, el consumo en un período constituye un bien diferente a consumir en otro periodo. Cada individuo de la sociedad tiene preferencias temporales respecto al consumo de un bien en diferentes periodos de tiempo. Esto es medido por su tasa marginal de preferencia en el tiempo (TMPT). Si un individuo es indiferente entre consumir en forma extra 1 US$ en un año o bien, 1.10 US$ en el siguiente, se dice que posee una TMPT de 10% por año.
La palabra marginal es usada debido a que una TMPT mide la preferencia individual entre pequeños incrementos de consumo en el tiempo. Esto presupone que el individuo tiene disímiles expectativas acerca del monto que consumirá en diferentes períodos.
Los conceptos anteriormente vertidos remarcan un punto verdaderamente importante: la preferencia en el tiempo considera preferencias en el consumo de un bien. Esto lleva a profundizar en el concepto de preferencias intertemporales, que en el caso de recursos renovables como los pesqueros adquiere una dimensión fundamental. En efecto, por dos grandes razones el análisis de las preferencias en el uso de este tipo de recursos no puede ser estático: 1) su naturaleza renovable implica variabilidad en el monto de recurso disponible, así como un cierto grado de incertidumbre en cuanto a su magnitud en diferentes periodos de tiempo; 2) según el tipo de pesqueria analizada, existirá una distinta preferencia marginal del uso de los recursos en el tiempo. Asi por ejemplo, en una pesqueria con sistema de libre acceso existirá probablemente una alta TMPT, dado que por lo general hay un mayor incentivo para incrementar el monto de ingresos en la actualidad con respecto al futuro debido a la naturaleza inherente a los recursos pesqueros (e.g. ocurrencia de externalidades; ver Capitulo 1). Considerando pesquerias con cierto grado de mecanización (e.g. pesquerias de mediana y gran escala), la inversión realizada en planificar y efectuar actividades de pesca no se paga de inmediato, sino que existe una vida útil de la unidad de pesca (buque, equipos y artes de pesca), que debe ser tomada en consideración para evaluar la magnitud de la inversión, costos presentes y futuros, asi como los probables ingresos que se deriven de dichas actividades. En estos casos es probable que bajo marcos conservativos de manejo y administración pesquera (e.g. entrada limitada de buques) ocurra una baja TMPT, a efectos de favorecer inversiones y al mismo tiempo explotar el recurso durante un lapso prolongado en el tiempo.
Siguiendo el análisis intertemporal reportado por Randall (1981), considere un pescador A que debe decidir cómo distribuir sus actividades de consumo en dos periodos de tiempo t1 y t2. Se asume que el consumo total en cada perido (Ψt) puede ser definido por su presupuesto en cada uno, esto es, Ψt1 en t1 y Ψent2 en t2 Asúmase que el pescador recibe un ingreso de Y en t1 e Y2 en t2, siendo y1 = y2. La Figura 4.1 muestra la curva de indiferencia la que define las preferencias (e.g. necesidades) del pescador A en el uso de los recursos en dos periodos de tiempo sucesivos. WW es la linea intertemporal de presupuesto, donde W = y1 + y2. WW tiene una pendiente negativa igual a-1, por lo cual se asume que el ingreso podria ser transferido de un periodo a otro en una base uno a uno. La curva de indiferencia pasa a través de un punto común representado por y1 e y2. Se dice que el individuo A tiene una preferencia neutra del tiempo si prefiere el mismo consumo en t1 que t2 (con Ψt1 = Ψt2 e y1 = y2).
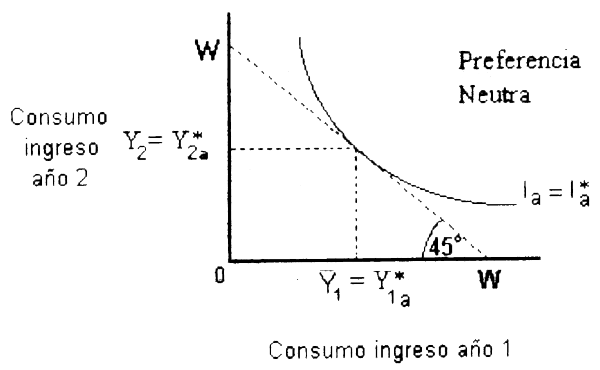
Figura 4.1 Preferencia intertemporal neutra (adaptada de Randall, 1981).
Ahora bien, considérese un pescador B y su respectiva función de utilidad (curva de indiferencia lb) en dos periódos de tiempo t1 y t2 (Fig. 4.2). Si fuera posible reasignar el consumo entre periodos (e.g. es posible transferir ingresos), el pescador B podria transferir parte de su consumo de t2 a t1, de tal manera que el consumo total seria Y*1b + Y*2b y en consecuencia lograria una curva de indiferencia más alta (l*b). El pescador B tiene un a preferencia positiva del tiempo o una alta TMPT, dado que prefiere un mayor consumo en el periodo inmediato que en posteriores. En otras palabras, está dispuesto a sacrificar un monto relativamente grande del consumo extra que dispondrá en el futuro a cambrio de un incremento el consumo acutal.
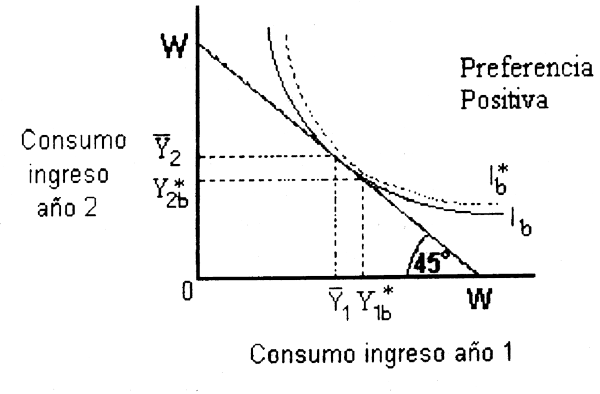
Figura 4.2. Preferencia intertemporal positiva (adaptada de Randall, 1981).
Por último, el pescador C (Fig. 4.3) está dispuesto a transferir parte de su consumo habitual del período actual al posterior, de tal mangera que su consumo será Y*10 + Y*2C y en consecuencia logrará la curva indiferencia más alta l*c. El pescador C tiene una preferencia negativa del tiempo, o bien, una baja TMPT.
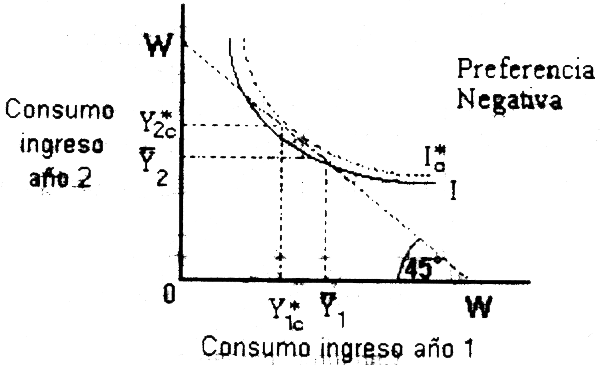
Figura 4.3. Preferencia intertemporal negativa (adaptada de Randall, 1981).
El sector público está capacitado para llevar a cabo inversiones en el manejo, desarrollo y conservación de recursos naturales renovables como los pesqueros. En este contexto, el economista pesquero debe evaluar la viabilidad y factibilidad de aquellas inversiones en el sector que minimicen los requerimentos de subsidio. En la mayoria de los casos, los proyectos o programas dirigidos al manejo y administración de recursos pesqueros son de larga vida, por lo cual no sólo se debe realizar un análisis estático de su eficiencia (e.g. Pareto eficiencia, ver Capitulo 6), sino incluir aspectos que supongan diferentes preferencias intertemporales en el uso de los recursos por parte de distintos sectores de la sociedad. Un proyecto, definido en un sentido amplio, es una forma de usar recursos, por lo cual la decisión concerniente a tomarlo o desecharlo es una elección entre diferentes alternativas de uso de los recursos en el tiempo. En tal sentido, la ejecución del proyecto por parte de la agencia pública pesquera tendrá como objetivo clave lograr una mejora en el bienestar social. La idea de cuantificar y evaluar un objetivo social es a veces problemática, particularmente cuando los bienes en consideración no tienen o son inadecuadamente reflejados en el precio de mercado debido a sus caracteristicas peculiares (e.g. arrecifes coralinos, manglares, reservas de la biósfera). Sin embargo, tales bienes reflejan las preferencias de la sociedad en la asignación de recursos de propiedad común por parte del Estado.
Las herramientas más comunes en la evaluación de proyectos se basan en el análisis benficio-costo (ABC) y métodos analiticos relacionados (ver Crooper y Oates, 1992). El ABC de un proyecto requiere la identificación de todos sus efectos en el bienestar individual de los miembros de una comunidad pesquera. Esos efectos son cuantificados a través de la comparación de los beneficios y costos derivados de la consecución del proyecto. El criterio más simple para evaluar diferentes alternativas, estrategias o proyectos es la Pareto-eficiencia intertemporal. Una estrategia o patrón del uso de un recurso en el tiempo es Pareto eficiente si y sólo si no es posible incrementar la utilidad de las partes afectadas en un período de tiempo sin disminuir las utilidades en otro perído. Por medio de este mecanismo se identifican, miden y comparan cambios en el bienestar de una sociedad. En el lenguaje de la Teoria de Bienestar (ver Capitulo 6), una mejora Pareto se producirá cuando una reorganización de la economia mejora el ingreso de un individuo sin perjudicar al resto de los miembros de la comunidad. En este contexto, un proyecto pesquero implicará una potencial mejora Pareto cuando la suma de dinero que los beneficiaríos estarian preparados a pagar para garantizar que el proyecto sea llevado a cabo excede la suma total de dinero que los potenciales perjudicados aceptarian como compensación por su ejecución. En esencia, el criterio Pareto-mejora potencial ó Pareto eficiencia requiere que los cambios en el bienestar de una comunidad pesquera sean medidos por su disponibilidad a pagar, o sea, el monto de dinero que los individuos están dispuestos a erogar por los beneficios de un proyecto pesquero, asi como por el monto que están dispuestos a aceptar como compensación por los daños impuestos a los grupos potencialmente perjudicados. De esto se desprende claramente que el criterio inherente en el ABC es el Valor Máximo del Producto Social y por tanto el daño económico es permisible si y sólo si la suma algebraica de los beneficios netos recibidos por los ganadores menos las pérdidas netas que enfrenten los perdedores sea mayor que cero y máxima.
El valor presente de un flujo de futuros ingresos es un concepto económico importante que permite realizar comparaciones monetarias en diferentes periodos de tiempo. En efecto, un igual monto de dinero a ser recibido ahora o en el futuro no significan lo mismo. En este contexto, la tasa de descuento (d) puede ser usada como un mecanismo para comparar el valor del dinero en el tiempo.
Por ejemplo, supóngase que un individuo tiene una TMPT de d por periodo. En consecuencia es indiferente entre una propuesta de consumo extra de 1 unidad en el periodo O y otra de consumo 1 + d unidades en el periodo 1. En forma análoga, será indiferente a la elección de las propuestas anteriores con respecto a un consumo de (1 + d)2 unidades extra de consumo en el período 2. Este razonamiento es similar a establecer que una unidad extra consumida en el periodo 1 tiene un valor presente de 1/(1 + d) unidades en el periodo O; del mismo modo, una unidad extra consumida en el periodo 2 tiene un valor presente de 1/(1 + d)2 unidades en el periodo O, y asi sucesivamente para t periodos (1/(1 + d)1). La tasa d a la cual los ingresos futuros son descontados a valores presentes es denominada tasa de descuento. Es importante remarcar que este término, a diferencia del término TMPT, no implica una interpretacién de la tasa a la cual hace referencia; una tasa de descuento es simplemente un número que es usado en una manipulación aritmética. En general, d es tratado como una constante.
Conceptos relacionados, tales como el factor de descuento y factor de compensación, pueden ser empleados para cálculos de este tipo. El factor de descuento vt,d es el valor presente en el periodo O de una suma de una unidad acumulada en el periodo t, si la tasa de descuento es d. Aritméticamente el factor de descuento es descrito por un patrón geométrico regular de la forma:

El factor de compensación ad es el valor presente en el periodo O de un flujo de ingresos consistente en la acumulación de una unidad en cada uno de los t periodos 1 a n, una tasa de descuento d. Aritméticamente,

donde: t = 1,2, …n.
En términos de factores de descuento:
ad=∑ v(t,d) (4.3)
donde: t = 1, 2, …n.
Es importante remarcar que el factor de compensación es útil cuando el flujo de costos y beneficios a lo largo del tiempo es el mismo (ver Sugden & Williams, 1990). Este no es el caso de pesquerías.
Dado que la evaluación de un proyecto involucra elecciones entre distintos cursos de acción, la utilidad de una estrategia puede ser determinada únicamente en relación a las alternativas posibles. En consecuencia, el costo de oportunidad de un proyecto es lo que se dejó de ganar en la siguiente mejor alternativa por haber adoptado el proyecto pesquero en cuestión (Shim & Siegel, 1995). De manera análoga, el retorno de un proyecto es el monto extra que se hubiera ahorrado si es puesto en marcha, en relación al generado si no es llevado a cabo.
Es importante remarcar que en la evaluación de proyectos, los costos y ingresos son relacionados con las estrategias o cursos de acción alternativos, lo cual implica una concepción diferente en la estimación de costos con respecto a la aproximación financiera, donde se estiman en base a cosas concretas (e.g. infraestructura, horas - hombre de trabajo). Varias razones explican esta diferente aproximación metodológica, las cuales serán desarrolladas a continuación:
El ABC no incluye costos de depreciación como costos reales, en razón de que no hay un costo de oportunidad involucrado. En efecto, éste se relaciona con el valor de los bienes de capital en la siguiente mejor alternativa. A modo de ejemplo, supóngase que una unidad de pesca desea concluir sus actividades de pesca. Dicha unidad habrá sido pagada en el pasado, considerando un precio de depreciación por unidad/año calculado por métodos convencionales. Sin embargo, esta estimación carece de directa relevancia a la hora de decidir entre concluir o no las actividades pesqueras. El costo de oportunidad de usar la unidad de pesca será el valor que tiene para el pescador en su siguiente mejor alternativa. Tal como se expondrá posteriormente, los criterios de decisión que sustentan el uso del ABC muestran: 1) el valor actual de los excedentes generados por encima de los que se hubiera logrado si se invirtiese a una tasa marginal de interés; y 2) que el procedimiento de descuento automáticamente da cuenta de la recuperación del capital inicial. En razón de estas consideraciones, cuando se incluyen en el tiempo cero (al inicio del proyecto) los costos de inversion, el flujo de costos de cualquier ABC no debe incluir ajustes por depreciación.
Los precios que el mercado otorga a cierto bien representan las preferencias y la habilidad de los individuos de comprar y vender bienes libremente en el mercado. Esto es, los precios que establece el mercado son apropiados en la medida en que éstos denoten las preferencias de la sociedad y la libertad de los individuos en consumir determinada cantidad de cierto bien a un precio fijo establecido. Este estará determinado por el nivel en el cual la demanda y la oferta se igualan; se asume que el precio de un bien es igual al valor de su producto marginal.
Cuando estos supuestos no son cumplidos, el precio que el mercado otorga a cierto bien no será necesariamente una buena aproximación de los costos sociales marginales del bien o servicio en cuestión. En este caso, en el ABC deben emplearse valores a efectos de tasar un bien que no son tomados directamente de precios reflejados por el mercado, los cuales son denominados precios sombra.
El precio sombra es un valor impuesto a un bien o servicio que carece de precio en el mercado (Pearce, 1981) o que es incorrectamente representado en éste. Los precios sombra son utilizados en ABC para representar el costo de oportunidad de producir o consumir un bien que generalmente no es comercializado en el mercado. Ejemplos tipicos de esto to contituyen especies en peligro de extinción, parques o reservas marinas, cierto nivel de calidad ambiental, o funciones bióticas y abióticas de un ecosistema especifico. Los precios sombra pueden ser estimados a partir de los costos marginales de producción o valor marginal de su uso como entradas al ABC.
A continuación serán desarrolladas tres alternativas diferentes factibles de ser seleccionadas como criterios de decisión: valor presente neto (VPN), cociente beneficio-costo (B/C) y tasa interna de retorno (TIR).
Como se ha explicado anteriormente, un cambio en determinada regulación gubernamental, al igual que la puesta en marcha de un proyecto pesquero de interés social, genera un flujo de efectos positivos (beneficios) y negativos (costos) a través del tiempo. La diferencia entre las tasas de beneficios y costos en un momento dado es denominada tasa de beneficio neto. Visto en términos de intervalos de tiempo discretos (e.g. nńos), el concepto de valor presente neto (VPN) puede expresarse de la forma siguiente:

donde BT(t) y CT(t) son los beneficios y costos totales en el tiempo t.
Este mecanismo permite la evaluación de diferentes alternativas o proyectos a través de un valor único, independientemente de la forma en que los costos y beneficios están distribuidos en el tiempo, lo cual posibilita la comparación de flujos de beneficios netos en el tiempo y facilita la decisión a ser tomada entre aquellos proyectos que produzcan diferentes flujos de beneficios netos. Es importante remarcar que la decisión dependerá esencialmente de la elección de la tasa de descuento d. De (4.4) se desprende que d tiene una influencia sustancial en las magnitudes calculadas de VPN y relativa en los ingresos netos logrados en periodos distantes de tiempo. A mayor valor de d, menor será el VPN. Un bajo valor de d tenderá a favorecer aquellos proyectos que generan mayores beneficios netos positivos en el largo plazo, pues son menos penalizados al ser traidos a valor presente que en el caso de haberse utilizado una d mayor. Considerando al sector pú blico como agente de inversión, es apropiado emplear estimaciones ded menores a aquéllas generadas por el mercado, aunque en general se utiliza la tasa de interés bancaria pues refleja de un modo u otro las preferencias de la sociedad. Tal como ya se ha mencionado, el objetivo de una agencia pública consiste en minimizar el valor presente de los requerimientos de subsidios netos en el tiempo, descontados a una tasa de descuento predeterminada por el Gobierno, ó “tasa de descuento testigo”. A este nivel, la analogia entre las agencias públicas y privadas se rompe, dado que es muy dificil infundir un criterio comercial a la agencia pública, de tal forma que elija una correcta tasa de descuento. Por ello es preferible emplear diferentes tasas de descuento que reflejen distintas preferencias en el uso de los recursos por parte de la sociedad.
Como regla de decisión, se considera que un proyecto o alternativa es ejecutable si el VPN es mayor a cero, y en consecuencia la inversión es aconsejable. Esta regla es mayormente viable en caso de no haber restricciones financieras. Ahora bien, dado que en la mayoria de los paises, en especial en aquéllos en vías de desarrollo, se suscitan restricciones financieras, la regla de decisión será seleccionar aquella alternativa que maximice el bienestar social y que al mismo tiempo tenga el máximo VPN (mayor que cero). Este criterio puede darse también en presencia de proyectos mutuamente excluyentes. Dado que, tal como se ha expresado anteriormente, el criterio inherente a esta selección es el de valor máximo del producto social, supone implícitamente daño económico, por lo cual s recomendable identificar a los beneficiarios y perjudicados de la ejecución del proyecto, mostrando los impactos distribucionales en la sociedad.
El cociente beneficio-costo (B/C) está dado por la ecuación:

donde: VPB y VPC son el valor presente de beneficios y costos respectivamente.
El criterio de decisión en este caso será llevar a cabo el proyecto si el cociente es mayor a uno, mientras que si son varias alternativas se escogerá aquélla con mayor valor de dicho cociente.
La tasa interna de retorno (TIR) de un proyecto es definida como la tasa de descuento que hace el VPN igual a cero. O sea:

siendo ρ la TIR.
Análogamente, ρ puede ser calculada llevando el valor descontado del flujo de beneficios netos igual al desembolso de capital inicial y resolviendo la ecuación resultante para el valor de la tasa de descuento. Esto es, una ecuación de la forma

es resuelta para d, siendo C0 el capital inicial. La ecuación (4.7) puede ser expresada en la forma:
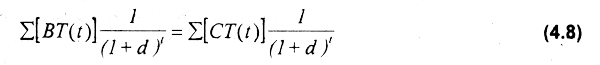
De (4.7) y (4.8) se obtendrá el mismo resultado, ya sea si se considera el valor presente del flujo de beneficios netos con respecto al capital inicial desembolsado, o bien el flujo de beneficios totales con respecto al flujo de costos totales. En ambas ecuaciones d es desconocido. El valor crítico dedque hace cero las ecuaciones (4.6) a (4.8) es la TIR (ρ). No existe un mecanismo simple para calcularla; sin embargo, una probable aproximación consiste en proponer una solución iterativa en base a la estimación de los valores presentes de costos y beneficios. Si el valor presente de éstos excede al de los costos, entonces la tasa escogida es demasiado pequeña y debe ser aumentada, y asi sucesivamente.
Un proyecto es aceptado cuando ρ es mayor o igual a un predeterminado valor de d que en general es la tasa de interés bancaria. En caso de proyectos mutuamente excluyentes o en presencia de restricciones financieras, se seleccionará el proyecto con máximo valor de ρ. Estas pueden ser consideradas como reglas de decisión.
El criterio de decisión para la inversión pública pesquera está basado en lograr la eficiencia económica en la asignación intertemporal de recursos con respecto a aquélla que hubiese logrado el sector privado. El argumento clave en este sentido ha sido considerar que una asignación eficiente de recursos en el tiempo será lograda si las tasas marginales de retorno en el uso de un recurso son iguales en los dos sectores. Cuando el sector público financia sus programas a través de préstamos ó impuestos provenientes del sector privado, las tasas de retorno derivadas de las inversiones no realizadas por estas causas, asi como aquéllas inferidas de la preferencia del tiempo en el consumo no efectuado, pueden ser consideradas como el costo de oportunidad de los recursos canalizados a la inversión de dichos programas. El argumento de eficiencia económica en este caso es que se ahorraría una tasa de retorno en los servicios aportados por el sector público al menos igual a su tasa de retorno en los servicios generados por el sector privado. Esto puede ser afirmado en base a la siguiente regla de inversión en el sector público: aceptar sólo aquellos programas que exhiben un VPN positivo, usando una tasa ponderada del costo de oportunidad del sector privado como tasa de descuento. Esto aseguraría una eficiente asignación de recursos entre los sectores público y privado.
Ahora bien, el VPN no provee información directa acerca de los requerimientos de capital de un proyecto en particular. Por ejemplo, si ei proyecto A tiene un VPN apenas mayor que otro B, pero mucho mayor requerimiento de capital inicial, no es claro que el proyecto A tenga mayor prioridad que B en presencia de restricciones financieras.
Tampoco una priorización por magnitudes en el caso del cociente beneficio-costo resulta estrictamente válido, dado que Bgr/c es un cociente entre beneficios y costos promedio y no marginales, los cuales constituyen la única alternativa posible de optimización.
En el caso de la TIR, tampoco la magnitud de ρ es un criterio válido para seleccionar proyectos en presencia de restricciones financieras. En efecto, dicho criterio es aplicable sólo en proyectos de inversión, donde los costos ocurren en forma temprana en el tiempo, mientras los ingresos son logrados a posteriori. En cambio no es aplicable a proyectos de desinversión, donde se producen beneficios a corto plazo y aumento de costos en el tiempo. Dado que altas tasas de descuento tenderán a favorecer aquellas alternativas con ocurrencia tardía de costos, cuanto más alta sea la tasa de interés, mejor considerado será el proyecto de desinversión. En consecuencia el valor crítico de ρ será el menor valor de la tasa de interés que justifique su ejecución. En otras palabras, un proyecto de desinversión sería ejecutable sólo si el verdadero valor de la tasa de interés es mayor que ρ, lo cual contradice el concepto de TIR. Una de las críticas de mayor peso efectuadas a la TIR es que su aplicación es problemática cuando se comparan proyectos cuyos flujos de costos y beneficios son muy diferentes en el tiempo, o sea se intercalan períodos donde los beneficios son mayores a los costos con otros donde ocurre el caso inverso. Dado que la TIR es resultado de la solución de una ecuación polinomial, es factible en el caso indicado obtener más de un valor de ρ posible. En efecto, si el polinomio es de grado n, habrán n raices, e.g. n valores de ρprobables. Por ejemplo, si la TIR de un proyecto tiene dos soluciones, 10% y 15%, y la tasa social de descuento es 12%, no hay un criterio evidente de aceptación ó rechazo. Por otra parte, la determinación de una TIR óptima cuando hay restricciones financieras no es muy sencilla, y no equivale a p = d, sino a aquél incremento de ρ que iguala a los incrementos de ρ para otros proyectos.
La TIR pondera en mayor grado a proyectos que acumulan sus beneficios en las primeras etapas de su ejecución con respecto a otros que generan beneficios en forma tardía en el tiempo. En efecto, 1 US$ invertido ahora tendrá una TIR de 100% si se acumulan 2 US$ al final del añ. Una inversión de 10 US$ que acumule 15 US$ al final de año tendrá una TIR de 50%. El empleo de la TIR como criterio de decisión favorecerá la primera alternativa, aún cuando a una tasa de descuento del 10% el VPN será respectivamente 0.8182 y 3.6364.
El uso de la TIR es complicado cuando se comparan proyectos mutuamente excluyentes, dado que no necesariamente el mejor proyecto es aquél que posee TIR más elevado. Considere los dos proyectos X e Y que se muestran en la Tabla 4.1 (Pearce & Nash, 1981), ambos con una vida de 10 años. Basándose en el TIR como regla de decisión, X es preferible a Y; sin embargo, de acuerdo a la regla de VPN, Y es preferible a X.
| Proyecto | Costo | Beneficio | TIR | VPN |
|---|---|---|---|---|
| X | 1 | 0.20 | 15 | 0.34 |
| Y | 2 | 0.36 | 12 | 0.42 |
| “Y-X” | 1 | 0.16 | 9 | -- |
En este caso la TIR como regla de decisión es falsa, dado que discrimina en contra de Y debido a la magnitud de capital desembolsado. Para evitar este problema, es necesario calcular la tasa de retorno en un proyecto hipotético “Y - Y”, o sea, basado en la diferencia entre capitales. Dado que la TIR en “Y-X” es mayor que el valor de d usado en el ejemplo, Y es preferible a X. En consecuencia, el contexto de exclusión mutua requiere de una regla de dos partes a efectos de que el proyecto Y sea aceptado:
1)TIRy > d
y además:
2)TIR(y-x)>d
donde d es un valor predeterminado. Esta regla ha sido usualmente descrita como la “tasa de retorno sobre costo” de Fisher (Pearce & Nash, 1981).
Del desarrollo de este Capitulo, resulta evidente que la TIR es un criterio de decisión más controvertido, ambiguo y con menor aplicabilidad que VPN y B/C. Sin embargo, las limitaciones que en común poseen los tres criterios surgen a raiz de su propia simplicidad, de su intento de resumir una gran cantidad y variedad de información en un simple número. Como respuesta a esto, ninguna de las tres aproximaciones provee un “ranking” estricto en la eventualidad de existir varios proyectos. Dificultades similares surgen a la hora de seleccionar el tamaño óptimo de un proyecto, dado que dicha estimación requiere del cálculo del VPN, B/C y TIR para cada incremento en el tamaño de cada proyecto en consideración (e.g. desarrollo de análisis marginales). Los autores sugieren por tanto el uso de VPN o B/C como criterios de decisión. La elección entre éstos provendrá de una decisión alternativa: saber cuando B/C >0 contiene más o menos información que B/C >1.
Un responsable de administrar recursos pesqueros está analizando tres alternativas de artes de pesca A, B y C, factibles de ser empleadas para desarrollar una pesqueria de una especie de langosta en el Estado de Yucatán (México). Se le ha solicitado al especialista en bioeconomía pesquera que estime el VPN y el B/C de dichas alternativas, explicar sus resultados al administrador pesquero y efectuar recomendaciones con respecto a la mejor alternativa de arte de pesca. El flujo temporal de costos y beneficios (en millones de dólares) se presenta a continuación:
| Año | Costos | Beneficios | ||||
|---|---|---|---|---|---|---|
| A | B | C | A | B | C | |
| 0 | 4.0 | 2.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 1 | 8.0 | 4.0 | 2.0 | 7.0 | 4.0 | 6.0 |
| 2 | 6.0 | 4.0 | 4.0 | 7.0 | 5.0 | 7.0 |
| 3 | 4.0 | 4.0 | 6.0 | 8.0 | 6.0 | 8.0 |
| 4 | 3.0 | 4.0 | 8.0 | 9.0 | 7.0 | 9.0 |
| 5 | 2.0 | 4.0 | 8.0 | 8.0 | 9.0 | 8.0 |
Resultados
En el ABC se ha optado por incluir 3 valores distintos de la tasa de descuento d a fin de reflejar diferentes preferencias intertemporales en el uso del recurso.
El VPN fue estimado para cada alternativa de arte de pesca en particular, en base a la maximización del valor presente de los beneficios netos dada por la ecuación (4.4):
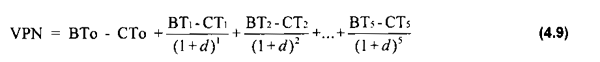
donde:
BT(t) son los beneficios totales en los añ 1 a 5.
CT(t) son los costos totales en los años 1 a 5.
d es la tasa de descuento (5%, 10% y 15%).
Un criterio análogo se siguió con B/C, en este caso estimado en base a (4.5), tomando en cuenta el flujo de beneficios y costos en los 5 años. Los resultados derivados del análisis se muestran a continuación:
| ALTERNATIVA | 5% | 10% | 15% | |||
|---|---|---|---|---|---|---|
| VPN | B/C | VPN | B/C | VPN | B/C | |
| A | 9.06 | 1.369 | 6.76 | 1.299 | 4.93 | 1.237 |
| B | 7.03 | 1.363 | 5.48 | 1.319 | 4.29 | 1.358 |
| C | 8.08 | 1.329 | 7.30 | 1.347 | 6.64 | 1.363 |
Tal como se ha argumentado anteriormente, el criterio de VPN maximiza la diferencia entre costos y beneficios, por lo cual si es mayor que cero, las alternativas son factibles de ser desarrolladas con éxito. Sin embargo, asumiendo restricciones financieras y/o que los proyectos son mutuamente excluyentes, debe hacerse un análisis comparativo de las distintas alternativas. Dicho análisis muestra que la alternativa C maximiza la relación beneficio-costo en base al empleo de tasas de descuento del 10% y 15%, y la oportunidad de llevar a cabo el proyecto de desarrollo es de 7.3 y 6.6 millones de US$ al valor presente (e.g. año cero) respectivamente. Para el caso del empleo de una tasa de descuento del 5%, el VPN se maximiza en la alternativa A, dado que otorga mayores beneficios netos al presente (9.06 millones US$).
Por su parte, el análisis del cociente beneficio-costo muestra que todos los valores obtenidos de B/C son mayores a 1, por lo cual las alternativas son factibles de ser desarrolladas con éxito. Asumiendo proyectos mutuamente excluyentes, el análisis comparativo muestra que la alternativa C maximiza el cociente beneficio-costo en base al empleo de tasas de descuento del 10% y 15%. El empleo de una tasa de descuento del 5% maximiza la alternativa A, dado que otorga mayores beneficios netos al presente.
De acuerdo a los resultados y análisis comparativo anteriormente expuesto, la selección del arte de pesca es sensible a la tasa de descuento empleada. La alternativa C sería la adecuada en caso de existir una alta preferencia intertemporal por el recurso, dado que optimiza el VPN y B/C para tasas de descuento mayores (10% y 15%). Estas a su vez tenderán a favorecer aquellas alternativas con ocurrencia de costos relativamente tardía y beneficios lográndose en el corto plazo. En el caso hipotético que la especie de langosta fuera de ocurrencia ocasional e impredecible, se le recomendaría al administrador del recurso utilizar el arte de pesca C para desarrollar la pesquería. Si por el contrario, los estudios de la biología y dinámica poblacional de la especie muestran que es de larga vida, con cierta constancia en la disponibilidad de biomasa a ser extraída, y que por otra parte se desea favorecer inversiones y explotarlo a largo plazo, el arte de pesca A junto al empleo de una tasa de descuento del 5% sería el curso de acción adecuado, dado que dicha estrategia otorga mayores beneficios al presente con una baja preferencia intertemporal. Por tanto beneficia a aquellos usuarios, presentes o futuros, que desean conservar el recurso a fin de favorecer su óptima explotación.
Tal como se ha expresado anteriormente, el ABC es aplicado a problemas asociados con las preferencias intertemporales de la sociedad como un todo, para lo cual se aplica el criterio Pareto-eficiencia. Dicho criterio provee las herramientas adecuadas para hacer afirmaciones acerca de la contribución de un proyecto a la eficiencia económica y bienestar social, pero no provee ninguna guía sobre la diversidad de efectos del proyecto en la distribución del ingreso. En este entorno juega una decisión clave el administrador ó tomador de decisiones, quien debe escoger entre las distintas alternativas y en consecuencia hacer juicios de valor acerca de las diferentes formas en las que se plantea la distribución del ingreso.
En este contexto, un ABC puede ser considerado como compuesto como compuesto de dos etapas distintas: a) la primera consiste en evaluar, en términos monetarios, las ganancias y pérdidas generadas en cada uno de los sectores de la sociedad afectados por el proyecto. b) La segunda etapa consiste en combinar dichos flujos costo-beneficio en una cuantificación simple que represente de un modo u otro los cambios en el bienestar social. Es en esta etapa en la cual se integran al análisis juicios de valor sobre la distribución del ingreso derivados de la consecución del proyecto. El criterio de Pareto-eficiencia, que implica que los beneficios y costos son ponderados en una simple operación algebraica, es sólo un juicio. Sin embargo, la forma más conveniente de expresar dichos juicios es a través del uso de coeficientes de distribución. Supóngase que el efecto de un produce cambios en los beneficios netos de dy1, dy2, …., dyn a cada uno de los miembros de la comunidad 1, 2,…, n. El cambio neto en el bienestar social dW es una suma ponderada de las pérdidas y beneficios individuales:
dW = w1dy1+ w2dy2 + ... + wndyn (4.10)
En este caso, cada uno de los valores de w denotan los coeficientes de distribución, expresando los valores relativos sociales de incremento en el ingreso de los diferentes individuos. Un beneficio de 1 US$ en el individuo 1 tiene la misma significación en el bienestar social que uno de w1/w2 US$ para el individuo 2. En este contexto, el criterio de Pareto-eficiencia implica que ocurra un conjunto particular de valores de w:
w1 = w2 = ... = w n = 1 (4.11)
Estos valores son denominados coeficientes de distribución unitarios.
dU = UM1dy1+UM2dy2+...+UMn dyn (4.12)
Los coeficientes de ponderación expresan de manera algebraica juicios de los administradores acerca de la redistribución del ingreso en los distintos sociales como consecuencia de la puesta en marcha de un proyecto. En estos términos, el objetivo propio de un gobierno es maximizar la suma de las utilidades correspondients a cada uno de los miembros de la comunidad. Suponiendo que un proyecto produce beneficios netos (en dinero) dy1, dy2,…., dyn a cada uno de los miembros de la comunidad 1, 2, …, n, se generará una utilidad marginal del ingreso (UMn), esto es, la utilidad extra conferida a un aumento en el ingreso de 1 US$.
El cambio neto en la utilidad total, o bienestar social, es entonces una suma ponderada de los cambios en el ingreso de los individuos; la ponderación en cada caso estará dada por la respectiva utilidad marginal en el ingreso. Dado que un incremento en una misma cantidad de dinero significa una utilidad marginal mucho mayor para un individuo con bajos ingresos, cuanto más bajo sea el ingreso promedio de determinado núcleo social, mayor será su coeficiente de distribución.
En la práctica, la adopción de distintos coeficientes de distribución (e.g. no unitarios) dificulta en grado sumo al ABC, debido a que la información tradicionalmente recolectada (e.g. precios del mercado, cantidades de bienes consumidos y vendidos) permite la determinación del excedente del consumidor y productor en forma agregada, o sea, mide beneficios o pérdidas totales de los consumidores en general y implícitamente coeficientes de distribución unitarios. Es muy difícil obtener información para aplicar coeficientes de distribución ponderados por núcleo social, inclusive por la dificultad inherente a la propia identificación de dichos grupos. Otra dificultad radica en que los beneficios y costos sociales netos a partir de un cambio en el precio de un bien pueden ser calculados únicamente a partir de su curva de demanda, y este concepto está intimamente ligado al concepto de Pareto-eficiencia, e.g. coeficientes unitarios de distribución.
El ABC es aplicado a problemas que incluyen la dimensión del tiempo como factor clave. Debe escogerse entre consumir en la actualidad o en periodos subsiguintes, a través de la aplicación de la tasa de descuento “apropiada”, que en este caso es la tasa social de descuento. Esta debe ser determinada a partir de las preferencias individuales de cada uno de los miembros de la sociedad. Estos podrían tener la misma TMPT, la cual reflejaría la tasa de interés en el mercado. En la práctica no existe ninguna tasa de interés patrón, sino que reproducen de una u otra manera la coyuntura económica, niveles de riesgo e incertidumbre asociados a la estabilidad política y desarrollo económico de un país. Por tanto, es más razonable asumir que los individuos que componen una sociedad no poseen la misma preferencia del tiempo, hecho que se agudiza si se consideran niveles distintos de ingreso e inclusive la propia expectativa de vida de cada individuo. Como resultado de estas disimilitudes, se hace necesario arribar a una tasa que de una u otra forma refleje las preferencia de la sociedad en su conjunto. Así habrán beneficiados y perjudicados como resultado de la ejecución de un proyecto (en el entendido que una evaluación personal del proyecto puede derivarse en un VPN negativo si se tiene en cuenta su propia TMPT).
En este contexto, el Gobierno, representado por los administradores y tomadores de decisión, debe escoger dicho valor, para lo cual es factible seguir dos aproximaciones diferentes: la primera se basa en lograr cierta concordancia entre las tasas de descuento generadas en los sectores público y privado; la segunda se basa en el concepto de preferencia social del tiempo.
En el primer caso, se ha enfatizado que es posible interpretar las decisiones tomadas por firmas privadas en la evaluación de un proyecto como si proviniesen de un ABC. Esto es, en vez de considerar a las reglas de decisión de las empresas como provenientes de un análisis financiero (considerando una tasa de interés del mercado), tomar dichos resultados como si fuesen costos y beneficios sociales en función de una tasa social de descuento implícita. La toma de decisiones en el ámbito privado podrá ser considerada consistente para las agencias públicas siempre que la tasa social de descuento usada por éstas para un ABC sea igual a la tasa social de descuento implícita usada en el sector privado. Dicha tasa es también denominada costo de oportunidad social del capital, en razón de que mide el costo de oportunidad social de derivar recursos invertidos por el sector privado.
La segunda alternativa supone el concepto de preferencia social del tiempo, la cual considera las preferencias temporales de la sociedad en el consumo, o sea, la cuantificación de efectos relativos en el bienestar de la sociedad a partir de cambios en el consumo en diferentes años. La selección de una tasa de descuento social (única) involucra un juicio de valor por parte de quien la selecciona. Este es en general el tomador de decisiones como puede ser el administrador pesquero, y su elección dependerá en gran medida de la coyuntura socio-económica, volumen de empleo complementario y disponibilidad de alimento entre otros factores. Sin embargo, la elección de un valor adecuado surgirá de un compromiso entre factores biológicos y socio-económicos (ver Sudgen y Williams, 1978).
Es común la tendencia a identificar valores altos de d como sinónimo de “anticonservación”, asi como bajos valores a inversión y explotación sostenible en el largo plazo (Clark, 1985). La importancia de este principio como herramienta para un adecuado manejo de recursos renovables ha sido ampliamente analizada en la literatura (e.g. Clark, 1976; Dasgupta y Heal, 1979). Se ha argumentado que en el caso de recursos recursos renovables en los cuales la sociedad como un todo es responsable de su conservación (no sólo los usuarios actuales sino también las futuras generaciones), el empleo de una tasa de descuento cero (Page, 1976) o muy pequeñas, sería una adecuada aproximación como tasa social de descuento. Dadas las características inherentes de los recursos pesqueros y libre acceso a la explotación (ver Capítulo 1), así como su variabilidad en diferentes fases del sistema (e.g. recurso + impacto humano), la divergencia “micro-motivos macro-resultados” también se refleja a la hora de definir la tasa social de descuento adecuada: para los pescadores, a quienes concierne en mayor grado el corto plazo y que están sujetos a un fuerte componente de incertidumbre en su actividad, la elección de altos valores de d es preferible. Por el contrario, los biólogos pesqueros y administradores del recurso tenderán a suponer bajos valores de d con criteros de largo plazo (e.g. conservación). Estos conceptos realzan la necesidad de emplear análisis dinámicos que tomen en cuenta la preferencia del tiempo para el manejo de recursos pesqueros.
A efectos de abordar este tópico, es importante distinguir los conceptos de riesgo e incertidumbre (Pearce & Nash, 1981). La existencia de riesgo en la ocurrencia de un evento implica que hay cierto conocimiento de las probabilidades de llevarlo a cabo, mientras que la incertidumbre supone variabilidad que no puede ser cuantificada debido al desconocimiento de dichas probabilidades de ocurrencia. A continuación se analizan brevemente ambos conceptos en el contexto del ABC en pesquerías, ya que en el Capítulo 8 se discuten más a fondo en el marco del manejo precautorio de pesquerías.
Riesgo
La ejecución de un proyecto pesquero lleva asociado en general un componente de riesgo, más si se están considerando recursos naturales renovables como los pesqueros. Los criterios de decisión se verán afectados por dicho componente, en el sentido que los resultados de un ABC derivados del análisis de distintas alternativas podrán ser diferentes a los teóricamente esperados de acuerdo al clásico criterio determinístico presente en las reglas de decisión del ABC. En efecto, es probable que ocurra más de un valor de VPN en el caso de analizar posibles estrategias de desarrollo de un plan pesquero. En este caso, será en mayor grado apropiado considerar los resultados de un proyecto en términos de distribución de probabilidades de ocurrencia de las alternativas y seleccionar los cursos de acción adecuados en base a la media ponderada derivada de dicha distribución probabilística. Las decisiones alternativas pueden ser el resultado de la comparación de diferentes proyectos o bien de diferentes opciones de manejo o desarrollo para un mismo proyecto. En todos los casos deberá especificarse claramente la preferencia del tiempo (TMPT) asociada a la probabilidad de ocurrencia de cada alternativa (Schmid, 1989).
A modo de ejemplo, supóngase que la magnitud de capturas de un recurso (y por tanto el flujo de ingresos totales asociados a un ABC) está asociada a la ocurrencia de diferentes condiciones ambientales, tales como magnitud de precipitaciones. La probabilidad de éxito del proyecto estará asociada a la ocurrencia de n alternativas posibles pero mutuamente excluyentes para desarrollarlo. La probabilidad de ocurrencia de cada altemativa es P1, P2, …, Pn. Si se considera que el resultado de cada una genera un beneficio neto de x1, x2, …, xn, el valor esperado de dichos beneficios (VE) será:
VE = P1X1+P2x2+...+Pnxn (4.13)
Esta evaluación ponderada de la utilidad de distintas alternativas se denomina criterio de valor esperado (VE), y puede resultar útil a efectos de atenuar el riesgo derivado del determinismo inherente al ABC. El VE puede constituir un criterio de decisión aceptable si, dada una serie de observaciones realizadas sobre el comportamiento del recurso en función de ciertas variables (e.g. climáticas) y estrategias de manejo, se asume como probable que los beneficios netos respondan al promedio de las expectativas generadas en dichos casos. El uso del VE como regla de decisión supone implícitamente que la variabilidad derivada de una serie estadisticamente consistente de observaciones sea despreciable. En caso de que no existan muchas alternativas o que la serie de observaciones no sea numerosa, es adecuado considerar la variabilidad de cada estrategia asociada al criterio de VE.
Incertidumbre
Se ha enfatizado anteriormente que existen situaciones donde el riesgo inherente a llevar a cabo ciertas alternativas existe, sin embargo se conoce la distribución de probabilidades de su ocurrencia. En el manejo de pesquerias este caso ocurre sólo eventualmente. La situación que prevalece en mayor grado es un importante grado de incertidumbre acerca de la ocurrencia de dichas probabilidades, así como en lo referido a características del stock, magnitud del esfuerzo pesquero, proyecciones de costos y precios. La evaluación de un proyecto pesquero entonces llevará asociado en general un componente de incertidumbre. En efcto, en el ABC dirigido a evaluar la factibilidad de desarrollo de actividades pesqueras debieran tomarse en consideración dos componentes importantes de incertidumbre:
a) Incertidumbre inherente al ABC. El desarrollo de las Secciones anteriores muestra que los criterios de decisión del ABC son determinísticos. Esto es, la viabilidad o factibilidad de un proyecto es definida a través de un valor único, sin especificar el grado de variabilidad asociado a su ejecución. Esto se debe a que los resultados obtenidos de un ABC son esencialmente proyecciones de flujos de costos y beneficios estimados de la planificación de actividades pesqueras y por tanto sujetas a un grado variable de incertidumbre.
Por otra parte, el proyecto afectará en mayor o menor grado a los diferentes sectores de la sociedad, debido al criterio inherente de decisión que lo sustenta (e.g. valor máximo del producto social). Puede considerarse entonces que se dará incertidumbre también en esta etapa, para lo cual será adecuado incluir de un modo u otro una proyección del impacto que el proyecto generará en cada sector de la sociedad.
A la hora de evaluar proyectos relacionados con pesquerías será necesario comparar los resultados provenientes del criterio de decisión empleado (sea preferiblemente VPN ó B/C) generados de distintas alternativas. Para ello, es conveniente emplear un amplio rango de valores de d que reflejen diferentes preferencias intertemporales en el uso de los recursos. Eventualmente podrá considerarse como patrón la tasa de interés existente en el mercado. Por ejemplo, si ésta es de 10%, podrían emplearse valores que oscilen entre 5 y 20%, representando respectivamente baja y alta TMPT. El empleo de tasas de descuento bajas beneficiará a aquellos usuarios (presentes ó futuros) de los recursos que desean conservarlo y en consecuencia explotarlo en un lapso prolongado en el tiempo. Este sería un ejemplo de un marco conservativo de manejo y al mismo tiempo una forma de estimular la inversión. La selección de altos valores de d, (e.g. alta TMPT por el recurso) tenderá a favorecer aquella alternativas con ocurrencia de costos relativamente tardia y beneficios produciéndose a corto plazo, ya que a mayores valores de d, mayor será la tasa de explotación del recurso. Es importante resaltar que una sola soución estaría mostrando las preferencias de sólo un sector de la sociedad, por lo que en cada evaluación realizada con determinado valor de d deberá especificarse el impacto distribucional que cada alternativa genera en los diferentes usuarios del recurso.
b) Incertidumbre inherente a los recursos pesqueros. La mayoría de los modelos desarrollados en ciencias pesqueras han sido de carácter determinístico (ver Capítulo 2). Sin embargo, el cuerpo de conocimiento teórico-práctico generado en las últimas dos décadas, dirigido a adoptar decisiones inteligentes para el manejo de los recursos pesqueros, permite afirmar que tanto las pesquerías como los recursos que las sustentan no se comportan en base a tal aproximación, y brindan en general resultados incorrectos sobre la elección de la captura óptima (Hannesson, 1987). En efecto, los recursos naturales renovables, en especial los pesqueros, poseen un importante grado de variabilidad temporal en su magnitud. Ello impide predecir con certeza las fluctuaciones de su biomasa y abundancia a través del tiempo, y por ende la factibilidad de desarrollo de una pesqueriía, los costos de explotación (en caso de que éstos sean dependientes de la magnitud del stock) y dimensionamiento del fenómeno extractivo. Dicho de otra manera, existe un fuerte componente de incertidumbre en las proyecciones de captura, y en consecuencia en los beneficios y costos incluidos como entrada en un ABC. Este hecho se ve agravado si se considera que los proyectos de pesca son en general a largo plazo, e incluyen componentes de inversión (e.g. barco de pesca) que tienen una vida útil que en general supera la década y presentan un bajo o nulo costo de oportunidad debido a la especialización de la actividad.
Tres tipos de incertidumbre referidas a los recursos pesqueros deben ser tomadas en consideración a la hora de realizar un ABC (Lewis, 1982; Seijo, 1986): b1) incertidumbre en el tamaño del stock, el cual dependerá a su vez del nivel de esfuerzo efectuado en años anteriores y el grado en que éste afecto al stock; b2) fluctuaciones impredecibles en las variables ambientales, que a su vez inducen a variabilidad en el tamaño del stock y en consecuencia en la magnitud de la captura; b3) incertidumbre en la predicción de la demanda y precio del producto, así como en los costos de captura, en general debida a altibajos en la situación económica local o regional y aspectos coyunturales del mercado internacional.
La incertidumbre asociada a la evaluación de un proyecto pesquero indicaría de una u otra manera que la decisión de llevarlo a cabo deba contener en forma explícita alguna corrección que considere dicha variabilidad. En este contexto, la generación de intervalos de confianza a través de enfoques tales como el Método de Monte Carlo puede ser empleada en aquellas variables críticas (e.g. proyecciones de captura, biomasa y diferentes niveles de esfuerzo) y considerar el límite del intervalo a efectos de brindar resultados en un marco de acción precautorio.
Ahora bien, qué criterio emplear como regla de decisión para escoger dentro de ese rango de alternativas aportadas por la aproximación estocástica? La decisión será dependiente de la visión e intereses sociales del administrador, y ésta a su vez del punto de vista de la sociedad frente a la adopción o no de nuevos cursos de acción. La toma de decisiones en la ejecución de proyectos se agrava aún más en aquéllos con una larga vida útil, donde las futuras generaciones puedan verse perjudicadas por su puesta en marcha, sin haber tomado parte en dicho proceso de decisión. Al respecto, resulta de significación la elección de una adecuada tasa de descuento, fundamentalmente en caso de recursos de larga vida e importancia en un contexto socio-económico (e.g. recursos demersales) donde las estrategias de manejo repercutirán en su disponibilidad para futuras generaciones.
En el Capítulo 2 se desarrolló el modelo bioeconómico clásico en sus versiones estática y dinámica. Se presentaron los conceptos de máximo rendimiento sostenible (MRS), máximo rendimiento económico (MRE) y rendimiento en equilibrio bioeconómico (EBE), es decir, estimaciones bioeconómicas bajo condiciones de equilibrio. Asimismo, se presentaron las ecuaciones dinámicas que muestran la trayectoria de la biomasa, el rendimiento, la renta y el esfuerzo de pesca en el tiempo. Si bien los primeros constituyen conceptos claves en bioeconomia pesquera, el hecho de que provengan de un análisis estático les disminuye su potencialidad como predictores y en consecuencia como adecuadas herramientas de manejo. Las trayectorias en el tiempo de las variables mencionadas anteriormente, es decir, la versión dinámica del modelo Gordon-Schaefer, permite contar con los flujos intertemporales de los costos y beneficios resultantes de diferentes niveles de esfuerzo de pesca. La influencia que la dinámica del esfuerzo tiene en la magnitud del stock, en las capturas, y en consecuencia en los flujos de costos y beneficios derivados de la pesquería, hacen que ésta deba ser manejada en base a la maximización de un patrón dinámico de explotación más que por un especifico (estático) nivel de rendimiento sostenible (MRE; MRS). En efecto, dado que una pesquería será económicamente eficiente si maximiza el valor presente neto de las capturas, y que éstas están autocorrelacionadas en el tiempo (e.g. el nivel de explotación en un año repercutirá en forma directa en la magnitud del stock y en consecuencia en las capturas de años subsiguientes), el análisis bioeconómico basado en curvas de rendimiento sostenible pierde significación a efectos del manejo de un recurso pesquero.
Desde la perspectiva del administrador de pesquerías se busca identificar el nivel de esfuerzo pesquero f(t) que permita maximizar el valor presente del flujo de ingresos netos generados en el tiempo. Esto es:

donde VPπ es el valor presente de los ingresos notos π (t) en el tiempo.
Clark (1985) desarrolla el modelo económico dinámico basado en el concepto de un solo propietario de la pesquería (que por ejemplo podría ser el Estado). Este concepto no significa un monopolio, ya que en éste se posee el control del mercado y en consecuencia se fija el precio del producto. Por el contraio, el modelo dinámico Gordon-Schaefer desarrollado por Clark (1985) supone que la industria es tomadora de precios que se asumen fijos y constantes. El modelo considera la tasa de descuento d en su forma continua. Esto es, el factor de descuento definido en (4.1) es expresado en su forma exponencial como:
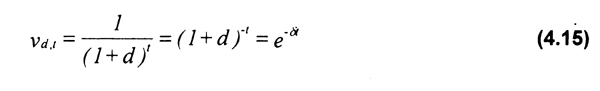
En esta expresión δ es denominada tasa de descuento continua anual. De acuerdo a (4.15) δse relaciona con d de la siguiente forma:
δ= 1n ( 1 + d) (4.16)
El valor presente del flujo de los ingresos netos π(t) en un intervalo de tiempo dt será:

Asumiendo largo plazo (e.g. T=+ω) y sustituyendo en (4.17) a π(t), el objetivo de un solo propietario será maximizar el valor presente de la renta económica que genera el recurso:
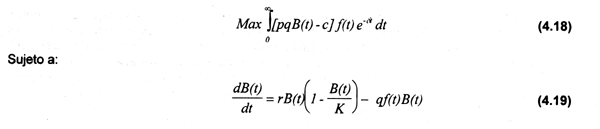
Debe considerarse asimismo la restricción de no negatividad en el monto del esfuerzo pesquero, de tal forma que f(t)≥0. Por otra parte se asume que B(t)≥ 0 y que la biomasa inicial Bo es conocida.
El nivel óptimo de biomasa BOPserá función decreciente de δ y en consecuencia tenderá a acercarse a la biomasa en equilibrio bioeconómico (BEBE) en caso que δ→+∞ (Clark, 1985). Resolviendo para f(t) en (4.19), sustituyendo en (4.18) e integrando por partes se obtiene una expresión para la biomasa óptima dada la tasa de descuento especificada:
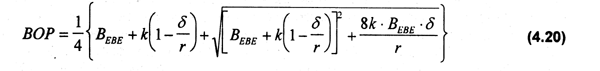
donde BEBE es definida como c/pq.
Ahora bien, el rendimiento óptimo sostenible (ROS) y el esfuerzo óptimo (fop) para el precio del tiempo especificado con el parámetro δ se obtiene con la siguiente expresión:
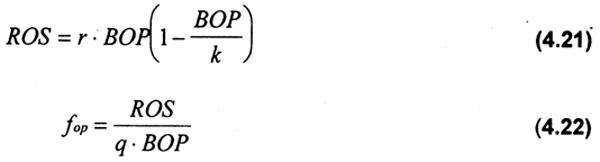
La propuesta de Clark (1973; 1985) anteriormente desarrollada, ha sido discutida en la literatura por Hannesson (1986; 1987). El concepto clásico, que implica que altos valores de δ aumentan la probabilidad de sobreexplotación, es rechazado por Hannesson (1986) al expresar que tal propuesta ignora las implicaciones derivadas de un alto valor de la tasa de interés en el costo del capital, efecto previamente establecido por Farzin (1984) para recursos no renovables. Según ambos autores, un alto valor de d aumentará el costo de extracción del recurso, dado que su explotación súbita requerirá inversiones a corto plazo en artes, equipos, etc.
Hannesson (1986) discute la ambigüeded de δ: por un lado expresa la tasa de retorno requerida para un beneficio creciente obtenido en el corto plazo, de tal manera que mayores valores de d implicarán una mayor tasa de explotación y una disminución en el tiempo del stock explotable. Por otro, δ expresa el costo de oportunidad del capital a ser invertido en la unidad de pesca (e.g. buque, artes, equipos), por lo cual un alto valor de δ implicará mayores costos de operación y por tanto una explotación óptima menos intensa que en el caso anterior y un stock disponible de mayores magnitudes.
El éxito en el desarrollo y sustentabilidad de una pesqueríra que la suma del valor presente de los ingresos netos totales sea maximizada. Esto significa que los niveles adecuados de captura en el tiempo dependerán de los valores esperados de costos y precios, fluctuaciones temporales en la tasa de crecimiento poblacional, y la situación económica y de mercado imperante en la región, probablemente reflejada en el valor de la tasa de interés. Las expectativas de cambios en los costos, precios y magnitud del stock deben ser incluidas en el estudio a través de un análisis ponderado de la distribución de probabilidades de diversas alternativas o cursos de acción. Estas razones suponen la necesidad de emplear aproximaciones dinámicas estocásticas para el manejo de un recurso pesquero. En este contexto, la tasa de descuento juega un papel fundamental para la adopción de un adecuado curso de acción a efectos de la explotación de un recurso pesquero. La elección de un valor de d será un paso crucial en la estrategia de explotación, y dependerá de la variabilidad esperada en variables intrínsecamente relacionadas al stock o bien al contexto socio-económico de los usuarios del recurso. Así pues, valores de δ que tiendan a +∞, debidos por ejemplo a una caída en el precio del producto o prdicción de una drástica disminución del stock, supondrán estrategias de explotación que maximizarán los ingresos a corto plazo, no importando el efecto adverso en el largo plazo. En estos casos el MRE dinámico tendrá a un valor cercano al EBE. Cuando por el contrario, las características del recurso favorecen una explotación a largo plazo, hay cierta estabilidad en los precios y costos, y se desea favorecer la inversión, δva a tender a 0 y en consecuencia el MRE dinámico coincidirá con el MRE estático. En general, el MRE dinámico fluctuará entre estas dos situaciones extremas (Anderson, 1986).