Table 1.5 Assumed Growth Rate of Real GDP (% per year), 1994-2010. (cont.)

Table 1.5 Assumed Growth Rate of Real GDP (% per year), 1994-2010. (cont.)

Table 1.5 Assumed Growth Rate of Real GDP (% per year), 1994-2010. (cont.)

1.5 Wood supply assumptions

In the current version of the GFPM, the supply of industrial roundwood in each country is a function of the price of industrial roundwood. The price elasticity of supply used in the model is 0.8, except for Asia, where the elasticity varies by country. This price elasticity indicates the percentage change in supply that would result from a 1% change in price, other things being equal. In addition, the supply equations are assumed to shift over time, to simulate changes in supply independent of prices. The rates of shift show how much timber supply would change, without any change in price. These rates of shift vary by country, and are based on various information regarding past production, forest area and stock, growth rates, extent of plantations, and policies of each country. In some countries of Asia, upper bounds were set on the timber supply, regardless of price, to reflect perceived limits on the potential sustainable timber production of the country. Estimate of the rate of shift to use in the GFPM relied mostly on the analysis of the FAO's Global Fibre Supply Model (FAO, 1999), with the rate of shift being equal to the annual percentage change in the commercially available wood supply projected by the GFSM. The resulting aggregate average rates of shift of industrial roundwood supply, by region, were 0.71% in America, 0.63% in Europe, 1.14% in Africa, and 1.43% in Asia. The detailed rates of shift used in this outlook are presented in Table 1.6.

Supply curves for fuelwood and charcoal, and for industrial roundwood used in the round (other industrial roundwood) were assumed to be horizontal, so that supply in each country was equal to the projected demand, at current prices and projected income. The statistics presented in FAOSTAT for these two variables are believed to be quite unreliable in many cases. Thus, the forecasts presented here should be treated with some caution. FAO, as part of the Global Forest Products Outlook Study, is conducting an in-depth review of FAO's fuelwood statistics and hopes to produce a more detailed and specific fuelwood forecast based on this review.

The supply of other fibre pulp and for waste paper used in paper manufacture was also assumed to be horizontal. However, the supply of waste paper in each country has an upper bound defined by the previous year's consumption and the maximum recycling rate for the country.

Table 1.6 Sawlog and pulpwood supply in 1994 and rate of shift of supply up to 2010.

Table 1.6 Sawlog and pulpwood supply in 1994 and rate of shift of supply up to 2010. (cont.)

Table 1.6 Sawlog and pulpwood supply in 1994 and rate of shift of supply up to 2010. (cont.)

Note: 1994 data is estimated by this study.

1.6 Other assumptions

Other assumptions governing the projections concerned changes in capacity, fibre input mix, and trade inertia constraints. In the GFPM, capacity is governed by past production and by relative profitability. Capacity data were estimated from the most recent production data. Thereafter, for pulp and paper products, and for all years for other products, the simplest capacity projection allowed by PELPS was used. This consisted of distributed-lag functions linking capacity changes to changes in past production at the global level, followed by allocating capacity growth to different countries according to the shadow price (the marginal value of one unit of additional capacity) revealed by the equilibrium computations (see: Gilless and Buongiorno 1987; and Zhang et al. 1993).

The technology, defined by input-output coefficients was held constant at the 1994 level, except for paper and paperboard. The input-output coefficients were changed substantially relative to those used in the Provisional Outlook, in that fewer constraints were put on the input-output coefficients to satisfy the national statistics. Instead, the coefficients were based on the national statistics, tempered with expert opinion as to what these coefficients could reasonably be expected to look like. This gave coefficients which varied by much less than previously across countries. It also means that the model's projections for roundwood and pulp production in the base-year do not always match national statistics, where the input-output coefficients would suggest that these figures might have been under or over-reported. Thus, the forecasts given here are not directly comparable with the statistics given for 1994 in some countries (e.g. industrial roundwood production in India which, it is suspected, is vastly under-reported in national statistics). For paper and paperboard, it was assumed that the fibre input mix for newsprint, printing and writing paper and paper and paperboard would change substantially between 1994 and 2010 with a progressively greater use of recycled fibre.

With the implementation of the GATT Uruguay Round underway, many countries are projected to reduce or eliminate trade tariffs and non-trade barriers in the near future. Thus, it was assumed that forest products would be traded more freely world-wide between 1994 and 2010 in response to market forces. However the adjustment of trade flows between countries or regions is bound to take time, thus inertia constraints were introduced to limit trade in a given year to be within a specified fraction of the previous year's trade (Buongiorno and Gilless 1984, Kallio et al. 1987, Nagy and Andersson 1988, Zhang et al. 1997).

1.7 Mathematical formulation of the GFPM

The Global Forest Products Model (GFPM) simulates dynamic market equilibrium for the global forest sector. Every year, demand, supply, trade and prices are computed that clear markets for all products and in all regions (static phase). Then, the model parameters are updated to reflect exogenous and endogenous changes from one year to the next (dynamic phase). Exogenous changes include economic growth, technical change, potential timber supply and trade inertia. Endogenous changes include capacity growth and availability of recycled fibres, which are determined by the model. The model then computes the quantity-price equilibrium next year as shaped by the intervening changes. It reiterates the static and dynamic phases for every year until the end of the projection.

1.7.1 Static phase:

The equilibrium for each year of the projection is obtained with an optimization model that simulates world markets. It finds the production, consumption and trade that maximize the total value of consumption minus the total cost of production for all products in all countries, in a given year. All the variables refer to that year.

Objective function:

[1]

where:

i,k = country, commodity,

P = price in US dollars,

D = final product demand,

S = raw material supply,

Y = quantity manufactured,

m = cost of manufacture.

Demand for final products:

[2]

where:

D_-1 = demand in the previous year,

X = gross domestic product, in real US dollars,

= elasticities with respect to price, GDP, and past demand.

Wood supply:

[3]

where:

P⁰ = cost of production.

S^u = potential supply.

Material balance:

[4]



where:

a_ikn = input of commodity k per unit of n.,

T = trade flow. Each country exports to and imports from a "world market", T^u,T^L= upper and lower bounds on imports and exports.

Manufacturing capacity:

[5]

where:

K = current capacity of production.

Waste paper recovery:

[6]

where:

r = recycled paper,

S^U = upper bound on recycled paper supply.

1.7.2 Dynamic phase:

Yearly changes in the market equilibrium conditions are brought about by:

1) shifts of the demand curves, due to changes in X at the projected GDP growth rate.

2) shifts of the upper bounds on wood supply, S, at the assumed rate of growth of potential supply.

3) changes of manufacturing coefficients m to reflect technical change, especially increasing use of paper recycling.

4) changes of capacity, determined as follows:

At global level, capacity change is a function of changes in production during the past three years:

[7]

then, global capacity change is allocated to each country in proportion of its production level and the marginal value of capacity revealed by the shadow price of capacity in the static phase.

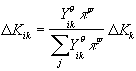[8]

where:

= yearly change,

= shadow price of capacity (endogenous, from constraint (5)),

= parameters.

5) Changes in waste paper recovery:

[9]

w_ikr= maximum possible recovery rate (exogenous).

6) Trade inertia:

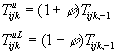[10]

= upper bound on relative change in trade flow (exogenous).

1.7.3 Regional sub-models:

The above calculations are performed first for the world model then repeated for each regional sub-model. However, when a regional sub-model is solved, total exports and imports of all countries in that region, must in every year, be equal to aggregate regional imports and exports predicted by the global model.