9. TOPOGRAPHICAL PLANS AND MAPS
9.0 Introduction
|
What are topographical plans and maps?
|
|
1. Topographical plans and maps are drawings which show the main
physical features on the ground, such as buildings, fences, roads,
rivers, lakes and forests, as well as the changes in elevation between
land forms such as valleys and hills (called vertical relief). You base
these plans and maps on the information you collect from topographical
surveys.
2. Plans are usually large-scale drawings; maps
are usually small-scale drawings. Depending on the scale you use
to make the drawing (see Section 9.1):
- it is a plan if the scale is larger than 1 cm
for 100 m (1 : 10 000), for example 1 cm for 25 m;
- it is a map if the scale is equal to or smaller
than 1 cm for 100 m (1 : 10 000), for example 1 cm for 200 m or 1 cm
for 1000 m.
|
|
Plan
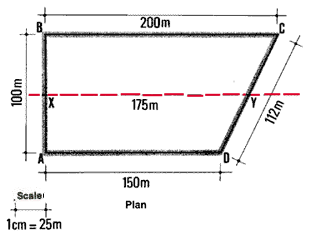
|
| |
|
|
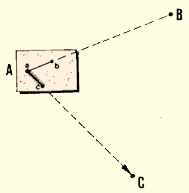
|
Example
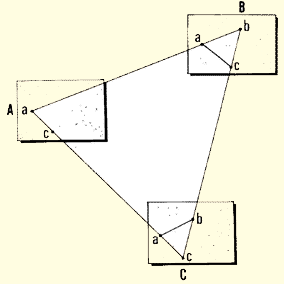
- An engineering plan could show information you need for building
fish-farm features such as dikes, ponds, canals or outlet structures,
at the scale of 1 cm for 25 m (1 : 2 500).
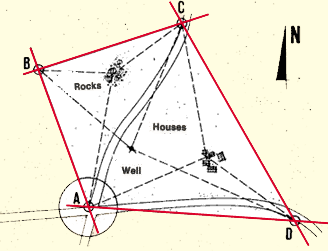
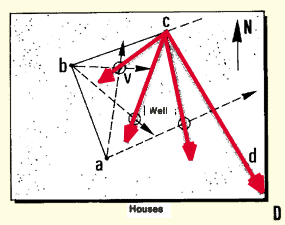
- A topographical map could show a fish-farm site (scale 1 cm for
200 m or 1 : 20 000) or a region of a country (scale 1 cm for 1 000
m or 1 : 100 000).
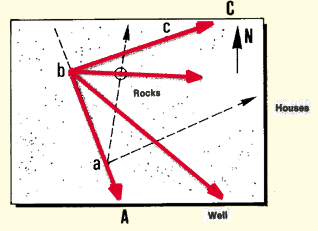
3. Plans and maps have two main purposes in fish-farm construction.
They help guide you in choosing a site, planning the fish-farm, and designing
the structures that are needed for the farm. Plans and maps also guide
you as you lay out marks on the ground, so that you can follow the plan
you have made of the fish-farm, and build the structures on it correctly.
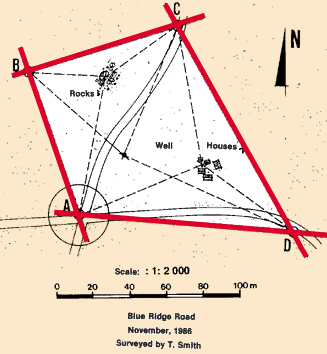
|
|
Map
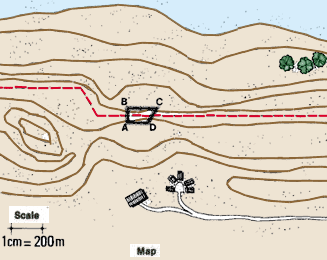
|
Starting topographical plans and maps
4. Before you begin a topographical survey, you should try to get any available
topographical plans and maps of the area, even though they may not be exactly
the kind of plan or map that you need. General topographical maps
are available from governmental organizations which are responsible for geological
surveys or land surveys, for example. National geographical institutes, soil
survey departments and agricultural development agencies can also usually provide
existing topographical maps. The cadastral department (that calculates land
taxes) of your local government may provide local topographical plans.
5. You will often have to make the topographical plans and maps yourself, however.
You will base them on a plan survey (see Chapter 7) and direct levelling (see
Chapter 8). In the following sections, you will learn how to:
- make the plan or map directly in the field by plane-tabling (see Section
9.2); or
- make the plan or map from the field measurements recorded in your notebook
(see Sections 9.3-9.6).
6. On topographical plans or maps, you should always look
for:
- the name of the area or piece of land mapped, and/or the name
of the type of project for which it is used;
- the exact location of the piece of land;
- the name of the person or people who made surveys on which the
plan or map is based;
- the date(s) on which the surveys were made;
- the direction of magnetic north;
- the scale at which the plan or map was drawn (see Section 9.1);
- the contour interval, if the vertical relief is shown (see Section
9.3);
- a key, or guide, to the symbols used in the drawing.
This information is often located in one corner of the map. It is called the
legend.
9.1 How to make scales for plans and maps
|
What is the scale of a plan or map?
|
|
1. To represent distances you have measured in the field on a piece of
paper, you need to scale them down. This means that you must
reduce the size of the distances proportionally according to a scale.
The scale expresses the relationship which exists between the
distance shown on a drawing or map and the actual distance across the
ground.
|
|
|
| |
|
|
|
Example
- 1 cm on the plan represents 20 m (or 2000 cm) on the ground,
or scale 1:2000.
- 1 cm on the map represents 100 m on the ground, or scale 1:10000.
- 1 cm on the map represents 1250 m on the ground, or scale 1:125000.
|
|
|
| |
|
|
|
Note: a ratio with a smaller number is a larger
scale, that is, 1: 500 is a larger scale than 1 : 1000.
|
|
|
Expressing a scale
2. There are three ways of
expressing the scale of a drawing:
- as a numerical equivalent such as " 1 cm = 20 m",
which you should read as "1 cm on the plan represents 20 m on the ground";
- as a ratio such as " 1: 2 000" which you should
read as " 1 cm on the plan represents 2 000 cm = 20 m on the ground";
- graphically, with a line that is marked off into drawing
distances that correspond to convenient units of distance on the ground.
3. Table 11 gives the numerical
equivalents of the most common scales, expressed as fractions.
Scales for both distances (in metres) and surface areas (in square metres) are
shown also.
Choosing a scale
4. General topographical maps usually have scales ranging from 1:50000 to 1:250000.
These are small-scale maps. In most countries, 1 :50000 maps
are now available. You can use these for general planning of aquaculture development,
including the planning of your fish-farm.
5. To show greater detail, plans are drawn to a larger scale,
showing individual structures or land areas. The scales most often used in plans
are 1 :500, 1 :1000, 1 :2000, 1:2500 and 1:5000. Detailed engineering drawings
use scales much larger than 1:500, for example
1 : 100 or 1: 10.
Note: special rulers, called "Kutsch" scales
or reduction scales, make it easy to transfer ground distances onto
drawings.
TABLE 11
Distances and surface areas expressed by scales
|
Scale
|
Distance: 1 cm equals (m)
|
Surface area: 1 cm2 equals
(m2)
|
| 1: |
300
|
3
|
9
|
| |
500
|
5
|
25
|
| |
600
|
6
|
36
|
| |
1000
|
10
|
100
|
| |
1200
|
12
|
144
|
| |
1500
|
15
|
225
|
| |
2000
|
20
|
400
|
| |
2500
|
25
|
750
|
| |
5000
|
50
|
2500 (0.25 ha)
|
| 1: |
10000
|
100
|
10000 (1 ha)
|
| |
25000
|
250
|
62500 (6.25 ha)
|
| |
50000
|
500
|
250000 (25 ha)
|
| |
100000
|
1000 (1 km)
|
1000000 (100 ha) (1 km2)
|
| |
125000
|
1250
|
1562500 (156.25 ha)
|
| |
200000
|
2000
|
4000000 (400 ha)
|
| |
250000
|
2500
|
6250000 (625 ha)
|
|
9.2 How to make a map by plane-tabling
|
|
1. In Section 7.5, you read that you can
use a plane-table to make a reconnaissance survey and to plot details.
In this section, you will learn how to do this. It is best
to use an alidade for this method (see Section 7.5, steps 21-28),
but you can use a simple ruler, and a series of tailor's pins to show
the observed directions, instead.
2. First, choose an appropriate scale for the map you will
draw (see Section 9.1, steps 4 and 5). Get an estimate of the longest
distance you need to map, and decide upon the size of the map you require.
If the map is to be fairly large, you can draw it on several sheets of
paper, and glue them together.
|
|
|
| |
|
|
|
Example
- You have a plane-table, size 40 x 55 cm.
- You estimate the longest distance to be mapped = 400 m.
- From Table 11, you find that if you use a 1 : 1 000 scale (where
1 cm is equivalent to 10 m), you will need 40 cm to draw this distance
on your sheet of paper.
- If this scale is large enough for your purposes, you can use
just one sheet of paper.
|
|
|
| |
|
|
| 3. Cover the board of your plane-table with paper
(see Section 7.5, steps 34-39). Set up the plane-table
(see Section 7.5, steps 40-44) on or near some major feature A
of the area you need to map, such as a large rock, a path, a river or a
tall tree.
4. Using a well-sharpened pencil with a hard lead, mark a small point
and circle on your paper. This is point a, the location
of the major feature, where you have set up your plane-table. Be
sure to choose a section of the paper from which you can later map the
entire area. For example, if you will be mapping only ahead of point A,
begin near the centre of the bottom margin of the plane-table.
Note: you will identify physical features in the
field that you need to map with capital letters. You will identity
the corresponding points that you draw on the plane-table sheet with lower-case
letters.
|
|
Set up the plane-table at point A

|
| |
|
|
|
5. Rotate the table so that you will be drawing the map in the orientation
you need. Using your magnetic compass
as a guide, draw arrows showing the magnetic north (see Section 7.5, steps
45-46).
Note: you should always try to locate the north
facing the top of your map. This is a rule which is always applied in
professional topographical maps. You may not be able to follow the rule,
however, depending on the direction of the longest distance and on the
scale you select.
|
|
|
| |
|
|
|
6. Using your alidade, sight
from the first marked point a to another major feature
B which you can see from the plane-table location. This could be
a small hill, a bend in a path or a ranging pole. Draw a thin line
ax in this direction.
Note: you can use the alidade much more easily
if you place a pin at point a on the board, and
then swivel the alidade around the pin until you can sight
the second point.
|
|
Draw ax

|
| |
|
|
|
7. Measure the horizontal ground distance from the plane-table
station A to the major feature B. Then mark this
distance along line ax, starting at point a
and scaling it down as line ab.
8. Without moving the plane-table from point A,
repeat this process for all other major features C, D, etc.
which you can see, and draw lines ac, ad, etc.
|
|
Draw ay
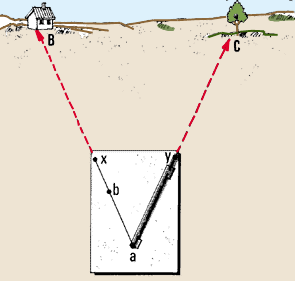
|
| |
|
|
|
9. Move the plane-table to one of the major features
you have just mapped, such as C. Choose a feature from which
you can easily map another part of the area, such as the route of a path
or the course of a river.
10. Set up the plane-table over this point C. Reorient the table.
Use the compass and the magnetic north arrows you have already drawn (see
step 5 above), or, instead, use the alidade, backsighting
along a drawn line which passes through the new station C and a known
major feature such as A (see Section 7.5, step 47).
|
|
|
| |
|
|
|
11. From this new station C, map in the new major
features which you can see, as explained above.
12. If necessary, move to other stations to complete the mapping of the
entire area. If you need more details in the map, go back to one of the
mapped features, reorient the table by backsighting on another mapped
feature, and map the details as required.
|
|
|
13. You can
use the above procedure for plane-tabling in several different situations in the field,
such as:
Usually, you will use a combination of some of
these surveying methods to map an entire area.
Open traverse
|
|
Closed traverse
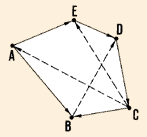
|
| |
|
|
Radiation
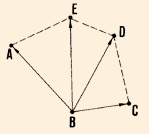
|
|
Triangulation
|
Mapping
an open traverse with a plane-table
|
|
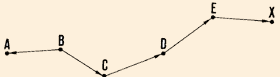
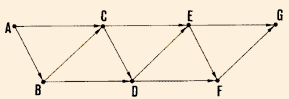
14. You may need to map an open traverse ABCD. To do this,
you can, for example, first set up the plane- table at point B, which
has a fixed position and from which a line BA of known direction already
exists on the ground. Map the location of station B, the direction of
BA and the distance BA in turn.
15. Draw the direction of the next station C, measure distance BC,
and map point c.
|
|
|
| |
|
|
|
16. Move the plane-table to station C, orient it along CB, and, using
the same procedure as above, map point d.
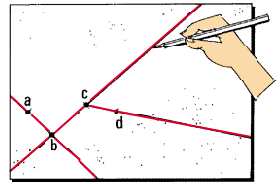
Note: if the traverse sections ba, cb,
etc. on the map are very short, you should mark their directions on
the edge of the paper. This will provide longer lines, so that you can
line up the alidade along them when you must reorient the plane-table
at a new station by backsighting.
|
|
At C, take a backsighting to B, and map D
|
| |
|
|
| |
|
Prolong lines for easier orientation
|
Mapping a closed traverse with
a plane-table
|
|
17. You need to map a closed traverse ABCDEA. First, set up
the plane-table at station A and plot this on paper as point a;
choose a scale and a location on the paper which will allow you to plot
the other stations within the limits of the sheet of paper.
18. Using the alidade, take a foresight through point a to
station B and draw line ax. Measure distances AB
and map point b on line ax.
|
|
|
| |
|
|
| 19. Move the plane-table to station B, set it up over the
point, and orient it by backsighting along line ba on
station A. Take a foresight to station C, measure distance BC, and map point
c. |
|
|
| |
|
|
| 20. Using this procedure, map the locations of the remaining
points on the closed traverse. At the end of the traverse, when you plot
the initial station A again, you can see any error of closure.
If this error is within reasonable limits, correct
it, using the graphic method explained in Section 7.1, step 19. |
|
|
| |
|
|
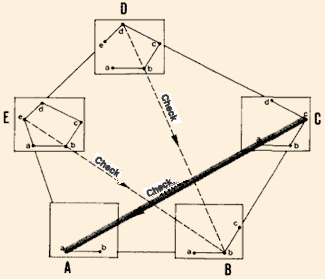
| 21. From one station on the traverse, you may be able to see
two or more of the preceding stations which are not on the same straight
line as the station where you are standing (for example, from C to A, from
D to B, or from E to B). In this case, check the other parts of the traverse.
Example
From station C, station A is visible. You should check from C the
position of point a by backsighting on Station A.
|
|
Take additional backsights to check your work
|
|
Mapping with a plane-table
by radiating
|
|
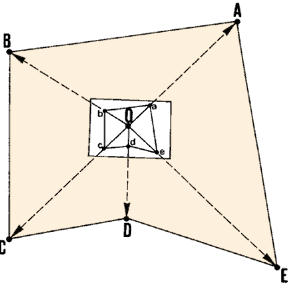
22. To use this method, set up the plane-table at a central station
0, from which you can see all the points you need to map. Orient
the table. On the map, draw lines representing the directions to these
ground points; to do this, pivot the alidade around the mapped location
of station 0. Measure horizontal distances OA, OB, OC, OD and OE, and
scale them along each of the drawn lines to map points a, b, c, d
and e.
|
|
Move the alidade, but not the plane-table
|
| |
|
|
Mapping with a plane-table
by triangulation
|
|
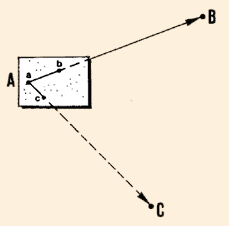
23. Before you start plane-tabling, you need to find a base line
determined by two known points visible from each other.
This base line can be a known section of an existing traverse, or a line
between two points fixed by a previous triangulation. If such a base line
is not available, you must accurately determine and measure one.
24. Draw the base line AB on the plane-table sheet. Choose
a location which will allow you to plot the other features of the map
within the limits of the sheet of paper.
25. Set up the plane-table over one of the two end-points of this base
line, at point A, for example. Then, with ranging poles, clearly mark
the second end-point B, and the third point C that you need to map. You
should be able to see point C from both point A and point B.
26. Align the alidade along line ab, which represents the
base line; orient the plane-table by sighting at the other end-point B
of the base along AB.
|
|
Start from the known base-line
|
| |
|
|
|
27. Place a pin at point a and rotate the alidade around it
until you sight point C. Draw a thin line from point
a along the edge of the alidade in the direction of point C.
|
|
Map C from A...
|
| |
|
|
|
28. Move the plane-table to B. Orient the table with line ba on
the map pointing in the direction of ground point A. Place a pin at b
and rotate the alidade around it until you sight point C. Draw a thin
line from point a in the direction of C. Point c is located
on the map at the intersection of line ac (step
27) and line bc.
|
|
... and from B

|
| |
|
|
|
29. Point C is now known, and you can use it in a similar way to determine
other points, taking, for example, BC as a base line to determine D. You
can then repeat this mapping process, using each point as it becomes known,
as long as each point you need to map is visible from two other known
points.
|
|
Move to the next triangle

|
| |
|
|
|
30. To check how accurately you have mapped a new point, set up the plane-table
over the corresponding point in the field. Then orient the table along
one line in the field and take a backsight to check that the second line
on the map corresponds with the correct line in the field.
Note: you can obtain the best results if you use
triangles with equal sides. The summit angles in
these triangles are all equal to 60�. In all cases, you should avoid angles
smaller than 15� or larger than 165�.
|
|
Check your work by backsighting
|
Mapping with a plane-table by combined methods
|
|
31. In most cases, you will map an area with a plane-table by using a
combination of the methods of traversing, radiating and triangulation.
32. You need to map site ABCDA, which includes such features as a rocky
area, a group of houses and a well. Clearly mark points A, B, C and D
with ranging poles.
|
|
Site ABCDA
|
| |
|
|
|
33. Set up the plane-table at corner A of the area. Locate the mapped
position of A on the sheet of paper. Be sure to choose a point which will
allow you to plot the other features of the map within the limits of the
sheet of paper at the drawing scale you have chosen. Orient the sheet
by drawing the direction of magnetic north.
34. From station A, you can see the rocks and the houses. By radiating,
determine the directions of the rocks and the houses from this station.
Then measure and map AB.
|
|
|
| |
|
|
|
35. Move the plane-table and set it up over corner B. Roughly orient
the board by backsighting to A, and check this orientation with the magnetic
compass.
36. From station B, you can see the rocks and the well. By radiating
and triangulation, locate and map the rocks, and determine the direction
of the well. Measure and map BC.
|
|
At B
|
| |
|
|
|
37. Repeat this process at point C, from which you can check on the position
of the rocks and locate the well and the houses. Measure and map CD.
|
|
At C
|
| |
|
|
| 38. Repeat this process at point D, from which you can check
on the positions of the houses and the well. Measure and map DA. |
|
At D

|
| |
|
|
|
39. Check the error of closure of traverse ABCDA and correct it, if possible.
If the error is too great, repeat the survey.
40. Finish the map, checking that you have
included all the information you need (see Section 9.0, step 6).
|
|
Finished map
|
|
9.3 How to map by protractor and scale
|
|
1. When you map in the office, using field records, you will usually
plot horizontal distances with a ruler/scale, and
the horizontal angles with a
protractor (see Section 3.3).
2. First, using the scale you have chosen, make a rough sketch of the
area to determine its size and shape. From this sketch, decide how large
a piece of paper you will need to make everything fit and determine the
position of your map on the sheet of paper.
|
|
|
| |
|
|
|
3. Draw the first line in the right place on the paper and determine
its length AB, using the selected scale. Using a pencil with a hard lead,
accurately mark points A and B on the paper as two dots with a small circle
around each.
Note: draw the line so that it will extend
beyond the next angle-point B, a distance greater than
the radius R of the protractor.
|
|
|
| |
|
|
|
4. Place the protractor along line AB so that:
- its centre is exactly on the second angle-point B; and
- marks 0� and 180� line up exactly with line AB.
|
|
|
| |
|
|
| 5. Plot the angle, which you have obtained from your field
notes, remove the protractor, and draw the second line. Locate and map point
C according to the measured distance and scale. |
|
|
| 6. Place the protractor along this last line with its centre
opposite point C. Lay out the measured angle, and draw the third line. Locate
and map point D according to the measured distance and scale.
7. Repeat this process until you have mapped the entire traverse.
|
|
|
| |
|
|
|
8. Locate the details on the plan from this traverse line.
Plot the positions of buildings, fences, rocky areas, streams, paths,
etc., using the scale for distances and the protractor for angles.
9. You can use a method similar to this one to map survey information
which you have obtained by radiating, by triangulation, and by offsets.
|
|
|
9.4
How to map contours
What is a contour line?
What are the characteristics of contour lines?
1. Contour lines are lines drawn to join points of equal elevation.
On a plan or map, they represent the contours you found and marked in the field
(see Section 8.3). Contour lines show the three-dimensional ground topography
of a site on a two-dimensional map or plan.
2. As you have already learned (see Section 8.3, step 7), contours are surveyed
on the basis of a selected contour interval. Similarly,
contour lines are drawn at equal vertical intervals. You should always clearly
state the contour interval of the mapped contour lines.
Hill
|
|
Peak
|
| |
|
|
Two hills
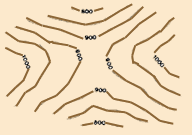
|
|
Valley
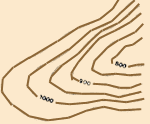
|
|
Contour interval = 50 m
|
| |
|
|
3. If you clearly understand the characteristics of contour
lines (CL), you will be able to survey, make contour maps and read
maps much more easily. The facts to remember are:
- all points on a contour line are at the same elevation;
- contour lines cannot cross each other or divide in any way (such as
branching or splitting off);
- contour lines always close on themselves, either within or outside
the limits of the map. When they close within the map's limits, they
indicate either a summit (such as a hill) or a depression
(such as a valley);
- straight, parallel contour lines indicate horizontal ground;
- evenly spaced contour lines indicate a uniform, or regular, ground
slope;
- the closer the contour lines, the steeper the slope (see Note);
- widely spaced contour lines indicate a gentle slope;
- closely spaced contour lines indicate a steep slope;
- the steepest slope is always at right angles to the contour lines;
- contour lines cross ridges perpendicularly;
- contour lines cross river valleys following a U- or V-shaped path.
Note: when two contour lines of equal elevation
are near each other, the land between them is often flatter than the general
trend of slope but its slope is indeterminate (unknown).
Areas of indeterminate slope
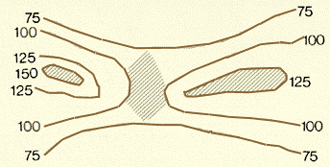
|
|
|
Choosing the contour interval of contour lines
|
|
4. Before drawing the contour lines on a plan or map, you must choose
the contour interval you will use. The contour interval mainly
depends on the accuracy or scale you need for the drawing, and on the
topography of the area (see Table 12). A smaller contour
interval, such as 0.15 m, 0.25 m or 0.5 m, is generally used for flat
or gently sloping areas. Remember that most fish-farm sites are located
in such areas.
|
|
|
| |
|
|
TABLE 12
Contour intervals (metres)
|
Topography
|
Map Scale
|
|
Greater than 1:1000
|
1:1000 to 1:10000
|
Smaller than 1:10000
|
| Flat |
0.15 to 0.3
|
0.3 to 0.6
|
0.6 to 3
|
| Gently sloping |
0.3 to 0.6
|
0.6 to 1.5
|
1.5 to 3
|
| Hilly |
0.6 to 1.5
|
1.5 to 3
|
3 to 6
|
|
| |
|
|
Making a contour map
|
|
5. First prepare a planimetric map of the area. This is
a map showing the boundaries of the land, the surveying stations, the
major physical features and all available details (see Sections 9.2
and 9.3).
6. Add the points of known ground elevation to the map.
To locate these points on the map, use a distance scale and, if necessary,
a protractor for determining any angles. Write the elevations next to
the points.
|
|
|
7. Find the points of lower ground elevation.
Then, according to the contour interval you have chosen, determine
which elevation represents the first contour line you need to draw.
8. The first contour line will pass between ground points
with elevations which are lower and higher than the elevation of the contour
points. Carefully locate the path of the contour line between these higher and
lower points, as you draw. Note that contour lines are usually curved, not straight.
You should draw them free-hand, rather than using a ruler to connect the points.
|
9. Using the same procedure, draw the other contour lines. Show the progressively
higher elevations as multiples of the selected contour interval.
Note: contour lines are only drawn
for elevations which are multiples of the contour interval. Show the elevations
of the contours by writing in numbers at appropriate intervals; the contour
line is usually broken to leave a space for the number.
|
|
|
| |
|
|
| 10. This general procedure may vary, depending
on the contour surveying method you have used in the field.
(a) If you have used a direct method (see Section
8.3, steps 10-29), the plan survey of the contours you have identified
gives you all the information you need to map the corresponding contour
lines. You will reduce the measured distances to scale, and use the
parallel lines marked on the ground as a background to the contour
lines.
(b) If you have used an indirect method (see Section
8.3, steps 30-33), you will lay out the pattern of lines roughly
in the drawing, map the points of known elevation and note their elevations.
Then, estimate the position of the contour lines, as explained above.
|
|
|
9.5 How to plot longitudinal profiles
Why are longitudinal profiles plotted?
1. Longitudinal profiles are plotted to show relative elevations on a
plan. When you design a fish-farm, longitudinal profiles help you to determine
the route and the bottom slope of such works as water-supply and drainage canals.
They are also useful when you need to estimate the amounts of earth you need
to dig out or build up on a site (called the volumes of earthwork), and when
you choose sites for the construction of reservoir dams and river barrages (small
dams that channel the water into ditches or canals).
Information from which longitudinal profiles can be plotted
|
|
2. You plot a longitudinal profile as a continuous line drawn through
points of known elevations. The information you use for
this can be:
|
|
|
| |
|
|
Scales to be used for longitudinal profiles
|
|
3. You need two different scales to be able to plot longitudinal profiles:
- a horizontal scale, which reduces horizontal ground distances;
- a vertical scale, which reduces vertical elevations.
Both scales should use the same unit of length. This is usually
the metre.
4. The horizontal scale of the profile should preferably be
the same as the scale of the plan or map.
Example
If the scale of the plan is 1 cm per metre, the horizontal scale
of the longitudinal profile should also be 1 cm per m.
|
|
|
| |
|
|
|
5. In most aquaculture surveys, the differences in elevation are very
small in comparison to the horizontal distances. When you plot longitudinal
profiles for such a survey, you will therefore need to make the differences
in elevation seem larger. You can use a vertical scale which is from 10
to 100 times larger than the horizontal scale.
|
|
|
| |
|
|
|
Example
| Horizontal scale |
Vertical scale |
| 1 cm per 25 m |
1 cm per 2.5 m |
| 1 cm per 10 m |
1 cm per 0.25 m |
|
|
|
|
Plotting profiles from contour
maps
|
|
6. Get some sheets of square-ruled millimetric paper. Or,
use one sheet as a guide only, placing it under a sheet of transparent
tracing paper on which you will plot your profiles.
7. On the contour map, draw line AB along which you
need to determine the longitudinal profile. Study the range of the elevations
you will plot, choose the vertical scale, and decide where to start your
drawing so that it will fit within the limits of the sheet of paper. Choose
the horizontal scale equal to the scale of the contour map.
|
|
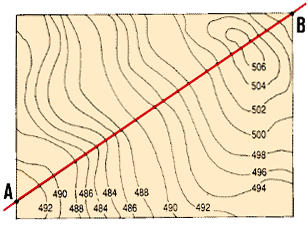
Contour interval 2 m
Horizontal scale: 1 cm = 20 m
Total vertical distance: 506 m - 484 m = 22 m
|
| |
|
|
|
Example
Contour map with contour interval = 2 m;
contour lines from 484 m to 506 m;
horizontal scale 1 cm = 20 m (map and profile);
vertical scale 1 cm = 0.25 m.
|
|
|
| |
|
|
|
8. Cut a strip of paper a little longer than the longitudinal
profile AB you need to draw and about 2 cm wide. Place this paper strip
on the contour map with one edge exactly on line AB.
9. Mark points A and B with thin vertical lines to indicate the end-points
of the longitudinal profile. In a similar way, mark the position
of each of the contour lines along the edge of the strip. Note the
elevations of the main contour lines next to their mark.
|
|
|
| |
|
|
|
10. Place the paper strip on the drawing sheet. Its marked
edge should line up with the horizontal line representing the lowest
elevation present (484 m) in the longitudinal profile.
Align point A on the strip with the starting point of the drawing.
11. Transfer all the pencilled marks from the paper strip to the drawing
and note the main elevations next to their marks.
|
|
|
12. Using the vertical scale as a reference, transfer each of these
marks vertically up to the horizontal line that corresponds
to its elevation. Using a sharp pencil with a hard lead, make a small circled
dot at each of these points on the lines.
13. Join these points with a continuous line, which represents
the longitudinal profile of the ground along selected line AB.
Note: you can only apply this method if the horizontal
scale of your drawing is the same as the distance scale of the contour map.
Plotting profiles from your own field
survey
|
| 14. You can use measurements of distances and elevations from
a field survey to plot profiles. Along the horizontal axis, first plot the
positions of the survey stations which you have located, for example at regular intervals along a centre-line
(see Section 8.2) using the horizontal scale (here 1 cm = 10 m) as a
basis. Next to each of these points, mark its distance from the starting
point of the profile, the cumulative distance* (in m). |
|
|
| |
|
|
|
15. For each of these points, plot the elevations on vertical
lines, using the vertical scale (1 cm = 5 cm) and the two extreme elevations
(1.34 m and 1.06 m) as bases.
16. Join these points with a continuous line, which represents
the profile of the ground along the centre-line.
17. Add more information, such as the elevations of
the bench-mark (BM) and of any turning point (TP). If you also plot the
proposed canal slope (0.15 cm/m = 7.5 cm/ 50 m), you
can use the drawing to easily locate areas where you need to raise the
land to a required level (called a fill*), or places where
you need to dig a channel (called a cut*). Then
you can use the drawing to estimate the amount of earthwork these will
require.
|
|
|
9.6 How to plot cross-section profiles
|
|
1. You can plot cross-section profiles either from
contour maps or from levelling-survey information.
2. A good example of when to use a cross-section profile plotted from
a contour map is for a study of a river valley when you want
to create a water reservoir, or build a small barrage that will raise
the water level and fill the fish-ponds by gravity.
3. If you use the information from a levelling survey, you can plot cross-section
profiles to calculate volumes of earthwork when you are building water
canals and fish-ponds, for example (see next manual on Constructions,
in this series).
|
|
|
| |
|
|
| |
|
|
| |
|
|
Plotting cross-section profiles
from contour maps
|
|
4. On the contour map, draw the lines along which you will study the
profiles. These lines should be perpendicular to a longitudinal profile.
5. Get several sheets of square-ruled millimetric paper, or
use one sheet as a guide only, under transparent tracing paper. Plot
the cross-section profiles with the help of a marked paper strip (as described
in Section 9.5, steps 8-13).
|
|
Scale: 1 cm = 20 m

|
| |
|
|
|
6. Remember that:
- the horizontal scale of the drawing should be the same
as the distance scale of the contour map; and
- the vertical scale of the drawing should be from 10 to
20 times larger than the horizontal scale.
|
|
Cross-sections of a valley 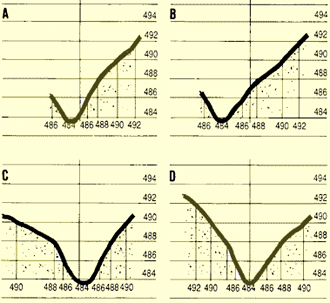
|
| |
|
|
|
Plotting
cross-section profiles for earthwork estimates
|
|
7. To estimate how much earthwork you need to do, you can usually plot
cross-sections to a scale of either 1 cm per metre or 1
cm per 0.5 m. Use the larger scale when the amount of
a cut or fill is small. Horizontal scales and vertical scales
should be identical, so that you can obtain a true surface area from the
scaled dimensions.
8. You can plot best on square-ruled millimetric paper or use one sheet
of such paper as a guide placed under a sheet of transparent tracing paper.
9. Draw a vertical centre-line (LL) representing the centre-line
of the cross-section profile. LL should follow one of the heavier lines
of the squared-ruled paper.
10. On both sides of this centre-line, draw the ground profile
EFD on the basis of your levelling data, using the horizontal scale for
distances and the vertical scale for elevations.
|
|
|
| |
|
|
|
11. From your longitudinal profile, locate point A on line
LL. In the example, it represents the elevation
of the bottom of the canal at this particular levelling station (see Section
9.5, step 17).
12. Through point A, draw a horizontal line BAC to show the
canal bottom. Make sure that AB = AC, and each is half the width
of the canal bottom.
|
|
|
| |
|
|
|
13. Through B and C, draw lines BE and CD representing the sides
of the canal (for example, with a slope of 1.5: 1). These
two lines intersect the ground surface at points E and D.
14. The cross-section EBACDFE represents a vertical section of the earth.
You can then easily calculate the area of this cross-section
(see, for example, Section 10.3). Using this area
as a basis, you can estimate the volume of earth you need to remove from
this location along the centre-line of the canal.
|
|
|
| |
|
|
| |
|
|
