2. MEDICIÓN DE DISTANCIAS HORIZONTALES
2.0 Introducción
|
Medición de distancias siguiendo líneas
rectas
|
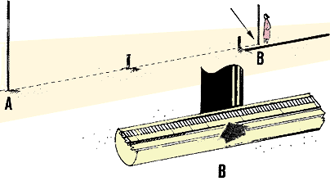
| 1. Cuando se lleva a cabo un levantamiento topográfico,
las distancias se miden siguiendo líneas rectas. Tales
rectas se trazan uniendo dos puntos o, a partir de un punto fijo, siguiendo
una dirección dada. Se marcan sobre el terreno con piquetes, pilares
o jalones. |
|
|
Cómo expresar las distancias en forma de medidas
horizontales
|
| 2. Las distancias siempre se
miden horizontalmente. En algunas ocasiones se trata de medir
distancias sobre un terreno plano o sobre un terreno cuya pendiente es muy
leve, o sea inferior o igual al 5 por ciento
(ver Sección 4.0). Las distancias medidas sobre tales tipos de
terreno son prácticamente iguales o muy parecidas a las distancias
horizontales. Al contrario, si la pendiente de un terreno supera el
5 por ciento, en ese caso de debe determinar la distancia horizontal.A
tal efecto, o se corrige la medida efectuada sobre el suelo (ver Sección
4.0)o se utiliza otro método (ver las secciones siguientes). Los
terrenos accidentados también requieren métodos especiales
de medición. |
|
|
| |
|
| |
|
| |
|
| |
Las distancias se deben medir siempre rectas y horizontales, aunque el terreno no lo sea

|
Medición de distancias a lo largo de líneas
rectas interrumpidas por obstáculos
|
| 3. Muy frecuentemente, todos los puntos de la recta que se
debe medir, resultan accesibles. Pero en algunos casos, cuando existe un
obstáculo, un lago, un río, un campo cultivado, se deben efectuar
mediciones indirectas. Dicho de otro modo, se debe determinar
la distancia horizontal a trav�s del c�lculo siguiendo la l�nea recta considerada
(ver Sección 2.9). |
|
 Midiendo con una cuerda Midiendo con una cuerda |
Elección del método más adecuado
4. Existen muchas maneras de medir correctamente una distancia. La elección
del método depende de varios factores:
- la precisión que se requiere;
- el equipo a disposición;
- el tipo de terreno.
Las siguientes secciones indican cómo utilizar los diferentes métodos
de medida. El Cuadro 1 ayuda a comparar tales métodos y a elegir el más
adecuado a cada necesidad.
|
CUADRO
1
M�todos de medici�n de distancias
| Sección1 |
M�todo
|
Distancia
|
Error2 por 100 m2
|
Comentarios
|
Equipo3
|
| 22* |
Cuenta de pasos
|
Media a larga
|
1 to 2 m o más
|
Para un estimado rápido y aproximado
|
Ninguno
|
| 22* |
Contraje con un pasómetro o un podómetro
|
Larga
|
1 to 2 m o más
|
Para un estimado rápido y aproximado
|
Pasómetro o podómetro
|
| 21* |
Regla
|
Corta
|
0.05 to 0.10 m
|
Especialmente útil para terrenos inclinados
|
Regla (nivel de albañil, línea
de plomada)
|
| 23** |
Medición con una cuerda
|
Media a larga
|
0.5 to 1 m
|
Bajo costo
|
Liana o cuerda, cordel, marcador
|
| 24** |
Medición con una cinta metálica
o de agrimensor
|
Media a larga
|
Menos de 0.05 m
|
Mejores resultados con una cinta metálica
|
Cinta metálica o cinta de agrimensor
|
| 25** |
Medición con cadena
|
Media a larga
|
0.02 to 0.10 m
|
Mejor calidad
|
Cadena de agrimensor
|
| 27*** |
Clisímetro
|
Media
|
1 to 2 m
|
Para un estimado rápido y aproximado
|
Clisímetro (lira-)
(mira de 2 m)
|
| 28*** |
Taquimétrico
|
Media a larga
|
0.1 to 0.4 m
|
Para un estimado rápido y preciso
|
Telescopio con hilos estadimétricos,
mira graduada
|
1 * Fácil ** más difícil *** muy difícil.
2 El error aumenta cuando el terreno es más accidentado
(pendiente, vegetación, obstáculos).
3 Además de los jalones (para trazar las líneas),
piquetes de marcaje (puntos intermedios), y el lápiz y cuaderno.
Se destaca en cursiva el equipo que usted mismo puede hacer, según
las explicaciones del texto. |
Cálculo de los perímetros
|
| 5. El perímetro de una superficie constituye su
límite exterior. El perímetro de las figuras geométricas
regulares se puede calcular mediante las fórmulas matemáticas
que se publican en el Anexo 1,
al final del Volumen 2 de este manual.

AB + BC + CD + DE + EF + FA = Per�metro ABCDEFA
|
|
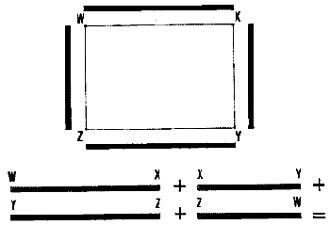 Per�metro WXYZW
Per�metro WXYZW |
2.1 Cómo medir distancias cortas
con una regla graduada
1. Para medir distancias cortas, es conveniente utilizar una regla graduada
de 4 a 5 m de longitud. Uno mismo puede confeccionar una vara de este tipo siguiendo
el procedimiento indicado a continuación. Una regla graduada es especialmente
útil para medir distancias horizontales sobre un terreno inclinado.
Fabricación artesanal de una regla graduada
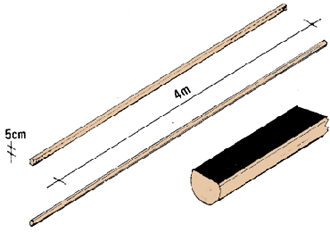
2. Para fabricar una regla graduada se debe disponer de una vara de madera
recta y plana, de unos 5 cm de ancho y de al menos 4 m de largo. Se puede utilizar
una vara más corta si se trata de medir distancias inferiores.
3.Es preferible usar una vara o estaca cuya superficie sea plana, pero si no
es posible, basta una vara rectilínea. En tal caso, conviene cepillar
al menos una de las superficies.
Medici�n con una regla
|
|
Es mejor usar un list�n plano ...
 ... pero tambi�n se puede aplanar un lado de una vara
... pero tambi�n se puede aplanar un lado de una vara
|
4. El siguiente paso es graduar la regla. Las graduaciones son trazos
que indican las medidas exactas en centímetros, decímetros, metros,
etc. A tal efecto se pueden utilizar dos cintas métricas graduadas
listas para ser empleadas, tales como las cintas métricas utilizadas
por los sastres. Una de estas cintas se encola sobre la superficie cepillada
de la vara de madera. Es importante alinear perfectamente el cero de la cinta
métrica con una de las extremidades de la vara. La segunda cinta métrica
se encola a continuación de la primera, con lo cual se habrá prácticamente
alcanzado la otra extremidad de la vara. Conviene asegurar las cintas con varios
clavos pequeños de cabeza grande.
5. Las marcas de graduación también las puede hacer uno
mismo. Con la ayuda de una regla o de una cinta métrica, se marcan
con lápiz las graduaciones sobre la superficie de la vara. Con un cuchillo
o un serrucho, se hacen pequeños cortes cada 10 cm. Si se utilizan herramientas
de carpintero, obviamente se logrará una mayor precisión. A continuación
se identifican las graduaciones con números (por ejemplo,
cada 50 cm) dibujadas con pintura o tinta. También se puede utilizar
un alambre o hierro caliente para marcar a fuego las graduaciones y las cifras
correspondientes sobre la superficie de la madera.
 Usar cola y clavos para asegurar las cintas
Usar cola y clavos para asegurar las cintas |
|
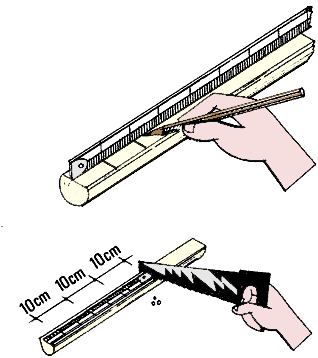 Hacer las marcas de la regla con precisi�n
Hacer las marcas de la regla con precisi�n |
Medición de distancias cortas con una regla
|
| 6. Si se debe medir una distancia corta sobre un terreno
horizontal, se procede primero a señalar cada extremidad
con un jalón. Se apoya la regla sobre el suelo, haciendo coincidir
el principio con el primer jalón, verificando que siga la dirección
de la recta que se quiere medir. Se marca con una estaca el otro extremo
de la regla. Se desplaza la regla hasta que su extremo coincide con la
estaca recién colocada. Se repite la operación hasta llegar
al otro extremo de la recta que se quiere medir, cuidando de anotar el
número de veces que se ha desplazado la regla. En general, basta
una parte de la longitud de la regla para medir el último segmento
de la recta. Es importante estar seguro de leer correctamente la graduación
de la regla. |
|
|
| |
|
|
| |
|
 Leer las escalas cuidadosamente
Leer las escalas cuidadosamente |
7. Si se debe medir una distancia sobre un terreno
en pendiente, la regla será especialmente útil para
determinar las distancias horizontales. Trabajando en sentido descendente,
en cada medición:
- verificar, con un nivel de alba�il
que la regla esté perfectamente horizontal (ver Sección
6.1);
- determinar con una plomada sujeta
a uno de los extremos de la regla, el lugar donde colocar el piquete
o estaca (ver Sección 4.8).
|
|
 Nivel de alba�il Nivel de alba�il |
| |
|
|
| Nota: cuando se mide una distancia
sobre un terreno en pendiente, se debe siempre proceder en sentido descendente,
o sea cuesta abajo. |
|
 L�nea de plomada
L�nea de plomada |
2.2 Cómo medir distancias contando pasos
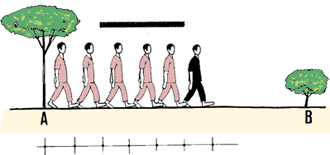
1. Las distancias pueden ser medidas aproximadamente contando pasos.
En otras palabras, de debe contar el número de pasos normales necesarios
para cubrir la distancia entre dos puntos en línea recta.
La cuenta de pasos puede ser especialmente útil para efectuar levantamientos
de reconocimiento, para trazar curvas de nivel a través del método
de la cuadrícula (ver Sección 83) y para verificar rápidamente
las medidas determinadas con cuerda o cadena (ver Secciones 2.3 to 2.5).
2. Para medir con precisión, es necesario conocer la longitud media
de los pasos, considerando una marcha normal. Tal longitud se llama paso
normal. La medición del paso se hace siempre a partir del extremo
del dedo pulgar del pie de atrás hasta el extremo del dedo pulgar del
pie de adelante.
 Cuente los pasos mientras camina
Cuente los pasos mientras camina |
|
|
Determinación del propio coeficiente de pasos.
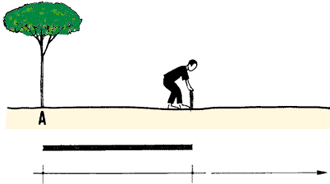
3. . Para medir la longitud promedio del propio paso normal (coeficiente
de pasos o CP)::
- caminar 100 pasos normales sobre un terreno horizontal, siguiendo una línea
recta, a partir de un punto A bien señalado. Para dar el primer paso,
se coloca el pie detrás del punto A, haciendo coincidir la extremidad
del dedo pulgar con dicho punto;
- señalar el final del último paso colocando el piquete B en
el extremo del dedo pulgar del pie que va adelante;
- medir la distancia AB (en metros), por ejemplo con una cinta métrica
y calcular el coeficiente de pasos (en metros) de la siguiente manera:
 Camine 100 pasos
Camine 100 pasos |
|

|
| |
|
|
| Ejemplo
Si la distancia recorrida con 100 pasos es de 76 m, el coeficiente de pasos se calcula de la siguiente manera: CP = 76 � 100 = 0,76 m
|
|
 Marcar la distancia
Marcar la distancia |
| Nota: para determinar con mayor precisión
el coeficiente de pasos:
- recorrer una distancia mayor (al menos 250 pasos);
- repetir la medición al menos tres veces y calcular
el promedio CP.
Ejemplo
La distancia recorrida con 250 pasos es sucesivamente 185, 190 y 188 m; en total, 3 veces x 250 = 750 pasos, con los cuales se ha recorrido 185 + 190 + 188 m = 563 m; lo que da un coeficiente promedio de pasos igual a CP = 563 � 750 = 0,75 m
|
|
|
| |
|
|
4.La longitud de cada paso depende por otra parte del tipo
de terreno que se va a medir. Es importante saber que los pasos son
más cortos:
- sobre un terreno con maleza alta;
- si se marcha subiendo una cuesta más que bajándola;
- sobre un terreno en pendiente en comparación a un terreno
plano;
- sobre un suelo blando en comparación a un suelo duro.
|
|
|
| |
|
|
| Para lograr un mejor resultado conviene que la longitud de
los pasos sea lo más regular posible. A tal efecto es necesario contar
los pasos con los que se recorre una distancia conocida, tanto
sobre un terreno plano como sobre un terreno accidentado o en pendiente.
Se debe corregir el paso de modo que resulte lo más regular posible. |
|
|
Medición de distancias horizontales contando pasos
|
| 5. Señalar claramente las líneas rectas
que se deben medir por medio de piquetes o estacas de madera. Si es necesario,
cortar las malezas altas que constituyen un obstáculo.
6. Caminar siguiendo las líneas rectas trazadas, contando cuidadosamente
los pasos.
7. Multiplicar el número de pasos N por el coeficiente de pasos
CP (en metros) para obtener una estimación aproximada de la distancia
en metros, de la siguiente manera:
|
|
 Se�ale las rectas que se quieren medir
Se�ale las rectas que se quieren medir |
| |
|
|
| |
|
|
| |
|
|
|
Ejemplo
Para cubrir el recorrido ABCD, el n�mero de pasos efectuado ha sido el siguiente:
AB = 127 pasos, BC = 214 pasos y CD = 83 pasos. ABCD = 127 + 214 + 83 = 424 pasos. Si CP = 0,75 m, ABCD = 424 x 0,75 m = 318 m.
|
|
|
| |
|
|
| |
|
|
| |
|
|
|
Nota: para evitar errores cuando se cuentan pasos:
- contar sólo zancadas o pasos dobles y multiplicar
el total obtenido por 2;
- contar centenas de pasos con los dedos (un dedo por cada
cien pasos);
- contar miles de pasos escribiéndolos en un trozo
de papel;
- considerar el número de pasos, de zancadas o medio pasos que
se efectúan para salvar obstáculos tales como
cercas o pequeños cursos de agua.
|
|
 Calcule el tama�o de los obst�culos
Calcule el tama�o de los obst�culos |
Contar los pasos con un pasómetro
o podómetro
|
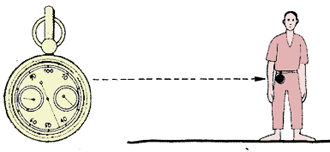
| 8. Es posible contar mecánicamente el número
de pasos efectuados gracias a un dispositivo muy simple conocido con el
nombre de pasómetro. El pasómetro tiene más
o menos el tamaño de un reloj de bolsillo y se lleva encima, cerca
del centro de gravedad del cuerpo, sujeto por una correa o cinturón.La
sacudida creada por cada uno de los pasos hace que se mueva una aguja dentro
del aparato. La aguja indica el número de pasos. |
|
 El pas�metro cuenta los pasos
El pas�metro cuenta los pasos |
| |
|
|
| 9. El podómetro es un dispositivo similar,
pero que registra las distancias, en general expresadas en kilómetros
y fracciones de kilómetros. 10. Es importante verificar la precisión
de ambos dispositivos antes de utilizarlos. Para verificar la exactitud
de un pasómetro se debe cubrir un trayecto efectuando algunos centenares
de pasos, contándolos cuidadosamente. Se compara el total obtenido
con los pasos registrados por el pasómetro y se efectúan
los ajustes necesarios. Para verificar la exactitud de un podómetro
se recorre una distancia conocida describiendo pasos normales
y regulares. Se compara la distancia recorrida con aquella registrada
por el podómetro y si fuese necesario se calibra el dispositivo. |
|
 El pod�metro mide las distancias
El pod�metro mide las distancias |
|
2.3 Cómo medir utilizando
una cuerda de agrimensor
|
|
1. Si se quiere efectuar una medición más precisa, sobre
todo si se trata de terrenos accidentados, es posible utilizar una cuerda
de agrimensor. Según la distancia que se deba medir, se puede confeccionar
una cuerda de 10, 20 ó 30 metros de longitud.
|
|
|
Cómo confeccionar una cuerda de agrimensor
|
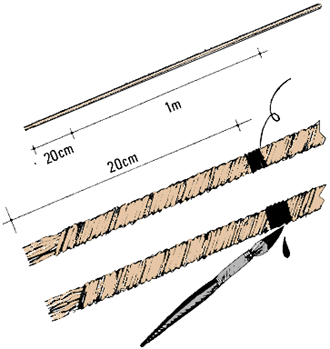
2. Se necesita una cuerda que tenga una sección
de 1 a 1,5 cm, de fibra natural. Las cuerdas de fibra artificial,
por ejemplo nylon, tienden a modificar su longitud mientras que las fibras
naturales, el yute por ejemplo, se contraen o estiran muy poco. Incluso
es preferible emplear una cuerda usada de sisal antes que una nueva. También
es posible utilizar un trozo de liana, elemento fácil de encontrar
en una selva.
3. Se traza una primera señal -el cero- a 20 cm de uno
de los extremos de la cuerda. A partir de ese punto, se mide con precisión
metro por metro hasta completar la longitud deseada. Se dejan otros 20 cm
en la otra extremidad de la cuerda. Se marca cada metro con pintura
a prueba de agua, tintura, tinta o con un lápiz de cera de
color. Es importante que las marcas sean lo más finas posible para
evitar tomar medidas poco precisas. También se pueden utilizar cuerditas
delgadas enfiladas en la cuerda grande lo cual asegura que la posición
de las marcas no se modificará.
4. Es importante reforzar los dos extremos de la cuerda graduada,
enrollando una cuerdita o un hilo, bien apretados, en los últimos
10 cm de cada extremo. |
|
Seleccionar una cuerda de tama�o apropiado
|
| |
|
|
 Hacer marcas bien visibles
Hacer marcas bien visibles |
|
 Reforzar los extremos con cordel
Reforzar los extremos con cordel |
Medición de distancias horizontales mediante una
cuerda
|
| 5. Se marcan claramente las rectas que se deben medir,
por ejemplo con estacas de madera. Se limpia la zona a ambos lados de
las rectas, quitando las malezas y las piedras grandes que pudiera haber.
6. Si la distancia que se quiere medir es inferior o semejante a la longitud
de la cuerda, se puede medir directamente. A tal efecto se extiende la
cuerda con cuidado, de una estaca a la otra. Si la distancia queda comprendida
entre dos de las marcas de la cuerda, realizadas de metro en metro, se
mide el último segmento con una regla o una cinta métrica
graduada en centímetros. |
|
 Limpiar el terreno donde se trabaja
Limpiar el terreno donde se trabaja |
| |
|
|
| 7. Si la distancia que se debe medir supera la longitud de la cuerda,
entonces se debe utilizar alguno de los m�todos de medici�n que se describen
m�s adelante (ver Sección 2.6). Tales métodos son aplicables
a todos los instrumentos de medición de agrimensura, especialmente
las cintas y bandas métricas, las cuerdas o las cadenas. |
|
 Tensar la cuerda
Tensar la cuerda |
| |
|
|
| |
|
 Medir la diferencia con una regla
Medir la diferencia con una regla |
2.4 Cómo
efectuar una medición por medio de cintas métricas o de
agrimensor
|
| 1. La cinta de agrimensor se puede adquirir en
el comercio. Se trata de una cinta metálica, que en general se
fabrica de 6 mm de ancho y de 30 ó 50 m de longitud, en la cual
están claramente marcados metros, decímetros y centímetros.
La cinta se enrolla sobre un eje, mediante una manivela de rebobinado,
en un armazón abierto. |
|
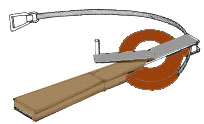 Cinta de medir met�lica
Cinta de medir met�lica |
| |
|
|
| 2. La cinta métrica puede ser de acero,
de tejido metálico o de fibra de vidrio. Su longitud en general
es de 10 a 30 m o más. Normalmente están marcados los metros,
salvo en los primeros y últimos tramos, en los cuales aparecen
los decímetros y centímetros. Se enrollan en una caja mediante
una manivela de rebobinado. La utilización de cintas métricas
presenta algunas dificultades. Efectivamente, las metálicas tienden
a torcerse y romperse y las de tejido son menos precisas porque la longitud
suele modificarse. |
|
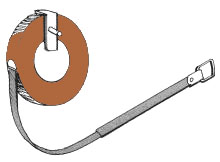 Cinta de medir de agrimensor
Cinta de medir de agrimensor |
| |
|
|
| |
|
|
Medición de distancias horizontales mediante una cinta métrica
metálica o una cinta de agrimensor
3. Se marca la recta que se quiere medir. Si la distancia que se quiere medir
es semejante o inferior a la longitud de la cinta métrica o de agrimensor,
se mide directamente. Basta extender la cinta métrica o de agrimensor
de un piquete a otro.
4. Si la distancia es superior a la longitud de la cinta m�trica
o de agrimensor, entonces se debe utilizar alguno de los m�todos descritos m�s
adelante (ver Sección 2.6).
Nota: la cinta de agrimensor y la cinta métrica deben estar
bien extendidas de manera que no presenten pliegues, sobre todo en el caso de
largas distancias. Por otra parte es importante no tensarlas demasiado, sobre
todo en el caso de cintas de fibra de vidrio, para no correr el riesgo de medir
incorrectamente.
 Mantenga la cinta derecha y pegada del suelo
Mantenga la cinta derecha y pegada del suelo |
|
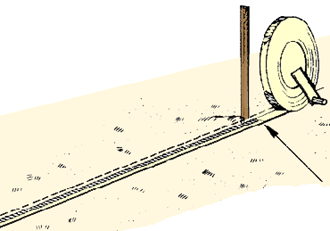 Mida haciendo coincidir el cero de la escala con la estaca
Mida haciendo coincidir el cero de la escala con la estaca |
2.5 Cómo efectuar una medición
con una cadena de agrimensor
|
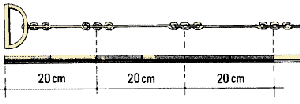
| 1. La cadena de agrimensor también se puede
adquirir en el comercio. Se trata de una serie de eslabones de acero, todos
de la misma longitud, en general de 20 cm, unidos entre sí mediante
anillos del mismo material. La longitud de cada eslabón
es la suma del largo de la porción rectilínea, sus extremos
redondeados y la mitad de los dos anillos que lo amarran al eslabón
siguiente. En general cada metro de la cadena está marcado con un
anillo de latón. Cada extremo de la cadena está
constituido por una empuñadura metálica o manija
cuya longitud debe ser tenida en cuenta cuando se realiza la medición.
La longitud total de la cadena habitualmente es de 10 ó 20 m. Las
cadenas son menos precisas que las cintas métricas o de agrimensor,
pero mucho más resistentes. |
|
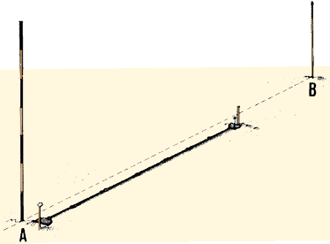 Medición con una cadena de agrimensor
Medición con una cadena de agrimensor |
| |
|
|
| |
|
|
| |
|
|
| 2. Cuando se utiliza una cadena de agrimensor se deben
tomar las siguientes precauciones:
- verificar que el extremo redondeado del eslabón no se ha enredado
con el final del eslabón siguiente, lo cual acortaría
la longitud de la cadena; cuando se va a usar la cadena, conviene repasarla
en toda su longitud enderezando todos los eslabones;
- no dejar la cadena al sol pues el calor la dilata;
- asegurarse de haber extendido completamente la cadena para obtener
una medición exacta.
|
|
Asegurarse de que los eslabones est�n rectos
Medir la longitud de cada eslab�n con una regla
Comprobar la longitud de la cadena
|
| 3. Cuando se utiliza una cadena por primera vez, conviene
medir con una regla la longitud de cada eslabón. No olvidar
que se debe considerar la parte rectilínea de cada eslabón,
los dos extremos redondeados y la mitad de ambos anillos que lo amarran
al eslabón siguiente. En cada extremo de la cadena, la longitud de
la empuñadura más la longitud del eslabón al que está
amarrada -que es más corto que los demás- más la longitud
del medio anillo de conjunción, debe corresponder a la longitud de
un eslabón normal. Después de haber verificado la longitud
de los eslabones es importante comprobar que 1 m de cadena comprende la
cantidad de eslabones prevista. |
|
Ejemplo
Si cada eslab�n mide 0,20 m de largo, cada metro de cadena estar� compuesto por cinco eslabones. .
|
| 4. La cadena de agrimensor siempre se debe plegar de la siguiente
manera: |
- ambas empuñaduras se sujetan con la mano izquierda, con la
cadena doblada por la mitad;
|
|
- con la mano derecha se recogen los eslabones de dos en dos disponiéndolos
oblicuamente.
|
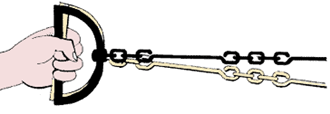 Tome ambas empu�aduras con su mano izquierda
Tome ambas empu�aduras con su mano izquierda |
|
Recoja los eslabones de dos en dos
|
| |
|
|
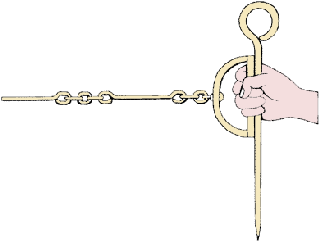
| 5. Cuando se quiere desplegar la cadena, se sujetan ambas
empuñaduras con la mano izquierda y se lanza la cadena en la dirección
en la cual se va a medir. |
|
 Lance la cadena hacia donde va a medir
Lance la cadena hacia donde va a medir |
Medición de distancias horizontales con cadena de agrimensor.
6. La cadena de agrimensor se usa para medir la longitud de líneas rectas,
cuyos extremos se marcan con estacas. Se requiere la ayuda de un asistente.
El m�todo de encadenado que se aplica en cada caso depende del
tipo de terreno (ver Sección 2.6).
 Para medir con una cadena se necesita un ayudante
Para medir con una cadena se necesita un ayudante |
|
 Sostenga firmemente la cadena en direcci�n a la marca
Sostenga firmemente la cadena en direcci�n a la marca |
2.6 Cómo medir distancias por encadenamiento
1. Ya se ha explicado que los instrumentos de medición
pueden ser cintas, bandas, cuerdas o cadenas de agrimensor. Cuando se miden
distancias largas, el modo de usar el instrumento de medición depende
de la pendiente del terreno. Si el terreno es plano o casi plano (quiere decir,
con una pendiente de 5 por ciento o menos de eso
- ver Sección 4.0), es posible medir distancias horizontales siguiendo
la superficie del suelo. Tal método es el que comúnmente se emplea
para el trazado de instalaciones de acuicultura, en las cuales se evitan las
pendientes muy fuertes. Si la pendiente del terreno supera el 5 por ciento, las distancias
horizontales se deben medir con gran cuidado teniendo presente que en ese caso
siempre las medidas tomadas en el suelo superan las horizontales.

En terreno plano, mida directamente
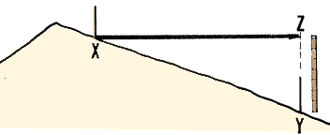
La verdadera distancia es la horizontal
|
|
 ... la medida de la superficie es m�s larga
... la medida de la superficie es m�s larga |
Medición
por encadenamiento de una superficie horizontal
|
| 2. Se marca cada línea recta que se debe medir
colocando un jalón en cada extremo. En el caso que las líneas
midan más de 50 m de largo, se colocan marcas intermedias a intervalos
regulares.
3. Para medir distancias largas con precisión, es necesario disponer
de piquetes o estacas. A tal efecto se pueden utilizar estacas
de madera de unos 25 cm de largo, que se pueden transportar fácilmente
en una canasta pequeña. Tales estacas se deben hundir verticalmente
en el suelo, a medida que se avanza con el encadenamiento.
|
|
|
| |
|
|
| |
|
|
| |
|
|
| 4. El encadenamiento requiere del concurso de dos personas,
o sea un encadenador trasero y un encadenador delantero.
El primero es responsable de tomar las medidas, de anotar los resultados
y de dirigir al encadenador que va adelante para asegurar que las mediciones
sucesivas se llevan a cabo siguiendo la línea recta entre los puntos
marcados en el suelo. |
|
|
| |
|
|
| 5. Comience las mediciones en uno de los extremos de la
línea recta. Quite el jalón y exactamente en el mismo sitio
clave el primer piquete de marcar.
6. El encadenador trasero coloca el extremo de su instrumento de medición
contra la estaca. El encadenador delantero se aleja siguiendo la línea
recta con el otro extremo de la cuerda o cinta de agrimensor, llevando
consigo varios piquetes de marcar.
|
|

TEl de atr�s se queda en el primer punto ...
|
| |
|
|
| 7. El encadenador delantero se detiene cuando la cuerda o
cinta de agrimensor está completamente desenrollada y extendida sobre
el suelo. Mira hacia el encadenador trasero. Si la cuerda no describe exactamente
una línea recta, éste último le indica cómo
corregir la posición de la cuerda. |
|
 ... y ayuda al otro a encontrar el segundo punto
... y ayuda al otro a encontrar el segundo punto |
| 8. Una vez que la cuerda está colocada correctamente,
el encadenador trasero indica al encadenador delantero que coloque un
segundo piquete en el extremo de la cuerda.
9. El encadenador delantero anota inmediatamente tal medida.
10. El encadenador trasero quita el primer piquete de marcar, lo coloca
en su canasta y coloca nuevamente el jalón en el punto
de partida. |
|
 Cuando se pone el segundo piquete
Cuando se pone el segundo piquete |
| |
|
|
 ... el hombre de atr�s anota la medida
... el hombre de atr�s anota la medida |
|
 ... y pone el primer piquete en la cesta
... y pone el primer piquete en la cesta |
| |
|
|
| 11. Sosteniendo ambos extremos de la cuerda, los dos encadenadores
caminan hacia adelante, siguiendo la línea recta, manteniendo
siempre la cuerda o cinta bien estirada. Esta precaución
es muy importante cuando se usa una cadena de agrimensor.
12. El encadenador trasero se detiene en el segundo piquete
y coloca junto a él, el extremo de su cuerda.
13. El encadenador delantero coloca la cuerda sobre el suelo,
corrige su posición siguiendo las instrucciones del encadenador
trasero y coloca un tercer piquete de marcar al final de la cuerda, cuando
recibe tal indicación. |
|
 Los dos hombres se desplazan
Los dos hombres se desplazan |
| |
|
|
| |
|
 ... para medir la distancia entre el segundo piquete y el tercero
... para medir la distancia entre el segundo piquete y el tercero |
| |
|
|
| 14. El encadenador trasero anota la medición
efectuada. A continuación coloca el segundo piquete en su canasta,
antes de abandonar el sitio.
15. . El procedimiento descrito en los puntos 10 a 14 se debe repetir
en cada segmento de la línea recta hasta llegar al extremo. |
|
 El hombre de adelante anota cada distancia
El hombre de adelante anota cada distancia |
| Nota 1: si se usa un conjunto de 11 piquetes
de marcar es más fácil llevar la cuenta de las mediciones
efectuadas. Cuando el encadenador trasero tiene diez piquetes en su canasta,
quiere decir que ya se ha medido diez veces la longitud total del instrumento
usado. Se anota esa cifra y se le devuelven los diez piquetes
al encadenador delantero, dejando el undécimo en el suelo;
ése es el punto de partida de una nueva serie de mediciones. |
|
|
| |
|
|
| Nota 2: si se usa un conjunto de 11 piquetes
de marcar es más fácil llevar la cuenta de las mediciones
efectuadas. Cuando el encadenador trasero tiene diez piquetes en su canasta,
quiere decir que ya se ha medido diez veces la longitud total del instrumento
usado. Se anota esa cifra y se le devuelven los diez piquetes
al encadenador delantero, dejando el undécimo en el suelo;
ése es el punto de partida de una nueva serie de mediciones. |
|
 El n�mero de piquetes en la cesta ayuda a llevar la cuenta
El n�mero de piquetes en la cesta ayuda a llevar la cuenta |
| |
|
|
| |
|
 Se ha medido 10 veces la longitud de la cadena
Se ha medido 10 veces la longitud de la cadena |
| |
|
|
|
Ejemplo
Usando una cadena de 10 m de largo, el encadenador trasero ha
marcado 4 x 10 piquetes en su cuaderno. Tiene 6 piquetes en su canasta.
A partir del sitio donde está clavado el otro piquete en el suelo,
ha medido una distancia de (4 x 10) + 6 = 46 longitudes de cadena o
46 x 10 m = 460 m. |
|
|
Medición por encadenamiento de un terreno en
pendiente
|
| 16. La medida de un terreno cuya pendiente supera el 5 por ciento (ver Sección
40) requiere que el mismo tipo de instrumento de medición se
use de una manera diferente para medir las distancias horizontales.
17. Proceda de acuerdo a las indicaciones de la sección precedente.
Marque la línea recta con jalones en los extremos y con piquetes
intermedios. Recuerde que debe trabajar pendiente abajo para
obtener mayor precisión.
18. En este caso, el encadenador delantero debe sostener horizontalmente
el instrumento de medición. |
|
|
| |
|
|
| 19. Cuando el instrumento de medición está
correctamente instalado y bien extendido, el encadenador delantero determina
el punto exacto en el que colocar la estaca de marcar, mediante una
plomada (ver Sección
4.8).
20. Keep proceeding in this way along the slope. Continúe las
operaciones de la misma manera a lo largo de la pendiente.
Nota: en terrenos con una pendiente más pronunciada
conviene utilizar un instrumento de medición más corto
(por ejemplo, de 5 m en lugar de 10 m). |
|
|
21. Cuando se miden terrenos en pendiente, recuerde las siguientes importantes
reglas:
- · mantener el instrumento de medición en posición
horizontal;
|
|
- mantener el instrumento de medición bien estirado
|
 Cuerda de medici�n horizontal
Cuerda de medici�n horizontal |
|
 Cuerda de medici�n bien tensa
Cuerda de medici�n bien tensa |
| |
|
|
- · colocar exactamente los piquetes de marcar.
|
|
|
 Colocaci�n precisa de los piquetes
Colocaci�n precisa de los piquetes |
|
Nota: también se pueden medir distancias
sobre el suelo en un terreno en pendiente. De todos modos, para obtener
distancias horizontales es necesario corregir
tales mediciones sobre el suelo mediante la aplicación de fórmulas
matemáticas (ver Secciones 40 y 50). |
Medición de terrenos accidentados
|
| 22. Frecuentemente las distancias se deben medir sobre
terrenos accidentados, o sea con crestas, montículos, rocas,
zanjas o cursos de agua. En muchos la cuerda, cadena o cinta de medición
se debe alzar por encima de los obstáculos. En tales
ocasiones es importante observar las siguientes reglas:
- mantener el instrumento de medición bien extendido.
En caso de necesidad, la cinta o cuerda se puede acortar enrollándola
en la mano;
|
|
|
| |
|
|
| |
|
|
| |
|
|
|
|
|
|
| 23. En lugar de la plomada, se pueden utilizar piquetes
más largos, por ejemplo jalones clavados verticalmente
en el suelo. |
|
 Los jalones son m�s altos que los piquetes de marcaje
Los jalones son m�s altos que los piquetes de marcaje
|
| |
|
|
| 24. En suelos muy duros o terrenos rocosos,
es imposible utilizar estacas para señalar. En esos casos conviene
señalar los puntos intermedios mediante objetos fácilmente
visibles, por ejemplo, piedras pintadas o trozos de madera. Será
importante verificar que tales marcas no se vuelen con el viento y no rueden.
También se puede trazar una señal sobre el suelo con un bastón
o con una marca de tiza sobre una piedra. |
|
Pinte una roca o un bloque


|
Cómo mejorar la precisión de una medición
|
| 25. Para mejorar la precisión de un encadenamiento
conviene repetir al menos una vez la medición. Una vez
completada la primera medición, conviene volver a medir en sentido
inverso la misma recta, comenzando desde el último punto señalado.
Esta segunda medición no debe resultar muy diferente de la primera
(ver la tabla más abajo).
26. Si ambas medidas coinciden en forma aproximada,
se puede sacar el promedio de las dos, que se considerará
como la medida real.
|
|
 Marque con un palo o una tiza
Marque con un palo o una tiza |
| |
|
|
| |
|
|
| |
|
|
 AB + BA
= Promedio
AB + BA
= Promedio
2 |
|
Diferencia m�xima admisible entre dos mediciones consecutivas considerando segmentos de 100 m:
Cinta métrica de acero |
0.1 m
|
Otro tipo de cinta |
0.2 m
|
Cadena de agrimensor |
0.2 m
|
Cuerda de agrimensor
fabricada por uno mismo
|
1.0 m
|
|
|
Ejemplo
Las siguientes medidas han sido tomadas con cadena de agrimensor:
- primera medida: 312,6 m;
- segunda medida: 313,2 m;
- diferencia: 313,2 - 312,6 = 0,6 m;
- diferencia admisible: 0,2 m x (312,6 m ÷ 100) = 0,2 m
x 3,12 m = 0,62 m, lo cual supone un valor superior a la diferencia
constatada; por lo tanto se considera que ambas mediciones concuerdan;
- valor promedio de la distancia (312,6 m + 313,2 m) ÷
2 = 312,9 m.
|
|
 Primera medici�n
Primera medici�n |
| |
|
|
| |
|
 Segunda medici�n
Segunda medici�n |
| |
|
|
| |
|
|
| 27. Si la diferencia entre las dos mediciones es muy grande,
entonces es necesario tomar por tercera vez la medida. Se comparan las tres
y se calcula el promedio de las dos más parecidas, como se indica
a continuación: |
|
 Primera medici�n
Primera medici�n
|
| |
|
|
|
Ejemplo
Las siguientes medidas han sido tomadas con una cinta métrica
metálica:
- primera medida: 754,4 m;
- segunda medida: 753,2 m;
- diferencia real: 754,4 m - 753,2 m = 1,2 m;
- diferencia admisible: 0,1 m x 7,54 m = 0,75 m, o sea un valor
inferior a la diferencia registrada entre las dos mediciones, las cuales
no coinciden;
- tercera medida: 753,9 m;
- diferencia: 754,4 m - 753,9 m = 0,5 m; esta vez la diferencia
es admisible pues es inferior a 0,75 m;
- distancia promedio: (754,4 m + 753,9 m) ÷ 2 = 754,15.
|
|
 Segunda medici�n
Segunda medici�n |
| |
|
| |
 Tercera medici�n
Tercera medici�n |
2.7 Cómo medir
distancias con un clisímetro
|
| 1. El clis�metro en forma de lira es un instrumento
simple que se puede utilizar para medir distancias. También es útil
para medir la pendiente de un terreno (ver
Sección 4.5). Menos preciso que un instrumento de agrimensor, permite
sin embargo una estimación rápida de las distancias
sin necesidad de recorrer la totalidad de la recta que se quiere medir.
La medición que se obtiene será menos precisa cuanto mayor
sea la distancia considerada, por lo tanto conviene utilizarlo solamente
en el caso de distancias inferiores a 30 m. En el caso de estimaciones
aproximadas, el límite es de 150 m. |
|
 Clis�metro plegado
Clis�metro plegado |
| |
|
|
| 2. El clisímetro se compone de un visor,
un anillo de suspensión y un elemento pesado
que sirve para estabilizar el instrumento en posición vertical. El
clisímetro se pliega dentro del peso lo cual facilita el transporte. |
|
 Viendo con un clis�metro
Viendo con un clis�metro |
| |
|
|
3. Si se mira por el visor, se ven tres escalas verticales.
Una escala consiste en una serie de rayas paralelas trazadas sobre una línea,
a intervalos regulares. La escala central, o escala estadimétrica
se utiliza para medir distancias horizontales. Dicha escala central comprende
dos partes:
- la parte superior, en la cual las marcas corresponden a
las distancias 150, 100 ... 7 m;
- la parte inferior, en la cual las marcas corresponden a
las distancias 150, 100 ... 10 m.
4. Medir distancias con el clisímetro exige la presencia de un
asistente y la definición de una altura de referencia
(llamada base). La manera de utilizar el clisímetro depende del
tipo de base.
- Se puede utilizar una base de 2 m, marcada claramente
sobre un piquete de madera llamado mira; en ese caso se utiliza
la parte superior de la escala existente, identificada con la mención
BASE 2,00 m.
- En otro caso, la altura del asistente puede ser utilizada
como base; en ese caso se utiliza la parte inferior de la
escala de distancias, con la mención BASE 1,70 m.
|
|
Escala dentro del clis�metro

|
Cómo construir una mira artesanal
|
| 5. Se debe conseguir un trozo rectilíneo de madera
de 2,50 m de longitud. Lo mejor es utilizar un listón rectangular
de 8 x 4 cm de sección transversal, pero se lo puede sustituir
con un piquete redondo de 6 a 8 cm de diámetro.
6. También se necesitan dos tablas de madera de 30 cm x 40 cm
cada una.
7. Las dos tablas se clavan sobre el mismo eje, a 10 cm de cada extremo
del listón, como se indica en la figura.
|
|
 Materiales
Materiales |
| |
|
|
| 8. Se traza una línea horizontal, en el medio
de una de las tablas. Esta línea se llama línea mediana.
9. A partir de dicha línea se miden exactamente 2 m a lo
largo del listón. El punto que se determina de este modo
se debe encontrar en la mitad de la segunda tabla. A continuación
se traza otra línea horizontal sobre la segunda tabla.
10. Con la ayuda de una regla y de un lápiz se divide en secciones
de 10 cm la parte del listón que queda comprendida entre las
dos tablas, cuya longitud debe ser 1,70 m.
11. Se pintan de color rojo vivo las dos secciones de ambas tablas
situadas a ambos extremos del segmento de 2 m. Luego se pinta
de rojo la primera sección de 10 cm de longitud contigua a cada
tabla y luego una de cada dos de las secciones restantes.
12. Se pintan de blanco todas las otras secciones de las
planchas y del listón, incluidos ambos extremos de 10 cm de longitud.
Completada la pintura, la mira ya se puede utilizar para medir distancias.
Nota: para medir distancias más cortas se puede utilizar
una mira simplificada. Se toma un listón o asta de 2 m exactos
de longitud y se pintan bandas sucesivas en rojo y blanco, como ya se
ha indicado. |
|
|
Cómo medir distancias con una mira
|
| 13. Se le pide al asistente que lleve la mira al primer
punto marcado sobre la línea recta que se quiere medir. El asistente
sostiene la mira en una posición lo más vertical
posible y dirige hacia el operador el lado pintado.
14. Se sostiene el clisímetro con una mano y se observa la mira
a través del visor. Se hace coincidir el cero de la
escala central con la línea mediana de la tabla inferior de la
mira.
15. Se observa la parte superior de la escala central (BASE
2,00 m) del clisímetro y se lee la distancia en metros correspondiente
a la graduación que coincide con la línea mediana
de la tabla superior.
16. Se anota cuidadosamente dicha medida en un cuaderno.
17. Se le pide al asistente de mover la mira y de reemplazarla con
una marca o piquete y, a continuación, de caminar hacia el siguiente
punto de medida.
18. El operador se desplaza hasta el piquete que el asistente acaba
de clavar y se repite la operación, hasta llegar al
extremo de la línea recta.
Nota: es importante tener en cuenta que los segmentos medidos
de esta manera deben ser inferiores a 30 m, si se pretende alcanzar
una cierta precisión.
|
|
 Mirando a una mira se usa la escala superior
Mirando a una mira se usa la escala superior |
Medición de distancias sin mira
|
| 19. Si no se dispone de una mira, se puede utilizar la
altura del asistente como base de referencia. Como este método
exige partir de una base de 1,70 m, es conveniente medir la estatura del
asistente. Si la altura difiere mucho de aquel valor, se debe proceder
de la siguiente manera:
- si la estatura del asistente supera 1,70 m, se debe medir la altura
de los ojos o de la boca con relación al piso y elegir el valor
más cercano a 1,70 m;
- si la estatura del asistente es inferior a 1,70 m, se le pide que
coloque algún objeto sobre su cabeza (por ejemplo una lata de
conserva, una botella o un trozo de madera), para así completar
una altura lo más cercana posible a 1,70 m.
|
|
 Determine un punto de referencia a 1,70 m de altura
Determine un punto de referencia a 1,70 m de altura |
| |
|
|
| 20. Se le pide al asistente que camine a lo largo de la línea
recta que se desea medir; al llegar al punto escogido se le pide que se
voltee hacia el operador y se mantenga lo más derecho posible. 21.
Se sostiene el clisímetro con una mano y se mira por el visor hacia
el asistente. Se hace coincidir la línea de mira cero de la escala
central con la altura de 1,70 m escogida previamente, o sea la parte más
alta de la cabeza, los ojos o el extremo de una botella apoyada sobre
la cabeza.
22. Se observa la parte inferior de la escala central (BASE 1,70 m) y
se lee la distancia en metros que aparece en la graduación que
coincide con el nivel del suelo a los pies del asistente.
23. Se anotan cuidadosamente dichas medidas en un cuaderno.
24. Se le dice al asistente que clave una señal en el suelo exactamente
donde él se encuentra y que camine hacia el siguiente punto de
medida.
25. El operador se desplaza hasta la señal que el asistente acaba
de colocar y se repite la operación apenas descrita, tantas veces
como sea necesario. Las distancias medidas de este modo deben ser siempre
inferiores a 30 m si se pretende una buena precisión.
|
|
 Mirando al asistente se usa la escala inferior
Mirando al asistente se usa la escala inferior |
Medición de distancias sobre terrenos en pendiente
26.La medición de distancias sobre terrenos cuya pendiente supera el 5 por ciento ,
exige una corrección de los valores leídos en el clisímetro
para obtener la distancia horizontal real. A tal efecto se debe utilizar
una formula matemática, siguiendo las indicaciones de la Sección
4.0.
2.8 Cómo medir distancias por el método taquimétrico
|
| El método taquimétrico o estadimétrico
es rápido y preciso para medir distancias largas, pero su aplicación
exige la adquisición de un costoso equipo topográfico
y además hay que aprender a utilizarlo. Por tal razón, el
siguiente párrafo se limita a una descripción sintética
del método para facilitar la comprensión de los principios
básicos en los cuales se basa.
1. El equipo empleado por este método consiste en un dispositivo
óptico perfeccionado llamado telescopio. Se mira a través
de dos hilos entrecruzados; el dispositivo tiene además dos hilos
horizontales suplementarios llamados hilos estadimétricos.
La mayor parte de los lentes de nivelaci�n
(ver Sección 5.8) incluye hilos estadimétricos, situados
a igual distancia de un lado y del otro de los hilos horizontales.
2. Para medir una distancia tambi�n se necesita una mira graduada con claridad
en centímetros (ver Sección 5.0).
3. Se instala el lente de nivelación en el punto desde el cual
se va a medir la distancia.
Se le indica al asistente que coloque la mira graduada verticalmente en
el siguiente punto de la línea recta. La mira puede estar situada
a una distancia de varios centenares de metros.
4. A través de la lente del telescopio se leen las marcas de la
mira graduada (en metros) que coinciden con el hilo estadimétrico
superior y con el hilo estadimétrico inferior.
Se anotan las medidas así determinadas.
5. Se resta el valor medido menor del valor medido mayor. La cifra que
se obtiene corresponde al intervalo que separa los dos hilos y se llama
intervalo estadimétrico.
6. Para obtener la distancia (en metros) se multiplica el intervalo estadimétrico
por un valor fijo llamado coeficiente estadimétrico. Dicho valor
está indicado en cada telescopio, pero en la mayor parte de los
casos es igual a 100.
Nota: Para proceder a una medición sobre un terreno
en pendiente, dicho valor debe ser corregido para obtener la distancia horizontal real (ver Secci�n 4.0). |
|
 Observaci�n de una mira con el telescopio
Observaci�n de una mira con el telescopio |
| |
|
| |
 Escala que se ve en la lente del telescopio
Escala que se ve en la lente del telescopio |
| |
|
| |
Ejemplo
- Lectura del hilo estadim�trico superior: 1,62 m;
- Lectura del hilo estadim�trico inferior: 0,52 m;
- Intervalo estadim�trico = 1,62 m - 0,52 m = 1,10 m;
- Factor estadim�trico = 100;
- Distancia AB = 1,10 m x 100 = 110 m.
|
2.9 Cómo medir distancias cuando aparecen obstáculos sobre
la línea recta
|
| 1. Para aplicar los métodos apenas
descritos, es necesario poder recorrer toda la longitud de la línea
recta y tomar las medidas directamente. Pero en algunos casos puede
haber obstáculos sobre la línea en cuestión que
impiden la medición directa de las distancias. En efecto, la
línea recta puede estar interrumpida, por ejemplo, por un espejo
de agua, un lago, un estanque o un río, o quizás un campo
cultivado. En muchas circunstancias será necesario realizar mediciones
indirectas sobre un segmento de la recta considerada, utilizando
algunos de los m�todos estudiados en la Secci�n
1.6.
Medición de una distancia a través de un lago o de un
campo cultivado
2. A partir de un punto A de la recta XY interrumpida por un obstáculo,
se marca otra línea recta AZ que evite el obstáculo en
cuestión.
3. Desde esta nueva recta, se traza una , l�nea perpendicular CB que encuentra
la recta inicial en el punto B más allá del obstáculo
(ver Sección 3.6).
4. Se miden los dos nuevos segmentos AC y CB y se calcula la distancia
AB por medio de la siguiente fórmula matemática:
|
|
 La l�nea XY cruza un lago
La l�nea XY cruza un lago |
| |
|
| |
 Trazar la l�nea AZ
Trazar la l�nea AZ |
| |
|
| |
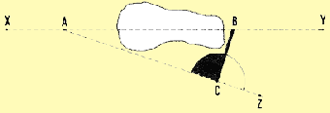 Trazar la perpendicular CB
Trazar la perpendicular CB |
| |
|
| |
|
Medición de una distancia interrumpida por un
curso de agua
|
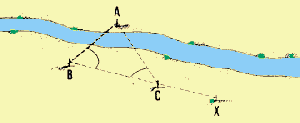
| 5.En este caso, el obstáculo (un curso de agua),
no puede ser evitado pero en general los puntos donde la recta se interrumpe
son visibles desde ambos lados. En tal caso existen numerosos métodos
geométricos que se pueden aplicar. A continuación se describen
dos de ellos.
6. Supongamos que se debe medir la distancia GH trazada sobre un curso
de agua. Utilizando jalones o piquetes se marca el punto C que prolonga
la recta GH. Se trazan las perpendiculares GZ y CX a partir de los puntos
G y C. Sobre cada una de las rectas se determinan los puntos E y F,
que se unen con el punto H, en la otra orilla, determinando la
recta FY. Se miden las distancias accesibles GE, GC y CF y se
calcula la distancia inaccesible GH aplicando la siguiente fórmula:
|
GH = (GE x GC) �(CF - GE)
|
|
|
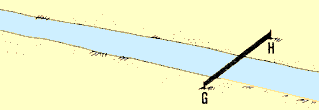 GH cruza un rio
GH cruza un rio |
| |
|
| |
 El punto H es visible desde el punto G
El punto H es visible desde el punto G |
| |
|
|
 Prolongar hacia atr�s la l�nea hasta el punto C
Prolongar hacia atr�s la l�nea hasta el punto C |
|
 Trazar las perpendiculares GZ y CX
Trazar las perpendiculares GZ y CX |
| |
|
|
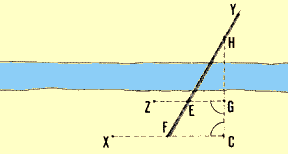 Hallar los puntos E y F en la l�nea FEHY
Hallar los puntos E y F en la l�nea FEHY |
|
 Calcular la distancia GH
Calcular la distancia GH |
| |
|
|
| Ejemplo
Medici�n de la distancia GH sobre la recta trazada a trav�s de un curso de agua:
- se prolonga la recta GH hacia atrás hasta el punto C;
- se trazan las rectas perpendiculares GZ y CX;;
- se determinan los puntos E y F sobre la recta FEH;
- se miden las distancias GE = 34 m; GC = 36 m, CF = 54 m;
- se calcula GH = (34 m x 36 m) ÷ (54 m - 34 m), GH =
1 224 m ÷ 20 m = 61,2 m.
|
|
|
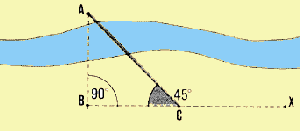
| 7. Supongamos que se quiere medir la distancia
AB sobre la recta trazada a través de un curso de agua. Se determina
la recta BX perpendicular a AB sobre una de las orillas. Se marca el punto
C sobre dicha perpendicular, desde el cual el punto A situado sobre la
otra orilla es visible determinando un
�ngulo de 45� (ver ejemplo Sección 36, punto 63). Se
mide la distancia CB que será igual a la distancia inaccesible
AB. |
|
 La l�nea AB cruza un rio
La l�nea AB cruza un rio |
| |
|
| |
 Trazar la perpendicular BX
Trazar la perpendicular BX |
| |
|
|
Trazar el �ngulo de 45� BCA
Calcular la distancia AB
|
|
Ejemplo
Medición de la distancia AB::
- desde el punto B, se traza la perpendicular BX;
- se determina el punto C, elegido de tal modo que el ángulo
BCA sea igual a 45°;
- se mide BC = 67 m;
- la distancia AB = BC = 67 m.
|
