Physical processes in coastal lagoons are influenced most by winds, tides and morphometry. Among the most important morphometric factors are: pass dimensions; lagoonal width to length to depth ratios; bottom topography; and, mean depth. Inlet dimensions control the exchange of water, including the dissolved and suspended material that it contains, and this in turn determines flushing rates and residence times. Bottom topography, including both natural and man-made channels, plays an important role in guiding the tidal and nontidal circulation of the lagoon. Mean depth may the most important of the three geometric factors. Lagoons are characteristically shallow, with a large horizontal to mean depth ratio, and several hydraulic and hydrographic features arise as a direct consequence.
First, shallow water is especially responsive to heating and cooling processes. Even over diurnal time scales, warming and cooling is distinct. Second, wind effects cause intense vertical mixing and significant wave action and these mixing processes can extend to the bottom. As a result, shallow lagoons favor vertical homogeneity, and significant density gradients in the vertical are uncommon. Third, in shallow water the bottom frictional influence may extend to the surface, and currents are quickly damped once forcing ceases. To maintain well-defined circulation patterns forcing must be continuous. Tidal forcing is continuous in a periodic sense, but tidal motions arise from exchanges with adjacent continental shelf waters, and inlet jetting can result in rapid dispersion and attenuation of the tidal current. Thus, as noted above, passes may have a significant constricting effect. Tidal motions may be significant only in the immediate vicinity of the pass. Wind forcing can be both local and non-local (by changing sea level outside passes), but it is intermittent in time, and variable in speed and direction. Thus, near passes, tidal currents are often dominant, while in the interior of the lagoon, wind forcing is primarily responsible for maintaining the circulation of the lagoon. Finally, shallow water enhances the residual, or net motion that occurs over any complete tidal cycle. The circulation of a coastal lagoon is highly variable in both space and time.
The objectives of this chapter are to survey the three most important physical processes in coastal lagoons: (1) the water balance, which discusses processes which add, remove and redistribute water within the lagoon; (2) the salt balance, which explains the mechanisms by which salt is gained or lost, thereby maintaining or altering the estuarine characteristics of the lagoon; and (3) the heat balance, which describes warming and cooling processes. All of the above processes not only affect water movement, but also the transport of properties associated with water masses, such as sediments and larvae. An understanding of physical processes is coastal lagoons is fundamental to their proper management.
The basic objective in an investigation of the water balance of a coastal lagoon is an accounting of the gains and losses of water - for the lagoon as a whole, or for some sub-area of interest - and a description of the mechanisms by which water is redistributed within the lagoon. A thorough study of water balance evaluates all the processes which contribute or remove water. These processes are represented by terms in the hydrologic equation, an equation of continuity that explains volume changes in terms of processes that involve both salt water and fresh water:
dv/dt = P - E + D + G + A, (2.1)
where V is the volume of the lagoon or study area, P is the precipitation rate, E is the evaporation rate, D is freshwater discharge, G is groundwater seepage and A is the advective gain or loss of water through a transverse cross-section. Depending upon the area chosen for study, the cross-section may be at an pass and describe lagoon-shelf exchanges, or it may be within the lagoon and describe the gain (or loss) of water to (from) a particular study area.
Precipitation (P) can be estimated using a network of rain gauges surrounding the lagoon, with individual readings weighted according to the fraction of the lagoon they represent (Thiessen 1911). Evaporation (E) estimates require a measure of humidity along with wind readings that are representative of over-water conditions. Freshwater discharge values (D) are obtained from gauges on major freshwater canals, rivers or streams emptying into the lagoon.
Groundwater seepage (G) is an integral part of lagoon hydrography, but it is usually difficult to quantify. Freshwater entering the lagoon will be by surface runoff and groundwater seepage. In lagoons with few natural streams or drainage canals, groundwater will contribute a substantial fraction of the total. Groundwater seepage is greatest in a band which is characteristically several tens of meters wide and which runs parallel to the shore on the landward side of the lagoon. The flow rate decreases roughly exponentially with distance from shore. Advective transport (A) is conceptually straightforward, but it is especially complex and difficult to estimate because gradients of current speed in both vertical and horizontal directions are significant.
The temporal variability of the individual terms in equation (2.1) is considerable. Precipitation varies greatly over time scales of hours to months, but seasonal variations are repeated in a general way from one year to the next. Evaporation may show a degree of seasonality, and there may be a diurnal variation in response to wind speed and humidity, but this term is relatively stable. Freshwater discharge shows considerable variation over time scales ranging from days to seasons. High-frequency fluctuations are damped somewhat, however, as rainwater percolates through soil enroute to the canal or river. Groundwater seepage is damped even more than freshwater discharge, because of the greater distances involved when water percolates all the way to the lagoon. The advective movement of water within the lagoon is the most rapidly fluctuating term, because shallow waters are highly responsive to temporal variations in windstress and therefore most likely to affect particle transport. Significant changes in current patterns are commonly recorded over time scales on the order of a few hours. This is superimposed on to much slower variations in response to weather systems moving through the area, and to seasonally changing wind patterns.
Assembling the data base necessary for evaluating the terms on the right hand side of equation (2.1) can be a formidable task. Under certain conditions, some terms can be assumed to be small, and it may be possible to estimate still others as residuals. In some studies, an alternate approach is taken which places an emphasis on effects, rather than causes. dv/dt is evaluated by assembling water level records and multiplying the change in water level by the surface area of the lagoon (see Pritchard 1960).
The concept of water balance is fundamental in calculating two commonly used measures of lagoon flushing-hydraulic replacement time, Th' and freshwater residence time, Tf. The hydraulic replacement time is given by
Th = V / Of, (2.2)
where V is the mean volume of the lagoon, and Of is the total net freshwater discharge. The freshwater replacement time is defined by
Tf = Th (So - S1)/S0, (2.3)
where So and Sl are the mean salinities of adjacent inner shelf waters and the lagoon, respectively. In practice, the net freshwater discharge must be the sum of the surface runoff, groundwater seepage and direct precipitation, less a correction for evaporation. Failure to evaluate these terms and incorporate all the significant terms can lead to substantial over- or under-estimates in the flushing rate. Unpublished data from Corpus Christi Bay, Texas, for example indicate a freshwater residence time of 0.27 years if freshwater discharge is uncorrected for evaporation. Similar calculations indicate a hydraulic replacement time of 1.87 years. If calculations are corrected for evaporation, however, the freshwater residence time increases to 1.03 years, and the hydraulic replacement time increases to 7.34 years.
It is important to distinguish between more general water balance studies and more highly focused mass flux, or mass continuity studies. The latter intentionally take a more limited approach and concentrate specifically on the advection term to describe transport processes. An example of this is one of the first papers on the subject of water balance (Pritchard 1958), which describes water balance in terms of mass or volume continuity. In contrast to this approach, a description of exchange rates in Chincoteague Bay (Pritchard 1960) takes a more complete approach by incorporating freshwater inflow data, and estimating freshwater runoff, precipitation and evaporation.
The circulation of a coastal lagoon can be sub-divided in one sense into “local wind-driven, or frictional,” and “gravitational” components. The local wind-driven component includes the direct downwind drift. Any upwind return flow that may arise in response to the wind-driven set-up and set-down of lagoon water levels is due to the barotropic pressure gradient set-up in the downwind direction. Additional circulation due to water surface slope can arise from water level variation outside the passes caused by tide and wind effects over the shelf. It may have barotropic, baroclinic, and freshwater discharge components. Freshwater discharge, for example, will move through the lagoon toward a pass as a result of the water surface variation it creates where it entered the lagoon. Similarly, both tidal and nontidal exchanges may be driven by the high and low water conditions occuring outside the lagoon over the inner continental shelf.
The circulation within a coastal lagoon will be in response to both local and nonlocal, or “remote” forcing. Within the lagoon, local forcing is of two kinds: windstress acting on the surface of the lagoon produces the frictional circulation; and, horizontal density gradients, associated with either fresh water entering the lagoon from the land side, or salt water entering from the seaward side, produce pressure gradients which influence the gravitational circulation. Both tidal and low-frequency variations in coastal sea level result in the nonlocal forcing of lagoonal circulation. Shelf tides force the ebb and flood of water through passes. The low-frequency rise and fall of coastal sea level in response to changes in surface pressure and wind conditions produce a similar inflow and outflow, but over longer time scales.
The measured flow at a given place and time may be a complex mix of tidal and nontidal currents, which are a response to both local and nonlocal forcing. The analysis of current measurements often begins with an attempt to understand the forcing to which the observed flow has responded. Two basic features of the flow which aid in identifying the dominant forcing mechanisms are the time scales over which it varies, and the vertical structure of the current speed. Tidal motions are rigorously periodic, with prominant semi-diurnal and diurnal variations in time series measurements. Nontidal motion is quasi-periodic at best, but fluctuations in response to passing weather systems occur over the same time scales found for rainfall, evaporation, freshwater discharge and groundwater seepage.
Local and non-local forcing can be distinguished easily when data are available in profile form. Both tidal and non-tidal currents forced by lagoon-shelf exchanges through passes will decrease logarithmically with height above bottom. Locally wind-driven currents will decrease exponentially with distance below the surface. This is shown schematically in Figure 2.1.
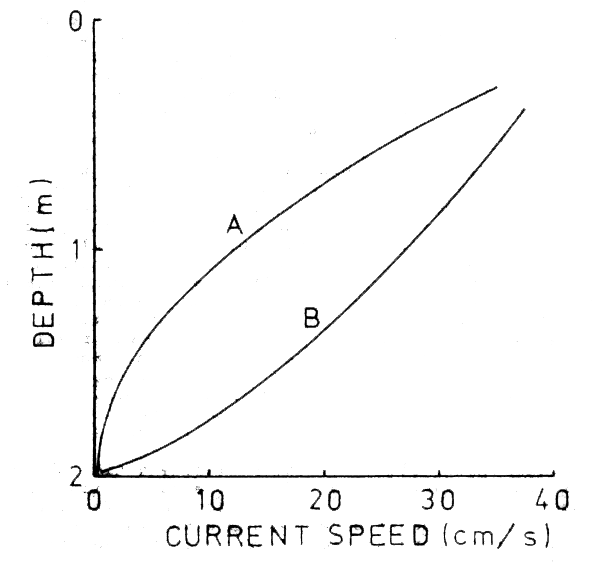
Figure 2.1 Hypothetical current profiles representing (A) locally forced wind-driven flow, and (B) tidal or nontidal flow forced by lagoon-shelf exchanges.
The complex mix of current components which may be superimposed at a particular time and place can be sorted out to some degree when observations in a time series are decomposed into three components. It is customary to separate the quasi-steady flow from the time-varying motion, and to expand the time-varying flow into its periodic and residual parts. Thus, for each measurement, u, in a time series, we can write at each time
u = <u> + U + u', (2.4)
where <u> is the mean over some time period, which is a multiple of the tidal period. U is the sinuosidal ebb and flood of the tide and u' is the non-steady, non-periodic residual. Each term may vary in space. This approach is an oversimplification insofar as many tidal constituents may influence a study area, but it is a useful breakdown nonetheless. To describe tidal currents in detail, a careful harmonic analysis of the data must be conducted.
Depending upon the questions being addressed and the physical characteristics of the lagoon under investigation, the appropriate decomposition of the measured current may be quite different. For example, it may be desirable to consider deviations from cross-sectional means rather than temporal means. Or it may be preferable to consider deviations from vertical means if vertical shear is significant. In coastal lagoons with little tidal motion, most of the instantaneous observation may be comprised of the quasi-steady mean and a nontidal deviation from that mean. A careful decomposition of the available current data can be very helpful in determining the nature of the advective gain or loss of water within the lagoon or study area.
Although a well-defined ebb and flood of the tide may be confined to portions of the lagoon relatively close to a pass, the tidal circulation is significant as a baseline level of circulation. Tidal currents are as predictable as they are periodic. Thus, they should be quantified in any comprehensive study of lagoonal circulation.
Tidal motions arise in response to forces associated with the interaction of the earth-moon-sun system. The response to this forcing is quantified by individual tidal constituents at approximately semi-diurnal, diurnal, monthly, annual and other periodicities. Each constituent is represented by harmonic constants-amplitudes and phase angles-which define the magnitude of the rise and fall in water level (or ebb and flood of the current) for that constituent, as well as the time at which high and low water (or maximum flood and ebb) occur. Harmonic constants are the basic input for all tidal predictions. A description of the tides is available from many sources and at levels ranging from introductory (Clancey 1969), Redfield 1980) to advanced (Dronkers 1964). Background information will not be repeated here, however a few points should be made which support the recommendation in Chapter 5 of this manual to conduct measurements over extended periods of time. For example, it is important to note that individual tidal constituents cycle in and out of phase to produce the familiar “spring” and “neap” tide conditions (Fig. 2.2, curve a). A similar interaction of diurnal constituents results in tropic and equatorial tidal conditions.
The interaction of semi-diurnal and diurnal tidal constituents results in a diurnal inequality of high and low water levels (Fig. 2.2, curve b), as well as flood and ebb currents. As a result, sampling must be continued through a 14-day period to include both maximum and minimum tidal ranges, and sampling must include two consecutive tidal cycles to average “higher-high” and “lower-high” water.
The residual flow of water past a study site during a complete tidal cycle is an important consideration in transport studies of all kinds. Van de Kreeke and Cotter (1974) have shown that residual flow is proportional to the ratio of tidal amplitude to water depth. Thus, a significant residual flow requires either a large amplitude tide or shallow water. Coastal lagoons generally do not have prominant tides, but they do provide shallow water and thus exhibit residual flow. Residual motion is made up of two components, relating to the steady flow of water and to oscillatory motions. The first is referred to as “Eulerian residual flow,” and is simply the average of the individual current measurements made over a time interval such as a tidal period. Eulerian residual flow is given by
QE = < U >, (2.5)
where U is the current speed and the diamond brackets indicate a temporal average over a tidal cycle or other appropriate time interval. Eulerian flow quantifies freshwater outflow, all long-period wind-driven transport and other nontidal flow in response to lagoon-shelf exchanges onto which tidal oscillations are superimposed.
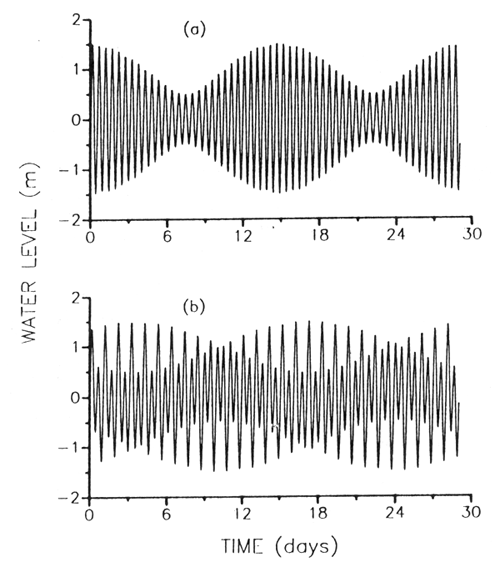
Figure 2.2 Composites showing: (a) the fortnightly “beat frequency”, resulting in spring and neap tide conditions, when two semi-diurnal tidal constituents are combined; and, (b) the diurnal inequality in high and low tides when semi-diurnal and diurnal constituents are combined.
The second, termed “mass transport Stokes drift,” arises from the correlation of the rise and fall in water level (H) with the ebb and flood of the current. The mass transport Stokes drift is given by
Qs = <U' H'> / <H>, (2.6)
where U' = U - <U> and H' = H - <H>, i.e. the differences between the individual measurements and the temporal mean values. A Stokes drift in the direction of tidal wave propagation will arise when over half of the flood tide coincides with water levels above the tidal cycle mean. While QS is especially well-suited for describing transport in a co-oscillating current system, the Eulerian residual current generally has to be evaluated as well. In lagoons with both quasi-steady and oscillatory currents, the mass transport residual current, QL = QE + QS, is calculated to quantify the total transport.
In lagoons with a single pass, the Eulerian and Stokes residual motions often transport water in opposite directions. For example, the Stokes drift may be transporting water into the lagoon, while the quasi-steady Eulerian transport is providing the compensating return flow, in addition to the freshwater outflow. In lagoons with two or more passes, residual tidal motions arise as a result of differences in mean water level, tidal conditions at the passes, or differences in the passes themselves. van de Kreeke and Cotter (1974) have shown that the residual flow will be toward the pass at which the tidal amplitude is greater, or at which the tidal phase is lagged-all other factors being equal. Alternately, a residual transport will be directed toward the pass of greater length, narrower width or greater depth-again, all other factors being equal. Inlet dimensions may differ in many ways, thus it is difficult to predict the direction and magnitude of a residual flow. But the existence of residual tidal motion must be recognized and sampling must be designed to detect and quantify it.
In view of the vertical variation in maximum tidal current speeds noted earlier, it follows that both the tidal excursion over any half tidal cycle, and the residual motion over a full tidal cycle will vary with depth. Because strongest flood and ebb current speeds are recorded at near-surface levels, transport will be greatest at these levels too. This feature of tidal transport is significant when dissolved or suspended material is unequally distributed through the water column.
As noted above, the nontidal circulation of a coastal lagoon is comprised of the wind-driven component--with both local and non-local sub-components--and the pressure gradient driven (gravitational) component. In lagoons with sufficiently restricted exchanges the local wind-driven circulation will dominate all other forms of locally or remotely forced nontidal circulation. An important feature of the local wind-driven current, and one that may set it apart from the ebb and flood of the tide, stems from the seasonality in wind forcing. Seasonal changes in characteristic wind speeds and directions will result in corresponding changes in the wind-driven circulation, and thus in the net transport. It is common for wind forcing in temperate regions to be stronger during fall, winter and spring months, then decrease significantly during summer months. In contrast, tidal circulation is dominated by semi-diurnal and diurnal constituents which vary only slightly in magnitude or in phase over the course of a year.
Local forcing by windstress produces initially a direct downwind transport regardless of the wind direction. This in turn will set up water levels along the downwind shore and set down water levels along the upwind shore. This will be especially pronounced if the lagoon is elongated and the wind direction parallels the longitudinal axis of the lagoon. The slope of the lagoon surface will be on the order of τPgH, where H is the total depth and τ is the wind stress, p is the water density, and g is local gravitational acceleration. This normally ranges from 10-5 to 10-6 for moderate winds and depths of 1-10m. Thus, a significant water level response would require a lagoon with a longitudinal axis on the order of several tens of kilometers.
The secondary response to the wind, and the primary response to the barotropic pressure gradient established by the down-wind rise of water level, is an upwind-directed return flow. This generally occurs at near-bottom levels, and in the deeper waters along the middle of the lagoon. An upwind return flow may be aided by navigational channels. Both natural and man-made channels serve as conduits by locally expanding the layer between the downwind-directed windstress itself, and the bottom frictional force which resists the upwind return flow.
Apart from the direct response to the windstress, the circulation of a coastal lagoon occurs in response to the pressure gradient term. The pressure, p, at any level z above a horizontal reference plane, is given by p = pa + pg (h-z), where Pa is the atmospheric pressure taken to be uniform, and h is the height or free surface area above the reference plane. Both density and the depth below the surface (h-z) can vary horizontally spatially, especially along the longitudinal axis of the lagoon. Thus, a horizontal plane at the study site will be at greater or shallower depths below the free surface at differing locations according to the surface slope - whether this is in response to a set-up or set-down, fresh water entering the lagoon, or tidal or nontidal exchanges through the pass. The pressure gradient driving the gravitational circulation is therefore given by
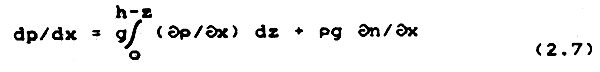
The second term in (2.8) is independent of depth and is due to the tilt of the free surface, n,; this is called the barotropic pressure gradient. The first term in (2.7) varies locally with distance below the free surface and is caused by horizontal variations; this is called the baroclinic pressure gradient.
From equation (2.7), it follows that a pressure gradient related flow will arise from the density gradients that exist where a wedge of fresh water lies over a similar wedge of salt water, as well as from the surface distortion associated with wind effects or the addition of fresh and salt water at opposite ends of the lagoon. An evaluation of the magnitude of the two terms on the right hand side of equation (2.7) suggests that baroclinic forcing, involving density gradients, will generally be of lesser importance, except possibly in strong frontal regions. It is important to note, however, that the gravitational circulation associated with density gradients is directly related to depth below the free surface. Thus, it typically increases in importance at intermediate and especially near-bottom layers if the horizontal density gradient either increases or remains constant with increasing depth.
Temperature (T) and salinity (S) are the principal determinants of the density of lagoon water. But while their effects on density are opposite, one unit of change in T does not have the same effect on density as does the effect of one unit change of S. We can express this in the ratio ΑT to Β, where Α is the coefficient of thermal expansion and where Β is the coefficient of bulk expansion. The question is, what are the relative number of T and S units which will produce an equivalent density change in water? At 30°C, this ratio is about 2.4; at 10°C, about 7; and at 5°C, about 10. The ratio is positive at all combinations, but increases as temperature declines. Thus at temperate winter temperatures, salinity is the major determinant of density since it takes about 10°C to produce the same density change as a 1ppt change in salinity. In summer, temperature changes may contribute more to density currents, for example, since the ratio has fallen to about 3 or 4°C/1ppt. Especially in shallow lagoons, diel fluctuations in temperature of this magnitude are not uncommon. However, under most circumstances, salinity is a far more important determinant' of water density in lagoons and estuaries because temperature differences either across or from top to bottom in a lagoon are small compared to salinity differences. Using the equation of state:
(p) = (Po) ([1+B(S-So)-a(T-To)] (2.8)
where the zero subscripts indicate the “means”, one can readily see this effect.
It is important to note that the strength of density-driven currents is proportional to the horizontal spatial gradients of T and S. For example, T may fluctuate much more than S, but if the changes in T occur everywhere in X or Y, then the net effect on circulation is O. The gradients of S are the important quantities in the absence of point sources of heat, such as thermal outfalls.
The baroclinic pressure gradient force will always be directed toward regions of lower salinity assuming that the effect of temperature on density is minimal. This force is from regions of high pressure towards regions of low pressure, i.e., down the density gradient. Thus, in a brackish-water lagoon, the baroclinic pressure gradient will tend to force near-bottom water into the lagoon. In a hypersaline lagoon, on the other hand, baroclinic forcing will act to force high salinity water out the pass. The barotropic pressure gradient is not a function of depth, and thus it will be felt equally at all sub-surface levels.
Owing to the relatively poor connections, understanding the mechanics of water exchange with the adjacent coastal ocean is of paramount importance for three reasons. First, it is one determinant of lagoon water quality. Second, the ocean is the source of much of the biota of lagoons, particularly larval forms which colonize lagoons. Third, over temporal scales longer than that of lunar tides, the lagoon tends to rise and fall in concert with the coastal ocean, thus adding an important hydraulic component. A conceptual scheme of the important forcing functions and their time and space scales is presented in Figure 2.3.
Nontidal lagoon-shelf exchanges occur when coastal winds raise or lower coastal sea level. Coastal sea level responds directly to the cross-shelf wind component, with set-up and set-down water levels when directed landward and seaward, respectively. More importantly, coastal sea level also responds to along-shelf winds, although indirectly. Along-shelf winds drive an along-shelf circulation. In an equilibrium condition in the Northern Hemisphere, the Coriolis force will be balanced by an opposing pressure gradient, and sea level will slope upward to the right, looking downstream. Thus, for along-shelf winds and currents with the coast on the left, coastal sea level will fall, and water will be drawn out of the lagoon. When the wind and current reverse direction, coastal sea level will slope upward toward the coast, and the lagoon will fill. The resulting inflow into, or outflow from the lagoon is much like a tidal exchange, although it characteristically occurs over time scales on the order of days, as synoptic-scale weather systems move through the study area.
Pass morphometry plays a central role in the hydraulics of a coastal lagoon. The constriction of a pass acts as a filter on lagoon-shelf exchanges in the sense that the damping effect it has on exchanges is directly related to the frequency of the rise and fall in coastal sea level. For a sufficiently constricting pass, tidal amplitudes in a lagoon may be greatly reduced below amplitudes found nearby on the continental shelf, yet low-frequency variations over time scales in excess of a few days may be nearly identical in lagoon and coastal waters. The degree to which semi-diurnal and diurnal tidal motions will be damped depends upon the dimensions of the pass and the area of the lagoon, but in every case semi-diurnal constituents will be preferentially damped. The total volume of water exchanged increases with the period of the tide for a fixed amplitude tide. This will enhance the diurnal constituents, and in some cases they will replace the semi-diurnal constituents in the lagoon as the dominant constituents. The “form number,” f, is defined by the sum of the amplitudes of the two principal semi-diurnal tidal constituents, divided by the sum of the amplitudes of the two principal diurnal constituents:
f = (M2+S2) / (K1+O1). (2.9)
The form number characteristically decreases in magnitude within a coastal lagoon. As noted above, it may be greater than unity in shelf waters, but less than unity well inside the lagoon.
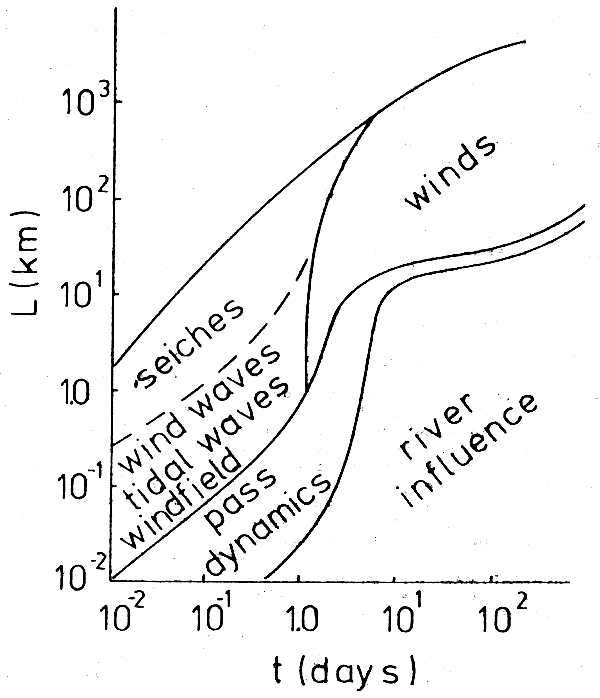
Figure 2.3 Relevant time and space scales of forcing in lagoons.
To obtain a more quantitative description of exchange through a pass due to sea level variations outside the pass associated with either tidal- or wind-forced events, we consider an idealized pass of width W and length L with W/L >> 1. The water depth in the vicinity of the pass, taken as uniform, is H. If the sea level outside, but in the vicinity, of the pass rises by an amount h in time T, then the pressure gradient in the vicinity of the pass is of magnitude pgh/W. Neglecting frictional effects, this pressure gradient will cause the water to accelerate through the pass. The pressure gradient will balance either the temporal acceleration term U/T or the advective acceleration term U2/T, whichever is larger. An analysis balancing the pressure gradient with the acceleration terms leads to the following conclusions.
If the pass is “wide” (W > CT √h/2H), then V=ghT/W, where current speed, C = √gH and the total volume of water passing through the pass in time T is QT= ghT2H. This follows from linear dynamics, i.e., if W < CT√h/2H. If the pass is “narrow” (W < CT√h/2H), then V = √2gh and QT = √2gh THW. This is the non-linear dynamics estimate V2/2W = gh/W. For typical passes C ≈ 10m/s, and if T ≈ 104 sec (semi-diurnal tide) and if √h/2H ≈ 0.1, the critical pass width separating “narrow” form “wide” is 10km. Thus most passes are “narrow” and QT = √2gh THW. This is a useful estimate of the volume exchanged through the pass in time T, though it is an overestimate for two reasons. First, neglected frictional terms will reduce the transport. Second, and more importantly, as water flows into the lagoon, the water level in the lagoon will rise and the pressure gradient, thus the volume flow, decreases. The water level inside the lagoon forced by the flow cannot exceed h. The estimate QT=√2gh THW is useful for estimating the response of mean water level in the lagoon to coastal forcing. The mean rise of water level h1 in a lagoon of cross-sectional area A, is:
h1=QT/A=?2gh THW/A (2.10)
If CTW/A √h/2H << 1, the Oean water level rise in the lagoon is small compared to h, and QT is a reasonable estimate, apart from frictional factors, for the water exchanged. We note that the water level rise near the pass may be comparable to h. On the other hand, if CTW/A √h/2H >> 1, this suggests that the water level in the lagoon will rise directly with h (since, in reality, h1 √ h), and QT must actually be hA, i.e., the pressure gradients will be reduced outside the pass by the water level rise in the lagoon to support just this amount of transport. We summarize our (frictionless) discussion for “narrow” passes (W < CT√h/H) as follows: if CTW/A √h/2H << 1, then h1/h = CTW/A √h/2H and QT = √2gh THW. If CTW/A √h/2H >> 1, h1 and QT = hA. Thus, pass dynamics depend on the time and magnitude of coastal sea level rise, the depth and width of the pass, and the surface area of the lagoon.
The above discussion applies to situations where the pass is short. In the case of a relatively long pass, both friction and pass configuration contribute more to the actual flow, and the “frictionless” prediction becomes less than adequate. In such cases the equation for flow through a pass becomes akin to that through a pipe.
The flow of water through such a pass is a function of four variables: water level difference (or head) along the axis of the pass from outside to inside the lagoon; pass cross section; pass length; and pass “roughness”,

where Q=flow
R=hydraulic radius of the pass
P1 - P2=head, or pressure difference
η=viscosity
L=length of the pass and n=coefficient of roughness.
Head is the difference in water height at either end of the pass. As we have seen, in lagoons this is rarely a simple function of the tidal amplitude, which can be used in cases where the sea level in the lagoon and coastal ocean rise and fall with comparable magnitude.
Flow through a long pass is partially inversely proportional to its length and directly proportional to its cross-sectional area, because the sides and bottom extract momentum from the moving water mass. Alternatively, if the cross-sectional area narrows in one direction, the velocity will accelerate to conserve volume flux, so velocity is also inversely proportional to the area. Clearly, there is a trade-off between wall roughness and the funnel or Venturi effect. Of particular importance is the minimum cross section, or constriction (equivalent to a kink in a hose).
Pass “roughness” represents resistance to flow. Except for extremely low flow conditions, the effects of surface roughness, such as caused by rip-rap, can be neglected. The momentum lost along the edges and bottom of all but a very long and narrow pass is small. More generally important are the pass curvature, or departure of a pass from a straight line (equivalent to a bend in a pipe)- and the degree of convergence or divergence of the walls; both effects are most important in the case of long passes.
Thus, the volume flow can be adequately predicted for many cases with a knowledge of the head and the pass cross-sectional area. The difficulty is predicting the head, since, in addition to lunar tidal, wind forcing is responsible for substantial water level fluctuations both inside lagoons and in near coastal waters. The flow of water through a pass can be markedly reduced by a cross-channel constriction, such as a partial dam or gates. The astronomical tidal amplitude in the lagoon can thus be easily reduced. We now turn to other considerations of pass dynamics which are particularly relevant to larval transport through passes.
Even in narrow passes the velocity of water is not uniform across a pass. Flow goes to O at the boundaries, owing to the no-slip condition, i.e., given the fact that pass walls generally do not move, at the wall the fluid must have zero velocity. In passes with large cross-sectional areas, ebbing water may flow on one side, while flooding water on the other - the ebb and flood channels familiar to navigators. Even flow reversals at the sides have been observed, and certainly there are “dead” areas at the inside edges of bends in a pass, or in bottom depressions.
Density stratification makes the prediction of flow somewhat more complex. The ebb flow may consist almost entirely of a less dense surface stratum, and the flood water may be mostly ocean water. Under conditions of a strong density gradient, pressure gradient forcing may cause saltier water to continue to enter the lagoon well after the upper layer begins to ebb. Furthermore, if the lagoon is vertically stratified, the probability that the same water mass will leave on the ensuing ebb is considerably less. In general, this means that more salt water will enter and more fresh water will leave on any particular tide cycle than under unstratified flow conditions. Thus, other things being equal, the mean flushing time will be shorter and a stratified lagoon will be more saline, on average. Perhaps of more import, larval entry and retention will be facilitated under stratified conditions, if the larvae can remain near the bottom: 1) because it is less likely that the same flood water mass (and larvae) will leave on the ebb; and, 2) because flood conditions near the bottom will persist for a larger fraction of a tidal cycle.
In the long run, the ebb volume must equal the flood volume plus the freshwater inflow volume. If tidal flow through a pass was between two identical basins, it would be symmetrical. This is never the case because, in general, there is more resistance to flood flow than ebb flow, given the fact that the typical coastal ocean has a strong longshore current which consists of relatively heavy water and thus accommodates the outwelling buoyant plume by riding underneath it. Zhang et al.(1987) recently showed that a strong coupling exists between shelf flows and outwelling plumes.
In tropical and subtropical regions, it is not uncommon for coastal lagoons to exhibit hyper saline conditions during at least part of the year if there are distinct wet and dry seasons. At those times, a lagoon becomes a negative estuary, defined as an estuary in which the relatively high salinity near-bottom layers occur in response to local evaporation, rather than as a result of advective exchanges with the inner continental shelf. In a negative estuary, the scenario described in the preceding paragraph is reversed: A net inflow exists in surface layeras; bottom layers exhibit a net outflow onto the inner shelf (e.g., Meshal 1987). The horizontal salinity gradient is directed seaward, especially in the near-bottom layers, and the gravitational circulation favors the export of high density lagoonal water. Conversely, ocean water floods into the lagoon relatively freely as a low-density surface layer. With the exchange process enhanced on both the flood and ebb cycles, the flushing rate will be increased proportionately.
Even if ebb and flood tides were symmetrical, most lagoons would entrain ocean water. Relatively dense flood water more or less “jets” into the lagoon, while buoyant ebb water is able to exit the pass without density gradient opposition (Fischer etal. 1979). Lee and Rooth (1972) suggest a rule of thumb that jetting extends inland about 500 times the pass depth. The flood water mass is also usually displaced away from the pass vicinity by both the tidal residual and sub-tidal frequency circulation in the lagoon.
If the incoming water mass is not entrained into the internal circulation pattern of the lagoon and advected away from the vicinity of the pass, much of the same water mass may be displaced back out the pass on the next ebb. The extreme case is where water enters a pass and is confined to a channel; the same water that enters on the flood will leave on the ebb. The channel length multiplied by the ratio of the mean channel depth to tidal excursion provides an approximation of the distance into the lagoon flood water will travel. If the water is stratified during the tidal cycle and the pass is deep and long, or jettyed into the lagoon, much of the “new” water that enters the lagoon will return to the ocean on the next ebb. The ratio of “new” water to the total ebb volume is the ebb tidal exchange ratio. While the salt balance does not distinguish “new” from “old” salt, this ratio has great implications for the ability of the lagoon to retain colonizing organisms. Zimmerman (1988) draws attention to the concept of local time scales and local ages of different sources (parcels) of water, and the inadequacy of hydrologic models to make these distinctions. On the ocean side, the buoyant outwelling plume will generally turn either right or left (Zhang et al. 1987) and meld into the nearshore circulation which is generally longshore, so that the return of the same ebb water to the lagoon is less likely. Again, jettys extending oceanward will tend to reduce the amount of new ocean water entering the lagoon.
Serendipity also plays a vital role in the ability of a lagoon to entrain and retain coastal water. Winds which blow either with the coast to the right (in the Northern Hemisphere) or towards the coast will elevate sea level on the seaward side of a pass. These same winds may, depending on the alignment and configuration of the lagoon, blow waters away from the pass head creating a drop in water height along the pass axis. This creates a pressure gradient force which acts in concert with a flood tide, to advect entrained water farther into the lagoon. The same winds will counter an ebbing tide and restrict transport out of the pass. Opposite winds (and sea level changes) will increase the tidal exchange ratio.
Similar good fortune, assuming larval retention is a positive feature, would couple a flooding tide with the flow induced by the sea to land breeze when, as above, the wind vector is located in the quadrant in which it is directed with the coast to its right or onshore. While the sea-land breeze phenomenon is diurnally coupled, the astronomical M2 tide, with a period of 12.42h, progresses around the daily clock so the two phenomena are only periodically synchronous.
A special case exists where two (or more) passes connect the lagoon to the ocean. Depending on the distance separating the passes, there may be a phase lag in the tides. Even if not, it is unlikely that wind-driven changes in water level in the lagoon are either equivalent or synoptic at both locations. Under normal circumstances there will be unequal circulation among passes, and the likelihood exists that such inequalities may augment the internal circulation pattern of the lagoon. This will tend to increase the one-way circulation in the lagoon, thus reducing the mean residence time as kind of a shunt. Depending upon the orientation of the wind-driven “set up” of the lagoon, this could either increase or decrease the tidal flux through a particular pass. When either the winds or longshore currents persist in one direction, one pass may more or less always act as an inlet and another as an outlet, e.g. Terminos Lagoon in Mexico (Yanez-Araccibia and Day 1982).
In an estuary or embayment with an unrestricted connection to the ocean, the ocean astronomical tide is most often the major forcing function with regard to estuary-ocean exchange processes. In a lagoon, this is rarely the case. Except in small lagoons with sufficiently wide and/or numerous passes, wind-forcing is frequently a more important determinant of water level change in the lagoon than the astronomical ocean, and certainly, lagoonal tide. This results in most lagoons having severely damped water level changes on the time scale of lunar tides.
In general, the M2 tidal forcing is relatively weak in lagoons. However, there is the possibility that the basin size may match identically with the wavelength of the tide and create basin resonance. In this case (only) the reflected waves may reinforce each other, resulting in more water movement than would be predicted by pass configuration and tidal amplitude alone - the phenomenon of resonance. Basically, this could only occur where the basin dimension approximates 1/2 the tidal wavelength, or integer multiples thereof. Conversely, it is possible that a basin's dimensions may dampen tidal forcing of water movements if its diameter is equal to 1/4 tidal wavelength, or some integer multiple. The wave period is 12.4h for a semi-diurnal tide. The wave speed, or celerity (c) is related to depth according to the equation:
c2 = hg (2.12)
where g is the gravitational constant and h is the water depth.
For a mean depth of 5m, the celerity is 7m s-1. This means the M2 tidal wave would have a length of about 316km. Resonant dimensions would be about 158km, or 79km, or 40km, etc. For a 1m deep lagoon the corresponding wavelength is 140km, with resonant dimensions of 70, 35 and 18km, etc. These dimensions are not exceptional for lagoons, so it is not unlikely that some are resonant. However, since in most lagoons, the M2 tide is restricted from entering freely, the amplitude of the tide, thus the energy, is reduced considerably. Higher harmonics of the tide are basically higher order additions (or corrections) to the fundamental mode. So, given a low amplitude fundamental motion, then the higher harmonic terms generally add little amplitude to the attenuated tide.
Owing to the possible effects of resonance, and the fact that these dimensions are not unusually large or small, the calculation of the resonant dimensions of any lagoon is worthwhile, particularly if its depth and diameter are close to the above relationships. In all cases wind forcing can swamp such effects. In even rarer cases, a wind blowing with the principal tidal axis, then relaxing, could set up a seiche in concert with such resonant, ocean tidal-forced waves. The effect on the circulation could be noticeable.
The nature of the “pump” represented by the pass plus tidal forcing in any situation varies greatly both among and within lagoons. It is to be expected that different lagoons and pass configurations will vary widely in this respect. It is also clear that ocean-estuary exchange processes can be quite different among lagoons and most estuaries which have relatively unrestricted mouths. This will be amplified further.
The most important point in the above discussion is that little insight into ocean-lagoon exchange processes through passes can be gained without a clear understanding of both direct and indirect wind effects upon both the lagoon and the coastal ocean. This is particularly true in cases where multiple passes are present. Given coastline alignment and relative inlet locations, connective pathways between the inlets may be established under certain sets of wind and tidal conditions, while under other circumstances the inlets may function independently. The effect of connective pathways could be to reduce water residence time considerably in the region between passes, and possibly isolate certain other (more remote) regions of the lagoon.
The importance of understanding the salt balance of a coastal lagoon stems not only from the role salt plays in determining the estuarine characteristics of the lagoon, but also from the fact that salt transport is similar to pollutant transport. Salt serves as a convenient natural tracer, and thus may be helpful in water quality studies. The salt balance of a coastal lagoon is intimately related to the water balance, with the qualification that salinity measurements must be incorporated into the analysis. For a simplified one-dimensional situation, consider a long narrow lagoon. Neglecting molecular diffusion, and ignoring salinity changes that result from the gain or loss of fresh water by precipitation, evaporation, freshwater discharge and groundwater seepage (see equation 2.1), the time rate of change in salinity at a point for small depth variations and due to advection is given by
ds/dt = -d(us)/dx, (2.13)
where u and s are instantaneous measurements of current and salinity, respectively.
Salt flux, like mass flux, results from advection and turbulent fluxes, or dispersion. Recalling equation (2.4), we can decompose salinity exactly as we decomposed current speed. Each measurement in a time series is comprised of a temporal mean value and a deviation from the mean:
s = <s> S + s', (2.14)
where <s> is the time average, S is the tidal period variation of salinity, and s' is the time varying residual. The product us in equation (2.10) then expands into
us = <u><s> + <u>S + <u>s' + U<s> + US + Us' + u'<s> + u'S+ u' s'. (2.15)
The x-derivative of the right hand side of equation (2.12) quantifies the convergence or divergence of salt. The resulting increase or decrease in salt at a point in the lagoon is the contribution of advection to the local balance. We note that in the absence of time varying wind-driven currents, u' and s' may be considered turbulent fluctuations.
When the cross-products are averaged over one or more tidal periods and the x-derivative is taken, several terms will drop out and equation (2.11) is simplified. Either individual terms are not correlated with each other, the sum of the products is zero, or the spatial variation is zero. Dyer (1973) has thoroughly discussed this. For example, both the <u>s' and u'<s> terms should drop out over a tidal cycle, because the residual fluctuations will have a zero mean. Similarly, it is unlikely that the tidal period variation in salinity is correlated with the mean velocity, or that the tidal current is correlated with the mean salinity. Thus, <u>S and U<s> drop out. The tidal velocity and salinity variations may be highly correlated, but unless this correlation changes along the axis of the lagoon, d (US)/dx will be negligible. Thus, while this term may explain salt transport, it will not result in a change in salinity, ds/dt. Similarly, while it is logical to assume that larger fluctuations might be embedded in stronger tidal currents, it does not follow that they will be consistently correlated, or that a longitudinal gradient in this correlation will exist. Finally, an increase in the amplitude of the tidal current might produce both a larger tidal variation in salinity and turbulent fluctuations, but the longitudinal variation in this relationship may be negligible.
Thus, in some studies, one is left with
d<s>dt = -d (<u> <s>)/dx - d<u’s’>/dx, (2.16)
which states that a change in salinity results from advection and/or from an eddy diffusion process. If, in the long term, a steady state exists, then the downstream advection associated with the mean flow will be balanced by an upstream turbulent transport.
The upstream diffusion of salt against the salinity gradient and opposing the advective transport is treated mathematically by introducing a coefficient of longitudinal dispersion which is called the effective eddy-diffusion coefficient (Kx). For simplified, one-dimensional flow, this is written as
d<s>/dt = -d(<u> <s>)/dx + d/dx Kx d<s>/ dx. (2.17)
In a steady-state condition, <s> will be constant in time, and the two right hand side terms in equation (2.14) will balance. While it is tempting to simplify the expression in this way, in practice it is rare to find steady- state conditions, except over the longest time scales. Most studies are not continued beyond several consecutive tidal cycles. Salinity fluctuates significantly over time scales ranging from hours to seasons, and it is generally preferable to retain ds/dt and work with a time-varying system.
Salt transport by advection is relatively easy to quantify; the diffusion terms are considerably more difficult. Thus, it is common practice to make simplifying assumptions appropriate to the estuarine system under investigation. That is, in many coastal lagoons, one may assume vertical homogeneity, ds/dz = 0, and perhaps lateral homogeneity, ds/dy = 0, thereby reducing salt flux to a one-dimensional process. It should be noted that lateral homogeneity is less likely, because both surface discharge and ground water seepage can reduce salinity on the landward side of the lagoon.
In a well-mixed, homogeneous lagoon, the longitudinal eddy-diffusion coefficient, Kx, can be calculated if the corrected freshwater outflow, Ft = R + D + G - E, from equation (2.1) is known, in addition to the mean longitudinal salinity gradient, d<s>/dx, and the cross-sectional area, A. Then,
Kx = (Ft <s> / (A d<s> / dx). (2.18)
Once Kx is known for a given study area, temporal variations in salinity, ds/dt, can be predicted if salinity and current patterns are known.
An alternate form of decomposition involves deviations from lateral or depth mean values of current speed and salinity, and the correlation of the corresponding cross-products. Murray and Siripong (1978) have taken this approach and used deviations from cross-sectional mean values of velocity and salinity to estimate the relative importance of vertical and lateral fluxes in the longitudinal salt flux in a well-mixed estuary. They found that the longitudinal flux due to lateral gradients was greater than that associated with vertical mixing. In well-mixed coastal lagoons, it is probable that lateral gradients in salinity combine with tidal and low-frequency co-oscillations to give rise to an upstream dispersive flux of salt which balances the downstream advective transport.
Warming and cooling in coastal lagoons is a straightforward response to a net gain or loss of heat energy. Temperature data obtained over sufficiently long study periods indicate that warming and cooling occurs over three distinct time scales. A diurnal rise and fall in temperature occurs as a logical response to heating by incoming solar radiation and cooling by net outgoing longwave radiation and evaporation. Over time scales on the order of 1–2 weeks, warming and cooling occurs as synoptic scale weather systems pass over the coastal zone, affecting cloud cover, wind speed, and perhaps air temperature and humidity. Finally, seasonal warming and cooling produces and annual cycle onto which all higher frequency fluctuations are superimposed.
Heat budget studies are conceptually similar to water balance studies in the sense that the heat budget equation, like the hydrologic equation, contains terms representing both local processes and advection. Local processes produce vertical fluxes through the air-water and water-sediment interfaces; advection results in a horizontal flux, as heat is brought in or removed by currents. The relative importance of local processes may be considerably greater in heat budget studies than in water budget studies. This is especially true for lagoons which have restricted exchanges with adjacent shelf waters.
The heat budget of a coastal lagoon is summarized by the well known heat budget equation:
dQ/dt = (Qs - Qb) + (Qh -Qe) + Qm + Qa (2. 19)
where dQ/dt is the temporal change in total heat energy, which is proportional to the change in mean temperature with time, Qs represents heating by insolation, Qb is the net longwave radiative energy loss, Qh is the sensible heat flux, Qe is the latent heat flux, Qm represents conductive heat exchanges with the underlying sediments, and Qa is the advective heat flux.
Qs and Qb have been combined because they are often considered together. They are both radiation terms, and they both vary inversely with cloud cover. An overcast sky, for example, reflects incoming solar radiation, thereby decreasing heating. Cloud cover also insulates the lagoon against longwave radiative energy losses. Similarly, Qh and Qe are often considered together, because they both respond to the overlying air mass. Warm, humid maritime tropical air, for example, will inhibit sensible heat losses as well as evaporative cooling.
Conductive exchanges with underlying sediments have received the least attention of all the terms in equation (2.19), because instantaneous fluxes are characteristically small, and because the net gain or loss over the longest time scales is negligible. The advection term is the most difficult of all to quantify, and in many studies it is calculated as a residual--the difference between what can be estimated for the other terms, and what has been observed at the study site.
Miller (1981) and Reed (1976a, 1978) discuss the calculation of insolation over a water surface. Several expressions are available for estimating solar heating. Basically, they consist of a correction to the solar constant to account for seasonal variations in the earth-sun distance, a second correction to account for the sun angle between sunrise and sunset, a third for atmospheric turbidity, a fourth for cloud-top reflection, and a fifth correction for surface reflectivity at the air-water interface. The result is a value for the insolation entering and thus heating the lagoon. Lagoonal heat budget studies show that without exception the insolation term is the dominant heating term (Smith 1981a, 1981b).
Net outgoing longwave radiation is based upon the Stefan-Boltzmann equation, but again corrections are needed to account for the insulating effect of humidity and cloud cover. Reed (1976b) has discussed this at some length. Radiative cooling is a significant term in the heat budget equation, but it is often dominated by evaporative cooling (latent heat flux).
Sensible and latent heat fluxes have been discussed by Hsu (1978). Although sensible heat fuxes can both warm and cool a lagoon, in practice cooling is considerably more efficient than heating. When warm air comes in contact with relatively cool water, both the lower atmosphere and the upper layers of the water column will stratify as they approach a common temperature, and further heat transfer will be reduced significantly. Themost common forms of the expression used to evaluate the sensible heat flux term include either the air-water temperature difference, or the temperature gradient in the lowest layers of the atmosphere and wind speed at a standard height above the lagoon (see Priestley and Taylor 1972). In these calculations, a bulk aerodynamic coefficient for heat is introduced as a proportionality factor to relate the wind speed and temperature gradient to the heat flux that they produce. Hsu (1978) has summarized values of the bulk aerodynamic coefficient wfound in several previous studies. The importance of sensible heat fluxes depends upon the time scale of the study. In the short term, air-water temperature differences may be significant. Over longer time scales, however, a shallow lagoon will warm and cool much like the overlying atmosphere, and sensible heat exchanges will be relatively slight.
Latent heat losses due to evaporation (Qe) are generally greater than sensible heat losses. Unsaturated air parcels are brought down to the water surface on turbulent eddies, gain humidity, and then are carried away from the surface by the eddying motion. The loss of water vapor to the air is balanced by evaporation at the surface which extracts energy from the water. Expressions for latent heat fluxes are similar to those for sensible heat fluxes (see Hsu 1978). Latent heat flux can be evaluated from wind speed, a measure of atmospheric moisture and the bulk aerodynamic coefficient for water vapor. In most studies, Qe is the primary cooling term balancing heating by insolation.
Conductive heat exchanges with underlying sediments can be evaluated from the product of the thermal conductivity of the sediment and the vertical gradient in temperature (Sellers 1965). In many cases, however, bottom sediments are layered, and either a mean value or a depth-varying value must be used in the calculations. Substituting representative values for conductivity (see Geiger 1965), calculations suggest that temperature changes at depths 2–3m below the water-sediment interface may be small enough to neglect, even over the longest time scales. Heat fluxes through the water-sediment interface are characteristically 1–2 orders of magnitude smaller than fluxes through the air-water interface (Smith 1982), because at the surface individual processes may act to warm and cool the water column simultaneously, and their net effect may be small.
An example of a heat budget study conducted in a subtropical lagoon in winter months is shown in Figure 2.4.
Only local fluxes were considered in this study. Insolation and net outgoing longwave (“back”) radiation are combined at the top of the plot. Insolation averaged 236 Watts m-2 during the study, but day-to-day variations in the daily means occurred in response to changes in cloud cover. Back radiation, in contrast, is relatively stable in time. Sensible and latent heat fluxes, shown in the middle of the plot, are similar in many respects, reflecting their response to the overlying air mass. Water-sediment conduction, at the bottom of the plot, is relatively insignificant. The mean over the study period was only 3 Watts m-2. While the plot and the mean values are study site specific, the relative magnitudes of the local heat flux terms are more generally representative. On average, the heat balance of this coastal lagoon involves a gain by insolation balanced by losses due to latent heat fluxes, outgoing longwave radiation, and to a lesser extent sensible heat flux.
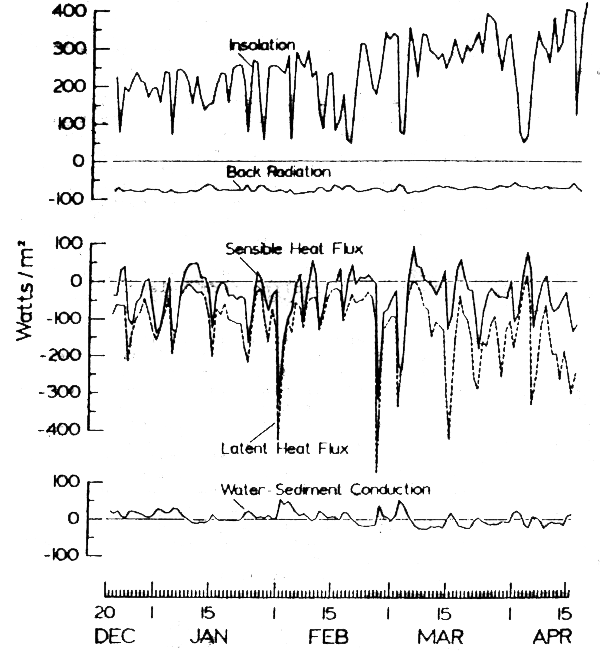
Figure 2.4 Local heat fluxes calculated for the Indian River Lagoon, Florida, December 1981 to April 1982.
Advective heat fluxes are computed from the product of the water temperature T, density p, specific heat cp, and current speed u:
Qa = cp T(y, z) u(y, z) dA, (2.20)
where u is the current component normal to the y-z cross-section, extending from shore to shore. In practice, vertical and perhaps lateral temperature gradients (and thus density gradients) may be significant, and the temperature structure of the lagoon must be known and monitored in time. More importantly, both lateral and vertical current shear in the longitudinal current component must be known. It is rare that one can quantify temporal variability in both temperature and velocity structure. Thus, one either interpolates based upon limited available measurements, approximates, calculates this term as a residual, or ignores it altogether.
A common problem in heat budget studies involves the use of weather data collected some distance from the study site. In the coastal zone, it is common for significant spatial gradients to exist--usually oriented across the coast, rather than parallel to it. Cross-shelf gradients in air temperature, wind speed and perhaps cloud cover are most pronounced. During summer months, the diurnal cycle of air temperature can be significantly greater over a land surface than over a water surface. The resulting variations in density produce a pressure gradient which drives the familiar land and sea breezes. Furthermore, stronger surface heating will increase convective activity and thus cloud cover over a land surface. Conversely, during winter months, cloud cover affecting the heat budget of a coastal lagoon may be greater than that recorded at an inland weather station, because of the heat and moisture put into the atmosphere over the continental shelf. Thus, observations at an inland weather station may be unrepresentative of conditions at the coast to which the lagoon is responding. This matter has been discussed further by Smith (1985).
Comparison of simultaneous measurements of over-land wind speed, S1, and over-water wind speeds, Sw, by Hsu (1981) has resulted in empirical expressions for estimating over-water conditions from routine weather station data. For over-land wind speeds greater than 1 m s-1, the expression
Sw = 1.17 + 1.63 S1 (2.21)
is recommended. This subject has been considered in somewhat greater detail by Richards, et al. (1965) who have incorporated effects of stratification and fetch, 7in addition to wind speed itself.
The circulation in lagoons has been shown to be dependent on the geometry of the lagoon, the geometry of the passes, the wind field, the amplitude of the tide, and, to a lesser extent, on the freshwater inflow. The overall influence of the tide- and wind-driven variations in shelf sea level on the lagoon circulation depends on pass geometry, and some lagoons may be relatively insensitive to external influences due to narrow and shallow passes. Wind forcing, on the other hand, will be important in nearly all lagoons, especially large and narrow lagoons with their long axes oriented with the wind. The magnitude of the currents are proportional to wind speeds, while water level fluctuations are proportional to wind speed squared and inversely proportional to depth. Overall salinity variations are dependent on tidal exchanges and freshwater influx, while overall temperature variations depend primarily on solar input and evaporative heat loss.