Transpiration component
(Kcb ETo)
Evaporation component (Ke
ETo)
Calculating ETc
Like Chapter 6, this chapter also deals with the calculation of crop evapotranspiration (ETc) under standard conditions where no limitations are placed on crop growth or evapotranspiration. This chapter presents the procedure for predicting the effects of specific wetting events on the value for the crop coefficient Kc. The solution consists of splitting Kc into two separate coefficients, one for crop transpiration, i.e., the basal crop coefficient (Kcb), and one for soil evaporation (Ke):
ETc = (Kcb + Ke) ETo (69)
The dual crop coefficient approach is more complicated and more computationally intensive than the single crop coefficient approach (Kc) of Chapter 6. The procedure is conducted on a daily basis and is intended for applications using computers. It is recommended that the approach be followed when improved estimates for Kc are needed, for example to schedule irrigations for individual fields on a daily basis.
The calculation procedure for crop evapotranspiration, ETc, consists of:
1. identifying the lengths of crop growth stages, and 'selecting the corresponding Kcb coefficients;2. adjusting the selected Kcb coefficients for climatic conditions during the stage;
3. constructing the basal crop coefficient curve (allowing one to determine Kcb values for any period during the growing period);
4. determining daily Ke values for surface evaporation; and
5. calculating ETc as the product of ETo and (Kcb + Ke).
Basal crop coefficient (Kcb)
Determination of daily Kcb values
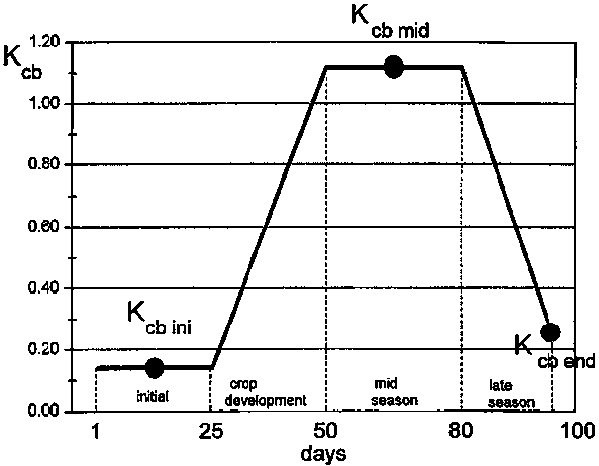
The basal crop coefficient (Kcb) is defined as the ratio of the crop evapotranspiration over the reference evapotranspiration (ETc/ETo) when the soil surface is dry but transpiration is occurring at a potential rate, i.e., water is not limiting transpiration (Figure 22). Therefore, 'Kcb ETo' represents primarily the transpiration component of ETc. The Kcb ETo does include a residual diffusive evaporation component supplied by soil water below the dry surface and by soil water from beneath dense vegetation.
As the Kc values of Chapter 6 include averaged effects of evaporation from the soil surface, the Kcb values lie below the Kc values as illustrated in Figure 26 and a separate table for Kcb is required. Recommended values for Kcb are listed in Table 17 for the same crops listed in Table 12. As with Table 12, the values for Kcb in the table represent Kcb for a sub-humid climate and with moderate wind speed. For specific adjustment in climates where RHmin differs from 45% or where the wind speed is larger or smaller than 2 m/s, the Kcb mid and Kcb end values larger than 0.45 must be adjusted using the following equation:
(70)
where
Kcb (Tab) the value for Kcb mid or Kcb end (if ³ 0.45) taken from Table 17,u2 the mean value for daily wind speed at 2 m height over grass during the mid or late season growth stage [m s-1] for 1 m s-1 £ u2 £ 6 m s-1,
RHmin the mean value for daily minimum relative humidity during the mid- or late season growth stage [%] for 20% £ RHmin £ 80%,
h the mean plant height during the mid or late season stage [m] (from Table 12) for 20% £ RHmin £ 80%.
For a full discussion on the impact of the climatic correction, and the numerical determination of Kcb mid and Kcb end, the user is referred to the discussions on Kc mid and Kc end in Chapter 6.
Table 18 summarizes the general guidelines that were used in deriving Kcb values from the Kc values listed in Table 17. Where local research results are available, values for Kcb from Table 17 can be modified to reflect effects of local conditions, cultural practices or crop varieties on Kcb. However, local values for Kcb should not be expected to deviate by more than 0.2 from the values in Table 17. A greater deviation should signal the need to investigate or evaluate the local research technique, equipment and cultural practices. Where local Kcb values are used, no adjustment for climate using Equation 70 is necessary.
EXAMPLE 29. Selection and adjustment of basal crop coefficients, Kcb
|
Select Kcb ini, Kcb mid and Kcb end for the dry bean crop of Box 15. |
|
Kcb ini, Kcb mid and Kcb end can be selected directly from Table 17 for dry beans as 0.15, 1.10 and 0.25. When adjusted for climate using Eq. 70: Kcb ini = 0.15 Height for beans was taken from Table 12 as 0.4 m. |
|
The corresponding Kcb curve is shown in Figure 37. |
TABLE 17. Basal crop coefficients, Kc, for non stressed, well-managed crops in subhumid climates (RHmin » 45%, u2 » 2 m/s) for use with the FAO Penman-Monteith ETo.
|
Crop |
|
|
| |
|
a. Small Vegetables |
0.15 |
0.95 |
0.85 | |
|
Broccoli |
|
0.95 |
0.85 | |
|
Brussel Sprouts |
|
0.95 |
0.85 | |
|
Cabbage |
|
0.95 |
0.85 | |
|
Carrots |
|
0.95 |
0.85 | |
|
Cauliflower |
|
0.95 |
0.85 | |
|
Celery |
|
0.95 |
0.90 | |
|
Garlic |
|
0.90 |
0.60 | |
|
Lettuce |
|
0.90 |
0.90 | |
|
Onions |
|
|
| |
|
|
- dry |
|
0.95 |
0.65 |
|
|
- green |
|
0.90 |
0.90 |
|
|
- seed |
|
1.05 |
0.70 |
|
Spinach |
|
0.90 |
0.85 | |
|
Radishes |
|
0.85 |
0.75 | |
|
b. Vegetables - Solanum Family (Solanaceae) |
0.15 |
1.10 |
0.70 | |
|
Egg Plant |
|
1.00 |
0.80 | |
|
Sweet Peppers (bell) |
|
1.002 |
0.80 | |
|
Tomato |
|
1.102 |
0.60-0.80 | |
|
c. Vegetables - Cucumber Family (Cucurbitaceae) |
0.15 |
0.95 |
0.70 | |
|
Cantaloupe |
|
0.75 |
0.50 | |
|
Cucumber |
|
|
| |
|
|
- Fresh Market |
|
0.952 |
0.70 |
|
|
- Machine harvest |
|
0.95 |
0.80 |
|
Pumpkin, Winter Squash |
|
0.95 |
0.70 | |
|
Squash, Zucchini |
|
0.90 |
0.70 | |
|
Sweet Melons |
|
1.00 |
0.70 | |
|
Watermelon |
|
0.95 |
0.70 | |
|
d. Roots and Tubers |
0.15 |
1.00 |
0.85 | |
|
Beets, table |
|
0.95 |
0.85 | |
|
Cassava |
|
|
| |
|
|
- year 1 |
|
0.703 |
0.20 |
|
|
- year 2 |
|
1.00 |
0.45 |
|
Parsnip |
|
0.95 |
0.85 | |
|
Potato |
|
1.10 |
0.654 | |
|
Sweet Potato |
|
1.10 |
0.55 | |
|
Turnip (and Rutabaga) |
|
1.00 |
0.85 | |
|
Sugar Beet |
|
1.15 |
0.505 | |
|
e. Lugumes (Leguminosae) |
0.15 |
1.10 |
0.50 | |
|
Beans, green |
|
1.002 |
0.80 | |
|
Beans, dry and Pulses |
|
1.102 |
0.25 | |
|
Chick pea |
|
0.95 |
0.25 | |
|
Fababean (broad bean) |
|
|
| |
|
|
- Fresh |
|
1.102 |
1.05 |
|
|
- Dry/Seed |
|
1.102 |
0.20 |
|
Grabanzo |
|
1.05 |
0.25 | |
|
Green Gram and Cowpeas |
|
1.00 |
0.55-0.256 | |
|
Groundnut (Peanut) |
|
1.10 |
0.50 | |
|
Lentil |
|
1.05 |
0.20 | |
|
Peas |
|
|
| |
|
|
- Fresh |
|
1.102 |
1.05 |
|
|
- Dry/Seed |
|
1.10 |
0.20 |
|
Soybeans |
|
1.10 |
0.30 | |
|
f. Perennial Vegetables (with winter dormancy and initially bare or mulched soil) | ||||
|
Artichokes |
0.15 |
0.95 |
0.90 | |
|
Asparagus |
0.15 |
0.907 |
0.20 | |
|
Mint |
0.40 |
1.10 |
1.05 | |
|
Strawberries |
0.30 |
0.80 |
0.70 | |
|
g. Fibre Crops |
0.15 |
|
| |
|
Cotton |
|
1.10-1.15 |
0.50-0.40 | |
|
Flax |
|
1.05 |
0.20 | |
|
Sisal 8 |
|
0.4-0.7 |
0.4-0.7 | |
|
h. Oil Crops |
0.15 |
1.10 |
0.25 | |
|
Castorbean (Ricinus) |
|
1.10 |
0.45 | |
|
Rapeseed, Canola |
|
0.95-1.109 |
0.25 | |
|
Safflower |
|
0.95-1.109 |
0.20 | |
|
Sesame |
|
1.05 |
0.20 | |
|
Sunflower |
|
0.95-1.109 |
0.25 | |
|
i. Cereals |
0.15 |
1.10 |
0.25 | |
|
Barley |
|
1.10 |
0.15 | |
|
Oats |
|
1.10 |
0.15 | |
|
Spring Wheat |
|
1.10 |
0.15-0.310 | |
|
Winter Wheat |
0.15-0.511 |
1.10 |
0.15-0.310 | |
|
Maize |
|
|
| |
|
|
- Field (grain) (field corn) |
0.15 |
1.15 |
0.50,0.1512 |
|
|
- Sweet (sweet corn) |
|
1.10 |
1.0013 |
|
Millet |
|
0.95 |
0.20 | |
|
Sorghum |
|
|
| |
|
|
- grain |
|
0.95-1.05 |
0.35 |
|
|
- sweet |
|
1.15 |
1.00 |
|
Rice |
1.00 |
1.15 |
0.70-0.45 | |
|
j. Forages | ||||
|
Alfalfa Hay |
|
|
| |
|
|
- individual cutting periods |
0.3014 |
1.1514 |
1.1014 |
|
|
- for seed |
0.30 |
0.45 |
0.45 |
|
Bermuda hay |
|
|
| |
|
|
- averaged cutting effects |
0.50 |
0.9515 |
0.80 |
|
|
- Spring crop for seed |
0.15 |
0.85 |
0.60 |
|
Clover hay, Berseem - individual cutting periods |
0.3014 |
1.1014 |
1.0514 | |
|
Rye Grass hay - averaged cutting effects |
0.85 |
1.0015 |
0.95 | |
|
Sudan Grass hay (annual) - individual cutting periods |
0.3014 |
1.1014 |
1.0514 | |
|
Grazing Pasture |
|
|
| |
|
|
- Rotated Grazing |
0.30 |
0.80-1.00 |
0.80 |
|
|
- Extensive Grazing |
0.30 |
0.70 |
0.70 |
|
Turf grass |
|
|
| |
|
|
- cool season 16 |
0.85 |
0.90 |
0.90 |
|
|
- warm season 16 |
0.75 |
0.80 |
0.80 |
|
k. Sugar cane |
0.15 |
1.20 |
0.70 | |
|
l. Tropical Fruits and Trees | ||||
|
Banana |
|
|
| |
|
|
- 1st year |
0.15 |
1.05 |
0.90 |
|
|
- 2nd year |
0.60 |
1.10 |
1.05 |
|
Cacao |
0.90 |
1.00 |
1.00 | |
|
Coffee |
|
|
| |
|
|
- bare ground cover |
0.80 |
0.90 |
0.90 |
|
|
- with weeds |
1.00 |
1.05 |
1.05 |
|
Date Palms |
0.80 |
0.85 |
0.85 | |
|
Palm Trees |
0.85 |
0.90 |
0.90 | |
|
Pineapple 17 (multiyear crop) |
|
|
| |
|
|
- bare soil |
0.15 |
0.25 |
0.25 |
|
|
- with grass cover |
0.30 |
0.45 |
0.45 |
|
Rubber Trees |
0.85 |
0.90 |
0.90 | |
|
Tea |
|
|
| |
|
|
- nonshaded |
0.90 |
0.95 |
0.90 |
|
|
- shaded 18 |
1.00 |
1.10 |
1.05 |
|
m. Grapes and Berries | ||||
|
Berries (bushes) |
0.20 |
1.00 |
0.40 | |
|
Grapes |
|
|
| |
|
|
- Table or Raisin |
0.15 |
0.80 |
0.40 |
|
|
- Wine |
0.15 |
0.65 |
0.40 |
|
Hops |
0.15 |
1.00 |
0.80 | |
|
n. Fruit Trees | ||||
|
Almonds, no ground cover |
0.20 |
0.85 |
0.6019 | |
|
Apples, Cherries, Pears 20 |
|
|
| |
|
|
- no ground cover, killing frost |
0.35 |
0.90 |
0.6519 |
|
|
- no ground cover, no frosts |
0.50 |
0.90 |
0.7019 |
|
|
- active ground cover, killing frost |
0.45 |
1.15 |
0.9019 |
|
|
- active ground cover, no frosts |
0.75 |
1.15 |
0.8019 |
|
Apricots, Peaches, Stone Fruit 20, 21 |
|
|
| |
|
|
- no ground cover, killing frost |
0.35 |
0.85 |
0.6019 |
|
|
- no ground cover, no frosts |
0.45 |
0.85 |
0.6019 |
|
|
- active ground cover, killing frost |
0.45 |
1.10 |
0.8519 |
|
|
- active ground cover, no frosts |
0.75 |
1.10 |
0.8019 |
|
Avocado, no ground cover |
0.50 |
0.80 |
0.70 | |
|
Citrus, no ground cover 22 |
|
|
| |
|
|
70% canopy |
0.65 |
0.60 |
0.65 |
|
|
50% canopy |
0.60 |
0.55 |
0.60 |
|
|
20% canopy |
0.45 |
0.40 |
0.50 |
|
Citrus, with active ground cover or weeds 23 |
|
|
| |
|
|
70% canopy |
0.75 |
0.70 |
0,75 |
|
|
50% canopy |
0.75 |
0.75 |
0.75 |
|
|
20% canopy |
0.80 |
0.80 |
0.85 |
|
Conifer Trees 24 |
0.95 |
0.95 |
0.95 | |
|
Kiwi |
0.20 |
1.00 |
1.00 | |
|
Olives (40 to 60% ground coverage by canopy)25 |
0.55 |
0.65 |
0.65 | |
|
Pistachios, no ground cover |
0.20 |
1.05 |
0.40 | |
|
Walnut Orchard 20 |
0.40 |
1.05 |
0.6019 | |
1 These are values for Kcb representing conditions having a dry soil surface. These values are intended for use with the dual Kcb ini + Ke approach, only. Values for maximum crop height, h, are given in Table 1 2 for adjusting Kcb for climate.2 Beans, Peas, Legumes, Tomatoes, Peppers and Cucumbers are sometimes grown on stalks reaching 1.5 to 2 meters in height. In such cases, increased Kcb values need to be taken. For green beans, peppers and cucumbers, 1.10 can be taken, and for tomatoes, dry beans and peas, 1.15. Under these conditions h should be increased also.
3 The misdseason values for cassava assume nonstressed conditions during or following the rainy season. The Kcb end values account for domancy during the dry season.
4 The Kcb end value for potatoes is about 0.35 for long season potatoes with vine kill.
5 This Kcb end value is for no irrigation during the last month of the growing season. The Kcb end value for sugar beets is higher, up to 0.9, when irrigation or significant rain occurs during the last month of the growing season.
6 The first Kcb end is for harvested fresh. The second value is for harvested dry.
7 The Kcb for asparagus usually remains at Kcb ini during harvest of the spears, due to sparse ground cover. The Kcb mid value is for following regrowth of vegetation following termination of harvest of spears.
8 Kcb for sisal depends on the planting density and water management (e.g., intentional moisture stress).
9 The lower values are for rainfed crops having less dense plant populations.
10 The higher value is for hand-harvested crops.
11 The two Kcb ini values for winter wheat are for less than 10% ground cover and for during the dormant, winter period, if the vegetation fully covers the ground, but conditions are nonfrozen.
12 The first Kcb end value is for harvest at high grain moisture. The second Kcb end value is for harvest after complete field drying of the grain (to about 18% moisture, wet mass basis).
13 If harvested fresh for human consumption. Use Kcb end for field maize if the sweet maize is allowed to mature and dry in the field.
14 These Kcb coefficients for hay crops represent immediately following cutting; at full cover; and immediately before cutting, respectively. The growing season is described as a series of individual cutting periods.
15 This Kcb mid coefficient for bermuda and ryegrass hay crops is an overall average Kcb mid coefficient that averages Kcb for both before and following cuttings. It is applied to the period following the first development period until the beginning of the last late season period of the growing season.
16 Cool season grass varieties include dense stands of bluegrass, ryegrass, and fescue.. Warm season varieties include bermuda grass and St. Augustine grass. The 0.90 values for cool season grass represent a 0.06 to 0.08 m mowing height under general turf conditions. Where careful water management is practiced and rapid growth is not required, Kcb's for turf can be reduced by 0.10.
17 The pineapple plant has very low transpiration because it closes its stomates during the day and opens them during the night. Therefore, the majority of ETc from pineapple is evaporation from the soil.
18 Includes the water requirements of the shade trees.
19 These Kcb end values represent Kcb prior to leaf drop. After leaf drop, Kcb end » 0.15 for bare, dry soil or dead ground cover and Kcb end » 0.45 to 0.75 for actively growing ground cover (consult Chapter 11).
20 Refer to Eq. 94, 97 or 98 and footnotes 22 and 23 for estimating Kcb for immature stands.
21 Stone fruit category applies to peaches, apricots, pears, plums and pecans.
22 These Kcb values can be calculated from Eq. 98 for Kc min = 0.15 and Kcb full = 0.70, 0.65 and 0.70 for the initial, mid season and end of season periods, and fc eff = fc where fc = fraction of ground covered by tree canopy (e.g., the sun is presumed to be directly overhead). The midseason value is lower than initial and ending values due to the effects of stomatal closure during periods of peak ET. For humid and subhumid climates where there is less stomatal control by citrus, values for Kcb ini, Kcb mid, and Kcb end can be increased by 0.1 - 0.2, following Rogers et al. (1983).
23 These Kcb values can be calculated as Kcb = fc Kcb ngc + (1 - fc) Kcb cover where Kcb ngc is the Kcb of citrus with no active ground cover (calculated as in footnote 22), Kcb cover is the Kcb for the active ground cover (0.90), and fc is defined in footnote 22. Alternatively, Kcb for citrus with active ground cover can be estimated directly from Eq. 98 by setting Kc min = Kcb cover. For humid and subhumid climates where there is less stomatal control by citrus, values for Kcb ini, Kcb mid, and Kcb end can be increased by 0.1 - 0.2, following Rogers et al. (1983). For non-active or only moderately active ground cover (active indicates green and growing ground cover with LAI > about 2 to 3), Kcb should be weighted between Kcb for no ground cover and Kcb for active ground cover, with the weighting based on the "greeness" and approximate leaf area of the ground cover.
24 Conifers exhibit substantial stomatal control due to reduced aerodynamic resistance. The Kcb can easily reduce below the values presented, which represent well-watered conditions for large forests.
25 These coefficients represent about 40 to 60% ground cover. Refer to Eq. 98, example 43, and footnotes 22 and 23 for estimating Kcb for immature stands.
Primary sources: Kcb ini: Doorenbos and Kassam (1979); Kcb mid and Kcb end: Doorenbos and Pruitt (1977); Pruitt (1986); Wright (1981, 1982), Snyder et al. (1989)
TABLE 18. General guidelines to derive Kcb from the Kc values listed in Table 12
|
Growth stage |
Ground condition, irrigation and cultural practices |
Kcb |
further adjustment |
|
|
Initial |
Annual crop - (nearly) bare soil surface. |
0.15 |
|
|
|
Perennial crop - (nearly) bare soil surface |
0.15-0.20 |
- |
||
|
Grasses, brush and trees - killing frost |
0.30 - 0.40 |
- |
||
|
Perennial crop - some ground cover or leaf cover |
|
|
||
|
|
- infrequently irrigated (olives, palm trees, fruit trees,...) |
Kc ini (Tab.12) - 0.1 |
- |
|
|
|
- frequently irrigated (garden-type vegetables,...) |
Kc ini (Tab.12) - 0.2 |
- |
|
|
Mid- season |
Ground cover more than 80% |
Kc mid (Tab.12) - 0.05 |
Climate (Eq. 70) |
|
|
Ground cover less than 80% (vegetables) |
Kc mid (Tab.12) - 0.10 |
Climate (Eq. 70) |
||
|
At end of season |
infrequently irrigated or wetted during late season |
~ Kc end - 0.05 |
- |
|
|
frequently irrigated or wetted during late season |
Kc end - 0.1 |
Climate (Eq. 70) |
||
Climate: adjustment for climate using Eq. 70 where Kcb > 0.45
As outlined in Chapter 6, only three point values are required to describe and to construct the crop coefficient curve. After dividing the growing period into the four general growth stages and selecting and adjusting the Kcb values corresponding to the initial (Kcb ini), mid-season (Kcb mid) and end of the late season stages (Kcb end), the crop coefficient curve can be drawn (Figure 37) and the Kcb coefficients can be derived (Example 30).
EXAMPLE 30. Determination of daily values for Kcb
|
Calculate the basal crop coefficient for the dry beans (Example 29, Figure 37) at the middle of each of the four growth stages. |
|
Initial stage (Lini = 25 days), at day 12 of the growing period: Kcb = Kcb ini = 0.15 Crop development stage (Ldev = 25 days), at day (25 + 25/2 =) 37 of the growing period, using Eq. 66: Kcb = 0.15 + [(37 - 25)/25] (1.14 - 0.15) = 0.63 Mid-season stage (Lmid = 30 days), at day (25 + 25 + 30/2 =) 65 of the growing period: Kcb = Kcb mid = 1.14 Late season stage (Llate = 20 days), at day (25 + 25 + 30 + 20/2 =) 90 of the growing period, Eq. 66: Kcb = 1.14 + [(90 - (25 + 25 + 30))/20] (0.25 - 1.14) = 0.70 |
|
The basal crop coefficients, Kcb, at days 12, 37, 65 and 90 of the growing period are 0.15, 0.63, 1.14 and 0.70 respectively. |
FIGURE 37. Constructed basal crop coefficient (Kcb) curve for a dry bean crop (Example 29) using growth stage lengths of 25, 25, 30 and 20 days
Calculation procedure
Upper limit Kc max
Soil evaporation reduction coefficient (Kr)
Exposed and wetted soil fraction (few)
Daily calculation of Ke
The soil evaporation coefficient, Ke, describes the evaporation component of ETc. Where the topsoil is wet, following rain or irrigation, Ke is maximal. Where the soil surface is dry, Ke is small and even zero when no water remains near the soil surface for evaporation.
Where the soil is wet, evaporation from the soil occurs at the maximum rate. However, the crop coefficient (Kc = Kcb + Ke) can never exceed a maximum value, Kc max. This value is determined by the energy available for evapotranspiration at the soil surface (Kcb + Ke £ Kc max) or Ke £ (Kc max - Kcb).
When the topsoil dries out, less water is available for evaporation and a reduction in evaporation begins to occur in proportion to the amount of water remaining in the surface soil layer, or:
Ke = Kr (Kc max - Kcb) £ few Kc max (71)
where
Ke soil evaporation coefficient,Kcb basal crop coefficient,
Kc max maximum value of Kc following rain or irrigation,
Kr dimensionless evaporation reduction coefficient dependent on the cumulative depth of water depleted (evaporated) from the topsoil,
few fraction of the soil that is both exposed and wetted, i.e., the fraction of soil surface from which most evaporation occurs.
In computer programming terminology, Equation 71 is expressed as Ke = min (Kr (Kc max - Kcb), few Kc max).
Following rain or irrigation Kr is 1, and evaporation is only determined by the energy available for evaporation. As the soil surface dries, Kr becomes less than one and evaporation is reduced. Kr becomes zero when no water is left for evaporation in the upper soil layer.
Evaporation occurs predominantly from the exposed soil fraction. Hence, evaporation is restricted at any moment by the energy available at the exposed soil fraction, i.e., Ke cannot exceed few Kc max, where few is the fraction of soil from which most evaporation occurs, i.e., the fraction of the soil not covered by vegetation and that is wetted by irrigation or precipitation.
The calculation procedure consists in determining:
· the upper limit Kc max;
· the soil evaporation reduction coefficient Kr; and
· the exposed and wetted soil fraction few
The estimation of Kr requires a daily water balance computation for the surface soil layer.
Kc max represents an upper limit on the evaporation and transpiration from any cropped surface and is imposed to reflect the natural constraints placed on available energy represented by the energy balance difference Rn - G - H (Equation 1). Kc max ranges from about 1.05 to 1.30 when using the grass reference ETo:
(72)
where
h mean maximum plant height during the period of calculation (initial, development, mid-season, or late-season) [m],Kcb basal crop coefficient,
max ( ) maximum value of the parameters in braces {} that are separated by the comma.
Equation 72 ensures that Kc max is always greater or equal to the sum Kcb + 0.05. This requirement suggests that wet soil will always increase the value for Kcb by 0.05 following complete wetting of the soil surface, even during periods of full ground cover. A value of 1.2 instead of 1 is used for Kc max in Equation 72 because of the effect of increased aerodynamic roughness of surrounding crops during development, mid-season and late season growth stages which can increase the turbulent transfer of vapour from the exposed soil surface. The "1.2" coefficient also reflects the impact of the reduced albedo of wet soil and the contribution of heat stored in dry soil prior to the wetting event. All of these factors can contribute to increased evaporation relative to the reference.
The "1.2" coefficient in Equation 72 represents effects of wetting intervals that are greater than 3 or 4 days. If irrigation or precipitation events are more frequent, for example daily or each two days, then the soil has less opportunity to absorb heat between wettings, and the "1.2" coefficient in Equation 72 can be reduced to about 1.1. The time step to compute Kc max may vary from daily to monthly.
Soil evaporation from the exposed soil can be assumed to take place in two stages: an energy limiting stage, and a falling rate stage. When the soil surface is wet, Kr is 1. When the water content in the upper soil becomes limiting, Kr decreases and becomes zero when the total amount of water that can be evaporated from the topsoil is depleted.
Maximum amount of water that can be evaporated
In the simple evaporation procedure, it is assumed that the water content of me evaporating layer of the soil is at field capacity, q FC shortly following a major wetting event and that the soil can dry to a soil water content level that is halfway between oven dry (no water left) and wilting point, q WP. The amount of water that can be depleted by evaporation during a complete drying cycle can hence be estimated as:
TEW = 1000 (q FC - 0.5 q WP) Ze (73)
where
TEW total evaporable water = maximum depth of water that can be evaporated from the soil when the topsoil has been initially completely wetted [mm],q FC soil water content at field capacity [m3 m-3],
q WP soil water content at wilting point [m3 m-3],
Ze depth of the surface soil layer that is subject to drying by way of evaporation [0.10-0.15m].
Where unknown, a value for Ze, the effective depth of the soil evaporation layer, of 0.10-0.15 m is recommended. Typical values for q FC, q WP and TEW are given in Table 19.
TABLE 19. Typical soil water characteristics for different soil types
|
Soil type (USA Soil Texture Classification) |
Soil water characteristics |
Evaporation parameters |
|||
|
q FC |
q WP |
(q FC - q WP) |
Amount of water that can be depleted by evaporation |
||
|
|
|
|
stage 1 REW |
stages 1 and 2 TEW* (Ze = 0.10m) |
|
|
|
m3/m3 |
m3/m3 |
m3/m3 |
mm |
mm |
|
Sand |
0.07 - 0.17 |
0.02 - 0.07 |
0.05 - 0.11 |
2 - 7 |
6 - 12 |
|
Loamy sand |
0.11 - 0.19 |
0.03 - 0.10 |
0.06 - 0.12 |
4 - 8 |
9 - 14 |
|
Sandy loam |
0.18 - 0.28 |
0.06 - 0.16 |
0.11 - 0.15 |
6 - 10 |
15 - 20 |
|
Loam |
0.20 - 0.30 |
0.07 - 0.17 |
0.13 - 0.18 |
8 - 10 |
16 - 22 |
|
Silt loam |
0.22 - 0.36 |
0.09 - 0.21 |
0.13 - 0.19 |
8 - 11 |
18 - 25 |
|
Silt |
0.28 - 0.36 |
0.12 - 0.22 |
0.16 - 0.20 |
8 - 11 |
22 - 26 |
|
Silt clay loam |
0.30 - 0.37 |
0.17 - 0.24 |
0.13 - 0.18 |
8 - 11 |
22 - 27 |
|
Silty clay |
0-30 - 0.42 |
0.17 - 0.29 |
0.13 - 0.19 |
8 - 12 |
22 - 28 |
|
Clay |
0.32 - 0.40 |
0.20 - 0.24 |
0.12 - 0.20 |
8 - 12 |
22 - 29 |
*TEW = (q FC - 0.5 q WP) Ze
FIGURE 38. Soil evaporation reduction coefficient, Kr

Stage 1: energy limiting stage
At the start of a drying cycle, following heavy rain or irrigation, the soil water content in the topsoil is at field capacity and the amount of water depleted by evaporation, De, is zero. During stage 1 of the drying process, the soil surface remains wet and it is assumed that evaporation from soil exposed to the atmosphere will occur at the maximum rate limited only by energy availability at the soil surface. This stage holds until the cumulative depth of evaporation, De, is such that the hydraulic properties of the upper soil become limiting and water cannot be transported to the soil surface at a rate that can supply the potential demand. During stage 1 drying, Kr = 1.
The cumulative depth of evaporation, De, at the end of stage 1 drying is REW (Readily evaporable water, which is the maximum depth of water that can be evaporated from the topsoil layer without restriction during stage 1). The depth normally ranges from 5 to 12 mm and is generally highest for medium and fine textured soils. Typical values for REW are given in Table 19.
Stage 2: falling rate stage
The second stage (where the evaporation rate is reducing) is termed the 'falling rate stage' evaporation and starts when De exceeds REW. At this point, the soil surface is visibly dry, and the evaporation from the exposed soil decreases in proportion to the amount of water remaining in the surface soil layer:
(74)
where
Kr dimensionless evaporation reduction coefficient dependent on the soil water depletion (cumulative depth of evaporation) from the topsoil layer (Kr = 1 when De, i-1 £ REW),De, i-1 cumulative depth of evaporation (depletion) from the soil surface layer at the end of day i-1 (the previous day) [mm],
TEW maximum cumulative depth of evaporation (depletion) from the soil surface layer when Kr = 0 (TEW = total evaporable water) [mm],
REW cumulative depth of evaporation (depletion) at the end of stage 1 (REW = readily evaporable water) [mm].
EXAMPLE 31. Determination of the evapotranspiration from a bare soil
|
Determine the evapotranspiration from a bare loamy soil surface (Kcb » 0.15) for ten successive days following a heavy rain. The reference evapotranspiration during the drying period is ETo = 4.5 mm/day, and the climate is subhumid with light wind. | |||||||
|
From Table 19 |
For Loam: TEW » 20 mm and REW » 9 mm | ||||||
|
For rain on bare soil |
few = 1 | ||||||
|
From Eq. 72 |
Kc max = 1.20 | ||||||
|
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
|
Day |
De start mm |
Stage |
Kr |
Ke |
Ke ETo mm/day |
De end mm |
ETc mm/day |
|
1 |
0.00 |
1 |
1 |
1.05 |
4.73 |
4.73 |
5.4 |
|
2 |
4.73 |
1 |
1 |
1.05 |
4.73 |
9.45 |
5.4 |
|
3 |
9.45 |
2 |
(20 - 9.45)/(20 - 9) = 0.96 |
1.01 |
4.53 |
13.98 |
5.2 |
|
4 |
13.98 |
2 |
(20 - 13.98)/(20 - 9) = 0.55 |
0.57 |
2.59 |
16.57 |
3.3 |
|
5 |
16.57 |
2 |
(20 - 16.57)/(20 - 9) = 0.31 |
0.33 |
1.47 |
18.04 |
2.1 |
|
6 |
18.04 |
2 |
(20 - 18.04)/(20 - 9) = 0.18 |
0.19 |
0.84 |
18.88 |
1.5 |
|
7 |
18.88 |
2 |
(20 - 18.88/(20 - 9) = 0.10 |
0.11 |
0.48 |
19.36 |
1.2 |
|
8 |
19.36 |
2 |
(20 - 19.36)/(20 - 9) = 0.06 |
0.06 |
0.27 |
19.64 |
0.9 |
|
9 |
19.64 |
2 |
(20 - 19.64)/(20 - 9) = 0.03 |
0.03 |
0.16 |
19.79 |
0.8 |
|
10 |
19.79 |
2 |
(20 - 19.79)/(20 - 9) = 0.02 |
0.02 |
0.09 |
19.88 |
0.8 |
|
(1) |
Day number. | ||||||
|
(2) |
Depletion at beginning of the day (= depletion at end of previous day). | ||||||
|
(3) |
Soil evaporation stage (stage 2 starts if De > REW = 9 mm). | ||||||
|
(4) |
Kr (Kr = 1 for stage 1. Use Eq. 74 for stage 2). | ||||||
|
(5) |
From Eq. 21: Ke = Kr (Kc max - Kcb) = Kr (1.20-0.15) = 1.05 Kr £ 1.20. | ||||||
|
(6) |
Evaporation component: Ke ETo = Ke (4.5 mm/day). | ||||||
|
(7) |
Depletion at end of day = (2) - (6). | ||||||
|
(8) |
ETc = (Kcb + Ke) ETo = (0.15 + Ke) ETo = (0.15 + Ke) 4.5 mm/day, where Kcb ETo = (0.15 ETo) » 0.7 mm/day is basal, "diffusive" evaporation from the soil, possibly from beneath the Ze depth (~ 0.10 to 0.15 m). Since the soil in this situation is bare, one could set the Kcb equal to zero so that maximum Ke becomes Ke = Kc max = 1.20. Then all of the evaporation would be deducted from the surface soil layer. | ||||||
|
The example demonstrates that the estimation of Kr requires a daily water balance calculation. This is further developed in the section on the daily calculation of Ke. | |||||||
few: calculation procedure
In crops with incomplete ground cover, evaporation from the soil often does not occur uniformly over the entire surface, but is greater between plants where exposure to sunlight occurs and where more air ventilation is able to transport vapour from the soil surface to above the canopy. This is especially true where only part of the soil surface is wetted by irrigation.
It is recognized that both the location and the fraction of the soil surface exposed to sunlight change to some degree with the time of day and depending on row orientation. The procedure presented here predicts a general averaged fraction of the soil surface from which the majority of evaporation occurs. Diffusive evaporation from the soil beneath the crop canopy is assumed to be largely included in the basal Kcb coefficient.
Where the complete soil surface is wetted, as by precipitation or sprinkler, then the fraction of soil surface from which most evaporation occurs, few, is essentially defined as (1 - fc), where fc is the average fraction of soil surface covered by vegetation and (1 - fc) is the approximate fraction of soil surface that is exposed. However, for irrigation systems where only a fraction of the ground surface is wetted, few must be limited to fw, the fraction of the soil surface wetted by irrigation (Figure 39). Therefore, few is calculated as:
few = min(1 - fc, fw) (75)
where
1 - fc average exposed soil fraction not covered (or shaded) by vegetation [0.01 - 1],
fw average fraction of soil surface wetted by irrigation or precipitation [0.01 - 1].
The 'min( )' function selects the lowest value of the '1 - fc' and 'fw' values. Figure 39 illustrates the relation of few to (1 - fc) and fw.
The limitation imposed by Equation 75 assumes that the fraction of soil wetted by irrigation occurs within the fraction of soil exposed to sunlight and ventilation. This is generally the case, except perhaps with drip irrigation (Figure 39).
In the case of drip irrigation, where the majority of soil wetted by irrigation may be beneath the canopy and may therefore be shaded, more complex models of the soil surface and wetting patterns may be required to accurately estimate total evaporation from the soil. In this case, the value for fw may need to be reduced to about one-half to one-third of that given in Table 20 to account for the effects of shading of emitters by the plant canopy on the evaporation rate from wetted soil (Example 34). A general approach could be to multiply fw by [1-(2/3)fc] for drip irrigation.
fw: fraction of soil surface wetted by irrigation or precipitation
Table 20 presents typical values for fw. Where a mixture of irrigation and precipitation occur within the same drying period or on the same day, the value for fw should be based on a weighted average of the fw for precipitation (fw = 1) and the fw for the irrigation system. The weighting should be approximately proportional to the infiltration depths from each water source.
TABLE 20. Common values of fraction fw of soil surface wetted by irrigation or precipitation
|
Wetting event |
fw |
|
Precipitation |
1.0 |
|
Sprinkler irrigation |
1.0 |
|
Basin irrigation |
1.0 |
|
Border irrigation |
1.0 |
|
Furrow irrigation (every furrow), narrow bed |
0.6...1.0 |
|
Furrow irrigation (every furrow), wide bed |
0.4... 0.6 |
|
Furrow irrigation (alternated furrows) |
0.3...0.5 |
|
Trickle irrigation |
0.3... 0.4 |
Alternatively, on each day of the application, the following rules can be applied to determine fw for that and subsequent days in a more simplified manner:
· Surface is wetted by irrigation and rain: fw is the fw for the irrigation system;
· Surface is wetted by irrigation: fw is the fw for the irrigation system;
· Surface is wetted by significant rain (i.e., > 3 to 4 mm) with no irrigation: fw = 1;
· Where there is neither irrigation nor significant precipitation: fw is the fw of the previous day.
1 - fc: exposed soil fraction
The fraction of the soil surface that is covered by vegetation is termed fc. Therefore, (1 - fc) represents the fraction of the soil that is exposed to sunlight and air ventilation and which serves as the site for the majority of evaporation from wet soil. The value for fc is limited to < 0.99. The user should assume appropriate values for the various growth stages. Typical values for fc and (1 - fc) are given in Table 21.
TABLE 21. Common values of fractions covered by vegetation (fc) and exposed to sunlight (1 - fc)
|
Crop growth stage |
fc |
1 - fc |
|
Initial stage |
0.0 - 0.1 |
1.0 - 0.9 |
|
Crop development stage |
0.1 - 0.8 |
0.9 - 0.2 |
|
Mid-season stage |
0.8 - 1.0 |
0.2 - 0.0 |
|
Late season stage |
0.8 - 0.2 |
0.2 - 0.8 |
Where fc is not measured, fc can be estimated using the relationship:
(76)
where
fc the effective fraction of soil surface covered by vegetation [0 - 0.99],
Kcb the value for the basal crop coefficient for the particular day or period,
Kc min the minimum Kc for dry bare soil with no ground cover [» 0.15 - 0.20],
Kc max the maximum Kc immediately following wetting (Equation 72),
h mean plant height [m].
This equation should be used with caution and validated from field observations. Kc min is the minimum crop coefficient for dry bare soil when transpiration and evaporation from the soil are near baseline (diffusive) levels. Kc min » 0.15 - 0.20 is recommended. The value of Kc min is an integral part of all Kcb coefficients. Kc min ordinarily has the same value as the Kcb ini used for annual crops under nearly bare soil conditions (0.15 - 0.20).
Equation 76 assumes that the value for Kcb is largely affected by the fraction of soil surface covered by vegetation. This is a good assumption for most vegetation and conditions. The '1+0.5h' exponent in the equation represents the effect of plant height on shading the soil surface and in increasing the value for Kcb given a specific value for fc. The user should limit the difference Kcb - Kc min to ³ 0.01 for numerical stability. The value for fc will change daily as Kcb changes. Therefore, the above equation is applied daily.
Application of Equation 76 predicts that fc decreases during the late season period in proportion to Kcb, even though the ground may remain covered with senescing vegetation. This prediction helps to account for the local transport of sensible heat from senescing leaves to the soil surface below.
EXAMPLE 32. Calculation of the crop coefficient (Kcb + Ke) under sprinkler irrigation
|
A field of cotton has just been sprinkler irrigated. The Kcb for the specific day (during the development period) has been computed using Table 17 and Eq. 70 and then interpolated from the Kcb curve as 0.9. The ETo = 7 mm/day, u2 = 3 m/s and RHmin = 20%. Estimate the crop coefficient (Kcb + Ke). |
|
Assuming h = 1 m, from Eq. 72, Kc max for this arid climate is:
From Eq. 76, where Kc min = 0.15: fc = [(Kcb - Kc min)/(Kc max - Kc min)] (1 + 0.5h) = [(0.9-0.15)/(1.3-0.15)] (1 +0.5(1)) = 0.53. As the field was sprinkler irrigated, fw = 1.0 and from Eq. 75: few = min(1 - fc, fw) = min(1- 0.53, 1.0) = 0.47. Assuming that the irrigation was sufficient to fill the evaporating layer to field capacity, so that Kr = 1, evaporation would be in stage 1. From Eq. 71: Ke = 1.00 (1.30 - 0.90) = 0.40 The value is compared against the upper limit few Kc max to ensure that it is less than the upper limit: few Kc max = 0.47 (1.30) = 0.61, which is greater than the value for Ke. Therefore, the value for Ke can be used with no limitation. |
|
The total Kc for the field, assuming no moisture stress due to a dry soil profile, is Kc = Kcb + Ke = 0.9 + 0.40 = 1.30. This value is large because of the very wet soil surface, the relatively tall rough crop as compared to the grass reference, and the arid climate (u2 = 3 m/s and RHmin = 20%). In this situation, Kc happens to equal Kc max, as the field has just been wetted by sprinkler irrigation. |
EXAMPLE 33. Calculation of the crop coefficient (Kcb + Ke) under furrow irrigation
|
The cotton field in the previous example (Ex. 32) has been irrigated by furrow irrigation of alternate rows rather than by sprinkler, and the fraction of the field surface wetted by the irrigation is 0.3. |
|
The few in this case is calculated from Eq. 75 as: few = min(1 - fc, fw) = min(1 - 0.53, 0.3) = 0.3. Assuming that the irrigation was sufficient to fill the few portion of the evaporating layer to field capacity, so that Kr = 1, evaporation would be in stage 1. From Eq. 71: Ke = 1.00 (1.30 - 0.9) = 0.40 The value is compared to the upper limit few Kc max which is 0.30 (1.30) = 0.39. Because 0.40 > 0.39, Ke from the few surface area is constrained to 0.39. |
|
The total Kc for the furrow irrigated field, assuming no moisture stress due to dry soil, is Kc = Kcb + Ke = 0.9 + 0.39 = 1.29. This value is essentially the same as for the previous example (Ex. 32) because the procedure assumes that the soil between alternate rows is the portion that is wetted by the irrigation, so that the majority of the field surface has either vegetation cover or wet soil. |
EXAMPLE 34. Calculation of the crop coefficient (Kcb + Ke) under drip irrigation
|
The cotton field in the previous example (Ex. 32) has been irrigated by drip irrigation, where the emitters are placed beneath the cotton canopy. The fraction of the field surface wetted by the irrigation is 0.3. |
|
The few in this case is calculated from Eq. 75 as few = min(1 - fc, fw). Because the emitters are beneath the canopy so that less energy is available for evaporation, the value for fw is reduced by multiplying by 1 - (2/3)fc, so that: few = min[(1 - fc),(1 - 0.67 fc) fw)] = min[(1-0.53), (1 - 0.67(0.53))(0.3)] = 0.19 Assuming that the irrigation was sufficient to fill the fw portion of the evaporating layer to field capacity, so that Kr = 1, evaporation would be in stage 1. From Eq. 71: Ke = 1.00 (1.30-0.90) = 0.40. The value is compared to the upper limit few Kc max = 0.19 (1.30) = 0.25. Because 0.25 < 0.40, Ke from the fw fraction of the surface area is constrained by the available energy. Therefore Ke = 0.25. |
|
The total Kc for the drip irrigated field, assuming no moisture stress due to dry soil, is: Kc = Kcb + Ke = 0.9 + 0.25 = 1.15. This Kc value is less than that for sprinkler and furrow irrigation (Examples 32 and 33). |
Daily water balance
The estimation of Ke in the calculation procedure requires a daily water balance computation for the surface soil layer for the calculation of the cumulative evaporation or depletion from the wet condition. The daily soil water balance equation for the exposed and wetted soil fraction few is (Figure 40):
FIGURE 40. Water balance of the topsoil layer
(77)
where
De, i-1 cumulative depth of evaporation following complete wetting from the exposed and wetted fraction of the topsoil at the end of day i-1 [mm],De, i cumulative depth of evaporation (depletion) following complete wetting at the end of day i [mm],
Pi precipitation on day i [mm],
ROi precipitation run off from the soil surface on day i [mm],
Ii irrigation depth on day i that infiltrates the soil [mm],
Ei evaporation on day i (i.e., Ei = Ke ETo) [mm],
Tew, i depth of transpiration from the exposed and wetted fraction of the soil surface layer on day i [mm],
DPe,i deep percolation loss from the topsoil layer on day i if soil water content exceeds field capacity [mm], fw fraction of soil surface wetted by irrigation [0.01 - 1],
few exposed and wetted soil fraction [0.01 - 1].
Limits on De, i
By assuming that the topsoil is at field capacity following heavy rain or irrigation, the minimum value for the depletion De, i is zero. As the soil surface dries, De, i increases and in absence of any wetting event will steadily reach its maximum value TEW (Equation 73). At that moment no water is left for evaporation in the upper soil layer, Kr becomes zero, and the value for De, i remains at TEW until the topsoil is wetted once again. The limits imposed on De, i are consequently:
0 £ De, i £ TEW (78)
Initial depletion
To initiate the water balance for the evaporating layer, the user can assume that the topsoil is near field capacity following a heavy rain or irrigation, i.e., De, i-1 = 0. Where a long period of time has elapsed since the last wetting, the user can assume that all evaporable water has been depleted from the evaporation layer at the beginning of calculations, i.e., De, i-1 = TEW = 1000 (q FC - 0.5 q WP) Ze.
Precipitation and runoff
Pi is equivalent to daily precipitation. Daily precipitation in amounts less than about 0.2 ETo is normally entirely evaporated and can usually be ignored in the Ke and water balance calculations. The amount of rainfall lost by runoff depends on: the intensity of rainfall; the slope of land; the soil type, its hydraulic conditions and antecedent moisture content; and the land use and cover. For general situations, ROi can be assumed to be zero or can be accounted for by considering only a certain percentage of Pi. This is especially true for the water balance of the topsoil layer, since almost all precipitation events that would have intensities or depths large enough to cause runoff would probably replenish the water content of the topsoil layer to field capacity. Therefore, the impact of the runoff component can be ignored. Light precipitation events will generally have little or no runoff.
Irrigation
Ii is generally expressed as a depth of water that is equivalent to the mean infiltrated irrigation depth distributed over the entire field. Therefore, the value Ii/fw is used to describe the actual concentration of the irrigation volume over the fraction of the soil that is wetted (Figure 31).
Evaporation
Evaporation beneath the vegetation canopy is assumed to be included in Kcb and is therefore not explicitly quantified. The computed evaporation is fully concentrated in the exposed, wetted topsoil. The evaporation Ei is given by Ke ETo. The Ei/few provides for the actual concentration of the evaporation over the fraction of the soil that is both exposed and wetted.
Transpiration
Except for shallow rooted crops (i.e., where the depth of the maximum rooting zone is < 0.5 to 0.6 m), the amount of transpiration from the evaporating soil layer is small and can be ignored (i.e., Tew = 0). In addition, for row crops, most of the water extracted by the roots may be extracted from beneath the vegetation canopy. Therefore, Tew from the few fraction of soil surface can be assumed to be zero in these cases.
EXAMPLE 35. Estimation of crop evapotranspiration with the dual crop coefficient approach
|
Estimate the crop evapotranspiration, ETc, for ten successive days. It is assumed that: - the soil is a sandy loam soil, characterized by q FC = 0.23 m3 m-3 and q WP = 0.10 m3 m-3, - the depth of the surface soil layer that is subject to drying by way of evaporation, Ze, is 0.1 m, - during the period, the height of the vegetation h = 0.30 m, the average wind speed u2 = 1.6 m s-1, and RHmin = 35%, - the Kcb on day 1 is 0.30 and increases to 0.40 by day 10, - the exposed soil fraction, (1 - fc), decreases from 0.92 on day 1 to 0.86 on day 10, - all evaporable water has been depleted from the evaporation layer at the beginning of calculations (De, i-1 = TEW), - irrigation occurs at the beginning of day 1 (I = 40 mm), and the fraction of soil surface wetted by irrigation, fw = 0.8, - a rain of 6 mm occurred at the beginning of day 6. | |
|
From Tab. 19 |
REW » 8 mm |
|
From Eq. 73 |
TEW = 1000 (0.23-0.5(0.10)) 0.1 = 18 mm |
|
From Eq. 72 |
Kc max = 1.2 + [0.04(1.6 - 2) - 0.004(35 - 45)] (0.3/3)0.3 = 1.21 |
|
All evaporable water has been depleted at the beginning of calculations, De, i-1 = TEW = 18 mm
| |
|
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
(10) |
(11) |
(12) |
(13) |
(14) |
(15) |
(16) |
(17) |
|
Day |
ETo |
P-RO |
I/fw |
1 - fc |
fw |
few |
Kcb |
De, i start |
Kr |
Ke |
E/few |
DPe |
De, i end |
E |
Kc |
ETc |
|
|
mm/d |
mm |
mm |
|
|
|
|
mm |
|
|
mm |
mm |
mm |
mm/d |
|
mm/d |
|
start |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
18 |
- |
- |
- |
|
1 |
4.5 |
0 |
50 |
0.92 |
0.8 |
0.80 |
0.30 |
0 |
1.00 |
0.91 |
5.1 |
32 |
5 |
4.1 |
1.21 |
5.5 |
|
2 |
5.0 |
0 |
0 |
0.91 |
0.8 |
0.80 |
0.31 |
5 |
1.00 |
0.90 |
5.6 |
0 |
11 |
4.5 |
1.21 |
6.1 |
|
3 |
3.9 |
0 |
0 |
0.91 |
0.8 |
0.80 |
0.32 |
11 |
0.70 |
0.62 |
3.0 |
0 |
14 |
2.8 |
1.04 |
4.0 |
|
4 |
4.2 |
0 |
0 |
0.90 |
0.8 |
0.80 |
0.33 |
14 |
0.40 |
0.35 |
1.8 |
0 |
16 |
1.5 |
0.70 |
2.9 |
|
5 |
4.8 |
0 |
0 |
0.89 |
0.8 |
0.80 |
0.34 |
16 |
0.20 |
0.18 |
1.1 |
0 |
17 |
0.8 |
0.52 |
2.5 |
|
6 |
2.7 |
6 |
0 |
0.89 |
1 |
0.89 |
0.36 |
11 |
0.75 |
0.64 |
2.0 |
0 |
13 |
1.7 |
1.00 |
2.7 |
|
7 |
5.8 |
0 |
0 |
0.88 |
1 |
0.88 |
0.37 |
13 |
0.53 |
0.45 |
3.0 |
0 |
16 |
2.6 |
0.82 |
4.7 |
|
8 |
5.1 |
0 |
0 |
0.87 |
1 |
0.87 |
0.38 |
16 |
0.20 |
0.17 |
1.0 |
0 |
17 |
0.9 |
0.55 |
2.8 |
|
9 |
4.7 |
0 |
0 |
0.87 |
1 |
0.87 |
0.39 |
17 |
0.09 |
0.08 |
0.4 |
0 |
18 |
0.4 |
0.47 |
2.2 |
|
10 |
5.2 |
0 |
0 |
0.86 |
1 |
0.86 |
0.40 |
18 |
0.05 |
0.04 |
0.2 |
0 |
18 |
0.2 |
0.44 |
2.3 |
(1) Day number.(2) ETo is given. Note that ETo would be forecast values in real time irrigation scheduling but are known values after the occurrence of the day, during an update of the calculations.
(3) (P-RO) are known values after the occurrence of the day, during an update of the calculations.
(4) Net irrigation depth for the part of the soil surface wetted by irrigation.
(5) (1 - fc) is given (interpolated between 0.92 m on day 1 and 0.86 m on day 10).
(6) If significant rain: fw, i = 1.0 (Tab. 20)
If irrigation: fw, i = 0.8 (given),otherwise: fw, i = fw, i-1.
(7) Eq. 75. Fraction of soil surface from which most evaporation occurs.
(8) Kcb is given (interpolated between 0.30 on day 1 and 0.40 on day 10).
(9) De, i start (depletion at start of day)
If precipitation and irrigation occur early in the day then the status of depletion from the soil surface layer (at the start of the day) should be updated:
= Max(De, i-1 - In, i/fwi - (P-RO)i, or 0).where De, i-1 is taken from column 14 of previous day.
If precipitation and irrigation occur late in the day, then column 6 should be set equal to De, i-1 (column 14 of previous day).
(10) If De, i £ REW Kr = 1
If De, i > REW Kr = Eq. 74.
(11) Eq. 71 where Ke = Kr (Kc max - Kcb) £ few Kc max. (e.g., Ke = min (Kr (Kc max - Kcb), few Kc max).
(12) Evaporation from the wetted and exposed fraction of the soil surface = (Ke ETo)/few.
(13) Eq. 79 where DPe ³ 0. (This is deep percolation from the evaporating layer).
(14) De, i (depletion at end of day) is from Eq. 77 where De, i-1 is value in column 14 of previous day.
(15) Mean evaporation expressed as distributed over the entire field surface = Ke ETo.
(16) Kc =Kcb + Ke.
(17) Eq.69.
The daily water balance calculation for the surface layer, even for shallow rooted crops, is not usually sensitive to Tew, as Tew is a minor part of the flux from the Ze depth for the first 3-5 days following a wetting event. Tew can, therefore, generally be ignored. The effects of the reduction of the water content of the evaporating soil layer due to Tew can be accounted for ulteriorly when it is assumed that Tew = 0 by decreasing the value for Ze, for example from 0.15 to 0.12 m or from 0.10 to 0.08 m.
Deep percolation
Following heavy rain or irrigation, the soil water content in the topsoil (Ze layer) might exceed field capacity. However, in this simple procedure it is assumed that the soil water content is at q FC nearly immediately following a complete wetting event, so that the depletion De, i in Equation 77 is zero. Following heavy rain or irrigation, downward drainage (percolation) of water from the topsoil layer is calculated as:
(79)
As long as the soil water content in the evaporation layer is below field capacity (i.e., De, i > 0), the soil will not drain and DPe, i = 0.
Order of calculation
In making calculations for the Kcb + Ke procedure, for example when using a spreadsheet, the calculations should proceed in the following order: Kcb, h, Kc max, fc, fw, few, Kr, Ke, E, DPe, De, I, Kc, and ETc.
The calculation procedure lends itself to application by computer, either in the form of electronic spreadsheets (Example 35) or in the form of structured programming languages. The calculation procedure consists in determining:
a. Reference evaporation, ETo:
Estimate ETo: the procedure is given in Chapter 4.
b. Growth stages:
Determine the locally adjusted lengths of the four growth stages (for general information consult Table 11):
- Initial growth stage: Lini,
- Crop development stage: Ldev,
- Mid-season stage: Lmid,
- Late season stage: Llate.
c. Basal crop coefficient, Kcb:
Calculate basal crop coefficients for each day of the growing period:
- select Kcb ini, Kcb mid and Kcb end from Table 17;
- adjust Kcb mid and Kcb end to the local climatic conditions (Equation 70);
- determine the daily Kcb values· initial growth stage: Kcb = Kcb ini,
· crop development stage: from Kcb ini to Kcb mid (Equation 66),
· mid-season stage: Kcb = Kcb mid,
· late season stage: from Kcb mid to Kcb end (Equation 66).
d. Evaporation coefficient, Ke:
Calculate the maximum value of Kc, i.e., the upper limit Kc max (Equation 72), and Determine for each day of the growing period:
- the fraction of soil covered by vegetation, fc (Table 21 or Equation 76),- the fraction of soil surface wetted by irrigation or precipitation, fw (Table 20),
- the fraction of soil surface from which most evaporation occurs, few (Equation 75),
- the cumulative depletion from the evaporating soil layer, De, determined by means of a daily soil water balance of the topsoil (Equation 77),
- the corresponding evaporation reduction coefficient, Kr (Equation 74), and
- the soil evaporation coefficient, Ke (Equation 71).
e. Crop evapotranspiration, ETc:
Calculate ETc = (Kcb + Ke) ETo (Equation 69).
|
BOX 16. Case study of dry bean crop at Kimberly, Idaho, the United States (dual crop coefficient) Results from applying the Kcb + Ke procedure for a snap bean crop harvested as dry seed are shown in the figure below. This example uses the same data set that was used in the case study of Box 15. The measured ETc data were measured using a precision lysimeter system at Kimberly, Idaho. Values for Kcb ini, Kcb mid, and Kcb end were calculated in Example 29 as 0.15, 1.14, and 0.25. The lengths of growth stages were 25, 25, 30, and 20 days. The Kcb values are plotted in Fig. 37. The value for Kc max from Eq. 72 for the mid-season period averaged 1.24, based on u2 = 2.2 m/s and RHmin = 30% for Kimberly. The soil at Kimberly was a silt loam texture. Assuming that the depth of the evaporation soil layer, Ze, was 0.1 m, values for TEW = 22 mm and REW = 9 mm, based on Eq. 73 and using soil data from Table 19. The occurrence and magnitudes of individual wetting events are shown in the figure below. Nearly all wetting events were from irrigation. Because the irrigation was by furrow irrigation of alternate rows, the value for fw was set equal to 0.5. Irrigation events occurred at about midday or during early afternoon. The agreement between the estimated values for daily Kcb + Ke (thin continuous line) and actual 24-hour measurements (symbols) is relatively good. Measured and predicted Kcb + Ke was higher following wetting by rainfall or irrigation, as expected. The two wet soil evaporation 'spikes' occurring during the late initial period and early development period (between days 160 and 180) were less than Kc max, because this evaporation was from wetting by furrow irrigation where fw = 0.5. The value for few was constrained to fw by Eq. 75 during these two events, because during this period, fw < 1 - fc. Therefore, less than all of the 'potential energy' was converted into evaporation due to the limitation on maximum evaporation per unit surface area that was imposed by Eq. 71.
Measured (symbols) and predicted (thin line) daily coefficients (Kcb + Ke) and the basal crop curve (thick line) for a dry bean crop at Kimberly, Idaho. P in the figure denotes a precipitation event and I denotes an irrigation (data from Wright, 1990). |