5.1 Introduction
5.2 Characteristics of sampling
5.3 Estimation of population values
5.4 Construction of error graphs
5.5 Measurement errors in school sizes
5.6 Precision increasing methods
5.7 Rotation system of acoustic surveys
5.8 The accuracy problem of calibration coefficient
5.9 Variance of products
In this chapter we discuss, in summary, various parts of the sampling process as they are encountered in the design and execution of acoustic surveys. The methods of obtaining estimates of the population values and of the sampling errors from the sample values are also discussed.
For the choice of the proper type of sampling for acoustic surveys one should take into account the factors which affect the precision of the calculated estimates. Our experience with acoustic surveys has proved that the resulting sample distribution is assymetrical and that the precision of fish biomass estimates based on line sampling is a function of the following two groups of factors:
1. Properties of the surveyed population, i.e., its density and its degree of clumping.12. Characteristics of the sampling, i.e., the sampling method employed and the size of line sample.
1 Generally speaking, acoustic data follow the negative binomial distribution. The distribution is defined by two parameters, m and k, where m is the mean and k is the positive exponent. The biological meaning of this last parameter has been considerably discussed: k is called “a measure of aggregation”, a “measure of degree of clumping”, a “measure of relative levels of over dispersion”. (see also Appendix 1).
5.2.1 Methods of line transect sampling
It is interesting to note that the sampling method which is considered appropriate for acoustic surveys is the method of line sample. Further, along the sample tracks, covered by the research vessel the required items of information are obtained from the underwater survey objects by transmitting sound waves and observing the returned echoes (see chapter 1). Furthermore, in order to obtain quantitative estimates of the target fish population covered by an acoustic system consisting of an echo-sounder with T.V.G. (Time Varied Gain) and echo-integrator, the value of the proportionality coefficient C is estimated through calibration experiments. Specifically, the estimated average biomass (m.t) per n.mi2 is equal to the average integrator ouput (mm) per n.mi multiplied by the proportionality coefficient C.
From a sampling point of view, line sampling is an alternative to point sampling and is used in agricultural and forestry surveys for the estimation of the geographical pattern of the target population. In fisheries acoustic surveys the methods of line transect sampling used can be grouped under the following two headings.
a) Regular line transect samplinga) Regular line transect sampling
b) Random line transect sampling
The method of regular line transect sampling is the most common method used for obtaining acoustic samples. It is mainly used in practice for its convenience. Another advantage of the method is that it is easy to check whether survey operations have been conducted according to the instructions. In this method of sampling the track pattern crosses isotherms or isobaths and follows regular tracks (zigzag) or parallel transects.2 The method can be based on a stratified or non-stratified sample. The transect pattern and the spacing of the sample transects is determined by the survey objectives and by taking into account, time available and cost involved. Transect sampling with a spacing interval of 10 n.mi (or even 20 n.mi) could be considered as sufficiently large to cover the required domains of study adequately.
2 The direction of transects can be optimized if the distribution of the survey biomass is approximately parallel to the cost. In such a case the location of the tracks should be across counter lines of biomass abundance, making, at the same time, some degree of offshore/inshore stratification possible (post-stratification).Sample observations are usually obtained continuously (day, night) on a 1 n.mi basis which is considered as the elementary sampling distance unit (ESDU) of the acoustic survey.
The line transect sample is selected at the design process of the acoustic survey and is usually kept fixed over time, i.e., replications of the survey are made on the pre-selected line sample (see also section 5.7). One of the main reasons for using a “fixed sample” in acoustic surveys is our interest in calculating estimates of changes that are taking place over time.
Below we present track patterns of regular line transect sampling used for acoustic surveys (Figs. 5.2.1a, b, c, d). Specifically, Figures 5.2.1a, b portray transect patterns of parallel grids. Figures 5.2.1c, d portray transect patterns of zigzag sampling.
b) Random line transect sampling
It has been argued that, in the method of regular line transect sampling there are two statistical complications with the statistical data; firstly, observations are not randomly distributed over the survey area but are made along specific lines, and, secondly, successive observations are serially correlated.3
3 Because serial correlation results in an underestimation of the overall standard deviation per unit to correct for this (Hogg and Craig, 1968) the standard deviation is calculatedIn the method of random line transect sampling a probabilistic approach is used for the selection of the sample tracks. Specifically, the survey area is first divided into a number of space domains (= strata) and a number of randomly located transects is selected within each established stratum. In the case of large-scale acoustic surveys the method is a time consuming one and creates a number of practical problems concerning the proper location of the randomly selected tracks, specifically during night-time survey operations.
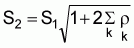
whereS1: uncorrected standard deviation
rk: serial correlation coefficient of lag k
S2: corrected standard deviation
Regular line transect sampling
Method of parallel grids
Figure 5.2.1a

Figure 5.2.1b
Regular line transect sampling
Method of zigzag
The surveyed area is to be closed under a rectangle. Zigzag is drawn from one side to the opposite side and then from the opposite side to the same and so on to cover the whole of the surveyed area.
Figure 5.2.1c: Zigzag method
Figure 5.2.1d: Zigzag method with replicated tracks
5.3.1 Regular line transect sampling
5.3.2 Random line transect sampling
In this section we discuss the process of estimating population values and their sample variances by using the respective estimating formulae. To reduce the work of estimating sample variances we have used simple estimation methods. Both the reliability and cost of such estimates may be less than those of very precise estimates of sampling errors, but if the accuracy is sufficient for the estimates to be useful and if there is a saving in cost, such estimates may be worthwhile. It should be noted that, in most cases the loss of precision is small.
a) Method of collapsed strata
In the case of regular line transect sampling, i.e., equally spaced tracks covering the survey area or zigzag method, the type of sampling used can be considered as “one-dimensional systematic sampling”. In this kind of sampling, a short-cut method for estimating sample variances is the method of collapsed strata.4
4 See Bazigos, G.P. (1976), The design of fisheries statistical surveys; inland waters. Populations in non-random order, sampling methods for echo surveys, double sampling. FAO Fish.Tech.Pap., (133) Suppl. 1:46 p.The method achieves greater homogeneity by carrying the stratification to the point that only one sample track is allocated per stratum. Specifically, a stratum is formed by considering the surface area up to
 n.miles on either side of a given sample track (post-stratification, c is the
spacing interval between sample tracks). Since only one sample track is selected
from a stratum it is not possible to make rigorous estimates of the sample variance
of the estimated totals; the sample variance is estimated by pairing the strata
to form collapsed strata. The number of strata should be at least 20, to allow
a minimum of 10 degrees of freedom in the estimated variance from the pairs.
n.miles on either side of a given sample track (post-stratification, c is the
spacing interval between sample tracks). Since only one sample track is selected
from a stratum it is not possible to make rigorous estimates of the sample variance
of the estimated totals; the sample variance is estimated by pairing the strata
to form collapsed strata. The number of strata should be at least 20, to allow
a minimum of 10 degrees of freedom in the estimated variance from the pairs.
According to the rules of the method, the population totals for the two members of a pair should not differ greatly and the allocation into pairs should be made before seeing the sample results. In acoustic surveys, for estimating sample variances we made collapsed strata by pairing adjacent strata,
|
|
|
Formation of collapsed strata |
||||||
|
1. |
Strata(i) |
1 |
2 |
3 |
4 |
|
19 |
20 |
|
2. |
Collapsed strata (1) |
1 |
2 |
|
10 |
|||
Suffix i: stands for a given stratum (i = 1, 2....., I)Estimated total biomass (m. tons):Suffix 1: stands for a given collapsed stratum (1 = 1, 2....., L, L =
)
ni: total number of ESDU’s in the ith sample track, within the ith stratum (j = 1, 2,....ni ESDU’s, 1 ESDU = 1 n.mi).
yi: total integrator readings (mm) of the ith sample track
Ai: total area of the ith stratum
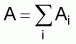
: estimated calibration coefficient
Estimated sample variance:: estimated total biomass5 in the ith stratum, where
(1)
:
: estimated total biomass (target population), (2)
5 Another expression of the above formula (1) is
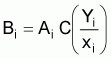
wherexi = length of the ith sample track in n.mi
The estimated sampling error of: estimated variance of total biomass in the 1 collapsed stratum,
(3)
: estimated variance of the estimated total fish biomass (target population) (4)
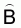 is given
by
is given
by
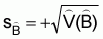 , (5)
, (5)
The estimated coefficient of variation of B is
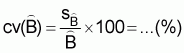 , (6)
, (6)
Exercise 1 at the end of the sub-section illustrates the theory presented above.
b) Yates’ method of mean square successive differences
In the case of one-dimensional systematic samples, i.e., equally spaced transects covering the survey area, no fully valid estimates of the sampling error can be made because the sampling units (= transects) are not located at random within defined areas. Approximate estimates can be made in various ways. Strata may be taken to contain pairs of successive units, so that the error variance is estimated from the members of the pairs. Each difference contributes one degree of freedom.
Notation:
n = total number of sample transects (i = 1, 2,....., n)Estimated sample variance:mi: number of ESDU’s in the ith transect (j = 1, 2,....., m.), tracks are approximately equal in size, 1 ESDU = 1 n.mi
yi: total integrator readings (mm) of the ith transect
n-1: total number of first differences, (yi+1 - yi)
A: total survey area (n.mi2)
The estimated variance of 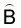 (Yates’
method) can be calculated as follows:
(Yates’
method) can be calculated as follows:
1. The error variance per transect is given byExercise 2 at the end of the sub-section illustrates the theory presented above.where
,(7)
d = yi+1-yiSince there are n sample transects the sample variance of
(8)
2. The estimated variance of
is
(9)
where
a is the total sample area (note; 1 n.mi sailing distance represents an area of 1 n.mi2, after having applied the. calibration coefficient).
Exercise 1 (Method of collapsed strata)
The next table provides hypothetical sample observations (echo-integrator readings, mm). The line transect sample of the survey is based on the method of parallel grids. The sample tracks have been designed perpendicular to the coastline. The sample tracks are equal in size, 10 n.mi (n = ni = 10 ESDU’s). The tabulated data provide the following items of information:
a) Log number of sample transect (i)By using the method of collapsed strata estimate the size of total biomass in the survey area and its absolute and relative sampling errors.b) Total integrator readings (mm) on a sample transect basis (yi).
(Note: the individually formed strata are equal in size Ai = 400 n.mi2. The value of the estimated calibration coefficient is C = 5 m.t/n.mi2 ref. 1 mm/n.mi).
|
Transect log no. |
No. of ESDU’s |
Total integr. reading (mm) |
Formed strata, area (n.mi2) |
Estimated biomass(m.t) |
Estimated sample variance |
|
|
|
col. str. |
|
||||
|
1 |
10 |
420 |
400 |
84,000 |
1 |
924,160 |
|
2 |
10 |
268 |
400 |
53,600 |
||
|
3 |
10 |
133 |
400 |
26,600 |
2 |
43,560 |
|
4 |
10 |
100 |
400 |
20,000 |
||
|
5 |
10 |
342 |
400 |
68,400 |
3 |
2,662,560 |
|
6 |
10 |
600 |
400 |
120,000 |
||
|
7 |
10 |
120 |
400 |
24,000 |
4 |
33,640 |
|
8 |
10 |
149 |
400 |
29,800 |
||
|
9 |
10 |
174 |
400 |
34,800 |
5 |
38,440 |
|
10 |
10 |
205 |
400 |
41,000 |
||
|
11 |
10 |
275 |
400 |
55,000 |
6 |
484,000 |
|
12 |
10 |
165 |
400 |
33,000 |
||
|
13 |
10 |
286 |
400 |
57,200 |
7 |
10,240 |
|
14 |
10 |
270 |
400 |
54,000 |
||
|
15 |
10 |
184 |
400 |
36,800 |
8 |
302,760 |
|
16 |
10 |
97 |
400 |
19,400 |
||
|
17 |
10 |
344 |
400 |
68,800 |
9 |
158,760 |
|
18 |
10 |
281 |
400 |
56,200 |
||
|
19 |
10 |
92 |
400 |
18,400 |
10 |
88,360 |
|
20 |
10 |
139 |
400 |
27,800 |
||
|
Total |
200 |
4,644 |
8,000 |
928,800 |
|
4,746,480 |

2. The estimated total biomass equals

3. The estimated variance of 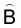 is
is
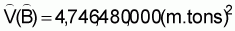
4. The estimated sampling error of 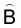 is
is
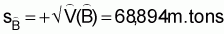
5. The estimated coefficient of variation6 of  is
is

6 It should be noted that in actual large-scale acoustic surveys the estimatedExercise 2 (Method of mean square successive differences)is much higher than the one calculated above (see section 5.4)
By using the tabulated data of Exercise 1, estimate the sampling error of the estimated total biomass by using the method of mean square successive differences.
|
Transect log no. |
No. of ESDU’s |
Total integr. reading (mm) |
d2 = (yi+1-yi)2 |
Remarks |
|
1 |
10 |
420 |
- |
A = 8,000 n.mi2 a = 200 n.mi2 |
|
2 |
10 |
268 |
23,104 |
|
|
3 |
10 |
133 |
18,225 |
|
|
4 |
10 |
100 |
1,089 |
|
|
5 |
10 |
342 |
58,564 |
|
|
6 |
10 |
600 |
66,564 |
|
|
7 |
10 |
120 |
230,400 |
|
|
8 |
10 |
149 |
841 |
|
|
9 |
10 |
174 |
625 |
|
|
10 |
10 |
205 |
961 |
|
|
11 |
10 |
275 |
4,900 |
|
|
12 |
10 |
165 |
12,100 |
|
|
13 |
10 |
286 |
14,641 |
|
|
14 |
10 |
270 |
256 |
|
|
15 |
10 |
184 |
7,396 |
|
|
16 |
10 |
97 |
7,569 |
|
|
17 |
10 |
344 |
61,009 |
|
|
18 |
10 |
281 |
3,969 |
|
|
19 |
10 |
92 |
35,721 |
|
|
20 |
10 |
139 |
2,209 |
|
|
Total |
200 |
4,644 |
550,143 |
|
2. Estimated sample variance:
1. Estimated variance per track
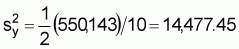
2. Estimated variance of


3. Estimated variance of
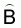
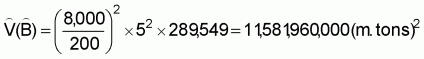
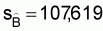
, (see footnote 6).
In the method of random line transect sampling a probabilistic approach is used for the selection of the sample transects. Specifically, the survey area is pre-stratified into area domains using the proper control characteristics for stratification, e.g., depth, bottom type and a number of randomly located tracks are selected within the established strata. In such a case the type of sampling used can be considered as “stratified cluster sampling”. The analogy is made here between transects and clusters with the elements of clusters being equivalent to the ESDU’s along the sample tracks.
Suffix h: stands for a given stratumEstimation of total biomassSuffix i: stands for a given transect in the hth stratum, i = 1, 2,... nh
Suffix j: stands for the jth ESDU in the ith transect, j =1, 2,... mhi
yhi: total integrator readings (mm) in the ith sample transect
Ah: stratum area (n.mi2),
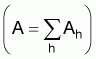
: estimated calibration coefficient
1. A simple estimate of the average integrator readings per ESDU in stratum
h, (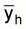 ), can be obtained by calculating
the mean of the cluster (transect) averages (
), can be obtained by calculating
the mean of the cluster (transect) averages (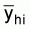 ),
),
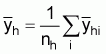 (10)
(10)
where
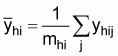 , (11)
, (11)
2. An estimate of the total biomass (m. tons) in stratum h, is given by
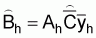 (12)
(12)
3. An estimate of the overall biomass (m, tons) is obtained by adding the strata totals,
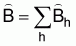 ,(13)
,(13)
Estimated sample variance
1. From the above (12) it is obvious that an estimate of the variance of 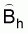 is given by
is given by
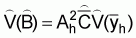 (14)
(14)
where
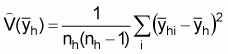 (15)
(15)
(Note: In the above formula (15) the finite population correction (fpc) is ignored - see footnote No. 7)
2. The estimated variance of  is
is
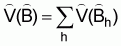 (16)
(16)
The sampling error of 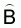 is
is
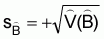 (17)
(17)
The coefficient of variation of 8 is
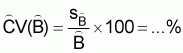 (18)
(18)
Exercise 3 below illustrates the theory presented above.
In large-scale acoustic surveys estimate of the sampling error of the survey total biomass should be calculated on a space/depth domain basis, marginal total space domain basis, marginal total depth domain basis and for the population as a whole. In such a case, other procedures must be followed when sampling errors are required separately for the different parts of the surveyed population.
The simplest and most convenient device to obtain the sampling error of the estimates is to make use of error graphs. For the construction of an error graph the estimated values of the coefficient of variation are plotted against the respective estimates, and a smooth curve is drawn to fit the points, as closely as possible. This curve gives the variance law from which revised estimates of the coefficient of variation can be obtained for any given value of the survey magnitude.
In the error graph below (Fig. 5.4a) the x-axis has been designated to the estimated various values of total biomass (small pelagic schools, off the southern coast of India) and y-axis has been designated to the estimated coefficients of variation of the estimates.
In order to obtain the sampling error (coefficient of variation) of a given point estimate the following procedure should be used:
1. Enter the error graph and locate the total biomass value on the horizontal axis (x-axis).Exercise 3 (Method of stratified cluster sampling)2. Draw a perpendicular to the x-axis at this point and extend the perpendicular to intersect the curve of the error variance.
3. At the intersection, drop a perpendicular to the y-axis. The intersection gives the value of the estimated coefficient of variation of the given value of total biomass.
In an acoustic survey programme (echo-integrator) the survey area was divided into four strata (h = 1, 2, 3, 4) and random sample of three tracks (nh = 3) was selected within each of the established strata. The tabulated data provide details of the obtained sample data. By using the method of random cluster sampling, calculate estimates of the following two magnitudes:
a) total biomass (m. tons); b) sampling error of the estimated biomass,Figure 5.4a Errorgraph(C = 2 m. tons/n.mi2 ref. 1 mm/n.mi).
a. Sample observations
|
Strata |
Sample transects |
||||||
|
(h) |
Area, n.mi2 |
i |
ESDU’s |
Integrator readings mm |
|
|
Remarks |
|
1 |
400 |
1 |
10 |
160 |
16,0 |
4 |
a1= 28 n.mi2 |
|
2 |
10 |
180 |
18.0 |
0 |
|||
|
3 |
8 |
160 |
20.0 |
4 |
|||
|
|
28 |
500 |
|
t1 = 8.0 |
|||
|
2 |
600 |
4 |
12 |
240 |
20.0 |
25 |
a2 = 38 n.mi2
|
|
5 |
14 |
210 |
15.0 |
0 |
|||
|
6 |
12 |
120 |
10.0 |
25 |
|||
|
|
38 |
570 |
|
t2= 50.0 |
|||
|
3 |
300 |
7 |
8 |
240 |
30,0 |
177.7 |
a3 = 22 n.mi2 |
|
8 |
6 |
300 |
50.0 |
44.5 |
|||
|
9 |
8 |
400 |
50.0 |
44.5 |
|||
|
|
22 |
940 |
|
t3= 266.7 |
|||
|
4 |
500 |
10 |
10 |
50 |
5 |
1.8 |
a4 = 32 n.mi2 |
|
11 |
12 |
120 |
10 |
13.5 |
|||
|
12 |
10 |
40 |
4 |
5.4 |
|||
|
|
32 |
210 |
|
t4 = 20.7 |
|||
|
Total |
1,800 |
|
120 |
2,220 |
|
|
|
b. Estimated totals
|
Str. |
Estimated biomass m.t |
Estimated sample variance |
||||
|
h |
|
|
|
|
|
|
|
1 |
14,400 |
0.1667 |
0.9300 |
8.0 |
640,000 |
793,759 |
|
2 |
18,000 |
0.1667 |
0.9367 |
50.0 |
1,440,000 |
11,242,648 |
|
3 |
25,998 |
0.1667 |
0.9267 |
266.7 |
360,000 |
14,832,019 |
|
4 |
6,330 |
0.1667 |
0.9360 |
20.7 |
1,000,000 |
3,229,846 |
|
T |
67,728 |
|
30,098,272 |
|||
1. Estimated total biomass
2. Estimated variance of
,
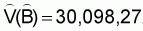
3. Estimated sampling error of
,
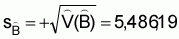
4. Estimated relative sampling error of
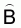
cv(
) = (5,486.19/67728) × 100 = 8.10%) (see footnote 6)
7 If fpc is taken into account, then the above formula (15) is given by
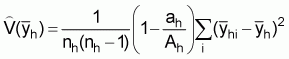
where ah is the area (n.mi2) covered by the sample transects (Note: sailing distance of 1 n.mi represents to an area of 1 n.mi2, after having applied the calibration coefficient).
Any consistent error in echo traces will give rise to bias, and because of that any calculated estimate of school size will be biased too. This problem has been studied in some detail by S. Olsen (1969). It was observed that, small schools tend to be more circulara and bigger ones become more elongatedb with size (axes ratio increases with school size). It was also observed that the expected probability of hitting a school of a certain type is smaller when the school is circular in horizontal extension, and for oblong schools it increases roughly proportionally to the square root of the ratio of the two axes. Volume estimates based on echo recordings are systematically biased;
a) Underestimating the small schools (by a factor)
b) Overestimating the big ones
c) Little or no bias at some intermediate school sizea Cylindrical schools:

where
V(m): volumeb Elliptical schools:
d(m): diameter
h(m): height or thickness of school
p= 3.14
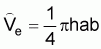
where
, p, h: as a)
a(=B, m): short diameter
b(=L, m): long diameter
It has been discussed that the precision of fish biomass estimates based on the method of line transect sampling is a function, on the one hand, of the properties of the target population and, on the other, of the characteristics of the sampling. A simple precision increasing process for fish biomass estimates has been suggested by Bazigos (see also page 51). It was observed that, in the case of over-dispersed populations, i.e., fish populations located in individualized domains of low and high levels of fish concentrations, the estimated sample variance based on a pre-selected regular line transect sample might be very high. It is a simple matter to get better sample data during the survey operations, by increasing the sample size (reducing the spacing interval between the sample tracks) when the R/V come across high fish concentrations. This, in turn, means that there might be differences between the size of the “pre-selected” sample of the survey on the one hand, and the size of the “actual” sample of the acoustic survey, on the other. For this purpose, allowances should be made at the design process of the survey.
Acoustic surveys should be considered as current surveys rather than as one-time enquiries. By taking into account the dynamic aspect of the fish population a rotation system of surveys should be established at the designing process of an acoustic programme. It is suggested that in the first year of a research programme at least two large-scale acoustic surveys should be conducted, the one at “peak” biomass density and the other at “low” biomass density. Small-scale acoustic surveys could be carried out on a current basis (sub-sampling) in the period between the two extreme densities of the population (peak biomass and low biomass), with the object of determining changes over time in the size of the target fish population.
For the sampling scheme of a current acoustic survey a number of alternatives can be considered.
a) Fixed sample: The same line transect sample is used on each occasion.Accurate estimates on changes of the fish population Can be estimated by re-survey of a fixed line transect sample or a sub-sample of the main sample.b) Independent sample: A new sample is taken each time.
c) Partial replacement: A part of the sample is retained, the remainder being replaced for the next occasion.
d) Surveying only these areas in which high biomass densities were observed at the main survey.
It should be noted that, other things being equal, estimated changes in the size of the target population over time should be reflected in the results of the current catch assessment survey and current stock assessment survey covering the same body of water (a lead-lag relationship between the surveyed magnitudes might be observed).
5.8.1 Estimated precision
It has been discussed that, in order to obtain a quantitative estimate of the target population surveyed with sonar system consisting of an echo-sounder with T.V.G. and echo-integrator, the value of the calibration coefficient C (= proportionality coefficient) must be calculated (estimated) in the echo-integrator equation (see also chapter 1).
 (19)
(19)
where
One of the most reliable methods for estimating the value of proportionality coefficient is direct calibration on live fish. This method was described by Johannesson and Losse (1977)= average integrator deflection (mm) per elementary distance sampling unit
= proportionality coefficient 8
= average biomass density (t/n.mi2).
8 The usual form of the proportionality coefficient is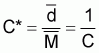
It is the reciprocal of the proportionality coefficient given in equation (19).
The concept of the direct method of calibration on live fish lies in measuring
the value of the integrated echo signal  ,
caused by a known biomass density of fish
,
caused by a known biomass density of fish 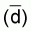 ,
and then determining the mathematical model (= regression line) which determines
the relationship between
,
and then determining the mathematical model (= regression line) which determines
the relationship between 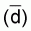 and
and  from the results of several such experiments. According to the above integrator
equation we should obtain a proportional relationship between
from the results of several such experiments. According to the above integrator
equation we should obtain a proportional relationship between 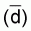 and
and .
.
The overall level of accuracy of the estimated calibration coefficient depends on the extent to which the calibration process takes into account the relative contributions of the independent random errors and avoids or minimizes systematic errors. Implicit in this method of direct calibration is the fundamental assumption that the encaged fish have the same species characteristics and behaviour as their counterparts in the wild. Clearly the understanding of this method requires understanding of the behaviour of fish species of interest. The behaviour of fish and their condition (especially any mortality) must be observed during the experiment, for instance by a diver or underwater camera. The calibration should be carried out after a few hours acclimatizing the fish, first in the keep-net and then in the cage.
Since this type of calibration is invariably performed at shallow depths, variation in fish target strength versus depth and/or depth adaptation time would not be evident in the results. Direct calibration is typically used in mixed-species fisheries investigations.
The concept of calibration experiments on live fish is portrayed in chapter 1.
If a number of replications are performed in a calibration experiment with different densities of fish, the value of the calibration coefficient C* (see footnote on page 70) can be estimated by fitting a linear regression model to the experimental values of the variables d = x (biomass density) on M = y (integrator deflection).
dc = A + C*M (20)
The estimated linear regression equation is
x = a’ + b’ y (20a)
In the above equations the regression parameters stand
b’ = C*: slope of the regression line, equal to the calibration constant value.All values of b’ in the regression equation (20a) will give unbiased estimates, and consequently any value b’ which appears appropriate to the data under analysis may be used.
a’ = A: intercept of the regression line.
The regression coefficient, b’, of x on y is calculated from the unweighted values of x and y
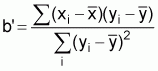 (21)
(21)
where
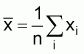 ,
, 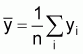
and
n = number of pairs of measurements (xi, yi).The variance of b’ is calculated in the ordinary manner from the regression. Specifically, by using the sample observations the estimated variance of b’ is given by
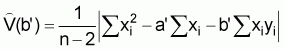 (22)
(22)
The sampling error of b’ is
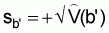
Note: In the method of direct calibration, an estimate of the calibration constant is calculated by using the method of least squares. However, it can happen that the value of the intercept of the regression line is large, and that the regression line does not fit the empirical data properly. This in turn indicates that the assumed physical model of calibration does not correspond to reality. It can happen if the cage is not placed in the centre of the transducer’s beam (the current diverts the cage from its central position, or the cage is not aligned within the transducer’s acoustic axis or if the fish are not uniformly distributed within the volume of the cage, see, J. Burczynski, p. 59-62).
Excercise 1
The tabulated data below provide the empirical observations of calibration experiment on sardines (Sardina pilchardus) conducted within the framework of an acoustic survey programme, (Morocco, 1980). Calculate (estimate) the value of the calibration coefficient and its level of precision.
Calibration experiment on sardinus (Sardina pilchardus), Morocco, 1980
|
Experiment |
Integrator deflection (mm) |
Biomass density (tons) |
Remarks |
|
1 |
19.05 |
5250.00 |
yi: average integrator readings per experiment (mm) |
|
2 |
21.81 |
6707.00 |
|
|
3 |
27.87 |
8164.00 |
|
|
4 |
23.18 |
8742.00 |
|
|
5 |
44.92 |
11421.00 |
xi: known weight of fish (biomass) per experiment (tons) |
|
6 |
0.55 |
89.30 |
|
|
n = 7 |
2.16 |
136.30 |
|
|
|
|
|
|
1. Variance of y: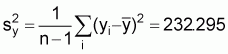
2. Variance of x:
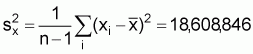
3. Linear regression model:
xc = a’ + b’y,orxc = 319.174 + 274.297yi, (b’ = 274.297)4. Estimated precision of calibration coefficient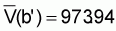
,
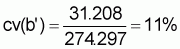
A simple expression was presented in this chapter for the estimation of total biomass,
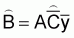 , (23)
, (23)
where
In the above equation (23)= estimated total biomass (m. tons)
= estimated calibration (= proportionality coefficient) (m. tons/n.mi2 ref. 1 mm/n.mi)
= average integrator readings (mm) per n.mi
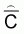 and
and 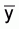 are unbiased estimators which are calculated independently. In such a case a more
profound expression for the estimated sample variance of
are unbiased estimators which are calculated independently. In such a case a more
profound expression for the estimated sample variance of 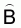 is
is
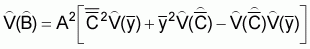 , (24)
, (24)