10.1 Introduction
10.2 Methods of sampling
10.3 Verification of the counts obtained
10.4 Random sampling
Trawling surveys (pelagic, demersal) are carried out concurrently with the main acoustic survey aiming to supply the material needed for the verification of the counts attained at the main acoustic survey, species identification of the survey biomass and the collection of biological information concerning the survey stocks.
A variety of sampling systems have been employed in the past for the collection of the required information. In each individual case a choice is made by assessing the objectives of the overall survey system and resources available, i.e., vessel’s availability, research vessel only, research vessel plus auxiliary trawler.
From a sampling point of view, the trawling sample methods used can be grouped under the following headings:
1. Concurrent systematic sampling (C-SS)In the case of C-SS a systematic sample of fishing stations is selected along the sample tracks of the main acoustic survey. Fishing is usually carried out by the research vessel. For the location of the fishing stations the following criteria are used:
2. Systematic sampling with time lag (L-SS)
3. Random sampling (RS)
a) Pelagic trawling: Sampling (fishing) is conducted when concentration of fish is recorded by the acoustic survey-irregular C-SSIn the case of L-SS, an auxiliary trawler is used for fishing operations. A time lag might be observed between the acoustic survey and trawling survey.b) Demersal trawling: Fishing is conducted either at preselected sampling stations by using supplementary information - regular C-SS, or when changes in the concentration of fish are recorded by the acoustic survey-irregular C-SS.
In the case of random sampling (RS), fishing operations are usually conducted after the completion of the main acoustic survey. Specifically, by using the chart of the relative fish abundance of the main acoustic survey, the survey area is first divided into a number of density domains, here called strata, and a random number of fishing stations is selected within the established strata. In this procedure every possible trawling site in each stratum has an equal chance of being selected and the probability of sampling a particular depth (or ecological niche) within a stratum is proportional to the area represented by that depth (or niche) in the stratum.
It should be noted that, behavioural changes may alter the vertical distribution of fish. Also, intensity of light (day, night) may affect the activity of fish which, in turn, affects the catchability coefficient. Because of that, sampling (fishing) in daytime and night-time is important and the ratio of night to day may be useful in detecting anomalies in catchability or gear selectivity.
If trawling surveys based on C-SS have been used in an acoustic survey programme the trawl data can be used for the validation of the obtained echo-integrator readings. Specifically, simple statistical approaches can be used for this purpose. It is expected that a linear model should be fitted to the matched sample data of the two concurrent surveys (integrator readings, catches). The estimated model describes the existing association between the two variables. A critical evaluation of the findings provides some indication of the validity of the obtained echo-integrator values.
10.4.1 Estimated indices
10.4.2 Estimated abundance
10.4.3 The sample size
10.4.4 The logarithmic transformation and the estimation of the confidence limits (small samples)
If random sampling (demersal trawling) has been used in an acoustic survey programme, the obtained results can be used, among other things, to calculate abundance estimates. In the sections below we describe the methodology used for this purpose.
Random sampling within each stratum provides valid estimates of sampling error (variance) and the catch-per-haul indices (standard) are unbiased in the sense that every (trawlable) habitat has an equal chance to be included in the sample.
Notation:
Suffix h: stands for a given stratumStratum estimates:
Suffix i: stands for a given sample tow
Ah: area of the hth stratum
yhi: sample catch of the ith standard tow
nh: stratum sample size
The standard abundance index is the stratified mean catch per haul for the strata which encompasses the population or stock of interest. The formulae for the stratified mean: sample mean catch per standard tow in the hth stratum
: sample variance in the hth stratum
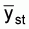 and its variance
V(
and its variance
V(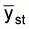 ) are
) are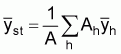 ,
(
,
( )
)
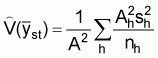 ,
(estimated)
,
(estimated)
and
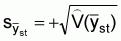
It should be noted that, unadjusted survey indices have a consistent bias in the sense that they reflect only that portion of fish in the path of the trawl which is actually caught. That is, the mean catch per haul is only a relative abundance index and must be adjusted by the average catchability coefficient (q) to represent absolute abundance. The catchability coefficient is the proportion of the fish in the path of the gear that is actually retained by the net. Values of the catchability coefficient which have been used in stock assessment studies are: Southeast Asian waters, q = 0.5, Western Indian Ocean, south of the equator, q = 1.0.
Estimation of standing stock can be calculated by using the sample observations.
Notation:
a: average area swept per standard haulThe estimated absolute abundance in the hth stratum is,
Ah: area of the hth stratum
q: average catchability coefficient: sample mean catch per standard tow in the hth stratum
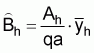
The estimated variance of
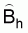 , is
, is
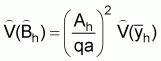
or
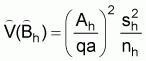
where

The estimated absolute total biomass for the strata which encompasses the population or stock of interest is
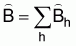
The estimated variance of
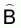 is
is
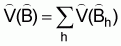
and
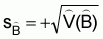
Sample size vs. precision
Some first approxomiations can be worked out of the relation between precision of stratified means and sample size (overall number of hauls). The calculations are based on the general formulae of stratified random sample for estimating required sample size for given precision.
Notation:
N: total number of possible standard hauls in the area represented by strata in the set (N = A/a).where
Nh: total number of possible standard hauls in the hth stratum (Nh = Ah/a).: variance per haul in the hth stratum (an estimate of
is given by
, above).
VO: desired variance of the stratified mean. Specifically
CV((An estimate of): desired coefficient of variation of
e.g., 10%
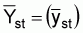 is obtained by using the
results of a pilot survey or the results of a previously conducted
survey)
is obtained by using the
results of a pilot survey or the results of a previously conducted
survey)n: required sample size (overall number of hauls for a given precision (= VO).In the case of proportional allocation the required n for given VO is
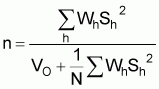
In the case of optimum allocation the required n for given VO is
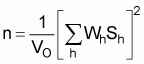 ,
(
,
( , negligible)
, negligible)
Usually, Values of n are calculated (estimated) for the set of species we are interested in and for the given VO values. The estimated maximum n represents the required sample size.
Sample size for normal approximation
The distributions we usually have to deal with in trawling
demersal surveys are usually highly positively skewed and because of cost
considerations our samples are of a size of which the assumption that
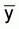 is normally distributed
might be far from the mark.
is normally distributed
might be far from the mark.
A rule of thumb (Cochran) for use in the normal approximation is the sample size should be greater than 25 times the square of the coefficient of skewness G1 (Fisher) of the surveyed population,

where
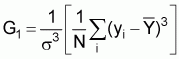
The value of G1 can be estimated by using the results either of a pilot trawling survey or of a previously conducted survey.
Sample size for a given cost
In practice, large-scale trawling surveys are cost-oriented surveys and the overall sample of the survey (= sample stations) is determined by the sample cost function
C = overall cost of the surveyFrom the above cost function the estimate of the overall sample size nc is calculated by
c0 = fixed cost encountered
c1: average travel cost between sample stations
c2: average cost of sampling a given station (duration of an individual tow plus time needed to set and haul up the net).
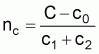
The actual sample size
In the previous three sub-sections we presented the methodology for advanced sample size estimates:
n: overall sample size for a given precisionThe final decision on the actual sample size of the survey should be a striking balance between cost and the objectives of the survey.
n*: overall sample size for normal approximation
nc: overall sample size for a given cost
In sample surveys the normal approximation is used primarily to calculate confidence limits. Generally speaking, when 95% confidence limits are computed for the population mean m by the normal approximation, we make the following statement:

With repeated sampling, we claim that statements of this type will be wrong only 5% of the time. Consequently we might say that the normal approximation is accurate enough if such statements are in fact wrong between 4% to 6% of the time. Some workers may be satisfied with wider limits.
For populations in which the principal deviation from
normality consists of marked positive skewness, the above statement is valid
under the assumption that the sample is large enough so that the distribution of
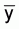 shows some approach to
normality.
shows some approach to
normality.
When the samples are of a size for which the assumption of
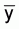 is normally distributed it
is not justified, then any confidence statement using the above described
procedure is wrong. In such a case the logarithmic transformation is usually
employed for the estimation of confidence limits.
is normally distributed it
is not justified, then any confidence statement using the above described
procedure is wrong. In such a case the logarithmic transformation is usually
employed for the estimation of confidence limits.
For a sample of n observations, the mean of the transformed values equals the logarithm of the geometric mean of the actual values.2 For example, if
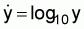
then
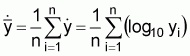
or
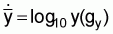 , where
gy is the geometric mean of y.
, where
gy is the geometric mean of y.
2 For the transformation , the following relations have been worked out,Also,a)b)
,
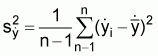
For the calculation of confidence limits for the population mean (m) there are two compromise solutions to the problem:
1. To use the factor derived from the logarithmic transformation and apply this factor to the arithmetical mean of the sample.Example:2. As the geometric mean is always less than the arithmetical mean, the estimated confidence limits will underestimate the true confidence interval of the population mean. A solution to the problem is to adjust the geometric mean before it is used for the calculation of confidence limits of m. The adjusted geometric mean (approximation) is given by,
The catches (kg) per standard tow of a pilot trawling survey are 90, 20, 70, 220, 50. Calculate the confidence interval of the population mean (P = 90% or a = 10%):
Solution:
|
a) n = 5 |
|||
|
|
|||
|
|
Sample mean,
Sample variance per unit,
Clearly
Because there are no zeros in the raw data (sample data) the transformation3 used is
3 If there are zeros in the sample data and |
||
|
|
|||
|
b) The transformed values
|
|||
|
|
|||
|
|
(gy = Antilog
|
||
|
|
|||
|
|
|
(i) Estimated confidence limits: |
|
|
|
|||
|
|
|
|
(i) Using the sample mean: |
|
|
|||
|
|
|
|
The estimated lower (L1) and upper (L2)
confidence limits for a = 10% are, |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 90 × 1.8339 =165.0510 kg |
|
|
|||
|
|
|
(ii) Using the adjusted geometric mean: |
|
|
|
|||
|
|
|
|
= Antilog (1.8283 + 1.15 × 0.1438) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2 = Antilog (1.9937 + 0.2600) = 179.3494
kg |