Appendix 1: Derivation of cost-benefit equations
Appendix 2: Equations for estimating recovery rates
Consider an individual with the utility function u(y). Positive elements of y represent consumption (demand), negative supply, e.g. items like labour.
In a static framework, the individual attempts to solve the problem:
(A.1) Maximize u(y) subject to y0 - p×y,where y0 represents the monetary value of the consumers assets and p is the vector of prices corresponding to y.
Among the necessary conditions for solving (A.1) are the equations:
(A.2) du(y)/dy(j) = l p(j),where l is the individual’s shadow value of assets.
Now, the change in utility caused by a government action dx is:
Which, on the basis of (A.2) may be rewritten as:
Now, considering a change social welfare function, W(u), we find:
Substituting (A.4) into (A.5) yields:
or
Consider a release n(a,a) at time a and let the number of surviving fish be n(a,t) at each subsequent time t. Let the recovery rate and natural mortality of these fish at each subsequent time t be represented by f(a,t) and m(a,t), respectively. Then clearly
Integrating we find:
where, for conformity with available data, it is assumed that the recovery and natural mortality rates are constant during each period and
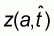represents this
constant.By definition instantaneous recoveries from release a at time t are:
(A-3) y(a,t) = n(a,t)× f(a,t).Integrating (A-3) over one time period,
, say, yields:
