Chapter three A macro model of the agricultural terms of trade and taxation

Contents - Previous - Next

In this Chapter the discussion of the terms of trade of agriculture that began in Chapter 1 will be formalized and extended in order to understand the relation between taxation of agriculture and macroeconomic equilibrium and adjustment.

Influencing the prices of products received by agricultural producers, or the prices paid by agricultural consumers is a widespread practice in developing countries. These interferences, of course, have as a consequence changes in relative prices faced by producers and consumers, and hence changes in demands and supplies for various products. The question is how such policies impinge on macroeconomic balance and growth, and how they influence the pattern of adjustment under internal and external shocks. In this Chapter a simple two sector macro model is outlined and discussed in order to clarify these issues.

Consider a developing economy composed of two sectors agriculture and non-agriculture. The agricultural sector will be assumed to produce with labour and capital, which can include land, machinery, dams, etc., and which can be thought of as fixed in the short and medium run. Agricultural production in the aggregate will be assumed to exhibit diminishing returns to labour

(3.1)

where X_a is aggregate agricultural production (namely agricultural gross domestic product (GDP)), L_a is the amount of the economy's labour employed in agriculture, is a constant which is a function of the agricultural capital stock, and is a positive parameter which is smaller than one.

(3.2)

This latter parameter denotes the labour share in agricultural production.

Production in non-agriculture will be assumed to utilize capital, labour and a non-domestically produced imported intermediate good, with a Cobb-Douglas production function

(3.3)

In (3.3) X_n is the volume of non-agricultural gross production, L_n is labour employed in non-agriculture, M is the quantity of imports, is a constant which is a function of non-agricultural capital, and b , g are positive parameters, denoting the labour and import share in the gross value of non-agricultural production, whose sum is smaller than 1.

(3.4)

Notice that it is assumed that agriculture does not utilize an intermediate good. This is, of course, an approximation as agricultural production in almost all countries utilizes some fertilizer or pesticides. However, the share of purchased inputs in the gross value of agricultural output is usually quite small (in Africa it is smaller than 5 percent), and for analytical convenience it is assumed equal to zero.

The product of the agricultural sector will be assumed to be traceable, while that of non-agriculture as non-traceable. These, again are convenient assumptions, and are meant to capture the stylized fact that the share of traceable products in agriculture appears to be much higher than the share of traceable products produced in non-agriculture.

With the specification of non-agricultural production assumed, imports will only be used as inputs to non-agriculture. This is an alternative to assuming that all imports are "imperfect substitutes" with nonagricultural products. The choice of specification is mostly a matter of convenience, as far as the analytics are concerned, but for the issues dealt with in this paper, it turns out that the "imperfect substitutes" model is not as appropriate.

The key behavioural conditions assumed about the economy are the following. First it is assumed that production in non-agriculture occurs according to profit maximization. In other words non-agricultural producers maximize profits P , where

(3.5)

where p_n is the domestic price of the non-agricultural good, p_m is the domestic price of the imported good, and w is the nominal wage in non-agriculture. The profit-maximizing assumption ensures that the supply curve of non-agriculture is upward sloping, and that the demand curve for imports M is downward sloping.

Secondly it is assumed that there is full employment, namely

(3.6)

where is the fixed amount of labour force available in the economy. The full employment assumption is made in order to capture the fact that wages in developing countries are responsive to economic conditions. Rigidity in wages is a feature mostly of the formal-unionized sectors in all countries. While, however, these sectors are substantial in developed countries, they are rather small in developing countries. Also, a large labour "sink" in the form of informal activities is prevalent in developing countries, a feature that makes labour markets there much more flexible.

The third behavioural assumption made is that labour is supplied from agriculture to non-agriculture according to the condition that the nonagricultural wage, which is equal to the marginal product of labour in non-agriculture, is equal to the average product of agricultural labour.

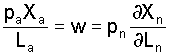(3.7)

Condition (3.7) says that the unit reward -of labour in non-agriculture is equal to the average product of labour in agriculture. In most developing countries agriculture is organized along owner-operated units, and hence the relevant return to agricultural activity is the (value of) the average product of labour. The non-agricultural sector in all developing countries is composed of two subsectors the formal and the so-called informal one. Formal sector nominal wages are usually set by legislative means, while informal sector wages are usually free to respond to supply and demand. While there are differences in nominal wages between these two sectors, what is normally neglected in analyses of the labour market is that the effective wage for formal activities, defined as reward per effective labour input, can vary substantially by varying the labour input. It is well known, for instance, that when nominal wages in the formal sector are kept fixed nominally in the presence of inflation, workers work less, and take up other activities. This implies that the labour market in developing countries is more flexible and unified than suggested by the distinction between formal and informal sectors. In the framework here the wage variable w is meant to represent average rewards to non-agricultural labour in this wider sense.

Condition (3.7) can also be looked at as a migration condition. Traditional migration models of the Harris-Todaro vintage (Harris and Todaro, 1970) equilibrate the labour market by equating average labour returns in agriculture with expected non-agricultural wage. Here, full employment is assumed, and hence the expected non-agricultural wage which in the Harris-Todaro model is defined as unemployment adjusted nominal wage, but here is assumed equal to the marginal product of labour in non-agriculture, is equivalent to the effective non-agricultural wage. Full employment seems a reasonably good assumption in developing countries, as the informal sector usually acts a sink that absorbs the unemployment. Household budget surveys, especially in Africa, usually show that open unemployment is quite small.

It should be noted that if (3.7) is replaced by a condition, whereby the nonagricultural wage is equated to the marginal rather than the average product of labour, in agriculture the subsequent results would not change. Condition (3.7) is kept, both because of convenience, as well as because it reflects the small scale atomistic nature of agricultural production in most countries.

Commodity balance (supply equals demand) in the two sectors is as follows:

(3.8)

(3.9)

In (3.8) E is the net exports of the product of agriculture which as already mentioned, is assumed to be the only traded good produced in the economy. C_a and C_n denote the quantities of domestic private consumption of the agricultural and non-agricultural products respectively. They are functions of consumed income and relative prices. S denotes the "surplus" of non-agriculture, namely the quantity of good X_n which is available for either public consumption G or investment (public and private) I.

(3.10)

It is assumed in (3.9) that only the product of non-agriculture is used for investment. While this is not strictly true, since livestock and trees are two well-known forms of investment of the agricultural product, it is becoming increasingly accepted that much of this type of investment of the agricultural product is for consumption smoothing and not for productive purposes (Deaton, 1990). Even trees for cash crops in many countries are viewed as old-age insurance.

Private income Y or value added in the economy is composed of agricultural and wage income and profits. Because of the full employment assumption, and the migration condition (3.7), non-profit income can be written simply as wage income in the economy

(3.11)

A fourth behavioural assumption is that only wage income is consumed, while all non-agricultural profits are saved. Hence the domestic demands for the two products can then be written in standard form as follows

(3.12)

(3.13)

where the relevant functions in (3.12) and (3.13) are homogeneous of degree zero.

Total domestic savings, however, do not arise only out of profits. They can be generated by taxing export and import trade, as well as by foreign borrowing.

Denote by and the international prices of the exportable agricultural product and the imported product respectively. The country is assumed small so that it cannot influence these international prices. Also denote by e the nominal foreign exchange rate. Then the tax income T. which is due to the differences between domestic and world prices can be written as follows:

(3.14)

It can easily be shown (by multiplying the commodity balances (3.8) and (3.9) by the respective domestic prices, adding, and using the assumption that only wage income is consumed) that the following modified "savings-investment" identity holds

(13.15)

where F is "foreign savings", namely autonomous or more typically accommodating foreign exchange inflows.

(13.16)

The negative of F is usually referred to by multilateral institutions such as the World Bank as the "Resource Balance".

If we had written S in its more traditional form 13.10), namely as the sum of public consumption G and total investment 1, and transferred G to the left hand side of (3.15), then we would obtain the traditional savings-investment identity of macro-models. The left hand side of (3.15) would be composed of private savings (P ) public savings (T-G) and foreign savings (eF). By writing this identity in the form (3.15), we separate the problem of total surplus from the problem of composition of the surplus among public current spending and total (public and private) investment. The first problem is the more traditional "scissors" problem, namely of what is a good internal terms of trade policy to maximize domestic surplus. The second problem of composition of the surplus is more relevant in the context of structural adjustment.

Notice that if it is assumed that private investment I_p is fixed (by animal spirits or other considerations) and equal to private profits P then the "modified surplus" p_n (S - I_p) is equal to total current and development public expenditure. In this case domestic taxation just generates public funds.

Notice that in equations (3.8) and (3.9) the terms E and S. namely exports and the "surplus" of the economy, are in a sense residuals of total domestic supply minus domestic private consumption. The amount of exports E, through the foreign exchange balance (3.16), is utilized to "pay" for imports that go into the production of the non-agricultural good, which in turn is used for consumption and investment.

The model as outlined is homogeneous in the domestic prices p_a, p_n and p_m Hence we can choose one of these prices as the numeraire. We choose the price of the non-agricultural good as the unit of measurement, and we therefore set p_n = 1. We also note that the balance of payments ex-post equilibrium condition 13.16), can be written in units of any foreign currency. We, therefore, for simplicity choose units so that = 1. Thus will symbolize the foreign terms of trade facing the country. An external terms of trade improvement will be synonymous with a rise in . Also p_a in this model with the above conventions symbolizes the domestic terms of trade of agriculture vis-à-vis non-agriculture.

Since agriculture is the only sector producing traded goods, and since the price of non-tradeables was normalized to equal one, the price p_a in equilibrium could also denote the real exchange rate, namely the relative price of tradeables to non-tradeables.

The model exhibited above differs in several ways from the model utilized by Sah and Stiglitz (1987). In their formulation they assumed that agricultural producers make only income from agriculture, and spend the value of surplus production (net of own consumption) on the non-agricultural good. Workers in turn have potentially different spending patterns. in the current model, the structure of income is left aggregated. However, the only assumption made is that all agricultural income and wage income is consumed, and those with such incomes have similar spending patterns. Sah and Stiglitz have very different assumptions about the labour market. They assumed fixed labour input in the two sectors, while here labour shifts across sectors in response to price signals. Wages in their model were either determined by fiat by the government, or derived through assumptions about workers wage bargaining. Finally in their model both products are fully traded, and hence no real exchange rate effects can be discussed.

The way in which the present model balances is through the labour market. Labour is assumed mobile between agriculture and non-agriculture. Hence a decline in the production of agriculture, which can occur only by labour leaving agriculture, will imply an increase in the production of non-agriculture. Hence we abstract from situations, which have been fairly prevalent in SSA in the early eighties, whereby the productivity of the whole economy declined because of deterioration in the overall capital (in the model this would be represented by declines in the constants and ).

Contents - Previous - Next