Dans certaines circonstances les gestionnaires des pêcheries peuvent être à même d'établir une limite supérieure à l'intensité de pêche au-delà de laquelle on s'accorde à penser que la pêcherie se trouverait dans un état très préjudiciable. Ainsi qu'on a pu l'évoquer, ce point est appelé Point de Référence Limite (PRL). Pour des raisons de simplification mathématique, nous considérerons dans ce qui suit que Fmsy est une valeur acceptée par convention, et non entachée d'erreur. Dans l'exemple suivant nous supposerons de plus que le PRL utilisé ici est une valeur pré-établie pour une mortalité par pêche correspondant aux conditions de la MSY.
Les gestionnaires reconnaissent qu'ils agissent dans un environnement incertain et que le status quo actuel de la pêcherie, et la valeur de F pour la saison précédente (Fact) ne sont pas précisément connus, mais que quelques estimations grossières de l'écart-type peuvent être faites. Dans le cas théorique en question, il apparaît nettement que, l'année précédente, l'intensité de pêche était inférieure à Fmsy et on suppose que si le même effort de pêche devait être déployé durant la saison à venir, la distribution de probabilité des taux de mortalité par pêche resterait la même. Les gestionnaires ressentent cependant qu'il serait utile de définir un Point de Référence Cible de manière telle que le risque de ne pas dépasser Fmsy soit prédéfini et faible.
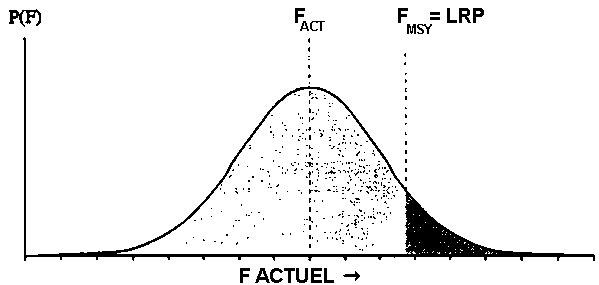
Etant donnée cette situation, nous indiquons ci-dessous une procédure permettant de calculer les valeurs cibles appropriées de Fact qui permettent, avec une probabilité prédéfinie, qu'un PRL adopté soit respecté. Dans cet exemple on suppose que le PRL est une valeur prédéfinie pour Fmsy = 0,6. Bien que la littérature scientifique n'indique pas clairement la fonction de distribution la plus appropriée à retenir pour F, on considère que l'incertitude quant à la position relative de Fact < Fmsy peut raisonnablement être exprimée par une distribution normale (voir Fig. 18 ci-dessous), bien que des calculs similaires puissent facilement être réalisés pour d'autres fonctions de distribution.
Considérons que le niveau actuel de mortalité par pêche, F, est inférieur au Point de Référence Cible Fmsy. Pour simplifier l'aspect mathématique nous supposons que Fmsy est connu sans incertitude. Nous considérons d'autre part que l'incertitude portant sur F est décrite par une distribution log-normale où, avec une probabilité équivalente (c'est-à-dire avec des niveaux de confiance équivalents), la valeur actuelle de F dans la pêcherie peut être moitié moindre ou double du paramètre estimé Fact. Nous cherchons à trouver une valeur pour ce Point de Référence Limite, Fact, qui se situe suffisamment loin de Fmsy, ne laissant qu'une probabilité suffisamment faible à la vraie valeur du F actuel d'être, en fait, supérieure à Fmsy.
Mathématiquement, la procédure suggérée est la suivante: le niveau de risque que la pêcherie peut tolérer (quantifiée dans la figure 18 de l'annexe comme la zone ombrée à l'extrémité supérieure de la distribution normale) est équivalent à l'intégrale de la probabilité que F actuel dépasse notre Point de Référence Limite. Si l'on appelle P (F>Fmsy) le niveau de risque acceptable choisi, nous devons trouver la valeur de Fact qui corresponde au Point de Référence Cible permettant cette marge de sécurité. La probabilité cumulée pour la partie supérieure de la distribution peut s'écrire sous la forme:
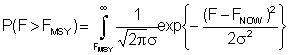
De ceci nous pouvons tirer Fmsy en utilisant un logiciel permettant de résoudre de telles équations (ex: Maple, Mathematica).
L'écart-type de F peut alors, en théorie, être estimé à partir des données rétrospectives en comparant les F prédits et les valeurs "vraies" obtenues rétrospectivement par APV, ou en s'accordant sur une marge d'erreur "probable" connaissant la variance estimée pour les estimations de la taille de la population. De plus, ce type de comparaison sur des données rétrospectives pourrait permettre aux gestionnaires des pêcheries de décrire plus précisément la nature de la distribution de l'incertitude sur F.
Tableau annexe: En supposant que Fmsy = 0,6, le tableau suivant donne les valeurs indicatives de Fact qui pourraient être utilisées comme Points de Référence Cible pour les combinaisons de (en colonnes): -proportions de temps acceptable où Fact. > Fmsy, et (en lignes): écarts-types de Fmsy.
|
|
[P(x)]
|
ECART-TYPE: |
||
|
s = 0.25 |
=0,5 |
=1,0 |
||
|
P(Fact > Fmsy) |
30% |
0,53 |
0,475 |
0,39 |
|
|
20% |
0,50 |
0,42 |
0,33 |
|
|
10% |
0,45 |
0,365 |
0,26 |
Figure 18: Illustre l'incertitude quant à l'intensité de pêche actuelle, Fact par rapport au Point de Référence Limite (ici assumé être FMSY). Une faible probabilité P(F) de la valeur de F > FMSY est représentée en gris foncé dans la courbe normale de distribution.