Tabela 4.4.5.1 Curva de captura linearizada baseada em dados de composição
de comprimento do Upeneus vittatus da Baía de Manila,
Filipinas (de Ziegler, 1979).
L∞ = 23.1 cm, K = 0.59 por ano. (Ver Fig.4.4.5.1)
| A | B | C | D | E | F | G | H |
| L1–L2 | C(L1,L2) | t(L1) | Δt | 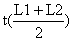 | 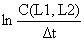 | Z | observações |
| a) | b) | c) | |||||
| (x) | (y) | ||||||
| 6– 7 | 3 | 0.510 | 0.102 | 0.56 | 3.38 | - | não usados, não estão totalmente explor. |
| 7– 8 | 143 | 0.612 | 0.109 | 0.67 | 7.18 | - | |
| 8– 9 | 271 | 0.721 | 0.116 | 0.78 | 7.76 | - | |
| 9–10 | 318 | 0.837 | 0.125 | 0.90 | 7.86 | - | |
| 10–11 | 416 | 0.961 | 0.134 | 1.03 | 8.04 | - | |
| 11–12 | 488 | 1.096 | 0.146 | 1.17 | 8.11 | - | |
| 12–13 | 614 | 1.242 | 0.160 | 1.32 | 8.25 | - | |
| 13–14 | 613 | 1.402 | 0.177 | 1.49 | 8.15 | - | porção usada na análise de regressão |
| 14–15 | 493 | 1.579 | 0.197 | 1.67 | 7.83 | - | |
| 15–16 | 278 | 1.776 | 0.223 | 1.88 | 7.13 | 2.64 | |
| 16–17 | 93 | 2.000 | 0.257 | 2.12 | 5.89 | 3.61 | |
| 17–18 | 73 | 2.257 | 0.303 | 2.40 | 5.48 | 3.20 | |
| 18–19 | 7 | 2.560 | 0.370 | 2.74 | 2.94 | 4.03 | |
| 19–20 | 2 | 2.930 | 0.473 | 3.15 | 1.44 | 4.19 | |
| 20–21 | 2 | 3.404 | 0.659 | 3.70 | 1.11 | - | não usado prox. demais de L∞ |
| 21–22 | 0 | 4.064 | 1.094 | 4.53 | - | - | |
| 22–23 | 1 | 5.160 | 4.047 | 6.19 | -1.40 | - | |
| 23–24 | 1 | - | - | - | - | - |
Pormenores das cinco análises de regressão
| L1–L2 | declive b Z | número de obs. n | distrib. Student 95% tn-2 | variância do declive sb2 | limites de confiança |
| Z ± tn-2*sb | |||||
| 13–14 | - | 1 | - | - | - |
| 14–15 | - | 2 | - | - | - |
| 15–16 | 2.64 | 3 | 12.70 | 0.198 | 2.64 ± 5.65 |
| 16–17 | 3.61 | 4 | 4.30 | 0.283 | 3.61 ± 2.28 |
| 17–18 | 3.20 | 5 | 3.18 | 0.121 | 3.20 ± 1.11 |
| 18–19 | 4.03 | 6 | 2.78 | 0.198 | 4.03 ± 1.24 |
| 19–20 | 4.19 | 7 | 2.57 | 0.087 | 4.19 ± 0.76 |
| a) Eq. 3.3.3.2 | |||||
| b) Eq. 4.4.5.1 | |||||
| c) Eq. 4.4.5.2 | |||||
O segundo argumento acima é muito importante para a curva de captura linearizada em comprimentos, sendo uma boa razão para nunca usar os pontos correspondentes aos peixes das classes de comprimento maiores.
Voltemos agora ao exemplo da Tabela 4.4.5.1. Somente os dados correspondentes às classes de comprimento entre 13 cm e 20 cm foram usados para a análise. Para verificar a sensibilidade do resultado em função da escolha dos pontos a serem excluídos dos cálculos, a inclinação b = Z foi calculada com 3, 4… e 7 pontos, como se pode ver na parte inferior da Tabela 4.4.5.1. A primeira estimação de Z foi calculada só com os dados dos Comprimentos entre 13 e 16 cm, o próximo Z com os de 13 a 17 cm, …etc. Os intervalos de confiança foram calculados usando o método descrito na Secção 2.4. Neste caso, a conclusão é: usando as seis classes, desde 13 a 19 cm, o valor de Z deve estar entre 4.03-1.24 = 2.8 e 4.03+1.24 = 5.2 por ano. Para as classes entre 16 e 20 cm, Z*Δt > 1 não é um valor pequeno, e, portanto, a aproximação assumida na curva de captura, na qual (ln[1 - exp(-x)] = ln x - x/2, (ver Secção 4.4.4), é grosseira neste caso.
(Ver Exercício (s) na Parte 2).
Para converter a “curva de captura acumulada” (Eq.4.4.4.1) em uma equação que possa ser utilizada para uma análise baseada em comprimentos, a equação inversa de von Bertalanffy (Eq. 3.3.3.2)
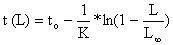
deve ser substituida na equação da curva de captura acumulada (Eq. 4.4.4.1):
ln C(t,∞) = d - Z*t
o que resulta:
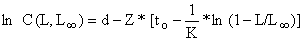
e pode ser convertida em:
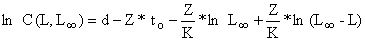
Como os primeiros três termos são constantes, podem receber nova denominação:
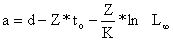
Obtendo assim a “Equação de Jones e van Zalinge”:
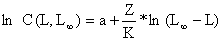 | (4.4.6.1) |
onde C(L,L∞) significa a captura acumulada dos peixes a partir do comprimento L. O declive estimado pela regressão linear da Eq. 4.4.6.1 representa Z/K, e portanto uma estimação de Z é obtida através de:
Z = K*inclinação
Exemplo 15: Método de Jones e van Zalinge, Upeneus vittatus
A Tabela 4.4.6.1 e a Fig. 4.4.6.1 mostram uma aplicação da Eq. 4.4.6.1 para Upeneus vittatus (os mesmos dados usados na secção anterior). Note que os dados básicos para aplicação deste método são também provenientes de uma amostra, e não do total capturado (ver Secções 4.4.4 e 4.4.5). Os resultados da análise de Jones e van Zalinge usando as classes de 13 e 19 cm são similares aos obtidos com a análise anterior da curva de captura linearizada (Tabela 4.4.5.1).
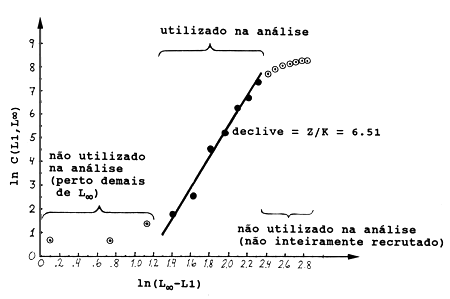
Fig. 4.4.6.1 Curva de captura acumulada baseada em dados de composição de comprimentos para Upeneus vittatus.A recta desenhada foi estimada a partir de sete pontos. Dados da Tab. 4.4.6.1
A Fig. 4.4.7.1 mostra um resumo das diversas versões da curva de captura linearizada (Eq. 4.4.2.1) discutidas na Secção 4.4. Todas elas originaram-se na equação de captura (ou equação de Baranov), a Eq. 4.2.7. Foram apresentados os seguintes modelos, três baseados em dados de composição em idades:
Curva de captura linearizada com intervalos de tempo constantes Eq. 4.4.3.1
Curva de captura linearizada com intervalos de tempo variáveis Eq. 4.4.4.2 (Eq. 4.4.3.1 generalizada)
Curva de captura acumulada Eq. 4.4.4.1
e dois baseados em dados de composição de comprimentos:
Curva de captura linearizada convertida para comprimentos, 4.4.5.3, derivada da Eq. 4.4.4.2
Método de Jones e van Zalinge. 4.4.6.1, derivado da Eq. 4.4.4.1
Sparre (1990) observou que existem problemas com métodos de avaliação de mananciais baseados em comprimentos, quando o crescimento é sazonal, e em particular com o método da curva de captura baseada em comprimentos. Na mesma edição da Fishbyte, Pauly (1990) descreveu um novo método para construção da curva de captura convertida para comprimentos. O erro em estimar Z para pequenas espécies de vida curta, que estão sujeitas a fortes variações sazonais no crescimento devido a mudanças nas condições ambientais, é em grande parte atenuado por este método. O autor fornece valores para Z muito menores que os obtidos com os métodos convertidos em comprimentos descritos nas Secções 4.4.5 e 4.4.6.
Tabela 4.4.6.1 Curva de captura acumulada baseada em dados de composição
de comprimentos para Upeneus vittatus da Baía de Manila,
Filipinas (de Ziegler, 1979)
L∞ = 23.1 cm, K = 0.59 por ano (ver Fig. 4.4.6.1)
| L1–L2 | captura C(L1,L2) | captura acumulada C(L1,L∞) | In da captura acumulada In C(L1,L∞) (y) | In (L∞-L1) (x) | declive Z/K | observa. |
| 6– 7 | 3 | 3816 | 8.25 | 2.84 | - | não usados, não estão sob exploração total |
| 7– 8 | 143 | 3813 | 8.25 | 2.78 | - | |
| 8– 9 | 271 | 3670 | 8.21 | 2.71 | - | |
| 9–10 | 318 | 3399 | 8.13 | 2.65 | - | |
| 10–11 | 416 | 3081 | 8.03 | 2.57 | - | |
| 11–12 | 488 | 2665 | 7.89 | 2.49 | - | |
| 12–13 | 614 | 2177 | 7.69 | 2.41 | - | |
| 13–14 | 613 | 1563 | 7.35 | 2.31 | - | parte usada na análise de regressão |
| 14–15 | 493 | 950 | 6.86 | 2.21 | - | |
| 15–16 | 278 | 457 | 6.12 | 2.09 | 5.61 | |
| 16–17 | 93 | 179 | 5.19 | 1.96 | 6.20 | |
| 17–18 | 73 | 86 | 4.45 | 1.81 | 5.98 | |
| 18–19 | 7 | 13 | 2.56 | 1.63 | 6.86 | |
| 19–20 | 2 | 6 | 1.79 | 1.41 | 6.51 | |
| 20–21 | 2 | 4 | 1.39 | 1.13 | - | não usados, proximos demais a L∞ |
| 21–22 | 0 | 2 | 0.69 | 0.74 | - | |
| 22–23 | 1 | 2 | 0.69 | 0.10 | - | |
| 23–24 | 1 | 1 | 0.00 | -2.30 | - | |
| Pormenores das 5 análises de regressão: | ||||||
| L1–L2 | declive*K Z | no de observ. n | distrib. Student 95% tn-2 | variância do declive sb2 | limites de confiança Z Z ± K*tn-2*sb |
| 13–14 | - | 1 | - | - | - |
| 14–15 | - | 2 | - | - | - |
| 15–16 | 3.30 | 3 | 12.71 | 0.131 | 3.30 ± 2.71 |
| 16–17 | 3.66 | 4 | 4.30 | 0.118 | 3.66 ± 0.87 |
| 17–18 | 3.53 | 5 | 3.18 | 0.047 | 3.53 ± 0.41 |
| 18–19 | 4.05 | 6 | 2.78 | 0.202 | 4.05 ± 0.74 |
| 19–20 | 3.84 | 7 | 2.57 | 0.110 | 3.84 ± 0.50 |
MODELO GERAL DA CURVA DE CAPTURA LINEARIZADA
ln C(t1,t2) = d - Z*t1 + ln[1 - exp(-Z*(t2-t1))]
(Eq. 4.4.2.1)
| Modelos baseados em composição de idades | Δt = t2-t1 é constante CURVA DE CAPTURA LINEARIZADA COM INTERVALOS DE TEMPO CONSTANTES ln C(t, t+Δt) = g - Z*t (Eq. 4.4.3.1) | |
| Δt = t2-t1 é variável | ||
| Δt = pequeno | Δt = ∞ | |
CURVA DE CAPTURA LINEARIZADA COM INTERVALOS DE TEMPO VARIÁVEIS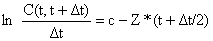 (Eq. 4.4.4.2) | EQUAÇãO DA CURVA DE CAPTURA ACUMULADA ln C(t,∞) = d - Z*t | |
| Conversão das idades para comprimentos | 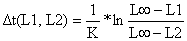 | 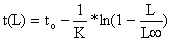 |
| (Eq. 4.4.5.1) e | (Eq. 3.3.3.2) | |
| t+Δt/2 ≈ | ||
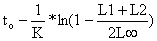 | ||
| (Eq. 4.4.5.2) | ||
| Modelos baseados em composição de comprimentos | CURVA DE CAPTURA LINEARIZADA CONVERTIDA PARA COMPRIMENTOS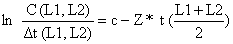 (Eq. 4.4.5.3) | MÉTODO DE JONES E VAN ZALINGE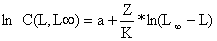 (Eq. 4.4.6.1) |
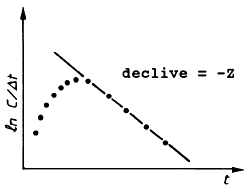 | 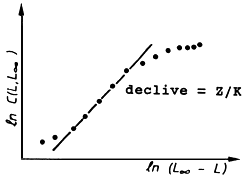 |
Fig. 4.4.7.1 Resumo dos modelos apresentados na Secção 4.4
O primeiro método que apresentaremos nesta secção permite estimar Z a partir do comprimento médio nas capturas e dos parâmetros K e L∞ da equação de von Bertalanffy. Portanto, são requeridos menos dados para este método do que para os métodos da curva de captura linearizada, para os quais o tamanho relativo (não necessariamente o absoluto) da composição das capturas deve ser conhecida (ver Secção 4.4.4 a 4.4.6). No entanto, o cálculo da equação de Beverton e Holt para estimar Z, é um pouco mais complicada do ponto de vista matemático. A seguir tenta-se demonstrar e justificar o método através de um exemplo numérico, evitando os cálculos matemáticos. É demonstrado também que mesmo L∞ pode ser estimado junto com uma estimação de Z/K.
Assumindo que foram colhidas amostras da composição por comprimentos das capturas nos anos 1960, 1970 e 1980, e que os resultados são os apresentados na Tabela 4.5.0.1. O exemplo é construído com um conjunto de dados hipotéticos, ou seja, um conjunto de dados de que se conhece previamente os parâmetros. As classes de comprimento representam somente a parte do manancial que está sob exploração total (ver a discussão na Secção 4.4.5) e onde Z é assumido como constante. Evidentemente, Z pode ser diferente para os três anos em questão.
Além disso, devemos conhecer os parâmetros K e L∞ de von Bertalanffy. Para o exemplo da Tabela 4.5.0.1 estes são:
K = 0.3 por ano, L∞ = 100 cm
Tabela 4.5.0.1 Composição em comprimentos de amostras de capturas (exemplo hipotético para ilustrar o método). Os comprimentos médios foram calculados como demonstra a Secção 2.1 (Tabela 2.1.2). L' é o comprimento a partir do qual os peixes estão sob exploração total
| ano | 1960 | 1970 | 1980 | 1960 | 1970 | 1980 | |
| classe de comprimento L1–L2 | compr. médio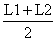 | número capturado | número * comp. médio | ||||
| C | 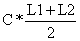 | ||||||
| L'= 45–50 | 47.5 | 256 | 268 | 212 | 12160.0 | 12730.0 | 10070.0 |
| 50–55 | 52.5 | 237 | 226 | 161 | 12442.0 | 11865.0 | 8452.5 |
| 55–60 | 57.5 | 211 | 180 | 116 | 12132.5 | 10350.0 | 6670.0 |
| 60–65 | 62.5 | 187 | 141 | 79 | 11687.5 | 8812.5 | 4937.5 |
| 65–70 | 67.5 | 161 | 105 | 52 | 10867.5 | 7087.5 | 3510.0 |
| 70–75 | 72.5 | 138 | 76 | 31 | 10005.0 | 5510.0 | 2247.5 |
| 75–80 | 77.5 | 113 | 50 | 7 | 8757.5 | 3875.0 | 1317.5 |
| 80–85 | 82.5 | 87 | 30 | 8 | 7177.5 | 2475.0 | 660.0 |
| 85–90 | 87.5 | 62 | 15 | 3 | 5425.0 | 1312.5 | 262.5 |
| 90–95 | 92.5 | 36 | 6 | 1 | 3330.0 | 555.0 | 92.5 |
| 95–100 | 97.5 | 12 | 1 | 0 | 1170.0 | 97.5 | 0.0 |
| Total, n | 1500 | 1098 | 680 | ||||
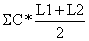 | 95154.5 | 64670.0 | 38220.0 | ||||
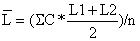 | 63.44 | 58.90 | 56.21 | ||||
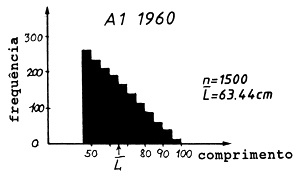
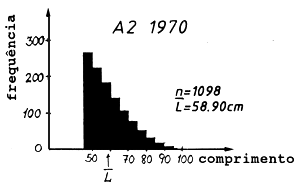
As Figs. 4.5.0.1A1 a 4.5.0.1A3 mostram as distribuições de comprimento. O comprimento médio L tem uma tendência decrescente com o tempo. Assim, em 1980 num determinado comprimento sobreviveram menos peixes comparando com 1970 e com 1960. Se esta alteração do comprimento médio do manancial é causada apenas por alteração da mortalidade por pesca, vem que:
(F em 1960) < (F em 1970) < (F em 1980)
Em outras palavras, quanto menor o comprimento médio na captura, maior é o F. Sob suposição que M permanece constante, a mesma conclusão vem para a mortalidade total, Z = F+M.
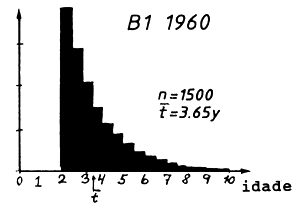
| A: COMPRIMENTO | B: IDADE |
|---|---|
| Exploração fraca: Z = 0.6y-1 | |
 |  |
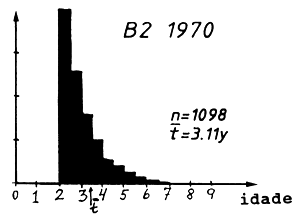
| Exploração moderada: Z = 0.9y-1 | |
 |  |
| Exploração intensa: Z = 1.2y-1 | |
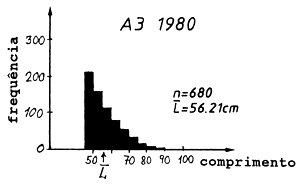 | 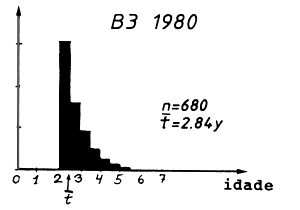 |
Fig. 4.5.0.1 Exemplo hipotético para ilustrar a equação de Beverton e Holt para estimar Z (Eq. 4.5.0.1). K = 0.3, L' = 45 cm e L∞ = 100 cm
Beverton e Holt (1956) demonstraram que a relação funcional entre Z e L é:
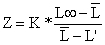 | (4.5.1.1) |
Onde L é o comprimento médio dos peixes com comprimento L' ou maiores, sendo L' o “comprimento a partir do qual todos os peixes deste comprimento ou maiores sofrem exploração total”. Note que L' é o limite inferior do intervalo da classe correspondente. Para a escolha de L', são válidos os mesmos comentários das Secções 4.4.2 e 4.4.6. No nosso exemplo foi escolhido L' = 45 cm.
Os valores de Z para os três anos, no exemplo, são (compare com a Tabela 4.5.0.1 e Fig. 4.5.0.1A):
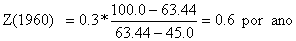
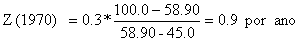
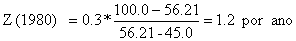
O método está melhor discutido na Secção 4.5.4.
(Ver Exercício (s) na Parte 2).
Assim como para a curva de captura linearizada, o método de Beverton e Holt baseado em comprimentos, tem um método paralelo baseado em idades. É mencionado principalmente porque ilustra uma característica básica da teoria de Beverton e Holt (Secção 1.3).
A composição em idades correspondente à composição em comprimentos da Tabela 4.5.0.1 é mostrada na Tabela 4.5.2.1 e na Fig. 4.5.0.1B. O mesmo raciocínio usado para o comprimento médio pode ser aplicado para a idade média: quanto maior é a mortalidade por pesca, menor é a idade média, t, na captura, ou quanto maior a idade média, menor o F. Isto pode ser considerado uma implicação da relação funcional existente entre idade e comprimento. No entanto, a verdadeira relação entre idade média e comprimento médio é um pouco complicada. Deve ser notado que a equação de von Bertalanffy não transforma a idade média em comprimento médio, porque o crescimento não é linear.
A equação paralela à Eq. 4.5.1.1, baseada em idades é um pouco mais simples. Beverton e Holt demonstraram que:
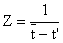 | (4.5.2.1) |
onde t é a idade média de todos os peixes de idade t' ou mais velhos, e t' é “uma idade a partir da qual todos os peixes desta idade ou mais velhos sofrem exploração total”. No exemplo temos que a idade, t', correspondente a L' = 45 cm é
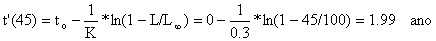
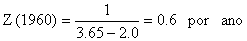
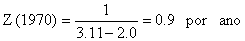
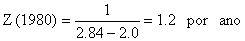
Tabela 4.5.2.1 Composição etária das amostras apresentadas na
Tabela 4.5.0.1
| grupo de idade | 1960 | 1970 | 1980 |
| 2.0– 2.5 | 390 | 399 | 308 |
| 2.5– 3.0 | 289 | 255 | 169 |
| 3.0– 3.5 | 214 | 162 | 92 |
| 3.5– 4.0 | 150 | 103 | 52 |
| 4.0– 4.5 | 118 | 66 | 28 |
| 4.5– 5.0 | 97 | 42 | 15 |
| 5.0– 5.5 | 64 | 27 | 8 |
| 5.5– 6.0 | 48 | 17 | 6 |
| 6.0– 6.5 | 35 | 11 | 2 |
| 6.5– 7.0 | 26 | 7 | - |
| 7.0– 7.5 | 19 | 4 | - |
| 7.5– 8.0 | 14 | 3 | - |
| 8.0– 8.5 | 11 | 2 | - |
| 8.5– 9.0 | 8 | - | - |
| 9.0– 9.5 | 6 | - | - |
| 9.5–10.0 | 4 | - | - |
| 10.0–10.5 | 3 | - | - |
| 10.5–11.0 | 2 | - | - |
| 11.0–11.5 | 2 | - | - |
| tamanho da amostra | 1500 | 1098 | 680 |
| ∑ número *idade | 5475 | 3415 | 1931 |
| idade média, t | 3.65 | 3.11 | 2.84 |
Existe uma terceira versão da equação, que matematicamente é equivalente à Eq. 4.5.1.1, mas conceptualmente diferente. Considere, por exemplo, a “curva de selectividade da arte”, para uma rede de arrasto, como mostra a Fig. 4.5.3.1. O eixo vertical representa a percentagem de peixes que entrando na rede é retida pela malha. Lc, ou L50%, é o comprimento no qual 50% dos peixes deste tamanho são retidos pela rede e 50% escapam através da malha. Note que Lc < L'. (No Capítulo 6 discutiremos mais propriedades da curva de selectividade).
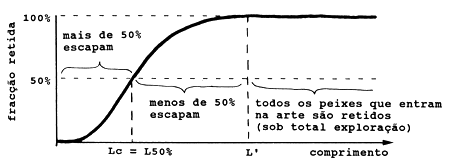
Fig. 4.5.3.1 Curva de selectividade da arte
A versão da equação de Beverton e Holt neste caso é:
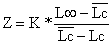 | (4.5.3.1) |
onde Lc é o “comprimento no qual 50% dos peixes que entraram na rede são retidos” e Lc é o “comprimento médio da captura total”.
A Eq. 4.5.3.1 tem se mostrado muito útil nos casos em que estimações de Lc e Lc estão disponíveis, e L e L' não são conhecidos.
Powell (1979), discutido em Wetherall et al. (1987), sugere uma aplicação particular da Eq. 4.5.1.1 na qual podem ser estimados L∞ e Z/K. Como L' pode assumir qualquer valor igual ou maior que o menor comprimento a partir do qual todos os peixes sofrem exploração total, a Eq. 4.5.1.1 pode dar uma série de estimações de Z, dependendo do valor de L' escolhido. Isto permite transformar a Eq. 4.5.1.1 numa análise de regressão com L' como variável independente. Uma série de manipulações algébricas mostram que a Eq. 4.5.1.1 é equivalente a:
| L-L' = a + b*L' | (4.5.4.1) | |
| onde | ||
| Z/K = -(1+b)/b e L∞ = -a/b | (4.5.4.2) | |
| ou | b = -K/(Z+K) e a = -b*L∞ |
Assim, marcando L-L' contra L' obtemos uma regressão linear, e a partir dos seus parâmetros, a e b, podemos estimar L∞ e Z/K (ver Fig. 4.5.4.1).
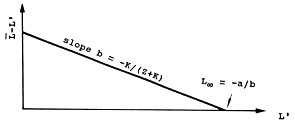
Fig. 4.5.4.1 Gráfico de Powell-Wetherall
Powell (1979) na verdade apresentou uma série de diferentes fórmulas adequadas para Z/K, das quais a Eq. 4.5.4.1 representa a aproximação mais simples. O método de Powell é especialmente adequado para situações que pouco ou nada se conhece sobre um determinado manancial de peixes. A estimação de L∞ é neste caso muito útil (comparar com Secção 3.3.2).
Deve ser lembrado que, assim como na fórmula de Beverton e Holt (Eq. 4.5.1.1) o método baseia-se na suposição da existência de um sistema de parâmetros constantes, o que reduz a sua aplicabilidade.
Exemplo 16: Método de Powell-Wetherall
Um exemplo do método de Powell-Wetherall é dado na Tabela 4.5.4.1 e na Fig. 4.5.4.2. Os cálculos para L começam com o comprimento médio da classe de maior comprimento, neste caso 46 cm. O próximo valor de L é calculado assim: (46*3+44*10)/13 = 44.462 e L' é o limite inferior de cada classe de comprimento. Os valores de L-L' são obtidos subtraindo-se de L o correspondente valor de L'. Por exemplo, 46.000-45 = 1.000 e 44.462-43 = 1.462. Estes valores são então marcados contra L', de forma a permitir uma ultimos avaliação dos pontos que se encontram em linha recta e portanto possam ser incluídos na análise de regressão linear. Neste exemplo os ultimos dois pontos foram excluídos, porque representam muito poucos peixes. (Note que o mesmo conjunto de dados foi usado para ilustrar a ogiva de selectividade estimada de uma curva de capturas, ver Secção 6.5)
Tabela 4.5.4.1 Método de Powell-Wetherall (ver Fig. 4.5.4.2).
Os mesmos dados foram usados na Tabela 6.5.1
| intervalo de comprimento L1–L2 (x) = L1 | número capturado C(L1,L2) | compr. médio dos peixes maiores que L', L | L-L' (y) | |
| 3– 5 | 37 | 21.101 | 18.101 | não usados na análise |
| 5– 7 | 56 | 21.291 | 16.291 | |
| 7– 9 | 86 | 21.552 | 14.552 | |
| 9–11 | 129 | 21.917 | 12.917 | |
| 11–13 | 188 | 22.419 | 11.419 | |
| 13–15 | 258 | 23.101 | 10.101 | |
| 15–17 | 319 | 23.998 | 8.998 | |
| 17–19 | 352 | 25.108 | 8.108 | |
| 19–21 | 351 | 26.394 | 7.394 | |
| 21–23 | 324 | 27.801 | 6.801 | |
| 23–25 | 283 | 29.279 | 6.279 | usados na análise |
| 25–27 | 239 | 30.792 | 5.792 | |
| 27–29 | 196 | 32.320 | 5.320 | |
| 29–31 | 158 | 33.852 | 4.852 | |
| 31–33 | 123 | 35.392 | 4.392 | |
| 33–35 | 93 | 36.926 | 3.926 | |
| 35–37 | 69 | 38.447 | 3.447 | |
| 37–39 | 48 | 39.982 | 2.982 | |
| 39–41 | 31 | 41.516 | 2.516 | |
| 41–43 | 18 | 43.032 | 2.032 | |
| 43–45 | 10 | 44.462 | 1.462 | não usados |
| 45–47 | 3 | 46.000 | 1.000 | |
| intersecção a: 11.671 | limites de confiança de a: [11.64, 11.70] | |||
| declive b: -0.2349 | limites de confiança de b: [-.2359, -0.2340] | |||
L∞ = -a/b = 49.7 Z/K = -(1+b)/b = 3.26 | ||||
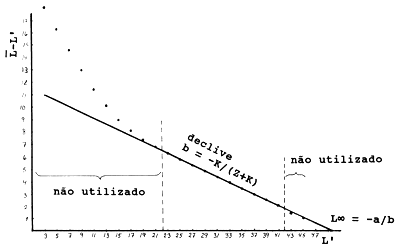
Fig. 4.5.4.2 Gráfico de Powell-Wetherall baseado nos dados da Tabela 4.5.4.1
Programas de computador
O programa “BHZWET” no pacote LFSA para microcomputadores (Sparre, 1987) pode executar a análise de Powell assim como a estimação de Z pela equação de Beverton e Holt. O pacote “COMPLEAT ELEFAN” (Gayanilo, Soriano e Pauly, 1988) e o FiSAT também contém programas similares.
A estimação de Z derivada dos métodos descritos nas secções anteriores pode, por vezes, ser usada para estimar F, a mortalidade por pesca e M, a mortalidade natural. Isto só é possível se existir pares de valores de estimações de Z e do esforço para uma série de períodos de tempo cobrindo uma grande amplitude de valores do esforço.
Seja Z(y) a mortalidade total e f(y) o esforço, no ano y. O método (Paloheimo, 1958, 1961 e 1980) está baseado na Eq. 4.2.3: Z = F+M, e na suposição que o esforço e a mortalidade por pesca estão relacionados simplesmente pela Eq. 4.3.0.7: F(y) = q*f(y), onde q é o coeficiente de capturabilidade. Substituindo a Eq. 4.3.0.7 na Eq. 4.2.3 resulta:
| Z(y) = M + q*f(y) | (4.6.1) |
Com Z como variável dependente e f como variável independente a Eq. 4.6.1 é uma regressão linear com declive q e a mortalidade natural, M, como intersecção. A mortalidade por pesca para o período y, F(y), é calculada de:
F(y) = Z(y) - M
Exemplo 17: Estimação de M e de q, de um peixe tropical
A Tabela 4.6.1 e Fig. 4.6.1 mostram uma aplicação da Eq. 4.6.1 para Selaroides leptolepis no Golfo da Tailândia (de Boonyubol e Hongskul, 1978). Neste caso, Z é calculado pela Eq. 4.5.3.1, ou seja, a partir de Lc, o comprimento de 50% de retenção e Lc, a média de comprimentos de todos os peixes na captura. O esforço é dado em milhões de horas de arrasto por ano. A Fig. 4.6.1 mostra o gráfico de Z contra o esforço.
Usando a regressão linear obtemos:
declive: q = 0.2532
intersecção: M = 2.034 por ano
Os limites de confiança calculam-se como descrito na Secção 2.4:
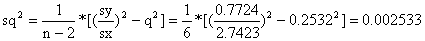
sq = 0.0503
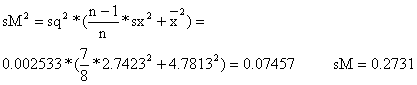
Os limites de confiança a 95% para q e M são
q: [q - sq*tn-2 , q + sq*tn-2] =
[0.253 - 0.0503*2.45 , 0.253 + 0.0503*2.45] = [0.13,0.38]
M: [M - sM*tn-2 , M + sM*tn-2] =
[2.03 - 0.2731*2.45 , 2.03 + 0.2731*2.45] = [1.36,2.70]
Tabela 4.6.1 Dados para a estimação de M e de q para Selaroides leptolepis
no Golfo de Tailândia (de Boonyubol e Hongskul, 1978).
K = 1.16 por ano, Lc = 10.0 cm, L∞ = 20.0 cm
| ano y | esforçoa) f(y) | comprimento médio Lc cm | 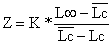 (Eq. 4.5.3.1) | |
| 1966 | 2.08 | 13.25 | 2.41 | |
| 1967 | 2.08 | 13.01 | 2.69 | |
| 1968 | 3.50 | 12.99 | 2.72 | |
| 1969 | 3.60 | 13.07 | 2.62 | |
| 1970 | 3.80 | 12.37 | 3.73 | |
| 1971 | - | - | sem dados | - |
| 1972 | 7.19 | 12.30 | 3.88 | |
| 1973 | 9.94 | 12.01 | 4.61 | |
| 1974 | 6.06 | 12.60 | 3.30 | |
| a) esforço em milhões de horas de arrasto | ||||
As estimações de M e de q obtidas por este método não são precisas. Por exemplo, baseiam-se na suposição de que o esforço é proporcional à mortalidade por pesca, ou seja, de que q é constante - uma suposição que pode ser sempre questionada devido à tendência a aumentar a eficiência na pesca. Uma hora de arrasto em 1970 pode não provocar a mesma mortalidade que uma hora de arrasto em 1980, porque os barcos de pesca estavam melhor equipados em 1980 (redes mais eficientes, motores mais potentes) que em 1970. Se é o caso, no nosso exemplo da Fig. 4.6.1 as observações mais recentes deveriam ser movidas para o lado direito, para compensar o aumento na eficiência, o que corresponderia a expressar todo o esforço em unidades de horas de arrasto de 1966. O resultado seria um declive menor e uma intersecção maior, ou seja, a estimação de M seria maior e a de q menor.
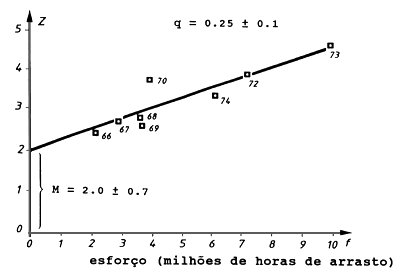
Fig. 4.6.1 Gráfico da mortalidade total, Z, contra o esforço, f, para estimar a mortalidade natural, M, e coeficiente de capturabilidade, q. Baseado nos dados da Tabela 4.6.1 (de Boonyubol e Hongskul, 1978)
Note que a aplicação deste método somente é possível se existir uma evidente variação nos valores do esforço durante o período considerado (ver Exercício 4.6). Se o esforço (a variável independente) permanecer constante durante o período não poderemos ajustar uma recta aos pontos.
Na Secção 4.7 continuaremos a discussão sobre a mortalidade natural, e sugerimos dois métodos simples alternativos para estimar M. Todos os métodos simples para estimar M são questionáveis e para avaliar a qualidade do M estimado, é sempre recomendável comparar os resultados com métodos alternativos e com valoras de M estimados para espécies similares.
(Ver Exercício (s) Parte 2).
Um método para estimar o coeficiente de mortalidade natural, M, já foi introduzido na Secção 4.6. Muitos outros procedimentos têm sido sugeridos na literatura. A maioria deles, ou talvez todos, permitem apenas uma estimação aproximada ou um “suposição qualificada”. Alguns destes métodos são usados muito frequentemente e outros poderão vir a ser mais usados no futuro. Por esta razão merecem ser discutidos.
Relembramos que a mortalidade natural é a mortalidade criada por todas as outras causas que não são a pesca, ou seja, predação incluindo canibalismo, doenças, “stress” devido à desova, fome, e velhice. A predação, a fome e algumas outras causas estão ligadas ao ecossistema ambiental. A mesma espécie pode ter diferentes taxas de mortalidade natural em diferentes areas, dependendo da densidade dos predadores ou competidores, cuja abundância é influenciada pelas actividades da pesca.
Como medidas directas de M são frequentemente impossíveis de serem obtidas, tem-se tentado identificar valores que sejam proporcionais a M e que sejam mais fáceis de serem quantificáveis (ou estimados).
Foi demonstrado que o parâmetro de curvatura, K, da equação de von Bertalanffy está correlacionado com a longevidade (Beverton e Holt, 1959), esta por sua vez está relacionada com a mortalidade (Tanaka, 1960; Holt, 1965 e Saville, 1977) (ver Eq. 4.5.2.1). Outros métodos que envolvem a longevidade serão tratados na Secção 4.7.1.
Duma maneira geral, as espécies com um alto valor de K têm valores de M altos, e espécies com valores de K baixos têm uma baixa mortalidade natural. Uma espécie de crescimento lento (K baixo) não pode ter uma mortalidade alta; se assim fosse, extinguia-se rapidamente. Beverton e Holt (1959) encontraram que os valores da relação M/K variam, na maioria das vezes, entre 1.5 e 2.5.
A mortalidade natural de uma espécie deve também estar relacionada com L∞ ou com o peso máximo, W∞, pois os peixes maiores encontram menos predadores do que os peixes pequenos. Foi sugerido que M poderia ser estimado a partir do tamanho do corpo de certos animais (Taylor, 1960, para bivalves; Peterson e Wroblewski, 1984, para peixes pelágicos).
Rikhter e Efanov (1976) (Secção 4.7.3) demonstraram que peixes com uma mortalidade natural alta atingem a maturação mais cedo, ou sejam começam a reproduzir-se mais cedo para compensar a alta mortalidade, M. Também pode ser mencionado que Gunderson e Dygert (1988) encontraram uma relação entre M e o índice gonadossomático (peso da gónada/peso do corpo). Isto parece razoável, porque os peixes devem compensar a alta mortalidade produzindo mais ovos.
Mais ainda, como a mairia dos processos biológicos se aceleram a altas temperaturas (naturalmente que dentro de certos limites) podemos imaginar que a mortalidade natural também está relacionada com a temperatura ambiental. A fórmula empírica de Pauly (Secção 4.7.2) descreve M como sendo uma função de K, L∞ e T, a temperatura do ambiente.
Intuitivamente, a longevidade parece estar mais ligada à mortalidade que a K, L∞ ou à temperatura do ambiente. O conceito básico dos coeficientes de mortalidade foi discutido na Secção 4.2 (Ver Fig. 4.2.1). Alagaraja (1984) sugere outra maneira de ilustrar o conceito do coeficiente de mortalidade. Ele definiu o ciclo de vida (ou longevidade) de uma espécie como a idade na qual 99% da coorte estaria morta se fosse exposta apenas à mortalidade natural (ou seja se Z = M). Se Tm significar a longevidade e M1% a mortalidade natural correspondente a 1% dos sobreviventes, então:
| M1% = -ln(0.01)/Tm | (4.7.1.1) |
Tabela 4.7.1.1 valores de M para as várias longevidades
| Tm | (meses) | 3 | 4 | 5 | 6 | 7 | 8 | 10 | 12 | |
| M1% | por ano | 18 | 14 | 11 | 9 | 8 | 6.9 | 5.5 | 4.6 | |
| M0.1% | por ano | 28 | 21 | 17 | 14 | 12 | 10.4 | 8.3 | 6.9 | |
| Tm | (anos) | 2 | 3 | 4 | 5 | 6 | 8 | 10 | 15 | 20 |
| M1% | por ano | 2.3 | 1.5 | 1.2 | 0.92 | 0.77 | 0.58 | 0.46 | 0.31 | 0.23 |
| M0.1% | por ano | 3.5 | 2.3 | 1.7 | 1.38 | 1.15 | 0.86 | 0.77 | 0.69 | 0.63 |
A Tabela 4.7.1.1 mostra um conjunto de valores de M definidos para a longevidade de 99%, assim como para a longevidade de 99.9%.
A Tabela 4.7.1.1 pode ser usada como uma primeira tentativa grosseira de estimar mortalidades em conjunto com uma análise de progressão de modas (particularmente para espécies tropicais). Se, por exemplo, na análise de progressão modal (ver Secção 3.4.2) encontram-se um número significante (mais de 1%) de indivíduos com idade superior a três anos, não deve ser aceite uma mortalidade Z maior do que 1.5. Caso sejam encontrados muitos poucos indivíduos com mais de três anos (menos do que 1 por mil) pode-se aceitar uma mortalidade maior que 2.3.
Sendo a longevidade tão difícil de ser observada tal como a mortalidade natural, a relação entre ambas não nos proporciona um método simples de estimar M, mas os conceitos são apresentados de um modo que talvez facilite a compreensão. A facilidade ou não de determinar a longevidade de uma certa espécie depende da dificuldade de determinar a idade dos indivídous mais velhos. Se a idade dos indivíduos mais velhos pode ser lida nas estruturas duras e se o manancial não esta sendo explorado pela pesca, será relativamente fácil obter uma estimação de Tm.
Os aspectos acima mencionados foram discutidos por Hoenig (1983), que também desenvolveu um modelo para estimar Z a partir de observações de longevidade. Este modelo é basicamente o mesmo que o de Alagaraja (1984), mas aplica-se a Z em lugar de M. Hoenig achou a seguinte equação linear baseada em observações de Z e de Tm:
ln Z = a + b*ln Tm com
a = 1.46 e b = -1.01 para peixes
(com base em 84 manancias de 53 espécies) e
a = 1.23 e b = -0.832 para moluscos
(com base em 28 manancias de 13 espécies)
Os resultados acima foram obtidos principalmente com dados de mananciais não explorados. Hoenig sugere que a idade máxima, Tm, deve ser estimada dos “indivíduos mais velhos” da amostra. Este procedimento, no entanto, é um pouco problemático pois a estimação de Tm depende do tamanho da amostra e da proporção da amostra que seja considerada representativa dos “indivídous mais velhos”.
Finalmente deve-se dar ênfase que a suposição de que M permanece constante para todos os grupos de idade (comprimento) dentro da mesma espécie, é altamente irrealista para certas idades. É evidente que um indivíduo menor está exposto a uma maior mortalidade por predação de que um maior, simplesmente pelo facto de que animais menores têm mais predadores do que animais maiores e esta diferença na mortalidade por predação, (que é talvez a maior causa da mortalidade natural para peixes pequenos) deve ser relativamente alta.
De facto, quando se estimou mortalidades por predação em análise de coortes multiespecíficas combinada com dados sobre conteúdos estomacais, o Grupo de Trabalho do ICES em multiespécies (ICES, 1986; Gislason e Sparre, 1987), encontrou que a mortalidade do grupo 0 dos peixes do Mar do Norte era 10 vezes maior que a do grupo 2 (ver também Secção 10.2).
Pauly (1980b) fez uma análise de regressão de M (por ano) contra K (por ano), L∞ (cm) e T (temperatura média da superfície em graus centígrados), com base nos dados de 175 diferentes manancias de peixes, e estimou a relação linear empírica.
| ln M = -0.0152-0.279*ln L∞+0.6543*ln K+0.463*ln T | (4.7.2.1) |
A Tabela 4.7.2.1 mostra valores de M por ano calculados pela “fórmula de Pauly” para várias combinações de L∞, K e T. Deve ser tomado em conta que as estimações de M obtidas através da Eq. 4.7.2.1 pertencem à categoria de “suposições qualificadas”.
Tabela 4.7.2.1 Mortalidade natural (por ano) calculada pela fórmula de Pauly para várias combinações de L∞, K e T
| T = 5 C° | T = 25 C° | |||||||
| L∞ | K 0.1 | 0.5 | 1.0 | 2.0 | 0.1 | 0.5 | 1.0 | 2.0 |
| 10 | 0.24 | 0.7 | 1.1 | 1.7 | 0.51 | 1.5 | 2.3 | 3.6 |
| 80 | 0.14 | 0.38 | 0.6 | 1.0 | 0.29 | 0.8 | 1.3 | 2.0 |
| 200 | 0.10 | 0.30 | 0.47 | 0.7 | 0.22 | 0.6 | 1.0 | 1.6 |
A Eq. 4.7.2.1 pode ser correcta para um “peixe típico”, mas pode não se aplicar a um determinado manacial de peixes. A fórmula indica que:
Isto implica que qualquer outro aspecto que possa influenciar a mortalidade natural é considerado “um ruído aleatório em torno da linha de regressão” (Eq. 4.7.2.1). Outros aspectos podem ser, por exemplo, o comportamento (agregação em cardumes, pelágico/demersal), a fisiologia da reprodução, o ecossistema (abundância de predadores). Pauly (1983) sugere a multiplicação por 0.8 para aplicar a fórmula da Eq. 4.7.2.1 a peixes em cardumes, de maneira a reduzir a estimação em 20%:
M = 0.8*exp[-0.0152 - 0.279*ln L∞ + 0.6543*ln K + 0.463*ln T ] (4.7.2.2)
Deve ser tomado em conta também que a qualidade dos dados que serviram de base para a análise da regressão da qual foi derivada a Eq. 4.7.2.1 pode ser questionada. Para chegar à Eq. 4.7.2.1 Pauly precisou de “observações” de M, que, como já foi discutido acima, são muito difíceis de serem obtidas. Qualquer valor de M usado para a estimação da Eq. 4.7.2.1 pode ser questionável. Por isso, é recomendável usar apenas uma casa décimal quando se apresentam os resultados da Eq. 4.7.2.1. Para algumas espécies o resultado parece ser duas vezes ou metade do que deveria ser. No entanto, quando não existe nenhuma outra informação sobre M, como na maioria dos casos, não devemos duvidar em aplicar a Eq. 4.7.2.1 ou a fórmula de Rikhter e Efanov discutida na Secção 4.7.3. Na realidade, somente para mananciais virgens, não explorados, (M = Z) é que estamos em condições de estimar M.
Note que a fórmula de Pauly é baseada somente em mananciais de peixes, e que o resultado depende de como foram medidos os peixes (comprimento total, comprimento padrão, comprimento furcal, etc). Porém, como a equação de Pauly dá apenas uma estimação grosseira de M, podemos ignorar este pormenor. Não usar a fórmula de Pauly para crustáceos, moluscos, cefalópodes ou quaisquer outros invertebrados, pois a fórmula não se aplica a estes grupos.
Beverton e Holt (1959) investigaram a relação existente entre a longevidade, Tm e a relação Lm/L∞, onde Lm é o comprimento da primeira maturação sexual. Holt (1962) observou também, que geralmente é aceite que a relação Lm/L∞ é aproximadamente 2/3 (com uma média de 0.64 e valores mínimos e máximos de 0.3 e 0.9, respectivamente).
Continuando estas investigações de dinâmica comparativa para mananciais de espécies de altas latitudes Rikhter e Efanov (1976) mostraram que existe uma associação entre M e Tm50%, a idade em que 50% da população está matura (tambem chamada de “idade de 1a maturação”):
| M = 1.521/(Tm50%0.720)-0.155 por ano | (4.7.3.1) |
Os autores sugerem também que Tm50% é igual à “idade óptima” definida como sendo a idade na qual a biomassa de uma coorte atinge o máximo.
A Eq. 4.7.3.1 dá os seguintes valores para Tm50%:
| Tm50% | 4 meses | 8 meses | 1 ano | 5 anos | 10 anos |
| M | 3.2 | 1.9 | 1.4 | 0.3 | 0.1 |