Este capítulo trata basicamente dos mesmos problemas do Capítulo 4, no entanto, a análise e os dados requeridos são mais pormenorizados. Os métodos do Capítulo 4 poderiam ser aplicados a conjuntos de dados originados de pequenas amostras de capturas comerciais ou de cruzeiros de investigação, enquanto que os métodos no Capítulo 5 requerem estimações do número total capturado pela pesca comercial.
Os métodos (ou modelos) descritos neste capítulo estão estritamente relacionados com os descritos no Capítulo 8. No Capítulo 5 trata-se de métodos que podem ser usados para analisar o efeito que uma pescaria tem sobre uma determinada classe anual do manancial e o Capítulo 8 trata dos métodos que podem ser usados para prever o efeito futuro dos diferentes níveis do esforço de pesca. Estes últimos são geralmente baseados nos resultados dos primeiros. Os métodos que focam o passado, usnado dados “históricos” são chamados “análise da população virtual (VPA) (virtual population analysis)” ou “análise de coortes”, enquanto que os que visam o futuro são chamados “métodos de projecção” ou “métodos de Thompson e Bell”.
A VPA e a análise de coortes foram desenvolvidos inicialmente como métodos baseados em idades. No entanto, nos anos recentes, os métodos baseados em comprimentos também têm sido desenvolvidos, o que é de particular interesse para as pescarias tropicais. Os métodos baseados em idades são discutidos nas Secções 5.1 e 5.2, enquanto que os métodos baseados em comprimentos são tratados nas Secções 5.3.
Foram também desenvolvidas versões da VPA multiespecíficas, mas fogem dos objectivos deste manual. Uma abordagem geral destes métodos é apresentada por Sparre, 1991.
Para aplicação desses métodos necessita-se de informações sobre as capturas, em termos do número de peixes. O desembarque total deve estar distribuido pelos grupos de idade (métodos baseados em idade) ou classes de comprimento (métodos baseados em comprimento). Os totais são obtidos pela ponderação da distribuição por idades ou comprimentos, das amostras aleatórias dos desembarques, usando informações sobre o total dos desembarques em toneladas. Tabelas de desembarque total em números, por idades ou comprimentos, por ano ou mês, têm que ser preparadas antes de iniciarmos a análise.
A análise da população virtual ou VPA é basicamente uma análise das capturas da pesca comercial, obtida através da estatística das pescas, combinadas com informações detalhadas sobre qual a contribuição de cada coorte para as capturas, que é geralmente obtida através de programas de amostragens ou leituras de idades. A palavra “virtual”, introduzida por Fry (1949) é baseada em uma analogia com a “imagem virtual”, conhecida da física. Uma “população virtual” não é a população real, mas é a única que é mensurável.
A ideia que fundamenta o método é analisar aquilo que é mensurável, a captura, de forma a calcular a população que deve ter existido para produzir essa captura (ver Fig. 5.1.1).
O desembarque total de uma coorte durante o seu tempo de vida é a primeira estimação do número de recrutas daquela coorte. É, no entanto, uma subestimação uma vez que alguns peixes devem ter morrido por causas naturais. Dada uma estimação de M podemos fazer um retrocálculo e determinar quantos peixes daquela coorte estavam vivos ano a ano e, finalmente, quantos recrutas haviam. Ao mesmo tempo podemos determinar os valores do coeficiente de mortalidade de pesca F, já que foram calculados os sobreviventes e sabemos quantos deles foram capturados em um ano particular.
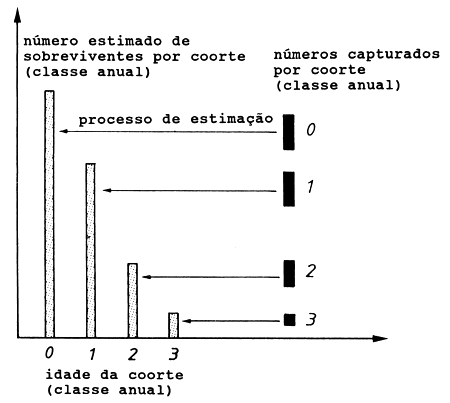
Fig. 5.1.1 Aspectos básicos da VPA. Para mais explicações ver texto
Portanto, a VPA lida com a população numa perspectiva histórica. A vantagem de utilizar uma VPA é que, uma vez conhecida a história dessa pescaria, torna-se mais fácil prever as capturas futuras, que é geralmente um dos objectivos mais importantes dos cientistas pesqueiros.
Uma revisão completa do desenvolvimento dos métodos da VPA é dada por Megrey (1989). O método originou-se na URSS, onde Derzhavin (1922) foi provavelmente o primeiro a combinar dados de idade com estatísticas de capturas. O método foi redescoberto por Fry (1949) e posteriormente modificado por muitos outros autores, incluindo Gulland (1965) e Pope (1972). As modificações feitas por Pope são geralmente referidas como “análise de coortes de Pope” e serão discutidas separadamente na Secção 5.2.
Pauly (1984) e Jones (1984) fizeram revisões práticas dos métodos da VPA, e também de outros.
A maneira mais fácil de explicar os conceitos da VPA é seguir um exemplo baseado em dados reais.
Exemplo 18: Análise da população virtual (VPA), badejo do Mar do Norte
Os dados apresentados na Tabela 4.4.3.1 são os necessários para se efectuar a análise da população virtual, VPA, isto é, o número total capturado por grupos de idade no total das capturas comerciais. Para expor os conceitos da VPA, vamos considerar a coorte de 1974 do badejo, números sublinhados na Tabela 4.4.3.1. A anotação usada é a mesma da Secção 4.4.3. C(y,t,t+1) = número capturado no ano y com idades entre t e t+1 anos (em milhões).
Os números capturados (em unidades de milhões) foram:
C(1974,0,1) = 599 , número capturado entre a idade de 0 a 1
C(1975,1,2) = 860 , número capturado entre a idade de 1 a 2
C(1976,2,3) = 1071 , número capturado entre a idade de 2 a 3
C(1977,3,4) = 269 , número capturado entre a idade de 3 a 4
C(1978,4,5) = 69 , número capturado entre a idade de 4 a 5
C(1979,5,6) = 25 , número capturado entre a idade de 5 a 6
C(1980,6,7) = 8 , número capturado entre a idade de 6 a 7
Iniciamos os cálculos a partir do fim, ou seja, com o número capturado entre as idades 6 e 7, C(1980,6,7) = 8 milhões de peixes. Suponha que sabemos que a mortalidade natural foi M = 0.2 por ano para todos os grupos de idade. Então se também soubéssemos a mortalidade por pesca para o grupo de idade entre 6 e 7 anos, o chamado grupo-6, poderíamos calcular quantos peixes haveriam no mar em 1 de Janeiro de 1980, N(1980,6), de modo a proporcionar uma captura de 8 milhões de badejos em 1980, usando a equação de captura (Eq. 4.2.7):
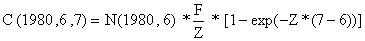
Se fizermos uma suposição inicial de F(1980,6,7) = 0.5 por ano, então Z = 0.5+0.2 = 0.7 e a equação de captura fica então:
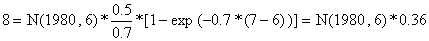
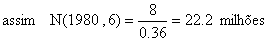
Agora que sabemos o número de sobreviventes no início de 1980, N(1980,6), que por sua vez, é igual ao número no fim de 1979, podemos calcular quantos indivíduos haveriam no mar em 1 de Janeiro de 1979 para que a captura durante 1979 fosse (em números): C(1979,5,6) = 25 milhões.
No entanto, em vez de supor o valor de F podemos também agora calcular qual é a mortalidade por pesca correspondente a esta captura. Para tal utilizamos novamente a Eq. 4.2.7, mas agora conjuntamente com o modelo exponencial decrescente (Eq.4.2.6). (O termo (t2-t1) = (t+1-t) foi omitido porque é igual a 1 neste exemplo).
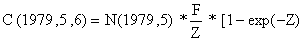 | (5.1.1) |
e
N(1980,6) = N(1979,5)*exp(-Z)
que é equivalente a:
| N(1979,5) = N(1980,6)*exp(Z) | (5.1.2) |
Substituindo o valor de N(1980,6) por 22.2 milhões calculado acima temos:
N(1979,5) = 22.2*exp(Z)
Substituindo este resultado e o número capturado, C(1979,5,6) = 25 milhões na Eq. 5.1.1 obtemos:
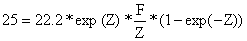
que depois dos cálculos é equivalente a
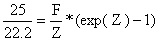
Assume-se que M é 0.2, então substituindo Z = F+M = F+0.2 obtemos:
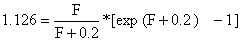
Desta forma obtivemos uma equação onde F é a única variável desconhecida. Resolvendo-a obtemos uma estimação de F. No entanto, a equação acima não pode ser resolvida com manipulações algébricas. A sua solução é obtida através do cálculo de tentativa e erro. Posteriormente, este problema técnico de ordem menor será discutido e veremos como pode ser contornado. Por enquanto, vamos esquecê-lo e aceitar que F = 0.696 é a solução, isto é:
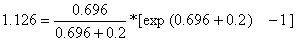
De F = 0.696 e M = 0.2 podemos derivar
Z(1979,5,6) = M + F(1979,5,6) = 0.2+0.696 = 0.896
Com a estimação de Z(1979,5,6) = 0.896, o número de peixes do grupo-5 em 1 de Janeiro de 1979 é facilmente encontrado através do modelo decrescente (Eq. 5.1.2):
N(1979,5) = N(1980,6)*exp(Z(1979,5,6)) ou
N(1979,5) = 22.2*exp(0.896) = 54.4 milhões
Os resultados dos cálculos feitos anteriormente podem ser resumidos como se segue:
| grupo idade | ano | no capturado durante ano y | Mort. por pesca durante ano y | no de sobreviventes em 1 Jan. do ano y |
| t | y | C(y,t,t+1) | F(y,t,t+1) | N(y,t) |
| 0 | 1974 | 599 | ⇑ | ⇑ |
| 1 | 1975 | 860 | ||
| 2 | 1976 | 1071 | ⇑ | ⇑ |
| 3 | 1977 | 269 | ||
| 4 | 1978 | 69 | ⇑ | ⇑ |
| 5 | 1979 | 25 | 0.70 | 54.4 |
| 6 | 1980 | 8 | 0.50 *) | 22.2 |
*) suposição inicial de F terminal
O próximo par N(1978,4) e F(1978,4,5) pode ser calculado aplicando-se exactamente o mesmo processo utilizado para 1979. Desta maneira podemos “retroceder no tempo” estimando o número de sobreviventes e a mortalidade por pesca para cada grupo de idade (conforme indicado pelas setas).
Note que, ao contrário dos métodos da curva de capturas, não se assume que F (e Z) sejam constantes, mas sim cada grupo de idade pode ter um valor diferente de F. Este método fornece, deste modo, uma análise mais detalhada da população, que qualquer outro método apresentado até agora. As duas equações da VPA derivadas acima têm a seguinte forma geral:
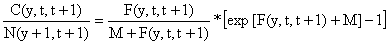 | (5.1.3) | |
| N(y,t) = N(y+1,t+1) * exp[F(y,t,t+1)+M] | (5.1.4) |
Para o ano 1978, no exemplo, obtemos:
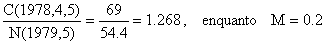
Substituindo estes valores na Eq. 5.1.3 obtemos por tentativa e erro:
F(y,t,t+1) = F(1978,4,5) = 0.757
e substituindo este valor de F e o número de sobreviventes em 1 de Janeiro 1979 na Eq. 5.1.4 obtemos o número de sobreviventes em 1 de Janeiro 1978:
N(1978,4) = N(1979,5)*exp[F(1979,4,5)+M] = 54.4*exp[0.757+0.2] = 141.9
Repetindo o processo para os anos 1977 a 1974 obtêm-se as estimações da mortalidade por pesca e os números de indivíduos do manancial como mostrado na Tabela 5.1.1.
Tabela 5.1.1 Resultados da VPA para a coorte de 1974 do badejo (dados da Tabela 4.4.3.1, números em milhões)
| grupo de idade | ano | no capturado durante ano y | mort. por pesca durante ano y | no de sobreviventes em 1 Jan. do ano y |
| t | y | C(y,t,t+1) | F(y,t,t+1) | N(y,t) |
| 0 | 1974 | 599 | 0.16 | 4390 |
| 1 | 1975 | 860 | 0.37 | 3054 |
| 2 | 1976 | 1071 | 1.11 | 1729 |
| 3 | 1977 | 269 | 0.99 | 465 |
| 4 | 1978 | 69 | 0.76 | 142 |
| 5 | 1979 | 25 | 0.70 | 54.4 |
| 6 | 1980 | 8 | 0.50 *) | 22.2 |
*) assume-se que é previamente conhecida
A Fig. 5.1.2 ilustra a dinâmica de uma coorte, descrita pela VPA, para o badejo do Mar do Norte (Tabela 5.1.1). Neste caso M é relativamente pequeno comparado com F, o que pode ser verificado se compararmos o número capturado (Eq. 4.2.8 com t2-t1 = 1):
| C(y,t,t+1) = F(y,t,t+1) * N(y,t,t+1) | (5.1.5) |
com o número de mortos naturais:
| D(y,t,t+1) = M(y,t,t+1) * N(y,t,t+1) | (5.1.6) |
A Fig. 5.1.2 apresenta os resultados como o número de sobreviventes, N, mas poderíamos perfeitamente ter escolhido a mortalidade por pesca, F, como resultado final pois:
F e C determinam N e
N e C determinam F
de forma que há uma correspondência entre N e F quando C e M são conhecidos.
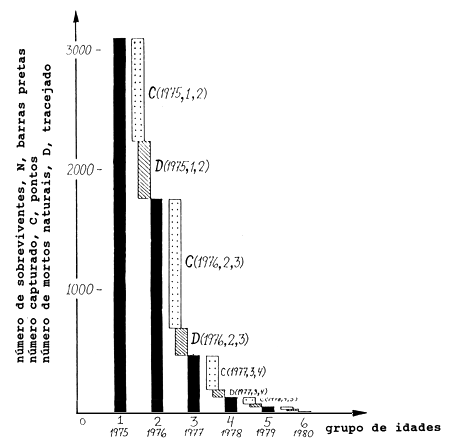
Fig. 5.1.2 Número de sobreviventes, N (barras pretas), número capturado, C = F*N e número de mortos naturais, D = M*N, calculados pela VPA da Tabela 5.1.1 para o badejo do Mar do Norte
VPA usando o grupo mais
No Exemplo 18 iniciámos com o cálculo de N(1980,6), mas não mencionamos os peixes com mais de 6 anos de idade. Esta aproximação é correcta, pois não é necessário considerar os grupos mais idosos. No entanto, pode haver muitos peixes com mais de 6 anos, e passamos a querer considera-los, mas como são difíceis de os separar em grupos de idade, juntamo-os em um grupo chamado grupo mais. Ao considerar este grupo é necessário modificar as fórmulas correspondentes.
Voltando ao exemplo e substituindo C(1980,6,7) pelo grupo mais:
C(1980,6+) = C(1980,6,7) + C(1981,7,8) + C(1982,8,9) + …
onde a soma contem todos os sobreviventes em número, ou as capturas em número de todos os peixes com 6 anos ou mais de idade.
Assumimos ainda que a mortalidade por pesca é a mesma para todas as componentes do grupo mais:
F(1980,6+) = F(1980,6,7) = F(1981,7,8) = F(1982,8,9) = …
A equação da captura do grupo mais velho (ver Exemplo 18):
C(1980,6,7) = N (1980,6)*(F/Z)*(1-exp(-Z(7-6)))
deve agora ser substituída por
C(1980,6+) = N(1980,6)*(F/Z)*(1-exp(-Z(∞-6)))
e porque [1-exp(-Z(∞-6))] = 1-0 = 1, o último termo desaparece de modo que
C(1980,6+) = N(1980,6)*(F/Z)
Assim, geralmente, nos casos onde a primeira observação é um grupo mais, a VPA é iniciada por
| C((y,t+) = N(y,t)*F(y,t+)/Z(y,t+) | (5.1.7) |
Teoricamente, os resultados devem ser iguais quer o último grupo de idade seja ou não um grupo mais.
O conceito de biomassa
O conceito de biomassa, associado à Tabela 5.1.1, é bastante directo, quando consideramos o peso de uma coorte num dado tempo; por exemplo, o peso de uma coorte no ano 1979 é N(1979,5)*w(5), onde w(5) é o peso do corpo de um badejo de 5 anos de idade. Porém o conceito de biomassa que reflecte a coorte durante todo o seu tempo de vida é mais difícil de entender.
A biomassa média em 1 de Janeiro durante os 6 anos de vida da coorte é:
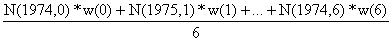
A biomassa média anual poderia ser definida como:
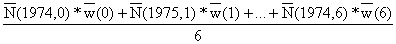
onde N é definido pela Eq. 4.2.9 como t2-t1 = 1 e w é o peso médio do corpo durante um ano. Os dois conceitos de biomassa são diferentes e não é evidente como e quando os usar. O mesmo tipo de problema surge quando se tenta definir o número médio de sobreviventes. Voltaremos ao conceito de biomassa nas seguintes secções.
Aspectos básicos da VPA
Do número capturado em cada grupo de idade, a VPA estima quantos peixes deveriam haver no mar, para que fosse obtida aquela captura, supondo que a mortalidade natural é conhecida (ver Fig. 5.1.1). Se a captura constitui uma pequena fracção do manancial (isto é, se F é pequeno) a estimação do tamanho do manancial torna-se menos precisa. Assim, quanto maior a mortalidade por pesca mais fiável é a VPA.
Assume-se que a mortalidade natural, M, é conhecida a partir de estudos independentes da VPA, mas, na verdade, na maioria dos casos ela é desconhecida. A confiança da VPA depende também do valor de M em relação a F. Geralmente a estimação de M é uma “suposição qualificada”, mas se M é pequeno em relação a F, não importa muito se a suposição de M é imprecisa. O significado de uma “suposição qualificada” foi discutido na Secção 4.7.
Uma série de equações só pode ter uma solução única apenas quando o número de equações se iguala ao número de variáveis desconhecidas. Se houver mais variáveis do que equações, haverá ilimitadas soluções.
No nosso caso, a série de equações utilizadas na VPA consiste em pares das Eqs. 5.1.3 e 5.1.4, para cada grupo de idade. Aparentemente, existem três variáveis desconhecidas em cada série de duas equações, que são N(y,t), N(y+1,t+1) e F(y,t,t+1). No entanto, em todos os casos, com excepção da primeira série que utiliza o grupo mais velho, N(y+1,t+1) é conhecido a partir da solução da série de equações anterior, e ficamos, então, com duas variáveis em duas equações e, portanto, com uma solução única.
O problema com a primeira série de equações, que pertencem ao grupo mais idoso, pode ser resolvido fazendo uma suposição aceitável e formulando-a como uma equação adicional. Podemos então obter uma solução que é condicionada por esta suposição. A solução no caso de uma VPA é assumir um valor para F do grupo mais idoso, o chamado “F terminal”.
Por exemplo, podíamos assumir que o F terminal é igual ao F do segundo grupo de maior idade, de modo que a equação adicional será:
F7 = F6 (assumindo que 7 é o grupo mais idoso)
Temos então quatro equações, duas séries de Eqs. 5.1.3 e 5.1.4, com quatro variáveis desconhecidas: F7, N7, N6 e N5.
No caso em que há mais equações do que variáveis desconhecidas não há, geralmente, solução. Neste caso usamos uma análise de regressão para determinar o melhor “ajuste” aos dados com o objectivo de encontrar uma solução, e podemos calcular limites de confiança. Na análise de regressão o conceito de “variáveis desconhecidas” substitui-se pelo conceito de “parâmetros”.
Para calcular os intervalos de confiança dos parâmetros estimados, o número de observações tem que ser maior que o número de parâmetros. O número de parâmetros na VPA (os N's e F para o grupo de idade mais velho) é igual ao número de observações (os C's) mais um. Desta forma não é possível calcular os limites de confiança dos N's estimados (ou dos F's dos outros grupos de idade).
Os dados usados no Exemplo 18 para ilustrar a VPA foram obtidos a partir das leituras directas de idade (otólitos). No entanto, os dados de entrada poderiam ter sido derivados de séries temporais de dados de frequências de comprimento decompostos em componentes de coortes, por exemplo, através do método de Bhattacharya (Secção 3.4). Este assunto é melhor discutido no fim da Secção 5.3.
A VPA é um método de análise de dados históricos que estima os parâmetros da população. O objectivo final dos parâmetros estimados é determinar a estratégia óptima de pesca, ou seja, a matriz de F à idade ou o chamado “padrão de pesca” que fornece, a longo prazo, o melhor rendimento do manancial em questão. Para avaliar as diferentes (futuras) estratégias de pesca necessitamos de um modelo que possa prever o nível do manancial e a captura para as várias hipóteses alternativas. O “modelo de Thompson e Bell” (Secção 8.6) é a versão que projecta o padrão de pesca a longo prazo.
Programas de computador
Mesnil (1988) apresenta um pacote de programas para microcomputadores, ANACO (ANAlise de COortes) que desenvolve os cálculos da VPA conforme descrito anteriormente e também oferece um número de opções adicionais, por exemplo a execução de análises de sensibilidade.
A VPA implica a solução da Eq. 5.1.3 por uma técnica numérica (método de tentativa e erro) que é um problema técnico sem grande importância quando se dispõe de um computador. No entanto, o problema pode ser contornado facilmente, de forma que a VPA possa também ser realizada com uma calculadora de bolso. A versão da VPA adaptada a calculadoras de bolso é a “análise de coortes” desenvolvida por Pope (1972), revista em Jones (1984) e Pauly (1984).
A análise de coortes é conceptualmente idêntica à VPA, mas a técnica de cálculo é mais simples. É baseada em uma aproximação, ilustrada na Fig. 5.2.1, que mostra o número de sobreviventes de uma coorte durante um ano. Na verdade, a captura é obtida continuamente durante o ano, mas na análise de coortes assume-se que todos os peixes são capturados em um único dia. Este dia é escolhido como sendo 1 de Julho, isto é, quando se passou metade do ano.
Consequentemente, na primeira metade do ano os peixes são submetidos somente à mortalidade natural, de maneira que o número de sobreviventes em 1 de Julho será:
N(y,t+0.5) = N(y,t)*exp(-M/2)
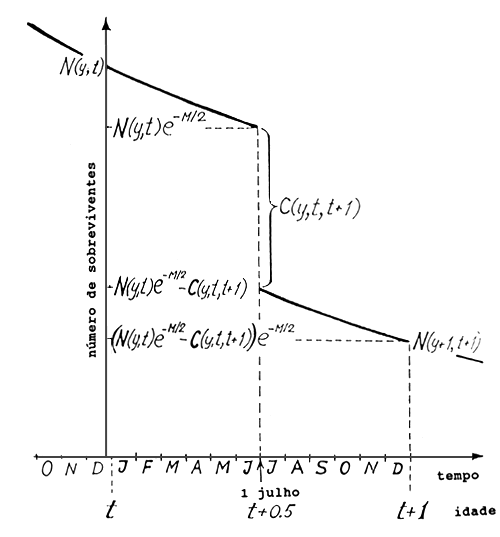
Fig. 5.2.1 Ilustração da aproximação básica da análise de coortes de Pope (ver mais explicações no texto)
A captura é, então, realizada instantaneamente e o número de sobreviventes passa a ser:
N(y,t)*exp(-M/2) - C(y,t,t+1)
O número de sobreviventes passa a sofrer apenas mortalidade natural na segunda metade do ano e finalmente o número de sobreviventes no fim do ano é:
N(y+1,t+1) = [N(y,t)*exp(-M/2) - C(y,t,t+1)]*exp(-M/2)
Por conveniência de cálculo a equação é rearranjada:
| N(y,t) = [N(y+1,t+1)*exp(M/2) + C(y,t,t+1)]*exp(M/2) | (5.2.1) |
Note que F, o responsável pelos problemas de cálculo na equação da VPA, não aparece aqui. Demonstramos o método com base no mesmo conjunto de dados, a coorte de 1974 do badejo do Mar do Norte.
Exemplo 19: Análise de coortes de Pope, badejo do Mar do Norte
Para aplicar a Eq. 5.2.1 ao exemplo do badejo começamos, de igual modo que a VPA, assumindo que F para o grupo mais velho “F terminal” é conhecido, F(1980,6,7) = 0.5, e M = 0.2, então começamos por calcular N(1980,6), da equação de captura:
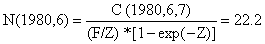
Então a Eq. 5.2.1 é aplicada para calcular N(1979,5):
N(1979,5) = [N(1980,6)*exp(M/2) + C(1979,5,6)]*exp(M/2)
= [22.2*1.1052 + 25]*1.1052 = 54.7
e assim continuamos da mesma forma:
N(1978,4) = [N(1979,5)*exp(M/2) + C(1978,4,5)]*exp(M/2)
= [54.7*1.1052 + 69]*1.1052 = 143.1
N(1977,3) = [143.1*1.1052 + 269]*1.1052 = 472.1
. . . . . . etc. . . . . . .
Assim, da mesma maneira que a VPA, andamos para trás no tempo estimando um novo número do manancial passo a passo. Os cálculos para os números no manancial, os N's, são dados na primeira metade da Tabela 5.2.1 (com uma notação menos extensiva).
As estimações da mortalidade por pesca são obtidas dos N's estimados, por:
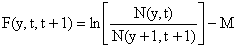 | (5.2.2) |
Tabela 5.2.1 Cálculos para a análise de coortes de Pope baseada em idades, ilustrada para a coorte de 1974 do badejo do Mar do Norte (da Tabela 4.4.3.1)
| ANÁLISE DE COORTES DE POPE BASEADA EM DADES | |
| M = 0.2 por ano | |
| FACTOR DE MORTALIDADE NATURAL: G = exp(M/2) = exp(0.2/2) = 1.1052 | |
| SUPOSIÇãO DO F TERMINAL: F6 = 0.5 | |
| Números do manancial: | 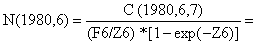 |
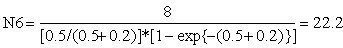 | |
| N(1979,5) = N5 = (N6*G + C5,6)*G = | |
| N5 = (N6*G + C5)*G = (22.2*G + 25)*G = 54.7 | |
| N4 = (N5*G + C4)*G = (54.7*G + 69)*G = 143.1 | |
| N3 = (N4*G + C3)*G = (143.1*G + 269)*G = 472.1 | |
| N2 = (N3*G + C2)*G = (472.1*G + 1071)*G = 1760.3 | |
| N1 = (N2*G + C1)*G = (1760.3*G + 860)*G = 3100.4 | |
| N0 = (N1*G + C0)*G = (3100.4*G + 599)*G = 4448.9 | |
| Mortalidade por pesca: | |
| F6 = (suposição inicial de F terminal) = 0.50 | |
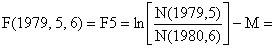 | |
| F5 = ln(N5/N6) - M = ln(54.7/22.2) - 0.2 = 0.70 | |
| F4 = ln(N4/N5) - M = in(143.1/54.7) - 0.2 = 0.76 | |
| F3 = in(N3/N4) - M = ln(472.1/143.1) - 0.2 = 0.99 | |
| F2 = ln(N2/N3) - M = ln(1760.3/472.1) - 0.2 = 1.12 | |
| F1 = ln(N1/N2) - M = ln(3100.4/1760.3) - 0.2 = 0.37 | |
| F0 = ln(N0/N1) - M = ln(4448.9/3100.4) - 0.2 = 0.16 | |
que segue do modelo exponencial decrescente resolvido para F:
N(y+1, t+1) = N(y,t)*exp[-F(y,t,t+1) - M]
Os F's estimados são apresentados na segunda metade da Tabela 5.2.1.
Comparando os resultados da VPA (Tabela 5.1.1) com os resultados da análise de coortes (Tabela 5.2.1) existem pequenas diferenças. Apesar das fontes de incertezas envolvidas neste tipo de cálculo, podemos dizer que as diferenças entre a VPA e a análise de coortes são insignificantes. Pope (1972) mostrou que para valores de F < 1.2 e M < 0.3 as diferenças são pequenas. A única vantagem da análise de coortes comparada á VPA é que pode ser facilmente realizada com uma calculadora de bolso. Para fazer a VPA com uma calculadora, é necessário realizar o tedioso cálculo de tentativa e erro para F (a não ser que a calculadora seja totalmente programável).
Example 19a: Análise de coortes para classes anuais sucessivas
A interpretação das mortalidades por pesca estimadas para uma classe anual durante toda a sua vida (Tabelas 5.1.1 e 5.2.1) não é clara. As mudanças com o tempo e com a idade, provavelmente devem-se a diferenças de esforço entre idades ou anos de pesca. A amostragem, no entanto, proporciona sempre dados para outras classes anuais (ver Tabela 4.4.3.1) que podem ser tratados da mesma forma. Os resultados de F e N estão na Tabela 5.2.2 onde as classes anuais de 1969–80 estão representadas por vários grupos de idade. O valor de 0.5 como F terminal foi escolhido para todas as classes anuais onde o grupo de idade 6 estava presente. Os valores de F estimados para a classe anual 1974 foram inseridos como F terminais para as classes anuais representadas somente pelos grupos mais jovens, que ainda não atingiram a idade 6. Os valores médios de F para cada grupo de idade (última coluna) são relativamente diferentes dos valores de F terminal usados. A análise pode ser repetida com as médias como valores finais de F.
Outra possibilidade, consiste em empregar a captura média por grupo de idade (Tabela 4.4.3.1, última coluna). Estes dados formam uma “pseudo-coorte” que representa a evolução média duma coorte em vez da verdadeira coorte de indivíduos, que nasceram todos na mesma altura. A Tabela 5.2.3 mostra os resultados. As mortalidades por pesca estimadas para os peixes mais velhos são maiores que as médias dos F individuais estimados na Tabela 5.2.3, o que se pode dever a alteração no esforço ou no tamanho da malha utilizados nestes anos. O grupo de peixes com 7 anos e mais (grupo 7+), está incluido na Tabela 5.2.3 pois as capturas erráticas deste grupo em anos individuais, são uma média. O número de peixes que entra neste grupo 7+, é estimado de:
N(7) = C(7+) * Z(7+)/F(7+)
que é outra expressão da equação
C(y,t+) = N(y,t) * F(y,t+) / Z(y,t+) da Secção 5.1.
F(7+) é o valor suposto de F terminal.
A utilização de psedo-coortes é importante para a análise de coortes baseada em comprimentos da Secção 5.3.
Os dados da captura na Tabela 4.4.3.1 não são os originais. Registrou-se, originalmente a captura total em peso, a distribuição de frequências ponderadas por comprimentos e realizaram-se leitura de otólitos em subamostras. A partir das leituras de idades, utilizaram-se chaves idade/comprimento (Secção 3.2.1), para transformar os números da distribuição de frequências de comprimentos em idades. A captura total em número por grupo de idade, foi estimada através do peso médio e do peso da captura total.
Neste processo existem muitas fontes de erros, exigindo que a distribuição de frequências de comprimentos seja realista. Isto é verificado multiplicando os números de cada grupo de idade pelo peso individual desse grupo de idade, calculados através dos parâmetros de crescimento conhecidos, ou da amostragem dos pesos médios para cada grupo de idade. Os pesos totais de cada grupo de idade são acumulados e o resultado é comparado com o valor conhecido do peso total da captura. Uma discrepância notória exige uma reexaminação dos dados e dos cálculos.
A biomassa para cada ano é calculada multiplicando os números da população (valores de N da Tabela 5.1.1) pelo peso do peixe.
A Eq. 5.2.1 foi calculada para um período de tempo de um ano. Como no caso da curva de capturas (compare Secção 4.4.4) podemos considerar a captura durante qualquer período de tempo, de t+Δt. Neste caso a Eq. 5.2.1 deve ser substituída pela expressão mais geral:
| N(t) = [N(t+Δt) *exp(M*Δt/2) + C(t,t+Δt)] *exp (M*Δt/2) | (5.2.3) |
O cálculo da Eq. 5.2.3 é similar ao da Eq. 5.2.1, conforme mostrado na Fig. 5.2.2. A equação correspondente à Eq. 5.2.2 é:
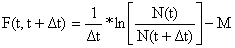 | (5.2.4) |
A principal razão para o índice do ano, y, ter desaparecido nas Eqs. 5.2.3 e 5.2.4, deve-se ao facto de as mesmas serem normalmente utilizadas sob suposição de um sistema de parâmetros constantes (cf. Secção 4.4.4). Além do mais, quando Δt varia não haverá correspondência com os intervalos de tempo e a notação usada para os grupos de idade deixa de ser adequada.
Tabela 5.2.2 Badejo do Mar do Norte. Estimação de mortalidades por pesca e números da população para todas as idades e classes anuais. As estimações de F para 1974 (sublinhados) são adoptados como F terminais em 1980.
| mortalidades por pesca, F(y,t,t+1) | |||||||||
| idade | classe anual | 1974 | 1975 | 1976 | 1977 | 1978 | 1979 | 1980 | média anos 1974–79 |
| 0 | (1974) | 0.16 | 0.11 | 0.16 | 0.30 | 0.39 | 0.35 | 0.16 | 0.24 |
| 1 | (1973) | 0.61 | 0.37 | 0.30 | 0.70 | 0.31 | 0.72 | 0.37 | 0.50 |
| 2 | (1972) | 1.11 | 0.89 | 1.12 | 0.74 | 0.53 | 0.69 | 1.12 | 0.85 |
| 3 | (1971) | 1.26 | 1.13 | 1.24 | 0.99 | 0.71 | 0.77 | 0.99 | 1.02 |
| 4 | (1970) | 1.03 | 0.94 | 1.04 | 0.92 | 0.76 | 0.77 | 0.76 | 0.91 |
| 5 | (1969) | 0.22 | 0.68 | 0.61 | 0.78 | 0.62 | 0.70 | 0.70 | 0.60 |
| 6 | (1968) | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 |
| números na população N(y,t) | |||||||||
| 0 | (1974) | 4449 | 2526 | 3166 | 2828 | 2351 | 1776 | 2456 | 2849 |
| 1 | (1973) | 1645 | 3100 | 1852 | 2208 | 1715 | 1305 | 1021 | 1971 |
| 2 | (1972) | 1806 | 733 | 1760 | 1126 | 899 | 1026 | 519 | 1225 |
| 3 | (1971) | 424 | 486 | 247 | 472 | 441 | 433 | 420 | 417 |
| 4 | (1970) | 69 | 98 | 128 | 59 | 143 | 177 | 164 | 112 |
| 5 | (1969) | 34 | 20 | 31 | 37 | 19 | 55 | 67 | 33 |
| 6 | (1968) | 3 | 22 | 8 | 14 | 14 | 8 | 22 | 12 |
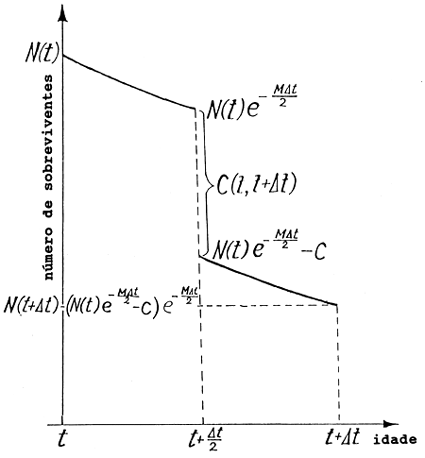
Fig. 5.2.2 Cálculo das fórmulas para a análise de coortes de Pope no caso de intervalos de tempo variáveis (Eqs. 5.2.3 e 5.2.4)
Table 5.2.3 Análise duma pseudo-coorte: captura média por grupo de idade em 1974–80. Badejo do Mar do Norte. Dados da Tabela 4.4.3.1
| idade | captura | № na população no princípio do ano | F |
| 0 | 488 | 3059 | 0.19 |
| 1 | 612 | 2063 | 0.40 |
| 2 | 601 | 1135 | 0.88 |
| 3 | 237 | 385 | 1.14 |
| 4 | 62.3 | 101 | 1.13 |
| 5 | 15.7 | 26.6 | 1.05 |
| 6 | 4.7 | 7.6 | 1.15 |
| 7+ | 1.4 | 2.0 | 0.50 |
As Eqs. 5.2.3 e 5.2.4 aplicadas sob a suposição de um sistema de parâmetros constantes são aplicações típicas da análise de coortes para manaciais de peixes tropicais. Elas podem ser aplicadas para todas as coortes durante um ano ou para a captura média anual durante uma sequência de anos. Retornaremos a este assunto na Secção 5.3.
(Ver Exercício(s) na Parte 2).