Nesta secção dispomos somente de dados de composição de comprimentos para o total das pescarias, para um ano (ou a composição de comprimentos médios para uma sequência de anos). O princípio é basicamente o mesmo da curva de capturas convertida para comprimentos (ver Secção 4.4.5). O termo “análise de coortes baseada em comprimentos” é um pouco enganador, já que não estamos tratando de coortes verdadeiras na presente análise. A coorte verdadeira é substituída pela “pseudo-coorte” que obtemos quando assumimos um sistema de parâmetros constantes (ver Secção 4.4.1). Assim, assumimos que o quadro apresentado por todas as classes de comprimento (ou idades) capturadas durante um ano reflectem o comportamento de uma coorte durante o seu tempo de vida. Voltaremos a este assunto mais adiante e o método será explicado, novamente, com base em um exemplo.
Exemplo 20: Análise de coortes de Jones baseada em comprimentos, pescada do Senegal
A Tabela 5.3.1 apresenta um conjunto de dados para a pesca da pescada na Costa do Senegal (CECAF, 1978), que podem ser usados como entrada para a análise de coortes baseada em comprimentos.
Tabela 5.3.1 Composição de comprimentos da captura total da pescada (Merluccius merluccius) da costa do Senegal (CECAF, 1978), dados de entrada para a análise de coortes baseada em comprimentos
| classe de comprimento cm L1–L2 | número capturado ('000) C(L1, L2) |
| 6–12 | 1823 |
| 12–18 | 14463 |
| 18–24 | 25227 |
| 24–30 | 8134 |
| 30–36 | 3889 |
| 36–42 | 2959 |
| 42–48 | 1871 |
| 48–54 | 653 |
| 54–60 | 322 |
| 60–66 | 228 |
| 66–72 | 181 |
| 72–78 | 96 |
| 78–84 | 16 |
| 84–∞ | 46 |
Da mesma forma que no caso da análise da curva de capturas (cf. Secção 4.4.5) as classes de comprimento podem ser convertidas em intervalos de idade pela equação inversa de von Bertalanffy (Eq. 3.3.3.2 e Eq. 4.4.5.1, respectivamente):
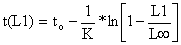 | (5.3.1) | |
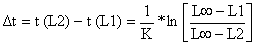 | (5.3.2) |
Para a pescada do Senegal (Tabela 5.3.1) foram estimados os seguintes parâmetros de crescimento de von Bertalanffy e o factor de mortalidade natural como:
K = 0.1 por ano, L∞ = 130 cm e M = 0.28 por ano.
Fazendo to = o (compare com a Secção 4.4.5) e aplicando as Eqs. 5.3.1 e 5.3.2 obtemos as idades relativas, t(L1) e Δt como apresentado na Tabela 5.3.2, colunas B e C, respectivamente.
Para converter a equação da análise de coortes (Eq. 5.2.3) numa versão baseada em comprimentos, somente o termo exp (M*Δt/2) tem que ser mudado. Isto é feito facilmente substituindo Δt pela Eq. 5.3.2.
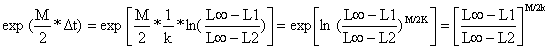 | (5.3.3) |
É conveniente utilizar símbolos em vez deste termo complicado, assim introduzimos os símbolos:
| N(L1) = N(t(L1)) | = número de peixes que atingem o comprimento L1 |
| = número de peixes que atingem a idade t(L1) (também chamado o número de sobreviventes) | |
| N(L2) = N(t(L1)+Δt) | = número de peixes que atingem o comprimento L2 |
| = número de peixes que atingem a idade t(L2) (= t(L1) +Δt) | |
| C(L1, L2) = C(t, t+Δt) | = número de peixes capturados entre os comprimentos L1 e L2 |
| = número de peixes capturados com idades entre t(L1) e t(L2) |

A Eq. 5.2.3 pode agora ser escrita usando os símbolos baseados em comprimentos, como:
| N(L1) = [N(L2) *H(L1,L2) + C(L1,L2)] *H(L1,L2) | (5.3.4) |
Os cálculos efectuados para a Eq. 5.3.4 são similares aos da análise de coortes baseada em idades (Eq. 5.2.1). Iniciamos com o último grupo e usamos a equação de captura:
 | (5.3.5) |
No caso da pescada do Senegal a última classe é a dos indivíduos com 84 cm e mais.
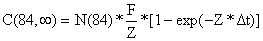
Neste caso Δt refere-se a todos os peixes maiores que 84 cm, de forma que Δt é muito grande. Teoricamente, a idade correspondente a L∞ é ∞, portanto Δt = ∞, e então:
exp(-Z*∞) = 0
A captura em números por classe de comprimento é conhecida (ver Tabela 5.3.1), assim, aproximadamente:
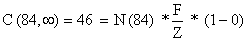
ou
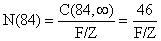
Tabela 5.3.2 Classes de comprimento da pescada (Merluccius merluccius) da costa do Senegal convertidos em intervalos de idade e factores H(L1,L2). K = 0.1 por ano, L∞ = 130 cm, M = 0.28 por ano
| A | B | C | D |
| classe de comp. cm L1–L2 | idade relativa t(L1) | Δt | factor de mortalidade natural H(L1,L2) |
| 6–12 | 0.473 | 0.496 | 1.0719 |
| 12–18 | 0.968 | 0.522 | 1.0758 |
| 18–24 | 1.490 | 0.551 | 1.0801 |
| 24–30 | 2.041 | 0.583 | 1.0850 |
| 30–36 | 2.624 | 0.619 | 1.0905 |
| 36–42 | 3.242 | 0.660 | 1.0967 |
| 42–48 | 3.902 | 0.706 | 1.1039 |
| 48–54 | 4.608 | 0.760 | 1.1122 |
| 54–60 | 5.368 | 0.822 | 1.1220 |
| 60–66 | 6.190 | 0.890 | 1.1337 |
| 66–72 | 7.087 | 0.984 | 1.1478 |
| 72–78 | 8.071 | 1.092 | 1.1652 |
| 78–84 | 9.163 | 1.226 | 1.1873 |
| 84–∞ | 10.389 | - | - |
| as colunas contém respectivamente: B 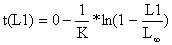 (Eq. 5.3.1, com to = 0) (Eq. 5.3.1, com to = 0)C 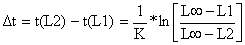 (Eq. 5.3.2) (Eq. 5.3.2)D 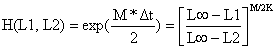 (Eq. 5.3.3) (Eq. 5.3.3)Note: Neste caso H(L1,L2), pode ser calculado quer da fórmula baseada em idades quer na fórmula baseada em comprimentos. Os resultados são os mesmos, mas os cálculos baseados em comprimentos são mais curtos pois não é necessário calcular Δt. | |||
Aqui é necessário novamente fazer uma suposição inicial, neste caso de F/Z (cf. Tabela 5.2.1). Se F/Z para a última classe de comprimento tomar o valor 0.5, então o número de indivíduos que atinge o comprimento de 84 cm será:
N(84) = 46/0.5 = 92
A Coluna D da Tabela 5.3.2 dá os valores de H(L1,L2) para a pescada do Senegal com M = 0.28 por ano e K = 0.1 por ano, isto é M/2K = 0.28/ (2*0.1)= 1.4. O número de pescadas que atingem o comprimento de 78 cm pode ser calculado inserindo na Eq. 5.3.4 o valor de N(L1) como valor de N(L2) obtido para a classe de comprimento maior e o correspondente valor de H da Tabela 5.3.2 Neste caso N(L2) = N(84) = 92 e H(78, 84) = 1.1873.
N(78) = [92*1.1873 + 16]*1.1873 = 148.7
Tabela 5.3.3 Cálculo da análise de coortes por comprimentos de Jones ilustrada para a pescada (Merluccius merluccius) do Senegal. K = 0.1 por ano , L∞ = 130 cm, M = 0.28 por ano. Assume-se o valor 0.5000 para F/Z terminal (indicado por *)
| A | B | C | D | E | F | G |
| classe compr. cm | factor mort.nat. | número capturado ('000) | número sobreviventes ('000) | taxa de exploração | mort. por pesca | mort. total |
| L1–L2 | H(L1,L2) | C(L1,L2) | N(L1) | F/Z | F | Z |
| 6–12 | 1.0719 | 1823 | 98919.3 | 0.1255 | 0.04 | 0.32 |
| 12–18 | 1.0758 | 14463 | 84392.7 | 0.5805 | 0.39 | 0.67 |
| 18–24 | 1.0801 | 25227 | 59475.8 | 0.7920 | 1.07 | 1.35 |
| 24–30 | 1.0850 | 8134 | 27623.0 | 0.6979 | 0.65 | 0.93 |
| 30–36 | 1.0905 | 3889 | 15967.8 | 0.6369 | 0.49 | 0.77 |
| 36–42 | 1.0967 | 2959 | 9861.5 | 0.6785 | 0.59 | 0.87 |
| 42–48 | 1.1039 | 1871 | 5500.5 | 0.6977 | 0.65 | 0.93 |
| 48–54 | 1.1122 | 653 | 2818.8 | 0.5792 | 0.39 | 0.67 |
| 54–60 | 1.1220 | 322 | 1691.5 | 0.5072 | 0.29 | 0.57 |
| 60–66 | 1.1337 | 228 | 1056.6 | 0.5234 | 0.31 | 0.59 |
| 66–72 | 1.1478 | 181 | 621.0 | 0.5890 | 0.40 | 0.68 |
| 72–78 | 1.1652 | 96 | 313.7 | 0.5817 | 0.39 | 0.67 |
| 78–84 | 1.1873 | 16 | 148.7 | 0.2823 | 0.11 | 0.39 |
| 84–∞ | - | 46 | 92.0** | 0.5000* | 0.28 | 0.56 |
| as colunas contém respectivamente B 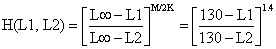 D N(L1) = [N(L2)*H(L1,L2) + C(L1,L2)] *H(L1,L2) ** N(84) = C(84,∞)/(F/Z) = 46/0.5 = 92 E F/Z = C(L1,L2)/[N(L1)-N(L2)] F F = M*(F/Z) / (1-F/Z) G Z = F+M | ||||||
Continuando os cálculos para os comprimentos anteriores (e assim no tempo) os seguintes números do manancial são obtidos:
N(72) = [148.7*1.1652 + 96]*1.1652 = 313.7
N(66) = [313.7*1.1478 + 181]*1.1478 = 621.0
. . . . . etc. . . . . .
Os números do manancial obtidos desta forma para todos as classes de comprimento são dados na Tabela 5.3.3.
Para estimar F poderíamos usar a Eq. 5.2.4, mas é mais conveniente calcular F por:
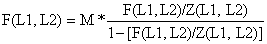 | (5.3.6) | |
| onde a taxa de exploração F/Z é obtida de: | ||
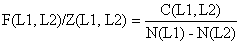 | (5.3.7) | |
Por exemplo, para simplificar escrevemos F/Z para F(L1,L2/Z(L1,L2) obtendo para a classe de comprimento 72–78 cm:
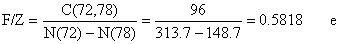
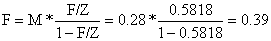
Os resultados completos deste cálculo para a análise de coortes por comprimentos são apresentados na Tabela 5.3.3.
Número médio e biomassa
Queremos agora calcular o número médio de peixes no mar e a sua biomassa. Da simples soma dos valores da coluna de N(L1) na Tabela 5.3.3, não resultaria o valor correcto, porque ao mudar o intervalo de classe resultariam diferentes somas: Os valores de N(L1) mão são mais que o número de indivíduos vivos em qualquer comprimento L1. O processo é encontrar o número médio em cada intervalo de classe e ponderá-lo pelo tempo Δt passado naquele intervalo de classe. É o mesmo problema ocorrido com as Eqs. 4.2.6 e 4.2.9, no qual algumas manipulações aplicadas a ambas resultam:
| N(L1,L2) *Δt = [N(L1)-N(L2)]/Z | (5.3.8) |
que é o número médio anual em cada classe de comprimento.
N(L2) = N(L∞) = 0 pode ser assumido para a última classe. O número médio total de peixes no mar com comprimentos acima do primeiro L1 (aqui 6 cm) será no geral:
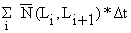 | (5.3.9) |
De forma correspondente, encontramos a biomassa média anual para cada classe de comprimento multiplicando pelo peso médio, w(L1,L2), da classe:
| B(L1,L2)*Δt = N(L1,L2)*Δt*w(L1,L2) | (5.3.10) |
O peso do corpo é calculado de:
| w(L1,L2) = q*[(L1+L2)/2]b | (5.3.11) |
onde q e b são constantes da relação peso-comprimento descrita na Secção 2.6. O peso do corpo do última classe pode ser calculado como w(L1,L∞).
A soma geral
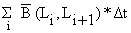 | (5.3.12) |
Tabela 5.3.4 Cálculo das capturas e da biomassa média na análise de coortes de Jones baseada em comprimentos, ilustrada para a
pescada (Merluccius merluccius) do Senegal.
q = 0.00001 kg/cm3, b = 3, K = 0.1 por ano, L∞ = 130 cm,
M = 0.28 por ano
| A | B | C | D | E | F | G | H |
| classe de compr. cm L1–L2 | número captur. ('000) C | número sobreviventes ('000) N(L1) | taxa mort. total Z | peso médio corpo kg w(L1,L2) | média N *Δt ('000) N(L1,L2)*Δt | biomassa média*Δt ton. B*Δt | capturas ton. Y(L1,L2) |
| 6–12 | 1823 | 98919.3 | 0.32 | 0.0073 | 45369 | 330.7 | 13.3 |
| 12–18 | 14463 | 84392.7 | 0.67 | 0.0338 | 37335 | 1260.1 | 488.1 |
| 18–24 | 25227 | 59475.8 | 1.35 | 0.0926 | 23664 | 2191.5 | 2336.3 |
| 24–30 | 8134 | 27623.0 | 0.93 | 0.196 | 12575 | 2475.1 | 1601.0 |
| 30–36 | 3889 | 15967.8 | 0.77 | 0.359 | 7919 | 2845.9 | 1397.6 |
| 36–42 | 2959 | 9861.5 | 0.87 | 0.593 | 5007 | 2970.1 | 1755.3 |
| 42–48 | 1871 | 5500.5 | 0.93 | 0.911 | 2895 | 2638.1 | 1704.9 |
| 48–54 | 653 | 2818.8 | 0.67 | 1.33 | 1694 | 2247.1 | 866.2 |
| 54–60 | 322 | 1691.5 | 0.57 | 1.85 | 1117 | 2068.6 | 596.3 |
| 60–66 | 228 | 1056.6 | 0.59 | 2.50 | 741 | 1852.8 | 570.1 |
| 66–72 | 181 | 621.0 | 0.68 | 3.29 | 451.1 | 1481.9 | 594.6 |
| 72–78 | 96 | 313.7 | 0.67 | 4.22 | 246.5 | 1039.9 | 405.0 |
| 78–84 | 16 | 148.7 | 0.39 | 5.31 | 144.9 | 770.1 | 85.0 |
| 84–∞ | 46 | 92.0 | 0.56 | 12.25 | 164.3* | 2012.7 | 563.5 |
| Totais | 26184.6 | 12977.2 | |||||
| as colunas contém respectivamente E w(L1,L2) = q*[(L1+L2)/2]b F N(L1,L2)*Δt = [N(L1) -N(L2)]/Z G B*Δt = w(L1,L2)*[N(L1)-N(L2)]/Z H Y(L1,L2) = w(L1,L2) * C(L1,L2) * N (L1,L∞)*Δt = N(84)/Z(84,∞) | |||||||
é uma estimação da biomassa média durante o tempo de vida de uma coorte, ou de todas as coortes durante um ano, e é independente do intervalo de classe.
O peso pode também ser usado para estimar as capturas em peso. O peso da captura pertencente à classe i será:
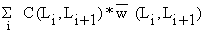 | (5.3.13) |
A Tabela 5.3.4 mostra os cálculos da captura e da biomassa média durante um ano.
Análise de coortes com várias frotas
A VPA e a análise de coortes, baseada em idades ou em comprimentos serve para estimar separadamente, as mortalidades por pesca, causadas por cada uma das várias frotas. Neste contexto, uma frota é um grupo de barcos de pesca com características comuns, como por exemplo a sua arte ou a sua nacionalidade, etc.. Para se poder analisar estes dados, são necessárias as estatísticas de captura de cada frota, tal como as distribuições de frequências de comprimento efectuadas por amostragem.
Table 5.3.5 Análise de coortes baseada em comprimentos para duas frotas.
M = 1, L∞ = 25 cm, K = 0.4.
Valor previsto para F terminal = 1.4
| no capturado ('000) por ano | fracção em | taxas de mortalidade por pesca | |||||||
| classe de comprimento cm | arrasto | rede de emalhar | total | arrasto | rede de emalhar | no de sobreviventes ('000) | total | arrasto | rede de emalhar |
| L1–L2 | C(1) | C(2) | C | C(1)/C | C(2)/C | N(L1) | F | F*C(1)/C = F(1) | F*C(2)/C = F(2) |
| 8–9 | 126 | 0 | 126 | 1.00 | 0 | 9945 | 0.091 | 0.091 | 0 |
| 9–10 | 200 | 0 | 200 | 1.00 | 0 | 8430 | 0.161 | 0.161 | 0 |
| 10–11 | 294 | 0 | 294 | 1.00 | 0 | 6989 | 0.271 | 0.271 | 0 |
| 11–12 | 360 | 0 | 360 | 1.00 | 0 | 5612 | 0.392 | 0.392 | 0 |
| 12–13 | 377 | 0 | 377 | 1.00 | 0 | 4334 | 0.503 | 0.503 | 0 |
| 13–14 | 351 | 11 | 362 | 0.97 | 0.03 | 3207 | 0.615 | 0.597 | 0.018 |
| 14–15 | 283 | 66 | 349 | 0.81 | 0.19 | 2256 | 0.795 | 0.644 | 0.151 |
| 15–16 | 194 | 195 | 389 | 0.50 | 0.50 | 1468 | 1.332 | 0.666 | 0.666 |
| 16–17 | 114 | 232 | 346 | 0.33 | 0.67 | 787 | 2.261 | 0.746 | 1.515 |
| 17–18 | 41 | 84 | 125 | 0.33 | 0.67 | 288 | 1.984 | 0.655 | 1.329 |
| 18–19 | 18 | 18 | 36 | 0.50 | 0.50 | 100 | 1.406 | 0.703 | 0.703 |
| 19–20 | 9 | 2 | 11 | 0.82 | 0.18 | 38.4 | 0.932 | 0.764 | 0.168 |
| 20–21 | 5 | 0 | 5 | 1.00 | 0 | 15.6 | 0.916 | 0.916 | 0 |
| 21–∞ | 3 | 0 | 3 | 1.00 | 0 | 5.14 | 1.400 | 1.400 | 0 |
A partir da equação de capturas, Eq. 5.1.5:
C = F*N
com N sendo o número médio anual da população de um grupo de idade ou de tamanho específico. Os índices de idade ou de comprimento, como por exemplo N(t) e N(L), foram omitidos por conveniência. Considerando as capturas de n frotas, tem-se que:
| C(1) = F(1) *N | |
| C(2) = F(2) *N | |
: | |
: | |
: | |
| C(n) = F(n) *N | (5.3.13a) |
| C = C(1)+C(2)+....+C(n); F = F(1)+F(2)+....+F(n) |
Dividindo a Eq. 5.1.5 por a Eq. 5.3.13a e reordenando ambos os termos, obtem-se a mortalidade por pesca, causada pela frota i:
| F(i) = F*C(i)/C | (5.3.13b) |
A Tabela 5.3.5 illustra como se efectua este processo simples para realizar a análise de coortes baseada em comprimentos, com duas frotas que utilizam diferentes artes: rede de arrasto e rede de emalhar, cada uma com tamanho de malha diferentes. contudo, o vector de valores de F total para ambas as frotas de forma combinada não é fácil de interpretar. Ao separar as mortalidades por pescas causadas pelo arrasto F(1) das causadas pela rede de emalhar, F(2) observa-se que F(1) aumenta em direcção a uma assimptota indicando uma curva de selectividade da arte, tal como se encontra representado na Fig. 4.5.3.1, ao passo que a mortalidade devido á rede de emalhar toma a forma de uma curva em sino.
Aspectos básicos de análise de coortes baseada em comprimentos
A análise de coortes por comprimentos definida pelas Eqs. 5.3.3 a 5.3.7 (ver Tabela 5.3.3) é chamada “análise de coortes de Jones baseada em comprimentos”. (Jones, 1976, e Jones e van Zalinge, 1981, revista por Jones, 1984 e Pauly, 1984). Conforme já mencionado, o método é normalmente aplicado a “pseudo-coortes”, ou seja, assumimos um sistema de parâmetros constantes (equilíbrio). De forma a simular uma condição de equilíbrio, é essencial que os dados cubram um período de tempo relativamente longo (digamos um ano ou vários anos), preferivelmente um número de anos completos.
Uma amostra de frequências de comprimento colhida durante um curto espaço de tempo não pode ser utilizada. Como exemplo olhemos para a amostra de camarões referente a Setembro mostrada na Fig. 3.4.2.6, que consiste somente em uma coorte. O método assume que um indivíduo maior seja igualmente o mais velho, neste caso assumimos que todos os camarões, independente do tamanho, são da mesma idade, e portanto, a parte descendente da figura em questão está relacionada com a variação das taxas de crescimento individual, e não com a mortalidade.
É possível aplicar o método de Jones a uma verdadeira coorte, mas isto implica que seja possível seguir a coorte através do tempo, ou seja que conhecemos a sua idade. No entanto, se este é o caso, uma vez que não existem problemas na conversão de comprimentos em idades, podemos perfeitamente usar a análise de coortes de Pope baseada em idades.
Como a análise de coortes de Jones baseada em comprimentos é baseada na análise de coortes de Pope baseada em idades (Secção 5.2), ambas possuem as mesmas limitações. A aproximação para a VPA é válida para valores de F*Δt até 1.2 e M*Δt até 0.3 (Pope, 1972).
A utilização da VPA baseada em comprimentos sem a aproximação da análise de coortes não requere mais que uma ligeira modificação nas fórmulas das Eq. 5.1.3 e Eq. 5.1.4. Primeiro, o intervalo de tempo de 1 ano é alterado par Δt:
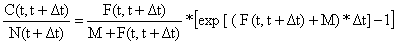
N(t) = N(t+Δt) * exp[F(t,t+Δt)+M)*Δt]
Sendo a idade t correspondente a L1 e a idade t+Δt a L2:
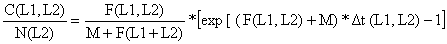 | (5.3.14) |
donde, usando a Eq. 4.4.5.1:
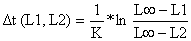
| N(L1) = N(L2) * exp[ (F(L1,L2) + M) *Δt(L1,L2)] | (5.3.15) |
Com a VPA tal como com a análise de coortes, a melhor estimativa do peso no grupo mais,+, obtem-se da Eq. 8.3.6:
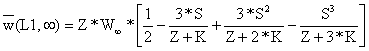 | (5.3.16) |
no qual Z = F(L1,∞) + M, S = 1 - L1/L∞
O peso médio depende de Z devido ao efeito da mortalidade na distribuição de frequências de comprimentos no manancial: quanto maior a mortalidade mais pequenos serão os peixes. De qualquer modo, tem pouca importância quando se trabalha com classes de tamanhos pequenos. Isto deve-se à formula da Eq. 5.3.11 ser aproximadamente simples.
Programas de computador
O programa “LCOHOR” no pacote LFSA para microcomputadores (Sparre, 1987) pode executar a análise de coortes de Jones baseada em comprimentos, segundo a apresentação acima. O pacote “COMPLEAT ELEFAN” (Gayanilo, Soriano e Pauly, 1988) e o FiSAT também contêm rotinas para uma análise baseada em comprimentos semelhante ao programa LCOHOR.
(ver Exercício (s) na Parte 2).
Nos métodos baseados em idades, Secções 5.1 e 5.2, vimos que podemos facilmente seguir a vida duma coorte ano após ano, como ilustrado na Tabela 4.4.1.1. Isto não se verifica nos métodos baseados em comprimentos porque o tempo não é igual para todos os intervalos de comprimento. A análise de coortes baseada em comprimentos ou a VPA resolve o problema trabalhando com pseudo-coortes ou seja, a distribuição média das frequências de comprimentos durante um período no qual não houve alteracões significativas no esforço ou na malha utilizada. O período deve abranger o tempo suficiente para minimizar as flutuações na distribuição de frequências, causadas pelas variações no recrutamento sazonal e anual.
No caso duma amostragem anual de frequências de comprimentos é preferível manter os dados anuais separados, possibilitando assim a identificação de variações no recrutamento e alterações da mortalidade por pesca. Os peixes devem ser referidos por grupos de idade com intervalos fixos, geralmente um ano no caso de desova anual, onde o comprimento dum peixe com um ano, dois anos, etc., é calculado com os parâmetros de crescimento, podendo-se assim discernir as variações no recrutamento e na mortalidade. Os peixes menores do que o comprimento à idade 1 são referidos como o grupo-0, os que estão entre os comprimentos de idades 1 e 2 são referidos como o grupo-1, e assim por diante. Nalgumas classes de comprimento será necessário repartir proporcionalmente, ou seja distribuir as frequências entre os dois grupos de idade, como por exemplo, se o intervalo da classe de comprimento é 1 cm e os peixes da idade 1 têm 12.6 cm, então 6/10 dos peixes na classe 12–13 cm vão ser referidos ao grupo de idade 0 e 4/10 vão ser referidos ao grupo de idade 1. Se o intervalo de comprimento for 6 cm com uma classe de comprimento de 12–18 cm, então só a fracção 0.6/6 = 0.1 será referida ao grupo de idade 0 enquanto que 9/10 será referida ao grupo de idade 1.
Esta técnica é conhecida como a técnica da repartição “slicing technique”, existindo várias versões das quais é dificil atribuir os devidos méritos. Há dois problemas importantes a considerar; a idade verdadeira do peixe não ser conhecida e a análise de coortes baseada em comprimentos utilizar um valor arbitrário da to (normalmente 0), pois as diferenças entre as idades, Δt, são utilizadas em vez das idades própias, eliminando to. A escolha de to na técnica de reparticipação afecta a distribuição entre grupos de idades e a variação do recrutamento, mas isto é um problema menor quando se analiza uma pseudo-coorte. Na reparticipação de amostras anuais durante um período de vários anos é importante que todos os peixes da mesma coorte (classe anual) sejam atribuidos ao mesmo grupo de idade: grupo de idade 0 para um ano, grupo de idade 1 para o próximo ano, etc., e que não sejam distribuidos entre dois grupos de idade. O valor de to deve ser escolhido de tal forma que um pico na curva de distribuição, resultante duma classe anual forte, é atribuido, se for possível, a um grupo de idade para esse ano.
Mesmo uma escolha cuidadosa do to não pode evitar que alguns dos peixes sejam mal classificados por causa da variação do tamanho dentro duma coorte, como ilustrado na Fig. 1.4.1. Este problema pode ser ultrapassado com pressupostos sobre o desvio padrão do comprimento dos peixes dentro da coorte, assim como foi estimado para os peixes mais jovens com o método Bhattacharya, Secção 3.4, mas é dificil dizer se a técnica de repartição vai mesmo substituir a análise de coortes baseada em comprimentos.
As Tabelas 5.4.1 e 5.4.2 dão um exemplo simples da análise de coortes baseada em idades, seguida da repartição de uma pseudo-coorte de pescada, exemplo já utilizado para a análise de coortes baseada em comprimentos (ver Tabela 5.3.1). Na análise de coortes baseada em comprimentos o recrutamento é definido como o número de peixes que entra na primeira classe de comprimento de 6 cm, e to = 0 é uma escolha sem consequências. A escolha de to = 0 na técnica da repartição faz com que uma estimativa do recrutamento num comprimento nominal dos peixes e à idade 0 seja pouco útil, pois a idade estimada aos 6 cm (Tabela 5.3.2) era 0.473, o que daria um to = -0.473 anos.
Table 5.4.1 Exemplo de repartição. As capturas ('000) nas primeiras linhas da Tabela 5.3.1 são referidas por grupos de idade. Compare a aplicação dos resultados na Tabela 5.4.2
| idade t | comprimento à idade *) | classe de comprimento | fracção do grupo menor | captura total | captura por grupo idade | ||
| 0 | 1 | 2 | |||||
| L(t) | L1–L2 | C(L1,L2) | |||||
| 0 | 6.00 | 6–12 | 1.0000 | 1823 | 1823 | ||
| 1 | 17.81 | 12–18 | (17.81-12)/6 = 0.9683 | 14463 | 14005 | 458 | |
| 18–24 | 1.0000 | 25227 | 25227 | ||||
| 2 | 28.48 | 24–30 | (28.48-24)/6 = 0.7467 | 8134 | 6073 | 2061 | |
| 30–36 | 1.0000 | 3889 | 3889 | ||||
| 3 | 38.14 | 36–42 | (38.14-36)/6 = 0.3567 | 2959 | 1055 | ||
Captura total referente aos grupos de idade 0, 1 e 2: | 15828 | 31758 | 7005 | ||||
*) L(t) = 130*(1-exp(-0.1*(t+0.473)))
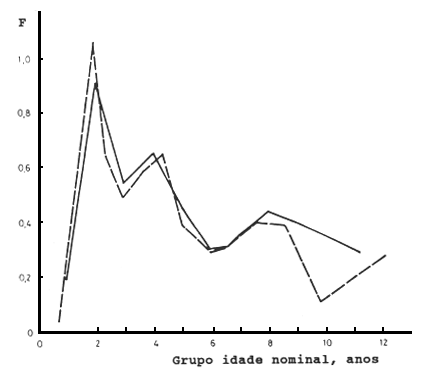
Fig. 5.4.1 Comparação de valores de F, por grupos de idade, da pescada do Senegal, estimados através da análise de coortes baseada em comprimentos (linha a tracejado) e da técnica da repartição. Ver Tabela 5.3.2, 5.3.3 e 5.4.1
Table 5.4.2 Análise de coortes baseada em idades depois de se utilizar a técnica de repartição. Pseudo-coorte da pescada do Senegal (Tabela 5.3.1) M = 0.28
| grupo idade nominal | captura ('000) | no no princípio do ano ('000) | mortalidade por pesca |
|---|---|---|---|
| t | C(t,t+1) | N(t) | F(t,t+1) |
| 0 | 15828 | 99818 | 0.20 |
| 1 | 31758 | 61680 | 0.91 |
| 2 | 7005 | 19008 | 0.55 |
| 3 | 3426 | 8276 | 0.65 |
| 4 | 1044 | 3276 | 0.46 |
| 5 | 354 | 1569 | 0.30 |
| 6 | 227 | 878 | 0.35 |
| 7 | 144 | 466 | 0.44 |
| 8 | 64 | 227 | 0.40 |
| 9+ | 58 | 116*) | 0.28 |
*) N(9) = C(9+)*Z(9+)/F(9+) (Eq. 5.1.7)
Na análise de coortes baseada em idades, após a técnica da repartição, atribuindo-se a idade 0 a esse peixe, também resulta num recrutamento com 6 cm de comprimento. Esta técnica de distribuição das capturas por grupos de idade está ilustrada na Tabela 5.4.1 e a consequente análise de coortes baseada em idades na Tabela 5.4.2. O recrutamento aos 6 cm de comprimento N(0) é agora estimado em 99.8 milhões em comparação com os 98.9 milhões obtidos pela análise de coortes baseada em comprimentos, considerando-se razoável. As mortalidades por pesca estimadas pelos dois métodos são comparados na Fig. 5.4.1, podendo-se ver que são similares excepto para os peixes mais velhos que são poucos nas capturas.