Nos vários métodos discutidos no Capítulo 4 parece que o completo intervalo de comprimentos (ou intervalo de idades) de peixes ou crustáceos de um manancial nem sempre é totalmente explorado. A maioria das artes de pesca, por exemplo, redes de arrasto, são selectivas para tamanhos maiores, enquanto que algumas artes (redes de emalhar) são selectivas somente para um certo intervalo de comprimento, excluindo assim a captura de peixes muito pequenos e muito grandes. Esta propriedade da arte de pesca é chamada “selectividade da arte” e é necessário ter em conta, quando queremos estimar a real composição de tamanhos dos peixes na área de pesca. Ao mesmo tempo, é uma importante ferramenta para os gestores das pescas que, através da regulamentação dos tamanhos da malha utilizada pela frota pesqueira, podem mais ou menos determinar o tamanho mínimo da espécie a capturar, para uma certa pescaria. A selectividade da arte está fortemente relacionada com a mortalidade total estimada, Z, com as análises de dados de arrastos de investigação em comparação com as pescarias comerciais e com a previsão de futuras capturas (Thompson e Bell, ver Capítulo 8). Uma recente edição da “Fisheries Research” oferece uma visão geral do problema das selectividades das artes de pesca, de bastante utilidade (MacLennan, 1992).
Como é conceptualmente mais fácil, primeiro discute-se a selectividade das artes de arrasto e depois a das redes de emalhar ou artes similares.
Uma completa descrição da rede de arrasto é dada na Secção 13.1. A parte final da rede com malhas finas, onde o peixe é retido, é chamada saco. Parece ser o “tamanho de malha” do saco que determina, em grande parte, a selectividade do arte de arrasto.
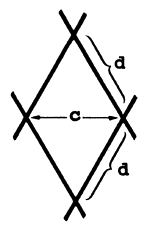
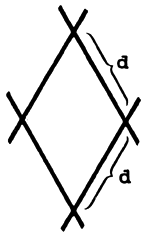 | O “tamanho de malha” é normalmente definido como o comprimento da malha esticada. O comprimento da malha da rede mostrada aqui é 2*d, onde d é o comprimento entre dois nós. |
Para uma detalhada discussão das definições de tamanho e técnicas de medição de malha, ver FAO (1978b).
É possivel determinar a quantidade e o tamanho dos peixes que escapam através das malhas do saco, cobrindo-o com um saco maior de malha menor, conforme ilustrado na Fig. 6.1.1. A selectividade da arte pode ser determinada comparando o tamanho dos peixes retidos no saco com os retidos no duplo saco. O “método do duplo saco” foi descrito por Pope et al., 1975 e Jones, 1976.
Exemplo 21: Experiência com o duplo saco, Nemipterus japonicus, Mar Sul da China
A experiência refere-se ao falso besugo Nemipterus japonicus, capturado com rede de arrasto com um saco de malha de 4 cm e um duplo saco com malha bem menor. A captura típica de um lance é dada na Tabela 6.1.1, para o saco e para o duplo saco, na forma de duas tabelas de frequências de comprimento respectivamente (colunas B e C). A fracção da captura total que foi retida pelo saco pode então ser calculada e é apresentada como a fracção retida (exemplo 1/7 = 0.14) de cada classe de comprimento. Quando a fracção retida é marcada, num sistema de eixos, contra o ponto médio da classe de comprimento correspondente, os pontos parecem seguir uma linha sigmoidal, que atinge o valor 1.00 (100% de retenção) para os comprimentos maiores e aproxima-se de 0.00 (0% de retenção) para os comprimentos menores. Esta curva sigmoidal é chamada “ogiva de selectividade da arte” e assemelha-se a uma distribuição normal acumulada.
A expressão matemática mais fácil de descrever a ogiva de selectividade é a chamada “curva logística”:
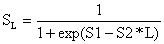 | (6.1.1) |
e L é o ponto médio (comprimento médio) do intervalo de comprimento. S1 e S2 são constantes (Paloheimo e Cadima, 1964; Kimura, 1977, e Hoydal et al., 1982).
A Eq. 6.1.1 pode ser reescrita como
| ln(1/SL - 1) = S1 - S2*L | (6.1.2) |
que representa uma recta, onde S1 = a e S2 = b. Assim, a observação das fracções retidas (coluna E) pode ser usada para determinar a curva logística que se ajusta às observações. A curva logística estimada (SLest) pode então ser usada para calcular as fracções que correspondem à curva (coluna H na Tabela 6.1.1).
Pode ser visto que se SL = 0 ou se SL = 1 a expressão na Eq. 6.1.2 não é definida.
Aplicando-se algumas manipulações algébricas, observa-se que existe uma correspondência entre S1 e S2 e L25%, L50% e L75%, os comprimentos nos quais 25%, 50% e 75% dos peixes são retidos, respectivamente, no saco. O intervalo de comprimentos compreendido entre L25% a L75%, que é simétrico em torno de L50%, é chamado “intervalo de selecção” (ver Fig. 6.4.3.1).
As fórmulas para calcular L25%, L50% e L75% são
| L25% = (S1 - ln 3) /S2 | (6.1.3) |
| L50% = S1/S2 | (6.1.4) |
| L75% = (S1 + ln 3) /S2 | (6.1.5) |
S1 e S2 podem ser calculados de L75% e L50% usando as seguintes fórmulas:
| S1 = L50%*ln(3) / (L75%-L50%) | (6.1.6) |
| S2 = ln(3) / (L75%-L50%) = S1/L50% | (6.1.7) |
A análise de regressão é feita para um intervalo de comprimentos entre a retenção zero (0) e a retenção total (1), excluindo assim os intervalos de comprimentos onde nenhuma retenção, ou a retenção total, é obtida, bem como todos os valores além destes pontos, mesmo que eles se encontrem entre 0 e 1.

Fig. 6.1.1 Experiência com o duplo saco
Para o Nemipterus japonicus a regressão fornece os seguintes resultados, conforme apresentados na Tabela 6.1.1 e Fig. 6.1.2:
a = S1 = 9.4875 e -b = S2 = 0.7193,
que resulta
SLest = 1/(1 + exp(9.4875 - 0.7193*L))
L25% = (9.4875 - ln 3) / 0.7193 = 11.7 cm
L50% = 9.4875/0.7193 = 13.2 cm
L75% = (9.4875 + ln 3) / 0.7193 = 14.7 cm
Como a probabilidade de um peixe escapar através da malha depende da sua forma, e, em particular, da relação entre a altura do corpo e o tamanho da malha, é natural assumir uma proporcionalidade entre d50% (altura do corpo na qual 50% dos peixes são retidos) e o tamanho da malha:
| d50% = A*(tamanho da malha) | (6.1.8) |
onde A é uma constante. Como a altura do corpo é aproximadamente proporcional ao comprimento do corpo (cf. Secção 2.4), aplica-se uma expressão similar da Eq. 6.1.8 ao comprimento do peixe:
| L50% = SF*(tamanho da malha) | (6.1.9) |
onde SF é chamado “factor de selecção”.
No caso do nosso exemplo (Tabela 6.1.1), encontramos L50% = 13.2 cm para um tamanho de malha de 4 cm e o factor de selecção é
SF = 13.2/4 = 3.3
Este factor de selecção pode agora ser usado para determinar L50% para diferentes tamanhos de malha. Por exemplo, o L50% do Nemipterus japonicus quando se utilizar malhas de 3 cm de comprimento será:
L50% = 3.3*3 = 9.9 cm
Mais aplicações do L50% e do SF serão discutidas no Cápitulo 8.
Tabela 6.1.1 Estimação da ogiva de selectividade das artes de pesca para Nemipterus japonicus a partir de uma experiência com duplo saco (de Jones, 1976, compare Fig. 6.1.2)
| A | B | C | D | E | F | G | H |
| interv. de comp. L1–L2 | no no saco | no no duplo saco | no total | fracção retida SLobs | ln(1/S(L)-1) (y) | comp.médio (L1+L2)/2 (x) | fracção retida SLest |
| 9–10 | 0 | 1 | 1 | 0 | - | - | - |
| 10–11 | 1 | 6 | 7 | 0.14 | 1.82 | 10.5 | 0.13 |
| 11–12 | 2 | 7 | 9 | 0.22 | 1.27 | 11.5 | 0.23 |
| 12–13 | 2 | 4 | 6 | 0.33 | 0.71 | 12.5 | 0.38 |
| 13–14 | 7 | 5 | 12 | 0.58 | -0.32 | 13.5 | 0.56 |
| 14–15 | 30 | 13 | 43 | 0.70 | -0.85 | 14.5 | 0.72 |
| 15–16 | 61 | 8 | 69 | 0.88 | -1.99 | 15.5 | 0.84 |
| 16–17 | 27 | 3 | 30 | 0.90 | -2.20 | 16.5 | 0.91 |
| 17–18 | 7 | 0 | 7 | 1.00 | - | 17.5 | 0.96 |
| 18–19 | 4 | 1 | 5 | 0.80 | - | 18.5 | 0.98 |
| intersecção = a = S1 = 9.4875 | -declive = -b = S2 = 0.7193 | ||||||
| L50% = S1/S2 = 13.2 cm | L75% = (S2 + ln 3) /S2 = 14.7 cm | ||||||
| SLest = 1/(1 + exp(9.4875 - 0.7193*L)) | |||||||
| (usada para calcular a curva na Fig. 6.1.2) | |||||||
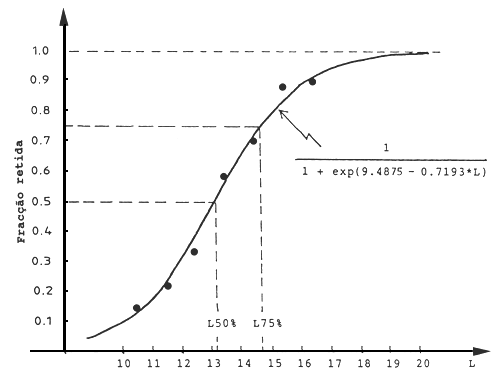
Fig. 6.1.2 Ogiva de selectividade para Nemipterus japonicus, capturado por uma rede de arrasto de tamanho de malha do saco de 4 cm (Jones, 1976)
Basicamente, as redes de emalhar são redes rectangulares onde a parte superior, o cabo mestre, possui flutuadores, enquanto que o cabo inferior possui pesos. As redes de emalhar (de deriva ou fixas) frequentemente são compostas por diversas redes com diferentes tamanhos de malha. Para descrições adicionais de redes de emalhar ver FAO (1978b), Nédélec (1982) ou Karlsen e Bjarnason (1986).
As propriedades de selectividade das redes de emalhar são revistas em Hamley (1975) e pode-se encontrar discussões sobre selectividade de redes de emalhar, por exemplo em Baranov (1948), McCombie e Fry (1960), Gulland e Harding (1961), Regier e Robson (1966), Hamley e Regier (1973) e Jensen (1986).
As redes de emalhar são “artes passivas”, isto é, os peixes têm que nadar para dentro da rede para serem capturados. Teoricamente, isto implica que peixes que se movam rapidamente têm uma maior probabilidade de encontrar as artes passivas, do que os peixes que se movam lentamente. Sabe-se ainda que peixes maiores movem-se mais rapidamente que os peixes menores da mesma espécie. A velocidade de natação pode ser aproximada por uma constante vezes uma função potência do comprimento:
A*LB, onde A e B são constantes (Yates, 1983).
Rudstam, Magnuson e Tonn (1984) incluiram a velocidade de natação (com B = 0.8 para o coregono, Coregonus artedii, de Wisconsin, USA) num modelo para a selectividade da rede de emalhar. Eles consideraram a selectividade como o produto de duas probabilidades:
(selectividade) = (probabilidade de encontro) * (probabilidade de ser capturado dado esse encontro)
Contudo, devemos lidar em seguida somente com o último factor, a probabilidade de ser capturado dado um encontro.
Para redes de emalhar simples, a curva de selectividade tem (ao contrário da curva de selectividade da rede de arrasto) uma inclinação descendente no seu lado direito. Os peixes pequenos podem passar através das malhas, tal como para a rede de arrasto, mas os peixes grandes também podem evitar serem capturados numa rede de emalhar porque as suas cabeças são tão grandes que eles não podem ser emalhados. Esta é a teoria simples que fundamenta a selectividade em redes de emalhar. Contudo, o quadro torna-se um tanto mais complicado quando são consideradas outras maneiras pelas quais os peixes podem ser presos numa rede de emalhar. Karlsen e Bjarnason (1986) reconhecem quatro maneiras do peixe ser capturado pela rede, como indicado na Fig. 6.2.1.1.
“Pegado”, quando a malha prende o peixe logo atrás do olho.
“Emalhado”, quando a malha prende o peixe logo atrás da abertura branquial
“Entalado”, quando a malha prende o peixe perto da barbatana dorsal
“Enredado”, quando o peixe se prende na rede pelos dentes, maxilares, barbatanas ou outras saliências, sem necessariamente ter penetrado na malha.
Modelo de Holt para dois tamanhos de malha
Para as três primeiras maneiras do peixe ser capturado, citadas acima, foi sugerido (Holt, 1963) que as curvas de selectividade tenham a forma de sino e possão ser descritas por uma distribuição normal (cf. Secção 2.2 e Fig. 6.2.2.2).
Assim, quando o peixe está pegado, emalhado através das brânquias e ou entalado até às barbatanas dorsais, usamos o seguinte modelo:
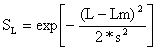 | (6.2.1.1) |
onde Lm é o “comprimento óptimo para ser capturado” e s é o desvio padrão da
distribuição normal. O factor 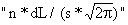 que aparece na expressão para
a distribuição normal (Eq. 2.2.1) não é utilizado aqui. Omitindo este
factor, SL torna-se numa fracção, ou seja, 0 < SL < = 1.
que aparece na expressão para
a distribuição normal (Eq. 2.2.1) não é utilizado aqui. Omitindo este
factor, SL torna-se numa fracção, ou seja, 0 < SL < = 1.
Holt (1963) sugeriu uma experiência para estimar Lm e s pelo uso de duas redes de emalhar com tamanhos de malha diferentes, ma e mb. Os dois tamanhos de malha devem ser escolhidos de modo que as suas curvas de selectividade se sobreponham. As duas redes são utilizadas para pescar na mesma área e ao mesmo tempo; as observações retiradas são o número de peixes capturados por classe de comprimento, para cada rede e os pressupostos que fundamentam este método são:
O comprimento óptimo Lm (o topo da curva de selectividade em forma de sino) é proporcional ao tamanho de malha (Lm = SF*m, onde SF é o factor de selecção, cf. Secção 6.1)
As duas curvas de selectividade têm o mesmo desvio padrão
As duas artes têm o mesmo poder de pesca. Isto implica que, quando caladas, devem ter o mesmo comprimento e a mesma altura.
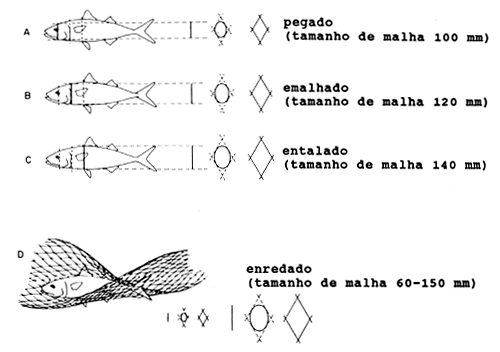
Fig. 6.2.1.1 Selectividades da rede de emalhar (de Karlsen e Bjarnason, 1986)
Exemplo 22: Estimativa das curvas de selectividade da rede de emalhar, Tilápia, Lago Victória
A Tabela 6.2.1.1 mostra um exemplo da experiência em Tilapia esculenta do Lago Victória. A coluna B contém as capturas, Ca, por classes de comprimento para a rede de malha menor (ma = 8.1 cm), e a coluna C contém as capturas correspondentes, Cb, para a rede de malha maior (mb = 9.1 cm). Os parâmetros a serem estimados são:
Lma: Comprimento óptimo para a rede de malha menor
Lmb: Comprimento óptimo para a rede de malha maior
s: O desvio padrão comum
Os dados de entrada para a análise, são os números capturados por classe de comprimento para cada rede, Ca e Cb, e os dois tamanhos de malha ma e mb. Os cálculos matemáticos são longos e são aqui omitidos.
Tabela 6.2.1.1 Cálculo das ogivas de selectividade das redes de emalhar para a Tilapia esculenta, Lago Victória (Garrod, 1961).
| A | B | C | D |
| ponto medio do intervalo de comprimento L (x) | número de peixes capturados com a malha de 8.1 cm Ca | número de peixes capturados com a malha de 9.1 cm Cb |  (y) |
| 18.5 | 7 | 0 | não utilizado |
| 19.5 | 90 | 1 | |
| 20.5 | 199 | 9 | -3.096 |
| 21.5 | 182 | 53 | -1.234 |
| 22.5 | 119 | 290 | 0.891 |
| 23.5 | 29 | 357 | 2.510 |
| 24.5 | 17 | 225 | - |
| 25.5 | 3 | 82 | não utilizado |
| 26.5 | 0 | 19 | |
| 27.5 | 0 | 10 | - |
| ordenada na origem = -41.907, declive = 1.894 | |||
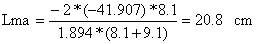 | |||
| Lmb = 20.8*9.1/8.1 = 23.4 cm | |||
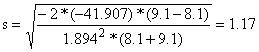 | |||
| Passo 1: | Calcular as razões logarítmicas | |
y = In(Cb/Ca) | ||
| para cada classe de comprimento (coluna D da Tabela 6.2.1.1). Somente os comprimentos onde as frequências se sobrepõem podem ser utilizados. | ||
| Passo 2: | Fazer uma análise de regressão dos log das razões (y = ln(Cb/Ca), coluna D) contra o ponto médio do intervalo (x = L, coluna A) e determinar a e b: | |
ln(Cb/Ca) = a + b*L | (6.2.1.2) | |
| Passo 3: | Os resultados são obtidos substituindo os valores de a, b, ma e mb nas seguintes expressões. | |
| O factor de selecção é estimado de | (6.2.1.6) | |
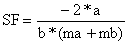 | ||
| O comprimento óptimo para as dois tamanhos de malha é Lma = SF*ma e Lmb = SF*mb. O desvio padrão comum é determinado pela variância | ||
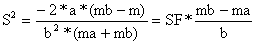 | (6.2.1.6a) | |
| Passo 4: | Os pontos da curva de selectividade são determinados dando valores a L, na Eq. 6.2.1.1: | |
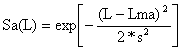 | ||
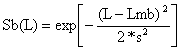 | ||
| Passo 5: | Dos pontos obtidos e das capturas Ca(L) e Cb(L) é estimado um índice do número de indivíduos na população, para cada malha: | |
Na(L) = Ca(L)/Sa(L) | (6.2.1.6b) | |
Nb(L) = Cb(L)/Sb(L) | ||
Os índices Na e Nb são, em princípio, iguais para o mesmo L, excepto quando há erros de amostragem. Estes, devem ser calculados somente, para classes de comprimento onde há um número fiável de indivíduos nas capturas da rede em questão. Se a suposição básica, da curva de selectividade seguir uma normal, não for cumprida, o número estimado da população deve ser restricto à zona da curva em que a suposição é cumprida quase na sua totalidade.
Os resultados estão apresentados na Tabela 6.2.1.2 e Figs. 6.2.1.1a e 6.2.1.2. Ao marcar os dados para a análise de regressão, Fig. 6.2.1.1a verifica-se que as curvas de captura são assimétricas, provavelmente devido ao efeito do enredado: os peixes maiores estão sobre representados em ambas as curvas. A estimativa foi restricta aos 4 pontos que se encontravam numa linha recta, que tem um número adequado de indivíduos. Na(L) e Nb(L) estão em acordo com os 4 pontos usados na regressão, no entanto, para os peixes maiores o ajuste é duvidoso devido à curva de captura ser assimétrica. É necessário um grande número de tamanhos de malha para cobrir a larga amplitude de tamanhos da estrutura da população.
Tabela 6.2.1.2 Estimativa da curva de selectividade da rede de emalhar para a Tilapia esculenta, Lago Victória (Garrod, 1961)
| ponto médio do intervalo de comprimento L (x) | número capturado | 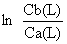 | selectividade | № estimado | |||
| ma = 8.1 Ca(L) | mb = 9.1 Cb(L) | (y) | Sa(L) | Sb(L) | Na(L) | Nb(L) | |
| 18.5 | 7 | 0 | - | 0.1333 | 0.0001 | 52 | - |
| 19.5 | 90 | 1 | -4.500 | 0.5164 | 0.0036 | 174 | (282) |
| 20.5 | 199 | 9 | -3.096 | 0.9583 | 0.0443 | 208 | 203 |
| 21.5 | 182 | 53 | -1.234 | 0.8519 | 0.2611 | 214 | 203 |
| 22.5 | 119 | 290 | 0.891 | 0.3627 | 0.7373 | 328 | 393 |
| 23.5 | 29 | 357 | 2.510 | 0.0739 | 0.9970 | 392 | 358 |
| 24.5 | 17 | 225 | 2.583 | 0.0072 | 0.6458 | (2492) | 348 |
| 25.5 | 3 | 82 | 3.308 | 0.0003 | 0.2003 | (8881) | 409 |
| 26.5 | 0 | 19 | - | 0.0000 | 0.0304 | (638) | |
| 27.5 | 0 | 10 | - | 0.0000 | 0.0021 | (4721) | |
ln (Cb(L)/Ca(L)) = a + b*L; a= -41.907; b = 1.894 | |||||||
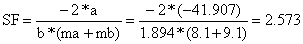 | |||||||
Lma = SF*ma = 20.84 cm Lmb = SF*mb = 23.41 cm | |||||||
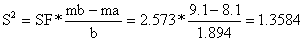 | |||||||
s = 1.1655 | |||||||
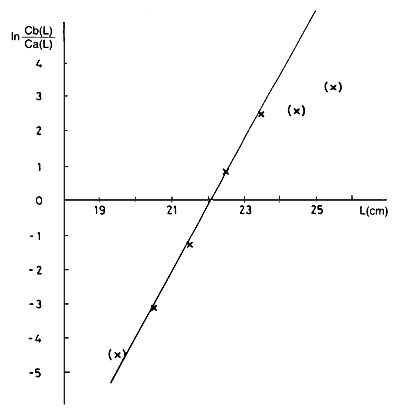
Fig. 6.2.1.1a Tilapia esculenta. Regressão do ln(Cb(L)/Ca(L)) contra o comprimento do peixe (Eq. 6.2.1.2)
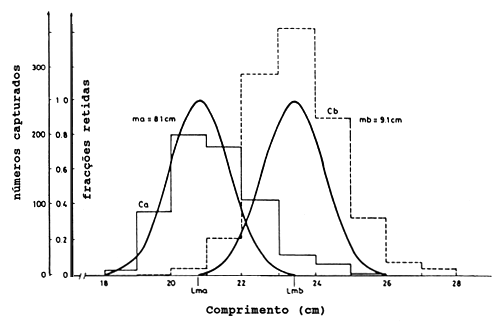
Figura 6.2.1.2 Curvas de selectividade para a Tilapia esculenta em redes de emalhar com tamanhos de malha de 8.1 cm e 9.1 cm, Lago Victória (Garrod, 1961)
Modelo para vários tamanhos de malha
Quando há n tamanhos de malha, usados todos juntos em redes do mesmo tamanho, existe n-1 declives, b, e ordenadas na origem, a, estimados de acordo com a Eq. 6.2.1.2, obtendo como resultado
[a(1), b(1)], [a(2), b(2)], . . . . ,[a(n-1), b(n-1)]
correspondendo aos tamanhos da malha:
[m(1), m(2)], [m(2), m(3)], . . . . ,[m(n-1), m(n)]
Cada grupo de dados (correspondendo a cada tamanho de malha) foi utilizado duas vezes para gerar as estimativas: para estimar a(1) e b(1), empregou-se o primeiro grupo com o segundo, e este novamente com o terceiro para estimar a(2) e b(2) e assim sucessivamente. Origina-se, assim, uma certa correlação entre pares consecutivos de a(i) e b(i) que é difícil de avaliar, mas pode ser importante quando apenas se dispôe de informação para poucos tamanhos de malha. Mantendo esta problemática em mente e reordenando a Eq. 6.2.1.5 dá uma recta que passa pela origem:
| -2*a(i)/b(i) = SF*[m(i)+m(i+1)], i = 1,2,…,n-1 | (6.2.1.7) |
do qual o factor de selecção é estimado como o declive. Com y(i) = -2*a(i)/b(i) e x(i) = m(i)+m(i+1) temos da Eq. 2.4.13:
SF = ∑[x(i)*y(i)]/∑x(i)2
A variância comum é estimada como a média das estimativas individuais para cada par consecutivo de tamanho da malha:
 | (6.2.1.9a) |
O comprimento óptimo para cada tamanho de malha, i, é obtido por:
| Lm(i) = SF*m(i) | (6.2.1.10) |
De seguida, calcular os pontos na curva de selectividade Si(L) para cada classe de comprimento. Somar os pontos obtidos a cada classe de comprimento para todos os tamanhos de malha e ajustar uma normal reduzida ao intervalo |0,1|, para obter uma curva de selectividade composta. Este último passo efectua-se dividindo os valores das somas pelo valor determinado mais alto.
Uma curva uniforme sobre uma grande gama de comprimentos indica que todas as classes de comprimento dessa gama foram amostrados uniformemente, de tal modo que a soma das capturas para cada classe de comprimento Ci(L) pode ser usado directamente como um índice do número de indivíduos da população. Se a soma das curvas de selectividade produz picos e depressões acentuadas, o número de indivíduos por classe de comprimento, tem que ser estimado dividindo as capturas originais pela probabilidade de retenção (≤ 1), determinada para cada respectiva classe de comprimento da curva de selectividade normal reduzida. No entanto, deve-se considerar do mesmo modo que pode haver classes de comprimento que não servem para calcular o índice do número de indivíduos da população.
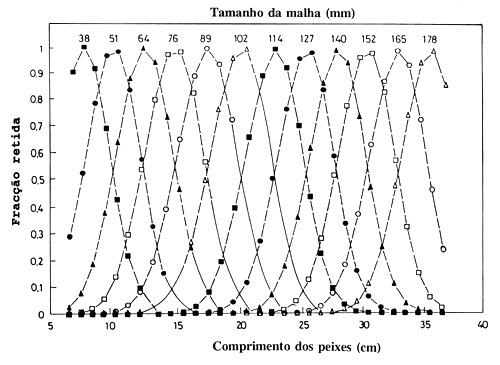
Fig. 6.2.1.2a Curvas de selectividade para um ciclídeo Serranochromis codringtoni no lago Kariba, África Sudeste, com redes de emalhar de 12 tamanhos de malha. Adaptado de: Zambia/Zimbabwe SADC Fisheries Project, Project Report № 26, 1993
As Figs. 6.2.1.2a e 6.2.1.2b mostram curvas de selectividade para um ciclídeo dum lago de África, onde 21000 indivíduos foram capturados num conjunto de 12 redes de emalhar com tamanhos de malha variando entre 38 e 178 mm. As curvas foram estimadas como acima descrito. Depois de somar e reduzir ao intervalo |0,1|, pode ser visto que a curva de selectividade resultante é achatada no topo para peixes com comprimento entre 11 e 31 cm. Assim, a captura total obtida com os 12 tamanhos de malha dá um índice bastante fiável da composição de tamanhos da população. O incremento na retenção observado no lado esquerdo da ampla curva, assemelha-se à curva de selectividade do arrasto (Fig. 6.1.2); a diminuição do lado direito não se observa nos resultados, pois não há peixes de tamanho tão grande, ou seja estimou-se um L∞ = 27 cm. Convém não esquecer que os dados provém de pesca experimental e a pesca comercial no lago é principalmente com rede de emalhar de um só tamanho de malha. Portanto, é de esperar que a mortalidade por pesca não se mantenha com um valor máximo a partir de um certo tamanho e maior, tal como na pesca comercial.
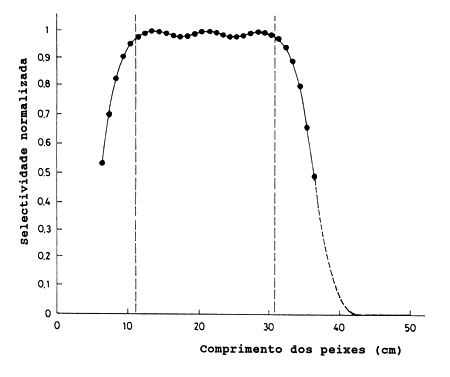
Fig. 6.2.1.2b Curvas de selectividade da Fig. 6.2.1.2a somada e reduzida ao intervalo |0,1|. Adaptado de: Zambia/Zimbabwe SADC Fisheries Project, Project Report № 26, 1993
Coeficiente de retenção
A selectividade da rede de emalhar é dependente duma variedade de factores para além do tamanho, tais como: construção da rede, visibilidade e elasticidade da rede, material da reder e forma e comportamento do peixe (Hamley, 1975). O enredado, mais do que o entalado e o emalhado, (cf. Fig. 6.2.1.1) é afectado pela construcção da rede. A probabilidade de um peixe ficar enredado depende da chamada “razão de retenção” ou “coeficiente de retenção” que é definido segundo (FAO, 1978b):
 | 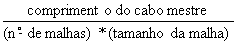 | |
| ou (ver figura): | ||
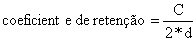 | (6.2.1.11) |
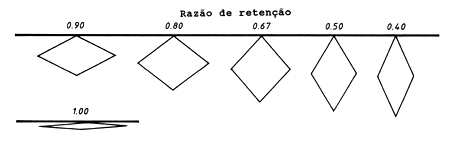
Fig. 6.2.1.3 Configuração de malhas com vários coeficientes de retenção para a rede de emalhar (FAO, 1978b)
Deste modo, para uma malha quadrada (d = c/√2) temos o coeficiente de retenção √2/2 = 0.707 que representa a abertura máxima. Os coeficientes de retenção, estão de um modo geral, no intervalo de 0.2 a 0.7 (ver Fig. 6.2.1.3). Quanto menor o coeficiente de retenção maior a probabilidade do peixe ficar enredado. Isto é demonstrado por Riedel (1963), que referiu capturas de Tilapia mossambica com redes de emalhar com 10 cm de tamanho de malha com três coeficientes de retenção diferentes:
| coeficiente de retenção | numero médio capturado/dia | Percente enredado | intervalo de tamanho captura |
| 0.707 | 9.3 | 0 | 18–23 cm |
| 0.36 | 29.5 | 24 | 13–23 cm |
| 0.24 | 81.0 | 80 | 8–22 cm |
Se o enredo é um factor importante, o método da distribuição normal descrito acima não é aplicável. Uma maneira de se estimar a curva de selectividade seria comparar as capturas das redes de emalhar às de uma arte não selectiva, por exemplo, às capturas da rede de arrasto. As capturas de uma arte não selectiva exerceriam o mesmo papel que a captura total no duplo saco e no saco de uma rede de arrasto quando operada segundo descrito na Secção 6.1. O mesmo processo utilizado na Tab. 6.1.1 pode ser aplicado. Neste caso necessitamos de uma curva de selectividade não simétrica do tipo mostrado na Fig. 6.2.2.1. Uma expressão matemática para este tipo de curva pode ser obtida multiplicando as duas curvas logísticas (Hoydal et al., 1982). A parte ascendente da curva é dada pela curva logística comum (cf. Eq. 6.1.1). Esta parte da curva reflecte a probabilidade de o peixe ser emalhado ou “entalado”, e chama-se “SL”, onde “L” representa “o lado esquerdo da curva de selectividade”:
| SLL = 1/(1 + exp(S1 - S2*L)) | (6.2.2.1) |
Este tipo de selectividade é a dominante até ao comprimento A (ver Fig. 6.2.2.1). Para comprimentos maiores que B a selectividade é o efeito combinado do emalhado, o “entalado” e o “enredado”. Esta parte da curva é exemplificada pela “curva logística inversa” e chama-se “SR” onde “R” representa o “lado direito da curva de selectividade”:
| SRL = 1/(1 + exp(D1 - D2*L)) | (6.2.2.2) |
Os parâmetros na função SR, D1 e D2, são números negativos, enquanto que os parâmetros na função SL, S1 e S2, são números positivos. Os comprimentos correspondendo a 50% e 75% da selectividade, D50% e D75%, estão relacionados com D1 e D2 pelas mesmas expressões matemáticas utilizadas para S1, S2, L50% e L75% (cf. Eqs. 6.1.4 a 6.1.7):
D50% = D1/D2 e D75% = (D1 + In 3)/D2
D1 = D50%*In(3)/(D75%-D50%) e D2 = D1/D50%
Multiplicando a curva ascendente, SL, pela curva descendente SR, obtemos o tipo desejado de curva, S. Quando SL é ascendente SR é “neutra” (ou seja, aproximadamente igual a 1.0), e quando SR é descendente SL é “neutra”:
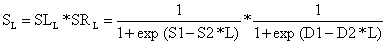 | (6.2.2.3) |
A expressão SL, supostamente, toma o valor máximo, 1.0, para pelo menos um valor L. Por conseguinte, a expressão da Eq. 6.2.2.3 (assim como a distribuição normal na Eq. 6.2.1.1) deve ser normalizada de forma ao valor máximo ser igual a 1.
Na prática isto é obtido da seguinte maneira. Seja S(i) o ponto na curva de selectividade que representa a classe de comprimento no i (estimado pela Eq. 6.2.1.1 ou 6.2.2.3) e seja MAX {S(j)} o valor máximo de S(j) entre todas as classes de comprimento, então a normalização é feita substituindo o valor de S(i) pelo valor:
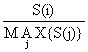
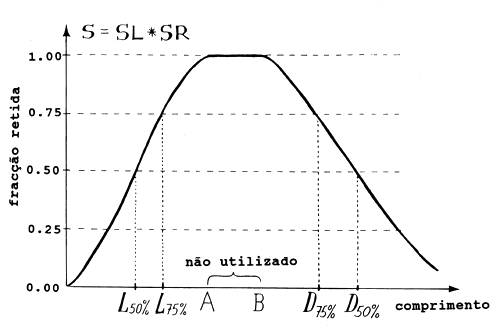
Fig. 6.2.2.1 Curva de selectividade assimétrica
Os parâmetros podem ser estimados tal como os parâmetros da ogiva de selectividade de rede de arrasto (cf. Secção 6.1). Para estimar S1 e S2 utilizar apenas as classes de comprimento abaixo de A (ver Fig. 6.2.2.1) e efectuar a análise de regressão:
| In(1/S - 1) = S1 - S2*L | (6.2.2.4) |
onde a variável independente, y = In (1/S - 1), é calculada por comparação com a arte não selectiva:
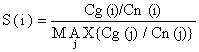 | (6.2.2.5) |
onde

O denominador na Eq. 6.2.2.5, “MAX {Cg(j)/Cn(j)}”, é o valor máximo da razão Cg/Cn entre todas as classes de comprimento com valores diferentes de zero de Cg e Cn. Assim S(i), tal como definido pela Eq. 6.2.2.5, assume valores entre 0 e 1 (incluindo 1).
A Eq. 6.2.2.5 é baseada na hipótese de que os números Cn são capturados por uma arte, que não é selectiva para todas as classes de comprimento capturadas pela rede de emalhar. Se não for o caso, a Eq. 6.2.2.5 deve ser substituida por:
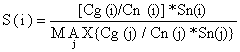 | (6.2.2.6) |
onde Sn(i) é a curva de selectividade para a “outra arte”.
O lado descendente da curva de selectividade (lado direito) é estimado utilizando os mesmos cálculos e as correspondentes observações às utilizadas para o lado esquerdo. Desta maneira, utilizamos os dados para as classes de comprimento acima do ponto B (ver Fig. 6.2.2.1) e procedemos à análise de regressão linear:
| In(1/S - 1) = D1 - D2*L | (6.2.2.7) |
O método dado acima, baseado no produto de duas curvas logísticas, é uma generalização que inclui a ogiva de selectividade da rede de arrasto (Eq. 6.1.1) e a curva simétrica (Eq. 6.2.1.1) como casos especiais. Designando os valores D1 = -∞ e D2 = 0, fazemos o factor 1/(1 + exp(D1 - D2*L)) na Eq. 6.2.2.3 igualar a 1 para todos os valores de L e então a Eq. 6.2.2.3 é igual à Eq. 6.2.1.1. Se a curva é simétrica estimamos os parâmetros de forma que:
L50% + D50% = L75% + D75%
mas não temos que fazer suposições prévias.
A curva simétrica criada pelo produto das duas curvas logísticas pode não ser a mesma, tal como a curva de distribuição normal. O produto das duas curvas logísticas pode assumir o valor máximo (1) para uma intervalo de valores (na Fig. 6.2.2.1 A a B), contudo, pode também aproximar-se muito à distribuição normal como foi mostrado para o exemplo da Fig. 6.2.2.2.
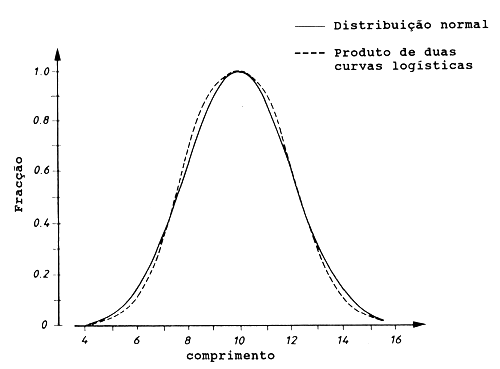
Fig. 6.2.2.2 Produto de duas curvas logísticas, que é quase idêntico à
distribuição normal. Os parâmetros são:
Distribuição normal: Lm = 10 e s = 2
Produto das duas curvas logísticas:
L50% = 7.645 L75% = 8.483
D50% = 2*Lm - L50% D75% = 2*Lm - L75%
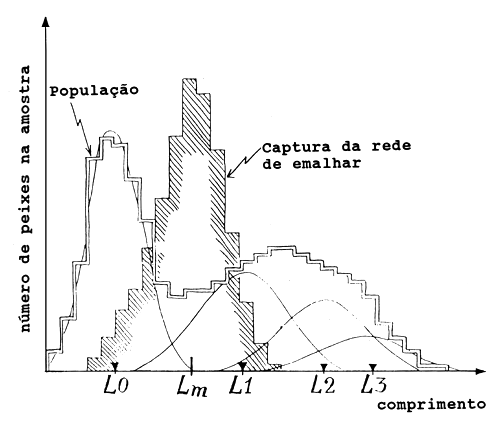
Fig. 6.2.2.3 Exemplo hipotético para ilustrar problemas de erro quando se usa dados da rede de emalhar para estimar os parâmetros de crescimento e as taxas de mortalidade
Sendo assim, se os dados para uma arte não selectiva (ou uma arte com curva de selectividade conhecida) são disponíveis, não há realmente necessidade de se usar o modelo tradicional, a distribuição normal, pois a mesma curva pode ser obtida como um caso especial da função logística (Eq. 6.2.2.3). Além do mais, esta última é versátil e fácil de lidar de um ponto de vista de cálculos. Utilizando o produto das duas curvas logísticas não somos forçados a fazer as hipóteses questionáveis de que as curvas de selectividade são distribuídas normalmente com um desvio padrão comum.
Finalmente, deve ser mencionado que os dados colhidos das capturas de redes de emalhar são difíceis de se utilizar para estimar os parâmetros de crescimento ou taxas de mortalidade. Isto é ilustrado na Fig. 6.2.2.3 como exemplo hipotético, consideramos uma amostra de frequências de comprimento representando a população (linha dupla), isto é uma amostra de uma arte não selectiva, e uma amostra representando as capturas da rede de emalhar (linha sombreada). A população contém quatro componentes ou coortes (distribuições normais), enquanto que a amostra da rede de emalhar parece conter apenas uma componente com valor médio Lm, que não coincide com nenhum dos quatro comprimentos médios das coortes (L0, L1, L2 e L3). Portanto, a amostra da rede de emalhar não dá nenhuma informação que possa ser utilizada para a separação das coortes e estimação dos comprimentos à idade.
As amostras colhidas durante todo o ano também dariam, mais ou menos, o mesmo quadro. Ou seja, somando uma série temporal durante um ano não daria uma curva muito diferente da curva de capturas da rede de emalhar da Fig. 6.2.2.3. Utilizando o declive descendente desta curva para estimar a mortalidade total a partir da análise da curva de capturas baseada em comprimentos, levaria a uma sobrestimação de Z. Antes de utilizar quaisquer dados da rede de emalhar para estimar os parâmetros de crescimento ou taxas de mortalidade, eles devem ser examinados criticamente. O resultado de tal exame pode resultar em, os dados não poderem ser usados ou poderem ser usados somente após ajustados para a selectividade das artes, como descrito na Secção 6.7.
As duas secções anteriores trataram da selectividade de redes de arrasto (artes activas) e redes de emalhar (artes passivas). A literatura científica que trata da selectividade tem se preocupado principalmente com estas artes porque é relativamente fácil conduzir experiências para estimar as suas curvas de selectividade. Outros tipos de artes são também mais ou menos selectivas e o padrão de selectividade pode ser modificado por ajustes apropriados da arte. Acredita-se que tanto o modelo de selectividade baseado na curva logística (Eq. 6.1.1) como o modelo baseado no produto de duas curvas logísticas (Eq. 6.2.2.3) são versáteis o suficiente para descrever a curva de selectividade de qualquer tipo de arte.
Segue-se abaixo uma discussão resumida das propriedades de selectividade de dois tipos de artes passivas: anzóis e armadilhas, e de um tipo de arte activa: rede de cerco.
Parece conhecer-se muito mais sobre a selectividade das redes de arrasto e redes de emalhar do que das pescarias de anzol. Para a pesca à linha e anzol, alguns autores relatam que a curva de selectividade possui uma forma de sino, do tipo da rede de emalhar, dependente do tamanho do anzol, enquanto outros optam por um tipo de selectividade semelhante à da rede de arrasto. A ideia básica do uso da curva de selectividade em forma de sino é que um peixe pequeno não pode abrigar um anzol grande na boca e que um peixe grande não é retido com segurança por anzois pequenos.
Uma discussão sobre selectividade de anzol pode ser encontrada em Ralston (1982), que observou um tipo de selectividade da rede de arrasto para a pesca à linha à mão do mar alto havaiano. De um experiência onde quatro tamanhos de anzois foram usados para capturar lucianos e garoupas, o autor encontrou que pequenos anzois foram quase tão eficientes quanto anzois grandes na captura de peixes grandes. Para a parte esquerda ascendente da curva de selectividade (do peixe pequeno) encontrou uma curva sigmóide. Pope et al. (1975) sugeriram a utilização do tipo de selectividade da rede de emalhar para a pesca de anzois, embora citem vários trabalhos que mostram o tipo de selectividade da rede de arrasto.
Pope et al. (1975) sugerem o tipo de selectividade da rede de arrasto para armadilhas argumentando que as armadilhas comportam-se como sacos na retenção do peixe. Munro (1974, 1983) discute a selectividade e outros aspectos da operação de armadilhas portáteis de peixes nas Antilhas. Estas armadilhas de 3 m de comprimento são feitas de arame para galinheiro com dois funis, em cujas bases estão as aberturas da entrada. São utilizadas para capturar peixes de recifes de coral. Munro (1974) desenvolveu um modelo para a capturabilidade das armadilhas como uma função do tempo de submersão (o tempo em que a armadilha está deixada na área de pesca).
A selectividade das armadilhas é complicada porque depende do peixe movimentar-se activamente para dentro dela. Para armadilhas pequenas (como as armadilhas mencionadas das Antilhas) pode-se esperar que apenas um indivíduo de uma espécie territorial possa ser capturado, mas o peixe apreendido pode ter sido substituido por outro antes da armadilha ser içada. Num outro extremo temos os peixes predadores, como os carapaus (Carangidae) que numa pesca de recifes de coral que abrange uma grande área num curto período de tempo e, portanto, tornam-se sobre representados nas capturas de armadilhas. Se um predador grande é capturado na armadilha ele pode manter potenciais peixes presas longe da entrada da armadilha. Se as espécies presas já estão dentro da armadilha, podem actuar como isco vivo e atrair grandes predadores, que por sua vez podem comer a presa antes da armadilha ser içada.
As capturas com armadilhas dependem da duração do tempo em que estas estão submersas (Munro, 1974). Há sempre uma possibilidade de que um peixe capturado encontre a abertura de entrada e escape através dela. Existem diferenças consideráveis entre as espécies. Algumas espécies saiem das armadilhas com grande facilidade (Munro, 1983). Assim, a selectividade da armadilha pode não ser apenas uma função do tamanho da malha utilizada na armadilha, por exemplo, o tamanho da abertura da entrada e o tempo de submersão podem ser importantes. A composição das espécies na área de pesca onde a armadilha é colocada também pode influenciar a selectividade, contudo, para o escape através das malhas, parece razoável assumir o tipo de ogiva de selectividade da rede de arrasto. Quando se considera a média das capturas de um grande número de armadilhas, algumas das complicações acima mencionadas podem desaparecer, isto é podem acabar sendo “interferências casuais” em torno da curva de selectividade.
Em princípio uma rede de cerco deve operar dum modo semelhante a uma rede de arrasto no que diz respeito à selectividade. No entanto, é mais difícil lidar com redes de cerco porque este tipo de arte é comumente utilizado para capturar cardumes de peixes, tais como sardinhas, cavalas e atuns. Estas espécies têm uma tendência a formar cardumes que consistem em peixes do mesmo tamanho. Assim sendo, devemos considerar um cardume como sendo uma unidade amostral (em vez de um único peixe).
A Fig. 6.4.1.1 mostra duas curvas de selectividade. A curva A tem um intervalo de selectividade de 3 cm e a curva B, a linha vertical grossa, tem um intervalo de selectividade de 0 cm. A curva B é a chamada “curva de selectividade fio da navalha” (Beverton e Holt, 1957). A selectividade fio da navalha deve ser considerada um modelo hipotético, pois na verdade nunca descreve uma situação real. No entanto, a selectividade fio da navalha é muitas vezes usada como uma aproximação da ogiva de selectividade. Para comprimentos abaixo de L50% os números seleccionados são subestimados e para comprimentos acima de L50% os números são sobrestimados. Estas duas fontes de erro têm sinais opostos e como as duas áreas “a” e “b” (ver Fig. 6.4.1.1) são simétricas compensam-se, apesar de os peixes da área “a” pesarem mais do que os da área “b”, pois o peso de um peixe corresponde ao cubo do seu comprimento.
Fig. 6.4.1.1 Curva de selectividade de arrasto em função do comprimento do corpo. Uma ilustração dos conceitos de selectividade fio de navalha e intervalo de selectividade
O recrutamento dos peixes à área de pesca, que ocorre quando eles saiem das áreas de desova e de crescimento para a área de pesca, é também dependente do tamanho, da mesma maneira que a curva de selectividade do arrasto. Isto significa que todos os tamanhos de peixes não estarão totalmente representados nas áreas de pesca, e, assim, quando há uma pescaria para os intervalos de comprimento que não estão ainda totalmente recrutados, a probabilidade de um peixe vir a ser retido pelo arte de pesca é de facto o produto de duas probabilidades:
A probabilidade de o peixe estar presente (tenha sido recrutado) na área de pesca.
A probabilidade de o peixe ser retido pelas malhas uma vez que tenha entrado na arte.
A Fig. 6.4.2.1 ilustra estes pontos. A curva R é a “curva de recrutamento”, a curva G é a “curva de selectividade da arte” e a curva S a “curva resultante”.
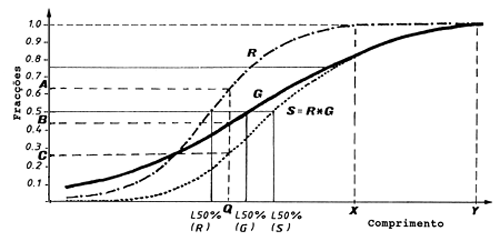
Fig. 6.4.2.1 Curvas representando: recrutamento à área de pesca (R), selectividade da arte (G), e a resultante (S = R*G) (ver também o texto)
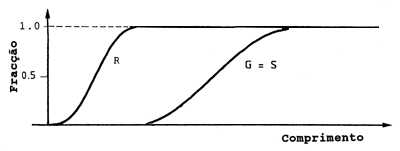
Fig. 6.4.2.2 Exemplo da igualdade entre a curva de selectividade da arte (G) e a curva resultante (S)
A probabilidade de um peixe de certo tamanho ser capturado é o produto da probabilidade do recrutamento e da selectividade. A probabilidade pode, portanto, ser descrita por uma “curva resultante”, S, onde S = R*G (ver Fig. 6.4.2.1).
O L50% para as três curvas, R, G e S, é diferente conforme indicado na Fig. 6.4.2.1. A probabilidade de captura dum peixe de comprimento Q é o produto da probabilidade A, relativa à curva de recrutamento, e da probabilidade B, relativa à curva de selectividade da arte, e o resultado é a probabilidade C.
Neste exemplo A*B = C ou R(Q)*G(Q) = S(Q) ou 0.62*0.42 = 0.26. No comprimento X praticamente todos os peixes foram recrutados à área de pesca, mas alguns são ainda bastante pequenos para escapar através das malhas. No comprimento Y a retenção da malha é completa e nenhum peixe escapa.
Quando as malhas são suficientemente grandes de forma a não haver sobreposição da curva de recrutamento com a da selectividade podemos ignorar o recrutamento. A curva resultante é então determinada apenas pela selectividade, ver Fig. 6.4.2.2.
Até agora a selectividade foi considerada como função do comprimento. Outro exemplo de curva de selectividade SL é dado na Fig. 6.4.3.1. Os valores de S1, S2, L50% e L75% correspondentes a esta curva são os seguintes:
S1 = 15*ln(3)/(18-15) = 5.4930 e S2 = ln(3)/(18-15) = 0.3662
L50% = 5.4930/0.362 = 15 cm e
L75% = (5.4930+ln 3)/0.3662 = 18 cm
O intervalo de selectividade é 2*(18-15) = 6 cm
Usando a equação de von crescimento de von Bertalanffy podemos expressar o comprimento em função da idade, e expressar S em função da idade, t:
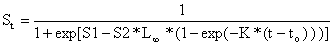 | (6.4.3.1) |
O gráfico desta expressão é aproximadamente igual ao gráfico equivalente à Eq. 6.1.1 baseada em idades, e definida por:
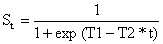 | (6.4.3.2) |
que pode ser reescrita na forma linear:
| ln(1/St - 1) = T1 - T2*t | (6.4.3.3) |
onde:
| T1 = t50%*ln(3)/(t75%-t50%) | (6.4.3.4) |
| T2 = ln(3)/(t75%-t50%) = T1/t50% | (6.4.3.5) |
(cf. Eqs. 6.1.6 e 6.1.7)
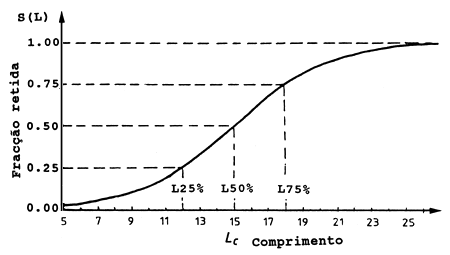
Fig. 6.4.3.1 A curva de selectividade referida no texto

Fig. 6.4.3.2 A: Ogiva de selectividade exacta transformada para idades
(Eq. 6.4.3.1)
B: Ogiva de selectividade aproximada (Eq. 6.4.3.2)
As fórmulas para t50% e t75% são:
| t50% = T1/T2 | (6.4.3.6) |
| t75% = (T1 + ln 3) /T2 | (6.4.3.7) |
(cf. Eqs. 6.1.4 e 6.1.5)
A Fig. 6.4.3.2 mostra as duas curvas de selectividade baseadas em idades. A curva A é baseada na transformação exacta de acordo com a Eq. 6.4.3.1, enquanto a curva B é a ogiva de selectividade aproximada, baseada na Eq. 6.4.3.2 e nas equações relacionadas 6.4.3.4. a 6.4.3.7.
É também possível expressar t50% e t75% em comprimentos e vice-versa, expressar L50% e L75% em idades, usando as seguintes fórmulas:
| t50% = to - (1/K)*ln(1 - L50%/L∞) | (6.4.3.8) | |
| t75% = to - (1/K)*ln(1 - L75%/L∞) | (6.4.3.9) | |
| e | ||
| L50% = L∞*[1 - exp(K*(to-t50%))] | (6.4.3.10) | |
| L75% = L∞*[1 - exp(K*(to-t75%))] | (6.4.3.11) |
Assumindo que L∞ = 50 cm, to = 0 ano e K = 0.3 por ano para o manancial de peixes associado à curva de selectividade baseada em comprimentos da Fig. 6.4.3.1, então:
t50% = 0 - (1/0.3)*ln(1 - 15/50) = 1.1889
t75% = 0 - (1/0.3)*ln(1 - 18/50) = 1.4876
T1 = 4.3727 e T2 = 3.6779
Os correspondentes L50% e L75% são:
L50% = 50*[1 - exp(0.3*(0 - 1.1889))] = 15.0 cm
L75% = 50*[1 - exp(0.3*(0 - 1.4876))] = 18.0 cm
que são os mesmos resultados obtidos para a curva de selectividade baseada em comprimentos.