Quando se usa uma curva de captura linearizada para estimar a mortalidade (por exemplo Fig. 4.4.5.1) é também necessário desprezar o lado esquerdo da curva porque os peixes jovens não são totalmente explorados ou não são totalmente recrutados. Uma maneira conceptualmente simples de se estimar quantos peixes estão a faltar em cada idade é extrapolar da recta, da qual o coeficiente de mortalidade total Z é estimado, a fim de encontrar o número de juvenis que “têm que existir”, (ver Fig. 6.5.1). As diferenças entre os números “esperados” e os reais deve dar a curva resultante do efeito combinado do recrutamento e da selectividade da malha. Como é mostrado abaixo, os cálculos são facilmente realizáveis. O problema é que é feita uma hipótese importante e, provavelmente, não realista, que a taxa de mortalidade total, Z = F+M, é a mesma para todas as idades. O F, isoladamente, não é constante porque tem que ser menor na fase de selectividade da malha e o M, por sua vez, é provável que seja maior para os peixes pequenos do que para os adultos. Por isso é possível que Z permaneça aproximadamente constante, embora até agora ninguém tenha provado. Todavia, o método tem alcançado uma popularidade considerável e portanto é aqui mencionado.
Para explicar este método (Pauly, 1984a), é utilizado o exemplo da Tabela 6.5.1. As colunas A-E contêm os dados de entrada e os cálculos para uma análise da curva de captura partindo de dados convertidos de comprimentos (cf. Secção 4.4.5). Neste caso calculamos a mortalidade total anual Z = 1.0 a partir dos parâmetros de crescimento, L∞ = 50 cm, K = 0.3 por ano (ver Fig. 6.5.1). O resultado da análise de regressão é:
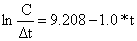
Em contraste ao exemplo discutido na Secção 4.4.5 agora temos uma utilidade para a intersecção (a = 9.208).
Sob a hipótese da mortalidade ser constante esperamos que os valores ln(C/Δt) estejam na recta de regressão ln(C/Δt) = a-Z*t. Assim, é esperado que a verdadeira frequência hipotética, o número total da população no mar, CT, preencha a equação:
| ln(CT/Δt) = a - Z*t. | (6.5.1) |
A ideia básica deste método é que o número de peixes no mar seja proporcional ao número capturado, ou seja

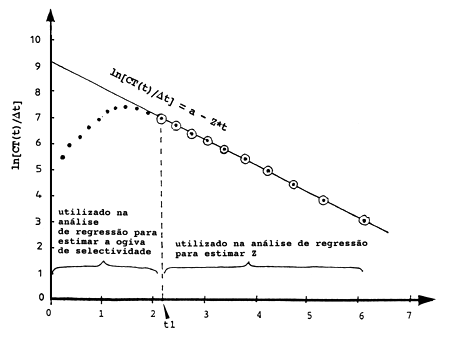
Fig. 6.5.1 Estimação da curva resultante a partir da análise da curva de capturas com os dados convertidos para comprimentos, na Tabela 6.5.1
Tabela 6.5.1 Exemplo para ilustrar a estimação da ogiva de selectividade de uma curva de captura (cf. Fig. 6.1.2.1). L∞ = 50 cm, K = 0.3 por ano, to = 0. (Os mesmos dados foram usados na Tabela 4.5.4.1)
| A | B | C | D | E | F | G | H |
| L1–L2 | t (x) | Δt (L1,L2) | C(L1,L2) | ln (C/Δt) (y') | St obs. | ln (1/S-1) (y) | St est. |
| 3– 5 | 0.278 | 0.145 | 37 | 5.54 | 0.034 | 3.35 | 0.03 |
| 5– 7 | 0.426 | 0.151 | 56 | 5.92 | 0.057 | 2.81 | 0.06 |
| 7– 9 | 0.581 | 0.159 | 86 | 6.29 | 0.097 | 2.23 | 0.10 |
| 9–11 | 0.744 | 0.167 | 129 | 6.65 | 0.163 | 1.64 | 0.16 |
| 11–13 | 0.915 | 0.176 | 188 | 6.97 | 0.267 | 1.01 | 0.27 |
| 13–15 | 1.095 | 0.186 | 258 | 7.23 | 0.416 | 0.42 | 0.42 |
| 15–17 | 1.286 | 0.196 | 319 | 7.39 | 0.590 | -0.37 | 0.59 |
| 17–19 | 1.487 | 0.208 | 352 | 7.43 | 0.750 | -1.10 | 0.75 |
| 19–21 | 1.703 | 0.222 | 351 | 7.37 | 0.870 | -1.90 | 0.87 |
| 21–23 | 1.933 | 0.238 | 324 | 7.22 | 0.943 | -2.80 | 0.94 |
| 23–25 | 2.180 | 0.257 | 283 | 7.00 | (0.976) | - | 0.98 |
| 25–27 | 2.447 | 0.278 | 239 | 6.76 | - | - | 0.99 |
| 27–29 | 2.734 | 0.303 | 196 | 6.47 | - | - | 1.00 |
| 29–31 | 3.054 | 0.334 | 158 | 6.16 | - | - | 1.00 |
| 31–33 | 3.406 | 0.371 | 123 | 5.80 | - | - | 1.00 |
| 33–35 | 3.798 | 0.417 | 93 | 5.41 | - | - | 1.00 |
| 35–37 | 4.243 | 0.477 | 69 | 4.97 | - | - | 1.00 |
| 37–39 | 4.757 | 0.557 | 48 | 4.46 | - | - | 1.00 |
| 39–41 | 5.365 | 0.669 | 31 | 3.84 | - | - | 1.00 |
| 41–43 | 6.109 | 0.838 | 18 | 3.04 | - | - | 1.00 |
| 43–45 | 7.068 | 1.122 | 10 | 2.19 | - | - | 1.00 |
| 45–47 | 8.419 | 1.702 | 3 | 0.57 | - | - | 1.00 |
as colunas contém, respectivamente
D C(L1,L2) = captura em números por classe de comprimento
E ln(C/Δt), variável dependente na análise de regressão da curva de captura (y')
H Stest. = 1/[1 + exp(T1 - T2*t)], ogiva de selectividade estimada (teórica)
Seja t1 a idade correspondendo à primeira classe de comprimento que supõe-se estar totalmente representada nas capturas e portanto é a utilizada na regressão da curva de captura (no caso da Tabela 6.5.1, temos t1 = 2.180, ver Fig. 6.5.1). Para idades acima de t1, CTt deve ser aproximadamente igual às frequências observadas, uma vez que a probabilidade de captura é 1, pois supostamente, a selectividade e o recrutamento já foram concluídos antes daquela idade. Mas para as idades abaixo de t1 esperamos que a população no mar seja maior que a representada nas capturas, isto é:
ln(CTt/Δt) > ln(Ct/Δt)
Como CTt é proporcional ao número da população, a razão
Ct/CTt
é a probabilidade estimada de um peixe de idade t estar na área de pesca e ser retido, se ele encontrar a arte, ou seja Ct/CTt pode ser usado como a curva resultante estimada St.
CT pode ser previsto pela Eq. 6.5.1 modificada:
| CTt = Δt*exp(a - Z*t) | (6.5.2) |
Assim, a curva pode ser estimada por:
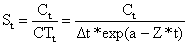 | (6.5.3) |
As fracções retidas da curva de selectividade observada são representadas na coluna F da Tabela 6.5.1. De forma a se obter a ogiva de selectividade teórica (estimada), a expressão para St dada como Eq. 6.4.3.3, é usada na forma linear:
| ln(1/St - 1) = T1 - T2*t | (6.5.4) |
A Eq. 6.4.3.3 possibilita estimar os parâmetros T1 e T2 por regressão linear. As colunas B (x) e G (y) da Tabela 6.5.1 contêm os dados de entrada para esta regressão. (Colunas C, D e E contêm o resultado da análise da curva de capturas utilizada para calcular a variável dependente, y, coluna G). A coluna H contém a curva de selectividade estimada. Apenas os valores de S(t) (coluna F) menores que 1 podem ser usados na expressão ln(1/S-1) (coluna G). Procedendo à análise de regressão vem:
a = T1 = 4.396 e -b = T2 = 3.701
que resulta, usando-se as Eqs. 6.4.3.6, 6.4.3.7, 6.4.3.10 e 6.4.3.11, em:
t50% = T1/T2 = 1.1877 ano
t75% = (T1 + ln 3) /T2 = 1.4846 ano
L50% = 50*(1 - exp(-0.3*(1.1877 - 0))) = 15.0 cm
L75% = 50*(1 - exp(-0.3*(1.4846 - 0))) = 18.0 cm
O exemplo da Tabela 6.5.1 é hipotético, construído para dar os resultados das Figs. 6.4.3.1 e 6.4.3.2. Como os dados são ideais, há uma concordância perfeita entre as fracções de retenção observadas (coluna F da Tabela 6.5.1) e as fracções de retenção teóricas (coluna H).
O exercício proporciona um controle da adequadabilidade da escolha dos pontos utilizados na análise de regressão para estimar Z. A conclusão da Tab. 6.5.1 é que o primeiro grupo de idade utilizado para estimar Z devia ter sido 27–29 cm, pois este grupo é o primeiro sob exploração total. Contudo, uma vez que a curva logística nunca alcança o valor 1, o conceito de “exploração total” é determinado pelo número de decimais na tabela.
Levando em conta que a curva logística é uma aproximação da curva real de selectividade, não se pode esperar obter uma estimação precisa para o primeiro comprimento sob exploração total. Se conseguirmos valores “próximo à vizinhança” de 1, a escolha do grupo do primeiro comprimento na regressão de captura estará suficientemente boa.
Como assinalado na introdução desta secção, os resultados do método descrito devem ser tratados com uma certa reserva.
(Ver Exercício (s) na Parte 2).
A mortalidade por pesca, F, está claramente relacionada com a curva de selectividade. Quando SL = O a mortalidade por pesca deve ser zero e quando SL = 1 a mortalidade por pesca está no seu nível mais alto. A relação óbvia entre a mortalidade por pesca e a selectividade é:
| FL = Fm*SL | (6.6.1.1) |
onde Fm é a “mortalidade por pesca máxima”. Assim, F, sendo uma função do comprimento tem a mesma forma de S, mas tem um nível diferente (ver Fig. 6.6.1.1A).
Na Eq. 6.6.1.1 consideramos F uma função contínua do comprimento, L. Na prática, no entanto, é muitas vezes conveniente substituir a função contínua por uma função por degraus como mostrado na Fig. 6.6.1.1B, onde se assume que F permanece constante dentro de cada classe de comprimento.
A curva de selectividade contínua SL também pode ser aproximada a uma função por degraus, S(j), na qual o valor para a classe de comprimento, j é S((L1+L2)/2), onde L1 e L2 são os limites inferior e superior da classe de comprimento, j. Quando usamos o índice da classe de comprimento, j, como argumento antes do comprimento L, podemos escrever um modelo da função por degraus para a mortalidade total, Z:
| Z(j) = M + Fm*S(j) | (6.6.1.2) |
onde M é o coeficiente de mortalidade natural (assumido aqui como sendo constante para todos as classes de comprimento), S(j) é a função por degraus da curva de selectividade e Fm a mortalidade por pesca máxima. Se Z, M e Fm são conhecidos, a selectividade pode ser estimada por (Pope et al., 1975 e Hoydal et al., 1982):
| S(j) = F(j)/Fm | (6.6.1.3) |
onde F(j) = Z(j) - M.
A Fig. 6.6.1.2 mostra F(j), Z(j) e S(j) como uma função do comprimento. Quando trabalhamos com uma função por degraus em vez da curva logística contínua, a selectividade é dada por uma matriz de valores de S, que pode substituir a expressão matemática (Eq. 6.6.1.1) ou pode ser aplicada para estimar os parâmetros da curva logística. Na verdade, uma matriz de valores de S é uma forma mais versátil de apresentar a curva de selectividade, já que nenhuma suposição tem que ser feita sobre a expressão matemática subentendida (cf. discussão de chaves de idade/comprimento versus equação de crescimento na Secção 3.2.1).
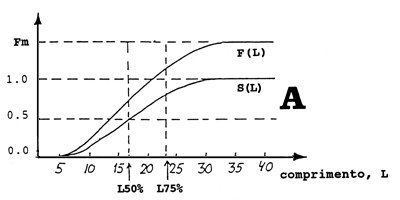
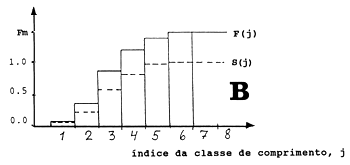
Fig. 6.6.1.1 Relação entre a curva de selectividade e a mortalidade por
pesca
A: Funções contínuas
B: Funçães-degrau correspondendo a A

Fig. 6.6.1.2 Relação entre a mortalidade e a curva de selectividade (para mais explicação ver o texto)
Os vários tipos de análise de coortes (Capítulo 5) produzem uma série de estimaçães do coeficiente F (o chamado “padrão de pesca”), por grupos de idade ou por classes de comprimento. Estes valores F oferecem dados para uma curva de selectividade da arte/recrutamento que é obtida por:
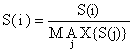 | (6.6.2.1) |
onde F(i) é a mortalidade por pesca para os grupos de idade, i; ou comprimento e MAX{F(j)} é o valor máximo da mortalidade por pesca entre todos os grupos de idade e comprimentos (cf. Eq. 6.6.1.3). A Eq. 6.6.2.1 aplica-se a qualquer arte ou qualquer combinação de artes com qualquer curva de recrutamento (Hoydal, et al. 1980 e 1982). O método não faz suposiçães quanto ao tipo de arte ou a como o peixe é capturado. Sendo assim, a curva de selectividade pode ser estimada apenas a partir dos dados da captura. A Eq. 6.6.2.1 dá os resultados reais das operaçães de pesca e portanto é chamada o “tamanho de malha efectivo”, isto é, os parâmetros de recrutamento/selectividade observados. O conceito de “tamanho de malha efectivo” também se aplica a artes sem malha, tais como o anzol e linha.
Esta abordagem possui um número de vantagens sobre as curvas de selectividade calculadas a partir das características das artes, por exemplo, o tamanho da malha. Ao considerar por exemplo a rede de arrasto e se assumir (como é frequentemente feito) que a curva de selectividade é determinada apenas pelo tamanho da malha no saco, então dois navios de pesca utilizando artes com o mesmo tamanho de malha deveriam ter a mesma curva de selectividade. No entanto, é provável que só se verifique se os dois navios operarem as artes exactamente da mesma maneira. Por exemplo, se um dos navios realiza arrastos de 5 horas de duração e o outro opera com arrastos de apenas uma hora, as propriedades selectivas podem ser diferentes por causa do entupimento da rede pela própria captura. A velocidade de arrasto também pode influenciar a selectividade. Uma velocidade maior pode fazer com que as malhas fiquem mais alongadas e causar um factor de selecção menor.
Quando se analisa uma amostra de frequências de comprimento, (isto é quando se procede à análise de Bhattacharya, Secção 3.4.1) a selectividade pode criar erros nos resultados. Como exemplo, vejamos a primeira parte da Tabela 3.2.1.1. Na coluna B da Tabela 6.7.1 mostra-se a amostra. Na verdade, a coluna B é a primeira componente estimada pela análise de Bhattacharya, como pode ser visto na coluna H da Tabela 3.4.1.1, que foi baseada nos mesmos dados. Estes dados hipotéticos representam uma amostra aleatória da população. Assim, no caso da Tabela 3.2.2.1 assumimos artes não selectivas. Se a amostra tivesse sido tomada com artes selectivas os resultados teriam sido diferentes.
Suponha agora que se utiliza uma arte com uma curva de selectividade do tipo da rede de arrasto, com L50% = 15 cm e L75% = 18 cm. Neste caso teríamos observado as frequêcias mostradas na coluna C da Tabela 6.7.1 e não as da coluna B. (Os valores na coluna C são hipotéticos e são calculados pelo produto da coluna B e da coluna D). As frequências da coluna C produzem um comprimento médio e um desvio padrão estimados errados, como pode ser visto nas duas últimas linhas da Tabela 6.7.1. No entanto, se a curva de selectividade é conhecida, é possível estimar a amostra não viciada, isto é, estimar a coluna B, que se obtém dividindo as frequências observadas (coluna C) pelas fracções retidas. Este processo de aumento dá a coluna E. Como poderia ser esperado, existem problemas com as frequências pequenas (comprimentos de 12–14 cm). O método não pode ser utilizado para aumentar uma frequência zero e não é fiável para pequenas frequências.
Tabela 6.7.1 Exemplo para ilustrar a estimação de uma amostra aleatória
a partir de uma amostra viciada por selectividade
(cf. Fig. 6.7.1)
| A | B | C | D | E |
| classe de comprimento cm | amostra observada não viciada (Tabela 3.2.1.1) | amostra viciada por selectividade | curva estimada SL | amostra não viciada estimada C/D |
| 12–13 | 1 | 0 | 0.30 | 0 |
| 13–14 | 4 | 1 | 0.37 | 3 |
| 14–15 | 11 | 5 | 0.45 | 11 |
| 15–16 | 24 | 13 | 0.55 | 24 |
| 16–17 | 38 | 24 | 0.63 | 38 |
| 17–18 | 42 | 30 | 0.71 | 42 |
| 18–19 | 33 | 26 | 0.78 | 33 |
| 19–20 | 20 | 17 | 0.84 | 20 |
| 20–21 | 7 | 6 | 0.88 | 7 |
| 21–22 | 2 | 2 | 0.92 | 2 |
| Total | 182 | 124 | 180 | |
| L médio | 17.3 | 17.6 | 17.3 | |
| s | 1.69 | 1.60 | 1.64 | |
| As colunas contém respectivamenta A classe de comprimento em cm B amostra não viciada da população (da Tabela 3.2.1.1) C amostra como teria sido obtida com uma rede de arrasto com uma curva de selectividade com L50% = 15 cm e L75% = 18 cm D ogiva de selectividade estimada (fracção retida) SL = 1/(1 + exp(S1 - S2*L) Eq. 6.1.1 onde S1 = L50%*ln(3)/(L75%-L50%) (Eq. 6.1.6) e S2 = S1/L50%(Eq. 6.1.7). E amostras não viciadas estimadas corrigidas para a selectividade, frequências da amostra viciada dividida pela fracção retida (C/D) (compare com a coluna B). | ||||
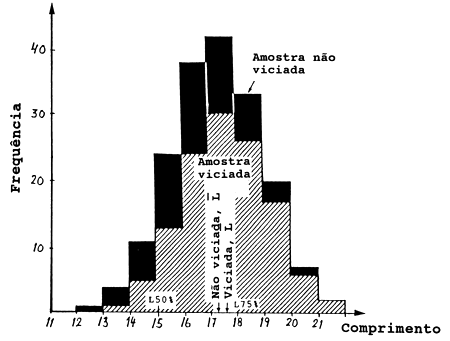
Fig. 6.7.1 Erro criado pela selectividade
Em geral, o efeito da selectividade de rede de arrasto é:
O erro causado pela selectividade é ilustrado pela Fig. 6.7.1.
A correcção dos erros deve ser feita preferenciavelmente através das curvas de selectividade determinadas por experiências, como o arrasto com o duplo saco (Secção 6.1) ou pela análise da matriz de mortalidades por pesca fornecida pela análise de coortes (Secção 6.6). Às vezes, podem ser utilizadas curvas de selectividade, para espécies intimamente relacionadas, com formas semelhantes.
Quando tais dados não são disponíveis, pode-se estimar a curva de selectividade talvez a partir de uma curva de captura linearizada (Secção 6.5). No entanto, fazendo de tal modo encontramos um problema lógico porque a estimação da selectividade é a última parte da análise da curva de capturas e portanto baseada em parâmetros estimados com erros devido aos efeitos da própria selectividade. Para iniciar a correção e, felizmente, é possível assim proceder, a sequência da análise pode ser como se segue:
| Passo 1: | Estimar L∞ pelo método de Powell-Wetherall. |
| Passo 2: | Corrigir as frequências de comprimento para a selectividade usando o valor 1.0 para o parâmetro de curvatura, K, e a estimação de L∞ obtida na Passo 1. |
| Passo 3: | Utilizar o método de Bhattacharya (Secção 3.4.1) na distribuição de frequências de comprimento corrigidas, para separar as componentes. |
| Passo 4: | Usar os valores estimados dos comprimentos médios das componentes na análise de progressão modal para estimar os parâmetros de crescimento K e L∞ (Secção 3.4.2). |
| Passo 5: | Estimar Z usando a análise da curva de capturas com comprimentos convertidos com os novos parâmetros de crescimento estimados (Secção 4.4.5). |
Este processo é aplicável porque a curva de selectividade estimada não é sensível à escolha do parâmetro de curvatura, K.
Aplicando o método de Powell-Wetherall para os dados na Tabela 6.5.1 coluna D (números capturados) encontramos L∞ = 49.7 cm (cf. Tabela 4.5.4.1 que usa os mesmos dados de entrada para estimar L∞ (pelo método de Powell-Wetherall)). Refazendo os cálculos da Tabela 6.5.1 com K = 1.0 obtemos os resultados apresentados na Tabela 6.7.2.
A ogiva de selectividade estimada, Stest, na Tabela 6.7.2, calculada com K = 1.0 por ano e L∞ = 49.7 cm é quase idêntica à apresentada na Tabela 6.5.1, calculada com K = 0.3 por ano e L∞ = 50 cm. Os valores de L50% e L75% são 14.8 cm e 17.8 cm respectivamente com K = 1.0, enquanto que foram de 15.0 e 18.0 cm respectivamente com K = 0.3.
Table 6.7.2 Exemplo para ilustrar o uso de uma curva de selectividade
para ajustar uma amostra de frequências de comprimento para
a selectividade, usando os mesmos dados de frequências de
comprimento apresentados na Tabela 6.5.1, com L∞ = 49.7 cm
(estimado pelo metodo de Powell-Wetherall),
K = 1.0 por ano e to = 0
| A | B | C | D | E | F | G | H | I |
| L1–L2 | t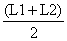 (x) | Δt (L1,L2) | C (L1,L2) obs | ln (C/Δt) (y') | St obs | ln (1/S-1) (y) | St est | C (L1,L2) est |
| 3–5 | 0.084 | 0.044 | 37 | 6.74 | 0.03 | 3.35 | 0.03 | 1121 |
| 5–7 | 0.129 | 0.046 | 56 | 7.11 | 0.06 | 2.81 | 0.06 | 1000 |
| 7–9 | 0.176 | 0.048 | 86 | 7.49 | 0.10 | 2.22 | 0.10 | 887 |
| 9–11 | 0.225 | 0.050 | 129 | 7.85 | 0.17 | 1.61 | 0.17 | 777 |
| 11–13 | 0.276 | 0.053 | 188 | 8.17 | 0.27 | 0.99 | 0.27 | 689 |
| 13–15 | 0.331 | 0.056 | 258 | 8.44 | 0.42 | 0.32 | 0.43 | 604 |
| 15–17 | 0.389 | 0.059 | 319 | 8.59 | 0.60 | -0.40 | 0.61 | 526 |
| 17–19 | 0.450 | 0.063 | 352 | 8.63 | 0.76 | -1.14 | 0.77 | 459 |
| 19–21 | 0.515 | 0.067 | 351 | 8.56 | 0.88 | -1.98 | 0.88 | 398 |
| 21–23 | 0.585 | 0.072 | 324 | 8.41 | 0.95 | -2.97 | 0.95 | 342 |
| 23–25 | 0.660 | 0.078 | 283 | 8.20 | 0.98 | -3.94 | 0.98 | 289 |
| 25–27 | 0.741 | 0.084 | 239 | 7.95 | 1.00 | 0.99 | 241 | |
| 27–29 | 0.829 | 0.092 | 196 | 7.66 | 1.00 | 197 | ||
| 29–31 | 0.925 | 0.102 | 158 | 7.35 | 1.00 | 158 | ||
| 31–33 | 1.032 | 0.113 | 123 | 6.99 | 1.00 | 123 | ||
| 33–35 | 1.152 | 0.128 | 93 | 6.59 | 1.00 | 93 | ||
| 35–37 | 1.289 | 0.146 | 69 | 6.16 | 1.00 | 69 | ||
| 37–39 | 1.446 | 0.171 | 48 | 5.64 | 1.00 | 48 | ||
| 39–41 | 1.634 | 0.207 | 31 | 5.01 | 1.00 | 31 | ||
| 41–43 | 1.865 | 0.261 | 18 | 4.23 | 1.00 | 18 | ||
| 43–45 | 2.166 | 0.355 | 10 | 3.34 | 1.00 | 10 | ||
| 45–47 | 2.598 | 0.554 | 3 | 1.69 | 1.00 | 3 | ||
| T1 = 4.428 T2 = 12.492 | ||||||||
| t50% = T1/T2 = 0.3545 ano t75% = (T1 + ln 3)/T2 = 0.4424 ano | ||||||||
| L50% = 49.7*(1 - exp(-1*(0.3545 - 0))) = 14.8 cm | ||||||||
| L75% = 49.7*(1 - exp(-1*(0.4424 - 0))) = 17.8 cm | ||||||||
A última coluna da Tabela 6.7.2 contém os resultados do Passo 2 do processo, as frequências de comprimento corrigidas para a selectividade. Uma comparação com os dados observados (coluna D) mostra imediatamente que um grande número de peixes não foram considerados no exemplo. O próximo passo (3), o método de Bhattacharya, será portanto bem diferente do aplicado aos dados originais.
Em princípio, o método supracitado pode ser aplicado a qualquer tipo de curva de selectividade das artes, porém quanto mais estreito o intervalo de comprimentos selecionado pelas artes, mais difícil é estimar as frequências de comprimento que se teria conseguido com artes não selectivas.
Para redes de emalhar ou quaisquer outras artes com uma curva de selectividade em forma de sino, é preciso ser cuidadoso na interpretação de amostras de frequências de comprimento. A moda observada (é comum haver somente uma moda para este tipo de artes) pode ter pouca relação com a coorte, mas pode reflectir primariamente a curva de selectividade da arte (cf. Secção 6.2).
(Ver Exercício (s) na Parte 2).