A base ideal para avaliação de mananciais de peixes é ter dados totalmente representativos do manancial, pelo menos a partir do momento em que é recrutado à área de pesca, sem qualquer erro sistemático ou vício. Embora na prática não seja possível obter dados com esta qualidade, deveria ser o objectivo de qualquer programa de amostragem de dados de uma pescaria, a obtenção de amostras que sejam totalmente representativas da população em estudo, ou, quando for o caso, a determinação das fontes de erros e as formas de corrigílos.
A teoria completa sobre amostragem é tratada por muitos manuais, largamente disponíveis, como Raj (1968), Som (1973) ou Cochran (1977).
Na primeira parte deste Capítulo, serão discutidos alguns aspectos básicos da amostragem, com ênfase para a amostragem aleatória. A segunda parte trata de um exemplo típico de pescaria demersal, onde muitas espécies são desembarcadas, parcialmente seleccionadas, para consumo humano, e parcialmente misturadas na forma de espécies acompanhantes (para produção de farinha de peixe ou outros propósitos). O objectivo deste exemplo é mostrar a complexidade que um esquema de amostragem pode assumir de maneira a fornecer uma amostra representativa de uma particular pescaria e como os factores de ampliação devem ser aplicados para a pescaria de uma determinada espécie como um todo.
Este exemplo foi elaborado com base na experiência obtida nos cursos da FAO/DANIDA sobre avaliação de mananciais de peixes, onde muitos grupos de dados apareciam incompletos ou viciados, devido a erros de estratégia de amostragemo e/ou a aplicação desta (ver Venema et al., 1988).
Bons programas de amostragem requerem altos investimentos a longo prazo em termos de pessoal e despesas gerais. Portanto, é importante que estes programas sejam desenhados de maneira a fornecer os dados necessários para a avaliação de mananciais das principais espécies e pescarias, e que estejam em acordo com os padrões formulados pelos grupos de trabalho internacionais e nacionais.
Os princípios de amostragem tratados neste capítulo também podem ser aplicados para trabalhos a bordo de cruzeiros de investigação, para os quais, adicionais detalhes específicos sobre amostragem de convés são apresentados na Secção 13.4.
Voltando ao problema de estimar o comprimento médio de uma coorte, conforme citado nas Secções 2.2 e 2.3. Uma estimação é dita não viciada se as repetidas estimações apenas se desviam do valor real de maneira estritamente aleatória. O “valor real” é o parâmetro que obteríamos se medíssemos todos os indivíduos da população inteira (ver Secção 2.3). Uma estimação é “viciada” se se desvia do valor real de maneira sistemática. Com uma estimação não viciada podemos obter a aproximação que desejamos em relação ao valor real aumentando o tamanho da amostra. Uma amostra viciada conterá sempre um desvio em relação ao valor real, e o desvio será independente do tamanho da amostra.
Para obter estimações não viciadas do comprimento médio necessitamos de uma “amostra aleatória”, isto é, uma amostra na qual qualquer peixe do manancial considerado tenha exactamente a mesma probabilidade de ser amostrado. Supondo-se que é possível obter uma amostragem aleatória (isto é muito difícil na prática), quantos peixes, n, seriam necessários na amostra para se obter um determinado grau de precisão?
Supor que se necessita de uma estimação do comprimento médio cujo desvio em relação ao comprimento real não seja maior que 7% e queremos estar 95% certos disto. Temos então que estabelecer que os limites de confiança inferior e superior, ao nível de 95%, não se desviem mais do que 7% da média estimada, x. Assim o desvio tn-1*s/√n deve ter um valor máximo de 0.07*x, ou
tn-1*s/√n = 0.07*x
ou mais geral: tn-1*s/√n = ε*x
onde ε representa o “erro máximo relativo” (no caso ε = 0.07).
Resolvendo esta equação em ordem a n resulta:
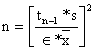 | (7.1.1) |
Para aplicar a Eq. 7.1.1 e estimar o tamanho requerido da amostra, devemos antes conhecer o desvio padrão, s, das amostras prévias.
Podemos também resolver a Eq. 7.1.1 em ordem a ε, usando, por exemplo a estimação de s = 2.20 e x = 15.07 da Tabela 2.1.2.
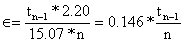
Na Figura 7.1.1 o erro máximo relativo, é mostrado como uma função do tamanho da amostra n. Note que o ganho em precisão para aumentos de n quando n > 50 é relativamente pequeno. No entanto, um incremento de n = 10 com n = 20 produz uma redução no erro relativo de 10.0% para 6.8%.
Se puderem ser obtidas amostras aleatórias não viciadas, não há problemas com a estimação do tamanho da amostra para qualquer grau de precisão estabelecido. No entanto, uma amostra, de uma forma ou de outra, é sempre viciada.
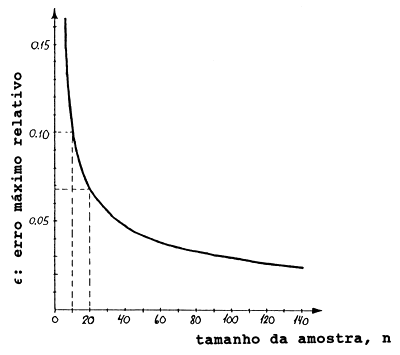
Fig. 7.1.1 Erro máximo relativo (ε) do comprimento médio estimado em função do tamanho da amostra (n) (usando dados da Tabela 2.1.2)
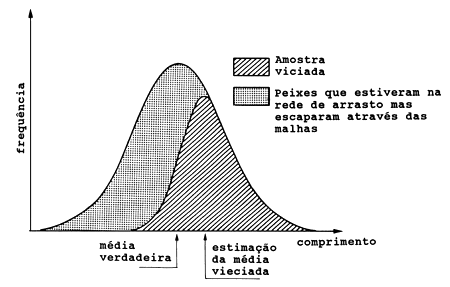
Fig. 7.1.2 Exemplo de erro: erro causado pela selectividade da arte
Se pequenos peixes escapam através das malhas da rede de arrasto obtemos uma sobrestimação do comprimento médio da população (ver Fig. 7.1.2). Isto é um exemplo de erro. Se um peixe grande pode nadar mais rápido que a velocidade do arrasto e então evitar a sua captura, temos outro tipo de erro.
No entanto, uma vez que se está prevenido para o erro, pode-se contorná-lo. No caso da selectividade da malha, por exemplo, poderíamos tentar estimar quantos peixes haveriam se todos tivessem sido retidos pela arte de pesca (ver Capítulo 6).
Outro tipo de erro ocorre se a distribuição espacial da população de peixes depende dos tamanhos. Por exemplo, quando os peixes jovens concentram-se nas áreas de crescimento e gradualmente migram para as áreas de pesca, pode ser introduzido um erro, caso não se compreenda bem este padrão de migração. O erro causado pela migração será discutido no Capítulo 11.
Outra possibilidade de erro de amostragem decorre em situações onde seria ineficaz medir toda a captura, como o caso de um arrasto volumoso. Depois de separar a captura por espécies, poderia-se tirar uma subamostra de, digamos, 100 peixes de uma espécie. Se os peixes fossem retirados um a um por recolha manual directa, poderia resultar num erro de amostragem, pois há uma tendência natural pela escolha dos exemplares maiores. Um procedimento correcto para evitar este problema seria colocar a captura daquela espécie em caixas com aproximadamente o mesmo peso e então seleccionar, aleatoriamente, algumas delas como subamostras.
Até agora considerámos uma população constituida de um grande número de peixes de forma que uma amostra é uma parcela insignificante da mesma. No entanto, algumas “populações” consistem de um pequeno número de unidades, de forma que uma amostra constitui uma grande parcela da mesma. Isto ocorre quando a “população” amostrada não é de peixes mas, por exemplo, dos locais de desembarques em uma certa área.
Supor que o objectivo de um esquema de amostragem é estimar o desembarque médio por local durante um certo período, digamos, um mês e supor que o número total de locais de desembarque é 100. Se amostramos todos os 100 locais, então a variância do desembarque médio estimado seria zero. Neste caso, simplesmente teriamos a verdadeira média da população. Se o pessoal disponível para amostragem é suficiente apenas para 50 locais, haveria uma certa variância na nossa estimação. No entanto, esta variância não seria s2 (conforme definida pela Eq. 2.1.2), já que só 50% da população é que produz a variância, o que difere do caso da população de peixes onde praticamente 100% da população é responsável pela variância.
Contornamos este problema aplicando o chamado “factor de correcção para populações finitas”:
(1 - n/N)
onde N é o tamanho da população (N = 100 no exemplo) e n é o tamanho da amostra. Seja Y(i) o desembarque no local de desembarque no i da amostra, i = 1,2,…n, e seja Y o desembarque médio para todos os locais de desembarque, então o desembarque médio estimado é dado por:
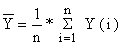
A variância da estimação será (conforme Eqs. 2.3.2 e 2.1.2):
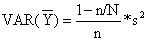 | (7.1.2) |
onde
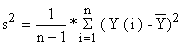 | (7.1.3) |
O intervalo de confiança de Y é (ver Eq. 2.3.1):
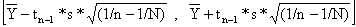
O desembarque total estimado é:
| Y = N*Y | (7.1.4) |
e a sua variância é
| VAR(Y) = N2 VAR(Y) | (7.1.5) |
Y é geralmente a quantidade em que estamos interessados. A Eq. 7.1.5 calcula-se da regra geral para a variável aleatória, Eq. 2.3.3, onde N é constante.
Note que a Eq. 7.1.2 é geral no sentido que também é aplicada a grandes populações (na prática infinitas) já que o factor de correcção para populações finitas, (1-n/N) torna-se 1.0 quando N é infinito.
Frequentemente a Eq. 7.1.4 é expressa como:
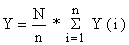 | (7.1.6) |
e dizemos que a amostra foi ampliada para o total, Y, pela aplicação do “factor de ampliação” N/n.
Considere novamente o problema da estimação do desembarque total, Y, de 100 locais durante um certo mês, conforme tratado na Secção 7.1. Supor que um programa de amostragem foi conduzido em anos anteriores baseado nos mesmos 100 locais de desembarque no qual foram divididos em três categorias, conforme mostrado na Tabela 7.2.1. Esta divisão da população é chamada “estratificação” e as categorias (grande, médio, pequeno) são chamadas “estratos”. A Tabela 7.2.2 mostra um exemplo numérico (de Gulland, 1966) correspondente à Tabela 7.2.1. Para obter uma estimação do desvio padrão dentro de cada estrato, s(j), j = 1,2,3,… foi conduzido um levantamento, durante um mês, cobrindo todos os locais de desembarques.
Tabela 7.2.1 Um exemplo de estratificação (de Gulland, 1966)
| categoria do local desemb. ou estrato | número de locais de desemb. por estrato | média de desemb. por estrato | desvio padrão dentro de cada estrato s(j) |
| 1 grande | N(1) | Y(1) | s(1) |
| 2 médio | N(2) | Y(2) | s(2) |
| 3 pequeno | N(3) | Y(3) | s(3) |
Tabela 7.2.2 Exemplo numérico de uma estratificação baseada em amostras de um mês (de Gulland, 1966)
| Y(j,i) = desembarques no local no i no estrato j. | ||||||||||||
| LOCAIS DE DESEMB. GRANDES: | Y(1,i) | |||||||||||
| N(1) | = | 10 | 45 | 59 | 87 | 41 | 71 | 25 | 9 | 69 | 10 | 7 |
| Y(1) | = | 42.3 | ||||||||||
| s(1) | = | 28.91 | ||||||||||
| LOCAIS DE DESEMB. MÉDIOS: | Y(2,i) | |||||||||||
| N(2) | = | 30 | 17 | 13 | 19 | 26 | 1 | 8 | 27 | 11 | 12 | 26 |
| Y(2) | = | 15.2 | 5 | 8 | 10 | 16 | 16 | 4 | 16 | 16 | 13 | 29 |
| s(2) | = | 8.57 | 14 | 25 | 29 | 27 | 20 | 25 | 2 | 7 | 3 | 12 |
| LOCAIS DE DESEMB. PEQUENOS: | Y(3,i) | |||||||||||
| N(3) | = | 60 | 2 | 6 | 7 | 0 | 1 | 2 | 1 | 5 | 4 | 7 |
| Y(3) | = | 4.2 | 8 | 9 | 3 | 2 | 5 | 4 | 2 | 0 | 2 | 8 |
| s(3) | = | 2.81 | 5 | 3 | 8 | 9 | 8 | 9 | 1 | 6 | 5 | 3 |
| 3 | 4 | 7 | 5 | 5 | 3 | 2 | 4 | 6 | 1 | |||
| 6 | 2 | 5 | 1 | 0 | 3 | 8 | 0 | 4 | 3 | |||
| 3 | 5 | 5 | 0 | 7 | 0 | 9 | 7 | 9 | 0 | |||
O desvio padrão, s(j), nas Tabelas 7.2.1 e 7.2.2 é a raiz quadrada da variância correspondente:
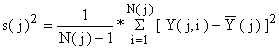 | (7.2.1) |
onde a média dos estratos é:
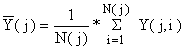 | (7.2.2) |
Note que as Eqs. 7.2.1 e 7.2.2 fornecem os parâmetros reais para o mês particular em que os dados foram amostrados.
Em geral não temos condições para amostrar todos os locais de desembarque. Vamos assumir que temos pessoal, etc. disponível apenas para amostrar n (n < 100) locais de desembarque. O tamanho da amostra pode ser escrito como a soma:
n = n(1)+n(2)+n(3)
onde n(i) é o número de locais de desembarque amostrados no estrato no i. “Delinear um esquema de amostragem” significa decidir qual o tamanho das amostras, n(1), n(2) e n(3), a ser aplicado a cada um dos três estratos.
Poderia ser questionado agora o porquê de complicar a amostragem com a introdução do estrato. A resposta é que (quase) sempre obtemos uma melhor precisão nas estimações da média da população com amostragem estratificada do que com amostragem aleatória simples. O quanto ganhamos com isto depende da escolha dos estratos. Se as observações dentro de um estrato são aproximadamente do mesmo tamanho (como no caso da Tabela 7.2.2) teremos certamente um ganho com a estratificação. Quanto menor a variação dentro do estrato maior o ganho com Por outro lado, por razões práticas, existe um limite do número de estratos.
A regra básica da amostragem estratificada é que o tamanho da amostra por estrato, n(j), deve ser grande quando:
A estas regras podemos acrescentar que, por razões económicas, a amostra deve ser grande quando:
A amostragem sai barata
Matematicamente as duas primeiras condições podem ser expressas como
| n(j) proporcional a N(j)*s(j) | (7.2.3) | |
| ou | ||
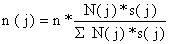 | (7.2.4) |
onde n é o tamanho total da amostra. Esta fórmula é chamada “equação da amostragem estratificada óptima” (ou “repartição de Neyman”).
As duas primeiras condições serão tratadas no Exemplo 25 abaixo e a terceira no Exemplo 26.
Exemplo 25: Amostragem aleatória estratificada
Vamos assumir que temos recursos disponíveis para executar 100 observações. Existem dois estratos e o tamanho dos estratos, N(j), e os seus desvios padrões, s(j), são:
| Estrato 1 | Estrato 2 | |
| N(j) | 1000 | 2000 |
| s(j) | 50 | 10 |
Então as 100 observações deveriam ser repartidas por cada estrato de acordo com a Eq. 7.2.4 nas seguintes proporções:
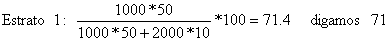
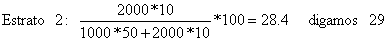
Geralmente os orçamentos disponíveis para a condução de programas de amostragem são limitados. O custo da amostragem será diferente de estrato para estrato e, portanto, devemos levar em conta o custo de uma unidade amostral (uma observação) quando delineamos um esquema de amostragem.
Seja c(j) o custo para se realizar uma unidade amostral no estrato j e seja Co o custo fixo adicional de todo o programa de amostragem. O custo total, C, para m estratos será então:
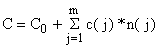 | (7.2.5) |
Pode ser demonstrado que para uma repartição óptima o tamanho da amostra deve ser proporcional a 1/√c(j).
Uma óptima aplicação dos recursos disponíveis é obtida (ver Eq. 7.2.3) quando o tamanho da amostra é proporcional a:
N(j)*s(j)/√c(j), ou se
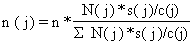 | (7.2.6) |
onde n é o tamanho total da amostra. Usando o critério, Eq. 7.2.6, minimizamos a variância da estimação do desembarque total, Y.
Se o orçamento total disponível é C e o custo fixo é Co então o número total de unidades amostrais em todas os estratos é dado por:
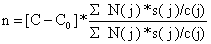 | (7.2.7) |
e o número de unidades amostradas no estrato j será dado por:
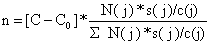 | (7.2.8) |
Exemplo 26: Amostragem aleatória estratificada, considerando os custos
Suponha que o orçamento total para o programa de amostragem dado no Exemplo 25 é de 1800 (unidades monetárias). O custo fixo é 444 e o custo por unidade amostral é:
| Estrato 1: | 16 |
| Estrato 2: | 9 |
Então, o número total de amostras, n, que pode ser obtido com os recursos disponíveis é determinado pela Eq. 7.2.7:
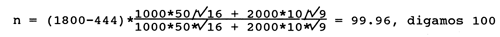
Estas 100 unidades amostrais seriam repartidas pelo estrato 1 e 2 respectivamente como se segue:
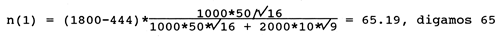
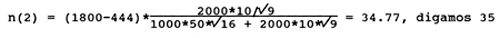
Note agora que 35 unidades amostrais são repartidas pelo estrato 2, de mais baixo custo, em comparação com 29 no Exemplo 25, onde o preço da unidade amostral não foi levado em consideração (ou foi assumido como sendo o mesmo para ambos os estratos).
Conclui-se, assim, a teoria da repartição óptima e voltamos à questão de como estimar os valores médios, os totais e as suas variâncias. Embora a teoria apresentada a seguir seja geral, podemos novamente particularizar o exemplo da Tabela 7.2.2. Tendo determinado o tamanho das amostras, n(j), obtemos um desembarque médio estimado para cada estrato, Y(j), por:
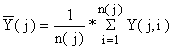 | (7.2.9) |
Seja m o número total de estratos (j = 1,2,…,m), então a estimação da média do total da população, isto é, o desembarque médio em todos os estratos, é:
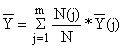 | (7.2.10) |
e, finalmente, o desembarque total estimado, Y, (ver Eq. 2.7.4) é:
Y = N*Y
Seja “VARst” o símbolo para a variância de uma estimação obtida de uma amostragem aleatória estratificada (“st”). A estimação da variância da média do total da população, Y, é:
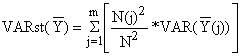 | (7.2.11) |
onde a estimação da variância da média estimada para cada estrato Y, VAR(Y(j)), é definida pela Eq. 7.1.2:
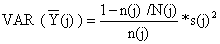 | (7.2.12) |
Note o factor de correcção para a população finita: 1 - n(j)/N(j)
A Eq. 7.2.11 calcula-se a partir das regras gerais da variância da soma de variáveis aleatórias independentes, dadas na Eq. 2.3.3 e 2.3.4.
A variância dentro do estrato j, definida pela Eq. 7.1.3, é:
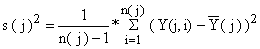 | (7.2.13) |
Substituindo a Eq. 7.2.12 na Eq. 7.2.11 esta, também pode ser escrita:
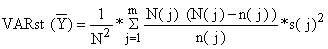 | (7.2.14) |
A Eq. 7.2.14 torna-se mais conveniente do ponto de vista de cálculos (ver Exercício 7.2).
A variância do desembarque total no estrato j é:
| VAR (Y(j)) = N (j)2*VAR(Y(j)) | (7.2.15) |
e a variância da captura total (todos os estratos) é:
| VARst (Y) = N2*VARst(Y) | (7.2.16) |
Nos exemplos dados anteriormente os estratos eram compostos por diferentes tamanhos de locais de desembarque em termos de peso desembarcado. As estratificações também se podem basear em outros critérios, como por exemplo:
Tipos de artes de pesca
Tipos de barco
Estações de pesca
Áreas de pesca
Espécies ou grupos de espécies
Tamanhos das categorias comerciais
Geralmente podemos obter vantagem em algum processo de estratificação. Algumas vezes somos forçados a estratificar a nossa amostragem, como é o caso das pescarias onde os desembarques já vêm separados por categorias comerciais. Em outros casos teremos um trabalho extra para estratificar, como é o caso da estratificação por tipo de barco. Se amostramos numa lota, no momento da venda do peixe, talvez tenhamos que investigar para saber de que barco provém aquela captura. Se temos que investir recursos extras (humanos, materiais, tempo, etc.) em um processo de estratificação, o ganho em precisão a ser obtido deve ser considerado em relação aos custos.
Em alguns casos (por exemplo, quando iniciamos os trabalhos), pode não ser conhecida a variância dentro do estrato, mas apenas o tamanho do estrato, N(j). Nesta situação recomenda-se o uso da “amostragem proporcional”, isto é, a repartição do número de amostras proporcionalmente ao tamanho do estrato. Aplicando a amostragem proporcional às 100 observações do Exemplo 25 dado acima, as amostras deveriam ser repartidas pelos dois estratos na seguinte proporção:
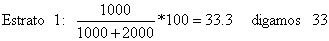
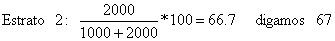
Compare com os valores obtidos pela repartição óptima no Exemplo 25, 71 para o estrato 1 e 29 para estrato 2, respectivamente.
Note que a amostragem proporcional apenas é idêntica à amostragem estratificada óptima no caso excepcional em que as variâncias de todos os estratos são iguais.
(Ver Exercício (s) na Parte 2).
Para realizarmos a avaliação de mananciais de peixes em exploração temos que dispor de dados adequados para cada espécie em investigação. Devemos conhecer o peso total das capturas e a composição por comprimentos e/ou idades do total capturado de cada manancial. Para a obtenção destes dados será necessário amostrar os desembarques das pescarias comerciais, de acordo com um esquema pré determinado. Tal esquema de amostragem deve levar em consideração os seguintes factores:
a área total de distribuição do manancial de cada espécie e
todas as actividades de pesca realizadas na área dirigidas para a captura daquelas espécies em particular. Isto pode incluir diferentes tipos de barcos (frotas) e diferentes tipos de artes de pesca. As frotas podem ser completamente nacionais ou incluir frotas estrangeiras que também exploram o mesmo manancial.
Uma vez que os mananciais de peixes podem ocupar áreas que ultrapassam os limites internacionais, o sistema de recolha de dados deve ser conduzido de maneira a permitir a utilização conjunta de dados de diferentes países. Nestes casos, é essencial que sejam feitos acordos entre os países para estabelecer os dados necessários e uma forma comum de amostragem. Tais acordos devem ser feitos através de organismos internacionais sendo também desejável a formação de grupos de trabalho internacionais para a condução dos mesmos. O mesmo critério aplica-se a grandes países onde vários organismos e institutos de investigação estão envolvidos no estudo e recolha de dados de um determinado manancial.
Os dados recolhidos devem ser verificados e armazenados em uma base de dados informatizada, que deve ser accessível a todos os cientistas interessados, que estejam autorizados a usá-la. A recolha de dados através de tais esquemas de amostragens não pode jamais ser considerada “propriedade” do investigador responsável pela sua recolha.
Devido à complexidade de muitas pescarias, particularmente nos trópicos, onde muitas artes diferentes são usadas para capturar uma mistura de espécies e onde os desembarques são sempre dispersos em várias localidades diferentes, é fundamental desenhar uma estratégia de amostragem baseado num conhecimento profundo das pescarias da espécie visada. Quando é seleccionada mais de uma espécie para investigação, pode ser possível combinar os esquemas de amostragem caso haja sobreposição dos locais de desembarques, frotas, etc.
Os esquemas de amostragem, uma vez estabelecidos, e em particular quando estão envolvidos acordos internacionais, devem ter fundos assegurados para longos períodos de tempo e, em alguns casos, praticamente para sempre.
As amostragens realizadas para a avaliação de mananciais possuem uma estreita relação com as amostragens ou sistemas de estimação dos totais, estabelecidos por estatísticos pesqueiros. Enquanto estes, estão mais interessados na obtenção das capturas de todas as espécies importantes, geralmente por arte de pesca e tipo de embarcação, o cientista pesqueiro está normalmente mais voltado para um número menor de espécies. Amostragens biológicas consomem muito tempo e, portanto, não é possível, na maioria dos casos, cobrir todos os desembarques em determinado local, no entanto, para a avaliação de mananciais também é necessário estimar quanto de uma determinada espécie foi desembarcado pelos barcos não amostrados, tanto no local onde a amostragem biológica foi realizada como nos outros locais. Assim, é óbvio que o trabalho do estatístico das pescas é de extrema importância para os biólogos pesqueiros, uma vez que as estatísticas gerais serão utilizadas para determinar os chamados “factores de ampliação”, que consistem em índices para relacionar o número total de unidades com o número amostrado. Factores de ampliação são, portanto, usados para ampliar os dados (por exemplo, frequências de comprimento) obtidos através das amostras, para a captura total. Contudo, quando as amostras são pequenas em relação ao desembarque total, o factor de ampliação pode ser muito grande e, caso a amostra contenha vícios, este será reflectido em maior escala nos totais.
Portanto, é muito importante que as amostras sejam aleatórias e que representem uma proporção razoável da captura total e, em vez de se pensar em medir centenas de peixes, deve-se fazer planos para medir milhares de peixes. Apenas assim disporemos de uma base confiável para a avaliação de mananciais. No exemplo dado na Tabela 4.4.3.1, as capturas totais de badejo de todas as classes anuais (coortes) foram estimadas em 2,021,800,000 peixes, enquanto que o número de otólitos de badejo amostrados em todos os países que actuam na exploração deste recurso e usados pelo grupo de trabalho internacional foi de aproximadamente 10,000. O factor de ampliação global das amostras para a captura total foi de aproximadamente 200,000.
Na Tabela 5.1.1, o número total de sobreviventes estimado para a coorte de 1974 foi de 9,856,600,000 badejos, ou seja, cerca de 3.4 vezes mais que o número capturado. Assim sendo, o número efectivamente amostrado representa apenas uma pequena fracção da real população no mar, apesar dos enormes esforços empregados.
A base de todo o esquema de amostragem é a decisão sobre a espécie a ser amostrada. Esta decisão é geralmente estabelecida levando-se em conta a importância económica da espécie (ou grupo de espécies) e no caso de recursos explorados por mais de um país, é considerado as necessidades dos grupos de trabalho internacionais.
Considerando-se que o padrão geral das pescarias comerciais de cada espécie seleccionada é conhecido, é possivel determinar que locais de desembarque e que frotas devem ser amostradas em cada época.
Com base no padrão, e conforme a disponibilidade de fundos e de pessoal, o sistema pode ser desenhado e testado.
A complexidade dos esquemas de amostragem e os vários factores de ampliação envolvidos são ilustrados no exemplo teórico a seguir, que em muitos aspectos assemelha-se a uma pescaria tropical de camarões e de peixes demersais.
Exemplo 27: Esquema de amostragem para uma pescaria tropical demersal
Os dois principais objectivos do esquema de amostragem ilustrado neste exemplo são:
Determinar a captura total em peso de uma espécie “s” (Secção 7.5) e
Determinar a composição por comprimentos da captura total da espécie “s” (Secção 7.6.).
Tabela 7.4.1 Processo para estimar a captura total em peso para uma espécie, s, durante um período, t. (compare Fig. 7.4.1)
| CAPTURA TOTAL DA ESPÉCIE “s” DURANTE O PERÍODO DE TEMPO “t” EM UNIDADES DE PESO | |||||||
| frota | local de desemb. | esforço E | captura observada W | CPUE por frota | captura estimada | captura total por frota e local desem. | captura total por frota |
| f | h | (t,f,h) | (s,t,f,h) | ∑W/∑E | CPUE*E | W(s,t,f,h) | W(s,t,f,*) |
| a | I | 15 | 57 | 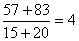 | - | 57 | |
| a | II | 20 | 83 | - | 83 | 172 | |
| a | III | 8 | - | 4*8 = 32 | 32 | ||
| b | I | 25 | 55 | 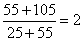 | - | 55 | |
| b | II | 55 | 105 | - | 105 | 184 | |
| b | III | 12 | - | 2*12 = 24 | 24 | ||
| c | I | 20 | - | 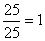 | 1*20 = 20 | 20 | |
| c | II | 25 | 25 | - | 25 | 75 | |
| c | III | 30 | - | 1*30 = 30 | 30 | ||
total geral estimado da captura: W(s,t,*,*) = 431 | |||||||
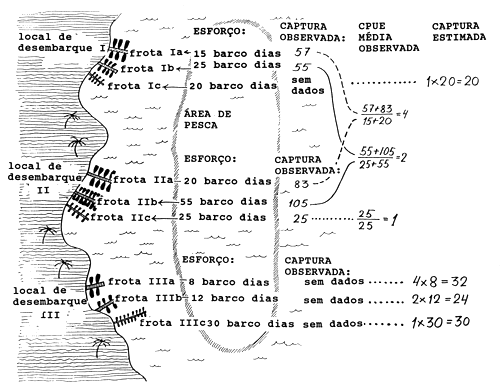
Fig. 7.4.1 Exemplo hipotético para ilustrar a estimação da captura total em peso da espécie, s, durante um período de tempo, digamos um trimestre
Assume-se que todos os indivíduos capturados da espécie “s” provém de um mesmo manancial e que todos os locais de desembarque destas capturas são cobertos pelo esquema de amostragem.
Os aspectos físicos do exemplo são mostrados na Fig. 7.4.1. Assumimos que o manancial está limitado a um banco pesqueiro explorado unicamente pelos barcos que operam nos três locais de desembarque, h, e com índices I, II e III. Existem três diferentes tipos de barcos, por exemplo:
Cada local de desembarque é porto de um certo número de barcos de cada tipo. Um grupo de barcos similares é chamado frota (índice f). Tendo em vista que a localização dos portos de desembarque é um factor de importância prática num esquema de amostragem, identifica-se cada frota de acordo com o local de desembarque, de forma que, de facto, trata-se de nove frotas, que serão diferenciadas por combinações das colunas f e h, por exemplo aI, bII, bIII etc. Na Fig 7.4.1 as frotas foram distribuidas pelos seus respectivos portos, enquanto que na Tabela 7.1.1 foram ordenadas por tipo de barco com o objectivo de facilitar os cálculos da captura por unidade de esforço (CPUE).
A próxima suposição importante que fazemos é que dispomos dos dados do esforço total de pesca, e para cada frota em cada local de desembarque. No presente exemplo, o esforço foi medido como o número de barcos/dias durante o período de tempo considerado. (Note que poderiam ter sido tomadas, um número de medidas alternativas do esforço. No pior dos casos, apenas o número de barcos em cada frota é conhecido. Neste caso, devemos assumir um número médio de unidades de esforço por barco por unidade de tempo. Se conhecemos, por exemplo, o número médio de barcos/dia, por frota, por mês para um local de desembarque, este número pode ser aplicado a locais de desembarque onde essa informação não esteja disponível).
O número de unidades de esforço de pesca aplicado durante o período de tempo, t, pela frota, f, do local de desembarque, h, é dado por:
E(t,f,h) = esforço
Os valores observados (ou estimados) do esforço E(t,f,h) dos nove grupos de barcos são mostrados na Tabela 7.4.1 e Fig. 7.4.1. Por enquanto, confinamos a descrição do sistema de amostragem para um único período de tempo, por exemplo o segundo trimestre de 1978, o que faz com que o índice “t” seja constante. Mais tarde, dados de períodos de tempos diferentes serão combinados e então “t” torna-se-á um índice variável.
Assumimos que, devido a limitações de recursos financeiros e de pessoal, as capturas totais não foram registadas para 1) nenhuma das frotas do local de desembarque III, 2) para a frota c do local de desembarque I. As capturas totais observadas das outras componentes são mostradas na Tabela 7.4.1 e Fig. 7.4.1. Sendo
W(s,t,f,h)
o peso total da espécie “s” desembarcado no período de tempo “t”, pela frota “f” no local de desembarque “h”.
Os dados do esforço e das capturas disponíveis podem agora ser combinados para calcular a CPUE média por tipo de barco e, estas podem então ser usadas para estimar a captura total para todas as frotas. (Note que a CPUE é medida em peso e não em número de peixes, compare Secção 4.3).
A fórmula é simples:
esforço*CPUE = captura estimada
os cálculos e os resultados são mostrados na Fig. 7.4.1 e Tabela 7.4.1.
Para evitar mais sinais de somatórios nos seguintes cálculos, introduzimos uma notação mais conveniente. Sempre que um índice for substituído por “*”, significa a soma relativa do índice em questão. Por exemplo, o peso total dos desembarques dos três locais “h”, da espécie “s”, no período “t”, pela frota “f” pode ser denotado por:
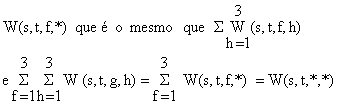
que é a captura total da espécie s durante o período de tempo t desembarcada por todas as frotas em todos os locais de desembarque (Tabela 7.4.1).
Voltando agora ao objectivo principal, o cálculo da composição por comprimentos da espécie s, ou seja, a determinação dos dados de entrada necessários à análise de coortes baseada em idades ou em comprimentos. Primeiro, é necessário esclarecer alguns aspectos gerais da espécie s amostrada para a composição por comprimentos. Como na maioria dos processos de amostragem, temos que ampliar o resultado da amostragem para a captura total do barco e, eventualmente, para a captura total de todas as frotas, é útil introduzir o sufixo “m” para as quantidades que foram amostradas. Outra coisa útil é distinguir quantidades das amostras das da captura total. Isto é feito usando letras maiúsculas para o total e minúsculas para a amostra. Por exemplo:
Wm = peso total da captura amostrada
Wm = peso da amostra
Cm = número total de peixes na captura amostrada
cm = número de peixes na amostra
Um processo de amostragem normalmente começa com a classificação das capturas por espécie e a pesagem ou estimação do peso da captura total de cada espécie, por exemplo, contando o número de cestos ou caixas. O próximo passo é seleccionar uma amostra aleatória e pesar a amostra, e depois disso, medir os comprimentos de toda a amostra.
Em alguns casos será necessário obter subamostras antes de poder medir os comprimentos de uma determinada espécie. Este é o caso das “espécies acompanhantes” como será demonstrado a seguir.
No presente exemplo, a amostra básica para estimar a composição por comprimentos está, neste exercício, associada a uma “viagem”. Cada frota de cada local de desembarque faz um número de viagens durante um período de tempo considerado. Na Fig. 7.6.1 considera-se a frota do local de desembarque I como exemplo. Durante o período, t, 15 viagens foram realizadas e no final, quatro delas foram amostradas no cais, por ocasião dos desembarques. (Note que, usualmente, é impossível tomar-se amostras de todas as viagens. Neste caso somente quatro dentro das 15 viagens foram amostradas. Deve-se tomar as medidas para que estas amostras sejam seleccionadas aleatoriamente, ver discussão na Secção 7.1).
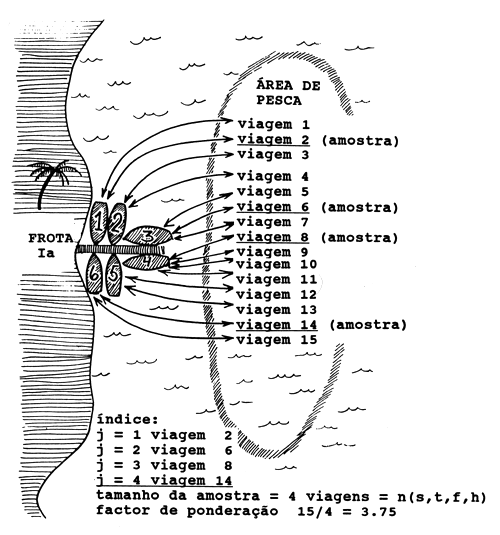
Fig. 7.6.1 Ilustração da amostragem para estimar a composição das capturas por comprimentos de uma frota de um local de desembarque
Seja o número de amostras denotado por
n(t,f,h)
No exemplo da Fig. 7.6.1: n(t,a,I) = 4. A cada amostra é dado um número ou um índice, j, para o controlo interno:
j = 1,2,…,n(t,f,h) (ver Fig. 7.6.1)
A situação complexa, geralmente envolvendo a amostragem de uma embarcação após uma viagem, é ilustrada na Fig. 7.6.2. Assumimos, neste caso, que a captura de uma viagem consiste em duas categorias:
PEIXES PARA CONSUMO HUMANO DIRECTO ou PEIXES PARA CONSUMO. Esta parte é classificada em espécies (ou grupos de espécies) e contém os tamanhos de mercado
ESPÉCIES ACOMPANHANTES. Esta parte não é classificada pelos pescadores. Contém peixes não utilizados no comsumo humano e inclui também espécies de peixes comestíveis, porém com tamanho inferior ao de comercialização. As quantidades relativas às espécies acompanhantes são diferenciadas das de consumo humano pelo sufixo “b”. O peso total de toda as espécies acompanhantes da viagem amostrada é denotado por Wbm (*,t,f,h,j).
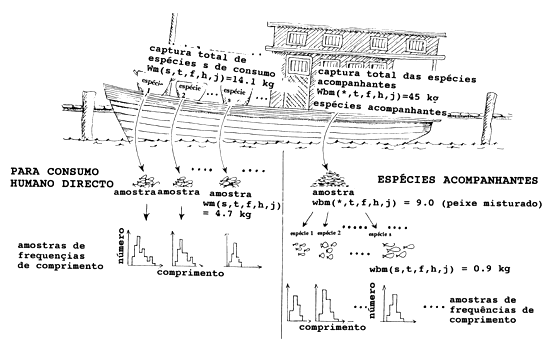
Fig. 7.6.2 Amostragem de uma única viagem (mais explicações no texto)
Das espécies seleccionadas para o programa de amostragem, tomam-se amostras de ambas as categorias, pois do ponto de vista biológico, ambas tem igual importância. Primeiro, trataremos da amostragem da categoria de peixes para consumo humano, e então das espécies acompanhantes e, finalmente, combinamos os dois conjuntos de dados. Todo o processo é ilustrado nas Figs. 7.6.2, 7.6.3 e 7.6.4.
Amostrar as capturas para consumo humano de uma viagem
O processo geral de amostragem dos dados de frequências de comprimento é abaixo descrito, baseado no exemplo da espécie s para consumo humano:
O peso da captura total amostrada da espécie s, da categoria de peixes para consumo humano, é registado:
Wm (s,t,f,h,j) = peso total da captura da espécie s da viagem amostrada j
Uma amostra é tirada aleatoriamente e o peso da amostra é registado como se segue:
wm(s,t,f,h,j) = peso de todos os indivíduos da espécie s na amostra j.
Toma-se então os comprimentos da amostra. Seja i o índice para uma classe de comprimento, então denotamos:
cm(s,t,f,h,j,i)
| Peixes para consumo: | ||
| Peso total da captura amostrada: | Wm = 14.1 kg | |
| Peso total da amostra: | wm = 4.7 kg | |
| Factor de ampliação: | Wm/wm = 14.1/4.7 = 3 | |
| Espécies acompanhantes: | ||
| Peso total das espécies acompanhantes amostradas: | Wbm = 45 kg | |
| Peso total da amostra (todas as espécies): | wbm = 9 kg | |
| Factor de ampliação: | Wbm/wbm = 45/9 = 5 | |
| Peixes para consumo (espécie s) | ||
| Amostra de frequências de comprimento | amostra de frequências de comprimento ampliada | |
| cm(s,t,f,h,j,i) | cm*Wm/wm = cm*3 | |
| tamanho da amostra = 37 | 37*3 = 111 | |
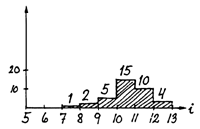 | 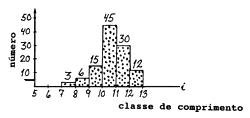 | |
| Espécies acompanhantes (espécie s) | ||
| Amostra de frequências de comprimento | amostra de frequências de comprimento ampliada | |
| cbm(s,t,f,h,j,i) | cbm*Wbm/wbm = cbm*5 | |
| tamanho da amostra = 24 | 24*5 = 120 | |
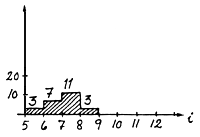 | 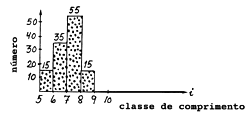 | |
| Captura total (espécie s) | ||
| frequências de comprimento estimadas da espécie s na captura total da viagem amostrada | amostra combinada de frequências de comprimento | |
| Cm(s,t,f,h,j,i) | Cm = cm*3 + cbm*5 = | |
| 111+120 = 231 | ||
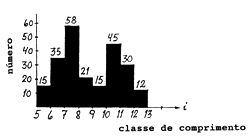 | ||
Fig. 7.6.3 Combinação das amostras de frequências de comprimento da espécie s encontradas na captura de peixes para consumo humano e na de espécies acompanhantes dos desembarques de uma viagem única (ver também Fig. 7.6.2)
O número de peixes da espécie s na classe de comprimento i, da amostra j, no local de desembarque h, capturado pela frota f, no período de tempo t.
O número total de peixes para todas as classes de comprimento da amostra é denotado por
cm(s,t,f,h,j,*)
Na Fig. 7.6.2 é mostrado que uma amostra de 4.7 kg = wm (s,t,f,h,j) foi tirada de uma captura total de 14.1 kg = Wm(s,t,f,h,j) da espécie s.
Foram tomados os comprimentos da amostra e obtidas as frequências, conforme apresentado na Fig 7.6.3, para uma amostra com tamanho total de 37 peixes = cm(s,t,f,h,j,*).
Esta amostra de frequências de comprimento tem que ser ampliada para a captura total do barco, para tal amplia-se cada frequência por um “factor de ampliação”, que é simplesmente o peso total da captura da espécie s dividido pelo peso da amostra.
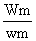
No caso da espécie s, o número total capturado estimado, na categoria para consumo, é dado por
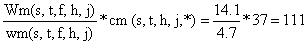
Amostrar as espécies acompanhantes de uma viagem
O processo de amostragem das espécies acompanhantes inclui um passo extra, que é a separação por espécies. Seja o peso total das espécies acompanhantes
Wbm(*,t,f,h,j) kg
(O índice “s” é substituído por “*” porque as espécies acompanhantes não estão separadas.)
Do Wbm kg tira-se uma amostra de
wbm(*,t,f,h,j) kg
Esta amostra é então separada por espécies (ver Tabela 7.6.2). Estamos interessados unicamente na espécie s. O peso da espécie s na amostra é:
wbm(s,t,f,h,j) kg
(Note que este não é o peso a ser usado para ampliar a amostra para a captura total.)
Estes peixes são medidos e os tamanhos registados (ver Fig. 7.6.3). O número de peixes por classe de comprimento i é denotado por:
cbm(s,t,f,h,j,i)
e o número total da espécie s no exemplo é:
cbm (s,t,f,h,j,*)
Neste caso o número é 24 (ver Fig. 7.6.3).
Estes números são ampliados, para se determinar a captura total das espécies acompanhantes, pelo factor de ampliação, que corresponde ao peso total das espécies acompanhantes dividido pelo peso total da amostra (e não apenas o peso da espécie s):
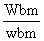
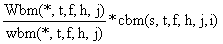
fornece as frequências de comprimento que correspondem à captura total das espécies acompanhantes.
No exemplo da Fig. 7.6.2, Wbm(*,t,f,h,j) = 45 kg, e o peso da amostra é wbm (*,t,f,h,j) = 9 kg de modo que o factor de ampliação fica Wbm/wbm = 45/9 = 5, e o número total de indivíduos de espécie s na categoria das espécies acompanhantes é 5*24 = 120.
Combinação das amostras das espécies para consumo e das amostras das espécies acompanhantes de uma viagem
Agora tem-se que combinar as frequências de comprimento ampliadas das duas categorias, de forma a obter o quadro completo das frequências de comprimento da espécie s na captura da viagem amostrada. Isto é feito pela simples adição das duas frequências ampliadas.
Obtém-se a captura total em número por classe de comprimento, C, estimada, simplesmente adicionando as estimações da espécie para consumo e as das espécies acompanhantes:
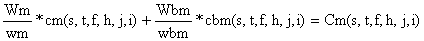
(ver Fig. 7.6.3).
Assim, por exemplo, o número total estimado para a classe de comprimento 8–9 cm vem:
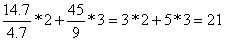
Somatório de amostras de várias viagens
De novo um simples somatório basta; o número capturado estimado por classe de comprimento, em todas as viagens (t,f,h) amostradas:
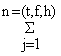 Cm(s,t,f,h,j,i) = Cm(s,t,f,h,*,i)
Cm(s,t,f,h,j,i) = Cm(s,t,f,h,*,i)
Na Fig. 7.6.4., por exemplo, o número total estimado de todas as quatro viagens amostradas para a classe de comprimento 8–9 cm é:
21+22+20+26 = 89
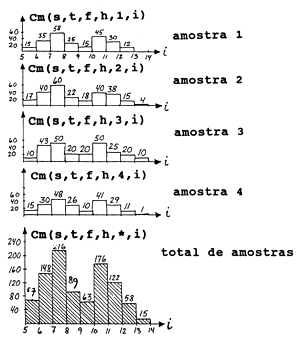
Fig. 7.6.4 Soma da composição de comprimentos, da espécie s, para as viagens amostradas. A amostra usada no exemplo da Fig. 7.6.3 aparece como amostra no 1
Ampliação das viagens amostradas para a captura total da frota, num local de desembarque
A composição total por comprimentos, das viagens amostradas Cm(s,t,f,h,*,i) pode ser ampliada para se obter a captura total no período t, pela frota f, para o local de desembarque h, usando um factor de ampliação baseado no número de viagens:
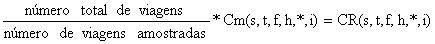
onde o sufixo “R” indica a “ampliação”. R foi usado aqui apenas para indicar o processo de ampliação que inclui quantidades que não foram amostradas (neste caso 11 das 15 viagens). No exemplo (Fig. 7.6.1) o factor de ampliação é 15/4 = 3.75 e o resultado é mostrado na Tabela 7.6.1. O número total estimado de indivíduos na classe de comprimento 8–9 cm para todas as viagens da frota f no local de desembarque h será:
89*3.75 = 333.75
Este processo de ampliação apenas é razoável se “uma viagem” for uma unidade de esforço bem definida. Se algumas viagens tivessem a duração de 1 dia de pesca e outras de 5 dias de pesca, então “dias de pesca” poderia ser a unidade de esforço mais apropriada. Porém, tanto a unidade de esforço “viagem” ou “dias de pesca” só fazem sentido, se os barcos da frota tiverem certas semelhanças, ou seja, se tiverem o mesmo “poder de pesca”. Outras possíveis unidades de esforço são “número de homens/dias”, “número de horas de arrasto”, “número de redes de espera”, etc.
Tabela 7.6.1 Ampliação das capturas das viagens amostradas para a captura total, em todas as viagens de uma frota em um local de desembarque (ver Fig. 7.6.1 e 7.6.4)
| classe de comprimento | total de viagens amostradas (de Fig. 7.6.4) | ampliado para o no de viagens no local amostrado de desembarque |
| (i) | Cm(s,t,f,h,*,i) | CR(s,t,f,h,*,i) |
| 5–6 | 57 | 213.75 |
| 6–7 | 148 | 555.00 |
| 7–8 | 216 | 810.00 |
| 8–9 | 89 | 333.75 |
| 9–10 | 63 | 236.25 |
| 10–11 | 176 | 660.00 |
| 11–12 | 122 | 457.50 |
| 12–13 | 58 | 217.50 |
| 13–14 | 15 | 56.25 |
| total | 944 | 3540.00 |
| = Cm(s,t,f,h,*,*) | = CR(s,t,f,h,*,*) |
Soma dos locais de desembarques amostrados, por frota e ampliação para todos os locais de desembarque
A composição total de comprimentos de todos os locais de desembarques amostrados (ver Fig. 7.4.1) é obtida pela simples adição:
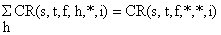
Este valor pode ser ampliado para o total de todas os locais de desembarques aplicando-se um factor de ampliação baseado no esforço dispendido em todos os locais de desembarques:
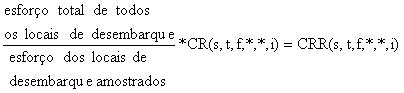
Somatório de frotas
Aqui também se efectua um simples somatório. A total composição por comprimentos da espécie s capturada durante o período de tempo t é:
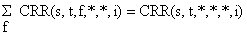
Obteve-se desta forma um quadro completo da distribuição de frequências de comprimento de todos os desembarques da espécie s em um trimestre do ano, t. Dependendo do tipo de análise requerida, poderemos parar o processamento dos dados de captura neste nível. O resultado neste caso, após um ano, são as quatro frequências de comprimento amostradas na Fig. 7.6.5A. Estas podem ser convertidas, por exemplo, em componentes de coortes pelo método de Bhattacharya (Secção 3.4), conforme mostrado na Fig. 7.6.5B. Os números capturados da mesma coorte em diferentes trimestres do ano (isto é, os números C1, C2, C3 e C4 indicados na Fig. 7.6.5B) constituem os dados de entrada para a análise de coortes de Pope (ver Secção 5.2).
Alternativamente, poderemos decidir aplicar a análise de coortes de comprimentos de Jones (ver Secção 5.3). Neste caso não separamos as coortes, mas procedemos como se segue:
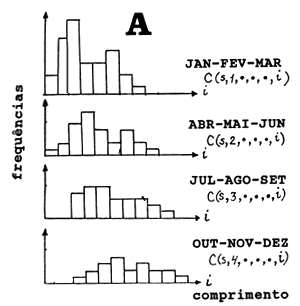 | 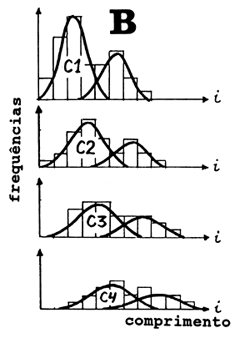 |
Fig. 7.6.5 A: Frequências de comprimento total por trimestre
B: Frequências de comprimento decompostas em componentes de
coortes normalmente distribuidas (dados de entrada para a
análise de coortes de Pope)
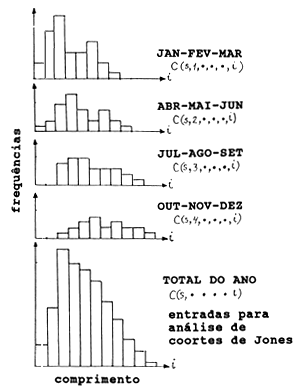
Fig. 7.6.6 Somatório da composição total por comprimentos para todos os períodos de tempo (a composição total por comprimentos como entrada para a análise de coortes baseada em comprimentos de Jones)
Somatório de períodos de tempo
Este é o passo final que dá a composição de frequências de comprimento de uma espécie para todo o ano. A adição é simples:
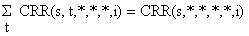
A Fig. 7.6.6 mostra um exemplo onde as composições por comprimentos trimestrais são adicionadas para se chegar a uma composição por comprimentos anual. Os últimos valores de “C” podem ser usados como dados de entrada para a análise de coortes por tamanhos. Podemos também usar valores médios para uma série de anos (ver Secção 5.3).
Análise de dados
A resolução das amostras de frequências de comprimento em componentes normalmente distribuidas, mostradas na Fig. 7.6.5, torna-se mais problemática quanto mais longo for o período de amostragem. As amostras trimestrais mostram uma certa estrutura de coortes, enquanto que para o ano todo as coortes são pouco evidentes (ver Fig. 7.6.6). Este exemplo ilustra que, para análise de coortes baseada em idades, devemos trabalhar com períodos de tempo relativamente curtos. De contrário, será impossível indentificar as coortes. A análise de coortes de Pope baseada em idades usa os números capturados por coorte.
Por outro lado, para uma análise de coortes pelo método de Jones, estamos interessados no declive do lado direito da distribuição de frequências combinadas, pois este reflecte a mortalidade total. No entanto, as frequências de comprimento combinadas deveriam representar um período de tempo longo, de forma que os declives das coortes individuais sejam nivelados.
Finalmente, deve-se ressaltar que o exemplo explicado acima pode ou não se adaptar a todas pescarias. A definição da unidade de esforço (viagem) poderá ser inapropriada para muitas pescarias. Igualmente, a suposição de que as amostras sejam retiradas dos barcos na altura dos desembarques, também pode não se adaptar a todos os casos. No exemplo foi assumido que houve o desembarque total da captura, o peixe para consumo e a mistura de espécies acompanhantes. Ou seja, não houve “rejeições”.
Rejeições são peixes capturados mas não desembarcados, isto é, devolvidos ao mar. Acredita-se que as rejeições não sobrevivem ao encontro com a arte de pesca, sendo assim, do ponto de vista biológico, as rejeições têm a mesma importância que os desembarques, pois o aspecto biológico importante é que os peixes foram mortos pela pescaria. Algumas pescarias, notavelmente o arrasto de camarão, rejeitam até 90%, ou mais, em alguns casos, do peso capturado. Vale a pena salientar que estas rejeições podem muito bem conter peixes adequados para o consumo humano, mas o seu valor é baixo quando comparado com o camarão. Na verdade, deve-se fazer uma cuidadosa distinção entre “desembarques” e “capturas”, estas últimas incluindo tanto desembarques como rejeições. A amostragem de rejeições é difícil ou dispendiosa, já que, para se obter estimações confiáveis seria necessário a colocação de observadores a bordo dos barcos comerciais. No entanto, se a rejeições representam quantidades importantes, devem ser empreendidos esforços para amostrá-las.
Programas de computador
Os pacotes de programas para microcomputador, FiSAT e LFSA contêm programas de manipulação de dados, como descrito neste capítulo, isto é: diferentes tipos de cálculos de somatório e ampliação para amostras de frequências de comprimento.