As capturas futuras e os níveis da biomassa dos mananciais podem ser previstos através de modelos matemáticos similares aos que fundamentam as análises de população virtual, VPA, e análises de coortes (ver Capítulo 5). As fórmulas matemáticas usadas na VPA e na análise de coortes, que analisam a história de uma pescaria, podem ser convertidas de tal maneira que o conhecimento do passado pode ser usado para prever a biomassa e as capturas em peso futuras, considerando-se diferentes níveis de esforço de pesca. Por outras palavras, estes modelos podem ser usados para prever os efeitos do incremento de uma pescaria e das medidas de regulamentação, tais como aumento ou redução da frota pesqueira, mudanças no tamanho da malha, períodos de defeso, vedas de áreas de pesca, etc. Portanto, estes modelos constituem uma ligação directa entre a avaliação de mananciais pesqueiros e a gestão dos mesmos.
Os modelos de projecção também podem incorporar outros factores como preços e rendimentos das capturas, tornando-os aplicáveis a análises bio-económicas, onde dados biológicos e económicos são usados para prever capturas futuras, níveis da biomassa e rendimento das capturas, sob todos os tipos de simulação. Este capítulo contém apenas uma introdução básica a aspectos bioeconómicos e, para um aprofundamento do assunto, recomenda-se a leitura de Sparre e Willmann (1992).
Os primeiros modelos de projecção foram desenvolvidos já na década dos trinta por Thompson e Bell (1934). No entanto, devido á enorme quantidade de cálculos requeridos, o chamado “modelo de Thompson e Bell” não obteve popularidade até à introdução dos computadores.
Durante este período, um modelo mais simples, baseado em suposições muito rigorosas, mas que, em compensação, requeria menos cáculos foi desenvolvido por Beverton e Holt (1957). Este modelo de “Captura por Recruta” foi largamente utilizado, mas actualmente vem sendo substituído pelo modelo de Thompson e Bell em locais onde a VPA e a análise de coortes são aplicadas.
O modelo de captura por recruta de Beverton e Holt pode ser considerado como uma aplicação especial do modelo de Thompson e Bell, o que significa que qualquer conclusão geral derivada do mesmo, também pode ser suportada pelo modelo de Thompson e Bell.
Embora não seja provável que o modelo de Beverton e Holt continue a ser muito utilizado no futuro, foi incorporado neste capítulo por razões históricas e didácticas. O modelo de captura em peso por recruta é adequado à utilização de calculadoras e, portanto, é muito útil para demonstrar certos aspectos da avaliação de mananciais. A segunda parte deste Capítulo (Secções 8.6 a 8.8) trata do modelo de Thompson e Bell, baseado em idades e em comprimentos e de aspectos da selectividade das artes de pesca relacionados com o mesmo.
O objectivo final da utilização dos modelos de projecção é oferecer aos reponsáveis pela gestão dos recursos pesqueiros informações sobre os efeitos biológicos e/ou económicos da actividade pesqueira sobre os mananciais. A partir dos resultados obtidos espera-se que os gestores tomem as medidas que permitam a exploração dos recursos a um nível no qual se obtenha o máximo rendimento, tanto no sentido biológico como no económico, numa base sustentável, ou seja, sem causar prejuizos ao manancial de forma a afectar futuras capturas.
Os gestores devem evitar situações onde a pressão de pesca seja muito forte e venha a provocar a “sobrepesca” do manancial. Uma previsão exacta das capturas futuras geralmente não é possível, pois, os mananciais raramente se encontram em condições de equilíbrio, o que é um pressuposto para a aplicação dos vários modelos. Foi demonstrado (Sharp e Csirke, 1984) que a abundância de certos mananciais, em particular pequenas espécies pelágicas que ocorrem em áreas de ressurgência, geralmente dependem muito dos factores ambientais que estão fora do controlo humano. Nestes casos, o valor previsivo dos modelos que a seguir são descritos é praticamente nulo. No entanto, no caso de algumas espécies pelágicas e para a maioria das pescarias demersais de peixes e camarões, os modelos têm se mostrado extremamente úteis.
Antes de se aprofundar estes dois modelos, vale a pena considerar primeiro um modelo mais simples e discutir o conceito de sobrepesca.
O modelo clássico que descreve uma pescaria sobre determinado manancial é apresentado por Russell (1931). O modelo é uma espécie de “caixa-preta” que representa o que Ricker (1975) definiu como “manancial utilizável”, o peso de todos os peixes maiores que um certo tamanho aproveitável. Os incrementos do manancial são o peso dos novos recrutas e o crescimento dos peixes que já fazem parte do manancial. As perdas decorrem das mortes por causas naturais e das capturas em peso das pescarias.
Em um manancial virgem o total dos incrementos é, em média, igual às perdas da biomassa por mortes naturais. Quando uma população começa a ser explorada o efeito reflecte-se em todos os outros factores, resultando um maior recrutamento, um crescimento mais rápido e uma redução nas mortes naturais. Isto porque a pesca abre “espaço” para mais recrutas, remove os peixes velhos, cujo crescimento é lento, que são substituídos por peixes menores de crescimento rápido, e remove peixes antes de virem a morrer por velhice ou outras causas naturais. Portanto, desde que seja dado tempo suficiente para o manancial ajustar-se à nova situação e que a pressão da pesca não se torne muito elevada, a pesca produz um efeito estimulante à productividade pesqueira, . Por outro lado, quando ocorre a “sobrepesca”, o crescimento individual dos peixes não iguala as mortes causadas pela pesca e, quando a intensidade de pesca é muito grande, também afecta o recrutamento, havendo, assim, dois tipos de sobrepesca, “sobrepesca de crescimento” e “sobrepesca de recrutamento”. A sobrepesca de crescimento ocorre quando o esforço de pesca é tão alto que as capturas totais diminuiem com o aumento do esforço. Os peixes são capturados antes de poderem atingir um tamanho suficiente para contribuir substancialmente para a biomassa. Em geral, é razoável dizer-se que um manancial está em sobrepesca de crescimento, no sentido biológico, quando F excede FMSY (cf. Fig. 8.2.3). O termo “biológico” é usado para indicar que somente é considerada a captura em termos de biomassa, medida em unidades de peso. Assim, o rendimento e o custo da pescaria não estão sendo aqui considerados.
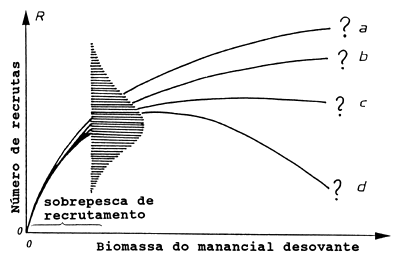
Fig. 8.0.1 Relação manancial-recrutamento em ligação com o conceito de
“sobrepesca de recrutamento”
Para entender o conceito de sobrepesca de recrutamento, é necessário considerar primeiro a relação existente entre o recrutamento e a biomassa do manancial desovante, de acordo com a ilustração da Fig. 8.0.1. Conforme indicado pelos pontos de interrogação, esta relação não é bem compreendida. O único ponto conhecido com segurança é (0,0), ou seja, quando não existe manancial progenitor não pode haver desova e é razoável assumir que para níveis baixos do manancial progenitor há uma relação linear directa positiva entre o tamanho deste e o número de nascimentos ou recrutas. Sob condições normais tal relação linear directa não é observada, mas quando ocorre, significa que o manancial progenitor caíu a um nível muito baixo e, neste caso, fala-se em sobrepesca de recrutamento.
O modelo de captura por recruta (Beverton e Holt, 1957), é, em princípio, um “modelo de condição de equilíbrio”, ou seja, um modelo que descreve o estado do manancial e a captura em uma situação cujo o padrão de pesca vem sendo o mesmo durante um tempo suficientemente longo, de modo que todos os peixes vivos vêm sendo submetidos ao mesmo padrão desde que foram recrutados. Existem extensões do modelo que tratam da fase de transição após uma mudança no padrão de pesca, mas raramente são utilizadas, pois os modelos do tipo Thompson e Bell (Secções 8.6 a 8.8) fornecem descrições mais simples de situações onde não se observa o equilíbrio.
Os pressupostos que fundamentam rigorosamente o modelo de Beverton e Holt são:
Recrutamento constante, mesmo que não especificado
Todos os peixes de uma coorte nasceram na mesma data
O recrutamento e a selectividade são do tipo “fio-de-navalha” (ver Capítulo 6)
A mortalidade natural e por pesca são constantes desde o momento que se inícia a fase explorada
Existe uma mistura completa no manancial
A relação peso-comprimento (Eq. 2.6.1) tem expoente 3, ou seja, W = q*L3
Um dos modelos que fundamenta o modelo de Beverton e Holt é o modelo exponencial decrescente que foi introduzido na Secção 4.2 e matematicamente é expresso pela Eq. 4.2.2. As definições e terminologia introduzidas na Secção 4.1 são também aplicáveis ao modelo de Beverton e Holt (por exemplo Tc,Tr,R = N (Tr)).
A história da vida de uma coorte assumida no modelo de Beverton e Holt, conforme a Fig. 8.1.1, é descrita como se segue:
Na idade Tr todos os peixes pertencentes a uma determinada coorte são recrutados ao mesmo tempo às áreas de pesca: “Recrutamento fiode-navalha”.
Da idade Tr à idade Tc a coorte não está exposta a qualquer mortalidade por pesca. (Assume-se que todo o peixe com idade entre Tr e Tc escapa através das malhas, caso entre na arte de pesca). Assim, durante este período estão sujeitos apenas à mortalidade natural, M, que, supostamente, permanece constante durante toda a vida da coorte.
Na idade Tc, a “idade de primeira captura”, assume-se que toda a coorte é, repentinamente, exposta à mortalidade por pesca, F, que, supostamente permanece constante durante o resto da vida da coorte. A curva sigmóide da selectividade da arte, introduzida no Ca-pítulo 6, é aproximada pela chamada “selectividade fio-de-navalha” (ver Fig. 6.4.1.1). A captura da coorte é, portanto, assumida como zero até que a mesma atinja a idade Tc.
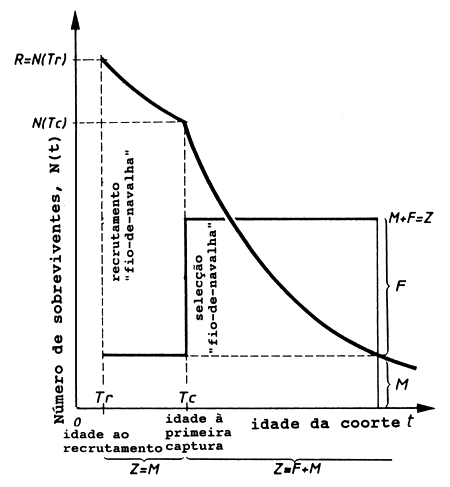
Fig. 8.1.1 A evolução de uma coorte conforme a suposição
assumida pelo modelo
de Beverton e Holt
O número de sobreviventes à idade Tr é o recrutamento à pescaria:
| R = N(Tr) | (8.1.1) |
O número de sobreviventes à idade Tc é:
| N(Tc) = R*exp[-M*(Tc-Tr)] | (8.1.2) |
O número de sobreviventes à idade t, onde t > Tc, é:
N(t) = N(Tc)*exp[-(M+F)*(t-Tc)] = R*exp[-M*(Tc-Tr) - (M+F) * (t-Tc)]
A fracção do recrutamento total N(Tr) ou R que sobrevive até a idade t é obtida dividindo-se ambos os lados da equação por R, resultando:
| N(t)/R = exp[-M*(Tc-Tr) - (M+F)*(t-Tc)] | (8.1.3) |
Isto significa que a Eq. 8.1.3 dá o número “por recruta” no tempo t, ou seja, a fracção que foi recrutada à pesca por cada recruta.
O outro modelo que fundamenta o modelo de Beverton e Holt é a “equação de captura” na forma da Eq. 4.2.10 conforme será explicado na secção seguinte.
Para calcular a expressão matemática do modelo de captura por recruta de Beverton e Holt toma-se (como de costume) um ponto de partida na equação de captura na forma da Eq. 4.2.10:
| C(t,t+Δt) = Δt*F*N(t) | (8.2.1) |
A Eq. 8.2.1 dá o número capturado de uma coorte, no período de tempo t a t+Δt, quando Δt é pequeno. Para obter a correspondente captura em peso multiplica-se este valor pelo peso individual. Se Δt é pequeno, então o peso do corpo permanecerá aproximadamente constante durante o período de tempo de t a t+Δt, e a captura em peso será:
| Y(t,t+Δt) = Δt*F*N(t)*w(t) | (8.2.2) |
onde w(t) é o peso de um peixe de idade t, conforme a definição da equação de von Bertalanffy baseada em peso (Eq. 3.1.2.1). Para obter a captura por recruta para o período de tempo t a t+Δt, a Eq. 8.2.2 é dividida pelo número de recrutas, R:
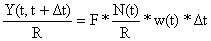 | (8.2.3) |
onde N(t)/R é definido pela Eq. 8.1.3.
A Eq. 8.2.3 é o “modelo de Beverton e Holt para um curto período de tempo”. Para obter a captura total em peso por recruta para toda a vida da coorte, Y/R, todas as pequenas contribuições definidas pela Eq. 8.2.3 devem ser acumuladas:
Y/R = Y(Tc,Tc+Δt)/R + Y(Tc+Δt,Tc+2Δt)/R +
Y(Tc+2Δt,Tc+3Δt)/R + Y(Tc+3Δt,Tc+4Δt)/R +
Y(Tc+4Δt,Tc+5Δt)/R + Y(Tc+5Δt,Tc+6Δt)/R +
....
....
+ Y(Tc+(n-1)*Δt,Tc+n*Δt)/R
onde “n” é um número grande, tão grande que o número de peixes mais velhos que Tc+n*Δt, isto é N(Tc+n*Δt), é tão pequeno que pode ser ignorado.
O próximo passo é converter o somatório apresentado acima em uma fórmula que possa ser facilmente calculada. Se o número de termos, n, no somatório é grande (e deve ser grande para que a aproximação para w(t) seja razoável) será necessário muito tempo para efectuar a soma. No entanto, usando uma série de cálculos matemáticos cuja explicação foge aos objectivos deste manual, é possível demonstrar que o somatório acima pode ser escrito de uma forma mais conveniente:
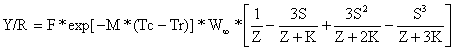 | (8.2.4) |
onde:
S = exp [-K*(Tc-to)]
K = parâmetro de crescimento de von Bertalanffy
to = parâmetro de crescimento de von Bertalanffy
Tc = idade da primeira captura
Tr = idade ao recrutamento
W∞ = peso assintótico
F = mortalidade por pesca
M = mortalidade natural
Z = F+M, mortalidade total
A Eq. 8.2.4 é o “modelo de captura por recruta de Beverton e Holt” (1957), modelo Y/R, escrito na forma sugerida por Gulland (1969). Embora a equação pareça complicada, é bastante fácil de ser executada com uma calculadora de bolso programável.
Como Beverton e Holt expressam as capturas em uma “base por recruta”, as capturas são relativas, isto é relativas ao recrutamento. Se, um recrutamento de 100 milhões de peixes fornece uma captura de 10 000 toneladas, então 200 milhões de recrutas forneceriam 20 000 toneladas, conforme o modelo. Esta suposição parece trivial, mas não é, pois, imagina-se que quanto mais abundante a espécie, piores serão as condições para cada indivíduo devido, por exemplo, à competição pelo alimento e ao canibalismo. Os resultados do modelo são expressos em unidades de captura por recruta (gramas por recruta). No exemplo acima a captura em peso será:
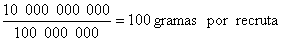
O modelo permite-nos calcular Y/R variando os valores de entrada dos diferentes parâmetros, tais como F e Tc, e então avaliar o efeito destes parâmetros sobre a captura por recruta da espécie sob investigação. É importante notar aqui que os dois parâmetros F e Tc são os que podem ser controlados pelos gestores da pesca, pois:
F é proporcional ao esforço (cf. Eq. 4.3.0.7)
Tc é uma função da selectividade da arte
Portanto, Y/R é considerado uma função de F e Tc. No entanto é mais frequente os gráficos de Y/R contra o F (ou esforço).
A Fig. 8.2.1 mostra o resultado da avaliação de uma captura com o modelo de captura por recruta. A idade de entrada à fase explorada, Tc, é mantida constante. A variável independente é o esforço expresso pelo coeficiente de mortalidade por pesca, F. A variável dependente é a captura anual por recruta, em gramas. Quando a captura anual total é conhecida em uma situação de equilíbrio, para um dado valor de F, então o número de recrutas pode ser calculado dividindo-se a captura total pela captura por recruta, em gramas.
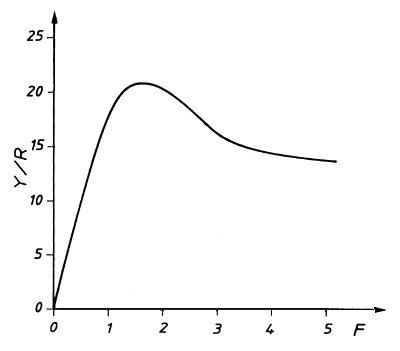
Fig. 8.2.1 Resultado de uma avaliação das capturas com o modelo de
captura por recruta
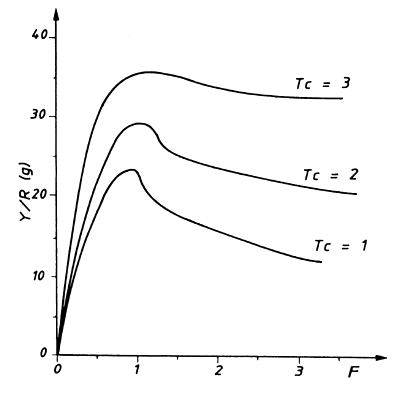
Fig. 8.2.2 Curvas de captura por recruta para diferentes idades de
primeira captura (Tc)
A “curva de captura por recruta” geralmente possui um ponto máximo: a “captura máxima sustentável (MSY)”. A posição do ponto máximo depende da idade à primeira captura, Tc, que por sua vez depende do tamanho da malha utilizada na pescaria.
Uma alteração no tamanho da malha, ou seja, em Tc, resultará num diferente MSY. A Fig. 8.2.2 mostra três curvas com diferentes valores de Tc. O MSY mais alto é obtido para o maior valor de Tc, com um nível de esforço, F, ligeiramente superior. A captura sustentável mais elevada, válida para uma certa combinação de Tc e F, pode ser determinada pela combinação de diferentes valores de Tc com diferentes valores de F. O termo sustentável significa que a captura pode ser mantida “para sempre”, desde que as condições não mudem, contudo, supondo que nada mais se altera, capturas mais altas podem ser obtidas com um aumento acentuado do esforço, mas não podem ser mantidas, e serão obrigatoriamente seguidas por um período com capturas bem mais baixas.
O modelo Y/R é originalmente um modelo baseado em idades, mas as idades podem facilmente ser convertidas em comprimentos, usando novamente os princípios da conversão da curva de captura (ver Secções 4.4.2 e 8.5).
Exemplo 28: Y/R como função de F, para uma espécie tropical
Como exemplo calcula-se Y/R para Nemipterus marginatus como função de F, usando os seguintes parâmetros:
| K = 0.37 por ano | Tc = 1.0 ano | to = -0.2 ano |
| M = 1.1 por ano | Tr = 0.4 ano | W∞ = 286 gramas |
Começamos pelo cálculo dos termos da Eq. 8.2.4 que são independentes de F:
S = exp[-K*(Tc-to)] = exp[-0.37*(1.0+0.2)] = 0.6415
3S = 1.9244, 3S2 = 1.2344 , S3 = 0.2639
M+K = 1.47, M+2K = 1.84, M+3K = 2.21
exp[-M*(Tc-Tr)]*W∞ = exp[-1.1*(1.0-0.4)]*286 = 147.8
Tabela 8.2.1 Capturas por recruta e biomassa média por recruta do Nemipterus marginatus como função de F. Parâmetros conforme indicados na legenda da Fig. 8.2.3
| F | Y/R | B/R | B/R como % de Bv | F | Y/R | B/R | B/R como % de Bv |
| 0.0 | 0 | 22.4 = Bv | 100 | 1.3 | 7.66 | 5.9 | 26 |
| 0.1 | 1.92 | 19.2 | 86 | 1.5 | 7.79 | 5.2 | 23 |
| 0.2 | 3.33 | 16.7 | 75 | 1.7 | 7.86 | 4.6 | 21 |
| 0.3 | 4.38 | 14.6 | 65 | 1.9 | 7.90 | 4.2 | 19 |
| 0.4 | 5.18 | 13.0 | 58 | 2.1 | 7.92 | 3.8 | 17 |
| 0.5 | 5.79 | 11.6 | 52 | 2.3 F(MSY) | 7.93 MSY/R | 3.5 MSB/R | 15 MSB/Bv |
| 0.6 | 6.26 | 10.4 | 46 | 2.5 | 7.92 | 3.2 | 14 |
| 0.7 | 6.62 | 9.5 | 42 | 3.0 | 7.88 | 2.6 | 12 |
| 0.8 | 6.91 | 8.6 | 38 | 4.0 | 7.77 | 1.9 | 8 |
| 0.9 | 7.14 | 7.9 | 35 | 5.0 | 7.66 | 1.5 | 7 |
| 1.0 | 7.32 | 7.3 | 33 | 6.0 | 7.57 | 1.3 | 6 |
| 1.1 | 7.46 | 6.8 | 30 |
Substituindo estes valores na Eq. 8.2.4 obtemos:
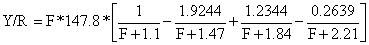
Para produzir um gráfico correspondente à Fig. 8.2.1 esta expressão deve ser calculada para uma gama de valores de F, obtendo-se um número de pontos suficientemente grande para ajustar a curva a olho.
Por exemplo, para F = 0.5:
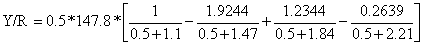
= 0.5*147.8*0.0785 = 5.8 gramas por recruta
Repetindo-se estes cálculos para a gama de valores de F = 0 a F = 6.0 obtêmse os resultados apresentados na primeira e quarta colunas da Tabela 8.2.1, que foram usados para elaboração do gráfico mostrado na Fig. 8.2.3.
Testando vários valores de F encontramos para F = 2.3 o valor máximo de Y/R, a “Captura Máxima Sustentável por Recruta” (MSY/R):
MSY/R = 7.9 gramas por recruta
que corresponde à mortalidade por pesca óptima:
FMSY = 2.3 por ano (ver Tabela 8.2.1 e Fig. 8.2.3).
Como o modelo Y/R assume um sistema de parâmetros constante (cf. Secção 4.4.1) os resultados obtidos apenas se aplicam depois de o sistema estar estabilizado durante um certo tempo. Alterações no valor de F implicam necessáriamente um certo tempo para que os valores de Y/R venham a ser previstos pela curva; o tempo necessário depende da longevidade da espécie em questão. Da Tabela 8.2.1 e Fig. 8.2.3 parece que o nível de FMSY não é determinado com grande precisão. De facto, para F > 1.5 o Y/R permanece constante para uma grande gama de esforços.
A curva B na Fig. 8.2.4 é um exemplo de curva de Y/R que difere na forma da curva da Fig. 8.2.3 (que está reproduzida como curva A). A curva B tem um máximo bem pronunciado, um valor mais baixo de FMSY e um valor mais alto de MSY/R quando comparada com a curva A, no entanto, a única diferença nos valores usados para determinação de ambas é o valor da taxa de mortalidade natural, M = 0.2 por ano para a curva B e M = 1.1 por ano para a curva A. As conclusões que podem ser obtidas das diferenças entre as duas curvas são:
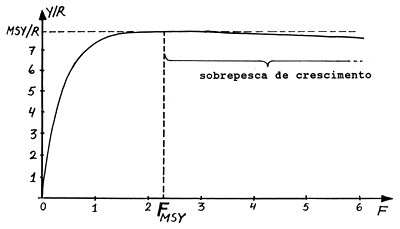
Fig. 8.2.3 Curva de captura por recruta do Nemipterus marginatus como
função de
F para os parâmetros:
| K = 0.37 por ano | Tc = 1.0 ano | to = -0.2 ano |
| M = 1.1 por ano | Tr = 0.4 ano | W∞ = 286 gramas |
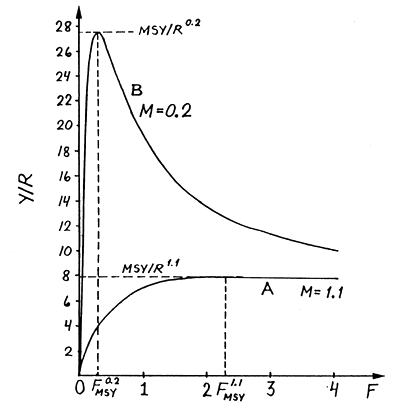
Fig. 8.2.4 Curva de captura por recruta como função de F para os parâmetros:
| A: | M = 1.1 por ano | B: | M = 0.2 por ano | |
| K = 0.37 por ano | Tc = 1.0 ano | to = -0.2 ano | ||
| Tr = 0.4 ano | W∞ = 286 gramas |
Um M mais baixo produz um FMSY mais baixo e um MSY/R mais elevado, enquanto que níveis de esforço de pesca acima de FMSY provocam uma severa redução da captura total
Se M é alto, é difícil estimar FMSY pela curva de Y/R
Estas conclusões são as consequências lógicas do efeito do nível da mortalidade natural, M, na produção de biomassa.
Se M é alto, o peixe atingirá rapidamente a idade onde as perdas por mortalidade natural excedem o ganho em biomassa pelo crescimento somático. Portanto, F tem que ser alto de forma a capturar os peixes antes que eles morram por causas naturais.
Se M é baixo o ganho em biomassa devido ao crescimento será maior que as perdas causadas pela mortalidade natural para grande parte da vida da coorte. Neste caso, compensa deixar o peixe crescer para tamanhos maiores o que significa, que para um nível de exploração óptima, F deve ser baixo.
Em alguns casos (cf. Exercício 8.3) a curva Y/R nem sequer tem um máximo e os gestores sem experiência podem chegar à conclusão errada que o esforço pode ser aumentado indefinidamente. Em tais casos, que são comuns em pescarias tropicais, é recomendável considerar também a curva de biomassa por recruta (B/R), que será introduzida na próxima secção. As duas curvas fornecem informações diferentes, sendo recomendável traçá-las sempre juntas. Y/R como função de Tc, idade à primeira captura, está estreitamente relacionada com a estimação do tamanho óptimo da malha (cf. Fig. 8.2.2, ver Exercícios 8.3 e 8.4).
O modelo de biomassa por recruta de Beverton e Holt expressa a biomassa média de sobreviventes como função da mortalidade por pesca (ou esforço). A biomassa média está relacionada com as capturas por unidade de esforço (cf. Secção 4.3). A Eq. 4.3.0.2 expressa a relação entre CPUE e os números capturados, CPUE(t) = q*N(t), que multiplicado pelo peso do corpo em ambos os lados resulta:
CPUE(t)*w(t) = q*N(t)*w(t)
ou, se N(t)*w(t) for substituído por B(t), o símbolo para biomassa:
| CPUEw(t) = q*B(t) | (8.3.1) |
onde CPUEw é o “peso da captura por unidade de esforço”. Assim, a biomassa deverá mostrar o mesmo declínio com o aumento do esforço de pesca, como mostra a curva da CPUEw na Fig. 8.3.1.
A captura em números por ano pode ser expressa como
C = F*N
(cf. Eq. 4.2.8 com t2-t1 = 1 ano). Com um argumento similar pode ser demonstrado que a captura por ano é
Y = F*B
onde B é a biomassa média durante um ano. Resulta que:
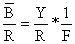

Fig. 8.3.1 Curva da CPUE (em peso) como função do esforço
Devido ao pressuposto de um sistema com parâmetros contantes (ver Secção 4.4.1) a captura de um manancial durante um ano é igual à captura de uma coorte individual durante toda sua vida.
Portanto temos a seguinte relação simples entre Y/R, (Eq. 8.2.4) e biomassa média por recruta, B/R:
| Y/R = F*B/R | (8.3.2) |
A fórmula usada para calcular B/R é a mesma da Eq. 8.2.4, dividida por F:
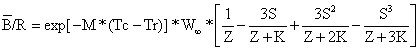 | (8.3.3) |
É sempre recomendado calcular Y/R e B/R juntos. A maneira mais fácil de fazer isto é começar pelo cálculo de B/R pela Eq. 8.3.3 e então usar a Eq. 8.3.2 para calcular Y/R. No caso de F = 0, o valor de B/R corresponde à chamada biomassa virgem por recruta, Bv/R, a biomassa de um manancial não explorado.
A biomassa média por recruta, conforme definido pelas Eq. 8.3.2 e Eq. 8.3.3, é a biomassa média da parte explorada da coorte, isto é a biomassa dos peixes de idade Tc ou acima.
Os valores de B/R relacionados com os valores de Y/R calculados na Secção 8.2 estão apresentados na Tabela 8.2.1, onde B/R também é dada como percentagem da biomassa virgem, Bv. Fica assim demonstrado que, para o Nemipterus marginatus, a biomassa correspondente ao nível óptimo biológico F, FMSY, é somente 15% da biomassa virgem, Bv. A Fig. 8.3.2 mostra a “curva da biomassa por recruta” que é sempre decrescente com o aumento do esforço de pesca. A curva é proporcional à captura por unidade de esforço com base nos pressupostos do modelo (ver Eq. 8.3.1). Isto significa que em qualquer pescaria seria esperado um decréscimo na captura por unidade de esforço e na biomassa quando o esforço (por exemplo, número de barcos) aumentasse. Portanto, um decréscimo na captura por unidade de esforço, não é per si um indicador de que um manancial está em sobrepesca, pois esta ocorre quando o esforço torna-se tão elevado que o crescimento não consegue contrabalançar com a mortalidade.
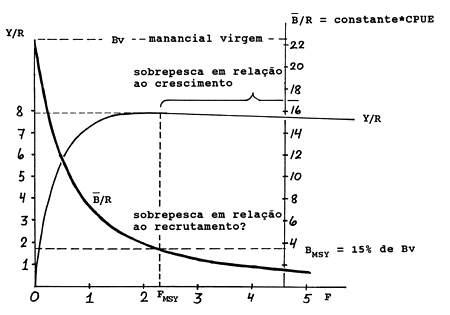
Fig. 8.3.2 Curva da biomassa por recruta do Nemipterus marginatus correspondente à curva de Y/R da Fig. 8.2.3 que aqui se encontra repetida
Outra maneira, às vezes mais apropriada, de usar a curva de B/R é interpretá-la como uma curva de CPUEw. Quando se gere uma pescaria é essencial considerar a possível entrada de receitas por barco e esta quantidade, obviamente, está relacionada com as CPUEw (ver Sparre e Willmann, 1992).
(Ver Exercício (s) na Parte 2).
Idade e tamanho médio na captura
O modelo de Beverton e Holt pressupõe que Z seja constante a partir da idade Tc (Tr quando Tr > Tc), facilitando assim a estimativa da idade média, do tamanho médio e do peso médio na captura anual. A idade média na captura anual é:
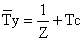 | (8.3.4) |
Esta equação também é aplicada em situações onde Z varia na fase explorada, mas mantém-se constante para os peixes mais velhos. A idade média dos peixes mais velhos é, assim, 1/Z mais a idade a partir da qual Z se torna constante.
O comprimento médio na captura anual é:
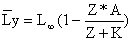 | (8.3.5) |
| S = exp(-K*(Tc-to)) = 1 - Lc/L∞ |
Tc ou Lc podem-se novamente, substituir por qualquer idade na qual os peixes têm uma mortalidade constante, obtendo-se, assim, um comprimento médio para essa parte da população.
O peso médio da captura calcula-se da mesma forma:
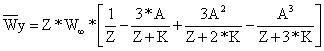 | (8.3.6) |
onde S é igual à Eq. 8.3.5. Esta expressão pode ser aplicada para o grupo mais da VPA, substituindo-se Tc ou Lc pela idade ou comprimento no início do grupo mais, ver Eq. 5.3.16.
Um aumento do Z, com um aumento do esforço, resulta sempre na diminuição de Ty, Ly e Wy, tal como da biomassa explorada e da captura por unidade de esforço (ver Fig. 8.3.3). Esta diminuição é mais acentuada para valores baixos de F (isto é do esforço), caracterizando as primeiras fases duma pescaria, após o seu início. Tc (determinada pela malha) é um parâmetro incluido nas três equações, o que implica que uma maior malha resulta numa captura onde a idade média é mais elevada e portanto obtem-se um comprimento médio maior nas capturas.
Pescarias caracterizadas por diminuições na captura por unidade de esforço e diminuições nos tamanhos dos peixes desembarcados são geralmente consideradas como o resultado de sobrepesca, mas no entanto, as Figs. 8.3.2 e 8.3.3 mostram claramente que a diminuição deve-se, logicamente, ao aumento do esforço de pesca e é importante notar, que estas diminuições são mais acentuadas nos níveis mais baixos do esforço de pesca; o que quer dizer que após a abertura duma pescaria sobre um manancial virgem as capturas rapidamente começarão a diminuir e a consistir de peixes pequenos. Em muitos casos, estes factores não foram considerados em estudos de praticabilidade de novas pescarias.
(Ver Exercício(s) na Parte 2).
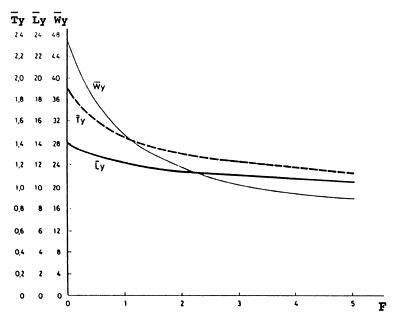
Fig. 8.3.3 Idade média (Ty), comprimento médio (Ly) e peso médio (Wy) na captura anual de Nemipterus marginatus correspondente à curva (CPUE) de biomassa da Fig. 8.3.2
Os valores absolutos de Y/R expressos em gramas por recruta não têm muita importância para o propósito da gestão pesqueira. Mas, é importante determinar as variações de Y/R para diferentes valores de F, por exemplo, se F aumentar em 20% a captura irá decrescer em 15%. Portanto, Beverton e Holt (1966) também desenvolveram um “modelo de captura relativa por recruta” que pode fornecer o tipo de informação necessária à gestão. Este modelo tem a grande vantagem de reguerer menos parâmetros, e, ao mesmo tempo, é especialmente útil para avaliar o efeito da regulametação do tamanho da malha. Pertence à categoria dos modelos baseados em comprimentos, porque está mais baseado em comprimentos do que em idades.
O “modelo de captura relativa por recruta de Beverton e Holt” é definido por:
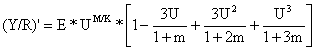 | (8.4.1) |
onde
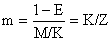 | |
| U = 1 - Lc/L∞, | a fracção de crescimento a ser completada depois de entrar para a fase explorada |
| E = F/Z, | taxa de exploração ou fracção de mortes provocadas pela pesca (cf. Secção 4.2). |
(Y/R)' é considerado uma função de U e E, e o único parâmetro é M/K. A equação dá um valor que é proporcional a Y/R conforme definido na Eq. 8.2.4 e que pode ser demonstrado por uma série de manipulações algébricas. Pode-se demonstrar que (Y/R)' = (Y/R)*exp[-M*(Tr-to)]/W∞.
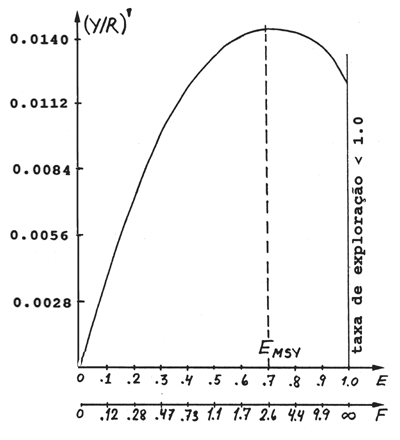
Fig. 8.4.1 Curva de captura relativa por recruta (Y/R)' de Beverton e Holt correspondente à curva de Y/R da Fig. 8.2.3 (Lc = 10.2 cm)
Note que não é necessária uma estimação separada de K como valor de entrada e que a Eq. 8.4.1 é baseada em comprimentos (L∞ e Lc em U) em vez de idades.
(Y/R)' pode ser calculado com valores de M/K, L∞ e Lc, para valores de E variando de 0 a 1, correspondendo a valores de F variando de 0 a ∞.
O gráfico de (Y/R)' contra E resulta numa curva com um valor máximo, EMSY, para um dado valor de Lc. Assim, quando Lc, F e M/K são conhecidos para uma certa pescaria, a taxa de exploração actual pode ser comparada com o nível de EMSY e as medidas de gestão propostas conforme as necessidades.
A Fig. 8.4.1 mostra a curva de (Y/R)' correspondente à curva de Y/R do Nemipterus marginatus (Fig. 8.2.3) no caso de:
Lc = L(Tc) = L(1.0) = 28.4*[1 - exp(-0.37*(1+0.2))] = 10.2 cm
onde L∞ = 28.4 cm (ver Secção 3.1.2 e Fig. 3.1.2.1).
U = 1 - Lc/L∞ = 1 - 10.2/28.4 = 0.641
Como exemplo calculamos (Y/R)' para E = 0.5:
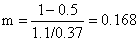
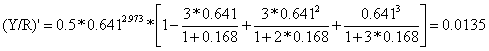
(Ver Exercício(s) na Parte 2).
Praticamente os mesmos cálculos algébricos referidos na Secção 8.4 transformam a equação de Y/R (Eq. 8.2.4) num modelo baseado em comprimentos. Os parâmetros e variáveis originais são F, M, W∞, K, to, Tr e Tc. No modelo transformado para crescimento temos L∞, Lr e Lc em vez de to, Tr e Tc. A nova equação é
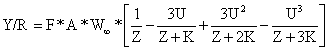 | (8.5.1) |
onde U = 1 - Lc/L∞ como na Eq. 8.4.1 e
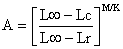
Uma vez que estão descritos nos capítulos anteriores, vários métodos de estimar parâmetros, será, também, interessante formular a Eq. 8.5.1 em termos de Z/K e M/K. Dividindo por K fora dos parênteses e multiplicando por K dentro dos parênteses, e substituindo z por Z/K obtém-se:
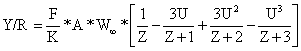 | (8.5.2) |
Esta equação contém F/K, M/K (em A) e Z/K (em z) e não requer uma estimação separada de K nem faz referência à idade.
Marten (1978), usando crescimento linear em vez do modelo de von Bertalanffy apresentou um modelo similar de Y/R baseado em comprimentos.
Conforme já dito na introdução deste capítulo o primeiro modelo de projecção foi desenvolvido, bem antes do modelo de Beverton e Holt, por Thompson e Bell (1934). O modelo de Thompson e Bell é exactamente o oposto dos modelos discutidos no Capítulo 5, VPA e análise de coortes. É utilizado para prever os efeitos de alterações no esforço de pesca nas capturas futuras, enquanto a VPA e a análise de coortes são usadas para determinar o número de peixes que deveriam ter estado presentes no mar, para explicar uma determinada captura sustentável, e o esforço de pesca que devia ter sido aplicado em cada grupo de idade ou de comprimento para obter dada captura em número (ver Secções 5.1 e 5.2). Portanto, a VPA e a análise de coortes são chamados modelos históricos ou retrospectivos, enquanto o modelo de Thompson e Bell é de projecção.
O método de Thompson e Bell consiste em dois passos principais: 1) Fornecimento de dados de entrada essenciais e opcionais e 2) cálculo dos resultados na forma de previsões das futuras capturas, níveis de biomassa e até mesmo o rendimento dessas capturas.
1) Fornecimento dos dados de entrada: A entrada principal é a chamada “matriz de referência de F-por-idades”, uma matriz de valores de F por grupos de idades. Em princípio, qualquer matriz-F pode ser usada como entrada, mas, é claro, não é qualquer uma que fornecerá resultados compatíveis com a situação real da pescaria. Portanto, é comum utilizar-se uma matriz-F obtida a partir de uma análise de dados históricos, em outras palavras, de uma VPA ou duma análise de coortes. No entanto, uma matriz-F de referência pode ser originada de outras fontes como é, na verdade, o caso do exemplo 29, dado abaixo.
Outro importante parâmetro de entrada é o número de recrutas, que pode ser igualmente obtido de uma VPA ou duma análise de coortes. Este parâmetro é necessário para obtenção de previsões absolutas de capturas, etc. Contudo, se este dado de entrada não estiver disponível, o modelo de Thompson e Bell pode, ainda assim, ser usado para fornecer resultados em números relativos, na forma, por exemplo, de unidades “por 1000 recrutas” (ver Exemplo 29).
O modelo requer ainda uma “matriz de peso por idades”, os pesos individuais dos peixes por grupos de idade. Para análises económicas o modelo também requer entradas de valores monetários, geralmente na forma de preço por kg por grupos de idade. (Para o modelo de Thompson e Bell baseado em comprimentos o mesmo tipo de dados de entrada são requeridos por classe de comprimento).
2) Resultados: Os resultados obtidos pelo modelo, relacionados com os valores de F para cada grupo de idade, são na forma de previsões das capturas em número, do número total de mortos, das capturas em peso, da biomassa média e do rendimento, por grupo de idade. Podem ser obtidos novos valores de F multiplicando-se a matriz-F de referência, como um todo, por um certo factor, geralmente chamado X, ou aplicando-se o factor somente a uma parte da matriz-F de referência. Este último caso aplica-se, por exemplo, no caso de alterações do tamanho mínimo da malha, ou para separar o efeito das frotas com diferentes características (por exemplo artesanal e industrial) em um particular manancial. Executando uma série de cálculos com diferentes valores de X (factores-F), podem ser elaborados gráficos que ilustram claramente os efeitos de F sobre as capturas, a biomassa média e o rendimento da captura.
O modelo de Thompson e Bell é uma ferramenta muito importante para o cientista pesqueiro demonstrar os efeitos que certas medidas de regulamentação, como mudanças no tamanho mínimo de malha, diminuição ou aumento do esforço de pesca, ou períodos de defeso, terão sobre a captura, a biomassa e o rendimento da captura. Como é requerido um grande número de cálculos, é essencial o uso de computadores.
Um aspecto importante do modelo de Thompson e Bell é que ele permite a incorporação do valor da captura. Portanto, o modelo tem se tornado a base para o desenvolvimento dos chamados modelos bio-económicos, que são extremamente úteis na formulação de previsões necessárias a decisões na gestão das pescarias.
Programas de computadores
O pacote LFSA contém programas para executar de forma relativamente simples as análises de Thompson e Bell, tanto baseada em idades como em comprimentos, e também foram incorporados programas similares ao pacote FiSAT. Uma série de programas de computadores para análise bio-económica das pescarias têm sido desenvolvidos e publicados pela FAO, os chamados programas BEAM (Bio-Economic Analytical Model), modelos analíticos bio-económicos, (BEAM 1 e 2, Coppola et al., 1992, BEAM 3, Cochet e Gilly, 1990 e BEAM 4, Sparre e Willmann, 1992).
Exemplo 29: Análise de Thompson e Bell baseada em idades, camarão tropical
Dados de Entrada
Para ilustrar o modelo usamos dados da pescaria de camarão do Kuwait (de Garcia e van Zalinge, 1982). As colunas de A a E na Tabela 8.6.1 contêm os dados de entrada. Neste caso as mortalidades por pesca, os F's, foram estimados dos dados das capturas e as estimações da biomassa obtidas pelo método da área varrida (cf. Capítulo 13). No entanto, a matriz F poderia também ter sido estimada através de uma análise de coortes ou da VPA.
Tabela 8.6.1 Modelo de Thompson e Bell baseado em idades, ilustrado com os dados da pescaria de camarão do Kuwait (de Garcia e van Zalinge, 1982). M = 3.0 por ano para todas as idades
| ENTRADA | RESULTADO | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K |
| idade *) | peso médio w(t) | rend. por g v(t) | mort. pesc. F(t) | mort. total Z(t) | número N(t) | mortos | captura C(t) | captura em peso Y(t) | biomassa média B(t) | rend. |
| N(t)- N(t+Δt) | ||||||||||
| Y*v | ||||||||||
| t meses | g | unidade monetária | por ano | por ano | na popul. *) | número | número | g | g | unidade monetária |
| 1=Tr | 5.7 | 0.73 | 1.20 | 4.20 | 1000.0 | 295.3 | 84.4 | 481 | 4809 | 351 |
| 2 | 9.3 | 0.93 | 1.32 | 4.32 | 704.7 | 213.0 | 65.1 | 605 | 5504 | 563 |
| 3 | 13.0 | 1.20 | 1.32 | 4.32 | 491.6 | 148.6 | 45.4 | 590 | 5367 | 708 |
| 4 | 17.6 | 1.45 | 1.44 | 4.44 | 343.0 | 106.1 | 34.4 | 606 | 5046 | 878 |
| 5 | 22.0 | 1.70 | 1.92 | 4.92 | 236.9 | 79.7 | 31.1 | 684 | 4276 | 1163 |
| 6 | 26.1 | 1.90 | 1.20 | 4.20 | 157.2 | 46.4 | 13.3 | 346 | 3463 | 658 |
| 7 | 30.3 | 2.08 | 1.56 | 4.56 | 110.8 | 35.0 | 12.0 | 363 | 2793 | 755 |
| 8 | 33.8 | 2.14 | 1.20 | 4.20 | 75.8 | 22.4 | 6.4 | 216 | 2161 | 462 |
| 9 | 37.0 | 2.18 | 1.20 | 4.20 | 53.4 | 15.8 | 4.5 | 167 | 1667 | 363 |
| 10 | 40.3 | 2.23 | 1.80 | 4.80 | 37.6 | 12.4 | 4.7 | 187 | 1250 | 418 |
| 11 | 43.1 | 2.24 | 2.76 | 5.76 | 25.2 | 9.6 | 4.6 | 199 | 863 | 445 |
| 12 | 44.7 | 2.27 | 2.52 | 5.52 | 15.6 | 5.8 | 2.6 | 117 | 559 | 267 |
| 13 | - | - | - | - | 9.9 | - | - | - | - | - |
| Total | 4561 | 37758 | 7031 | |||||||
| Biomassa média: | 37758/12 = 3146.5 | |||||||||
O tempo de vida do camarão Penaeus semisulcatus não é muito superior a um ano e por isso os grupos de idades na Coluna A da Tabela 8.6.1 são dados em meses, a espécie é recrutada à pescaria com a idade de um mês (Tr = 1). A Coluna B apresenta o peso médio por grupos de idade. A Coluna C contém um valor relativo, proporcional ao preço por kg de cauda com casca por grupo de idade. A Coluna D contém a mortalidade por pesca, a “matriz-F-por-idades de referência”, e a Coluna E a mortalidade total por ano por grupo de idade.
Na Coluna F começamos com 1000 recrutas, que têm a idade de 1 (um) mês no início do período. Em outras palavras, a população do grupo de idade 1 é 1000. Todos os cálculos subsequentes são relativos aos 1000 recrutas. Caso uma análise de coortes tivesse sido aplicada e o número real de recrutas estimado, os valores obtidos por 1000 recrutas poderiam ser convertidos em capturas e tamanho do manancial (ver Secção 5.2).
Resultados baseados na matriz-F-por-idades de referência
Com base nos valores de entrada apresentados nas Colunas A a E e no número de recrutas (1000) na idade de 1 (um) mês, a população por grupos de idade, expressa em números existentes no início de cada mês pode ser calculada (Coluna F). Podemos também calcular o seguinte: o número de mortos por mês (Coluna G), as capturas em número, equivalente ao número de mortos devido à mortalidade por pesca (Coluna H), a captura em gramas (Coluna I), a biomassa média em gramas (Coluna J), e o rendimento expresso em unidades monetárias (Coluna K).
Os cálculos serão agora apresentados, passo a passo, usando-se como exemplo numérico os cálculos para os três primeiros grupos de idade.
| Passo 1: | Calcular o número na população no início de cada período (mês): |
| N(1) = 1000, use | |
| N(t+Δt) = N(t)*exp(-Z*Δt), onde | |
| Δt = 1 mês = 0.08333 ano, para calcular os números subsequentes | |
| N(2) = 1000*exp (-4.20*0.08333) = 704.7 | |
| N(3) = 704.7*exp (-4.32*0.08333) = 491.6 | |
| Passo 2: | Calcular o número total de mortos em cada período: |
| Número total de mortos D(t) = N(t) - N(t+Δt) | |
| D(1) = 1000-704.7 = 295.3 | |
| D(2) = 704.7-491.6 = 213.1 | |
| D(3) = 491.6-343.0 = 148.6 | |
| Passo 3: | Calcular o número capturado em cada período: |
| C(t) = [N(t) - N(t+Δt)]*F(t)/Z(t) = D(t)*F(t)/Z(t) | |
| C(1) = 295.3*1.20/4.20 = 84.4 | |
| C(2) = 213.1*1.32/4.32 = 65.1 | |
| C(3) = 148.6*1.32/4.32 = 45.4 | |
| Passo 4: | Calcular a captura em peso em cada período: |
| Y(t) = C(t)*w(t) | |
| Y(1) = 84.4*5.7 = 481 | |
| Y(2) = 65.1*9.3 = 605 | |
| Y(3) = 45.4*13.0 = 590 | |
| Passo 5: | Calcular a biomassa média em cada período: |
| B(t) = Y(t)/[F(t)*Δt] | |
| B(1) = 481/(1.20*0.08333) = 4810 | |
| B(2) = 605/(1.32*0.08333) = 5500 | |
| B(3) = 591/(1.32*0.08333) = 5373 | |
Note: Este cálculo de biomassa é derivado da Eq. 4.2.8, C = F*Δt*N, que, multiplicada por w em ambos os lados, resulta
Y = F*Δt*B e B = Y/(F*Δt)
| Passo 6: | Calcular o rendimento em cada período: |
| V(t) = Y(t)*v(t) | |
| V(1) = 481*0.73 = 351 | |
| V(2) = 605*0.93 = 563 | |
| V(3) = 590*1.20 = 708 | |
| Passo 7: | Calcular a captura total, a biomassa média ao longo de todo o período e o rendimento total (ver a última coluna da Tabela 8.6.1): |
| A captura total é a soma de todas as capturas mensais. | |
| O rendimento total é a soma de todos os rendimentos mensais. | |
| A biomassa média aproximada é (cf. Fig. 4.2.3): | |
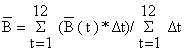 | |
| Como Δt = 1/12 e o período total é de 12 meses, neste caso | |
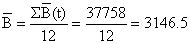 | |
O conceito de biomassa média no caso mais complicado, onde Δt não permanece constante, é discutido na Secção 5.3.
As seguintes equações resumem, de uma maneira geral, as fórmulas para o modelo de Thompson e Bell baseado em idades, incluindo X (factor-F). O índice i refere-se ao intervalo de idades (ti, ti+Δt). O índice ti refere-se ao início do intervalo e o índice ti+Δt ao final.
| intervalo de idade: i = (ti,ti+Δt) | |
| Zi = M + X*Fi | |
| N(ti+Δt) = N(ti)*exp(-Zi*Δt) | |
| Ci = [N(ti)-N(ti+Δt)]*X*Fi/Zi | |
| wi = w(ti+Δt/2) | (8.6.1) |
| Yi = Ci*wi | |
| Bi = Yi/[Fi*Δt*X] | |
| Vi = Yi*vi |
Thompson e Bell usando um grupo-mais
A última linha do grupo de idade na Tabela 8.6.1 (exemplo 29), idade 13, contém somente o número de sobreviventes e nenhuma das outras entradas, devido ao número de sobreviventes com idade superior a 12 meses ter sido considerado insignificante e, portanto, ignorado.
Em casos onde o número é significante existe uma maneira de explicá-los, mesmo quando levamos em conta apenas 12 grupos de idade. Tratando o grupo 12 como um “grupo-mais”, isto é, substituindo o número de mortos entre as idades 12 e 13, N(12)-N(13), pelo total de mortos depois da idade 12, e, como todos os indivíduos morrerão, este número é no Exemplo 29, N(12) = N(12+) = 15.6.
Assumindo ainda que os grupos mais velhos têm a mesma mortalidade que o grupo 12, o número de camarões capturados do grupo-mais será
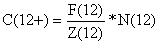
C(12+) = (2.52/5.52)*15.6 = 7.1
Assim, deixando de fora o grupo-mais na Tabela 8.6.1 uma captura de 7.1 -2.6 = 4.5 foi ignorada.
Se o crescimento tivesse parado na idade 12 então w(12) seria o peso máximo e a captura correspondente a C(12+) seria 44.7*4.5 = 201 g. Esta captura corresponde ao rendimento de 201*2.27 = 456 unidades monetárias, que representam algo em torno de 6% do total - uma quantidade significativa. Portanto, para estar seguro de que capturas significativas não estão sendo ignoradas, é melhor tratar sempre o último grupo como um “grupo-mais”.
Previsões, resultados baseados em diferentes matrizes-F
Com os resultados baseados na matriz-F de referência calculados acima, ficam disponíveis os dados básicos para a previsão dos efeitos de aumentos ou diminuições no esforço de pesca ou mortalidade por pesca. Novos valores para a captura total, biomassa média total e rendimento total podem ser obtidos ponderandose a mortalidade por pesca na Coluna D da Tabela 8.6.1 por uma certa percentagem. A matriz F apresentada na Tabela 8.6.1, chamada matriz-F de referência, é então substituída por uma nova, pela sua multiplicação, ou parte dela, por um factor X = (novo F) / (F de referência).
Se, por exemplo, o esforço aumentasse em 20 %, a nova mortalidade por pesca na Coluna D seria
1.20*1.20 = 1.44, 1.32*1.20 = 1.58, etc.
Executando novamente todo o cálculo, usando os novos F's, a correspondente captura total, biomassa média total e rendimento total são obtidos.
Um exemplo de resultados de uma série de cálculos deste tipo com X = factores-F variando de 0 a 3.0 é apresentado na Tabela 8.6.2. A matriz-F de referência, onde X = 1.0 fornece um rendimento total de 4560, uma biomassa média total de 3146 e um valor total de 7029. (Estes valores foram obtidos com os mesmos dados de entrada utilizados na Tabela 8.6.1, no entanto existem pequenas diferenças dos resultados da tabela devido ao facto do programa de computador usado para calcular a Tabela 8.6.2 utilizar o número máximo de dígitos em todas as operações. Estas pequenas e, sob o ponto de vista da avaliação de mananciais, insignificantes diferenças podem também ser observadas em outros cálculos apresentados neste manual).
Na Fig. 8.6.1 a captura total, a biomassa média total e o rendimento total correspondentes à Tabela 8.6.2 foram marcados contra X (factor-F) e as respectivas curvas traçadas. Notar que a curva de rendimentos possui um ponto máximo, o que não ocorre com a curva de capturas no intervalo de variação dos factores-F (X) considerados. Quando o preço por kg varia com o tamanho dos camarões as duas curvas terão os seus máximos em diferentes níveis de F.
Recordar que a biomassa é proporcional à captura por unidade de esforço (Secções 4.3 e 8.3). A Fig. 8.6.1 ilustra o sério conflito entre o desejo de maximizar a captura total de uma pescaria, em peso ou em valor, e a necessidade de permitir que pescadores e armadores obtenham receitas suficientes. A captura por barco diminui constantemente quando o esforço aumenta e pode, na prática, ficar tão pequena que torna a pescaria inviável economicamente, mesmo para níveis de esforço menores que os correspondentes ao máximo na curva de rendimento total da captura.
Tabela 8.6.2 Captura, rendimento da captura e biomassa para vários níveis de F. A matriz-F de referência é dada na coluna D da Tabela 8.6.1 (compare com a Fig. 8.6.1)
| factor-F X | captura total | biomassa média total | rendimento total |
| 0 | 0 | 5382 | 0 |
| 0.4 | 2549 | 4271 | 4209 |
| 0.8 | 4055 | 3466 | 6396 |
| 1.0 | 4561*) | 3146*) | 7031*) |
| 1.2 | 4954 | 2870 | 7465 |
| 1.5 | 5383 | 2522 | 7842 |
| 2.0 | 5814 | 2075 | 8025 |
| 3.0 | 6138 | 1497 | 7683 |
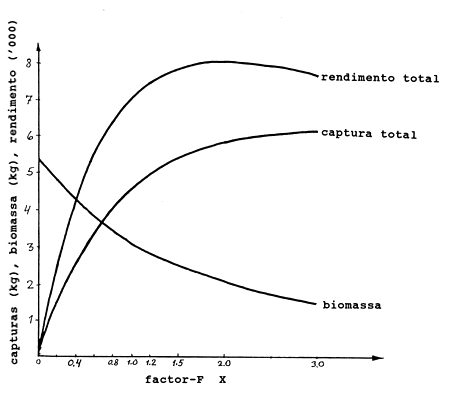
Fig. 8.6.1 Captura, biomassa e rendimento da captura por 1000 camarões calculados pelo modelo de Thompson e Bell baseado em idades. Baseado nos dados da Tabela 8.6.2
Previsão por frota
A pesca de camarões nas águas do Kuwait é composta de um “segmento artesanal” e um “segmento industrial”. A Tabela 8.6.3 mostra os resultados de uma divisão da mortalidade por pesca total dada na Tabela 8.6.1 em uma componente artesanal e uma industrial (de Garcia e van Zalinge, 1982). Este tipo de divisão, da mortalidade por pesca causada por diferentes frotas, está baseado, normalmente, na proporção do número de indivíduos (camarões ou peixes) capturados por cada frota.
Tabela 8.6.3 Divisão da mortalidade por pesca total, na pesca de camarão do Kuwait, em componentes artesanal e industrial (de Garcia e van Zalinge, 1982)
| idade (meses) | artesanal FA | industrial FI | total Ftotal |
| 1 | 0.720 | 0.480 | 1.20 |
| 2 | 0.960 | 0.360 | 1.32 |
| 3 | 0.840 | 0.480 | 1.32 |
| 4 | 0.480 | 0.960 | 1.44 |
| 5 | 0.600 | 1.320 | 1.92 |
| 6 | 0.480 | 0.720 | 1.20 |
| 7 | 1.080 | 0.480 | 1.56 |
| 8 | 0.480 | 0.720 | 1.20 |
| 9 | 0.084 | 1.116 | 1.20 |
| 10 | 0.120 | 1.680 | 1.80 |
| 11 | 0.240 | 2.520 | 2.76 |
| 12 | 0.240 | 2.280 | 2.52 |