Tabela 8.6.4 Divisão de capturas e rendimentos, da Tabela 8.6.1, em componentes artesanal e industrial (de Garcia e van Zalinge, 1982). Os factores-X são como na Tabela 8.6.2 (XA = XI) (ver Fig. 8.6.2)
| captura total | rendimento total | frota artesanal | frota industrial | ||||
| factor-F XA | captura | rendimento | factor-F XI | captura | rendimento | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2549 | 4209 | 0.4 | 1048 | 1531 | 0.4 | 1501 | 2678 |
| 4055 | 6396 | 0.8 | 1773 | 2486 | 0.8 | 2284 | 3910 |
| 4560 | 7029 | 1.0 | 2048 | 2815 | 1.0 | 2512 | 4216 |
| 4954 | 7465 | 1.2 | 2281 | 3073 | 1.2 | 2673 | 4392 |
| 5383 | 7842 | 1.5 | 2563 | 3354 | 1.5 | 2819 | 4488 |
| 5814 | 8025 | 2.0 | 2903 | 3627 | 2.0 | 2910 | 4398 |
| 6138 | 7683 | 3.0 | 3291 | 3783 | 3.0 | 2847 | 3900 |
Tabela 8.6.5 Avaliação do efeito da variação do esforço industrial (XI) com a manutenção do esforço artesanal constante (XA = 1.0) (ver Fig. 8.6.3)
| frota artesanal | frota industrial | ||||||
| captura total | rendimento total | factor-F | captura | rendimento | factor-F | captura | rendimento |
| XA | XI | ||||||
| 2479 | 3603 | 1.0 | 2479 | 3603 | 0 | 0 | 0 |
| 3522 | 5403 | 1.0 | 2289 | 3250 | 0.4 | 1234 | 2154 |
| 4270 | 6598 | 1.0 | 2124 | 2950 | 0.8 | 2146 | 3648 |
| 4560 | 7029 | 1.0 | 2048 | 2815 | 1.0 | 2512 | 4216 |
| 4811 | 7383 | 1.0 | 1979 | 2691 | 1.2 | 2832 | 4692 |
| 5120 | 7783 | 1.0 | 1883 | 2520 | 1.5 | 3237 | 5263 |
| 5501 | 8203 | 1.0 | 1740 | 2271 | 2.0 | 3761 | 5932 |
| 5951 | 8499 | 1.0 | 1510 | 1880 | 3.0 | 4441 | 6619 |
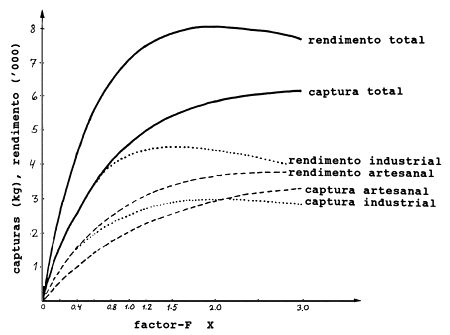
Fig. 8.6.2 Captura total e rendimento total da captura da Fig. 8.6.1 separados em componentes artesanal e industrial (cf. Tabela 8.6.4)
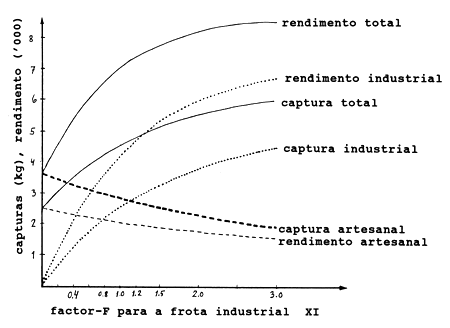
Fig. 8.6.3 Avaliação do efeito duma alteração na pescaria industrial mantendo a pesca artesanal a um nível constante (cf. Tabela 8.6.5)
A mortalidade por pesca exercida por uma frota, no i, F(i), é
| F(i) = Ftotal*C(i)/Ctotal | (8.6.2) |
onde C(i) é o número de camarões (ou peixes) capturados pela frota no i, e F(total) e C(total) são, respectivamente, a mortalidade por pesca e o número capturado por todas as frotas. F(total) pode ser derivado de uma análise de coortes. A divisão da captura (coluna H na Tabela 8.6.1) em componentes da frota é obtida por:
| C(i) = Ctotal*F(i)/Ftotal | (8.6.3) |
Assim, a captura e o rendimento são facilmente separados em componentes da frota. A Tabela 8.6.4 mostra a divisão, entre as duas frotas, da captura total e do rendimento dados na Tabela 8.6.2.
Neste caso os mesmos factores, XA = XI, são aplicados para valores-F das duas frotas, isto é no exercício apresentado na Tabela 8.6.4 foi assumido que o esforço da frota artesanal é sempre a mesma proporção do esforço total. A Fig. 8.6.2 mostra o gráfico correspondente à Tabela 8.6.4.
A Tabela 8.6.5 e a Fig. 8.6.3 mostram um exemplo onde o factor XA, para a frota artesanal é mantido constante enquanto o factor XI, para a frota industrial é alterado. Isto corresponde à situação onde a frota industrial está mudando, e a frota artesanal permanece no mesmo nível. Notar que a frota artesanal obtém uma menor porção da captura total à medida que se eleva o nível de esforço da frota industrial. Ou seja quando há um aumento no esforço da frota industrial o manancial reduz-se de modo que a frota artesanal fica com uma parte menor.
É possível avaliar de maneira semelhante o efeito de qualquer medida de regulamentação para uma das componentes da frota desde que seja possível converter o esforço regulamentado na mortalidade por pesca apropriada. Por exemplo, Garcia e van Zalinge (1982) usaram o modelo de Thompson e Bell para avaliar o efeito de um tempo de defeso.
O modelo de Thompson e Bell pode ser também utilizado para avaliar o efeito de uma alteração no tamanho da malha. Neste caso a curva de selectividade para a pescaria corrente poderia ser estimada usando-se um dos métodos descritos no Capítulo 6. O método será discutido na Secção 8.8.
A aplicação do modelo de Thompson e Bell acima descrito (incluindo a avaliação das malhas abaixo descrita) é, essencialmente, o método utilizado hoje em dia para a previsão das capturas e estabelecimento de quotas de pesca na área do ICES (Atlântico Nordeste) e em muitas outras áreas.
(Ver Exercício (s) na Parte 2).
Exemplo 29a: Previsões a curto e a longo prazo
Imediatamente a seguir a uma alteração do esforço ou do tamanho da malha, ocorre uma alteração nas capturas que só é sentida após todos os grupos de idade da população estarem sujeitos a esse novo esforço ou à nova malha. O exemplo 29 lida apenas com a estimativa do novo estado de equilíbrio.
Para calcular as capturas ano após ano depois duma alteração do esforço (F), continua-se com a análise de coortes ou VPA para os anos futuros, utilizando os números estimados, em cada grupo de idade, no final de cada período com o esforço antigo e o novo valor de F depois da alteração. Os cálculos iniciam-se com o grupo de idade mais novo e prosseguem para baixo na tabela, no sentido oposto à análise de coortes e VPA. O recrutamento não pode ser previsto e, portanto, é assumido como constante.
Voltando aos dados do badejo da análise de coortes baseada em idades, Secção 5.2, Exemplo 19a, usa-se o recrutamento médio, de 2849 milhões para o ano de 1974–79, ver Tabela 5.2.2. Poderemos estudar o efeito em duplicar o esforço. Assim o factor X do Exemplo 29 toma o valor de 2:
F(novo,t,t+1) = F(1980,t,t+1)*2
No entanto os valores de F para 1980 são “F terminais” ou seja são valores supostos. Na verdade, o valor de F estimado para a classe anual 1974 foi usado no exemplo 19a. A Tabela 5.2.2 mostra que não há nenhuma alteração do esforço durante o período de amostragem, consequentemente pode-se substituir o valor do F terminal pela média dos F estimados durante a amostragem de 1974–79, tal como dado na última coluna da Tabela 5.2.2. adoptando, assim, este valor como F(1980,t,t+1).
Alterando o valor de F terminal para 1980 é necessário também uma recalculação do número de indivíduos na população no início de 1980 e novamente a expressão do Exemplo 19 para o N terminal é usada:
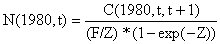
onde F = F(1980,t,t+1), Z = F+M, com M = 0.2. Os resultados estão na primeira coluna da Tabela 8.6.6.
Assume-se que a duplicação do esforço ocorre em 1 de Janeiro de 1981. Para se poder prever o efeito desta duplicação os números N(1981,t) têm que ser calculados dos F antigos e utilizados como ponto de partida. Assim:
N(1981,t+1) = N(1980,t)*exp[-(F(1980,t,t+1)+M)]
como por exemplo:
N(1981,4) = 412*exp[-1.02+0.2)] = 122
Ver Tabela 8.6.6. Para N(1981,0), utiliza-se o recrutamento médio de 1974 - 79, 2849 milhões da Tabela 5.2.2. Com um factor de X de 2 substitui-se os novos números em
N(1982,t+1) = N(1981,t)*exp[-(X*F(1980,t,t+1))+M)]
de modo que:
N(1982,5) = 122*exp[-2*0.91+0.2)] = 16
e igualmente para os restantes anos. Mantendo o factor X e o recrutamento constantes, a população acaba por estabilizar gradualmente à medida que a classe anual de 1980 vai desaparecendo. Em 1987 os números nos grupos de idade 0–6 anos estão todos estáveis e representam a projecção a longo prazo do efeito da duplicação do esforço.
Calculos similares, Tabela 8.6.7, são feitos para as capturas usando a Eq. 4.2.7:
C(y,t,t+1) = N(y,t) * [1 - exp(-Z)]*X*F(1980,t,t+1)/Z
onde:
Z = X*F(1980,t,t+1)+M
Assim, para a idade 4 no ano 1981:
Z = 2*0.91 + 0.2 =2.02
C(1981,4,5) = 122*[1 - exp(-2.02)]*2*0.91/2.02 = 95.
O peso da captura anual, mostrado na Fig. 8.6.5, é determinado multiplicando a captura pelo peso individual em cada grupo de idade. As capturas no primeiro ano depois do aumento do esforço são grandes devido ao manancial estar adaptado à situação anterior de esforço menor. No final do estado de equilíbrio (1987 e seguintes) as capturas de peixes com idade superior a 4 anos são praticamente neglígiveis, tal como se vê na Tabela 8.6.7.
Os resultados são influenciados pela data da alteração, 1 de Janeiro de 1981. A mesma alteração efectuada noutro ano daria resultados diferentes a curto prazo, dependendo da distribuição de idades do manancial nessa altura, no entanto as projecções a longo prazo seriam as mesmas. Para generalizar os efeitos de um aumento no esforço tem que se analisar a situação desde um estado de equilíbrio até ao outro. A Fig. 8.6.4 mostra tal efeito no arenque do Mar do Norte, neste caso o esforço aumentou e o tamanho da malha reduziu ao mesmo tempo. Alterações deste tipo ocorrem normalmente quando uma pescaria se desenvolve não estando regulamentada e já existe um nível de esforço próximo do MSY.
O efeito é un aumento imediato no número de capturas por peso (Fig. 8.6.4, C e A) seguido de um rápido declínio para um novo nível. A biomassa e o comprimento médio dos peixes diminuem permanentemente até um novo estado de equilíbrio ser alcançado (Fig. 8.6.4. B e D). Assim sendo, a tentação de aumentar o esforço, por exemplo melhorando a eficiência da arte e de reduzir o tamanho da malha, é óbvia pois o efeito observável imediato é um aumento das capturas.
Tabela 8.6.6 Projecções a curto e a longo prazo do número de indivíduos (milhões) após um aumentodo esforço (Fnovo) = 2*Fantigo), para o Badejo do Mar do Norte, das Tabelas 4.4.3.1 e 5.2.2. O recrutamento é constante. M = 0.2. Os peixes acima dos 7 anos foram desprezados. As capturas estão na Tabela 8.6.7
| número de indivíduos no início dos sucessivos anos | |||||||||
| grupo idade | 1 ano anterior à alteração | durante o ano anterior à alteração | 1oJan. do ano da alteração | novo F | alteração a longo prazo | ||||
| t | N(1980,t) | F(1980,t,t+1) | N(1981,t) | F(t,t+1) | N(1982,t) | N(1983,t) | N(1984,t) | … | N(1987,t) |
| 0 | 1700 | 0.24 | 2849 | 0.48 | 2849 | 2849 | 2849 | 2849 | |
| 1 | 801 | 0.50 | 1095 | 1.00 | 1443 | 1443 | 1443 | 1443 | |
| 2 | 614 | 0.85 | 398 | 1.70 | 330 | 435 | 435 | 435 | |
| 3 | 412 | 1.02 | 215 | 2.04 | 60 | 49 | 65 | 65 | |
| 4 | 146 | 0.91 | 122 | 1.82 | 23 | 6 | 5 | 7 | |
| 5 | 75 | 0.60 | 48 | 1.20 | 16 | 3 | 1 | 1 | |
| 6 | 22 | 0.50 | 34 | 1.00 | 12 | 4 | 1 | 0 | |
Tabela 8.6.7 Projecções a curto e a longo prazo das capturas (milhgões) após uma alteração do esforço, para o Badejo do Mar do Norte. O número de indivíduos da população estão na Tabela 8.6.6
| após a alteração do esforço | ||||||
| grupo idade | ano anterior à alteração | 1 o ano | 2 oano | 3 o ano | alteração a longo prazo | |
| t | C(1980,t,t+1) | C(1981,t,t+1) | C(1982,t,t+1) | C(1983,t,t+1) | … | C(1987,t,t+1) |
| 0 | 330 | 992 | 992 | 992 | 992 | |
| 1 | 288 | 638 | 841 | 841 | 841 | |
| 2 | 323 | 303 | 251 | 331 | 331 | |
| 3 | 243 | 175 | 49 | 40 | 53 | |
| 4 | 80 | 95 | 18 | 5 | 5 | |
| 5 | 31 | 31 | 10 | 2 | 1 | |
| 6 | 9 | 20 | 7 | 2 | 0 | |
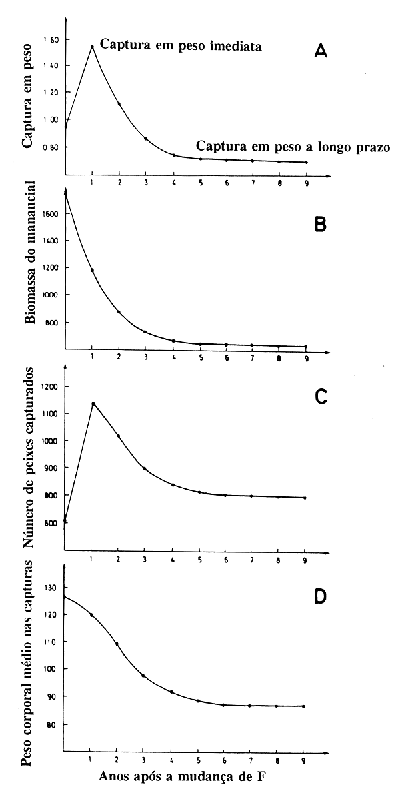
Fig. 8.6.4 Efeitos imediatos e a longo prazo devido ao aumento do esforço e redução do tamanho da malha, simultaneamente. Transição de um estado de equilíbrio para outro durante um período de 9 anos. Arenque do Mar do Norte (Clupea harengus). Adaptado de Beyer e Sparre (1983)
Voltando ao exemplo do badejo e examinando o efeito de reduzir a mortalidade por pesca (Tabela 8.6.6, coluna 3) para metade do valor presente, i. e. X = 0.5, é observado um aumento considerável de peixes mais velhos nas capturas de tal modo que não é aconselhável negligenciar os peixes do grupo 7 e mais. O grupo de idade 6 é portanto substituido pelo grupo mais, 6+. Isto não afecta os calculos para determinar o número, N(t) devido ao número no grupo de 6 anos no primeiro dia do ano ser a quantidade necessária. As capturas no grupo mais são definidas pela Eq. 5.1.7:
C(6+) = N(6) * F(6+) /Z(6+)
onde a mortalidade é definida pelo “F terminal” da VPA multiplicado pelo factor X, que é 0.5.
Se o número médio de todos os grupos de idade do grupo mais é necessário, este é dado pela Eq.:
N(6+) = N(6) /Z(6+)
O número de todas as idades no grupo mais no primeiro dia do ano pode ser encontrado pela soma da progressão geométrica do primeiro termo = N(6) e do quociente de exp(-Z(6+)):
| N (6+) = N (6) / [1-exp (-Z(6+))] | (8.6.3) |
Qualquer tratamento com o grupo mais é uma aproximação. A expressão acima assume que todas as classes anuais no grupo mais têm uma evolução idêntica: tiveram o mesmo recrutamento e a mesma mortalidade nos grupos de idade que ainda não pertenciam ao grupo mais. O efeito subsequente é um novo estado de equilíbrio ser alcançado para uma classe anual que nasceu antes da alteração do esforço actuar no grupo mais. Se o grupo mais fosse definido com 7+, em vez de 6+, isto aconteceria um ano depois, em 1988. Adoptando o grupo 8+, seria em 1989, etc. Usando o grupo 6+, como no exemplo, significa que se reconhece a necessidade de considerar peixes com 7 anos e mais, mas também à necessidade de tratar rapidamente dos dados.
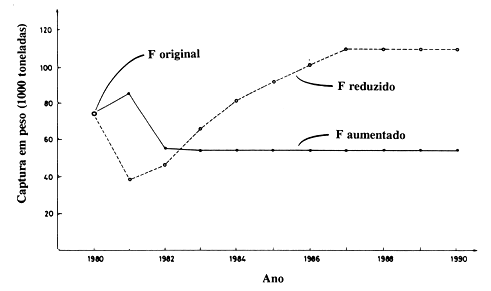
Fig. 8.6.5 Fase de transição depois duma alteração do esforço, badejo do
mar do Norte.
Capturas em 1000 de toneladas
Tabela 8.6.8 Projecções a curto e a longo prazo dos números do manancial e das capturas depois duma diminuição do esforço (Fnovo = 0.5*Fantigo). Badejo do mar do Norte. Peixes com mais de 6 anos estão no grupo mais. (Cf. Tabelas 8.6.6 e 8.6.7)
| numero no início dos anos sucessivos | capturas | ||||||||||
| depois da alteração do esforço | |||||||||||
| grupo idade | novo | altura da alter. | alter. longo prazo | último ano antes da alter. | 1o ano | 2 o ano | longo prazo | ||||
| t | F | N(1981) | N(1982) | N(1983) | ..... | N(1987) | C(1980) | C(1981) | C(1982) | ..... | C(1987) |
| 0 | 0.120 | 2849 | 2849 | 2849 | 2849 | 330 | 293 | 293 | 293 | ||
| 1 | 0.250 | 1095 | 2069 | 2069 | 2069 | 288 | 220 | 417 | 417 | ||
| 2 | 0.425 | 398 | 698 | 1319 | 1319 | 323 | 126 | 221 | 417 | ||
| 3 | 0.510 | 215 | 213 | 374 | 706 | 243 | 79 | 78 | 258 | ||
| 4 | 0.455 | 122 | 106 | 105 | 347 | 80 | 41 | 35 | 116 | ||
| 5 | 0.300 | 48 | 64 | 55 | 180 | 31 | 11 | 15 | 42 | ||
| 6+ | 0.250 | 34 | 29 | 39 | 109 | 9 | 19 | 16 | 61 | ||
A Tabela 8.6.8 dá os números do manancial em 1 de Janeiro e as capturas anuais depois da redução da mortalidade por pesca para metade do seu valor original. Depois duma queda, as capturas dos peixes maiores aumentam acentuadamente. A linha a tracejado na Fig. 8.6.5 ilustra o desenvolvimento das capturas em peso obtidas multiplicando as capturas em número pelo peso médio em cada grupo de idade. As capturas caiem para metade no primeiro ano e depois aumentam para valores próximos do valor inicial. A indústria pesqueira sofre uma falta imediata que pode influenciar o preço. Como a alteração afectará os navios de pesca individualmente, depende como a redução do esforço for realizada. Se a frota for reduzida para metade do tamanho, as capturas serão repartidas apenas por essa metade e a queda imediata será de metade da do ano anterior (de 76 000 toneladas para 38 000 toneladas) de tal modo que as capturas por unidade de esforço permanecerão constantes no primeiro ano, e aumentarão nos anos seguintes. Se por outro lado a redução do esforço for realizada através da proibição duma arte bastante eficiente ou por o estabelecimento duma época de veda, haverá na mesma, o mesmo número de barcos para partilhar as capturas reduzidas do primeiro ano de redução da mortalidade por pesca. Somente depois de uns poucos de anos as capturas atingirão o seu valor inicial ou ficarão maiores.
Sendo assim, quando na avaliação de mananciais é considerada uma redução do esforço é necessário olhar para o problema como se estivesse num período de transição, pois o dono das embarcações de pesca, com um capital pequeno, não se sustenta com a prospectiva de aumentar os rendimentos nos anos seguintes, se no primeiro ano ele for à falência.
Os dados de entrada para o “modelo de Thompson e Bell baseado em comprimentos” são obtidos de uma análise de coortes baseada em comprimentos. Os dados de entrada consistem na mortalidade por pesca para cada classe de comprimento, a matriz F por comprimentos, o número na menor classe, e o factor de mortalidade natural H por classe, que devem ser iguais aos utilizados na análise de coortes. Os dados de entrada adicionais são os parâmetros da relação peso-comprimento (ou o peso individual médio por classe de comprimento) e o preço médio por kg para cada classe de comprimento.
Os resultados são os mesmos do modelo baseado em idades, e consistem em: para cada classe de comprimento, o número no limite inferior da classe, N(L1), a captura em número, a captura em peso, a biomassa multiplicada por Δt, isto é o tempo requerido para um indivíduo crescer do limite inferior ao limite superior da classe e o rendimento. Finalmente, são obtidos os totais capturados, captura em peso, biomassa média * Δt e rendimento. Os cálculos são repetidos para uma gama de valores X (F-factor) e os resultados finais (totais) são marcados em gráficos. O princípio é o mesmo para os modelos baseados em idades acima descritos, somente as fórmulas são ligeiramente diferentes e podem ser derivadas das usadas na análise de coortes de Jones baseada em comprimentos, Eqs. 5.3.4 e 5.3.7 como se segue:
Primeiro a Eq. 5.3.7 é rearranjada:
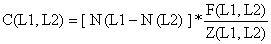 | (8.7.1) |
é, então, substituida na Eq. 5.3.4 que resulta:
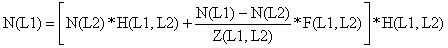
onde
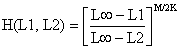
que é o mesmo factor usado na análise de coortes de Jones baseada em comprimentos (Eq. 5.3.3).
Resolvendo a equação em relação a N(L2) obtem-se:
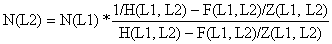 | (8.7.2) |
Para calcular a captura em peso por classe de comprimento, tem que se multiplicar a captura C (em números) pelo peso médio da classe, w(L1,L2), que é obtido da Eq. 5.3.11 da seguinte maneira:
w(L1,L2) = q*[ (L1+L2) /2]b
onde q e b são os parâmetros da relação peso-comprimento.
A captura desta classe de comprimento é então dada por
| Y(L1,L2) = C(L1,L2) * w(L1,L2) | (8.7.3) |
O rendimento é dado por:
| V(L1,L2) = Y(L1,L2) * v(L1,L2) | (8.7.4) |
onde v(L1,L2) é o preço médio por kg entre os comprimentos L1 e L2.
Durante o tempo Δt(L1,L2) que a coorte leva para crescer de L1 a L2, o número de sobreviventes decresce de N(L1) a N(L2). O número médio de sobreviventes daquela classe de comprimento é calculado da seguinte maneira:
| N(L1,L2) * Δt(L1,L2) = [N(L1)-N(L2)]/Z(L1,L2) | (8.7.5) |
A correspondente biomassa média * Δt é:
| B(L1,L2) * Δt(L1,L2) = N(L1,L2) * Δt(L1,L2) * w(L1,L2) | (8.7.6) |
A captura anual é simplesmente a soma da captura de todas as classes:
Y = ∑ Yi
O rendimento anual é, de forma semelhante, a soma dos rendimentos de todos as classes:
V = ∑ Vi
Conforme discutido na Secção 5.3
B = ∑ Bi*Δti
é a biomassa média estimada durante o tempo de vida de uma coorte, ou de todas as coortes durante um ano. No método baseado em idades, Secção 8.6, não foi necessário multiplicar cada biomassa pelo Δt porque este era uma constante e igual a 1/12 do ano, ou um mês, mas neste caso Δt é variável.
As Eqs. 8.7.1 a 8.7.6 têm sido apresentadas para uma classe de comprimento específica (L1,L2). Tal como na versão baseada em idades, o seguinte bloco de equações sumariza, de forma geral, as fórmulas para o modelo de Thompson e Bell baseado em comprimentos, incluindo X (factor-F). O índice i refere-se aqui, ao intervalo de comprimento (Li,Li+1). O índice Li refere-se ao limite inferior daquele intervalo de comprimento, enquanto o índice Li+1 refere-se ao limite superior.
| intervalo de comprimento: i = (Li, Li+1) | |
| Zi = M + X*Fi | |
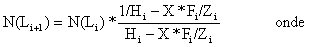 | |
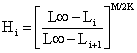 | |
| Ci = [N(Li)-N(Li+1)]*X*Fi/Zi | (8.7.7) |
| wi = q*[(Li+Li+1)/2]b | |
| Yi = Ci*wi | |
| Vi = Yi*vi | |
| Ni*Δti = [N(Li)-N(Li+1)]/Zi | |
| Bi*Δti = Ni*Δti*wi |
Aspectos básicos da análise de Thompson e Bell baseada em comprimentos
Como a análise de Thompson e Bell baseada em comprimentos é derivada da análise de coortes de Jones baseada em comprimentos (Secção 5.3) que por sua vez é baseada na análise de Pope baseada em idades (Secção 5.2), o método de Thompson e Bell baseado em comprimentos tem as mesmas limitações da análise de coortes de Pope baseada em idades. A aproximação com a VPA no modo previsivo é válida para valores de F*Δt até 1.2 e de M*Δt até 0.3 (Pope, 1972). Se os F's são altos, serão obtidos resultados sem sentido, tais como números negativos do manancial. Se este for o caso, será necessário a utilização de classes de comprimento menores e, portanto, menores valores de Δt.
No entanto, a aproximação não é necessária, pois a versão exposta da VPA não envolve uma solução iterativa para o F (Eq. 5.1.3). Usando a técnica VPA no modelo de Thompson e Bell necessitamos de substituir a segunda e terceira fórmula da Eq. 8.7.7 pela Eq. 4.2.6 e Eq. 4.4.5.1:
| N(Li+1) = N(Li) *exp(-Zi*Δti) | (8.7.8) |
onde:
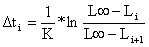
o peso médio da classe mais é dado pela Eq. 5.3.16.
Exemplo 30: Análise de Thompson e Bell baseada em comprimentos, pescada, Senegal
Como exemplo para a análise de Thompson e Bell baseada en comprimentos usamos os dados da Tabela 5.3.3 para a pescada (Merluccius merluccius) capturada nas águas do Senegal. São utilizados os seguintes parâmetros iniciais (cf. Secção 5.3):
L∞ = 130 cm, K = 0.1 por ano, M = 0.28 por ano, q = 0.00001 kg/cm3, b = 3, N (primeira classe de comprimento) = N(6) = 98919.3
Usando os valores-F e os factores de mortalidade natural, H, da Tabela 5.3.3 e os pesos calculados de wi = q*[(Li+Li+1)/2]b, a relação peso-comprimento, e alguns (neste caso seleccionados arbitrariamente) preços por kg para a pescada, os dados de entrada podem ser resumidos na Tabela 8.7.1.
Tabela 8.7.1 Dados iniciais para a análise de Thompson e Bell baseada em comprimentos, pescada, Senegal
| classe compr. (Li,Li+1) | F(Li,Li+1) | H(Li, Li+1) | w(Li, Li+1) | v(Li, Li+1 |
| kg | preços/kg | |||
| 6–12 | 0.04 | 1.0719 | 0.0073 | 1.0 |
| 12–18 | 0.39 | 1.0758 | 0.0338 | 1.0 |
| 18–24 | 1.07 | 1.0801 | 0.0926 | 1.0 |
| 24–30 | 0.65 | 1.0850 | 0.196 | 1.5 |
| 30–36 | 0.49 | 1.0905 | 0.359 | 1.5 |
| 36–42 | 0.59 | 1.0967 | 0.593 | 2.0 |
| 42–48 | 0.65 | 1.1039 | 0.911 | 2.0 |
| 48–54 | 0.39 | 1.1122 | 1.33 | 2.5 |
| 54–60 | 0.29 | 1.1220 | 1.85 | 2.5 |
| 60–66 | 0.31 | 1.1337 | 2.50 | 2.5 |
| 66–72 | 0.40 | 1.1478 | 3.29 | 3.0 |
| 72–78 | 0.39 | 1.1652 | 4.22 | 3.0 |
| 78–84 | 0.11 | 1.1873 | 5.31 | 3.0 |
| 84–∞ | 0.28 | - | 12.25 | 3.0 |
Usando as Eqs. 8.7.7 com X = 1 e os dados iniciais da Tabela 8.7.1 podemos calcular os números nas classes de comprimento subsequentes, a captura em número e em peso, a biomassa média * Δt e o rendimento, conforme apresentado no sequinte exemplo:
| N(12) | = | N(6)*[1/H(6,12) - F(6,12)/Z(6,12)]/[H(6,12) - F(6,12)/Z(6,12)] |
| = | 98919.3*[1/1.0719 - 0.04/0.32]/[1.0719 - 0.04/0.32] | |
| = | 84400.8 | |
| C(6,12) | = | [N(6)-N(12)]*X*F(6,12)/Z(6,12) |
| = | [98919.3-84400.8]*1*0.04/0.32 = 1814.8 | |
| w(6,12) | = | q*[(6+12)/2]b |
| = | 0.00001*93 = 0.007290 | |
| Y(6,12) | = | C(6,12)*w(6,12) |
| = | 1814.8*0.007290 = 13.23 |
| B(6,12)*Δt(6,12) | = | [(N(6)-N(12)]/Z(6,12)]*w(6,12) |
| = | [(98919.3-84400.8)/0.32]*0.007290 = 330.7 |
V(6,12) = Y(6,12)*v(6,12) = 13.23*1.0 = 13.23
Estes cálculos repetem-se até se atingir a última classe de comprimento e como esta é a chamada “classe mais” têm que ser feitas algumas suposições adicionais: N(∞) = 0 e w(84,∞) = w(84,90). Os resultados são:
| C(84,∞) | = | [N(84)-N(∞)]*F(84,∞)/Z(84,∞) |
| = | [92-0]*0.28/0.56 = 46 | |
| w(84,∞) | = | w(84,130) = q*[(84+130)/2]b |
| = | 0.00001*1073 = 12.25 | |
| Y(84,∞) | = | C(84,∞) * w(84,∞) |
| = | 46*12.25 = 563.5 | |
| B(84,∞)*Δt(84,∞) = [(N(84) -N(∞)]/Z(84,∞)] * w(84,∞) | ||
| = | [(92-0)/0.56]*12.25 | |
| = | 2012.5 | |
| V(84,∞) | = | Y(84,∞)*v(84,∞) |
| = | 563.5*3.0 = 1690.5 | |
Seguindo estes cálculos o resultado final encontra-se na Tabela 8.7.2. No entanto, deve ser notado que existem diferenças entre os resultados apresentados acima, calculados com uma calculadora de bolso, e os da Tabela 8.7.2, efectuados com 8 dígitos significativos em todas as etapas.
Notar que os valores de N(Li), C(Li,Li+1) e o rendimento (Li,Li+1) são exactamente os mesmos que os da Tabela 5.3.3, calculados pela análise de coortes de Jones baseada em comprimentos.
Estes cálculos podem agora ser repetidos para diferentes valores de X.
A Tabela 8.7.3 mostra os resultados correspondentes à Tabela 8.7.2 mas com factor-F X = 2.0, isto é a captura em peso, biomassa média * Δt e rendimento prevista sob o pressuposto de uma duplicação do esforço de pesca. Neste caso o efeito de duplicar o esforço seria uma queda dramática nas capturas em peso e no rendimento.
A Tabela 8.7.4 mostra os resultados para 16 diferentes factores-F (X). Cada linha está baseada em cálculos como os ilustrados nas Tabelas 8.7.2 e 8.7.3. A captura total, a biomassa média e o rendimento dados nas últimas linhas destas duas tabelas podem ser encontrados também na Tabela 8.7.4. As duas últimas linhas da Tabela 8.7.4 mostram a captura máxima sustentável (MSY) e o rendimento económico máximo sustentável (MSE) junto com o correspondente factor-F e a biomassa do manancial. Quando os preços por kg diferem de uma classe de comprimento para outra, o factor-F que corresponde ao MSY usualmente difere do factor-F que corresponde ao MSE. As Tabelas 8.7.2 a 8.7.4 foram calculadas pelo programa “MIXFISH” do pacote LFSA (Sparre, 1987), no qual calcula MSY e MSE através de uma técnica iterativa.
Tabela 8.7.2 Resultados da análise de Thompson e Bell baseada em comprimentos, pescada do Senegal, usando o factor-F X = 1.0. Pesos em toneladas (cf. Tabela 5.3.4)
| Classe comprimento (Li,Li+1) | F (Li,Li+1) X = 1.0 | N(Li) | C (Li,Li+1) | captura em peso (Li,Li+1) | biomassa média *Δt B*Δt | rendimento (Li,Li+1) |
| '000 unidades monetárias | ||||||
| '000 | '000 | tonneladas | tonneladas | |||
| 6–12 | 0.04 | 98919.3 | 1823 | 13.3 | 330.7 | 13.3 |
| 12–18 | 0.39 | 84392.7 | 14463 | 488.1 | 1260.1 | 488.1 |
| 18–24 | 1.07 | 59475.8 | 25277 | 2336.3 | 2191.5 | 2336.3 |
| 24–30 | 0.65 | 27623.0 | 8143 | 1601.0 | 2475.2 | 2401.5 |
| 30–36 | 0.49 | 15967.8 | 3889 | 1397.6 | 2845.9 | 2096.4 |
| 36–42 | 0.59 | 9861.5 | 2959 | 1755.2 | 2970.1 | 3510.5 |
| 42–48 | 0.65 | 5500.5 | 1871 | 1704.9 | 2638.4 | 3409.9 |
| 48–54 | 0.39 | 2818.8 | 653 | 866.2 | 2247.1 | 2165.5 |
| 54–60 | 0.29 | 1691.5 | 322 | 596.3 | 2069.4 | 1490.8 |
| 60–66 | 0.31 | 1056.6 | 228 | 570.1 | 1853.8 | 1710.3 |
| 66–72 | 0.40 | 621.0 | 181 | 594.6 | 1481.9 | 1783.8 |
| 72–78 | 0.39 | 313.7 | 96 | 405.0 | 1040.1 | 1215.0 |
| 78–84 | 0.11 | 148.7 | 16 | 85.0 | 772.0 | 255.1 |
| 84–∞ | 0.28 | 92.0 | 46 | 563.5 | 2012.6 | 1690.6 |
| Total | 59908 | 12977.3 | 26189.0 | 24567.1 |
Tabela 8.7.3 Resultados da análise de Thompson e Bell baseada em comprimentos, pescada do Senegal, usando o factor-F X = 2.0. (cf. Tabela 8.7.2)
| classe comprimento Li,Li+1 | F (Li,Li+1) X = 2.0 | N(Li) | C (Li,Li+1) | captura em peso (Li,Li+1) | biomassa media *Δt B*Δt | rendimento (Li,Li+1) |
| '000 unidades monetárias | ||||||
| '000 | '000 | toneladas | toneladas | |||
| 6–12 | 0.08 | 98919.3 | 3611.6 | 26.3 | 327.6 | 26.3 |
| 12–18 | 0.77 | 82724.1 | 26041.2 | 878.9 | 1134.4 | 878.9 |
| 18–24 | 2.13 | 47271.6 | 32863.1 | 3043.4 | 1427.4 | 3043.4 |
| 24–30 | 1.29 | 10092.9 | 5154.2 | 1014.5 | 784.2 | 1521.7 |
| 30–36 | 0.98 | 3823.1 | 1652.3 | 593.8 | 604.6 | 890.7 |
| 36–42 | 1.18 | 1699.7 | 881.6 | 523.0 | 442.5 | 1046.0 |
| 42–48 | 1.29 | 609.2 | 351.7 | 320.5 | 248.0 | 640.9 |
| 48–54 | 0.77 | 181.3 | 74.9 | 99.3 | 128.8 | 248.3 |
| 54–60 | 0.58 | 79.3 | 27.4 | 50.8 | 88.1 | 126.9 |
| 60–66 | 0.62 | 38.5 | 14.9 | 37.3 | 60.6 | 111.9 |
| 66–72 | 0.80 | 16.8 | 8.5 | 27.9 | 34.7 | 83.6 |
| 72–78 | 0.78 | 5.4 | 2.8 | 11.9 | 15.3 | 35.8 |
| 78–84 | 0.22 | 1.5 | 0.3 | 1.7 | 7.5 | 5.0 |
| 84–∞ | 0.56 | 0.8 | 0.5 | 6.7 | 12.0 | 20.2 |
| Total | 70685.0 | 6636.0 | 5315.9 | 8679.7 |
Os resultados da Tabela 8.7.4 foram traçados na Fig. 8.7.1. Os gráficos mostram claramente que o nível actual do esforço de pesca é bem acima daquele que fornece a captura máxima sustentável e a conclusão a ser tirada desta análise é que o manancial está sobrexplorado já que uma redução no esforço resultaria numa maior captura.
Tabela 8.7.4 Resultados da análise da Thompson e Bell baseada em comprimentos, pescada do Senegal. MSY = Captura Máxima Sustentável. MSE = Rendimento Económico Máximo Sustentável (valor) (cf. Fig. 8.7.1)
| A | B | C | D |
| factor-F X | captura total | biomassa média total *Δt | rendimento total |
| toneladas | toneladas | unidades monetáriaas | |
| 0.0 | 0 | 571297 | 0 |
| 0.2 | 18903 | 268193 | 48329 |
| 0.4 | 20717 | 135343 | 49701 |
| 0.6 | 18360 | 73209 | 40925 |
| 0.8 | 15474 | 42376 | 31836 |
| 1.0*) | 12977*) | 26189*) | 24567*) |
| 1.2 | 10999 | 17216 | 19168 |
| 1.4 | 9470 | 11976 | 15236 |
| 1.6 | 8287 | 8761 | 12370 |
| 1.8 | 7365 | 6697 | 10259 |
| 2.0**) | 6636**) | 5316**) | 8680**) |
| 2.2 | 6053 | 4357 | 7480 |
| 2.4 | 5580 | 3670 | 6554 |
| 2.6 | 5191 | 3163 | 5829 |
| 2.8 | 4868 | 2780 | 5253 |
| 3.0 | 4596 | 2484 | 4790 |
| MSY = 20919 para factor-F X = 0.343 Biomassa no MSY = 163296 | |||
| MSE = 51544 para factor-F X = 0.301 Biomassa no MSE = 188207 | |||
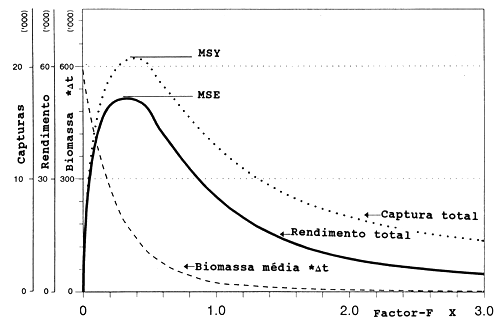
Fig. 8.7.1 Representação gráfica dos resultados da análise de Thompson e Bell baseada em comprimentos, pescada do Senegal (cf. Tabela 8.7.4)
No caso de interacção económica, onde várias frotas exploram um recurso as capturas previstas pela análise de Thompson e Bell baseada em comprimentos podem ser particionadas exactamente da mesma maneira mostrada na Secção 8.6 (cf. Tabelas 8.6.3 a 8.6.5).
O pressuposto que fundamenta a análise de Thompson e Bell baseada em comprimentos (e a análise de coortes de Jones baseada em comprimentos) é que o manancial permanece em um estado de equilíbrio, com todos os parâmetros (por exemplo recrutamento) constantes. Assim, obtemos uma previsão da “captura média a longo prazo”. Desvios na captura prevista são portanto prováveis em anos isolados.
(Ver Exercício(s) na Parte 2).
A regulamentação do tamanho das malhas é uma importante ferramenta de gestão para muitas pescarias. É, portanto, importante estar em condições de prever o resultado de possíveis alterações no tamanho da malha. Como uma alteração no tamanho da malha provocará alterações no padrão de pesca, ou seja na matriz de valores-F, podemos utilizar as fórmulas apresentadas na Secção 6.6.1 e 6.6.2 para chegarmos a uma previsão. Em outras palavras, usamos a situação “actual” para prever uma nova situação.
Podemos expressar a mortalidade por pesca actual pelo modelo baseado em idades ou em comprimentos (cf. Eq. 6.6.1.1):
| Ftactual = Fm*Stactual | (8.8.1) | |
| e | ||
| FLactual = Fm*SLactual | (8.8.2) |
onde Fm é a mortalidade por pesca máxima e Stactual ou SLactual a curva de selectividade para a arte de pesca actual, por exemplo, se é uma ogiva de selectividade da do tipo de arrasto:
| SLactual = 1/[1 + exp(T1 - T2*t)] | (8.8.3) | |
| e | ||
| SLactual = 1/[1 + exp(S1 - S2*L)] | (8.8.4) |
Os parâmetros T1 e T2 são definidos pelas Eqs. 6.4.3.4 e 6.4.3.5 respectivamente, enquanto S1 e S2 são definidos pelas Eqs. 6.1.6 e 6.1.7 respectivamente.
Os parâmetros t50% e t75% são as idades onde 50% e 75%, dos peixes são retidos pela arte. Usualmente conhecemos os comprimentos L50% e L75% que correspondem a t50% e t75% respectivamente.
Com os parâmetros L50% e L75% conhecidos para a arte de pesca actualmente em uso estamos em condições de calcular uma nova curva de selectividade baseada em idades ou em comprimentos para os novos valores de L50% e L75% (ou t50% e t75%). Desta nova ogiva de selectividade, e do Fm da pescaria actual, podemos calcular uma nova matriz de mortalidade por pesca usando a Eq. 6.6.1.1:
| Ftnovo = Fm*Stnovo | (8.8.5) | |
| e | ||
| FLnovo = Fm*SLnovo | (8.8.6) |
Os novos F's são então usados como entrada para o modelo de Thompson e Bell, e os resultados para os F's padrões alternativos, F(actual) e F(novo), podem ser comparados (Hoydal et al., 1980 e 1982). Este método é uma generalização dos métodos sugeridos por Gulland (1961), Jones (1961) e Kimura (1977).
Programas de computadores
O programa “MIXFISH” no pacote LFSA (Sparre, 1987) contém uma opção para avaliação das malhas, correspondente aos cálculos acima descritos. O resultado final apresenta-se sob a forma de uma tabela mostrando a captura total para várias combinações do esforço e L50%.
| Esforço Relativo | ||||||
| - 20% | - 10% | sem alterar | + 10% | + 20% | ||
| - 30% | ||||||
| Valor relativo de L50% | - 15% | |||||
| sem alter. | CAPTURA | |||||
| + 15% | ||||||
| + 30% | ||||||
O MIXFISH assume que L75% é proporcional a L50%. O MIXFISH permite testar todas as combinações entre o L50% e o esforço, possibilitando, desta forma, determinar a combinação óptima do L50% e do esforço. O quadrado central (marcado com “CAPTURA”) corresponde ao regime de pesca actual.
Um programa similar foi, também, incorporado no FiSAT.