Contrastando com os Capítulos 3 a 8, os Capítulos 9 e 13 não lidam com os “modelos analíticos”, mas sim com os “modelos holísticos” (ver Fig. 1.8.1), onde o manacial é visto como uma grande unidade de biomassa e não se considera a idade ou o comprimento nos cálculos. Os “modelos de produção geral” discutidos neste capítulo tratam do manancial como um todo, do esforço total e da captura total obtida do manacial, sem entrar em pormenores com parâmetros de crescimento e mortalidade ou efeitos do tamanho da malha na idade da captura dos peixes, etc. Apesar dos modelos de produção geral terem sido introduzidos por Graham (1935), faz-se mais frequentemente referência a eles como “modelos de Schaefer” (ver abaixo).
O objectivo da utilização dos “modelos de produção geral” é determinar o nível óptimo do esforço, ou seja, o esforço que leva à captura máxima que pode ser sustentada sem afectar a productividade do manancial a longo prazo, a chamada captura máxima sustentável (MSY). A teoria que fundamenta os modelos de produção de geral foi revista por muitos autores, por exemplo, Ricker (1975), Caddy (1980), Gulland (1983) e Pauly (1984).
Uma vez que os modelos holísticos são muito mais simples que os modelos analíticos, requerem menos dados para a sua aplicação. Não há, por exemplo, necessidade de determinar coortes e, portanto, de determinar idades, sendo esta uma das principais razões para a relativa popularidade dos modelos de produção geral na avaliação de manaciais de peixes tropicais. Os modelos de produção geral podem ser aplicados quando se dispõe de razoáveis estimações da captura total (por espécie) e/ou da captura por unidade de esforço (CPUE) por espécie e/ou a CPUE por espécie e o esforço correspondente para um certo número de anos. O esforço deve ter sofrido substanciais alterações ao longo do período coberto.
A captura máxima sustentável (MSY) pode ser estimada a partir dos seguintes dados:
f(i) = esforço no ano i, i = 1,2,…,n
Y/f = captura em peso por unidade de esforço no ano i.
Calcula-se Y/f a partir do captura, Y(i), do ano i, para a pescaria como um todo, e do correspondente esforço, f(i), por
| Y/f = Y(i)/f(i), i = 1,2,…,n | (9.1.1) |
A maneira mais simples de expressar a captura por unidade de esforço, Y/f, em função do esforço, f, é o modelo linear proposto por Schaefer (1954):
| Y(i)/f(i) = a + b*f(i) se f(i) ≤ -a/b | (9.1.2) |
A Eq. 9.1.2 é denominada “Modelo de Schaefer”.
O declive, b, deve ser negativo se a captura por unidade de esforço, Y/f, decresce para valores crescentes de f (ver Fig. 9.1.1). A intersecção a, é o valor de Y/f obtido imediatamente após o primeiro barco entrar na pesca e realizar, pela primeira vez, capturas do manacial. A intersecção é, portanto, sempre positiva. Assim, -a/b será positivo e Y/f igual a zero para f = -a/b. Como é absurdo um valor negativo para a captura por unidade de esforço Y/f, o modelo aplica-se apenas para valores de f menores que -a/b.
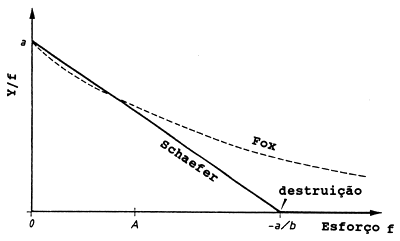
Fig. 9.1.1 Ilustração dos diferentes pressupostos básicos do modelo de Schaefer e do modelo de Fox
Fox (1970) introduziu um modelo alternativo, que fornece uma curva quando Y/f é marcado directamente contra o esforço, f, (ver Fig. 9.1.1) porém quando são marcados os logaritmos de (Y/f) contra o esforço obtém-se uma recta:
| ln (Y(i)/f(i)) = c + d*f(i) | (9.1.3) |
A Eq. 9.1.3 é denominada “Modelo de Fox”, e pode também ser escrita como se segue:
| Y(i)/f(i) = exp(c + d*f(i)) | (9.1.4) |
Ambos os modelos obedecem à condição que Y/f decresce quando o esforço aumenta, mas são diferentes, no sentido de que para o modelo de Schaefer existe um nível de esforço (f = -a/b) para o qual Y/f é igual a zero, enquanto que no modelo de Fox, Y/f é maior que zero para todos os valores de f.
Isto pode ser visto facilmente na Fig. 9.1.1 onde o gráfico de Y/f contra f dá uma linha recta no caso do modelo de Schaefer e uma linha curva, que se aproxima de zero somente para níveis muito altos do esforço, sem nunca atingi-lo (assintota), no caso do modelo de Fox.
Na Secção 8.3 foi demonstrado que CPUEw(t) = q*B(t) (Eq. 8.3.1). Como Y/f é também a captura por unidade de esforço em peso, podemos escrever
Y(i)/f(i) = q*B = a + b*f(i) para o modelo de Schaefer e
Y(i)/f(i) = q*B = exp(c + d*f(i)) para o modelo de Fox
onde B é a biomassa e q o coeficiente de capturabilidade (uma constante).
A Fig. 9.1.1 ilustra outra característica básica dos dois modelos. Para valores de f próximos dde zero Y/f apresenta valores máximos e, consequentemente, a biomassa também é máxima pois Y/f = q*B, onde q é uma constante. A biomassa correspondente a f = 0 é denominada de “biomassa do manancial virgem” ou “biomassa do manancial não explorado”, que é representada por “Bv”. Assim, substituindo Y/f por q*Bv nas Eqs. 9.1.2 e 9.1.4 obtém-se:
| q*Bv = a | ou Bv = a/q | (Schaefer) |
| q*Bv = exp(c) | ou Bv = exp(c)/q | (Fox) |
O valor de Bv para os dois modelos deve ser o mesmo. Quando aumentamos o valor de f de zero até o nível A (ver Fig. 9.1.1) as duas curvas são aproximadamente iguais, mas à direita de A as diferenças tornam-se cada vez maiores, portanto, a opção entre um ou outro modelo tem importância apenas quando são observados valores de f relativamente grandes. Não há como provar a superioridade de um modelo em relação ao outro. A solução pode passar por escolher o modelo que se acredita ser o mais razoável para cada caso particular ou aquele que fornece o melhor ajuste aos dados observados. No entanto, o modelo de Beverton e Holt está mais de acordo com o modelo de Fox, pois ambos possuem uma relação curvilínea semelhante entre a captura por unidade de esforço e o esforço (ver Fig. 8.3.1 e Fig. 9.1.1) e entre a biomassa média por recruta B/R e F (ver Fig. 8.3.2 e Fig. 9.1.1)
Exemplo 31: Modelos de Schaefer e de Fox, peixes demersais, Mar de Java
A Fig. 9.1.2 mostra um exemplo dos pontos marcados da CPUE, Y(i)/f(i), contra o esforço, f(i), e da captura, Y(i), contra o esforço. Os dados foram obtidos da pescaria de peixes demersais da costa norte de Java durante os anos de 1969–1977 (de Dwiponggo, 1979). Neste caso a captura, Y, refere-se à captura anual, expressa em unidades de 1000 toneladas, e Y/f corresponde à captura por milhares de barcos padrão em cada ano. O esforço é medido em unidades de barco padrão por ano.
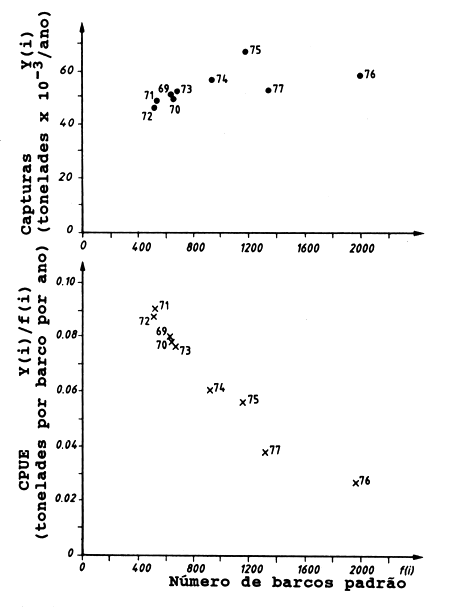
Fig. 9.1.2 Tendências de capturas, Y(i), e capturas por unidade de esforço Y(i)/f(i), no mar da costa Norte de Java (dados da Tabela 9.1.1)
Antes de se efectuar a soma dos esforços de todos os barcos para a obtenção do esforço total anual e como a frota consistia em diferentes tipos de barcos, estes foram agrupados por categorias e o esforço de cada categoria foi convertido à unidade de barco considerada padrão. Como era de se esperar a relação (Y/f) mostra uma tendência decrescente à medida que aumenta o esforço. Considerando-se a biomassa do manacial como um recurso limitado, o qual é compartilhado por todos os barcos participantes da pescaria, é de se esperar que quanto maior o número de barcos na pescaria menor é a captura individual por barco.
Neste caso não existe uma tendência clara na relação entre captura, Y, e esforço, f. Mostraremos agora como os dois modelos podem ser aplicados a este tipo de dados.
Os cálculos para se estimar os parâmetros (Schaefer: a e b, Fox: c e d) serão explicados com base nos dados apresentados na Tabela 9.1.1 e Fig. 9.1.2. Como estamos a lidar com uma recta, no caso do modelo de Schaefer, e de uma curva que foi linearizada através de logaritmos, no caso do modelo de Fox, a determinação de a,b e c,d requer duas regressões lineares, de f(i) contra Y(i)/f(i) e f(i) contra ln(Y(i)/f(i)) respectivamente. Os resultados das duas regressões são apresentados na Tabela 9.1.1, incluindo os desvios padrão dos declives e da intersecção. As rectas são mostradas na Fig. 9.1.3. Determinámos assim a relação entre a captura por unidade de esforço e o esforço para ambos os modelos.
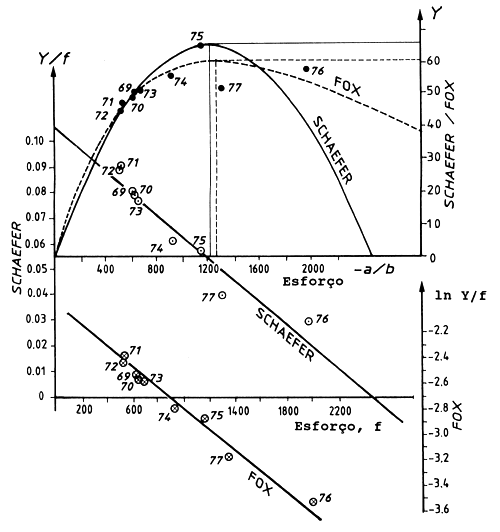
Fig. 9.1.3 Os modelos de Schaefer e de Fox ilustrados para as pescarias demersais da Costa Norte de Java (dados da Tabela 9.1.1)
O objectivo é, no entanto, estimar um valor da captura máxima sustentável (MSY) e determinar a que nível de esforço foi ou será atingido o MSY. Para tal é necessário reescrever as Eqs. 9.1.2 e 9.1.4 e expressar a captura em função do esforço, multiplicando ambos os lados da equação por f(i):
| Schaefer: | Y(i) = a*f(i) + b*f(i)2 | se f(i) < -a/b | (9.1.5) | |
| ou | Y(i) = 0 | se f(i) = -a/b | ||
| Fox: | Y(i) = f(i) *exp[c + d*f(i)] | (9.1.6) |
A Eq. 9.1.5, o modelo de Schaefer, é uma parábola (ver Fig. 9.1.3) a qual tem o seu valor máximo para Y(i), o MSY, a um nível do esforço
| fMSY = -0.5*a/b | (9.1.7) |
e a correspondente captura:
| MSY = -0.25*a2/b | (9.1.8) |
A Eq. 9.1.6, o modelo de Fox, é uma curva assimétrica com um ponto máximo (o MSY), apresentando um declive bastante acentuado no lado esquerdo e um mais suave no lado direito do ponto máximo (ver Fig. 9.1.3).
O MSY e fMSY para o modelo de Fox podem ser calculados por fórmulas que são derivadas da Eq. 9.1.6 por diferenciação de Y em relação a f e calculando o valor de f para dY/df = 0,
| fMSY = -1/d | (9.1.9) |
| MSY = -(1/d)*exp(c-1) | (9.1.10) |
Os resultados dos cálculos do exemplo são apresentados no final da Tabela 9.1.1.
Da Tabela 9.1.1 e Fig. 9.1.3 pode ser visto que os dois modelos fornecem resultados ligeiramente diferentes. De acordo com o modelo de Fox o nível de MSY é 60900 toneladas para um nível de esforço fMSY de 1274 barcos padrão, enquanto de acordo com o modelo de Schaefer o nível de MSY é bem mais alto (65800 toneladas) e a um nível mais baixo de fMSY, 1235 barcos padrão. Segundo ambos os modelos, o nível do esforço superou fMSY em 1976 e a captura foi abaixo do MSY (ver Fig. 9.1.2).
Até agora demonstrou-se principalmente os cálculos matemáticos a realizar, o que foi bastante simples. Assim sendo, porque nos preocupamos nós com modelos complicados, tais como o modelo de captura por recruta de Beverton e Holt, quando podemos facilmente estimar MSY através dos modelos de produção geral? Uma resposta é, que o ganho em simplicidade com os modelos de produção geral é feito às custas de uma série de suposições acerca da dinâmica dos mananciais pesqueiros, as quais podem ser (e quase sempre são) difíceis de serem justificadas. Algumas destas suposições são discutidas a seguir, baseando-se o raciocínio no modelo de Schaefer, mas aplicando-se também ao modelo de Fox.
(Ver Exercício(s) na Parte 2).
Tabela 9.1.1 Cálculos para estimar o MSY e fMSY através dos modelos de Schaefer e de Fox, utilizando dados de capturas e esforço de arrasto nas Costa Norte de Java (Dwiponggo, 1979) 1)
| ano i | capturas (1000 ton.) Y(i) | esforço (no de barcos padrão) f(i) x | SCHAEFER Y(i)/f(i) y | FOX ln(Y(i)/f(i)) y |
| 1969 | 50 | 623 | 0.080 | -2.523 |
| 1970 | 49 | 628 | 0.078 | -2.551 |
| 1971 | 47.5 | 520 | 0.091 | -2.393 |
| 1972 | 45 | 513 | 0.088 | -2.434 |
| 1973 | 51 | 661 | 0.077 | -2.562 |
| 1974 | 56 | 919 | 0.061 | -2.798 |
| 1975 | 66 | 1158 | 0.057 | -2.865 |
| 1976 | 58 | 1970 | 0.029 | -3.525 |
| 1977 | 52 | 1317 | 0.039 | -3.232 |
| valor médio | 923.22 | 0.0667 | -2.7648 | |
| desvio padrão | 485.14 | 0.02171 | 0.3873 | |
| intersecção (Schaefer: a, Fox: c) | 0.1065 | -2.0403 | ||
| declive (Schaefer: b, Fox: d) 1) | -0.00004312 | -0.0007848 | ||
| variânçia do declive: | ||||
| sb2 = [(sy/sx)2 - b2]/(9-2) | 2.041*10-11 | 3.087*10-9 | ||
| desvio padrão do declive, sb limites de confiança do declive: | 0.00000452 | 0.0000556 | ||
| b + t9-2*sb t7 = 2.37 | -0.000032 | -0.00065 | ||
| b - t9-2*sb | -0.000053 | -0.00092 | ||
| variânçia da intersecção: | ||||
| sa2 = sb2*[sx2*(n-1)/n + x2] | 0.00002167 | 0.003277 | ||
| desvio padrão da intersecção limites de confiança da intersecção | 0.0049 | 0.0572 | ||
| a + t9-2*sa | 0.118 | -1.90 | ||
| a - t9-2*sa | 0.095 | -2.18 | ||
| MSY: Schaefer: -0.25*a2/b | 65.8 | |||
Fox: -(1/d)*exp(c-1) | ||||
| fMSY: Schaefer: -0.5*a/b | 1235 | |||
Fox: -1/d | 1274 | |||
| 1) Nas fórmulas dadas nesta tabela a e b deveriam ser substituídos por c e d para o modelo de Fox | ||||
A suposição de uma situação de equilíbrio
Para explicar este conceito considera-se por exemplo uma situação na qual um manancial virgem começa a ser explorado em 1971 (ver Fig. 9.1.4), por, 1000 barcos. Suponha que a “recta de Schaefer” na Fig. 9.1.4 aplica-se a este manancial. De acordo com o modelo a captura em 1971, correspondente a 1000 barcos, deve ser x.
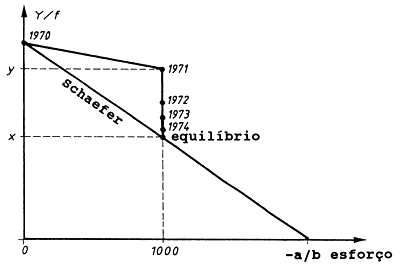
Fig. 9.1.4 Representação gráfica dos conceitos de uma situação de equilíbrio e período de transição (mais explicações são encontradas no texto)
Todavia, a captura resultante é y, isto é, um valor maior do que aquele previsto pelo modelo. Isto acontece porque quando a pesca foi iniciada em 1971 a biomassa era ainda a biomassa do manancial virgem Bv, e a biomassa apenas diminui depois de um certo período de exploração.
Quando a pesca continuou em 1972 a biomassa estava reduzida devido às perdas causadas pela pesca em 1971 e a captura de 1972 tornou-se, portanto, menor que a de 1971. O recurso é reduzido em cada ano que passa e esta redução é sempre menor à medida que um período de tempo maior decorre desde a entrada dos 1000 barcos na pesca. Eventualmente, o sistema estabilizará ao nível de x. Dizemos então que, após um “período de transição”, o sistema alcançou uma nova “situação de equilíbrio”.
Para a situação de equilíbrio a biomassa produzida por unidade de tempo t é igual à biomassa extraída pela pesca, ou captura por unidade de tempo, mais a quantidade de peixes que morreram por causas naturais. Isto também é ilustrado na Fig. 9.2.1.
A “situação de equilíbrio” do modelo de produção geral é comparável ao “sistema estabilizado de parâmetros constantes” do modelo de Beverton e Holt (ver Secção 8.1).
Os pressupostos biológicos
Os pressupostos biológicos do modelo foram adequadamente formulados por Ricker (1975):
“Próximo à densidade máxima do manancial, a eficiência da reprodu-ção é reduzida e frequentemente o número de recrutas é menor do que em níveis do manancial de menor densidade. Nesse caso, ao se reduzir o manancial obtém-se um aumento no recrutamento.
Quando a oferta alimentar é reduzida a conversão de alimento em peso é realizada com menor eficiência por um manancial maior do que por um manancial menor. Cada indivíduo do manancial maior obtém uma ração alimentar menor, daí resultando que a maior parte deste alimento é utilizado apenas para a manutenção das funções vitais do indivíduo, e uma porção menor será utilizada para o crescimento.
Num manancial não explorado há uma tendência de existirem indivíduos mais velhos em relação a um manancial explorado. Isto resulta numa produção decrescente, em pelo menos duas maneiras:
Peixes maiores utilizam alimentos maiores, portanto um degrau extra é acrescentado à pirâmide alimentar, com a consequente perda de eficiência de utilização da produção alimentar básica.
Os peixes mais velhos convertem uma menor fracção do alimento consumido em peso, em parte devido a peixes maduros utilizarem muita energia no desenvolvimento das gonadas.”
Contudo, é também possível considerar estes modelos puramente empíricos. Por exemplo, se as observações de Y/f marcados contra f resultam numa curva que se ajusta ao modelo de Fox, este modelo pode ser empregado sem se considerar as possíveis causas biológicas.
Pressupostos sobre o coeficiente de capturabilidade
Partindo-se do pressuposto que o coeficiente de mortalidade por pesca é proporcional ao esforço (Eq. 4.6.1):
F = q*f
Esta suposição não é em si contestável (se f for uma medida razoável do esforço). Os problemas surgem quando f é medido, por exemplo, em número de barcos/dias por ano durante vários anos, pois na maioria dos casos a eficiência dos barcos varia durante períodos de tempo longos; na maioria das vezes os barcos tornam-se maiores e melhor equipados. Assim, por exemplo, um esforço de 100 barcos/dia em 1978, pode resultar numa maior mortalidade por pesca, que num esforço de 100 barcos/dia em 1968. Isto significa que q é uma função de tempo, ou melhor, uma função do desenvolvimento tecnológico, o qual é geralmente uma função do tempo. Como é muito difícil considerar as variações de q resultantes de aumentos na eficiência da pesca, é bastante comum considerar-se q como constante. Portanto, recomenda-se tomar cuidado para não incluir séries de dados referentes a períodos de tempo muito longos nas análises que utilizam os modelos de produção geral. Alternativamente, devem ser tomadas em consideração alterações de q. Para pequenas espécies pelágicas em áreas de afloramento, por exemplo, a anchoveta do Peru e do Chile, no qual os peixes concentram-se em pequenas áreas devido a mudanças nas condições ambientais, não existe uma relação directa entre q, f e F, e o modelo de produção geral não pode ser aplicado.
Nesta secção considera-se a situação de mananciais pouco estudados. Para estes mananciais, séries históricas de dados de captura e esforço não se encontram disponíveis, mas dispõe-se da biomassa total estimada e da mortalidade natural.
Várias fórmulas empíricas foram desenvolvidas com o objectivo de fornecer uma primeira estimação grosseira do MSY, baseada nos poucos dados disponíveis. Estas fórmulas encontraram larga aplicação depois das primeiras biomassas estimadas serem obtidas a partir de um ou de uma série de levantamentos com rede de arrasto de fundo ou de levantamentos acústicos.
CONDIÇÔES DE EQUILÍBRIO
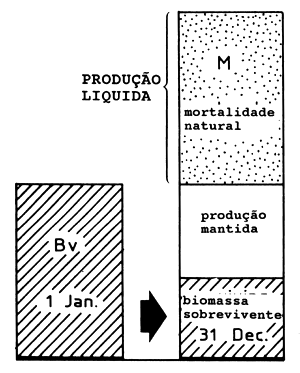 | 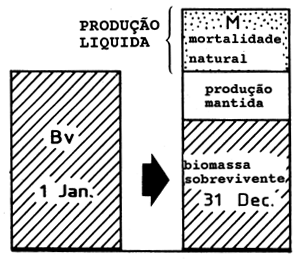 | ||
| A1: | Manancial virgem (Bv) M alto Alta produção líquida | B1: | Manancial virgem (Bv) M baixo Baixa produção líquida |
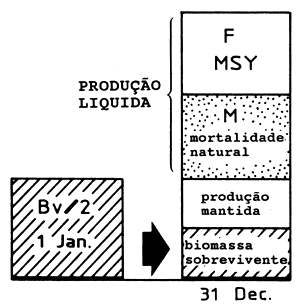 | 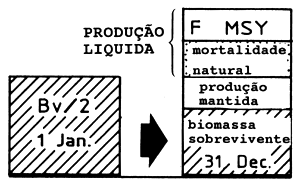 | ||
| A2: | Manancial explorado(Bv/2) M alto Alta produção líquida | B2: | Manancial explorado (Bv/2) M baixo Baixa produção líquida |
Fig. 9.2.1 Ilustração da fórmula de Gulland onde MSY = 0.5*M*Bv (para mais esclarecimentos consulte o texto)
A primeira fórmula foi desenvolvida por Gulland (1971), e uma modificação foi proposta por Cadima (em Troadec (1977), e finalmente um conjunto de fórmulas estritamente baseadas nos modelos de produção geral de Schaefer e Fox foram desenvolvidas por Garcia, Sparre e Csirke (1989).
Gulland (1971) sugeriu que se estimasse a captura máxima sustentável da seguinte forma:
| MSY = 0.5*M*Bv | (9.2.1) |
onde Bv é a biomassa do manancial virgem e M a mortalidade natural.
Esta fórmula tem sido utilizada especialmente para mananciais muito pouco estudados e ligeiramente explorados. A Bv estimada é muitas vezes obtida através do “método de área varrida” (Capítulo 13) e M é geralmente um valor já determinado para uma espécie semelhante numa área com características semelhantes àquela sob investigação. Uma vez que para utilizar esta fórmula necessita-se de uma estimação da biomassa do manancial virgem, Bv, na prática ela é aplicável apenas para mananciais não explorados e não existe uma justificação científica para a Eq. 9.2.1 (Gulland, comunicação pessoal). Contudo, as seguintes razões, que já foram levantadas por Tiurin (1962) e Alverson e Pereyra (1969), parecem razoáveis para justificá-la:
MSY deve depender da biomassa do manancial virgem, Bv
Um M elevado corresponde a uma produção elevada (este ponto é discutido com mais pormenor em baixo)
Se a biomassa = 0.5*Bv e F = M sob um regime de exploração óptimo, a Eq. 9.2.1 é realizada.
O ponto 2 acima é ilustrado na Fig. 9.2.1. Consideremos o balanço anual de biomassa para dois mananciais virgens: A1 com elevada taxa de produção e B1 com uma taxa de produção baixa. Para o manancial A1 a redução causada pela mortalidade natural é grande e para manter o manancial, a produção líquida deve igualar essas perdas. Para o manancial B1 a diminuição resultante da mortalidade por causas naturais é pequena e apenas uma pequena produção líquida é necessária para contrabalançar essas perdas. Os casos A2 e B2 lidam com os mesmos dois mananciais, mas depois de passarem por um período de regime de exploração óptima e de produzirem a captura máxima sustentável. Para o manancial A2 grande parte das mortes naturais foram substituidas por mortes devidas à pesca. Este é também o caso de B2, todavia, as possibilidades de substituição das mortes naturais por mortes ocasionadas pela pesca são menores para B2 do que para A2.
Ainda que largamente utilizada, a Eq. 9.2.1 tem merecido inúmeras críticas. Caddy e Csirke (1983) mostraram que a terceira suposição (F = M para um regime de exploração óptimo) não é aplicável para muitos casos, especialmente para mananciais de espécies presas (por exemplo, camarões). Beddington e Cooke (1983) concluíram, com base em testes simulados que a Eq. 9.2.1 geralmente sobrestima MSY por um factor de 2 a 3. Assim, substituindo “0.5” por “0.2” na Eq. 9.2.1 pode-se, talvez, obter um melhor (e consequentemente mais baixo) MSY estimado.
Uma versão mais geral da fórmula de Gulland foi proposta por Cadima (em Troadec, 1977) para mananciais de peixes explorados no qual dispõe-se apenas de dados limitados para avaliação dos mananciais.
Segundo Cadima a equação para se estimar MSY é:
| MSY = 0.5*Z*B | (9.3.1) |
onde B é a biomassa média (anual) e Z o coeficiente de mortalidade total. Uma vez que Z = F+M e Y = F*B, Cadima sugere que, na falta de dados sobre Z a Eq. 9.3.1 pode ser reescrita da seguinte forma:
| MSY = 0.5*(Y + M*B) | (9.3.2) |
onde Y é a captura total num derterminado ano e B é a biomassa média neste mesmo ano.
Como a maioria dos mananciais conhecidos já se encontram explorados esta equação é mais frequentemente utilizada para pescarias em desenvolvimento e para algumas pescarias desenvolvidas, onde séries históricas de dados de captura e esforço ainda não se encontram disponíveis, mas as biomassas estimadas já foram obtidas ocasionalmente através de, por exemplo, levantamentos acústicos ou com rede de arrasto.
Com base nas considerações apresentadas na secção acima, Garcia, Sparre e Csirke (1989) recomendaram duas maneiras alternativas para se estimar a captura potencial dos mananciais explorados, as quais têm basicamente o mesmo fundamento e aplicações que os estimadores propostos por Gulland e Cadima, mas que são consistentes com os modelos subjacentes. Os dois estimadores foram calculados a partir dos modelos de Schaefer e de Fox.
Para ambos os métodos assume-se que:
B (biomassa média) e Y (captura actual)
encontram-se disponíveis apenas para um ano. Considera-se também que a mortalidade natural, M, é conhecida e que existe uma relação entre M e fMSY da forma:
| fMSY = k*M | (9.4.1) |
onde k é uma constante.
Como f = Y/B e Y/f = B, as Eqs. 9.1.2 e 9.1.3, dos modelos de produção geral, podem ser reescritas da seguinte maneira:
| Schaefer: | B = a + b*(Y/B) | (9.4.2) |
| Fox: | lnB = c + d*(Y/B) | (9.4.3) |
Supondo-se que se dispõe dos dados B1 e Y1 e que se pode ter uma ideia do valor de M, então combinando-se com o pressuposto da Eq. 9.4.1 obtém-se:
| Schaefer: | B1 = a + b*(Y1/B1) e fMSY = k*M = -a/2b | (9.4.4) |
| Fox: | ln B1 = c + d*(Y1/B1) e fMSY = k*M = -1/d | (9.4.5) |
As constantes a, b e c, d podem ser obtidas através do modelo de Schaefer e do modelo de Fox, respectivamente:
| Schaefer: | 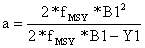 | 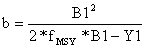 | (9.4.6) |
| Fox: | c = ln (B1) + Y1/(B1*fMSY) | d = -1/fMSY | (9.4.7) |
Uma vez obtido (a,b) ou (c,d) podemos estimar o MSY através das Eqs. 9.1.8 e 9.1.10:
| Schaefer: | MSY = -0.25*a2/b |
| Fox: | MSY = -(1/d)*exp(c-1) |
e traçar as curvas de captura (cf. Eqs. 9.1.5 e 9.1.6).
A equação correspondente a MSY pelo modelo de Schaefer é determinada substituindo-se a Eq. 9.4.6 na Eq. 9.1.8:
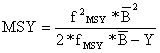 | (9.4.8) |
A curva de captura é determinada por a e b (Eq. 9.4.0.6). Quando fMSY não é conhecido (como acontece na maioria das vezes) pode-se substituir por k*M. No caso especial quando K = 0 e fMSY = M obtém-se:
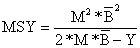 | (9.4.9) |
Se o manancial é não explorado (isto é, quando f = 0, Y = 0 e B = Bv) a Eq. 9.4.0.9 transforma-se na fórmula original de Gulland (Eq. 9.2.1).
Se o manancial em questão responde melhor ao modelo de produção de Fox (Eq. 9.1.10), obtém-se a expressão:
| MSY = fMSY*B*exp[Y/(fMSY*B) - 1] | (9.4.10) |
A curva de captura é determinada por c e d (Eq. 9.4.7). No caso especial em que k = 1 e fMSY = M, a Eq. 9.4.10 torna-se:
| MSY = M*B*exp[Y/(M*B) - 1] | (9.4.11) |
Quando Y = 0, o MSY estimado, considerando o estimador de Gulland, será:
| MSY = M*B*exp(-1) = 0.37*M*B | (9.4.12) |
Assim, um par de observações (B1, Y1) e suposições sobre o M e a relação entre M e fMSY (fMSY = k*M) são informações suficientes para obter uma primeira estimação grosseira da curva de captura (Schaefer: a, b ou Fox: c, d) da qual uma primeira estimação grosseira de MSY pode ser obtida.
O leitor interessado em mais pormenores deve procurar o trabalho original de Garcia, Sparre e Csirke, (1989).
Ao trabalhar com modelos matemáticos o cientista pesqueiro deve verificar se os requisitos básicos para a aplicação dos modelos são satisfeitos, aplicando-se, este conselho em particular, para as fórmulas empíricas mencionadas acima (Garcia, Sparre e Csirke, 1989). Por exemplo, a biomassa (B) representa a biomassa média explorada, e tanto a captura como a biomassa referida devem ter a mesma estrutura de idades (ou comprimentos). Por exemplo, dados de biomassa não devem incluir peixes pequenos que não se encontram disponíveis para a pesca. Esta biomassa representa a quantidade de biomassa anual; e as oscilações sazonais da biomassa causadas por variações no crescimento, mortalidade ou recrutamento, as quais provavelmente são mais importantes em espécies de ciclo de vida curto como camarões, lulas e biqueirões, deverão ser levadas em consideração e, na /medida do possível, ajustadas para se obter uma média anual apropriada da biomassa total.
Se as oscilações sazonais da biomassa são causadas por migração, então o pico da biomassa que representar o tamanho real do manancial deverá ser usado. Se um outro país explora o mesmo manancial numa outra estação do ano, em uma outra área, a captura deverá ser incluida nos cálculos e o MSY estimado deverá se referir ao total do manancial. A captura potencial estimada poderia também ser validada por comparação com outros mananciais para os quais houvesse melhores informações disponíveis.
Algumas questões a serem interrogadas são: O MSY/km2 estimado será idêntico a estimações para outros mananciais da mesma espécie que habita áreas ecológicas similares e exploradas sob um regime de pesca similar? A composição por comprimentos das capturas fornece o suporte para avaliações nas quais o manancial é intensamente sobrexplorado (por exemplo, onde há predominância de juvenis) ou subexplorado (isto é, onde predominam os indivíduos maiores e mais velhos)?
Deve ser ressaltado que uma verificação pormenorizada das distribuições de frequências de comprimento das capturas poderá fornecer indicações sobre os níveis relativos de exploração e estes devem ser um dos primeiros dados a serem recolhidos em qualquer pescaria em desenvolvimento, de modo a permitir estimar taxas de mortalidade total para comparação com estimações obtidas por outros métodos (cf. Capítulos 3 e 4).
Se o manancial em questão tem sido explorado durante algum tempo é provável que uma série histórica de dados de capturas esteja disponível, os quais deverão também ser examinados. Mesmo que não se encontrem disponíveis nenhuns dados detalhados do esforço a indicação de que após um período de aumento sustentado, a captura total permanece estável por algum tempo, pode significar que o nível de MSY foi alcançado, pelo menos para o actual regime de exploração. Por outro lado, se a captura diminui dum nível elevado pode significar que o manancial encontra-se sobrexplorado e, um valor médio das maiores capturas que ocorreram no passado podem fornecer uma estimação independente, que é próxima à do MSY. Ao se interpretar séries históricas de dados de capturas na forma acima sugerida, presume-se que as variações nas capturas são devidas a alterações no esforço e não o resultado de factores ambientais ou sócio-económicos.
Os modelos de produção geral são geralmente aplicados a séries de dados históricos de esforço e CPUE. Munro e Thompson (1983 e 1983a), contudo, aplicaram um modelo de produção geral a um conjunto de dados de pesca nos recifes de coral da Jamaica, todos recolhidos num mesmo ano mas representando diferentes áreas de pesca. A Fig. 9.5.1 mostra um mapa esquemático da Jamaica dividida em 9 áreas. Com excepção da área B, esta divisão coincide com a divisão territorial da Jamaica. A pescaria estudada por Munro e Thompson (1983) é a pesca realizada por canoas, utilizando armadilhas. Os peixes são de pouca mobilidade e foi assumido que em cada área ocorrem diferentes mananciais, independentes dos mananciais vizinhos (pouca mistura). Portanto, a suposição básica é que os “regimes ecológicos” em volta da ilha não diferem de modo substancial. Com base nesta premissa, faz sentido, ainda, assumir que a relação entre a captura e o esforço nas diferentes áreas seguirá o mesmo modelo.
A Tabela 9.5.1 apresenta os dados de esforço e CPUE obtidos nas várias áreas (Fig. 9.5.1) da plataforma da Jamaica em 1968. para a pesca das espécies que aí habitam
O esforço é expresso em unidades de canoas por km2 por ano, de modo a atender à suposição de que cada área possui o mesmo potencial relativo, ou seja, fornece a mesma produção por unidade de área. Assim, se forem explorados na mesma taxa (mesmo esforço por unidade de área por ano), todas as áreas deveriam oferecer a mesma captura por unidade de área por ano (kg/km2/ano) (ver coluna D da Tabela 9.5.1).
Tabela 9.5.1 Dados de entrada no gráfico de Munro e Thompson (para mais pormenores consulte o texto). De Munro e Thompson (1983a)
| A | B | C = lnB | D = A*B | |
| área (manancial) | esforço canoas | CPUE | ln(CPUE) modelo de Fox | captura |
| por km2 | kg por canoa por ano | kg por km2 por ano | ||
| A | 1.63 | 2367 | 7.769 | 3858 |
| B | 0.38 | 3279 | 8.095 | 1246 |
| C | 3.09 | 1407 | 7.249 | 4348 |
| D | 5.63 | 556 | 6.321 | 3130 |
| E | 4.43 | 974 | 6.881 | 4315 |
| (F) | 5.51 | 1306 | 7.175 | 7196 |
| G | 4.58 | 564 | 6.335 | 2583 |
| H | 4.20 | 767 | 6.642 | 3221 |
| I | 1.49 | 1875 | 7.536 | 2794 |
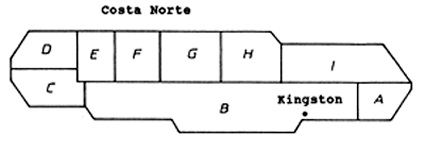
Fig. 9.5.1 Mapa esquemático da Jamaica mostrando as áreas usadas no “gráfico de Munro e Thompson” (Fig. 9.5.2)
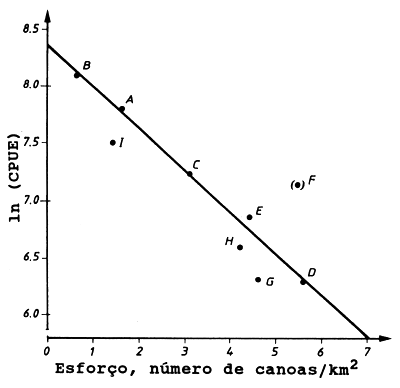 | 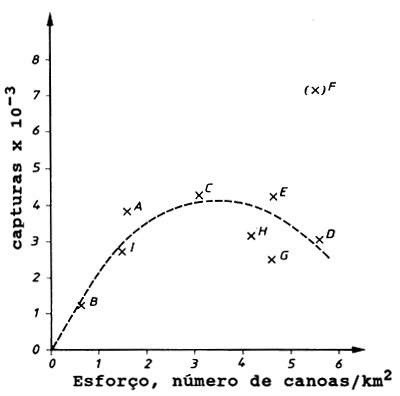 |
Fig. 9.5.2 O gráfico de Munro e Thompson. Baseado nos dados da Tabela 9.5.1 (de: Munro e Thompson, 1983)
A captura por unidade de área tomou por base a área da plataforma e dos bancos costeiros próximos a cada área. Para mais detalhes recomenda-se consultar o trabalho original (Munro e Thompson, 1983 e 1983a).
Assume-se que a relação entre CPUE e o esforço segue o modelo de Fox (Eq. 9.1.3). A Fig. 9.5.2 mostra o gráfico do ln(CPUE) contra o esforço bem como a captura por número de canoas por km2. Munro e Thompson tiveram as suas razões para excluirem a área F da análise regressão.
Ao aplicar o modelo gráfico de Munro e Thompson devemos ter o cuidado de excluir todos os peixes que podem mover-se livremente entre as áreas, como os grandes pelágicos.
O gráfico de Munro e Thompson pode ser útil em regiões onde se dispõe apenas de dados limitados de certas áreas, onde ocorre pescarias similares à dos recifes de coral ou outros recursos similares de baixa mobilidade.
Na Secção 4.3 indicou-se que o esforço é proporcional à mortalidade por pesca. Isto só é válido, obviamente, se definirmos o esforço como sendo proporcional à mortalidade por pesca, mas tal definição não é de aplicação prática. Na prática somos obrigados a escolher uma medida de esforço que se acredite estar relacionada com a mortalidade por pesca, ou melhor, com o “poder de pesca”. Existem várias opções de escolha possíveis. Para uma pescaria de arrasto pode-se considerar:
número de arrastões
número de arrastões-dias
número de arrastões padrão (tomando em consideração o tipo de barco)
número de arrrastões padrão-dias
… etc.
Para uma pescaria de linha e anzol pode ser mais apropriado considerar o número de pescador-dias ou o número de anzóis usados vezes o número de dias. Neste caso pode ser necessário levar em conta que os pescadores num mesmo barco competem entre si, e então, o esforço não é uma função linear do número de pescadores.
Em geral, uma medida de esforço que mostre ser linearmente relacionada com a taxa de captura é uma medida adequada. Isto é, se puder ser demonstrado que, operando nas mesmas condições, duas unidades de esforço capturam o dobro do que é capturado com uma unidade de esforço apenas, então esta unidade é uma medida adequada do esforço. Por exemplo, o número de horas a pescar vezes a potência do motor da embarcação pode ser uma medida adequada do esforço para determinada pescaria de arrasto, contudo, numa pescaria com rede de emalhar, o tipo de barco e o número de horas a pescar são provavelmente menos importantes que o número de redes lançadas por dia. Em ambos os casos acima mencionados o número de pescadores pode não estar linearmente relacionado com o poder de pesca.
Existem já consideráveis dificuldades para se definir medidas adequadas de esforço para uma única arte, conforme ficou mostrado acima. Quando se tenta definir o esforço para combinações de diferentes artes explorando os mesmos recursos depara-se com alguns problemas mais intrincados. Em pescarias tropicais usam-se diferentes artes para a captura do mesmos recursos e, portanto, discutiremos aqui diversos métodos de padronização de unidades de esforço.
Tabela 9.6.1 Exemplo (hipotético) para ilustrar a combinação de esforços para diferentes unidades de esforço
| ano | 1. REDE DE CERCO R1 (y) = | 2. REDE PARA A PRAIA R2 (y) = | ||||||
| CPUE1(y) | rel. | CPUE2 (y) | rel. | |||||
| y | Y1(y) | f1(y) | Y1/f1 | Y/f | Y2(y) | f2(y) | Y2/f2 | Y/f |
| 1971 | 100 | 10 | 10.00 | 1.089 | 300 | 800 | 0.375 | 1.047 |
| 1972 | 200 | 21 | 9.52 | 1.037 | 250 | 669 | 0.374 | 1.043 |
| 1973 | 400 | 43 | 9.30 | 1.013 | 200 | 543 | 0.368 | 1.028 |
| 1974 | 700 | 81 | 8.64 | 0.941 | 150 | 430 | 0.349 | 0.974 |
| 1975 | 1200 | 142 | 8.45 | 0.920 | 100 | 307 | 0.326 | 0.909 |
| CPUE1(y1,y2) = 9.18 | CPUE2(y1,y2) = 0.358 | |||||||
| ano | 3. LINHA E ANZOL R3(y) = | 4. CURRICO R4(y) = | ||||||
| CPUE3(y) | rel. | CPUE4(y) | rel. | |||||
| y | Y3(y) | f3(y) | Y3/f3 | Y/f | Y4(y) | f4(y) | Y4/f4 | Y/f |
| 1971 | 40 | 10000 | 0.00400 | 1.11 | 350 | 200000 | 0.00175 | 1.04 |
| 1972 | 80 | 20900 | 0.00383 | 1.06 | 344 | 200000 | 0.00172 | 1.02 |
| 1973 | 120 | 31100 | 0.00386 | 1.07 | 339 | 200000 | 0.00170 | 1.01 |
| 1974 | 80 | 23200 | 0.00345 | 0.96 | 333 | 200000 | 0.00167 | 0.99 |
| 1975 | 40 | 13700 | 0.00292 | 0.81 | 320 | 200000 | 0.00160 | 0.95 |
| CPUE3(y1,y2) = 0.00361 | CPUE4(y1,y2) = 0.00169 | |||||||
| Yi(y) = captur. das artes i no ano y. i = 1,..,4. y = 1971,…,1975. | ||||||||
| fi(y) = esforço das artes i no ano y | ||||||||
| CPUEi (y) = Yi (y)/fi(y) = captura por unidade de esforço das artes i no ano y | ||||||||
| Ri (y) = CPUEi (y)/CPUEi (y1,y2) = CPUE relativa | ||||||||
| ano | Y total amostrado | CPUE relativa | capt. total | esforço relativo | esforço rel. padroniz. |
| YS(y) | R(y) | YT(y) | YT(y)/R(y) | E(y) | |
| 1971 | 790 | 1.0524 | 7900 | 7507 | 0.653 |
| 1972 | 874 | 1.0341 | 8740 | 8452 | 0.735 |
| 1973 | 1059 | 1.0213 | 10590 | 10369 | 0.902 |
| 1974 | 1263 | 0.9590 | 12630 | 13170 | 1.145 |
| 1975 | 1660 | 0.9224 | 16600 | 17995 | 1.565 |
| Média YT/R 11499 | |||||
YS(y) = 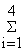 Yi(y) = soma das capturas das artes para os
quais o esforço é conhecido (capturas das
artes amostradas por ano) Yi(y) = soma das capturas das artes para os
quais o esforço é conhecido (capturas das
artes amostradas por ano)R(y) = 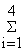 [Ri (y)*Yi(y)/YS(y)] = soma da CPUE relativa ponderada
pelas capturas no ano y [Ri (y)*Yi(y)/YS(y)] = soma da CPUE relativa ponderada
pelas capturas no ano yYT(y) = captura total de todas as artes (incluindo aquelas para as quais o esforço não é conhecido) YT(y)/R(y) = esforço relativo no ano y 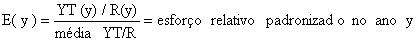 | |||||
Esforço relativo
Antes de discutirmos sobre a padronização das unidades de esforço devemos observar que:
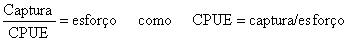 como CPUE = captura/esforço
como CPUE = captura/esforço
A seguir usaremos esta relação, não para capturas e esforços, mas para quantidades proporcionais às capturas, esforços e CPUE, de modo que o resultado final é uma medida proporcional ao esforço. Portanto, é chamada de “esforço relativo”. Também se assume que todas as unidades de esforço definidas são adequadas.
Exemplo 32: Combinação de esforço para diferentes unidades de esforço
No exemplo dado na Tabela 9.6.1 consideramos o esforço de quatro artes medidas em número de unidades por ano. Conforme pode ser visto, as unidades de esforço originais não são compatíveis. Capturas correspondentes ao esforço encontram-se também disponíveis através de um esquema de amostragem. As quatro artes mostradas na tabela representam apenas um décimo da captura total do manancial em questão. Para tornar as diferentes artes (unidades de esforço) compatíveis, cada unidade tem que ser transformada em CPUE, a qual por sua vez é convertida em “CPUE relativa” como pode ser visto na tabela. A captura relativa por unidade de esforço da arte i para o ano y é definida como:
 | (9.6.1) |
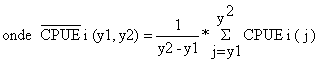 |
quando se considera um período de tempo de y1, y1+1,…,y2. (Na Tabela 9.6.1, y1 = 1971 e y2 = 1975).
Como a CPUE relativa de uma arte é adimensional, pode-se considerar que obtém-se unidades de CPUE compatíveis convertendo-as na CPUE relativa. As CPUEs relativas podem ser somadas.
No caso hipotético em que todas as observações da CPUE foram proporcionais ao tamanho da população (ver Secção 4.3) as CPUE's relativas seriam idênticas para todas as artes de pesca.
No entanto, na realidade alguns artes são menos importantes que as outras. A rede de cerco na Tabela 9.6.1 é a arte dominante no que se refere ao desenvolvimento da captura, enquanto a pescaria de linha e anzol é menos importante em termos de capturas. Isto é levado em conta quando calculamos a soma das CPUEs relativas ponderadas pelas correspondentes capturas. Por exemplo, para o ano de 1971 (ver Tabela 9.6.1):
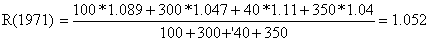
Dividindo a captura total das espécies consideradas, YT(y), incluindo também as capturas que não foram cobertas no plano de amostragem das capturas e esforços, pela soma ponderada das CPUEs relativas obtém-se valores proporcionais ao esforço total, R(y), mostrados na coluna “YT(y)/R(y)” da Tabela 9.6.1. A última coluna mostra o esforço relativo padronizado E(y). (Este conceito é apresentado para evitar que se confunda esforço relativo com esforço absoluto).
Tabela 9.6.2 Exploração do conceito de esforço relativo pradronizado para a combinação das várias artes (cf. Tabela 9.6.1)
| Da Tabela 9.6.1 | Se as capturas de cerco fossem apenas 10% daquelas mostradas na Tabela 9.6.1 | |
| ano | E(y) | E(y) |
| 1971 | 0.653 | 1.014 |
| 1972 | 0.734 | 1.018 |
| 1973 | 0.903 | 1.035 |
| 1974 | 1.146 | 0.984 |
| 1975 | 1.564 | 0.949 |
A primeira arte da Tabela 9.6.1, a rede de cerco, é a mais importante, uma vez que a tendência demonstrada na captura desta é a mesma que a do esforço relativo padronizado. O cerco para a praia mostra uma tendência oposta, mas por ser um tipo de arte de importância relativamente menor, tem menos influência sobre o esforço combinado. Se as capturas da rede de cerco fossem apenas 10% do que são, a tendência poderia mudar já que o cerco para a praia tornar-se-ia então o tipo de arte mais importante. Os valores de E(y) teriam então a mesma tendência da captura do cerco para a praia (Tabela 9.6.2).
O método acima descrito tem sido utilizado pelo Grupo de Trabalho do “Round Fish” do Mar do Norte (ICES, 1980). Este método não requer uma comparação directa dos diferentes tipos de barcos, necessita apenas do tipo de dados que normalmente se encontram disponíveis. O método pode ser questionado, e na realidade, os resultados alcançados pelo grupo de trabalho do ICES não foram absolutamente convincentes quando o grupo de trabalho correlacionou os dados do esforço relativo padronizado com os valores da mortalidade por pesca obtidos da Análise de População Virtual (VPA).
Poder de pesca relativo
Um método mais directo (e provavelmente mais confiável) para padronizar o esforço é o de Robson (1966) (o qual é discutido em Gulland, 1983). Este método, contudo, requer dados adicionais. Nele utiliza-se o conceito de “poder de pesca relativo” e é definido como o poder de pesca do barco B em relacão ao barco A sendo:
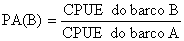 | (9.6.2) |
quando os dois barcos estiverem a pescar sob as mesmas condições (isto é, na mesma área de pesca e no mesmo período de tempo). O barco A denomina-se geralmente de “barco padrão”.
Suponha que os barcos que participam numa determinada pescaria podem ser agrupados em vários grupos homogéneos, de modo a que cada grupo é constituído por barcos com o mesmo poder de pesca. Suponha também que a CPUE é expressa em unidades de captura por unidade de tempo (por exemplo, captura por hora de arrasto), e que foram recolhidos os seguintes dados:
| Tipo de Barco | A (padrão) | B | C | D | E |
| Poder de pesca (PA) | 1.0 | PA(B) | PA(C) | PA(D) | PA(E) |
| Número de barcos (N) | NA | NB | NC | ND | NE |
| Número médio de dias | |||||
| de pesca/barco (d) | dA | dB | dC | dD | dE |
O esforço total seria então estimado por:
esforço total =
1.0*NA*dA + PA(B)*NB*dB + PA(C)*NC*dC + PA(D)*ND*dD + PA(E)*NE*dE (9.6.3)
Em certos casos pode-se considerar que o poder de pesca é proporcional a algumas características dos barcos ou das artes, que sejam relativamente fáceis de se obter, tais como, TAB (tonelagem de arqueação bruta) ou HP (potência do motor principal da embarcação), ou o seu produto para barcos de arrasto e, por exemplo, o número ou o comprimento das redes no caso de pescarias com redes de emalhar. Como geralmente o que interessa é o esforço relativo, os PA's na Eq. 9.6.3 podem simplesmente ser substituidos pelas características do barco/artes.
Um grupo de modelos que tentam assumir um compromisso entre os modelos de produção geral e os modelos estruturais de idades foram apresentados por, Deriso (1980), Ludwig e Walters (1985), Ludwig (1987) e Schnute (1985, 1987). Estes modelos, todavia, têm um uso restrito pois foram desenvolvidos para espécies de ciclo de vida longo (de crescimento lento), as quais não sofrem exploração na fase inicial do seu ciclo de vida. Eles são baseados em várias condições, que necessitam de serem satisfeitas de modo restrito, o que os tornam de difícil aplicação para determiadas espécies. Schnute (1985) afirma sobre estes modelos que: “Entre outras coisas, reflectem a inegável realidade de que a população consiste em várias coortes, que a cada ano que passa, tornam-se um ano mais velhas”. Isto mostra claramente que estes modelos não são aplicáveis a mananciais para os quais esta “realidade” pode ser negada, por exemplo, camarões. De facto, estes métodos fornecem resultados absurdos para tais espécies (por exemplo, biomassa negativa).
A base biológica teórica destes modelos é a mesma dos modelos já apresentados (o raciocínio é similar ao da análise de coortes de Pope), mas a teoria matemática apliciada para a obtenção das estimações é mais sofisticada do que para a maioria dos modelos apresentados neste manual. A principal diferença dos modelos estruturais de idades demonstrados neste manual é que a equação de Ford-Walford substitui a de von Bertalanffy para o crescimento em peso (Eq. 3.1.2.1).
Os modelos são altamente sofisticados e não são tão simples de aplicar. A sua descrição em uma linguagem não matemática necessitaria dum capítulo bastante extenso. Para o leitor interessado recomenda-se consultar os trabalhos de Deriso, Schnute e outros acima citados.