Até agora, os modelos e métodos descritos foram aplicados a um único manancial, explorado por uma única frota, contudo, esta situação é mais uma excepção do que uma regra. Na maioria dos casos uma frota explora vários mananciais e várias frotas competem na exploração dos mesmos recursos. Neste contexto, consideraremos três tipos principais de interacção entre componentes de um sistema multiespécie / várias frotas:
Interacção biológica significa interacção entre e dentro dos mananciais de peixes causada por predação e competição por alimento.
Interacção económica significa a competição entre frotas, por exemplo, entre pesca industrial e pesca artesanal. Quanto mais uma frota capturar de um recurso limitado, menos restará para os seus competidores.
Interacção técnica significa que a pescaria num manancial produz mortalidade por pesca sobre outros mananciais, quer seja porque se trata de pescarias multiespecíficas quer seja por causa da captura das espécies acompanhantes.
Este capítulo apresenta uma breve discussão de alguns aspectos dos três tipos de interacção acima mencionados, no entanto não se pretende explicar os modelos a um nível que permita ao leitor aplicá-los na prática, pois muitos aspectos dos modelos não estão ainda suficientemente estudados nem bem compreendidos. Portanto, a maioria dos mananciais de peixes de águas temperadas também são ainda avaliados por meio de modelos uniespecíficos.
Durante a última década foram sugeridos várias análises aos modelos, levando-se em consideração as interacções mencionadas. Estes modelos, na sua maioria, são extensões dos modelos “uma espécie/uma frota” apresentados nos capítulos precedentes, de modo que a teoria dos sistemas simples fornece os fundamentos necessários para a teoria multiespécies / várias frotas. A avaliação de multiespécies / várias frotas com referência especial a mananciais de peixes tropicais está revista em FAO (1978), Pope (1979, 1980), Saila e Roedel (1980) e Pauly e Murphy (1982).
A maneira mais simples de se lidar com um sistema multiespécies / várias frotas é aplicar os modelos de produção geral (ver Capítulo 9) à captura total de todas as espécies e ao esforço total de todas as frotas. A Fig. 10.1.1 mostra um gráfico da produção total das pescarias de arrasto no Golfo da Tailândia contra o esforço total (de Pauly, 1984, segundo SCSP, 1978). Aplicando, por exemplo, o modelo de Schaefer (Eqs. 9.1.2 e 9.1.5) às capturas de todas as espécies capturadas por todas as frotas forneceria um MSY total estimado para a área considerada. Esta aproximação, no entanto, combina tantas interacções complexas num modelo tão simples que a sua aplicabilidade geral pode ser questionada. Por exemplo, os modelos de produção geral presupõem que a curva é reversível, o que não pode ser verdadeiro se cada manancial seguir o modelo de Schaefer. Este aspecto é ilustrado na Fig. 10.1.2, que mostra uma pescaria hipotética de três espécies. Depois do nível do esforço F1 (ver figura) a espécie A estará erradicada, e depois do nível do esforço F2 a espécie B desaparece. Assim, ao se retroceder no esforço a partir do nível F3, e de acordo com o modelo de Schaefer, seria ao longo da curva para a espécie C. Além disso, na suposição de que cada manancial se adapta ao modelo de Schaefer, a captura total de todos os mananciais pode não ser uma parábola. A parte descendente da curva de captura total assemelha-se mais com uma curva exponencial decrescente, como ilustrado na Fig. 10.1.2.
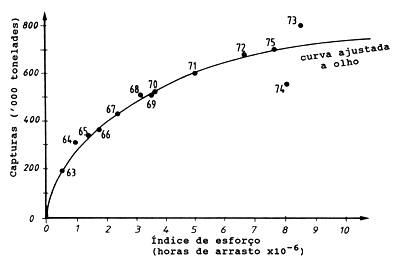
Fig. 10.1.1 Captura e esforço, da pesca de arrasto no Golfo da Tailândia (de Pauly, 1984. Dados de SCSP, 1978)
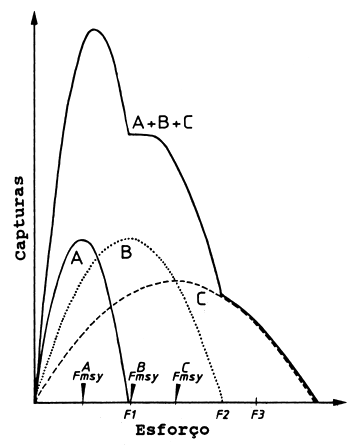
Fig. 10.1.2 Ilustração das alterações das capturas num sistema de três espécies segundo o modelo simples de Schaefer
Na prática, no entanto, muitas vezes observa-se um quadro diferente, como na Fig. 10.1.1, em que um aumento regular do esforço não produz uma queda da captura total de todas as espécies combinadas. A curva parece ter uma contínua tendência crescente e provavelmente terminaria num nível elevado de esforço. No entanto, ainda é difícil encontrar actualmente exemplos de um colapso na captura total de todas as espécies demersais em pescarias tropicais. Para uma pescaria demersal multiespecífica esperamos as seguintes alterações, juntamente com o aumento do esforço (Pauly, 1984) :
Um decréscimo (talvez extinção) dos peixes maiores, mais velhos, de crescimento lento e fáceis de capturar
Um decréscimo no tamanho médio dos peixes capturados
Um aumento na contribuição relativa de peixes de pequeno porte e de baixo valor. A remoção dos grandes predadores das espécies comerciais resulta numa redução da mortalidade natural
Um aumento de componentes do sistema, antes insignificantes (por ex., lulas, medusas), o que é também explicado pela remoção de predadores e competidores por alimento.
Assim, não é de esperar uma interpretação simples dos resultados do simples modelo de produção geral aplicado a uma pescaria multiespecífica. Uma discussão mais completa destes aspectos pode ser encontrada em Caddy (1980), Marten e Polovina (1982), Ursin (1982) e Pauly (1984). No entanto, pode-se ampliar os modelos de produção geral, de modo que a interacção entre as espécies seja explicitamente levada em conta no modelo, como será discutido na próxima secção.
Diversos autores têm utilizado, com relativo sucesso, modelos de avaliação uniespecíficos para abranger interacções biológicas entre espécies, introduzindo-se termos para a predação mútua e a competição por alimento. O mais prometedor destes modelos é, provavelmente, a “VPA (Análise de População Virtual) multiespecífica” (Helgason e Gislason, 1979; Gislason e Helgason, 1985; Pope, 1979a; ICES, 1984, 1986, 1987 e Gislason e Sparre, 1987). Consiste essencialmente, em várias VPAs paralelas, uma para cada manancial na área considerada. A segunda das duas equações da VPA (Eqs. 5.1.5 e 5.1.6):
C = F*N (número capturado) e D = M*N (número de mortes naturais) é
ampliada em:
D = (M1 + M2) *N
onde M2 é a “mortalidade por predação” e M1 a “mortalidade natural residual” (isto é, a mortalidade natural causada por doenças, fome, velhice, etc.). Mortalidade por predação para a espécie-presa i, M2 (i) é, em princípio, obtida da seguinte expressão (Andersen e Ursin, 1977):
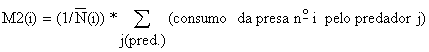
enquanto M1 tem que ser um valor assumido, como acontece com a mortalidade natural total, M, na VPA comum (ver Secção 5.1).
Além dos dados de captura, a VPA multiespecífica exige dados de conteúdos estomacais e dados sobre necessidades alimentares (a partir de experiências de alimentação). O consumo de presas por predadores é estimado a partir de dados de conteúdos estomacais dos predadores (Sparre, 1980 e Gislason e Sparre, 1987). A VPA multiespecífica foi testada no ICES, para o Mar do Norte, pela primeira vez em 1984 (ICES, 1984; Sparre, 1984; Gislason e Sparre, 1987), mas até agora ainda não foi empregada como base para a gestão das pescarias.
Pope (1980a) desenvolveu uma versão da VPA multespecífica com base em dados de comprimento. Este método é uma extensão da análise de coortes baseada em comprimentos, de Jones, para a análise de coortes multiespecíficas baseada em comprimentos.
Pope (1979, 1980) também estendeu o modelo de produção geral (o modelo de Schaefer) ao caso multiespecífico, introduzindo parâmetros de interacção biológica. Para uma situação de duas espécies, o modelo de Pope mostra (cf. com a Eq. 9.1.2):
| presa | : | Y1/f1 = a1 + b1*f1 + c1*f2 |
| predador | : | Y2/f2 = a2 + b2*f2 - c2*f1 |
Se os parâmetros da interacção, c1 e c2, tiverem valor zero, obtemos dois modelos de Schaefer independentes. Quando os parâmetros da interacção são positivos (c1 > 0 e c2 > 0), podemos interpretar o modelo de duas espécies como um sistema predador-presa, uma vez que o termo de interacção c1*f2 produz uma captura mais elevada da espécie-presa quando se aumenta o esforço sobre o predador, isto é, quando os predadores são removidos. O termo de interacção para o predador c2*f1, tem um efeito oposto. Se o esforço sobre a presa for aumentado, falta alimento para o predador e o manancial torna-se assim menos productivo, resultando uma redução nas capturas do manancial predador.
A interacção económica de várias frotas já foi introduzida com o modelo de Thompson e Bell, baseado em idades (Secção 8.6), para o qual o leitor é remetido. A interacção económica também pode ser descrita pelo modelo de Beverton e Holt de captura por recruta (Beverton e Holt, 1957), mas não será discutido neste caso.
Nas pescarias a captura consiste de uma mistura de diferentes espécies. Pauly (1984, p. 161) fornece uma tabela mostrando uma captura de arrasto típica do Mar de Java, contendo mais de 55 espécies distribuídas em 29 diferentes famílias. No entanto, as 10 espécies mais abundantes no arrasto constituíram 70% da captura, e a espécie mais abundante constituiu 32% da captura em peso. Desprezando as espécies raras, geralmente ocorrem 5 a 15 espécies de maior importância, do ponto de vista comercial e/ou ecológico.
Para ilustrar o problema consideramos um sistema simples de duas espécies, A e B, sendo A uma espécie de grande porte, crescimento lento e baixa mortalidade natural, e B uma espécie de pequeno porte, crescimento rápido e alta mortalidade natural. A forma típica da curva Y/R para espécies com as características de A e B são mostradas na Fig. 10.4.1.1. Se A for a espécie alvo da pescaria e se B for a (inevitável) espécie acompanhante então a curva Y/R para a espécie B terá pequena aplicabilidade prática. As medidas de gestão têm de ser direccionadas para a pescaria da espécie alvo, A. Se houver uma relação simples entre a mortalidade por pesca das duas espécies, por exemplo, linear:
F(A) = K*F(B)
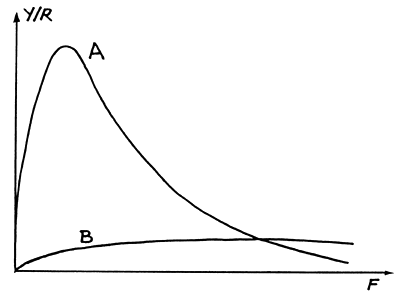
Fig. 10.4.1.1 A: Curva Y/R para uma espécie de grande porte e
crescimento lento, com baixa mortalidade natural
B: Curva Y/R para uma espécie de pequeno porte e
crescimento rápido com alta mortalidade natural
onde F(A) e F(B) são as mortalidades por pesca sobre as espécies A e B, respectivamente, e k é uma constante, os efeitos de várias estratégias de pesca sobre a espécie A podem ser facilmente convertidos para a espécie B.
Duas curvas de Y/R não podem ser adicionadas, pois têm diferentes unidades (captura “por recruta de A” é diferente da captura “por recruta de B”).
Se as estimações do recrutamento estiverem disponíveis, podemos transformar as curvas Y/R para unidades comparáveis (Sparre, 1980; Murawski, 1984). Por exemplo, se o número de recrutas da espécie A for, em média, 0.001 vezes ao da espécie B, podemos expressar a captura para a espécie A em “por recruta” e a captura para a espécie B em “por 1000 recrutas” e então, poderemos adicionar as duas curvas. Contudo, se os preços por kg das duas espécies forem diferentes, fará mais sentido, do ponto de vista da gestão, multiplicar pelo preço antes de adicionar as curvas. Se a espécie A for predadora da espécie B, a situação torna-se mais complicada, e uma adição simples das curvas de captura pode levar a conclusões erróneas (Sparre, 1979). Neste caso, seria mais adequado utilizar-se a VPA multiespecífica (Sparre, 1980).
Munro (1983) desenvolveu uma aproximação alternativa que exige menor quantidade de dados do que a VPA multiespecífica. O modelo representa, provavelmente, a maneira mais simples de extensão do modelo de Beverton e Holt, levando em consideração a interacção entre espécies. Murawski (1984) desenvolveu uma extensão da análise de Y/R de Beverton e Holt em que leva em consideração a interacção técnica numa pescaria mista.
Suponhamos que um certo tipo de arte de pesca comercial captura uma mistura de três espécies importantes, chamadas A, B e C. Uma rede de arrasto pode capturar até 50 diferentes espécies, dentro das quais três constituem a maior parte da captura, mas nenhuma destas pode ser considerada como a espécie alvo.
Assim, a captura consiste de uma mistura de espécies, a qual não é determinada pelas operações de pesca, mas pela disponibilidade dos peixes. As espécies em questão habitam as mesmas áreas de pesca e são capturadas em conjunto. Supõe-se que existem dados sobre a distribuição de comprimentos das três espécies principais e também que os preços por kg diferem entre as espécies e entre categorias de tamanho de cada espécie.
Neste caso, não se pode tratar cada espécie separadamente e, somar os resultados obtidos em termos de captura. Antes de somar as capturas devem ser convertidas para unidades de rendimento. Uma pescaria pode, por exemplo, capturar camarão como espécie alvo e lula como espécie acompanhante. Para os pescadores a captura de camarão é muito mais importante do que a de lula. Além disso, mesmo que a captura seja convertida em rendimento, ainda não é possível adicionar os resultados de avaliações para uma única espécie tal como as análises de Thompson e Bell baseadas em comprimentos. Como consequência, o nível de esforço que fornece o rendimento máximo económico (MSE) para a espécie A não é o mesmo para as espécies B e C.
A aproximação sugerida abaixo combina todas as espécies na estimação de MSE. Esta avaliação de uma pescaria mista baseada na distribuição de comprimentos funciona do seguinte modo:
| Passo 1: | Aplicar a análise de coortes para comprimentos a cada espécie separadamente, fornecendo assim, estimações do actual sistema de pesca para cada espécie, por exemplo, se o comprimento da espécie A varia de 5 a 25 cm, o padrão F terá a seguinte notação: |
FA (5,6), FA(6,7), FA(7,8),.....,FA (25, ∞). | |
| Assim, a espécie A é medida em classes de 1 cm. Se o comprimento da espécie B variar de 15 a 100 cm e for medida em classes de 5 cm, o sistema de pesca estimado pela análise de coortes terá a seguinte notação: | |
FB(15,20), FB(20,25), FB(25,30),....., FB(100, ∞) | |
| e os resultados para a espécie C podem ser: | |
FC(10,12), FC(12,14), FC(14,16),....., FC(50,∞). | |
| Para cada espécie obtemos ainda as frequências na primeira classe de comprimento (o número de recrutas) a partir da análise de coortes para comprimento. | |
| Passo 2: | Realizar três análises da captura com base nos comprimentos, segundo o modelo de Thompson e Bell, para as três espécies, como ilustrado pela Tabela 8.7.4. Usar o mesmo factor-F para cada um dos três sistemas de pesca em cada estimação e somar os valores da captura das três espécies. Os resultados desse exercício formam uma tabela semelhante à Tabela 8.7.4, a qual contém a captura, biomassa e rendimento para cada espécie, juntamente com a soma dos valores. |
| Pode-se, por exemplo, calcular 16 estimações como na Tabela 8.7.4, segundo a metodologia desenvolvida na Tabela 8.7.3 com as premissas sobre os padrões de pesca seguintes: | |
Primeira estimação: | |
0,0,............................................................................0 0,0,............................................................................0 0,0,............................................................................0 | |
Segunda estimação: | |
0.2*FA(5,6), 0.2*FA(6,7),.........,0.2*FA(25,∞) 0.2*FB(15,20), 0.2*FB(20,25),.......,0.2*FB(100,∞) 0.2*FC(10,12), 0.2*FC(12,14),.......,0.2*FC(50,∞) | |
Terceira estimação: | |
0.4*FA(5,6), 0.4*FA(6,7),.........,0.4*FA(25,∞) 0.4*FB(15,20), 0.4*FB(20,25),.......,0.4*FB(100,∞) 0.4*FC(10,12), 0.4*FC(12,14),.......,0.4*FC(50,∞) | |
.......................................... .......................................... | |
Décima-sexta estimação: | |
3.0*FA(5,6), 3.0*FA(6,7),.........,3.0*FA(25,∞) 3.0*FB(15,20), 3.0*FB(20,25),.......,3.0*FB(100,∞) 3.0*FC(10,12), 3.0*FC(12,14),.......,3.0*FC(50,∞) | |
| Passo 3: | Usar a soma dos valores para determinar o nível óptimo de esforço. A suposição básica é que quando se aumenta a mortalidade por pesca sobre a espécie A em, digamos, 20%, a mortalidade por pesca sobre as espécies B e C será automaticamente aumentada também em 20%. |
Esta aproximação pode ser usada, por exemplo, para avaliar o efeito combinado de alterações do tamanho da malha. Se as ogivas de selectividade forem determinadas para cada espécie, pode-se empregar a curva logística (ver Secção 6.1) para determinar o padrão de pesca. Portanto, os sistemas de pesca para as três espécies são determinados para os comprimentos de 50% e 75% de retenção, e a mortalidade por pesca, Fm, para as classes de tamanho totalmente exploradas (ver Fig. 6.1.1.4) é multiplicada pelo factor-F, X. O efeito de um aumento de 20% na largura da malha é estimado calculando-se três novos padrões de pesca, através dos parâmetros:
Espécie A: 1.2*L50%A, 1.2*L75%A, X*FmA
Espécie B: 1.2*L50%B, 1.2*L75%B, X*FmB
Espécie C: 1.2*L50%C, 1.2*L75%C, X*FmC
e então empregar a análise de Thompson e Bell com base em comprimentos para uma faixa apropriada de valores de factor-F (X), possibilitando a determinação do nível de F para MSE.
Programas de computador
A metodologia acima sugerida envolve um grande número de cálculos, recomendando-se o uso de um computador. O pacote LFSA contém o programa “MIXFISH”, que pode realizar a avaliação de uma pescaria mista. O programa executa a análise de Thompson e Bell baseada em comprimentos, para uma única espécie, bem como para as três espécies em conjunto, e calcula o MSE em cada caso, usando técnicas de iteracção. Um programa similar foi incorporado também ao FiSAT.
Na Secção 8.6 discutiu-se o caso de duas frotas competidoras (interacção económica) e na Secção 10.4.2 discutiu-se o caso onde um tipo de barco capturava várias espécies (interacção técnica ou pescaria mista). A maioria das pescarias apresenta aspectos de interacção económica e de interacção técnica, bem como de interação biológica (Secção 10.2). Nesta secção ignorase a interacção biológica e considera-se somente a combinação das interações económicas e técnicas.
A tabela 10.4.3.1 mostra um exemplo de dados de entrada para uma pescaria mista com várias frotas. São consideradas sete diferentes espécies pelágicas e quatro diferentes artes (frotas), assumindo-se que somente essas quatro artes (frotas) exploram os sete mananciais. Os dados inciais são o número de indivíduos capturados por classe de comprimento (ou grupo de idade):
| c(y,s,g,i) = | número de peixes na classe de comprimento (ou grupo de idade) i da espécie s, capturados pela arte (frota) g durante operíodo de tempo y | |
| s = 1,2,…,7 | g = a,b,c,d | |
| i = 1,2,…,n(s) | y = y1,y1+1,…,y2 | |
Tabela 10.4.3.1 Exemplo de dados iniciais para pescarias mistas de multifrota para um único período de tempo (por ex., um ano). C(s,g,i) = número de classes de comprimento i, peixes da especie s, capturados pela arte g. s = 1,2,…,7; g = a,b,c,d; * = soma de toda as artes i = 1,2,…,n(s)
| s | g arte (frota) | a | b | c | d | captura total (entrada VPA) | |
| rede emalhar | palangre | rede de cerco | linha e anzol | ||||
| espécie | |||||||
| 1 | Albacora | c(1,a,i) | c(1,b,i) | c(1,c,i) | c(1,d,i) | c(1,*,i) | |
| 2 | Gaiado | c(2,a,i) | c(2,b,i) | c(2,c,i) | c(2,d,i) | c(2,*,i) | |
| 3 | Merma-oriental | c(3,a,i) | c(3,b,i) | c(3,c,i) | c(3,d,i) | c(3,*,i) | |
| 4 | Judeu-liso | c(4,a,i) | c(4,b,i) | c(4,c,i) | c(4,d,i) | c(4,*,i) | |
| 5 | Serra | c(5,a,i) | c(5,b,i) | c(5,c,i) | c(5,d,i) | c(5,*,i) | |
| 6 | Agulhão-negro | c(6,a,i) | c(6,b,i) | c(6,c,i) | c(6,d,i) | c(6,*,i) | |
| 7 | Velerio | c(7,a,i) | c(7,b,i) | c(7,c,i) | c(7,d,i) | c(7,*,i) | |
Tabela 10.4.3.2 Resultados das sete análises de coortes baseadas em comprimentos individuais
| s | espécie | população (número) | mortalidade por pesca |
| 1 | Albacora | N(1) | F(1) |
| 2 | Gaiado | N(2) | F(2) |
| 3 | Merma-oriental | N(3) | F(3) |
| 4 | Judeu-liso | N(4) | F(4) |
| 5 | Serra | N(5) | F(5) |
| 6 | Agulhão-negro | N(6) | F(6) |
| 7 | Veleiro | N(7) | F(7) |
A Tabela 10.4.3.1 na realidade mostra somente uma pequena fracção dos dados, isto é, apenas uma série temporal, e cada índice i simboliza toda uma distribuição de comprimentos com i = 1,2,…,n(s) observações, onde n(s) é o número de classes de comprimento na gama de tamanhos da espécie s. A coluna mais à direita da tabela contém o número total capturado:
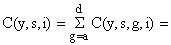 | número de peixes na classe de comprimento (ou grupo de idade) i da espécie s, capturados por todas as artes (frotas) durante o período de tempo y. |
Estes números por classe de comprimento (ou idade) e por período de tempo formam os dados iniciais para a análise de coortes ou VPAs para cada espécie.
Suponha agora que estamos a trabalhar com classes de comprimento e realizamos a análise de coortes de Jones, para comprimentos, utilizando o número médio de peixes capturados num período de tempo de vários anos, e estimamos o número médio na população e a mortalidade global por pesca para cada espécie. Os resultados das sete análises deste exemplo podem ser resumidos conforme o esquema da Tabela 10.4.3.2.
Cada entrada na Tabela 10.4.3.2 representa uma matriz (vector) :
N(s) = (N(s,1), N(s,2),…,N(s,n(s))
F(s) = (F(s,1), F(s,2),…,F(s,n(s))
onde cada elemento do vector corresponde a uma classe de comprimento. Cada valor de F de uma classe origina-se da mortalidade por pesca combinada e gerada por todas as quatro artes (frotas). O F total para cada uma das classes pode ser redistribuido nas quatro artes (frotas) usando-se:
F(s,g,i) = F(s,i) * C(s,g,i)/C(s,i)
Tabela 10.4.3.3 Mortalidades por pesca repartidas entre as artes (frotas) estimadas pela análise de coortes, e números capturados por cada arte de pesca
| s | g frota (arte) | a | b | c | d | mortalidade por pesca | |
| rede de emalhar | palangre | rede de cerco | linha e anzol | ||||
| espécie | |||||||
| 1 | Albacora | F(1,a) | F(1,b) | F(1,c) | F(1,d) | F(1,*) | |
| 2 | Gaiado | F(2,a) | F(2,b) | F(2,c) | F(2,d) | F(2,*) | |
| 3 | Merma-oriental | F(3,a) | F(3,b) | F(3,c) | F(3,d) | F(3,*) | |
| 4 | Judeu-liso | F(4,a) | F(4,b) | F(4,c) | F(4,d) | F(4,*) | |
| 5 | Serra | F(5,a) | F(5,b) | F(5,c) | F(5,d) | F(5,*) | |
| 6 | Agulhão-negro | F(6,a) | F(6,b) | F(6,c) | F(6,d) | F(6,*) | |
| 7 | Veleiro | F(7,a) | F(7,b) | F(7,c) | F(7,d) | F(7,*) | |
A Tabela 10.4.3.3 exemplifica o processo de subdivisão da mortalidade total por pesca, em mortalidades por pesca, por arte (ou frota). O tipo de dados apresentados nesta tabela, juntamente com o número do manacial estimado (Tabela 10.4.3.2), formam a entrada de dados necessários para a “estimação das capturas das pescarias mistas, de Thompson e Bell, baseadas em comprimentos”. O primeiro passo é fazer suposições sobre o valor da matriz-F para cada arte (frota), como discutido na Secção 10.4.2. Por exemplo, na hipótese de um aumento de 10% na pescaria de rede de emalhar, todas as matrizes na coluna “rede de emalhar” devem ser multiplicadas por 1.1. Outras suposições podem ser feitas para as outras artes de pesca.
O segundo passo é somar as mortalidades por pesca para cada espécie. O terceiro passo é fazer uma suposição da captura com base no modelo de Thompson e Bell, para cada manacial. O quarto passo é distribuir as capturas por classes de comprimento entre as frotas e converter quantidades em valores económicos. Finalmente, os rendimentos das capturas de diferentes espécies são somados para cada frota e para o total da pescaria das várias frotas.
Programas de computador
O pacote BEAM 4 para microcomputadores (Modelo Bio-Económico Analítico № Quatro, Sparre e Willmann, 1992) consiste de dois sub-modelos. O sub-modelo biológico/técnico do BEAM 4 é a versão do modelo de Thompson e Bell baseada em idades para pescarias mistas com várias frotas. Embora o BEAM 4 seja baseado em composição por idades, contém opções para converter dados de composição por comprimentos ou categorias de tamanhos comerciais em dados de composição por idades.
O modelo BEAM 4 dispõe também de opções para considerar a migração dos peixes e frotas entre áreas geográficas. O sub-modelo económico do BEAM 4 faz a ligação entre a análise de Thompson e Bell com uma análise de custos e receitas do sector das capturas e do sector do processamento de uma pescaria.