Vários dos métodos apresentados até agora mostram-se, muitas vezes, insuficientes quando aplicados a mananciais que migram ou que formam cardumes. Todos os métodos foram baseados na suposição de que se pode tomar amostras aleatórias representativas do manancial como por exemplo, toda a amplitude de frequências de comprimento. Quando os mananciais não estão vulneráveis à pesca, devido a migrações horizontais ou verticais para áreas não cobertas pela frota ou artes de pesca durante partes do seu ciclo de vida, geralmente não é possível amostrar tais mananciais durante esses períodos. Isto pode, no mínimo, conduzir a lacunas nas amostras por períodos curtos ou longos, mas também é possível que as amostras obtidas representem diferentes partes do manancial e, em tais casos, levem a conclusões erróneas sobre os mesmos. Em particular, os métodos baseados em comprimentos, tais como a análise de progressão modal e a análise da curva de captura, são difíceis de aplicar no caso de mananciais de peixes migratórios.
As migrações dos mananciais de peixes, que têm sido objecto de pescarias por séculos e de estudos científicos por vários anos, (o arenque do Mar do Norte, por exemplo), são suficientemente conhecidas para evitar erros na amostragem e má interpretação dos resultados. O conhecimento geral da maioria dos mananciais de peixes tropicais, no entanto, é frequentemente limitado e, portanto, facilmente ocorrem erros de amostragem.
Neste capítulo serão abordados alguns problemas relacionados com a migração, e serão apresentados alguns métodos que podem ajudar na interpretação de dados de frequências de comprimento de mananciais migratórios. Estes métodos devem ser considerados apenas como uma primeira aproximação para resolver problemas complexos.
Harden Jones (1968) identificou três tipos de “movimentos migratórios”: deriva com as correntes, movimentos locomotores aleatórios e movimentos locomotores orientados. Num trabalho posterior Harden Jones (1984) declara: “Eu emprego a palavra migração para descrever deslocamentos regulares em função das estações”. Gerking (1953) definiu o conceito de “retorno ao local de origem” como “o retorno para um local previamente ocupado, em vez de migração para outros locais igualmente prováveis”. O retorno ao local de origem é reconhecido como um importante aspecto da migração de muitos mananciais de peixes.
Do ponto de vista da avaliação, a explicação dos motivos pelos quais os peixes migram é de pequena importância. O que realmente interessa é, saber onde os peixes se encontram em certas épocas do ano.
Neste manual a migração será considerada, basicamente, como uma fonte de erro. Migração é definida aqui como “um tipo sistemático de movimentos de indivíduos pertencentes a um manancial” (a definição de erro é dada na Secção 7.1). Movimentos aleatórios não são considerados migrações no actual contexto porque estamos interessados apenas nos tipos de migração que produzem erros para um programa de amostragem de frequências de comprimento. Se os peixes se movem ao acaso, o movimento não modificará a probabilidade relativa de serem amostrados, no entanto a distinção entre movimentos aleatórios e movimentos sistemáticos não é óbvia. Os peixes podem encontrar concentrações de alimento ao se moverem ao acaso e, também com movimentos ao acaso permanecerem no local até que o alimento seja quase todo consumido. Se os movimentos devido ao alimento forem sistemáticos (por ex., determinado por correntes ou outros factores sistemáticos oceanográficos), devemos considerar o movimento trófico acima descrito como uma migração, embora seja composto de deslocamentos aleatórios.
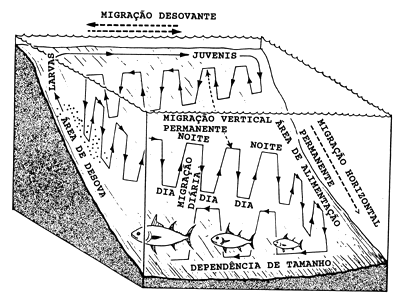
Fig. 11.1.1 Ilustração esquemática de cinco potenciais erros causados por migrações
Uma outra característica da migração é ser previsível, ou seja em alguns mananciais é possível prever onde e quando grandes concentrações de indivíduos podem ser encontradas.
Movimentos horizontais quer ao longo da costa, afastando-se da costa ou mesmo entre rios/lagoas e áreas marinhas, são as migrações que mais erros causam. Contudo, também as pequenas migrações verticais e diferenças, ao longo da coluna de água, na distribuição das classes de comprimentos (idades) da mesma espécie podem causar erros nos dados.
As migrações que geram erros podem ser classificadas em cinco principais tipos, dos quais alguns são ilustrados na Fig. 11.1.1.
| 1a. | Migração vertical diária (por ex., no fundo durante o dia e na coluna de água durante a noite). |
| 1b. | Migração horizontal diária (por ex., tem-se observado que o atum gaiado afasta-se e volta precisamente a um mesmo local em cada dia (Yuen, 1970). |
| 2. | Migração de desova (isto é, o retorno anual às áreas de desova seguido de um deslocamento para as áreas de alimentação ou, como no caso de alguns cefalópodes e camarões peneídeos, com apenas uma desova durante toda sua vida, migração para as áreas de desova seguida de morte. O retorno ao local de origem pode ser um importante aspecto deste tipo de migração). |
| 3. | Migração vertical de adultos dependente do tamanho, (por exemplo, os grupos de idade mais jovens do atum gaiado ocorrem em cardumes perto da superfície, enquanto os mais velhos migram para maiores profundidades). |
| 4. | Migração horizontal dependente do tamanho (isto é, os indivíduos maiores migram para águas mais profundas, enquanto realizam os movimentos acima mencionados). |
| 5. | Migrações dos jovens. Muitas vezes os jovens realizam migrações diferentes das dos adultos, podendo permanecer nas camadas superficiais dia e noite, enquanto os adultos ficam no fundo durante o dia. Podem também ocupar áreas de criação, onde não existem adultos. Para muitas espécies, um período numa área costeira ou de estuário é uma fase especial de sua vida (ver por exemplo, Blaber e Blaber, 1980). |
Um importante aspecto do complexo migração/erro, inerente principalmente à migração da desova, é a dependência do tamanho. Muitas vezes, cardumes com indivíduos maiores chegam primeiro à área de desova do que os indivíduos menores da mesma coorte. Além do problema do erro, existem outros motivos no qual a migração deve ser levada em conta em estudos de avaliação de mananciais. Um deles é a partilha do manancial entre vários países (ver Secção 4.1), conceito que fundamenta a definição da UNCLOS de espécies altamente migratórias.
As situações envolvidas na partilha de vários mananciais contêm problemas relacionados com a identificação dos mananciais e suas rotas de migração. A partilha de mananciais e a sua gestão estão discutidos em, por exemplo, Caddy (1982, 1987) e Caddy e Garcia (1986). Caddy (1982) classifica os recursos marinhos, com base nos seus movimentos relativos às ZEEs (Zonas Económicas Exclusivas), em cinco categorias:
Mananciais que se encontram quase totalmente numa única jurisdi-ção nacional.
Recursos não migratórios que se distribuem ao longo da fronteira entre zonas adjacentes, e que estão continuamente disponíveis em cada uma das zonas.
Espécies migratórias que se movimentam através de áreas de fronteira e disponíveis em cada zona apenas sazonalmente.
Mananciais do alto mar que estão disponíveis apenas ocasionalmente, ou parcialmente, dentro de zonas nacionais.
Mananciais de alto mar que ocorrem exclusivamente fora das ZEEs.
Especialmente para as categorias 3 e 4, a identificação dos mananciais é um pré-requisito para uma inteligente gestão, e a sua avaliação deve ser fundamentada no conhecimento das suas rotas migratórias.
Existem várias maneiras de se adquirir conhecimentos sobre as possíveis migrações da espécie em estudo. Uma delas, óbvia e barata, é aproveitar os conhecimentos dos pescadores que, certamente reconhecem as variações sazonais e diárias na disponibilidade das várias espécies alvos.
Tais flutuações podem também aparecer nos registos de desembarques dos vários tipos de barcos de pesca (estatística) e um conhecimento geral dos movimentos da frota. Ecosondas são extremamente úteis para a detecção de migrações verticais, enquanto equipamentos acústicos mais sofisticados podem ser usados para cartografar a distribuição e estimar a abundância, num tempo relativamente curto, principalmente de pequenos peixes pelágicos.
O método clássico de se estudar movimentos (e crescimento) de peixes e invertebrados é um programa de marcação. Marcas de identificação são fixadas externamente ou colocadas na cavidade corporal, o peixe é medido e libertado num local conhecido, de seguida oferecem-se recompensas para cada marca devolvida com informação sobre a data e local de captura. Tais programas de marcação, se bem sucedidos, podem fornecer muitas informações úteis sobre o deslocamento final entre os pontos de libertação e os de recaptura, mas não sobre o que aconteceu durante os intervalos entre esses momentos.
Marcas sofisticadas que utilizam as ondas de som e rádio possibilitam a observação contínua de um único indivíduo, sob o controlo de um navio de investigação. As últimas novidades incluem marcas que são libertadas num certo momento pré determinado, sobem à superfície e passam a transmitir para um satélite (aplicado no estudo das migrações dos atuns), e marcas que registam o rumo e o ângulo de inclinação dum peixe individual.
Na Secção 11.5 serão discutidos alguns aspectos dos programas de marcação.
Para ilustrar o problema, considere-se um manancial hipotético simplificado de peixes, como na Fig. 11.2.1. Este manacial passa metade do ano nas áreas de pesca e outra metade numa área onde não é explorado e que é também a sua área de criação. O manancial é composto de duas partes, A e B (pode-se considerar A como os peixes recrutados antes da monção e B como os recrutados depois da monção). As duas partes realizam as mesmas migrações mas em diferentes épocas do ano, como mostrado na Fig. 11.2.1. Suponhamos que a espécie tem uma esperança de vida de apenas dois anos e que as migrações ocorrem nos dias um de Janeiro e um de Julho e que existem amostras unicamente para as áreas de pesca.
Supondo-se ainda que não se conhece o padrão de migração, mas acredita-se, erroneamente, que todo o manancial está nas áreas de pesca durante todo o ano. Neste caso podem ocorrer sérias distorções na amostragem dos dados para estimar os parâmetros de crescimento porque dados importantes para a primeira metade do ano não estão disponíveis. Pode-se, assim, concluir erroneamente que a ausência de peixes pequenos é causada por selecção da arte de pesca. Podemos observar também um aparente crescimento negativo no período de Junho a Agosto se, supostamente, forem os mesmos peixes encontrados nesses meses, nas áreas de pesca. Em Junho, a parte A consiste de peixes com 1 e 2 anos de idade que, em Julho, serão substituídos por peixes da parte B com 0.5 e 1.5 ano de idade.
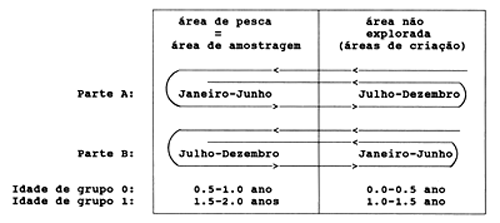
Fig. 11.2.1 Sistema hipotético simplificado para ilustrar os principais problemas na obtenção de amostras aleatórias de um manancial de peixes migratórios
Neste exemplo (não muito realista) provavelmente não haveria necessidade de amostrar a pescaria por muito tempo, para se conhecer a razão da ausência de dados sobre peixes pequenos e o aparente crescimento negativo. Na realidade, mananciais de peixes pelágicos apresentam comportamento migratório muito mais complexo, ocorrendo ainda o risco de se interpretar erroneamente os fenómenos causados pela migração. Um exemplo óbvio é confundir migração com mortalidade, por exemplo, se os peixes de um certo tamanho migrarem para águas mais profundas, onde não podem ser capturados pela pesca, a impressão obtida a partir das amostras é a de que os mesmos morreram.
O que normalmente ocorre é, que numa certa data e em certas áreas de pesca, as amostras podem ser tiradas somente de uma fracção do manancial, dependendo também da hora do dia e da arte utilizada. Esta secção é em parte baseada no trabalho de Sousa (1988), que discute fontes de erro na avaliação de mananciais de pequenos peixes pelágicos tomando a espécie Decapterus russelli, de Moçambique, como exemplo. O actual conhecimento sobre o comportamento migratório de peixes pelágicos em Moçambique é limitado, pois estes não têm sido objecto de experiências de marcação.
Sérias dificuldades, tais como crescimento negativo aparente, foram encontradas na utilização de análises de progressão modal em amostras de frequências de comprimento. A Fig. 11.2.2 mostra um exemplo duma série problemática de frequências de comprimento.
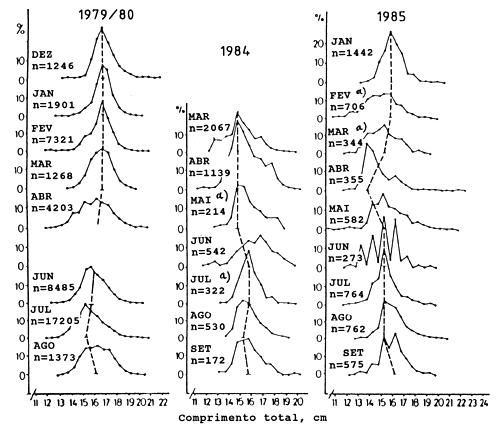
Fig. 11.2.2 Séries seleccionadas de frequências de comprimento de capturas comerciais de Decapterus russelli, banco de Sofala, Moçambique, ilustrando os problemas de interpretação da progressão modal (de Sousa, 1988)
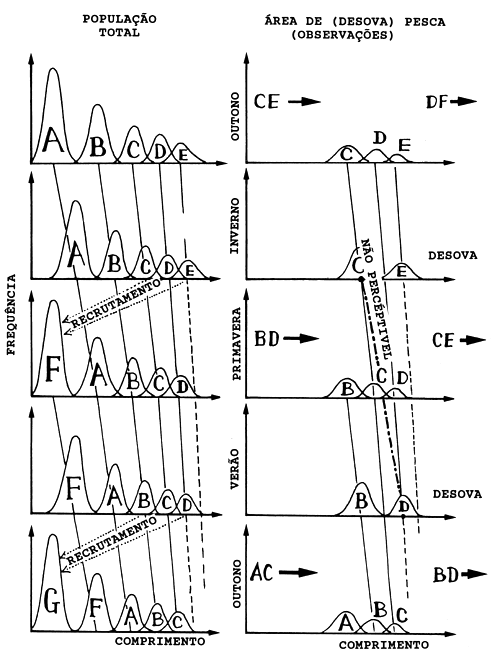
Fig. 11.2.3 Ilustração esquemática da hipótese de migração de pequenos pelágicos. Uma simplificação não realística é que as coortes não se sobrepõem. Para mais discussão ver o texto (de Sousa, 1988)
Na ausência de dados exactos sobre rotas migratórias, Sousa (1988) procurou nas séries temporais de frequências de comprimento as explicações plausíveis para algumas dessas anomalias. O primeiro passo foi sugerir hipóteses para o comportamento migratório e o seguinte, testar essas hipóteses com base nos dados disponíveis.
O raciocínio pressupõe a existência de padrões migratórios, ilustrados nas Figs. 11.1.1 e 11.2.3. A hipótese que fundamenta a Fig. 11.2.3 é:
Existem dois picos de recrutamento por ano, designados como “coortes de outono” e “coortes de primavera”.
Em cada ano, os peixes passam um certo tempo nas áreas de pesca que são, também, as áreas de desova, ficando afastados destas durante o resto do ano. As coortes de primavera não se encontram nas áreas de pesca na mesma época que as coortes de outono.
Os peixes passam o primeiro semestre fora das áreas de pesca.
O lado esquerdo da Fig. 11.2.3 ilustra a população total, onde A, C e E são as coortes de outono e B, D e F são as coortes de primavera. O lado direito da Fig. 11.2.3 mostra a parte do manancial que se encontra nas áreas de pesca. No outono, as coortes C e E estão a caminho das áreas de pesca e as coortes D e F estão se afastando das mesmas. Só uma parte de C e D já chegou, e só uma parte de E e F já saiu. No inverno, apenas C e E estão representadas nas áreas de pesca, mas todos os membros destas coortes encontram-se presentes. Os gráficos para a primavera e o verão devem ser explicados segundo esta metodologia.
Esta teoria poderia explicar porque parece ocorrer progressão tão insignificante nas modas de frequências de comprimento. O lado direito serve ainda para ilustrar o risco de se ligar picos de diferentes coortes. Na Fig. 11.2.3 simplificada (sem sobreposição entre coortes) é fácil ligar os picos adequadamente, mas com um conjunto real de dados a sobreposição entre coortes tornaria muito mais difícil a realização da análise da progressão modal.
A Fig. 11.2.4 ilustra o erro criado pela “migração dependente do tamanho” quando se procede à estimação de taxas de crescimento, em relação a duas coortes. As áreas sombreadas representam as fracções das duas coortes que não estão na área de amostragem (área de pesca). Pode-se dizer que formam a parte geradora do erro do manancial. A hipótese fundamental na Fig. 11.2.4 é que a migração anual (desova/alimentação) depende do tamanho individual.
Outra hipótese é que as coortes chegam às áreas de pesca no outono e as deixam durante a primavera. Nas amostras de outono alguns dos indivíduos pequenos (cardumes de pequeno tamanho médio) ainda não chegaram às áreas de pesca, resultando numa sobrestimação do comprimento médio das duas coortes. Nas amostras de primavera o quadro inverte-se, os peixes pequenos já chegaram, e alguns peixes maiores deixaram as áreas de pesca. Como consequência, verifica-se uma subestimação do comprimento médio. O efeito combinado destas duas fontes de erro é uma subestimação da taxa de crescimento. O que se observa é a taxa de crescimento correspondente à linha a tracejado, enquanto a verdadeira taxa média de crescimento da população é representada pela linha a cheio.
A Fig. 11.2.5 apresenta uma explicação plausível do crescimento negativo aparente tal como a Fig. 11.2.4. Assim, o crescimento negativo aparente pode-se explicar como o efeito combinado da migração anual e da dependência do tamanho. No entanto, outras explicações também são possíveis. O crescimento negativo aparente pode também ser causado por selectividade da arte, ou seja, se a pescaria variar sazonalmente em termos de distribuição geográfica e/ou arte empregada, pode resultar numa subestimação da taxa de crescimento. Em alguns casos pode ocorrer o contrario, isto é, uma sobrestimação da taxa de crescimento.
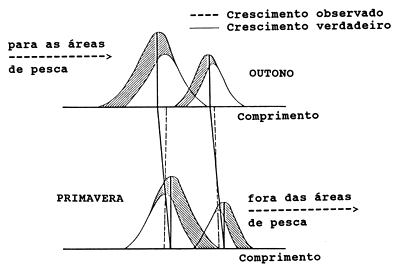
Fig. 11.2.4 Representação esquemática do erro causado pela migração dependente de tamanho. Áreas sombreadas indicam a parte da população que não é amostrada (de sousa, 1988)
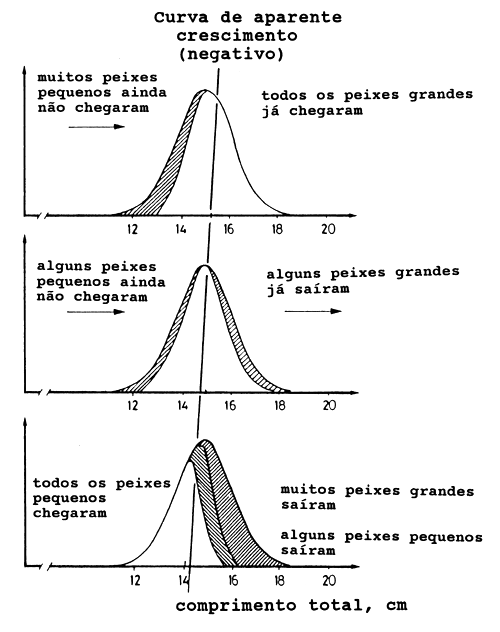
Fig. 11.2.5 Representação esquemática das possíveis razões pelas quais o crescimento negativo aparente pode ser observado (de Sousa, 1988)
A Fig. 11.2.6 ilustra o erro causado por migração vertical dependente do tamanho e/ou selectividade da arte de pesca. A Fig. 11.2.6A mostra dados obtidos das leituras de otólitos de 118 indivíduos de D. russelli capturados por duas diferentes artes: rede de arrasto de fundo e pelágica (Sousa, 1988). Neste caso, a observação de anéis diários permitiu a medição da idade em dias. Indivíduos menores foram capturados por arrasto pelágico e espécies maiores por arrasto de fundo. Os dois grupos parecem seguir diferentes curvas de crescimento, o que pode ser explicado por uma migração vertical vitalícia dependente do tamanho. Quanto mais lentamente os indivíduos crescerem, mais tempo eles permanecerão nas camadas superficiais. A curva de crescimento ajustada aos pontos na Fig. 11.2.6A é baseada em todas as observações, no entanto se fossem estimadas para cada grupo de tamanhos obteriase duas curvas diferentes entre si. O quadro torna-se mais claro na Fig. 11.2.6B, onde os resíduos (desvios em relação à curva de crescimento estimada na Fig. 11.2.6A) são marcados contra a idade. Alternativamente, é possível que os resultados evidenciados pela Fig. 11.2.6 possam ser explicados pela maior velocidade de natação dos peixes maiores, a qual reduz a capturabilidade destes indivíduos pelo arrasto pelágico.
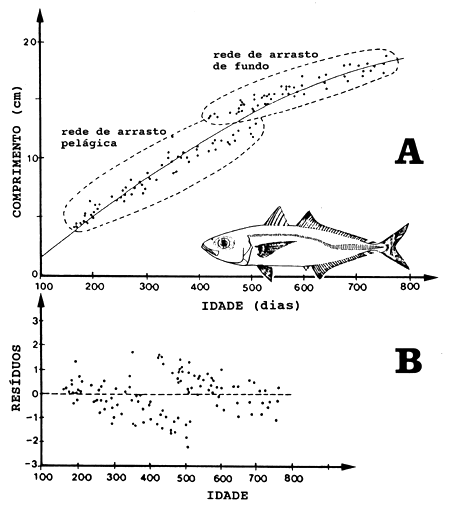
Fig. 11.2.6 Curva de crescimento de Decapterus russelli no Banco de Sofala, Moçambique, baseado em leituras de idade (anéis diários), de peixes amostrados pela pesca comercial de arrasto de fundo e levantamentos com arrasto pelágico, ambos em 1982 (de Sousa, 1988)
O método apresentado nesta secção é um simples caso especial do “método geral de amostras emparelhadas”, que será discutido na próxima secção, para estimar parâmetros do crescimento e de taxas de mortalidade de mananciais migratórios. Como outros métodos simples, é baseado em suposições bastante sólidas, mas a questão é saber se as mesmas são aproximações razoáveis de uma situação real.
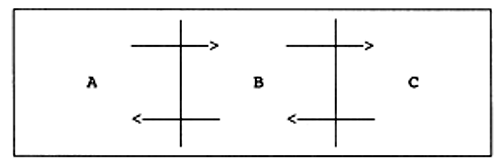
O método é baseado na suposição de que um manancial de peixes segue uma rota migratória previsível. Se esta for conhecida (por ex., a partir de experiências de marcação) no tempo e no espaço, torna-se possível seguir as coortes e “emparelhar” as amostras de modo que se originem da mesma coorte. Considere-se um modelo hipotético simples:
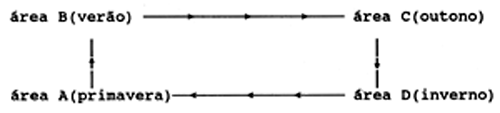
A, B, C e D simbolizam áreas geográficas. Supomos que o manancial realiza a mesma migração em cada ano, seguindo o esquema temporal acima mostrado. Para “emparelhar” amostras neste modelo para a coorte de primavera, realiza-se análises baseadas em amostras tomadas:
Na primavera, na área A, no verão, na área B,
no outono, na área C e no inverno, na área D
As amostras podem ser originadas apenas duma área, digamos A; nesse caso somente as amostras recolhidas na primavera (em anos diferentes) devem ser emparelhadas.
Este modelo pode ser ajustado para pequenos pelágicos como carapaus e cavalas da Índia, e sabe-se que se ajusta ao padrão de migração de pequenos pelágicos em águas temperadas (ver Secção 11.6). Pode ser usado para se estimar parâmetros de crescimento, conforme descrito a seguir.
A Fig. 11.3.1.1 mostra uma série de amostras de frequências de comprimento tomadas em cada quatro meses, por um período de 2 anos. Observe-se que as distribuições em períodos subsequentes muitas vezes indicam crescimento negativo. Seguindo-se o modelo podemos ligar as modas na distribuição para meses correspondentes em anos subsequentes (por ex., Jan. 1982, Jan. 1983 e Jan. 1984), como numa progressão modal normal.
O próximo passo é, utilizar o método de Chapman (Eq. 3.3.2.2), já que o intervalo de tempo Δt é relativamente longo, supondo-se sempre a duração de um ano:
L(t+Δt)-L(t) = c*L∞ - c*L(t) onde c = 1 - exp(-Δt*K)
Existem quatro estimações de ΔL/Δt com Δt = 1 ano, a saber: (L5-L1), (L6-L2), (L7-L3) e (L8-L4). O valor médio do incremento dessas quatro observações é 8 cm enquanto a média dos comprimentos médios das primeiras modas (L1+L2+L3+L4) /4 = 4.25 cm. Temos então:
a média de L(t+1) - L(t) = 8 cm e L(t) = 4.25 cm
8 = c*L∞ - c*L(t) = c*L∞ - c*4.25 ou
C = 8/(L∞ - 4.25) ou, como
K = -(1/Δt)*1n(1-c) (ver Secção 3.3.2) obtemos
K = -(1/1)*1n[1 - 8/(L∞ - 4.25)]
Se usarmos 18 cm como uma primeira estimação aproximada de L∞ obtemos:
K = -1n(1 - 8/(18 - 4.25)) = 0.87
Usando-se L∞ = 18 cm e K = 0.87 ao ano, obtemos a progressão modal de 4.3 a 12.2 cm nas idades 0.31 e 1.31 ano (Fig. 11.3.1):
L(0.31) = 18*(1 - exp(-0.87*0.31)) = 4.3 cm
L(1.31) = 18*(1 - exp(-0.87*1.31)) = 12.2 cm
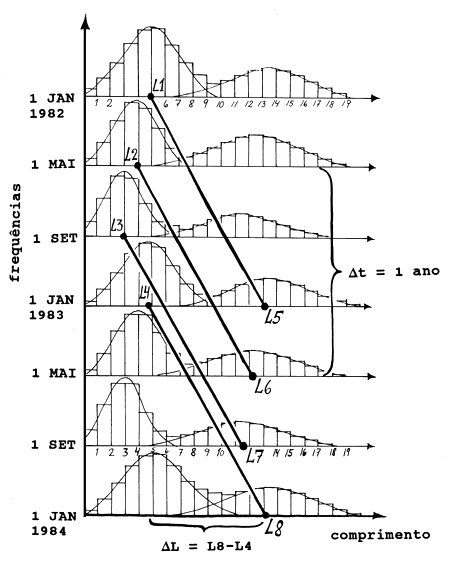
Fig. 11.3.1.1 Ilustração da estimação dos parâmetros de crescimento pelo método das amostras emparelhadas de retorno anual. Para mais detalhes ver o texto
Esta aproximação pressupõe que se tem conhecimento ou uma hipótese da rota migratória no tempo e no espaço e, portanto, torna-se possível “emparelhar” amostras de modo a que se originem da mesma coorte (ver o início da secção anterior).
Para ilustrar as características do método geral de amostras emparelhadas, para estimar a mortalidade total, foi construído um exemplo hipotético simples. Este exemplo simplificado trata de uma coorte migrando através de três áreas, A, B e C. A coorte desloca-se da área A para B e depois para C, onde permanece por algum tempo; daí volta para B e termina onde começou, na área A.
A Tabela 11.4.1 e Fig. 11.4.1 mostram o exemplo de números capturados por unidade de esforço. As curvas ajustadas na figura correspondem aos parâmetros do crescimento: L∞ = 10 cm, K = 2.0 ao ano e to = 0. As setas na Fig. 11.4.1 indicam a migração entre áreas. Ignorando-se a migração, interpretaríamos a primeira parte das frequências de comprimento na área A como uma coorte que se extinguia em Maio, e as taxas de mortalidade seriam estimadas da seguinte maneira (cf. com a Tabela 11.4.1):
| Z(JAN) | = | 1n(8465/5732) | = | 0.39 por mês |
| Z(FEV) | = | 1n(5732/2911) | = | 0.68 por mes |
| Z(MAR) | = | 1n(2911/986) | = | 1.08 por mês |
| Z(FEV) | = | 1n(986/167) | = | 1.77 por mês |
As verdadeiras mortalidades (incluindo-se toda a coorte nas três áreas) são (cf. com a Tabela 11.4.1):
| Z(JAN) | = | 1n(8465/(5732+1433)) | ||
| = | 1n(8465/7166) | = | 0.17 por mês | |
| Z(FEV) | = | 1n((5732+1433)/(2911+3154)) | ||
| = | 1n(7166/6065) | = | 0.17 por mês | |
| Z(MAR) | = | 1n((2911+3154)/(986+3614+534)) | ||
| = | 1n(6065/5134) | = | 0.17 por mês | |
| Z(FEV) | = | 1n((986+3614+534)/(167+2504+1670)) | ||
| = | 1n(5134/4346) | = | 0.17 por mês |
As diferenças entre os dois conjuntos de valores de Z são os “coeficientes de migração”.
A Fig. 11.4.2 ilustra as dificuldades geralmente encontradas quando se tenta estimar curvas de crescimento para espécies migratórias. A Parte C mostra a rota migratória para o manancial considerado. Neste exemplo hipotético supomos que as amostras são obtidas apenas das áreas de pesca, e que os peixes migram para dentro e para fora das áreas de pesca apenas em função do seu tamanho. Durante o primeiro ano de vida eles estarão disponíveis nas áreas de pesca quando tiverem comprimentos entre L1 e L2 e, para o segundo ano, comprimentos entre L3 e L4.
Tabela 11.4.1 Exemplo hipotético para ilustrar o “método de amostras emparelhadas”
| comprim. | Área A (número capturado por unidade de esforço) | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | total | |
| JAN | 8465 | 8465 | |||||||||
| FEV | 5732 | 5732 | |||||||||
| MAR | 1758 | 1153 | 2911 | ||||||||
| ABR | 629 | 357 | 986 | ||||||||
| MAI | 125 | 42 | 167 | ||||||||
| JUN | 0 | ||||||||||
| JUL | 0 | ||||||||||
| AGO | 0 | ||||||||||
| SET | 4 | 15 | 11 | 30 | |||||||
| OUT | 104 | 123 | 32 | 259 | |||||||
| NOV | 201 | 355 | 152 | 708 | |||||||
| DEZ | 178 | 424 | 264 | 866 | |||||||
| Total | 0 | 8465 | 5732 | 1758 | 1782 | 482 | 46 | 498 | 913 | 448 | 20124 |
| Área B | |||||||||||
| comprim. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | total |
| JAN | 0 | ||||||||||
| FEV | 1433 | 1433 | |||||||||
| MAR | 1905 | 1249 | 3154 | ||||||||
| ABR | 2306 | 1308 | 3614 | ||||||||
| MAI | 1870 | 634 | 2504 | ||||||||
| JUN | 271 | 606 | 111 | 988 | |||||||
| JUL | 94 | 74 | 168 | ||||||||
| AGO | 50 | 98 | 30 | 178 | |||||||
| SET | 98 | 351 | 239 | 688 | |||||||
| OUT | 422 | 499 | 129 | 1050 | |||||||
| NOV | 212 | 375 | 161 | 748 | |||||||
| DEZ | 43 | 103 | 64 | 210 | |||||||
| Total | 0 | 0 | 1433 | 1905 | 3555 | 3449 | 1482 | 1311 | 1246 | 354 | 14735 |
| Área C | |||||||||||
| comprim. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | total |
| JAN | 0 | ||||||||||
| FEV | 0 | ||||||||||
| MAR | 0 | ||||||||||
| ABR | 341 | 193 | 534 | ||||||||
| MAI | 1252 | 424 | 1676 | ||||||||
| JUN | 738 | 1650 | 302 | 2690 | |||||||
| JUL | 1650 | 1297 | 2947 | ||||||||
| AGO | 690 | 1350 | 418 | 2458 | |||||||
| SET | 216 | 771 | 526 | 1513 | |||||||
| OUT | 233 | 276 | 71 | 580 | |||||||
| NOV | 28 | 49 | 21 | 98 | |||||||
| DEZ | 0 | ||||||||||
| Total | 0 | 0 | 0 | 0 | 341 | 2183 | 4630 | 3981 | 1269 | 92 | 12496 |
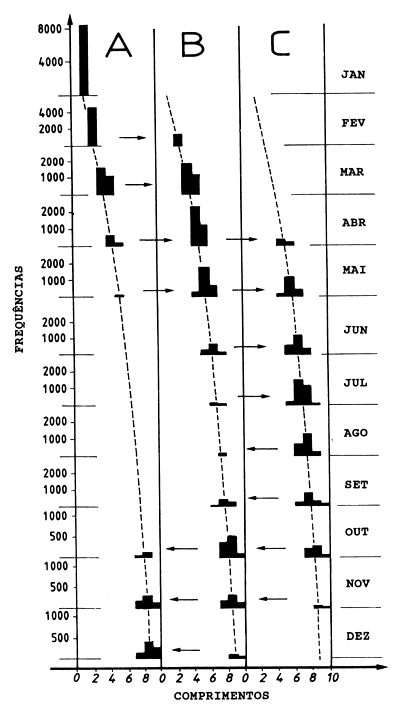
Fig. 11.4.1 Exemplo hipotético para ilustrar a estimação das taxas de mortalidade pelo “método de amostras emparelhadas”. Observe que as escalas diferem de um mês para o outro
 |  |
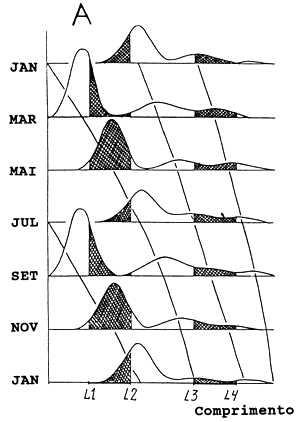Fig. 11.4.2 Ilustração dos problemas de erro quando se estima a curva de crescimento de uma espécie migratória a partir de amostras “não emparelhadas”
A Parte A mostra uma série temporal de amostras não viciadas de frequências de comprimento e as curvas de crescimento que seriam estimadas por essas amostras, obtidas simplesmente por um esquema de amostragem simples que cubrisse toda a amplitude de distribuição no tempo e no espaço. No entanto, não seríamos capazes de obter tais amostras não viciadas se todas as amostras fossem provenientes somente das áreas de pesca. Se os peixes chegassem às áreas de pesca exactamente com comprimentos L1 e L3 e as deixassem exactamente com comprimentos L2 e L4, seriam obtidas amostras representadas pelas partes sombreadas na distribuição de frequências de comprimento, na Parte A. Na prática, obviamente não se observaria um recrutamento tão instantâneo, do tipo “fio-de-navalha”, para as áreas de pesca, mas sim distribuições de frequências de comprimento apresentadas na Parte B, que mostram dois grupos distintos de peixes sem qualquer sobreposição de frequências. Os grupos de peixes pequenos mostram alguma progressão modal, enquanto que os grupos de peixes maiores estão abertos a qualquer interpretação e a classe de comprimentos intermediária está ausente. Este padrão generalizado é comumente observado quando se amostram frequências de uma área restrita, isto é, uma área que é apenas uma pequena parte da amplitude da distribuição do manancial considerado.
As curvas ajustadas na Parte B são as que seriam obtidas a partir da progressão modal, baseadas naquelas distribuições de frequências de comprimentos. Estas curvas são mais íngremes que as verdadeiras curvas de crescimento da Parte A. As modas dos peixes menores nas amostras da Parte B mostram alguma progressão, mas esta é menor do que nas modas da Parte A, que representa a verdadeira curva de crescimento. O efeito da migração dependente do tamanho (ver Secção 11.2), causa uma subestimação da taxa de crescimento nos peixes pequenos.
As modas aparentes dos peixes grandes na Parte B são de difícil interpretação em termos de crescimento. Na prática, estas modas podem ter pouco a ver com crescimento c, na verdade, reflectem ruidos aleatórios e/ou erros no sistema de amostragem. Neste caso as curvas de crescimento ajustadas aos peixes grandes representam uma subestimação da taxa de crescimento, mas em outros casos podem até induzir uma sobrestimação. Em geral, deve-se tomar o devido cuidado na interpretação da progressão modal para classes de comprimento próximas ao comprimento máximo da espécie.
O sucesso das experiências de marcação depende da habilidade e boa vontade dos pescadores e de outras pessoas que lidam com as capturas, para relatar onde e quando os peixes marcados foram recapturados. Se os dados forem usados também para estimar os parâmetros de crescimento, o comprimento dos peixes capturados também deve ser comunicado. A pescaria deve cobrir uma parte relativamente grande das distribuições espaciais e temporais do manancial para assegurar um número razoável de recapturas para os cálculos necessários. Supõe-se que os peixes marcados constituem uma amostra representativa da população, e assim têm os mesmos parâmetros básicos que a população não marcada. Modelos que adoptam esta premissa foram sugeridos por Gulland (1955), Paulik (1963), Seber (1973) e Jones (1977). Seber (1973) apresenta uma ampla discussão da análise de dados de captura e recaptura.
Kleiber, Argue e Kearney (1983) sugeriram um modelo para avaliação do atum gaiado do Pacífico baseado em dados de marcação. Este é o tradicional modelo da curva de captura (Eq. 4.2.7) com modificações para incluir mortalidade devida a marcação, perda de marcas e falhas na comunicação de recapturas. A equação básica do modelo para estimar o tamanho da população, P, e a “taxa de atrito, A”, (ver definição abaixo) é a seguinte:
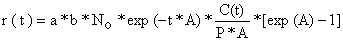 | (11.5.1) |
onde
| a | = | fracção de sobreviventes a curto prazo, enquanto 1-a = fracção de mortalidade a curto prazo, devido a traumas na marcação |
| A | = | taxa de atrito (inclui mortalidades (M e F) e perda de marcas, o crescimento além da vulnerabilidade da arte e migração para fora da área de exploração também são considerados) |
| b | = | fracção das marcas recapturadas devolvidas com informações úteis sobre a recaptura |
| C(t) | = | captura em unidades de biomassa no período de tempo t |
| No | = | número de peixes marcados no tempo t = 0 |
| P | = | manancial instantâneo em unidades de biomassa (supostamente constante com o tempo) |
| r(t) | = | número de marcas devolvidas durante o período de tempo t |
| t | = | índice do período de tempo |
Para tornar a Eq. 11.5.1 basicamente igual à equação da captura (Eq. 4.2.7), introduzimos:
| N(t) | = | No*exp[-(t-1)*A] = número de peixes marcados no início do período de tempo t. |
| F(t) | = | C(t)/P, mortalidade por pesca |
Supomos que a = b = 1 e A = Z (sem perda de marcas ou outro tipo de factores de atrito). Após substituir e rearranjar a Eq. 11.5.1 vem:
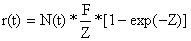isto é, a equação de captura (Eq. 4.2.7)
A descrição acima apresentada é apenas uma curta introdução à equação básica. Para uma completa descrição do modelo, o leitor deve consultar o trabalho original.
Como mencionado na Secção 11.2, em espécies de migração sazonal os peixes maiores e mais velhos às vezes começam a migrar mais cedo. Este aspecto é analisado em estudos bem documentados sobre o manancial da cavala do Atlântico Norte, Scomber scombrus. Este manancial vive nas regiões norte e oeste do Reino Unido e Irlanda. A principal rota migratória é mostrada na Fig. 11.6.1. O manancial realiza uma migração anual a partir da “área de permanência no inverno” para a “área de desova” e desta para a “área de alimentação”, e da área de alimentação de volta à área de inverno. A distância total percorrida é da ordem de 500–1000 milhas náuticas por ano. A desova ocorre de Março a Julho na área ao sul da Irlanda (ver Fig. 11.6.1).
Concentremo-nos nos aspectos relacionados com a migração dependente do tamanho, como discutido nas Secções 11.2 e 11.3, que foi demonstrada por Dawson (1986) e Eltink (1987). O que se segue está fundamentado nesses dois trabalhos, que chegam a conclusões semelhantes a partir de conjuntos independentes de observações.
Como se trata de uma espécie de águas temperadas, é relativamente fácil ler as idades da Scomber scombrus com otólitos. Os resultados encontrados por Dawson (1986) e Eltink (1987) baseiam-se em amostras aleatórias de cavalas capturadas por barcos de pesca comercial, bem como por barcos de investigação operando nas áreas de desova durante a época de reprodução. Registouse o comprimento, a idade e os estádios de maturação, sendo as amostras obtidas mensalmente. As principais rotas migratórias e as áreas de desova já eram previamente conhecidas através de outras investigações (por exemplo, experiências de marcação).
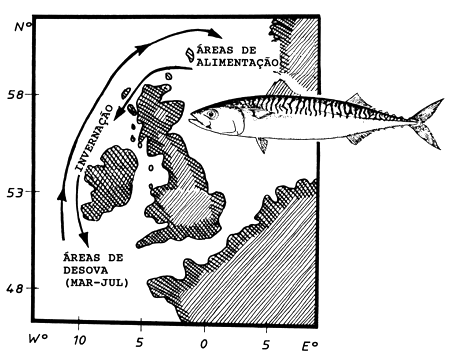
Fig. 11.6.1 Principal rota migratória anual de um manancial de cavala do Atlântico (Scomber scombrus) baseado em várias fontes, incluindo várias experiências de marcação (redesenhado de Eltink, 1987)
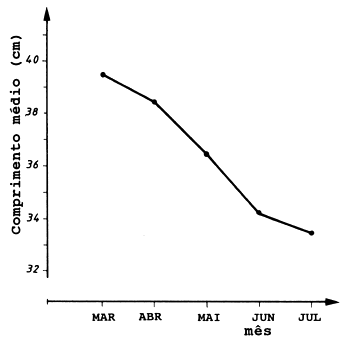
Fig. 11.6.2 Comprimento médio dos indivíduos durante a época de desova (estádo de maturação 6) da cavala do Atlântico (Scomber scombrus), por mês. Note que os maiores peixes desovam primeiro (redesenhado de Eltink, 1987)
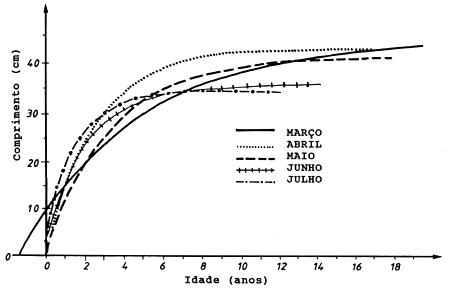
Fig. 11.6.3 Curvas de crescimento para a cavala do Atlântico Scomber scombrus) estimadas a partir de dados de idade/comprimento, de indivíduos amostrados nas áreas de desova, de Março a Julho - ilustração de um problema de erro (de Dawson, 1986)
Verificou-se que a migração da área de permanência invernal para a área de desova ocorreu numa sucessão idade-comprimento, em que os peixes mais velhos chegam antes dos jovens e partem primeiro que eles. Mesmo dentro de um grupo de idade os indivíduos maiores chegam primeiro que os menores. Isto é ilustrado na Fig. 11.6.2, que mostra o comprimento médio dos peixes no estádio de maturação 6, a partir de amostras aleatórias colhidas nas áreas de desova, em cada mês, durante a época de desova (Eltink, 1987), revelando que quanto maiores são os peixes, mais cedo desovam.
A Fig. 11.6.3 (de Dawson, 1986) ilustra a ocorrência de erros quando se estimam parâmetros do crescimento para um manancial migratório. Cada uma das cinco curvas de crescimento foi estimada pelo método das amostras emparelhadas (ver Secção 11.3), com base em dados colhidos durante um determinado mês, nas áreas de desova. Como era de se esperar, os dados colhidos no início da época de desova (Março) produzem uma curva para peixes grandes com um crescimento lento, enquanto os dados colhidos no fim da época de desova produzem uma curva mais íngreme com um L∞ menor.
