O problema do manancial e do recrutamento pode ser considerado como a procura da relação entre o tamanho do manancial progenitor e o recrutamento subsequente em número ou força da classe anual (ver Secção 8.3). Este é um problema central da dinâmica de populações de peixes, uma vez que isso representa o controlo natural do tamanho da população, estando ou não as populações sendo exploradas.
Este capítulo apresenta algumas considerações sobre o problema da relação S/R (Stock/Recruitment), manancial/recrutamento, embora não apresente métodos para resolver os problemas efectivamente. A razão pela qual é dado este tipo de tratamento à relação S/R não é devido ao assunto ser menos importante, mas sim porque ainda não se desenvolveram modelos realmente convincentes para lidar com o problema.
A dissertação que se segue sobre a relação S/R é baseada em Beyer e Sparre (1983) e Pauly (1984). Discussões da relação S/R com especial referência a mananciais de peixes tropicais são dadas, entre outros, por Murphy (1982) e Pauly (1984).
Para apresentar a relação S/R, foi escolhido um exemplo excepcionalmente claro (Fig. 12.0.1). O exemplo aborda a espécie Lactarius lactarius (peixe algodão) do golfo da Tailândia (Pauly, 1980a). Neste caso, parece haver uma relação bem definida entre o recrutamento e o tamanho do manancial desovante. Entretanto, como já foi mencionado na Secção 8.3 (Fig. 8.3.2) este não é um exemplo típico de um gráfico S/R. A Fig. 12.0.2 mostra o gráfico S/R para o arenque (Clupea harengus) do Mar do Norte, para os anos 1949–1978. As estimações dos tamanhos do manancial e do recrutamento (número de peixes de um ano de idade) são obtidas pela VPA, análise de população virtual (ver Secção 5.1). Este exemplo é mais representativo para gráficos de S/R em geral.
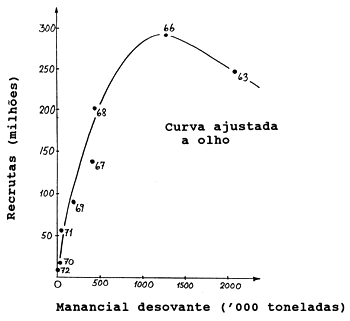
Fig. 12.0.1 Gráfico do manancial e recrutamento do Lactarius lactarius (peixe algodão) do golfo da Tailândia (de Pauly, 1980a)
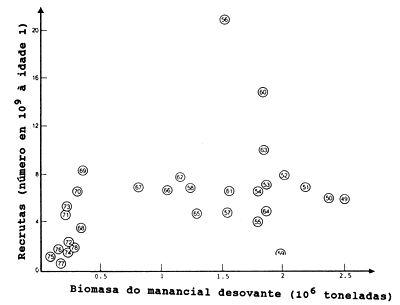
Fig. 12.0.2 Gráfico do manancial e recrutamento do arenque do Mar do Norte (Clupea harengus). Número de arenques de um ano de idade versus biomassa do manancial desovante. Dados obtidos da VPA (reproduzido de Beyer e Sparre, 1983)
Obviamente, não podem existir recrutas se não se permitir que os peixes adultos amadureçam, desovem e produzam ovos, os quais, após eclosão e crescimento das larvas se tornam recrutas. As fêmeas da maioria das espécies são extremamente fecundas, produzindo milhares, mesmo milhões de ovos durante a vida adulta. Esta enorme fecundidade tem levado muitos biologistas a supor que, mesmo um manancial progenitor muito pequeno deve ser capaz de restabelecer o manancial após cada estação de desova. Contudo, foi suposto que as características abióticas do meio ambiente (por exemplo, condições oceanográficas) eram os factores que determinavam quantos ovos desovados sobreviveriam para se tornarem recrutas. Assumia-se, assim, que a biomassa do manancial desovante (biomassa de peixes maduros) era virtualmente um factor irrelevante para a determinação do número de recrutas, excepto nos casos em que o tamanho do manancial fosse próximo de zero. Esta ausência da relação S/R foi sugerida, por exemplo, por Beverton e Holt (1957) (ver também Beverton, 1963). No entanto trabalhos posteriores (Parrish, 1973 e Saville, 1980) sugeriram que muitos mananciais de peixes apresentam uma relação S/R. Tem sido sugerido que a maioria dos mananciais de peixes que entraram em colapso em décadas recentes, sofreram de sobrepesca de recrutamento (ver Secção 8.3) (Murphy, 1966, 1977; Saville, 1980).
Contudo a relação S/R geralmente não pode ser estabelecida directamente pela marcação num sistema de eixos do número de recrutas (ou algum índice de recrutamento) e da biomassa do manancial desovante. De preferência, é necessário, simultaneamente, tomar-se em consideração a relação S/R e os factores bióticos e/ou abióticos que podem afectá-la. Csirke (1980) demonstrou um forte efeito das condições oceanográficas sobre o recrutamento da anchova do Peru.
Tem sido observado para muitos mananciais de peixes que o nível de recrutamento médio é quase constante numa grande faixa intermediária de variação do manancial progenitor (ver Figs. 12.0.2 e 12.1.1). No caso do arenque do Mar do Norte (Fig. 12.0.2) tem sido estimado que esta faixa intermediária abrange pelo menos um intervalo correspondendo a 1012-1013 ovos. O nível de recrutamento médio é de aproximadamente 8*109 peixes de um ano de idade. Assim, a probabilidade de um ovo em desenvolvimento vir a ser um recruta de um ano de idade é de aproximadamente 0.0001.
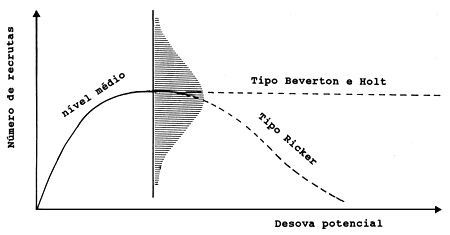
Fig. 12.1.1 Forma básica da curva de recrutamento. A distribuição sombreada indica a variação no recrutamento em torno do nível médio
Deve ser observado que esta baixa taxa de sobrevivência não tem relação nenhuma com a pesca, desde que se considere a mortalidade no estado de préexploração do ciclo de vida (o peixe mais jovem que Tr, ver Secção 4.1). O efeito da pesca é uma redução do potencial de desova (isto é, sobrepesca de crescimento, ver Secção 8.2), e não do recrutamento. O recrutamento é afectado somente quando a taxa de pesca é aumentada além de um certo nível (isto é, sobrepesca de recrutamento, ver Secção 8.3). No caso do arenque do Mar do Norte, tal transição de sobrepesca de crescimento parece ter acontecido em alguns períodos dos anos setenta. Porém, em princípio, não sabemos muito da própria localização desta zona de transição no gráfico de recrutamento. Apenas uma coisa é tida como certa, que é o ponto de extinção. Sabemos pouco sobre o outro extremo da curva de recrutamento. Beverton e Holt (1957) sugerem o seguinte tipo de relação S/R:
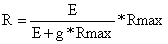 | (12.1.1) |
onde g é parâmetro e onde o número de recrutas, R, aumenta em direcção a um nível assintótico, Rmax, quando a produção de ovos, E = (número de fêmeas) * (produção média de ovos), aumenta. Este modelo é derivado de um modelo simples de mortalidade dependente de densidade:
| dN(t)/dt = -M(t)*N(t) e M(t) = m1 + m2*N(t) | (12.1.2) |
onde N(t) é o número de sobreviventes na idade t, M(t) é a taxa de mortalidade natural de juvenis e ml e m2 são parâmetros. Assim, quanto mais sobreviventes existem na idade t, maior a sua mortalidade. Este mecanismo equilibra as diferenças na sobrevivência causada por outros factores bióticos ou abióticos.
Pode ser mostrado (Beverton e Holt, 1957) que a Eq. 12.1.1 é a solução da equação diferencial 12.1.2.
Este é um exemplo de um modelo descrevendo a “mortalidade dependente da densidade”. A mortalidade dependente da densidade pode ser explicada pela competição pelo alimento. Se o alimento é limitado, o número de mortes por fome torna-se uma função do número de indivíduos que têm que repartir esse alimento.
A forma característica da curva S/R de Beverton e Holt é mostrada na Fig. 12.1.1. Os pontos S/R marcados na Fig. 12.0.2 são difíceis de serem descritos por uma curva, mas se uma curva for ajustada, será do tipo de Beverton e Holt.
Ricker (1954) sugeriu um modelo matemático diferente para a relação S/R (ver Fig. 12.1.1):
| R = R1*E*exp(-R2*E) | (12.1.3) |
onde R1 e R2 são parâmetros.
Neste modelo, o número de recrutas decresce de um nível máximo (de R1/(e*R2) quando E = 1/R2) em direção a zero, assim como a produção de ovos, E, aumenta. O declínio de recrutamento é explicado pelo canibalismo sobre os juvenis pelos adultos. Estes problemas são descritos mais amplamente por Ricker (1954, 1975).
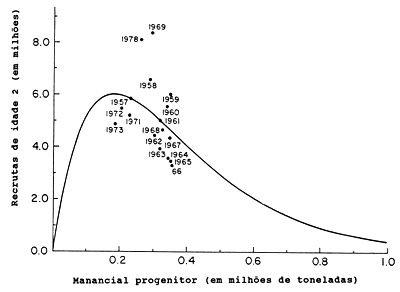
Fig. 12.1.2 Curva de Ricker ajustada à biomassa do manancial desovante e recrutamento do atum do sul. Dados obtidos através da análise de coortes (reproduzido de Murphy, 1982, com permissão)
A curva ajustada a olho na Fig. 12.0.1 é uma relação S/R do tipo de Ricker. No entanto, a parte descendente da curva é baseada em apenas um ponto. Umas poucas observações a mais para grandes mananciais desovantes podem mudar o quadro. A Fig. 12.1.2 mostra uma curva do tipo de Ricker ajustada a dados do atum do sul (Thunnus maccoyii) (Murphy, 1982). Este exemplo ilustra também as dificuldades frequentemente encontradas quando se tenta ajustar uma curva S/R. Como Murphy (1982) cita sobre este gráfico: “parece haver uma relação subjacente dependente da densidade, revestida por uma considerável variabilidade do meio ambiente”.
Essencialmente, o modelo de Beverton e Holt diz que acima de um certo nível de manancial desovante, não há relação entre o manancial progenitor e o recrutamento, enquanto que o modelo de Ricker diz que esta relação existe para todos os tamanhos do manancial desovante, e que existe um tamanho óptimo de manancial desovante (ver Fig. 12.1.1).
Deriso (1980) e Schnute (1985) sugeriram um modelo geral de manancial/recrutamento:
R = R1*E*[1 - R2*R3*E]1/R3
onde R1, R2 e R3 são parâmetros. Para grandes valores do parâmetro da “forma” R3, o modelo acima reduz-se ao modelo de Ricker e dessa maneira temos
R = R1*E*exp(-R2*E)
Se R3 = -1 temos o modelo de Beverton e Holt pela redefinição dos parâmetros
R1 = 1/g e R2 = 1/(g*Rmax) como
R = R1*E/[1 + R2*E] = (R1/R2)/(E + 1/R2)
A maioria dos dados disponíveis sobre o manancial e o recrutamento referemse à faixa média de variação dos desovantes. É aqui que a maioria das espécies parece manter constante um nível médio de recrutamento e isto constitui a motivação para a suposição de recrutamento constante em estudos clássicos de dinâmica de populações de peixes. Talvez o facto mais notável seja que o recrutamento mostra apenas variações relativamente pequenas em torno deste nível médio, considerando a grande redução em números desde o estado de ovo até à maturidade (Ursin, 1982).
A Tabela 12.2.1 dá variações relativas de recrutamento para onze espécies comercialmente importantes do Mar do Norte, no período 1963–75 (Ursin, 1982). A tabela é derivada de VPAs de vários relatórios do grupo de trabalho do ICES. Vemos, por exemplo, que as classes anuais de bacalhau mostram um factor seis na sua variação, do mais fraco para o mais forte.
Para considerar esta variação de amplitude à luz da amplitude de redução da população de bacalhau, durante o primeiro ano de vida, podemos aplicar a seguinte consideração como uma aproximação da situação dos anos setenta. O manancial maduro abrange cerca de 200000 toneladas de bacalhau, metade do qual são fêmeas. Uma vez por ano, cada fêmea desova 10% do seu peso em ovos, dando uma produção total anual de 10000 toneladas de ovos ou 2*1013 ovos, uma vez que cada ovo pesa cerca de 0.5 mg de peso húmido. O nível médio de recrutamento, no entanto, é de apenas 2*108 peixes de um ano de idade. Assim, em média, apenas um ovo dentro de 100000 sobrevive e cresce até chegar a um bacalhau de um ano de idade. O factor de seis na variação de recrutamento implica que a probabilidade de um peixe morrer no primeiro ano de vida, muda no máximo de 0.999997 em uma classe anual má, para 0.999983 em uma classe anual boa, ou em outras palavras, a probabilidade de um peixe sobreviver varia de 0.000003 a 0.000017.
Tabela 12.2.1 Variação de recrutamento em mananciais de peixes do Mar do Norte de 1963–1975. Números ajustados para um valor de 100 para as classes anuais mais salientes de cada espécie. “Ratio” é a razão entre o número na classe anual mais forte e a mais fraca (segundo Ursin, 1982)
| gadideos | peixes achatados | clupeideos | outros | ||||||||
| classe anual | bacalhau | arinca | badejo | escamudo | faneca noruuega | solha | lingua- | arenque do | espadi- | galeolha | cavala tas |
| 1963 | 52 | 1 | 14 | 17 | 4 | 100 | 100 | 100 | - | - | 10 |
| 1964 | 49 | 1 | 26 | 23 | 6 | 29 | 21 | 53 | - | - | 26 |
| 1965 | 70 | 2 | 30 | 18 | 0.5 | 28 | 11 | 47 | - | - | 43 |
| 1966 | 63 | 12 | 37 | 50 | 7 | 25 | 11 | 66 | 59 | - | 62 |
| 1967 | 20 | 100 | 100 | 51 | - | 21 | 18 | 65 | 62 | - | 10 |
| 1968 | 19 | 6 | 33 | 55 | 2 | 27 | 9 | 36 | 37 | - | 16 |
| 1969 | 82 | 2 | 30 | 29 | - | 32 | 26 | 78 | 41 | - | 100 |
| 1970 | 100 | 14 | 33 | 29 | 45 | 25 | 6 | 62 | 20 | 100 | 11 |
| 1971 | 18 | 21 | 68 | 30 | 7 | 20 | 14 | 41 | 19 | 21 | 17 |
| 1972 | 35 | 4 | 90 | 40 | 16 | 62 | 19 | 19 | 46 | 47 | 4 |
| 1973 | 31 | 21 | 63 | 100 | 100 | 40 | 18 | 47 | 91 | 28 | 15 |
| 1974 | 51 | 40 | 92 | 27 | 38 | 25 | 7 | - | 100 | 86 | 11 |
| 1975 | 27 | 9 | 37 | 50 | 18 | 37 | 22 | - | 79 | 41 | 4 |
| Ratio | 6 | 100 | 7 | 6 | 200 | 5 | 17 | 5 | 5 | 5 | 25 |
Podemos também considerar estabilidade em termos de recrutamento para o manancial maduro. Durante o seu ciclo de vida, uma fêmea de bacalhau deve produzir em média uma fêmea madura e um macho maduro. Se o manancial de bacalhau permanecer aproximadamente no seu nível actual, como aparentemente tem ocorrido nos últimos 150 anos ou mais, são apenas possíveis desvios extremamente pequenos deste número mágico, 2. Esta reposição aproximada de um para um entre gerações sucessivas, sustenta-se pelo menos desde que o manancial maduro esteja dentro da amplitude média de variação, como foi referido acima. Assim, se estamos a considerar uma situação em que a pesca é intensa, onde as fêmeas maduras de bacalhau, em média, desovam cerca de 2 milhões de ovos na sua curta longevidade, ou se estamos a considerar uma produção média de 40 milhões de ovos por fêmea num nível baixo de pesca, o número 2 sustenta-se ainda.
Não sabemos o que causa esta enorme redução, em número, desde o estado de ovo, que leva a este refinado ajustamento do número de recrutas, para o número de peixes maduros. Por outro lado, note que o arinca do Mar do Norte e a faneca da Noruega mostra uma notável instabilidade no recrutamento (ver a Tab. 12.2.1). Pode ser que não existam mecanismos de estabilização no Mar do Norte para estas duas espécies.
É difícil abordar o problema de recrutamento de um modo sensível, apenas através de meios estatísticos, por causa da pequena quantidade de dados úteis que, em geral, parecem estar disponíveis. Apenas alcançamos um novo ponto de dados por espécie em cada ano. Assim, para explicar a variabiliade de recrutamento, como por exemplo a ocorrência de classes anuais extremamente fortes, pode-se antecipar uma grande variedade de hipóteses conflituosas, todas elas levando a diferentes conclusões, mas nenhuma delas podendo ser rejeitada em termos dos dados disponíveis.
A situação não é melhor no que diz respeito a explicações de estabilidade de recrutamento. Não é possível discriminar-se entre modelos de recrutamento empíricos, como aqueles fornecidos pelas Eqs. 12.1.1 e 12.1.3. Nem é possível, de antemão, identificar mecanismos irrelevantes de regulação da mortalidade através dos dados. Aparentemente é necessário introduzir mais conhecimentos biológicos sobre as causas da mortalidade natural no primeiro ano de vida nos modelos de recrutamento. Ver também Sinclair (1988).