Relação peso/comprimento
W(i) = q*L(i)b | (2.6.1) |
Equação de crescimento de von Bertalanffy
L(t) = L∞*[1 - exp(-K*(t-to))] | (3.1.0.1) |
Taxa de crescimento, equação de crescimento de von Bertalanffy
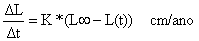 | (3.1.0.4) |
Equação de crescimento de von Bertalanffy baseada em pesos
W(t) = W∞*[1 - exp(-K*(t-to))]3 | (3.1.2.1) |
Equação de crescimento de von Bertalanffy invertida
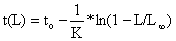 | (3.3.3.2) |
Modelo exponencial decrescente (1)
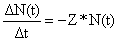 | (4.2.1) |
Modelo exponencial decrescente (2)
N(t) = N(Tr)*exp[-Z*(t-Tr)] | (4.2.2) |
Equação de Baranov ou equação de captura (1)
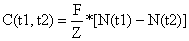 | (4.2.4) |
Equação de captura (2)
 | (4.2.7) |
Número médio de sobreviventes (de t1 a t2)
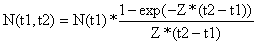 | (4.2.9) |
Mortalidade total a partir de dados de CPUE
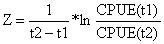 | (4.3.0.3) |
Curva de captura linearizada baseada em comprimentos
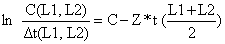 | (4.4.5.3) |
Fórmula de Pauly para M (baseada em 1n)
ln M = -0.0152 - 0.279*ln L∞ + 0.6543*ln K + 0.463*ln T | (4.7.2.1) |
Curva logística para selectividade de artes (baseada em comprimentos)
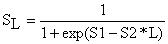 | (6.1.1) |
Modelo de Schaefer
Y(i) /f(i) = a + b*f(i) se f(i) ≤ -a/b | (9.1.2) |
Modelo de Fox
ln (Y(i)/f(i)) = c + d*f(i) | (9.1.3) |
Equações da VPA (baseadas em idades)
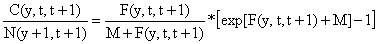 | (5.1.3) |
N(y,t) = N(y+1,t+1) * exp[F(y,t,t+1)+M] | (5.1.4) |
Análise de coortes de Pope baseada em idades (números)
N(t) = [N(t+Δt)*exp(M*Δt/2) + C(t,t+Δt)]*exp(M*Δt/2) | (5.2.3) |
Análise de coortes de Pope baseada em idades (mortalidade por pesca)
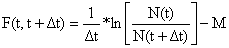 | (5.2.4) |
Análise de coortes de Jones baseada em comprimentos (números)
N(L1) = [N(L2)*H(L1,L2) + C(L1,L2)] *H(L1,L2) | (5.3.4) |
Equação de captura baseada em comprimentos
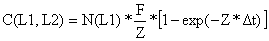 | (5.3.5) |
Análise de coortes de Jones baseada em comprimentos (mortalidade por pesca)
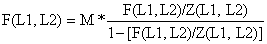 | (5.3.6) |
| onde a taxa de exploração F/Z é calculada de: | |
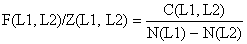 | (5.3.7) |
Conjunto de fórmulas para a análise de Thompson e Bell baseada em idades
intervalo de idade: i = (ti,ti+Δt) | |
Zi = M + X*Fi | |
N(ti+Δt) = N(ti)*exp(-Zi*Δt) | |
Ci = [N(ti)-N(ti+Δt)]*X*Fi/Zi | |
wi = w(ti+Δt/2) | (8.6.1) |
Yi = Ci*wi | |
Bi = Yi/[Fi*Δt*X] | |
Vi = Yi*vi |
Conjunto de fórmulas para a análise de Thompson e Bell baseada em comprimentos
intervalo de comprimento: i = (Li,Li+1) | |
Zi = M + X*Fi | |
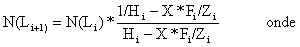 | |
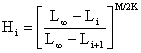 | |
Ci = [N(Li)-N(Li+1)]*X*Fi/Zi | (8.7.7) |
wi = q*[(Li+Li+1)/2]b | |
Yi = Ci*wi | |
Vi = Yi*vi | |
Ni*Δti = [N(Li)-N(Li+1)]/Zi | |
Bi*Δti = Ni*Δti*wi |