En los Capítulos 2 y 5 se mencionó que la naturaleza y comportamiento de las especies sedentarias hacen que el supuesto de agregamiento dinámico común a los modelos expuestos hasta ahora, no se satisfaga. En especies sedentarias de importancia comercial, que incluyen aquellos organismos con poca o nula movilidad tales como moluscos bivalvos, gasterópodos y equinodermos, la aplicabilidad del modelo clásico es limitada. Las caracteristicas inherentes a su biologia, dinámica poblacional y estrategias de explotación difieren de aquéllas observadas en organismos pelágicos para los cuales se desarrolló la teoria tradicional, y por consiguiente imponen importantes restricciones a su aplicación.
En efecto, los supuestos que subyacen a los modelos de producción excedente y de agrupamiento dinámico no son siempre válidos en recursos sedentarios por las siguientes razones: (1) su distribución espacial es generalmente agregada (Elliot, 1977; Hall, 1983); (2) la relativa o nula movilidad impide su redistribución en el área de pesca (Caddy, 1989a; b); (3) la estrategia de pesca tiende a exterminar secuencialmente los parches hasta que dejan de ser rentables (Hancock, 1973; 1979; Caddy, 1975; 1979a, b; Conan, 1984; Orensanz et al., 1991); (4) los parámetros básicos de crecimiento y mortalidad son dependientes de las condiciones ambientales y del tamaño poblacional en distintas escalas de espacio y tiempo (Orensanz, 1986; Holm, 1990; Raimondi, 1990; Possingham & Roughgarden, 1990; Defeo, 1993a).
Por todo lo anterior, el uso de la CPUE como indicador de abundancia en especies sedentarias es limitado: las hipótesis criticas del modelo de Schaefer analizadas en el Capítulo 2 no serian contrastadas y en consecuencia la aplicación de los “modelos captura - esfuerzo” seria invalidada. Debido a esto, dos aproximaciones (no excluyentes entre si) pueden ser apropiadas:
1) Relajar los supuestos de homogeneidad espacial del recurso y esfuerzo de pesca (Caddy, 1975; Sluczanowski, 1984; 1986). En tal sentido, stocks con amplia distribución geográfica, sujetos a cierta variabilidad ambiental que motiva fluctuaciones espaciales en su abundancia, crecimiento y mortalidad, pueden dividirse en subpoblaciones discretas (aún cuando el stock esté conectado por medio de dispersión larval) a ser consideradas como unidades de análisis independiente, para luego integrar los resultados (Seijo et al., 1994b, c).
2) Desarrollar modelos bioeconómicos comprensivos que integren las características inherentes a estos recursos. Considerar los componentes espaciales de la distribución, explotación, interacciones ecológicas y el efecto de gradientes ambientales en la distribución por tallas y/o edades de un stock. En vista de la incertidumbre inherente a variables biológicas, ambientales y económicas (Lewis, 1982; Anderson, 1984; Sissenwine, 1984a, b; Seijo, 1986; Hilborn, 1987), considerar modelos estocásticos donde se haga explicito un componente de error aleatorio conjuntamente con una distribución de probabilidades de la predicción en las relaciones causales establecidas en el modelo (Botsford, 1986; Seijo, 1987; 1989; Fogarty, 1989; Seijo & Defeo, 1994b; Seijo et al., 1994b).
Por otra parte, los estudios sobre la dinámica del esfuerzo pesquero se han enfocado usualmente a las decisiones de largo plazo de los pescadores. Esto es, el énfasis ha sido en la determinación de las tasas de entrada y salida a la pesqueria y en la caracterización de patrones generales de asignación de la intensidad de pesca (Smith, 1969; Clark, 1976; Mangel & Clark, 1983; Emerson & Anderson, 1989). Sin embargo, es en el corto plazo cuando los pescadores toman decisiones sobre la especie objetivo a capturar y sobre la asignación espacial de su esfuerzo pesquero (Hilborn & Ledbetter, 1979; Bockstael & Opaluch, 1983; Tanaka et al., 1991). Una vez que la especie objetivo ha sido seleccionada, se tiene que tomar la decisión de dónde iniciar el esfuerzo para capturarla. Como ha sido indicado por Eales & Wilen (1986), esta última pregunta ha sido poco abordada en la literatura de economía pesquera. En un estudio sobre el camarón de California, los autores antes mencionados encontraron que, en contraste con en el enfoque tradicional centrado en el exceso de capitalización de la flota, el problema parece ser más bien de que las rentas se disipan como resultado del exceso de movimiento de los pescadores en respuesta a la abundancia espacial relativa observada el dia previo de pesca. Este es usualmente el caso en las pesquerias de pequeña escala, en las que los pescadores toman decisiones a diario en un ambiente de incertidumbre respecto a los sitios de pesca alternativos, dadas sus restricciones de autonomía con respecto al puerto de origen (McKelvey, 1983; Salas et al., 1991). Por lo tanto, en este Capitulo se introducen consideraciones espaciales básicas, notablemente la distancia de los puertos de origen a los sitios alternativos de pesca, en el anámica de la intensidad de pesca en el espacio y en el tiempo. Esto permitirá entender mejor las decisiones de corto plazo de las pesquerias, en especial las artesanales. Asimismo, se amplia el grado de complejidad de las interdependencias tecnológicas discutidas en el Capitulo 3 al incorporar la dimensión espacial en el análisis.
Modelar la dinámica espacial de flotas heterogéneas en el corto plazo permite comprender mejor la asignación intertemporal del esfuerzo pesquero y consecuentemente ayudar al manejo de los recursos pesqueros. Asimismo, como se mencionó en la introducción, la necesidad de relajar el supuesto común de distribución homogénea del recurso y consecuentemente de esfuerzo, especialmente relevante para especies sedentarias. Hilborn & Walters (1987) y Gillis et al. (1993) entre otros, han identificado un conjunto de estrategias de asignación espacial de la intensidad de pesca, entre las que destacan:
(i) asignación proporcional a la abundancia espacial del recurso (Caddy, 1975);
(ii) asignación secuencial de la intensidad de pesca en parches de mayor abundancia relativa (Hilborn & Walters, 1987);
(iii) asignación con búsqueda aleatoria del recurso (Hilborn & Walters, 1987);
(iv) asignación por distribución libre de la intensidad de pesca (Gillis et al., 1993);
(v) asignación espacial de la intensidad de pesca proporcional a la quasi renta de los costos variables, (que incluyen los costos de transferencia del puerto de origen a los sitios alternativos de pesca), a la fricción de la distancia, es decir, los costos no monetarios asociados a la distancia, y a la probabilidad de encontrar el recurso en niveles rentables (Defeo et al., 1991; Seijo et al., 1994c; Cabrera, 1995; Hernández, 1995).
Con el objeto de incorporar al análisis las consideraciones anteriores, en las secciones siguientes se presentan dos modelos con diferente grado de resolución espacial y requerimientos de datos biológico-pesqueros y económicos. Los modelos se basan en el trabajo de Seijo et al. (1994c), quienes modelan la distribución espacio-temporal de la biomasa, intensidad de pesca y renta derivada de pesquerias sedentarias en función de diferentes insumos y supuestos.
ALLOC es un modelo bioeconómico de corto plazo que representa las interdependencias de dos tipos de flotas (e.g. artesanal e industrial) que, procedentes de diferentes puertos de origen, capturan la especie objetivo en sitios alternativos de pesca (Seijo et al., 1994c). La distribución espacio-temporal del esfuerzo de pesca es estimada en función de la distancia de los diferentes puertos de origen a las áreas alternativas de pesca, los ingresos netos obtenidos en los viajes de pesca previos, y la probabilidad de encontrar el recurso en niveles rentables en los sitios alternativos. ALLOC se basa en el simple modelo logístico (ver Capítulo 2) para biomasa, pero en forma desagregada en el espacio.
Modelar la dinámica espacial de flotas heterogéneas en el corto plazo permite comprender mejor la asignación intertemporal del esfuerzo de pesca y consecuentemente aportar pautas adecuadas para el manejo racional de los recursos pesqueros. Asimismo, como se mencionó en la introducción, surge de a necesidad de relajar el supuesto común de distribución homogénea del recurso y consecuentemente de esfuerzo, especialmente relevante para especies sedentarias.
Las dimensiones espacio y tiempo son incorporadas en ALLOC al especificar: (1) capturas por unidad de esfuerzo espacialmente heterogéneas por área de pesca, (2) distancias de diferentes puertos de origen a un conjunto de zonas de pesca heterogéneas, y (3) una relación que determina la asignación espacial de la intensidad de pesca en el corto plazo. Esta es modelada en ALLOC como una función de la distancia de los diferentes puertos a los sitios de pesca alternativos, de los ingresos netos obtenidos por las flotas artesanales e industriales en dichos sitios en el viaje previo de pesca, y de la probabilidad de encontrar el recurso en ellos en niveles rentables.
La asignación espacial de la intensidad de pesca de m flotas provenientes del puerto h en el sitio de pesca k en el tiempo t (fkhm(t+DT)), está dada por la siguiente ecuación:
fkhm(t)=SAEkhm(t)DP·Vhm(t) (7.1)
donde:
SAEkhm(t) = distribución (0,1) de barcos tipo m provenientes del puerto h en los sitios alternativos de pesca k, en el tiempo t.
DP = número promedio de dias efectivos de pesca por mes.
Vhm(t) = número de embarcaciones de la flota tipo m, registradas en el puerto h que asignan su esfuerzo pesquero a la especie objetivo en el tiempo t.
Debe mencionarse que intensidad de pesca es entendida aqui como esfuerzo efectivo por unidad de área (Gulland, 1983:44).
SAEkhm(t), es estimada por la ecuación (7.2) de la forma siguiente:
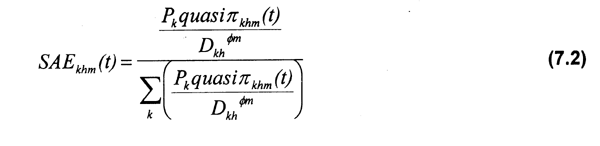
donde:
Pk =probabilidad de encontrar a la especie objetivo en niveles rentables en los sitios alternativos de pesca k. Este parámetro se calcula a partir del total de viajes a cada sitio de pesca y del número de ellos en los que se encontró la especie objetivo en niveles de abundancia que se tradujeron en valores de CPUE mayores o iguales a los costos variables del esfuerzo de pesca.
quasiπihm(t) = quasi renta de los costos variables recibidos por el tipo de embarcación promedio m proveniente del puerto h como resultado de pescar en el sitio k en el tiempo t.
Dkh = distancia del puerto h al sitio de pesca k.
φm = fricción de la distancia para el tipo de embarcación m.
Adicionalmente al costo de transferencia del puerto de origen a los sitios alternativos de pesca, un elemento considerado en este modelo como factor explicativo del comportamiento espacial de las flotas es la fricción de la distancia (Issard & Liossatos, 1979, Seijo et al., 1994c). Las embarcaciones artesanales con autonomía limitada enfrentan costos no-monetarios o insatisfacción (e.g. inseguridad asociada al distanciarse del puerto de origen, incomodidad en las condiciones de la embarcación que fomentan el no alejarse mucho para retornar al puerto de origen el mismo dia de ser posible, otros factores ambientales y culturales que le asignan costos no-monetarios a la distancia). Por lo tanto, a través de la expresión Dkhφm, ALLOC permite incorporar, si los hubiere, otros costos no-monetarios asociados a la distancia. El peso que tendrá la fricción de la distancia para un tipo especifico de embarcación m, estará dado por la potencia a la que se eleve la distancia entre los diferentes puertos y los sitios alternativos de pesca (Dkhφm en la ecuación 7.2).
Para observar el comportamiento de la flota en el corto plazo, se requiere también estimar la quasi renta percibida por la embarcación promedio del tipo m, proveniente del puerto h:
quasi πkhm(t)=ITDkhm(t)-CVkhm(t) (7.3)
Donde:
ITDkhm(t) = ingresos totales por dia recibidos por embarcación tipo m con puerto base h al capturar la especie objetivo en el sitio de pesca k en el tiempo t.
CVkhm(t) = costos variables del esfuerzo pesquero incurridos por la embarcación tipo m al pescar un dia en el sitio de pesca k en el tiempo t.
Los costos variables son estimados considerando: a) el costo de transferencia, el cual es definido en base a la distancia Dkh del puerto de origen al sitio de pesca multiplicada por el costo promedio de combustible y lubricantes por Km recorrido (θ); y b) el valor de la proporción (ω) de la captura que es asignada a la tripulación como pago por su esfuerzo pesquero. Otros costos variables tales como costos de carnada, mantenimiento, reemplazo de artes de pesca y avituallamiento, se agrupan en el parámetro denominado OCVm. Debe mencionarse que, en la dinámica de corto plazo, la permanencia de las embarcaciones en la pesquería estará condicionada a que los ingresos totales sean iguales o mayores que los costos variables, es decir, que la quasi renta de los costos variables sea igual o mayor que cero. Los costos variables son estimados por la ecuación (7.4) de la forma siguiente:
CVkhm(t)=ωqmBk(t)+θDkh+OCVm (7.4)
Debe observarse que inherente a la función SAEkhm(t) existe una familia de distribuciones espaciales de la intensidad de pesca. A continuación se describen cuatro casos:
(I) Caso 1: pesquerías artesanales litorales. Cuando la distancia es irrelevante en términos de los costos de transferencia del puerto de origen a los sitios alternativos de pesca (θ = 0) y la correspondiente fricción de la distancia es cero (φ = 0), es decir, no se perciben costos no monetarios para ir a pescar a los sitios alternativos de pesca, y existe la misma probabilidad de encontrar en niveles rentables al recurso en los sitios alternativos de pesca (P1=P2=…=Pk, donde k = 1..n), la distribución resultante de SAEkhm(t) es equivalente a la distribución proporcional de la abundancia espacial.
(ii) Caso 2: pesquerías de zonas costeras protegidas. Cuando son relevantes en términos monetarios las distancias para transferise de los puertos de origen a los sitios alternativos de pesca (θ < 0), pero con bajos o despreciables costos no monetarios asociados a la distancia por contarse con adecuadas condiciones de navegación y operación de pesca en áreas de pesca protegidas natural o artificialmente (fricción de la distancia igual a cero, φ = 0), es decir, no se perciben costos no monetarios para ir a pescar a los sitios alternativos de pesca, y existe la misma probabilidad de encontrar en niveles rentables al recurso en tales sitios (P1=P2=…=Pk, donde k = 1..n), la distribución resultante de SAEkhm(t) es equivalente a la distribución proporcional a la quasi renta espacial.
(iii) Caso 3: pesquerías de zonas costeras expuestas. Cuando son relevantes en términos monetarios las distancias para transferirse de los puertos de origen a los sitios alternativos de pesca (θ>0), existe fricción de la distancia (φ>0), y la misma probabilidad de encontrar en niveles rentables al recurso en tales sitios (P1=P2=…=Pk, donde k = 1..n), la distribución resultante de SAEkhm(t) es equivalente a la distribución proporcional a la quasi renta espacial e inversamente proporcional a la fricción de la distancia entre el puerto de origen y los sitios alternativos de pesca.
(iv) Caso 4: pesquerías con altos costos de información. Cuando son relevantes en términos monetarios las distancias para transferirse de los puertos de origen a los sitios alternativos de pesca (D>0 y θ>0), existe fricción de la distancia (θ>0), y heterogénea probabilidad de encontrar en niveles rentables al recurso en tales sitios (P1≠P2≠…≠Pk, donde k = 1..n), la distribución resultante de SAEkhm(t) es equivalente a la distribución proporcional a la quasi renta espacial y a la probabilidad de encontrar el recurso en niveles rentables e inversamente proporcional a la fricción distancia entre el puerto de origen y los sitios alternativos de pesca.
Lo anterior puede resumirse en la tabla siguiente:
| Aplicacién SAE | Costo monetario de la distancia | Friccién de la distancia | Probabilidad de encontrar recurso | Distribución esperada |
|---|---|---|---|---|
| Caso 1 | D1=D2=…=Dk θ=0 | φ=0 | P1=P2=…=Pk | Proporcional a la abundancia |
| Caso 2 | D1≠D2≠…≠Dk θ>0 | θ=0 | P1=P2=…=Pk | Proporcional a la quasi renta |
| Caso 3 | D1≠D2≠…≠Dk θ>0 | θ>0 | P1=P2=…=Pk | Proporcional a la quasi renta y a 1/Dφ |
| Caso 4 | D1≠D2≠…≠Dk θ>0 | φ>0 | P1≠P2≠…≠Pk | Proporcional a la quasi renta, a 1/Dφ y a Pk |
La renta económica por sitio de pesca obtenida por la flota tipo m, proveniente del puerto h a lo largo de la temporada de captura, se presenta en la ecuación (7.5):
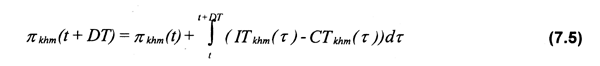
Donde:
ITkhm(t) = ingresos totales recibidos por la flota tipo m con puerto base h al capturar la especie objetivo en el sitio de pesca k, en el tiempo t.
CTkhm(t) = costos totales del esfuerzo pesquero incurridos por la flota tipo m al pescar en el sitio de pesca k en el tiempo t.
Expresiones para ITkhm(t), y CTkhm(t) son presentadas en las ecuaciones (7.6) y (7.7):
ITkhm(t)=(qmBk(t)Ptar+Cinc Pinc)fkhm(t) (7.6)
CTkhm(t)=FCmVm+CVkhm(t)fkhm(t) (7.7)
donde:
Ptar = precio promedio pagado al pescador por kg de especie objetivo.
Pinc = precio promedio ponderado pagado al pescador por kg de especies incidentales.
Cinc = captura promedio incidental por viaje de pesca de las embarcaciones tipo m.
qm = coeficiente de capturabilidad de la embarcación tipo m.
Bk(t) = biomasa de la especie objetivo en el sitio de pesca k en el tiempo t.
FCm = costo fijo diario por tipo de embarcación m.
Vhm = número de embarcaciones tipo m procedentes del puerto h.
Los costos fijos incluyen pago de intereses sobre capital prestado para comprar la embarcación, el motor y los artes de pesca. Asimismo, se incluyen en este rubro los gastos de administración, seguros y el costo de oportunidad de capital.
La tasa de captura dinámica es estimada por la ecuación siguiente:
Ckhm(t)=(qmBk(t)+RVkhm(t))fkhm(t) (7.8)
donde la variable aleatoria RVkhm(t) es generada con una función de densidad probabilística exponencialmente autocorrelacionada, utilizando la varianza observada de la captura por día. Esta variable aleatoria es incluida en el modelo para tomar en consideración la variabilidad en la captura por sitio de pesca no explicada por el esfuerzo pesquero, la capturabilidad correspondiente y la biomasa disponible en dicho sitio. Esta variable es generada para mostrar que variaciones aleatorias en las capturas en un punto en el tiempo no son independientes de sus valores previos: la captura de hoy es dependiente en cierto grado de la captura de ayer. La selección del sitio de pesca es parcialmente dependiente de la selección previa de las áreas de pesca. Factores ambientales (e.g. temperatura del fondo, corrientes, vientos etc.) que afectan la abundancia y distribución espacial del recurso, tienden a ser dependientes en cierta magnitud de valores previos. Para generar esta variable se puede emplear, tal como se hizo para la elaboración del modelo ALLOC, la subrutina EXACOR (Manetsch, 1986), utilizando la varianza de la captura observada para diferentes tipos de embarcaciones que asignan su esfuerzo pesquero en el sitio de pesca k. Esta subrutina utiliza una variable aleatoria uniformemente distribuida entre cero y uno para ser posteriormente transformada a la función de densidad exponencialmente autocorrelacionada. Debe mencionarse que las variables aleatorias pueden ser generadas con otras funciones de densidad probabilistica a través del uso del método de transformación inversa o bien utilizando métodos numéricos, dependiendo si la función de densidad probabilistica puede ser integrada analiticamente o no para obtener la función de distribución acumulada (Gottfried, 1984; Lewis, 1982).
La captura por unidad de esfuerzo de la embarcación tipo m obtenida en el sitio k en el tiempo t (CPUEkm(t)), es estimada por la ecuación (7.9):
CPUEkm(t)=qmBk(t) (7.9)
La biomasa especifica para cada sitio de pesca Bk(t) puede calcularse desagregando espacialmente la función logistica de crecimiento:
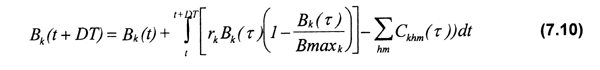
donde rk es la tasa intrinseca de crecimiento de la biomasa del recurso en el sitio de pesca k.
Ya que no necesariamente todas las embarcaciones entran a la pesqueria el primer dia de la temporada de captura, este modelo utiliza modelos de retraso distribuido para la incorporación de éstas a la pesqueria. Este elemento es introducido para suprimir el supuesto básico común a los modelos de pesquerias, el cual sugiere que todas las embarcaciones entran necesariamente el primer dia de la temporada. Para este propósito se utiliza el modelo de retraso distribuido explicado en Capitulo 5 (Manetsch, 1976; Seijo et al., 1987, 1994c). Aplicado a este tipo de problema de dinámica intraanual de flotas diferenciables m provenientes de diversos puertos de origen h (Vhm(t)), la función de retraso distribuido puede ser descrita a través de las siguientes ecuaciones diferenciales:
(7.11)
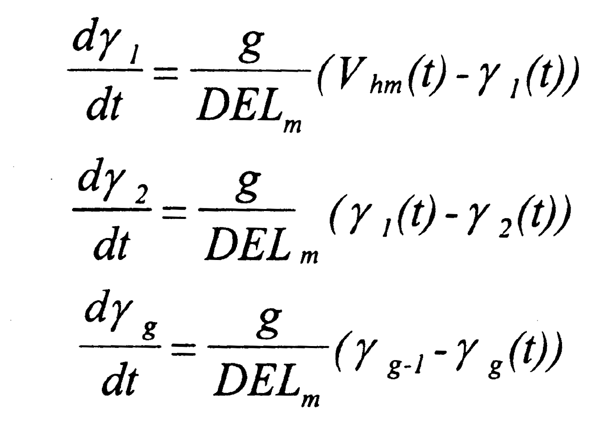
donde:
γg(t) = salidas del proceso de retraso (número de embarcaciones que entran a la pesquería a lo largo de la temporada).
γ1(t),…, γ2(t),…,γg-1(t) son la tasas intermedias del proceso de retraso.
DELm = valor esperado del tiempo de entrada de embarcaciones tipo m a la pesquería.
g = orden del proceso de retraso.
Finalmente, la asignación espacial de la intensidad de pesca acumulada a lo largo de la temporada para las flotas m provenientes del puerto h en el sitio de pesca k, fakhm(t), está dada por la siguiente ecuación:
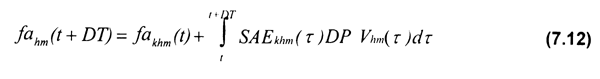
Algunos de los supuestos más importantes de este modelo son los siguientes:
(i) La asignación espacial de la intensidad de pesca entre sitios alternativos de pesca es función de la probabilidad de encontrar al recurso en niveles rentables, los ingresos netos obtenidos de diferentes sitios de pesca en viajes de pesca previos y la distancia de los puertos de origen a los diferentes sitios de pesca.
(ii) La captura por unidad de esfuerzo por sitio se estima en función de la capturabilidad y la biomasa del recurso en dicho sitio en el tiempo t.
(iii) Los sitios alternativos son considerados áreas ocupadas por organismos separados sin emigración e inmigración entre los mismos.
(iv) En este modelo no lineal, la estocasticidad inherente al proceso de obtención de capturas se puede representar a través de la generación de variables aleatorias con una función de densidad exponencialmente autocorrelacionada. La variabilidad en las capturas diarias no explicadas por cambios en abundancia espacial y temporal de la especie de interés es generada por la función de densidad antes mencionada utilizando la varianza de las capturas observadas.
(v) Se asume que los pescadores son tomadores de precio tanto de la especie objetivo como del costo de los insumos requeridos para realizar el esfuerzo de pesca (Clark, 1985).
(vii) Los costos de los insumos requeridos por viaje de pesca permanecen constantes a lo largo de la temporada de captura.
Para ilustrar el comportamiento de corto plazo de este sencillo modelo espacial, se recomienda al lector conducir experimentos de simulación bioeconómica espacial con el modelo ALLOC del paquete de software denominado SPATIAL publicado por la FAO (Seijo et al., 1994c).
Cuando la información bioeconómica espacial lo permite, algunos de los supuestos básicos del modelo ALLOC se pueden flexibilizar al incorporar elementos más realistas tanto en la dinámica de la estructura de la población como en el nivel de resolución espacial. CHART es un modelo que integra en forma dinámica el modelo YRAREA (modelo espacial de estructura por edades desarrollado por Caddy, 1975), con la dinámica de corto y largo plazo de la flota, utilizando un enfoque bioeconómico geográfico (Seijo et al., 1994c).
Para generar espacialmente la estructura inicial de la población, se especifican las capturas por unidad de esfuerzo máximas observadas en el área de distribución del recurso (CPUEmaxkl), donde k corresponde a la latitud y l a la longitud. La biomasa máxima en las coordenadas kl (Bmaxkl) se obtiene dividiendo la CPUEmaxkl entre el coeficiente promedio de capturabilidad por unidad de área. Ahora bien, el número de individuos a reclutarse cada año se puede especificar como: (i) reclutamiento constante, (ii) dinámico y determinístico, o (iii) dinámico y estocástico. Para los dos últimos, se emplea una función de reclutamiento del tipo Beverton & Holt (1957) de la forma siguiente:
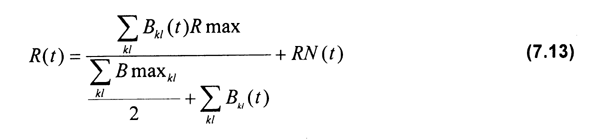
donde:
Rmax = reclutamiento máximo observado.
Bkl(t) = biomasa de la especie en el sitio con coordenadas kl en el tiempo t.
RN(t) = (0, var) variable aleatoria normalmente distribuida en el tiempo t a generarse en el caso en que se seleccione la opción de reclutamiento estocástico.
Después de estimar el número total de reclutas para el año en cuestión, se procede a distribuirlos estacionalmente utilizando la función de retraso distribuido definida anteriormente tomando en consideración el mes pico de reclutamiento y el período (en meses) en el que ocurre dicho reclutamiento. Posteriormente, el programa procede a reclutar espacialmente por parches a los individuos correspondientes al reclutamiento estacional.
Para representar la distribución espacial del reclutamiento por parches, el algoritmo computacional de CHART selecciona aleatoriamente las coordenadas del centro del parche y calcula la distribución de densidad del parche a partir del centro antes mencionado, utilizando la función de densidad probabilística normal bivariada:

donde:
Rkl(t) = número de reclutas asentándose a partir del centro del parche con coordenadas kl en el tiempo t.
NT(t) = número de reclutas a distribuir en el parche antes de verificar si se satisface o no la restricción de biomasa máxima en las coordenadas aleatoriamente seleccionadas.
x = distancia de la unidad de área kl al centro del parche
σ2 = desviación estándar de la densidad del parche (0 < σ < 1).
La distancia del centro del parche (x), es estimada por la siguiente ecuación:
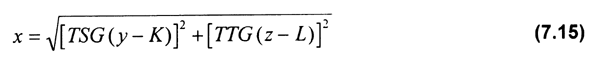
donde:
TSG = largo de la celda estimada a partir de la resolución espacial especificada (e.g. grados, minutos y segundos).
TTG = ancho de la celda estimada a partir de la resolución espacial especificada.
| i = 1, 2, 3,…, SG | y | SG = número de filas de la cuadricula geográfica. |
| j = 1, 2, 3,…, TG | y | TG = número de columnas de la cuadrícula geográfica. |
| y = SG/2 | y | z = TG/2. |
La biomasa en cada celda con coordenadas geográficas kl es estimada por la ecuación (7.16) de la forma siguiente:

donde Njkl(t) es el número de individuos de edad j localizados en el sitio kl en el tiempo t. El peso promedio de individuos de la edad j (Wj), es calculado por la ecuación de crecimiento en longitud (Lj) de von Bertalanffy y su correspondiente conversión en peso:
Lj=L∞(l-e(-kp(j-to))) (7.17)
Wj=aLbj (7.18)
donde:
a y b son constantes de la relación longitud-peso.
Ahora bien, la distribución en el espacio y en el tiempo de la estructura de la población Njkl(t) se estima de la forma siguiente:
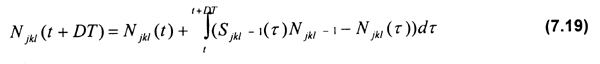
donde Sjkl(t) corresponde a la tasa finita de supervivencia de individuos de la edad j en el sitio con coordenadas geográficas kl en el tiempo t, la cual es estimada de la forma siguiente:
Sjkl(t)=[l-(l-e(-M+Fjkl(t)))] (7.20)
donde M representa la tasa instantánea de mortalidad natural y Fjkl(t) la tasa instantánea de mortalidad por pesca de individuos de la edad j en el sitio kl en el tiempo t, calculada al multiplicar el coeficiente de capturabilidad por edades (qj) por la intensidad de pesca ejercida en el sitio con coordenadas geográficas kl en el tiempo t(fkl(t)).
La captura por unidad de esfuerzo en el sitio kl en el tiempo t (CPUEkl(t)) es estimada en CHART con la ecuación siguiente:
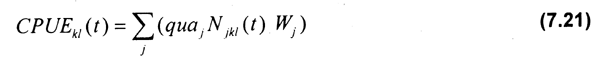
donde la capturabilidad por edad por unidad de área (quaj) es estimada utilizando la ecuación de área barrida de Baranov (1918) y la curva logística de selectividad (Sparre et al., 1989).
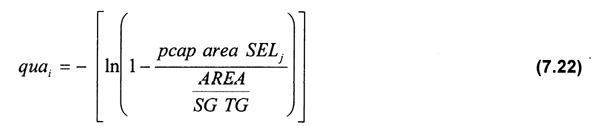
donde:
pcap = probabilidad de captura del arte de pesca utilizado.
area = área barrida por día.
SELj = selectividad del arte de pesca por edades.
AREA = área ocupada por stock.
La selectividad específica por edades es estimada según lo especificado en el Capítulo 5.
La asignación espacial de la intensidad de pesca en el corto plazo (e.g. períodos intra-anuales) se estima de manera análoga a la especificada para el modelo ALLOC con una variante: en CHART se asume que se cuenta con información espacial más precisa y por lo tanto se sustituye el parámetro Pk por el riesgo percibido (grado de peligro) por los pescadores para operar en el sitio de pesca con coordenadas geográficas kl.
La especificación de este factor permite capturar información cualitativa de la forma como los pescadores perciben el grado de peligro de su operación de pesca en sitios alternativos del área de distribución del recurso. Este parámetro se especifica con un intervalo ilustrativo de 1 a 3, donde 1 significa sin peligro y los valores 2 y 3 indican niveles crecientes de peligro en la operación de pesca.
La asignación espacial de la intensidad de pesca de las embarcaciones provenientes del puerto h en el sitio de pesca kl en el tiempo t, (fklh(t)), está dada por la siguiente ecuación:
fklh(t)=SAEklh=SAEklh(t)DP Vh(t) (7.23)
donde:
Vh(t) = número de embarcaciones registradas en el puerto h que asignan estacionalmente su esfuerzo pesquero a la especie objetivo.
SAEklh(t) = distribución (0, 1) de barcos provenientes del puerto h en los sitios alternativos de pesca kl, en el tiempo t.
SAEklh(t), en CHART es estimada por la ecuación (7.24) de la forma siguiente:
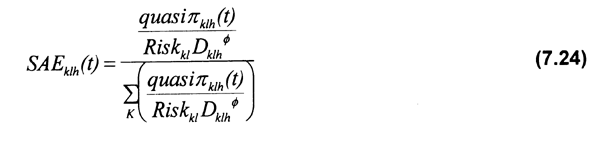
Donde:
Riskkl = riesgo o peligro percibido por los pescadores para realizar sus operaciones de pesca en los sitios alternativos de pesca kl.
La captura y la renta por sitio de pesca a lo largo de la temporada se calculan de manera análoga al modelo ALLOC.
En el largo plazo (i.e. períodos inter-anuales) la dinámica de flota, es decir, la entrada y salida de embarcaciones a la pesquería, es modelada en CHART a través de aplicar el modelo de Smith (1969) espacialmente desagregado:

donde φh es una constante positiva denominada parámetro de dinámica de la flota. La ecuación (7.24) establece que en el largo plazo y bajo condiciones de acceso abierto: (i) si la renta obtenida de todos los sitios de pesca a lo largo del año es mayor que cero, entonces habrá entrada de nuevas embarcaciones a la pesquería, (ii) si la renta antes mencionada es negativa, se esperarán salidas de embarcaciones y, (iii) si la renta es igual a cero, entonces se considera que la pesquería se encuentra operando bajo condiciones de equilibrio bioeconómico y por tanto no existe estímulo para entrar o salir de la misma.
(i) CHART es un modelo bioeconómico geográfico de estructura por edades cuyo reclutamiento es distribuido estacionalmente a través de funciones de retraso distribuido. Este componente del modelo se introduce para representar el hecho de que el reclutamiento no ocurre en un solo momento del tiempo sino en un período dado con una distribución específica.
(ii) El grado de extensión de los parches está determinado por la varianza de la densidad estimada.
(iii) La migración, la dispersión y el movimiento no son considerados, por lo cual su aplicación se limita a especies sedentarias.
(iv) La mortalidad natural se asume constante para todas las edades.
(v) La asignación espacial de la intensidad de pesca de las embarcaciones provenientes de diferentes puertos, se asume en función de la quasi-renta obtenida de los sitios alternativos de pesca, el riesgo (peligro) percibido por los pescadores para operar en dichos sitios y la distancia entre los puertos de origen y los sitios de pesca.
(vi) Las distancias entre los sitios de pesca y los puertos de origen son estimadas geográficamente sin consideración de posibles obstáculos en la ruta de navegación.
(vii) Para la dinámica de largo plazo se asume un parámetro de retraso promedio de seis meses, mientras que en el corto plazo, el usuario especifica el retraso correspondiente a la entrada de embarcaciones en el inicio de la temporada.
(viii) Como en el modelo ALLOC, la incertidumbre inherente a las capturas por día de pesca en los sitios alternativos, es modelada a través de la generación de variables aleatorias con una función de densidad probabilística exponencialmente autocorrelacionada.
(ix) Se asume que los precios de la especie objetivo y de los insumos del esfuerzo pesquero son constantes y se determinan exógenamente; sin embargo, pueden ser cambiados por el usuario en experimentos sucesivos de simulación.
Para ilustrar el comportamiento dinámico espacial de pesquerías en el corto y largo plazo se recomienda al lector conducir experimentos de simulación bioeconómica espacial con el modelo CHART del paquete de software denominado SPATIAL publicado por la FAO (Seijo et al., 1994c).
Teniendo en cuenta los conceptos anteriores, Seijo & Defeo (1994b) realizaron un análisis de corto y largo plazo de la pesquería de la almeja amarilla Mesodesma mactroides de Uruguay. Para ello se construyó un modelo dinámico estocástico no lineal que contiene las ecuaciones básicas de ALLOC para representar la dinámica espacial de corto plazo en la intensidad de pesca, pero además está construido para representar el comportamiento del recurso y los usuarios en el largo plazo.
La distribución espacio-tiempo del esfuerzo pesquero en el corto plazo fue representada en función de las estimaciones dinámicas de la CPUE en sitios de pesca alternativos, sus distancias a diferentes localidades, la probabilidad de encontrar a la especie a niveles rentables, y los correspondientes ingresos netos en el día de pesca previo. Muchos de los datos empleados a tales fines figuran en Defeo et al. (1991).
La dinámica de la pesquería en el largo plazo consideró aspectos biológicos tales como retrasos de tiempo entre el desove y el reclutamiento, así como una relación stock-reclutamiento “tipo Ricker”, i.e., con forma de domo que determinaba una inhibición del reclutamiento a altas densidades del stock parental (Defeo, 1993a, b). El reclutamiento en el tiempo fue también modelado en función de los patrones de reclutamiento aportados por Defeo et al. (1992) y distribuido a lo largo del año usando la función gamma de orden 3 en un modelo de retraso distribuido. La mortalidad natural por sitio de pesca se modeló en función de la densidad inicial de reclutas y variaciones en salinidad. La dinámica de la pesquería en el largo plazo, en lo referente a entrada y salida de los pescadores de la actividad, fue modelada por medio de la ecuación de Smith (1969) referida en el Capítulo 2. El modelo de retraso distribuido al cual se hizo alusión en páginas anteriores fue aplicado a tales propósitos (ver Seijo & Defeo, 1994b). Desde un punto de vista económico se consideraron además precios de la almeja amarilla en el mercado local, costo de oportunidad de la mano de obra y costos de operación por pescador (ver Defeo et al., 1991 para algunos datos básicos de entrada al modelo).
Conjuntamente con estos análisis, Seijo & Defeo (1994b) efectuaron experimentos de simulación con tres estrategias de manejo a efectos de observar el impacto dinámico en variables de desempeño de la pesquería, tales como densidad de adultos, captura y renta económica por localidad. El impacto de tres vectores de manejo fue simulado y comparado con la corrida base que representaba el esquema de manejo imperante en ese momento (talla mínima de captura de 50 mm y 50 permisos de pesca). Los vectores de manejo fueron los siguientes: 1) el esquema básico de manejo más una cuota anual global de captura de 50 ton; 2) reducción de la talla mínima comercializable a 43 mm (talla de madurez sexual) y aumento de permisos de pesca a 150; 3) aumento de permisos de pesca a 150, pero usando una talla mínima de captura de 50 mm.
El modelo reprodujo adecuadamente la variabilidad temporal en la abundancia de reclutas y adultos, y fue validado estadísticamente a través de la prueba no paramétrica de Kolmogorov-Smirnov. Las Figs. 7.1a y 7.1b muestran respectivamente, las variaciones temporales de las abundancias de adultos y reclutas observadas y simuladas por el modelo. Se puede observar el marcado incremento en la abundancia de adultos a partir de 1988, como resultado de un experimento de exclusión humana entre marzo de 1987 y noviembre de 1989 (ver Defeo, 1993a, b y Defeo & de Alava, 1995 para detalles sobre el experimento). Paralelamente, se observa la inhibición del reclutamiento para los dos últimos años observados (1989 y 1990), producto del fenómeno de sobrecompensación ante altas densidades del stock desovante. También como resultado de dicha inhibición, el modelo predice una disminución de la abundancia de adultos para años posteriores, lo cual trae aparejado marcadas connotaciones de manejo: el aumento de la abundancia de adultos como resultado de una clausura de la pesquería demasiado prolongada en el tiempo, puede determinar en el largo plazo (2 años) una merma en la disponibilidad de recurso a ser extraído (ver Defeo, 1993a, b).
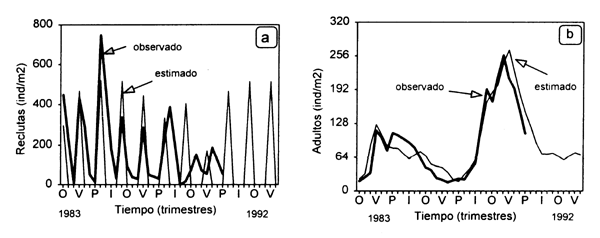
Figura 7.1 Mesodesma mactroides. Comparación de la abundancia observada y estimada por el modelo de largo plazo para reclutas (a) y adultos (b).
La pesquería mostró una fuerte incidencia estacional. El incremento de la captura en primavera y verano fue adecuadamente reproducido por el modelo, tanto en el corto como en el largo plazo. La Fig. 7.2 muestra la variabilidad espacial en la intensidad de pesca simulada para cada uno de los 4 sitios de pesca, la cual genera rentas diferenciales en cada zona.
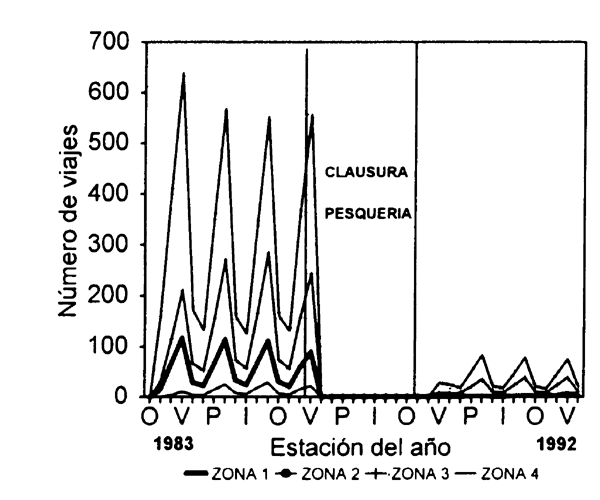
Figura 7.2 Variaciones trimestrales en la intensidad de pesca simulada por zona en base al modelo de largo plazo (1983–1992) para la pesquería de almeja amarilla Mesodesma mactroides de las costas de Uruguay.
En el corto plazo, el modelo explicó satisfactoriamente la marcada variabilidad estacional observada en los días efectivos de pesca, magnitud de las capturas e intensidad de pesca por zona (Fig. 7.3a; ver también Defeo et al., 1991), así como las oscilaciones espaciales en la renta económica generada por la pesquería. Los pescadores asignaron su esfuerzo de pesca en forma proporcional a la abundancia existente en cada zona de pesca (Defeo, 1993a, b); como resultado de ello, las zonas centrales de pesca 2 y 3, con mayor abundancia de stock, presentaron mayores valores de capturas (Fig. 7.3b) e intensidad de pesca. Cabe acotar que estas variaciones dentro y entre estaciones del año fueron correctamente representadas por el modelo.
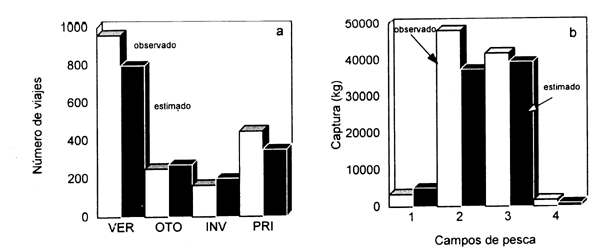
Figura 7.3 Mesodesma mactroides. Comparación de la intensidad de pesca observada y simulada por estación del año (a); variaciones espaciales de la captura por zona de pesca (verano 1985) observada y estimada por el modelo de corto plazo (b).
De acuerdo a los resultados logrados, se propone una técnica de rotación de áreas que considera períodos de desigual demanda del producto así como variaciones en la accesibilidad y abundancia del recurso (Defeo et al., 1991; Seijo & Defeo, 1994b).
La investigación bioeconómica sobre este recurso remarca la ya consabida tendencia de los recursos litorales con bajos costos operativos a lograr el equilibrio bioeconómico a altos niveles de esfuerzo pesquero. Ello incrementa seriamente el riesgo de sobreexplotación de este tipo de especies.