Sagary Nokoe
7.0 Performance objectives
7.1 Introduction
7.2 Statistical methods
7.3 Experimental design: basic concepts
7.4 Experimental designs for alley farming trials: Single-factor experiments
7.5 Experimental designs: multi-factor experiments
7.6 Notes on laying out field plots
7.7 On-farm alley trials
7.8 Summary
7.9 Feedback exercises: (Find out the answers from the text)
7.10 Suggested reading
7.11 References
Technical paper 7 is intended to enable you to:
1. List nine important factors to consider in designing alley farming trials.2. Differentiate among data collection, data screening, data transformation and data coding.
3. Recall six variables commonly used to compare treatment effects in alley farming trials.
4. Describe briefly various procedures to analyse data obtained from alley farming trials.
5. Define experimental design.
6. Explain terms: plot, treatment, experimental error, replication, randomization and blocking.
7. Identify twelve determinants in selecting appropriate experimental designs.
8. Differentiate between single factor and multi factor experiments.
9. Discuss distinguishing features and layouts of Completely Randomised Design (CRD), Randomised Complete Block Design (CRBD) and Latin Square (LS) design.
10. Describe objectives of incomplete block designs.
11. Recall major advantages of factorial experiments over a single factor experiment.
12. Explain main characteristics and uses of nested treatments and split-plot treatments in factorial experiments.
13. Differentiate between a fractional factorial design and a confounded design.
14. Recall and discuss six major factors to consider in laying out field plots for alley farming trials.
15. Discuss designs and experimental layouts for on-farm trials keeping in view different possibilities about farmers' plot sizes.
Scientific planning of each of the various operations in alley farming is based on proper experimentation that yields results which are statistically valid and easily verifiable. This paper has been written to assist researchers concerned with alley farming in designing appropriate experiments. Illustrations of designs and layouts are provided in Technical Paper 8, while the standard AFNETA experimental guidelines and trial designs are given in Volume I (Annex).
This paper's discussion of design and layout pertains to all major types of alley farming trials namely:
· multipurpose tree screening and evaluation
· alley farming management (e.g., mulching effects, crop productivity)
· livestock integration (e.g., feed supplementation, animal productivity)
· socio-economic assessment (e.g., economic returns)
The long-term nature of trials involving woody species and the varying objectives and expectations of alley farming trials demand that adequate caution be exercised in their design. Nine important issues worth noting include:
· restrictions on land availability and topography;· general increase in soil heterogeneity with increasing land area, and modification of soil characteristics by imposed hedgerow trees or shrubs;
· effect of types of land preparation on changes in soil fertility gradients;
· conferment of varying efficiencies on factors in layered or split-plot arrangements;
· consistency of design, to ensure the possibility of combined analysis;
· the need to reduce the number of factors and their levels to the basic minimum;
· the possibility of using farmers' plots (in on-farm trials) as replicates rather than as a complete experiments;
· required plot sizes and number of plots for efficient estimation of errors;
· edge effects and the rows of discards
7.2.1 Steps in Experimentation
7.2.2 Data Collection
7.2.3 Data Screening
7.2.4 Data Transformation and Coding
7.2.5 Variables
7.2.6 Data Analysis
In scientific research, the seven major steps in experimentation to find solutions to a problem are:
(1) define and state the problem;
(2) identify objectives and develop a hypothesis;
(3) design and conduct experiments to test the hypothesis;
(4) collect data;
(5) analyse the data;
(6) interpret the data;
(7) draw conclusions about the hypothesis.
Statistical methods are useful in the proper execution of each of the seven steps. We shall be briefly touching here the common methodologies Used in alley farming trials for data collection, data screening, data transformation and coding, selection of variables or observational parameters, and data analysis. Experimental design and procedures for establishing trials are discussed in a greater detail in the section to follow (7.3)
Specification of the objectives, definition of the problem, and formulation of a hypothesis are initial requirements for data collection strategies. The merit of any data will depend on their representativeness of the underlying population and their capacity for assessment and minimization of the various errors. For example, while studying the changes in soil properties as affected by alley farming it is always advisable to collect soil samples separately from alleys and hedgerows in order to assess the effects of mulching and nitrogen fixation. B. T. Kang (Pers. comm.) has observed great vertical and horizontal variation in soil properties between and across alleys and tree hedgerows.
There are three data collection strategies: experimentation, sampling, and routine observational data collection. Experimentation is discussed in much detail in a later section. Sampling procedures are used in on-farm surveys of farming practices and adoption rates, and in the collection of data from trial plots.
A sample from a real (not imaginary) population is defined as a sub-collection of that population. For statistical inference and for purposes of error minimization and reduction of observer-bias, these collections should be randomly obtained. The number and larger size of sampling units can be determined optimally by considering a cost/variance function. Generally, a highly variable population will require greater number of sampling units than for a fairly homogenous population.
A useful guiding principle for sampling is that the plot size and/or frequency should be large enough to include a good representation of the population, but small (or few) enough to ensure that sampling is achieved within a reasonable period of time. Further discussion on plot sizes and layouts is provided in the section "Notes on laying out Field Plots" (section 7.6).
In many cases, not all data collected will adequately represent the population under study. Two obvious reasons could be: faulty experimental or sampling technique, or wrongly derived data due to incorrect calculations or measuring scales. In data screening, unrepresentative or other wise faulty data is rejected.
A good practice is to assume the possibility of errors in data, and then perform screening procedures to test the assumption. The procedures include:
· re-checking of data, which could imply revisiting the study site or re examining the collected sample in cases of suspect observations;· re-computing derived values and checking for consistency in measuring units (inches or meters, kilograms or pounds, acres or hectares, etc).
When the suspect values are not due to measurement errors, one can further subject the data to statistically acceptable data screening procedures. These tests are usually referred to as "tests of outliers or spurious observations." They depend largely on the statistical distributions principle. A common procedure for data assumed to follow the normal distribution is to compute the 95% confidence limits on the mean of the observations. If the suspected outlier falls outside the limits, it is rejected from further statistical analysis.
Transformation of data may be carried out to achieve one or all of the following objectives:
· equalization of variances
· normalization of observations
· selection of appropriate regression variables
The overall aim, however, is to ensure the use of correct statistical procedures. Common transformations include the square root and logarithm for counts and the angular for percentages.
Data coding is different from data transformation. Ranking of data from original observations, reducing or increasing all data by a common factor are common forms of data coding. Sometimes this is done to simplify the arithmetic computations or in the case of species coding, to facilitate the use of conventional statistical procedures.
Variables are the characteristics a researcher intends to observe and compare among the various treatments. They are usually explicitly stated along with the statement of the problem. The six important types of variables related to alley farming trials are:
· Agronomic variables - germination and survival percentages, tree height and growth, stem form, biomass weight, crop yield, etc.;· Soil chemical variables - soil fertility (nutrients type and level) with regard to hedgerows or alleys;
· Plant chemical variables - levels of essential elements (N. P. K) etc.;
· Socio-economic variables perceived to be of importance to the farmers Examples include farmer views of the importance of a particular treatment, or the social costs and benefits of alley farming;
· Economic variables;
· Derived variables, e.g., differences in response of control and introduced treatments.
Analyses of alley farming trials are usually straight-forward and involve one or more of the procedures listed below. (The reader is referred to the suggested readings for detailed descriptions of data analysis procedures.)
· Treatment means comparisons procedures, using the t-test (for two means at a time) and the analysis of variance (for more than two comparisons at a time);· The use of regression procedures to establish or identify relationships between the independent and dependent variables;
· The use of covariance procedures;
· Non-parametric or distribution free procedures for assessing variables;
· The method or repeated measures analysis is particularly relevant in alley farming trials and long term studies. This procedure enables one to study differences between treatments at any particular period, differences between periods for specified treatments, interactions between period and treatments, and the identification of trends in response variables;
· Jolayemi (1989) has also suggested the method of differencing for removing the effects of auto-correlation which are inherent in repeated measures (time-dependent data) or adjacent plots. Routine analysis of variance may then be performed on such differenced data;
· The use of the land equivalent ratio could be considered when more than one crop are planted in the alley. This ratio is simply the sum of the ratios of the yields when planted on an area of the same size used for all the intercrops. This data conversion procedure is used to ensure the use of a single yield component for assessing different intercropping combinations.
· Additional Treatment means comparison procedures, such as the Duncans multiple range, the Student-Neuman-Keuls procedure, etc. The least significant difference and single degree of freedom contrasts could also be useful for pre-experimentation comparisons.
7.3.1 What is Experimental Design?
7.3.2 Basic Terminology and Concepts
7.3.3 Determinants in Selecting Experimental Designs
In experimentation we attempt to monitor the effects of certain inputs or material on the subject matter, of interest. The inputs could be different hedgerow leguminous plants planted under identical conditions, while the effects to be monitored could be the changes in soil fertility status, the yield of agricultural crops planted between the rows, the productivity of the animal being fed with the foliage from the tree crops, or the tree crop performance. The allocation of treatments (inputs) to the experimental units (plots) may be loosely referred to as the design.
The experimenter decides which individual unit is to receive which particular treatment according to a laid down procedure. The choice of procedure will often determine the basic design. What is important, however, is that during an experiment, the researcher has a choice as to how and when to apply the treatments. (In a survey situation, in contrast, there is no such choice). The choice of design is influenced by several considerations, notably the objectives, the amount of resources, and the time available. In till cases, however, the emphasis is on the reduction of unknown error and the elimination of systematic bias.
· The plot or experimental unit is the smallest unit receiving a certain treatment. The information or-data for comparison are from such single units. Examples include a single animal or group of animals receiving the same feed from the same source, a small plot having the same type of trees or agricultural crops, and so on.
· The treatment is the material being forced on the subject (unit) and whose effect is to be monitored. The treatment can be either qualitative (e.g., species, fertilizer types) or quantitative (e.g., time periods, quantified levels of a fertilizer type).
· The experimental error is a measure of the sum of variation between plots or units receiving same treatments. Suppose there are five different treatments with each treatment repeated or replicated four times. We could obtain the square of the deviation of each observation from its treatment mean, sum these up, and then obtain the average to give an idea of that treatment variance. There will be five such treatment variances. The "average" of these variances is roughly a measure of the experimental error. Inherent variability in the subject, uncontrolled external influences, and lack of uniformity in the application of treatments are possible causes of experimental error. Experimental error should be controlled so that we can estimate the treatment effects properly and compare effects of various treatments effectively.
· Types of Field Experiments: The several types of experimental trials include:
· variety trials;
· provenance trails;
· field germplasm or screening trials;
· fertilizer trials;
· cultural/agronomic trials;
· chemical (other than fertilizer) trials.
It is quite common to have more than one type of trial in the same experiment. For instance we can compare different hedgerow species under weeding and no-weeding, that is, a situation involving both variety and cultural trials. However, species screening trials are best done on their own, rather than mixed up with other trials. Having selected the most suitable species for a particular area, aspects of intra-row spacing and other agronomic/management inputs can then be investigated.
· Replication: Experiments of the same nature, when presented under similar conditions, should yield similar results. In other words, researchers would want to ensure consistency in their results. The simplest way to achieve this is through the "repetition," i.e. "replication," of the same treatment on several plots or experimental units. Repetition on the same plot is not recommended as observations are unlikely to be independent. Moreover, the use of several small plots instead of one large plot ensures minimization of the effect of uncontrolled variability in the field.
· Randomization: This refers to the allocation of treatments to plots in such a way that, within a specific experimental design, units are not discriminated for or against. Each unit is supposed to have the same chance of receiving a particular treatment. Randomization is a necessity as no two units or plots are exactly the same. Statistically, the randomization procedure allows elimination of bias and ensures the computation of valid sampling errors.
· Coverage or Blocking: A block is a relatively large area or several identical units receiving all or most of the treatments. One is encouraged to "block" if one can vouch for the homogeneity within blocks and the heterogeneity between blocks. Because of the limitation of homogenous plots and the relatively large area required for alley-farming and agroforestry trials, one could also consider a location as a "block." The distinction between "replication" and "blocking" should be evident. Blocking is another way of improving the estimation of the error term, but only if the blocking is justified.
To ensure the selection of appropriate experimental designs, the experimenter will need to respond to the following twelve issues:
· What are the specific study objectives?· What are the variables to be observed (i.e. the dependent variables)?
· Are these dependent variables quantifiable and/or measurable? If these are not measurable, what criteria will you use for later comparisons among treatments?
· What are the independent variables that is to say, the treatments to be applied)?
· Are these treatments fixed or random? In other words, do you have several treatments to choose from or do you have a fixed number of treatments among which specific comparisons are desired?
· Are the levels of treatments qualitative (e.g. Species - Acacia, Gliricidia, Eucalyptus or quantitative (e.g., solutions - 10 mg/l, 20 mg/l, 30 mg/l etc.)?
· How many replicates of each treatment can be available?
· Will all the replicates be available at the same time?
· How much land or material (to which the treatments are to be applied) are available?
· Are the subject materials or available land uniform enough to receive all treatments at a time?
· What will be the sampling unit? That is, indicate how small or large is the area or material to be observed. (In response, one may simply define the area.)
· How often will data (from dependent variables) be collected ?
7.4.1 Introduction to Single-Factor Experiments
7.4.2. Complete Block Designs
7.4.3 Incomplete Block Designs
Knowledge of experimental design is necessary for selection of simple designs that give control of variability and enable the researcher to attain the required precision. We have already discussed certain factors which are important in selecting an experimental design. The three most important among these are:
· type and number of treatments,
· degree of precision desired,
· size of uncontrollable variations.
We generally classify scientific experiments into two broad categories, namely, single-factor experiments and multifactor experiment. In a single-factor experiment, only one factor varies while others are kept constant. In these experiments, the treatments consist solely of different levels of the single variable factor. Our focus in this section is on single-factor experiments.
In multi-factor experiments (also referred to its factorial experiments), two or more factors vary simultaneously. The experimental designs commonly used for both types of experiments are classified as:
· Complete Block Designs- completely randomised (CRD)
- randomised complete block (RCB)
- latin square (LS)· Incomplete Block Designs
- lattice
- group balanced block
In a complete block design, each block contains all the treatments while in an incomplete block design not all treatments may be present. The complete block designs are suited for small number of treatments while incomplete block designs are used when the number of treatments is large.
We will discuss here three basic designs which come under the category of complete block designs, namely CRD, RCB, and LS.
The layout of the designs will be illustrated with the example of a modified research protocol on the "Evaluation of four Gliricidia accessions in intensive food production" (Atta-Krah, pers. comm.). The objective of the protocol is to evaluate top potential Gliricidia accessions under intensive feed garden conditions. The plot size is 8 x 5 m with 3 rows or columns of an accession in each plot. The available area is capable of containing a maximum of 16 plots.
Completely Randomised Design (CRD)
This is the simplest design. In CRD, each experimental unit has an equal chance of receiving a certain treatment. The completely randomised design for p treatments with r replications will have rp plots. Each of the p treatment is assigned at random to a fraction of the plots (r/rp), without any restriction. As stated above, if we have four Gliricidia accessions designated as A, B. C and D and we evaluate them using four replications in CRD, it is guise likely that any one of the accessions, say A, may occupy the first four plots of the 16 plots as illustrated in the following hypothetical layout.
|
A |
A |
A |
A |
|
B |
C |
C |
D |
|
D |
B |
C |
B |
|
D |
C |
B |
D |
A Useful assumption for the application of this design is homogeneity of the land or among the experimental materials. This design is rarely used in most trials involving woody vegetation, but could be used under laboratory and possibly green house conditions.
The total source of variation (error) is made up of differences between treatments and within treatments.
Randomised Complete Block Design (RCBD)
One possibility that could arise in design or layout of alley farming trials is differences in the cultural practices or crop-rotation history of the portions of land available for the study. Alternatively, there could be a natural fertility gradient or, in the case of pest studies, differences in prevailing wind direction. If any of these heterogenities are known to exist, one can classify or group the area into large homogenous units, called blocks, to which the treatments can then be applied by randomization.
Randomized Complete Block Design (RCBD) is characterized by the presence of equally sized blocks, each containing all of the treatments. The randomised block design for P treatments with r replications has rp plots arranged into r blocks with p plots in each block. Each of the p treatments is assigned at random to one plot in each block. The allocation of a treatment in a block is done independently of other blocks.
A layout for 16 accession plots, grouped in 4 blocks, may be as follows:
|
PREVIOUS CROPPING HISTORY |
BLOCK |
ACCESSION | |||
|
Fallow |
1 |
A |
C |
B |
D |
|
Maize |
2 |
A |
B |
D |
C |
|
Gmelina |
3 |
B |
D |
C |
A |
|
Maize/Gmelina |
4 |
B |
C |
A |
D |
The arrangement of blocks does not have to be in a square. The above arrangement can also be placed as follows:
|
A |
C |
B |
D |
|
A |
B |
D |
C |
|
B |
D |
C |
A |
|
B |
C |
A |
D |
|
|| |
|| |
|| |
|| |
|
|| |
|| |
|| |
|| |
|
|| |
|| |
|| |
|| |
|
|| |
|| |
|| |
|| |
where || represents 3 columns or rows of accession.
The actual field plot arrangement, with three columns of each accession for the first two blocks could be as follows:
|
<-----BLOCK 1-----> |
|
<-----BLOCK 2-----> | ||||||
|
a a a |
c c c |
b b b |
d d d |
|
a a a |
b b b |
d d d |
c c c |
|
a a a |
c c c |
b b b |
d d d |
|
a a a |
b b b |
d d d |
c c c |
|
a a a |
c c c |
b b b |
d d d |
|
a a a |
b b b |
d d d |
c c c |
|
a a a |
c c c |
b b b |
d d d |
|
a a a |
b b b |
d d d |
c c c |
|
a a a |
c c c |
b b b |
d d d |
|
a a a |
b b b |
d d d |
c c c |
|
a a a |
c c c |
b b b |
d d d |
|
a a a |
b b b |
d d d |
c c c |
The total source of variation may be categorized as differences between blocks, differences between treatments, and interaction between blocks and treatments. The latter is usually taken as the error term for testing differences in treatments.
The Randomized Complete Block Design (RCB) is the most commonly used, particularly because of its flexibility and robustness. However, it becomes less efficient as the number of treatments increases, mainly because block size increases in proportion to the number of treatments. This makes it difficult to maintain the homogeneity within a block.
In RCB, missing plots (values) leading to Unbalanced designs were problematic at one time. However, this is not much of a problem now due to the availability of improved estimation methods, for example, the use of generalized linear models. For situation with less than three missing values, one can still use the traditional computational procedure of RCB design.
Latin Square Design (LS)
The Randomised Complete Block design is useful for eliminating the contribution of one source of variation only In contrast, the Latin Square Design can handle two sources of variations among experimental units In Latin Square Design, every treatment ocurs only once in each row and each column. In the previous example, cropping history was the only source of variation in four large blocks Supposing in addition to this we have a fertility gradient at right angle to the "cropping history" as shown below:
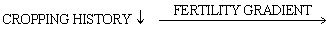
One may tackle this problem by using a Latin Square Design Each treatment (in this case, the Gliricidia accessions) is applied in ''each" cropping history as well as in "each" fertility gradient In our example, restriction on space allows us to have a maximum of only 16 plots, when, say, 64 might have been ideal. The randomization process has to be performed in such a way that each accession appears once, and only once, in each row (cropping history) and in each column (fertility gradient). The layout will be as follows:
|
CROPPING |
FERTILITY GRADIENT | |||
|
HISTORY |
1 |
2 |
3 |
4 |
|
Fallow |
A |
C |
B |
D |
|
Maize |
B |
D |
A |
C |
|
Gmelina |
C |
B |
D |
A |
The four blocks correspond to the four different cropping histories. The Latin Square (LS) design thus minimises the effect of differences in fertility status within each block. The total sources of variation are made up of row, column, treatment differences, and experimental error.
For field trials, the plot layout must be a square. This condition imposes a severe restriction on the site as well as on the number of treatments that can be handled at any one time. However, the principle can be extended to animal experimentation where a physically square arrangement does not necessarily exist. For instance, if the intention is to assess the nutritional effects of the accessions when fed to animals, the latter could be divided into four age and four size classes. The LS arrangement will thus be used to ensure that each age class and size class receives one and only one of each accession type.
The LS design can be replicated leading to what is commonly referred to as "Replicated Latin Squares". These Latin squares may be linked as shown below:
|
CROPPING |
FERTILITY GRADIENT | |||||||
|
HISTORY |
A |
C |
B |
D |
D |
A |
C |
B |
|
|
C |
B |
D |
A |
A |
B |
D |
C |
|
|
B |
D |
A |
C |
C |
D |
B |
A |
|
|
D |
A |
C |
B |
B |
C |
A |
D |
In the case of the above, the two squares have the same set of rows (cropping histories), leading to an increased degree of freedom for the error term. The rows are said to be linked. If, on the other hand, the rows are not linked, "Rows Within Squares" variability replaces the ordinary "Row" source of variation.
An additional restriction (source of variation) imposed on a basic LS design would lead to what is called "Graeco-Latin Square Design".
One precondition for both the RCB and LS designs is that all treatments must appear in all blocks and all rows (For RCB) or columns (For LS). Sometimes with large number of treatments (say 20 accessions), each requiring relatively large plot sizes, this condition may not be practicable. Latin Square and RCB then fail to reduce the effect of heterogeneity(s). The designs in which the block phenomenon is followed but the condition of having all the treatments in all blocks is not met, are called Incomplete Block designs. In Incomplete Block situations, the use of several small blocks with fewer treatments results in gains in precision but at the expense of a loss of information on comparisons within blocks. The analysis of data for incomplete block designs is more complex than RCB and LS. Thus where computation facilities are limited, incomplete block designs should be considered a last resort.
Among incomplete block designs, lattice designs are commonly used in species and variety testing. These are more complex designs beyond the scope of this paper, but covered in a number of text books cited at the end of this paper. It is always advisable to consult a statistician when using incomplete block designs.
7.5.1 Factorial Treatments
7.5.2 Nested Treatments/Nested Designs
7.5.3 Nested-Factorial Treatments
7.5.4 Split-Plot Arrangement
7.5.5 Multi-Factor, Incomplete Block Designs
We have so far concentrated on only one factor (i.e., one accession or other treatment). However, more than one factor will often need to be studied simultaneously. Such experiments are known as factorial experiments. The treatments in factorial experiments consist of two or more levels of the two or more factors of production.
Suppose we are interested in studying the yield of an agricultural crop in an alley farm where four different leguminous tree species and three cultural methods are of interest. The leguminous tree species could be Acacia sp., Cassia sp., Leucaena sp., and Gliricidia sp.
The cultural treatment could include two weedings, one weeding and no weeding; the agricultural crop is maize planted between hedgerows of the same tree species. For a complete factorial set of treatments, each level of each factor -must occur together with each level of every other factor. Thus in the present case we ensure that each cultural method is applied to each tree species. Since there are 4 species and 3 cultural methods, the total number of treatments will equal 12. In reality, what we have here is 12 treatments, with one treatment being made up of 2 factors having 4 and 3 levels, respectively. One might say, in this case, the factors are crossed.
This is not an "experimental design" but rather a "treatment design," because the 12 treatment combinations could be applied to any of the designs discussed previously. If we take the simplest design, the unrestricted randomized design, and four replications, then the conduct of an experiment with 4 leguminous species and 3 cultural methods will imply the randomization of " 12 treatments'' in 48 plots. If it is a Block design, we will have to ensure that each of the 12 treatments appears in all the blocks.
The advantages of the factorial arrangement are many. One major advantage is the reduction in the number of experiments, and a second the possibility of studying the interactions among the various factors. A significant interaction implies that changes in one factor may be dependent on the level of the other factor. If this happens, interpretation of the results has to be done cautiously to avoid inaccurate general statements on the individual factors.
The situation discussed above can be extended to two or more locations, and the results combined using the Combined Analysis Procedure. However, it does at times happen that species may be location specific, in which case the 4 leguminous tree species utilised in a particular location may not be suitable at other locations. One approach would then be to use 4 different species in each location. Or, a particular tree species may not appear in all the locations. This structure of treatments falls under the category of Nested Designs (or better, Nested Treatments). The tree species are said to be nested in locations, not crossed as in factorial treatment. It is necessary to emphasize that this nested-treatment arrangement can be applied to any of the basic designs, such as CRD, RCB and LS.
This type of treatment arrangement is followed when some factors in the same experiment are crossed (as in factorial treatment) while others are nested. For instance, if we impose three fertilizer levels to the trees nested in the example above a nested-factorial treatment arrangement is obtained - provided the same fertiliser levels are used for all trees and locations.
Split-plot experiments are factorial experiments in which the levels of one factor, for example tree species, are assigned at random to large plots. The large plots are then divided into small plots known as "sub-plots" or "split plots", and the levels of the second factor, say cultural practices, are assigned at random to small plots within the large plots.
This arrangement is often useful when we wish to combine certain treatments (as in factorial and nested), some of which require larger plots than others for practical and administrative convenience. Examples are situations requiring spraying insecticides, irrigation, tillage trials, etc. Usually, the treatment on which maximum information is desired is placed in the split-plot or in the smallest plot.
It is important to emphasize that the split-plot is not a design as such but rather refers to the manner in which treatments are allocated to the plots. A split-plot arrangement in an RCB design will usually have two error terms - one for testing the treatments in large plots (not efficient) and the other for the sub-plot treatments and interactions (very efficient).
A split plot design can be further extended to accomodate a third factor through division of each sub-plot into sub-sub-plots. This is then called a split-split-plot arrangement.
Although factorial experiments provide opportunities to examine interactions among various factors, they are difficult to conduct when the number of factors and their levels are many. Consider a situation involving 3 factors, each of which has 4 levels, making a total of 43 or 64 treatment combinations. The conduct of this experiment will require very large blocks if we employ randomised block design. Obviously in field plot experimentation this could be a major defect.
To overcome this difficulty, fractional factorial or confounding designs can be used. In a fractional factorial design, only a fraction of the complete set of factorial treatment combinations is included. Here the main focus is on selecting and testing only those treatment combinations which are more important. The fractional factorial design is used in exploratory trials, where the main objective is to examine the interaction between factors. In a confounding design all the treatment combinations of the factors and levels under study are tested with blocks containing less than the full replications of the treatment combinations.
The two procedures do not allow equal evaluation of all the effects and interactions. Depending on what is being confounded, some effects may not be estimated at all. This problem can be resolved through a conscious and objective selection of the input variables. With the limited number of variables in alley farming research, the need for confounding may not be as great as the need for fractional replications and or balanced incomplete blocks. To use the fractional factorial or confounding designs, the assistance of a statistician is a must.
7.6.1 Discards and Sample Units
7.6.2 Soil Heterogeneity
7.6.3 Plot Orientation
7.6.4 Plot Shape and Size
7.6.5 Selection of Experimental Site
7.6.6 Guidelines in Recording Data
As in any field crop experiment, not all the areas in alley farming experimental plots need to be observed during data collection. If we are comparing two or more hedgerow species for their effectiveness in enhancing soil fertility, the following possibilities in layout, subject to land restriction, could arise:
Subject to land restriction
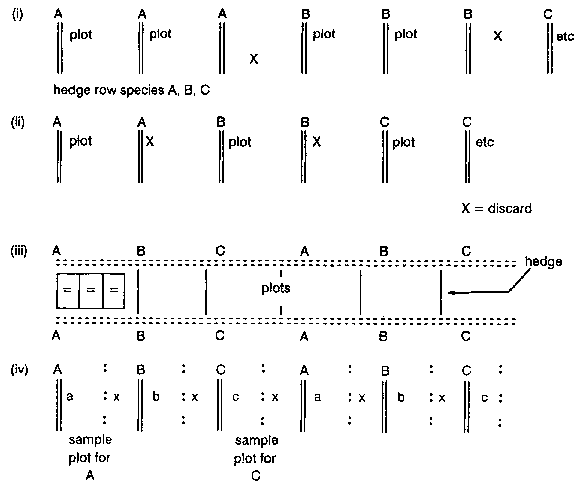
The arrangement in (i) provides two plots for each hedgerow species for soil nutrient or crop yield studies. One whole plot is discarded between the last row of a species and the first row of another species. If land is not limiting, this arrangement is ideal. Some practitioners will even go further to sample or observe the area surrounding only the middle hedgerow, i.e., one half-plot to the left and one half-plot to the right of the middle hedgerow of the same species.
For the assessment of the hedgerows themselves, the middle hedgerow constitutes an ideal sampling unit. However, in most practical situations, particularly where the hedgerow species are spaced widely apart from each other, examination of all hedgerows may be acceptable.
Arrangements (ii) and (iii) have been found useful when land is particularly limiting. In situation (iii), the area to sample lies between the two rows as marked in treatment A.
The arrangement in (iv) is not recommended, but has been used Under serious land limitation and species availability situations. The sample plots are half-plots. For consistency, either the right-hand or left-hand side of the hedgerow should always be chosen. Remember that the hedgerow species at the edges cannot be studied reliably. Given enough replications, these could be ignored. If the interest is in the yield of the hedge crop itself, then the arrangement in (iv) is very much appropriate, with the sampling Unit being the inner rows of the hedges. This implies ideally a minimum of three rows per species for effective assessment.
The areas marked "x" in the illustrations are usually planted with the agricultural crops, but not assessed. Unplanted gaps are not recommended as they are likely to aggravate the edge effects.
For long-term experiments involving perennial crops such as hedgerow species, agronomists have recognised the need to establish the nature and extent of soil heterogeneity through "blank" trials, before the conduct of the actual trial. This involves the planting of a bulk crop on the experimental field and monitoring its performance. On the other hand, if one is familiar with the cropping history of an area, this could be considered accordingly while laying out the trial so as to eliminate the delay in planting trials. When planting on farmer's plots the knowledge base of the farmer should not be ignored.
Irregularly sloped areas should be avoided, but there is no objection to the Use of area with a near constant slope provided the plots run up and down the slope. The same principle applies on a fertility gradient. For trials on terraces, one should ensure that all the treatments (except in incomplete block situations) appear on the same terrace, so that a terrace could be regarded as a block (Rao and Roger, 1 990).
In alley farming, plot shapes are more likely to be square or rectangular than any other shape. A square plot exposes the least number of plants to the edge effect. Avoid circular plots; on sloping grounds, circular plots tend to be ellipses. As regards plot size, plots that are too small yield unreliable results. On the other hand, excessively large plots waste time and resources.
The most important factor in selecting an experimental site is its representativeness of the area. It should be of appropriate shape and size for the conduct of the experiment. The land and soil characteristics as well as past cultural practices should be known as far as possible. It should have an access to a road and be distant from environmental modifiers.
Record only as much data as you can analyse and interpret. Use metric units to record the data. Always note the date of data collection. Use standard procedures for recording the data.
7.7.1 Farmers' Plot Sizes Unlimited
7.7.2 Farmers' Plots as Replicates
7.7.3 Farmers' Plots Inadequate for Complete Replicates
7.7.4 Farmers Plots as Single Experimental Plots
On-farm research, whether managed by the researcher or the farmer, requires simplicity in design. Sometimes this simplicity requirement may be due to limited resources such as land, or subject materials (treatments). However, it is more often due to the fact that complexity in design renders the management and data collection burdensome, especially for the farmer.
The statistical implications also encourage simplicity. If the treatments are not kept to a basic minimum of two or three, the whole experiment, with or without replications, cannot be carried out on one smallholder's property. This would require the Use of several farmers plots, either as replicates or single plots. This could result in increased variability and might make it impossible to compare effectively some treatments and/or farmers.
The following four possibilities may exist in the availability of experimental plots on farmers fields:
· Farmers' plot sizes unlimited;
· Farmers' plots as replicates;
· Farmers' plots inadequate for complete replicates:
· Farmers plots as single experimental plots.
This is a happy situation in which a complete trial is performed on each of the farmers. property. The unlimited nature of the available area would enable the use of all the treatments and the relevant replications on the same farmer's fields. The complete experiment is thus performed at each site. Any of the basic designs can be applied here, depending on the nature of the land and treatments being tested. These trials are time-consuming and are mostly researcher-managed. The obvious limitation is that only a small number of such farmers' plots would be available for experimentations.
This situation arises when the farmers plots are large enough to accommodate all the treatments, but not large enough to allow for replications. The fact that replications are not possible in this situation implies that the usual Completely Randomised Design (CRD) will not be applicable. What is more likely to be feasible is the Randomised Complete Block Design (RCB) in which a farmer's plot will be regarded as a block receiving all the treatments. This is illustrated below for four treatments (A, B, C, D).
|
(i) |
Farmer 1 |
A |
B |
D |
C |
|
|
Farmer 2 |
B |
A |
D |
C |
|
Farmer 3 |
C |
D |
A |
B |
The arrangement in (i) is a typical complete block layout. The minimum replications is only three farmers, but this can be increased depending on the availability of resources and time. We will, in the case of design (i), assume uniformity in land and other considerations within each farmers plot, but will allow for heterogeneity between the farmers plots. In a classical block arrangement, we often conclude that the block design is justified when the analysis indicates significant differences between blocks. This is not a necessity in the on-farm situation. The use of the farmers plots is to ensure reasonable replications (unless clearly observed differences are known to exist). The analysis however does not exclude comparisons between the farmers (i.e., between blocks).
In illustration (ii) below, we assume a situation similar to (i) except that each farmer's plot can be stratified into four units according to, say, soil type, crop type, management practices, etc. (a, b, c, d). We have assumed that four such farmers with all the four classifications (strata) are available. Although not easily identifiable, this arrangement is in fact a Latin Square. Notice that each treatment appears once and only once in each stratum and in each farmer's plots. The LS design can be seen more clearly below in (iii).
A, B, C, D = Species or accession
a, b, c, d = Clarification variable (e.g. soil types)
|
(ii) |
Farmer 1 |
a |
b |
c |
d |
|
|
|
A |
B |
C |
D |
|
|
Farmer 2 |
b |
a |
c |
d |
|
|
|
A |
D |
B |
C |
|
|
Farmer 3 |
c |
d |
a |
b |
|
|
|
D |
A |
B |
C |
|
|
Farmer 4 |
b |
c |
a |
d |
|
|
|
D |
A |
C |
B |
|
(iii) |
|
Strata | |||
|
|
|
a |
b |
c |
d |
|
|
Farmer 1 |
A |
B |
C |
D |
|
|
Farmer 2 |
D |
A |
B |
C |
|
|
Farmer 3 |
B |
C |
D |
A |
|
|
Farmer 4 |
C |
D |
A |
B |
Layout (ii) assumes a different ordering of the classification variable (a, b, c, d) for each farmer's plots. This is more likely than the hypothetical standard ordering given in (iii).
We consider a situation in which the subject materials (treatments) are not in limited supply, but plot size considerations do not allow for the allocation of all treatments in the same farmer's plot. We might thus wish to deny some farmers' plots certain treatments. This would mean an incomplete block design. A valid statistical design results if pains of treatments appear the same number of times. The only issue worth determining here is the number of farmers plots required to ensure this requirement.
If we assume each farmer's plot can accommodate a maximum of three treatments, then:
· For 4 treatments, we will need 4 farms;
· For 5 treatments, we will need 10 farms;
· For 6 treatments, we will need 20 farms;
· For 7 treatments, we will need 35 farms;
· For 10 treatments, we will need 120 farms.
In general, for t treatments and a block size of b (number of experimental plots on farmers field), the number of farmers for a balanced incomplete block arrangement is
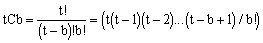
For this arrangement, it is important to keep the number of treatments to the basic minimum. A maximum of 5 treatments requiring 10 farmers should be more than adequate. An example of a possible treatment combination (not necessarily layout) for (i) is given as follows:
|
Farmer 1 |
A |
B |
C |
|
Farmer 2 |
A |
B |
D |
|
Farmer 3 |
A |
C |
D |
|
Farmer 4 |
B |
C |
D |
We note that pairs AB, AC, BD, etc., occur the same number of times, that is twice. For the field layout, each set of treatment will be randomised within each farm.
We consider two possibilities:
(i) Farmers plots identical
(ii) Farmer's plots variable
In experimentation, as already pointed out, we are interested in observing the effects of treatments when applied to identical units. Thus in situation-(i) we would simply assign the treatments to the farmers' plots as illustrated for a hypothetical set of 3 treatments (A, B. C) and 12 farmers, as follows:
|
Farmer 1 |
A |
Farmer |
7 |
A |
|
Farmer 2 |
B |
Farmer |
8 |
C |
|
Farmer 3 |
A |
Farmer |
9 |
C |
|
Farmer 4 |
C |
Farmer |
10 |
B |
|
Farmer 5 |
B |
Farmer |
11 |
B |
|
Farmer 6 |
A |
Farmer |
12 |
C |
However, if instead of assuming identical farmers' plots, we recognise that some plots have identical traits different from others, then we would group the similar farmers separately and apply the treatment accordingly. This is situation (ii), and could be illustrated as follows:
|
Group 1 Degraded soil, maize as only previous crop |
Group 2 Degraded Soil, maize & cassava previous crop |
Group 3 Fertile soil, maize as only previous crop | ||||||
|
Farmer |
1 |
A |
Farmer |
3 |
A |
Farmer |
2 |
B |
|
Farmer |
4 |
B |
Farmer |
5 |
C |
Farmer |
9 |
A |
|
Farmer |
8 |
C |
Farmer |
6 |
B |
Farmer |
10 |
D |
|
Farmer |
12 |
D |
Farmer |
7 |
D |
Farmer |
11 |
C |
These layouts can also be modified as in split-plot arrangements.
7.8.1 Summary of Important Points on Statistical Methodologies
7.8.2 Summary of Important Points on Experimental Design
7.8.3 Summary of Important Points on Field Layout and On-Farm Trials
Basic principles for the design. and layout of alley farming trials have been outlined and illustrated. These should not be taken as a complete presentation. Neither does the paper cover all possible field plot designs.
It is important to mention that appropriate experimental designs are the first step in the conduct of successful experiments. Accordingly, whenever we are not sure of the appropriateness of a design with regard to a particular scientific objective or to the availability of physical resources, we must consult a statistician.
While simplicity should be the watchword in deciding the design and layout for an alley farming trial, the basic requirements of randomization, replication and blocking should not be overlooked. The study of many factor and levels simultaneously, will necessarily lead to the use of complex designs for which assistance from a statistician is a must.
1. Alley farming trials are long term, due to the inclusion of woody species, and therefore require special caution in their designs.
2. Seven steps in experimentation are:
· define the problem
· identify objectives and develop a hypothesis
· design and conduct experiments to test the hypothesis
· collect data
· analyse data
· interpret data and
· draw conclusion about the hypothesis.
3. The definition of the problem and objectives of the experiments determine the type of data to be collected in a trial.
4. Data screening aims at identifying representative data for the population. Data is transformed to suit to appropriate statistical procedures. The ranking of data and the reduction or increase of all data are examples of data coding.
5. Variables refer to characteristics that will be measured for treatment effects in a trial.
6. The procedures used in data analysis depend on the objectives and methods of data collection.
1. Monitoring of the effects of certain inputs on a subject matter is known as experimentation.
2. The allocation of treatments to an experimental unit or plot is referred to as an experimental design.
3. A plot is the smallest unit of land receiving a treatment.
4. The treatment is the material being forced on the subject and whose effect is to be studied.
5. Experimental error is a measure of the difference between two units treated alike.
6. Replication is the number of times a complete set of treatments is repeated In an experiment.
7. Randomisation refers to the allocation of treatments to plots in such a way that within a specific experimental design, Units are not discriminated for or against.
8. A block is a large area or several identical units receiving all or most of the treatments.
9. Issues to consider in selecting art experimental design include the choice of dependent and independent variables, the availability of subject material, data collection procedures and timing.
10. In a single-factor experiment, only one factor varies while others are kept constant.
11. Experimental designs cart be broadly classified as:
· complete block
· incomplete block
12. Three important basic designs in the group of complete block designs are:
· Completely Randomised (CRD)
· Randomised Complete Block (RCBD
· Latin Square (LS)
13. Completely Randomized Design offers an equal chance of receiving a treatment by each experimental Unit. However, it is appropriate only for experiments with homogeneous experimental units.
14. Randomized Complete Block Design is characterized by the presence of equally sized blocks, each containing all of the treatments. It reduces the error of one source of variation among experimental units. It is one of the most popular designs for agricultural experimentation, but becomes less efficient with large number of treatments.
15. Latin Square Design is capable of handling two known sources of variations among experimental units. In this design every treatment occurs only once in each row and each column.
16. Incomplete block designs are those in which each block does-not contain all the treatments. These designs are Used to accommodate large number of treatments.
17. Experiments in which two or more factors vary simultaneously are known as multi-factor or factorial experiments.
18. The major advantage of a factorial experiment is that it offers an opportunity to examine interactions among various factors.
19. In factorial experiments, factorial treatments can be tested using any one of the basic designs used for single factor experiments.
20. The commonly used designs for factorial treatments other than the CRD, RCBD and LS are:
· Complete Block- Nested
- Split plot· Incomplete Block
- fractional factorial confounded
1. Use of appropriate sampling units is essential for the valid statistical analysis of the data.
2. Knowledge of soil heterogeneity is a prerequisite for the field plot layout of an experiment.
3. Irregularly sloped areas should be avoided for alley farming trials. On terraced land, a terrace may be treated as a block.
4. Rectangular and square plots are preferred for field experimentation. Plots that are too small yield unreliable results and too large plots waste time and resources.
5. An experimental site should be accessable, located away from environmental modifiers, representative of the area, and consistent with experimental design.
6. Use standard procedures for recording date.
7. For on-farm trials, one should use simple designs only.
8. The availability of experimental plots OPT farmers' fields could be visualised as follows:
· farmers' plot sizes unlimited
· farmers' plots as replicates
· farmers' plots not complete replicates
· farmers' plots as single experimental plot
10. Use conventional designs if availability of land in farmers, field is unlimited. If not consider possibilities for incomplete block arrangement, including the possible use of a farmer's plot as a single treatment unit.
1. Write the first four steps in a 7-step procedure for scientific experimentation.
1. ________________________
2. ________________________
3. ________________________
4. ________________________
2. Circle T for true and F for false.
|
a. The merit of any data depends much on the accuracy with which it is collected and not so much on its representativeness of the population. |
T |
F |
|
b. The "test of outliers and spurious observations" relates to data transformation. |
T |
F |
|
c. The coding of data is carried out for equalisation of variances or normalisation of observations. |
T |
F |
|
d. By "variable" we mean the observational parameters to compare the treatment effects. |
T |
F |
|
e. Data analysis depends on objectives and methods of data collection. |
T |
F |
3. Column 1, given below, lists certain terminologies used in connection with experimental design. Match each with its explanation in column 2.
1. experimental error
2. plot
3. experiment design
4. replication
5. blocking
6. treatmenta: rules for assigning treatments to experimental plots
b: difference between two plots treated alike
c: the unit on which random assignment of treatment is made
d: material being forced on the subject
e: repetition of some treatments on several plots
f: a large area or several identical units receives most or all treatments
4. Tick the correct answer(s).
a. What is a factorial experiment?
· it has many levels of the single factor treatments
· it tests two or more factors simultaneously, each one at one level
· it tests two or more factors at the same time, with two or more levels
· it is also called multi-factor experimentb. A Randomized Complete Block Design is characterised by:
· treatments assigned at random to an experimental unit
· treatments assigned at random to experimental units within a block
· appropriateness only for experiments with homogenous experimental units
· arrangement of blocks in a square
· reduction experimental error by elimination of a known source of error among experimental units
5. a Write one major advantage of the Latin Square design over the Randomised Complete Block Design and one distinguishing feature of its layout.
Advantage ______________________________________________
Distinguishing feature of layout ______________________________
________________________________________________________
b. What is the most important advantage of a factorial experiment over a single factor experiment?
________________________________________________________
c. In a split plot design, there are main plots and sub-plots. To which one of these you will allocate the treatments requiring higher precision?
________________________________________________________
d. How does a split-split-plot design differ from a split-plot design?
________________________________________________________
6. a. Define sampling unit and discard plot.
________________________________________________________
________________________________________________________
b. List two main considerations in locating sampling units in alley farming trials.
a. ____________
b. ____________
c. Tick the correct answer(s). Why are blank trials conducted before initiating an actual trial?
· to homogenise the experimental area
· to study the performance of test crops
· to study the extent and pattern of soil heterogeneity
· to treat the soil with a fertility restoring crop
d. List 4 important factors in selecting an appropriate experimental site.
1. ____________
2. ____________
3. ____________
4. ____________
Cochran W.G. and Cox G.M. 1957. Experimental Designs, John Willey & Sons, N.Y.
Hicks H. 1973. Basic Concepts in the Design of Experiments. 2nd edition.
Le Clerg E.L., Leonard W.H. & Clark A.G. 1966. Field Plot Technique, Burgess Pub. Co., Minn., USA
Gomez, K.A. and Gomez, A.A., 1984. Statistical Procedures for Agricultural Research. John Wiley & Sons, New York.
Mead, R. and Curnow, R.N, 1983. Statistical Methods in Agriculture and . Experimental Biology. Chapman and Hall, London.
Pearce S.C., Clarke G.M., Dyke G.V. & Kempson R.E. 1988. A Manual of Crop Experimentation. Charles Griffin & Co. Ltd., Oxford.
Sanginga, N. 1990. Summary comment on and finalization of country projects submitted to IFAD. Unpublished AFNETA document.
SAS Institute Inc. 1987. SAS/STAT Guide for Personnel Computers, Version 6. SAS Inst. Inc., Cary N.Y.
Jolayemi E.T. 1989. ANOVA under the autoregressive error model of the first type. Abacus, 18(2): 289 - 294.
Rao M.R. & Roger J.H., 1990. Agroforestry field experiments: Part 2 Agronomic considerations. Agroforestry Today, 2(2), 11-14.