Apéndice: El Dilema del prisionero y la pesca

Al tratar de la ordenación no cooperativa de recursos pesqueros transfronterizos hemos examinado brevemente uno de los más famosos de todos los juegos no cooperativos, el «Dilema del prisionero". Como hemos visto, el juego es también plenamente pertinente para la ordenación de las otras tres clases de poblaciones de peces compartidas. El juego consiste en que los jugadores están abocados inexorablemente a adoptar estrategias que saben que no son deseables. El nombre, se recordará, viene del relato utilizado para ilustrar el juego, en el que participan dos compañeros, A y B, los cuales han sido arrestados (de forma justificable) por la sospecha de un gran robo. En nuestro ejemplo, la cooperación resulta imposible porque los dos no pueden comunicarse entre sí. Si pudieran hacerlo, pero desconfiaran plenamente uno del otro (deshonor entre ladrones), de forma que el establecimiento de un acuerdo realmente vinculante entre ambos fuera imposible, obtendríamos el mismo resultado.

En cualquier caso, cada jugador (A y B) tiene ante sí dos estrategias: declararse culpable o declararse inocente. Si ambos se declaran inocentes, ambos saldrán de la cárcel tras cumplir una mínima condena. Sin embargo, ambos están inducidos a declararse culpables y, como consecuencia de ello, pueden prever condenas más largas. Podemos mostrar ahora el resultado o la «solución" del juego con más detalle, creando una matriz de pago. Los pagos se expresan en la matriz en términos de condenas a prisión. Consideremos la matriz siguiente adaptada de Luce y Raiffa (1957):

Supongamos que el Jugador B se declara culpable. El Jugador A estará mejor si se declara culpable. Supongamos que el Jugador B se declara inocente. El Jugador A también estará mejor en este caso si se declara culpable. Independientemente de cual de las dos estrategias adopte el Jugador B, la mejor estrategia para el Jugador A es declararse culpable. Por lo tanto, la declaración de culpabilidad es la estrategia dominante para el Jugador A. Lo que es verdadero para el Jugador A, lo es también para el Jugador B.

Colin Clark, en su libro Bioeconomic Modelling and Fisheries Management (Clark, 1985), presenta un ejemplo lúcido del Dilema del prisionero aplicado a la pesca. Consideremos un recurso pesquero compartido por dos países, en los que los costos de la captura son independientes del tamaño de la biomasa y los precios del pescado capturado y los costos del esfuerzo de pesca son iguales para los dos países y también constantes. Para cada país, el beneficio neto por cada unidad de pescado capturado es p-c, donde p es el precio del pescado capturado y c es el costo unitario de la captura. Para simplificar, supongamos que p-c = 1.

Supongamos que x denota la biomasa y G(x), el crecimiento de la biomasa y, por lo tanto, la captura sostenible para un determinado nivel de x. Supongamos que comenzamos en el nivel óptimo mundial de biomasa, es decir, el nivel de biomasa en el que los beneficios económicos mundiales del recurso se elevarán al máximo. Denotemos dicha biomasa con x*. El beneficio económico mundial del recurso en x = x* es el valor actual de la captura sostenible a lo largo del tiempo, que puede expresarse como: G(x*)/d, donde d es la tasa apropiada de interés o tasa de descuento, que se supone será común a los dos países.

Una posible política de captura es sencillamente agotar el recurso. Como los costos de la recolección son independientes del tamaño del recurso, éste podrá reducirse a cero. Si, partiendo de x = x*, se agota el recurso a cero, el rendimiento económico de esta actuación sería exactamente x*. Supongamos que x* es positivo, lo que implica, a su vez, que x * < G(x*)/d.

El país 1 se enfrenta con dos estrategias posibles: agotar el recurso o conservarlo. Si el país 1 adopta la estrategia de agotar, mientras que el país 2 adopta la de conservar, se supone que el País 1 puede agotar el recurso tan rápidamente que el País 2 no reciba nada. Lo que es verdad para el país 1, lo es también para el país 2, que se enfrenta con las mismas estrategias.

Por último, supongamos que los dos países tienen igual capacidad de negociación y de captura. Si los dos siguen las mismas estrategias, compartirán a partes iguales los beneficios económicos de la pesquería.

La matriz de pago adopta la forma siguiente:

Si ambos conservan, cada uno recibirá la mitad del valor actual de la captura sostenible, es decir:

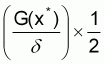
Si ambos agotan, cada uno recibirá

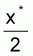
Como

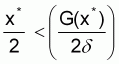
ocurre que, si los dos países pudieran comunicarse entre si y estuvieran dispuestos a concertar un acuerdo vinculante, cooperarían y terminarían por conservar el recurso.

Supongamos, por otra parte, que no hay ninguna cooperación ni comunicación entre los dos países. Supongamos, para empezar, que

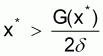
y consideremos el país 1. Si el país 2 siguiera la estrategia de conservación, el país 1 recibiría

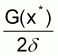
si conserva, y x*, si agota. Si el país 2 siguiera la estrategia de agotar, el país 1 recibiría 0, si sigue la estrategia de conservación y

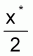
si sigue la estrategia de agotar. Es evidente que el país 1 debería adoptar la estrategia de agotar. Lo que es verdad para el país 1, lo es también para el país 2, y terminaríamos con un resultado de agotamiento. Este es un caso perfecto de Dilema del prisionero (Clark, 1985, pp. 151- 153).

Supongamos, por otra parte, que

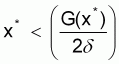
para el país 1 sería mejor conservar, si el país 2 siguiera la estrategia de conservación. Es posible que llegáramos en último término a un resultado de conservación. Sin embargo, dicho resultado es decididamente inestable. Supongamos que el país 1, sospechando que el país 2 va a conservar, adopta la estrategia de conservación, pero después se demuestra que se ha equivocado. El país 2 agota, con el resultado de que el país 1 se queda con 0, y es la «víctima".

En la teoría de juegos, existe un criterio famoso para elegir las estrategias en los juegos no cooperativos, el cual es particularmente aplicable cuando el oponente es agresivo e imprevisible. Se denomina el criterio maxmin. Este criterio establece que hay que buscar el peor resultado posible de cada estrategia y después compararlos. Elijamos la estrategia que tenga el menos malo de los resultados peores.

En el caso en examen,

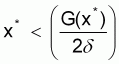
la matriz del pago nos dice que el peor resultado para el país 1, si sigue la estrategia de conservación, es que recibirá 0 (el resultado de «víctima"). El peor resultado para el país 1, si sigue la estrategia del agotamiento, es que recibirá

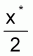
La aplicación del criterio maxmin inducirá al país 1 a elegir la estrategia de agotamiento. Si cada uno de los países 1 y 2 considera al otro como agresivo e imprevisible, podemos esperar un resultado de agotamiento. Podríamos denominar este caso como el caso imperfecto del Dilema del prisionero (Clark, 1985, ibid.; Bacharach, 1976).