C.A. Guerrero
Instituto Nacional de Investigación y Desarrollo Pesquero
Departamento de Aguas Continentales
Buenos Aires. Argentina.
3.1 RESUMEN
Se realizó un estudio de crecimiento de distintas poblaciones de perca de boca chica, Percichthys trucha, provenientes de cuatro lagos y lagunas de la Patagonia argentina. La edad fue leída en escamas provenientes de campañas realizadas entre los meses de mayo de 1983 y marzo de 1985, ajustada al modelo de crecimiento de Von Bertalanffy.
Se encontró una relación inversa entre la tasa de crecimiento y el largo asintótico que podrían alcanzar los individuos. En general, la tasa de crecimiento se correlacionó mejor con las variables ambientales que los otros parámetros de la curva de Von Bertalanffy. Los resultados muestran que el estado trófico del ambiente se correlaciona positivamente con las tasas de crecimiento, mientras que la correlación con el largo asintótico sería negativa. No parecería existir una relación entre el crecimiento y la composición específica de la comunidad de peces.
ABSTRACT
The growth of different populations of small mouth perch (Percichthys trucha) from four Patagonian lakes and ponds (Argentina) was studied. Age has been determined on scales obtained from samples performed since may 1983 to march 1985. Von Bertalanffy's growth curves have been adjusted to obtained data.
The individual growth rate was found to be inversely related to the asimptotic length. Generally, the growth rate correlated with environmentals characteristics better than the other Von Bertalanffy curve parameters. The results showed that the environment trophic characteristics correlate positively with the individual growth rate and negatively with the asimptotic length. It seems that there is no relation between growth and the specific composition of the fish community.
3.2 INTRODUCCION
El conocimiento que se tenga del crecimiento de los peces es una propiedad importante para el análisis de sistemas en ambientes acuáticos (Weatherley, 1972). Este mismo autor señala, también, que los peces están muy influenciados por el medio en que viven y que, además, esta relación no es unidireccional.
El estudio comparativo del crecimiento de los peces nos ofrece la oportunidad de investigar ciertos aspectos del estado de las poblaciones y de los ecosistemas que ocupan. Muchos autores han tratado este tema, y se han hallado relaciones entre el crecimiento y la temperatura (Sule, 1981 y Diana, 1984), la altitud y latitud (Hazel et al., 1983), el estado trófico de los ambientes (Campbell, 1971; Shafi y Maitland, 1971; Ryan y Harvey, 1977; Pivnicka, 1982), la interacción entre especies (Burrough y Kennedy, 1978), y la densidad poblacional (Havey, 1980).
Entre mayo de 1983 y marzo de 1985 se desarrólló un convenio entre el Instituto Nacional de Investigación y Desarrollo Pesquero y la Provincia del Chubut, para la evaluación del potencial pesquero de seis lagos y lagunas de dicha Provincia. Durante dicho convenio se realizaron muestreos limnológicos y pesqueros de los lagos Musters, Colhué Huapí, Rosario, Las Chultas, embalse Florentino Ameghino y laguna Esquel (Quirós, 1984). A través de ellos se pudo contar con material para la determinación de la edad en poblaciones de peces de distintos ambientes, caracterizados desde el punto de vista limnológico. Se iniciaron así estudios sobre aspectos demográficos de algunas poblaciones de Percichtidae patagónicos.
A pesar de estar presentes en casi todos los ambientes patagónicos argentinos (Ringuelet et al., 1967), pocos son los trabajos publicados hasta ahora sobre la biología de los percíctidos (López et al., 1981, 1982, 1987). Por ello se consideró importante desarrollar un estudio de crecimiento comparativo, sobre todo teniendo la posibilidad de poder correlacionar los resultados del mismo con variables ambientales, tanto físico-químicas como biológicas, tratando de encontrar cuáles son y en qué forma influyen dichas variables en el crecimiento de esta especie. Se trabajó con material de escamas de Percichthys trucha de los lagos Musters y Colhué Huapí, laguna Esquel y embalse Florentino Ameghino.
3.3 MATERIALES Y METODOS
El material utilizado proviene de los muestreos pesqueros realizados con baterías de redes agalleras de las siguientes medidas de malla: 42, 50, 60, 70, 78, 104, 120, 140 y 170 mm de malla estirada (Baigún y De Nichilo, 1984) Se calcularon las relaciones largo-peso en cada muestreo según:
W = a Lb
donde: W es el peso del individuo
L es la longitud total
a y b son constantes
Las constantes a y b fueron estimadas por regresión lineal (Rickler, 1973), luego de una transformación logarítmica de las variables peso y talla. Para la caracterización limnológica de los ambientes se consideraron los siguientes parámetros: superficie (A) en km2, profundidad media (.) en metros, lectura del disco de Secchi (LS) en metros, conductividad a 20 °C (K20) en μs/cm, fósforo total (PT) en mg/m3, nitrógeno orgánico total (NOT) en mg N/m3, nitratos (NO3) en mg N/m3, demanda química de oxígeno (DQO) en mg O2/1, pH, pigmentos fotosintéticos (Chl eq) en mg/m3 (Quirós y Scapini de Orfila, 1984 y Quirós et al., 1986), longitud media del macrozooplancton (crustáceos) (LP1) en μm, biomasa media del zooplancton (BP1) en μg/l (Menu Marque y Marinone, 1984 y 1986), la captura de peces por unidad de esfuerzo (CPUE) en kilogramos y la composición de la captura en peso, expresada en porcentaje de perca de boca chica (% PBC), perca de boca grande (Percichthys colhuapiensis) (%PBG), de aterínidos (%ATE) y trucha arco iris (Oncorhynchus mykiss) (%TAI) (Baigún y De Nichilo, 1984; Quirós y Baigún, 1986).
Las escamas fueron guardadas en seco durante los muestreos. En el laboratorio fueron limpiadas con una solución de hidróxido de potasio al 2% y se montaron en seco entre dos portaobjetos. De cada ejemplar se eligieron, de acuerdo con el tamaño y forma, entre cuatro y ocho escamas. Se midieron de dos a cuatro escamas por ejemplar, con un proyector óptico de perfiles, con un aumento de 20X; las medidas del radio total y del radio de cada marca se hicieron sobre las dos aristas del campo anterior, con una precisión de 1 mm de proyección, promediándose las lecturas entre aristas y entre escamas del mismo ejemplar.
Para retrocalcular las tallas a cada edad se estudió la relación entre el radio total de la escama (R) y la talla de los individuos (L). Se probaron distintos modelos de ajuste para cada ambiente, eligiéndose, en cada caso, el que ajustaba mejor a los datos. Así se obtuvieron ajustes lineales para los datos de Esquel, Colhué Huapí y Florentino Ameghino:
L = a + b R (1)
donde: L es la longitud total actual
R es el radio total actual de la escama
Las constantes fueron calculadas por el método de regresión lineal funcional de Ricker (1973). Para Musters se encontró que un modelo exponencial modificado ajustaba mejor a los datos:
L = k + a Rb (2)
Las constantes de este modelo fueron calculadas, ajustando el modelo lineal:
log (L - k) = log a + b log R
por el método de regresión lineal funcional, iterando varias veces sobre k. Se tomó el valor del coeficiente de correlación múltiple como estimador del ajuste. Para elegir el valor de k se partió de valores arbitrarios, y en cada iteración se elegían los dos valores de k que dieran los r2 más altos, usándose el promedio entre ambos para la nueva iteración. Se iteró hasta encontrar un valor de k que diera un r2 que fuera igual hasta el sexto decimal de los dos valores anteriores.
Para la interpretación y adjudicación de edad a cada una de las marcas en escama se procedió de la siguiente manera: se realizaron las descomposiciones de modas de las distribuciones de frecuencias de marcas en escama, en sus componentes unimodales, aplicando el método de Cassie (1954), modificado para ser usado con microcomputadoras (Guerrero y Tablado, 1985). Se realizó el retrocálculo de tallas para cada marca. En los ambientes donde la relación R-L era lineal, se tomó la ordenada al origen como una constante para todos los individuos y se calculó una nueva pendiente para cada uno de la siguiente manera:
lt = a + b' rt
donde: rt es la marca al tiempo t
lt es la talla retrocalculada al tiempo t
a es la ordenada al origen de (1)
b' es la pendiente para cada individuo
En el caso de Musters, se consideraron como constantes para todos los individuos a k y a,
lt = k + a Rb'
b' se calculó para cada ejemplar k y a son constantes de ajuste de (2)
Posteriormente se realizaron las descomposiciones de las distribuciones de tallas retrocalculadas, utilizando el mismo método que para las marcas. Luego se procedió a comparar las dos descomposiciones, la de marcas y la de tallas retrocalculadas, para adjudicar a cada marca de edad correspondiente. Para ello se tomaron en cuenta que tanto la marca como la talla retrocalculada estuvieran dentro de modas análogas. Para los cálculos de talla media a cada edad y para el ajuste de las curvas de Von Bertalanffy, se descartaron aquellos datos en los cuales había discrepancia entre la ubicación de la marca y la talla retrocalculada.
Se calcularon las tallas medias a cada edad, así como sus desviaciones estándar. El ajuste de las curvas de Von Bertalanffy se hizo por el método de Allen (1966). Se calcularon los coeficientes de correlación lineal entre las constantes de las curvas de Von Bertalanffy estimados y los parámetros ambientales, sin transformar y aplicando una transformación de los datos según ln (x + 1), con excepción de la variable pH.
3.4 RESULTADOS
En la Tabla 1 se encuentran los coeficientes de las curvas largo-peso para cada muestreo. En la Figura 1 se pueden ver los gráficos de dispersión de la relación entre el radio total de la escama (R) y la talla de los individuos (L), para cada ambiente. En dicho gráfico se puede apreciar que la relación R-L es distinta para cada ambiente. Sin embargo, se puede observar que en los cuatro, la dispersión aumenta con la talla. Además, parecería que en el rango de tallas entre 250 y 150 mm no habría grandes diferencias entre ambientes. Lamentablemente, dado el tipo de arte utilizado en la captura, no se pudo contar con ejemplares de tallas por debajo de 150 nm, por lo que no se puede afirmar que para las tallas menores exista un único modelo para esta relación. Los resultados de los ajustes de los datos de R-L fueron:
| Muster | L = 12+ 1,345 R1,249 | r = 0,936 |
| Colhue Huapi | L = -18,99 + 4,218 R | r = 0,932 |
| Emb. Ameghino | L = 24,52 + 2,988 R | r = 0,898 |
| Esquel | L = 12,30 + 3,513 R | r = 0,926 |
En las Figuras 2 a 5 están las distribuciones de frecuencias de marcas en escamas y de tallas retrocalculadas y sus respectivas descomposiciones en componentes unimodales. En las Tablas 2 a 5 estan los resultados de los mismos. En los casos de Colhué Huapí y Esquel se descartó como marca real a la primera moda que aparecía, basándose en su baja frecuencia de aparición y a que no aparecía en todos los individuos.
Además, en general, para las edades mayores se hallaron dificultades cuando se compararon las descomposiciones de marcas y tallas retrocalculadas. Para esas edades, siempre se tomó como edad verdadera a la que se deducía de la descomposición de marcas. Este problema es propio de la determinación de edades por escamas, ya que es conocido que a medida que los individuos son más viejos, la lectura de marcas en el borde se hace difícil, pudiendo llegar a haber reabsorción de la escama. Además hay que considerar los errores debidos a las dispersiones de la relación R-L, que a edades mayores presenta mayor superposición de tallas y que el período de marcación de la población puede ser extenso.
En la Tabla 6 y en la Figura 6 aparecen las tallas medidas retrocalculadas para cada edad y para cada ambiente. En la Tabla 7 se encuentran los resultados de los ajustes a las curvas de Von Bertalanffy para cada ambiente. Los datos ambientales seleccionados a priori se encuentran en la Tabla 8. En las Tablas 9 y 10 se encuentran los coeficientes de correlación encontrados, entre los parámetros de las curvas de Von Bertalanffy y las variables ambientales, con los valores sin transformar y transformados, respectivamente.
Existiría una correlación negativa entre el L∞ y el K de la curva de Von Bertalanffy (r = -0,854). Si bien, estadísticamente los valores de los coeficientes de correlación no son significativos, en genral las tasas de crecimiento K se correlacionan mucho mejor que los otros parámetros de la curva de Von Bertalanffy con las variables ambientales.
3.5 DISCUSION Y CONCLUSIONES
El conjunto de lagos elegidos estaría dentro del rango de meso a eutróficos (Menú Marque y Marinone, 1984, 1986; Quirós y Scapini de Orfila, 1984). Si bien la base de datos es limitada, se pueden ver ciertas relaciones entre el crecimiento y el estado trófico de los ambientes. Para esta especie, en el conjunto de lagos considerados se encontró una relación inversa entre la tasa de crecimiento (K) y el largo asintótico que alcanzarían los individuos (L∞).
Así, en ambientes relativamente más productivos, con mayor disponibilidad de alimento, se encuentran individuos que crecen rápido, pero que no alcanzan tallas elevadas, en tanto que en ambientes menos productivos, alcanzarían tallas mayores pero con un ritmo de crecimiento inicial menor, tal como lo señalaron distintos autores para otras especies (Leggett y Power, 1969; Campbell, 1971, 1979; Ryan y Harvey, 1977).
Si comparamos los resultados de las correlaciones entre el crecimiento y los factores físicos y químicos, que determinarían la productividad de los ambientes y las variables biológicas, que expresarían esa productividad. Se conocida la relación entre los niveles de nutrientes y de pigmentos foto-sintéticos con la productividad pesquera (Northcote y Larkin, 1956; Ryder, 1965; Oglesby, 1977; Hanson y Leggett, 1982; Quirós et al. 1986). Era de esperar, entonces encontrar, la misma relación entre la tasa de crecimiento y las variables físico-químicas y biológicas. Sin embargo, se obtuvieron relaciones inversas con los niveles de nutrientes, sólidos disueltos (PT, NOT, NO3 y K20) y con los niveles de clorofila.
Mo obstante, la tasa de crecimiento se correlacionó positivamente con la biomasa media del zooplancton (BPI) y con la captura de peces. Estos resultas se podrían explicar tomando en cuenta que, de los cuatro ambientes considerados, dos (Esquel y Colhué Huapí) serían casos excepcionales (Quirós y Scapini de Orfila, 1984), por ser ambientes de baja profundidad media (2 m).
El lago Colhué Huapí tiene muy altos niveles de nutrientes y sólidos disueltos, pero presenta una elevada turbidez inorgánica, que se ve reflejada en los bajos valores de lectura del disco de Secchi, lo que limitaría la producción primaria del fitoplancton, y la producción secundaria dependería en cierta medida del aporte de material alóctono de la cuenca.
La laguna Esquel presenta altos niveles de nutrientes, pero relativamente bajos niveles de clorofila, si bien tiene un importante desarrollo de la macrofilia arraigada al fondo, que contribuiría grandemente a la producción primaria del ambiente, si consideramos la relación entre la zona eufótica (LS) y la profundidad media (Quirós y Scapini de Orfila, 1984).
Se aprecia una baja correlación entre los parámetros del crecimiento y la composición específica de las capturas. Si bien la cantidad de ambientes no permite generalizer, esto estaría indicando que las interacciones con otras especies no afectarían en gran medida al crecimiento de Percichthys trucha, por lo menos en los lagos considerados.
Los resultados del presente trabajo coinciden con los encontrados por Lafarga y Guerrero (1987) y Lafarga et al. (1987) para la trucha arco iris (O. mykiss), en un conjunto parecido de lagos. Sería interesante contar con más datos de crecimiento de la especie en otros ambientes, tratando de que el conjunto fuera lo más heterogéneo posible, desde el punto de vista del estado trófico. Además, sería necesario conocer otros parámetros demográficos que tienen estrecha relación con el crecimiento, tales como la estructura de edades y la mortalidad, lo que permitiría predecir, en función de las variables ambientales, el comportamiento de la especie en otros cuerpos de agua.
3.6 AGRADECIMIENTOS
El presente trabajo forma parte de la Beca de Perfeccionamiento del autor, otorgada por el Consejo Nacional de Investigaciones Científicas y Técnicas, bajo la dirección del Lic. Lauce R. Freyre. Se agradece a la Dirección de Intereses Marítimos y Pesca Continental de la Provincia del Chubut, por la toma de muestras de escamas en el campo, y al Lic. Rolando Quirós, del Instituto Nacional de Investigación y Desarrollo Pesquero, por las sugerencias y el apoyo brindado.
3.7 BIBLIOGRAFIA
ALLEN, K.R. 1966. A method of fitting growth curves of the Von Bertalanffy type to observed data. J. Fish. Res. Bd. Canada. 23(2):163–179.
BAIGUN, C.A. y DE NICHILO, A. 1984. Pesca experimental. En: Editor Quirós, R. Evaluación del potencial pesquero en seis lagos de la Provinicia del Chubut. Informe de Avance № 1. INIDEP, Departamento Aguas Continentales. Mimeografiado.
BURROUGH, R.J. y KENNEDY, C.R. 1978. Observations on the brown trout and perch of Malham Tarn. Fld. Stud. 4:631–634.
CAMPBELL, R.N. 1971. The growth of brown trout Salmo trutta in northern Scottish lochs with special reference to the improvement of fisheries. IN: J. Fish. Biol. 3:1–28.
CAMPBELL, R.N. 1979. Ferox trout, Salmo trutta L., and charr, alvelinus alpinus (L.), in Scottish lochs. IN: J. Fish. Biol. 14:1–29.
CASSIE, R.M. 1954. Some uses of probability paper in the analysis of size frequency distributions. Aust. J. Mar. Freshw. Res. 5:513–522.
DIANA, J.S. 1984. The growth of largemouth bass Micropterus almoides, under constant and fluctuating temperatures. IN: J. Fish. Biol. 24(2): 165–172.
GUERRERO, C.A. y TABLADO. 1985. Programa BASIC para la descomposición de distribuciones polimodales. EN: Bol. Asoc. Cs. Nat. Litoral. 5(3):45–52.
HANSON, J.M. y LEGGETT, W.C. 1982. Empirical prediction of fish biomass and yield. IN: Can. J. Fish. Aquat. Sci. 39(2):257–263.
HAVEY, K.A. 1980. Stocking rate and the growth and yield of landloched Atlantic salmon at Long Pond, Maine. Trans. Am. Fish. Soc. 109(5):502–510.
HAZEL, P.P., LAMOUREUX, J., MAGNIN, E. y NAULT, R. 1983. Croissance de six especes de poissons vivant pres de leur limits de repartition en latitude et en altitude sur le territoire de la baie James. CYBIUM 3eme ser. 7(4):57–69.
LAFARGA, A.M. y GUERRERO, C.A. 1987a. Crecimiento de Salmo gairdneri y Percichthys trucha en dos ambientes lénticos de la Patagonia. EN: Reunión Argentina de Ecología, 13. Bahía Blanca, Argentina. 5–8 de abril.
LAFARGA, A.M. y GUERRERO, C.A. 1987b. Crecimiento de la trucha arco iris, Salmo gairdneri, en ambientes patagónicos (Argentina). EN: Curso Taller Latinoamericano Enfoques integrados para el estudio de lagos y reservorios, como base para su gestión. Santiago de Chile, 28 de septiembre–10 de octubre.
LEGGETTI, W.C. y POWER, G. 1969. Differences between two populations of landlocked Atlantic salmon (Salmo salar) in Newfoundland. IN: J. Fish. Res. Bd. Canada. 26:1585–1596.
LOPEZ, H.L., MENNI, R.C. y RINGUELET, R.A. 1981. Bibliografía de los peces de agua dulce de Argentina y Uruguay (1967–1981). Biología Acuática. 1:100.
LOPEZ, H.L. 1982. Bibliografía de los peces de agua dulce de Argentina y Uruguay. Suplemento 1982. Biología Acuática. 3:26.
LOPEZ, H.L. 1987. Bibliografía de los peces de agua dulce de Argentina y Uruguay. Suplemento 1986. Biología Acuática. 9:61.
MENU MARQUE, S. y MARINONE, M.C. 1984. Estudio del zooplancton y sus relaciones con algunos factores ambientales. EN: Editor Quirós, R. Evaluación del potencial pesquero en seis lagos de la provincia del Chubut. Informe Avance № 1. INIDEP, Dpto. Aguas Continentales. Mimeografiado.
MENU MARQUE, S. y MARINONE, M.C. 1986. El zooplancton de seis lagos del Chubut (Argentina) y sus probables relaciones con la ictiofauna y algunos factores ambientales. EN: Editoras Vila, I. y Fagetti, E. Trabajos presentados al Taller Int. sobre ecología y manejo de peces en lagos y embalses. Santiago, Chile, 5–10 de noviembre de 1984. COPESCAL. Documento Técnico. (4):90–114 p.
NORTHCOTE, T.G. y LARKIN, P.A. 1956. Indices of productivity in British Columbia lakes. IN: J. Fish. Res. Bd. Canada. 13(4):515–540.
OGLESBY, R.T. 1977. Relationships of fish yield to lake phytoplankton standing crop, production, and morphoedaphic factors. IN: J. Fish. Res. Bd. Canada. 34(12):2271–2279.
PIVNICKA, K. 1982. Growth capacity of some fish species in different environmental conditions. Vest. ds. Spolec. zool. 47:272–287.
QUIROS, R. y BAIGUN, C. 1986. Prospección pesquera en 33 lagos y embalses patagónicos (Argentina). En: Editoras Vila, I. y Fagetti, E. Trabajos presentados al Taller Internacional sobre ecología y manejo de peces en lagos y embalses. Santiago, Chile, 5–10 noviembre de 1984. COPESCAL. Documento Técnico. (4):159–179.
QUIROS, R., CUCH, S. y BAIGUN, C. 1986. Relación entre abundancia de peces y ciertas propiedades físicas, químicas y biológicas, en lagos y embalses patagónicos (Argentina). En: Editoras Vila, I. y Fagetti, E. Trabajos presentados al Taller Internacional sobre ecología y manejo de peces en lagos y embalses. Santiago, Chile. 5–10 noviembre de 1984. COPESCAL. Documento Técnico. (4):180–202.
QUIROS, R. y SCAPINI DE ORFILA, M.C. 1984. Características limnológicas de los ambientes. EN: Editor Quirós, R. Evaluación del potencial pesquero en seis lagos de la provincia del Chubut. Informe Avance № 1. INIDEP, Dpto. Aguas Continentales. Mimeografiado.
RICKER. W.F. 1973. Linear regressions in fishery research. IN: J. Fish. Res. Bd. Canada. 30(3):409–434.
RYDER, R.A. 1965. A method for estimating the potential fish production of north-temperate lakes. Trans. Am. Fish. Soc. 94:214–218.
RINGUELET, R.A., ARAMBURU, R.H. y ALONSO DE ARAMBURU, A. 1967. Los peces de agua dulce. La Plata, Buenos Aires, Argentina, Com. Inv. Cient. Prov. 602 p.
RYAN, P.M. y HARVEY, H.H. 1977. Growth of the rock bass, Ambloplites rupestris, in relation to the morphoedaphic index as an indicator of environmental stress. IN: J. Fish. Fish. Bd. Canada. 34:2079–2088.
SHAFI, M y MAITLAND, P.S. 1971. The age and growth of perch Perca fluviatilis (L.) in two Scottish Lochs. IN: J. Fish. Biol. 3(1):39–57.
SULE, M.J. 1981. First year growth and feeding of largemouth bass in a heated reservoir. IN: Bull. Nat. Hist. Surv. Illionois, U.S.A. 32(4):520–535.
WEATHERLEY, A.H. 1972. Growth and ecology of fish populations. London, England, Academic Press. 293 p.
Tabla No 1: Coeficientes de la curva Largo-Peso (W = a Lb para los cuatro ambientes, discriminados por muestreo.
| ESQUEL | MUSTERS | COLHUE HUAPI | F. AMEGHINO | ||
| 5/83 | a | 1,246×10-6 | 1,663×10-6 | 1,804×10-5 | |
| b | 3,397 | 3,340 | 2,907 | ||
| r | 0,988 | 0,975 | 0,937 | ||
| n | 29 | 93 | 342 | ||
| 8/83 | a | 2,323×10-6 | 2,128×10-5 | 7,357×10-5 | |
| b | 3,294 | 2,874 | 2,648 | ||
| r | 0,928 | 0,890 | 0,914 | ||
| n | 150 | 326 | 77 | ||
| 12/83 | a | 1,557×10-5 | 2,506×10-6 | 2,293×10-6 | 6,320×10-6 |
| b | 2,959 | 3,275 | 3,281 | 3,080 | |
| r | 0,970 | 0,982 | 0,981 | 0,975 | |
| n | 259 | 421 | 245 | 89 | |
| 3/84 | a | 1,412×10-5 | 1,692×10-6 | 3,318×10-6 | 8,463×10-6 |
| b | 2,984 | 3,325 | 3,206 | 3,039 | |
| r | 0,989 | 0,988 | 0,995 | 0,981 | |
| n | 539 | 165 | 81 | 66 | |
| 5/84 | a | 1,237×10-5 | 3,211×10-6 | 1,057×10-5 | |
| b | 3,015 | 3,227 | 2,984 | ||
| r | 0,990 | 0,978 | 0,994 | ||
| n | 11 | 194 | 5 | ||
| 9/84 | a | 6,319×10-6 | 3,641×10-7 | 2,305×10-6 | 1,474×10-5 |
| b | 3,135 | 3,597 | 3,286 | 2,927 | |
| r | 0,993 | 0,932 | 0,984 | 0,839 | |
| n | 63 | 219 | 176 | 19 | |
| 12/84 | a | 1,920×10-5 | 2,292×10-6 | 6,295×10-6 | 4,551×10-6 |
| b | 2,944 | 3,288 | 3,099 | 3,143 | |
| r | 0,946 | 0,970 | 0,960 | 0,980 | |
| n | 40 | 581 | 656 | 53 | |
| 3/85 | a | 3,127×10-6 | 7,108×10-7 | 4,654×10-6 | 2,107×10-6 |
| b | 3,248 | 3,477 | 3,148 | 3,285 | |
| r | 0,989 | 0,982 | 0,980 | 0,995 | |
| n | 17 | 188 | 594 | 28 |
Tabla No 2a: Resultados de la descomposición de la distribución de frecuencias de marcas en escama para Musters
| Moda (mm) | Desv. Std. | N |
| 25,22 | 5,669 | 140 |
| 45,52 | 4,970 | 111 |
| 63,06 | 5,243 | 99 |
| 74,90 | 3,380 | 56 |
| 84,92 | 3,208 | 51 |
| 93,15 | 2,070 | 26 |
| 99,71 | 5,100 | 10 |
| 108,71 | 0,663 | 3 |
Tabla No 2b: Resultados de la descomposición de la distribución de frecuencias de tallas retrocalculadas para Musters
| Moda (cm) | Desv. Std. | N |
| 9,34 | 2,385 | 129 |
| 17,88 | 2,421 | 103 |
| 24,89 | 1,681 | 73 |
| 31,03 | 1,882 | 67 |
| 36,24 | 1,741 | 48 |
| 40,88 | 0,841 | 21 |
| 44,38 | 0,341 | 8 |
| 47,39 | 0,298 | 3 |
Tabla No 3a: Resultados de la descomposición de la distribución de frecuencias de marcas en escama para Colhué Huapí
| Moda (mm) | Desv. Std. | N |
| 23,38 | 5,658 | 124 |
| 39,67 | 5,383 | 108 |
| 54,84 | 5,314 | 117 |
| 69,56 | 3,831 | 54 |
| 80,20 | 3,076 | 18 |
| 87,12 | 2,622 | 18 |
| 94,41 | 0,755 | 9 |
| 102,21 | 3,418 | 7 |
Tabla No 3b: Resultados de la descomposición de la distribución de frecuencias de tallas retrocalculadas para Colhué Huapí
| Moda (cm) | Desv. Std. | N |
| 4,52 | 1,054 | 29 |
| 10,42 | 3,186 | 160 |
| 18,53 | 2,085 | 122 |
| 24,39 | 1,938 | 72 |
| 30,32 | 1,823 | 35 |
| 34,42 | 0,340 | 14 |
| 37,43 | 0,339 | 13 |
| 40,52 | 1,584 | 11 |
Tabla No 4a: Resultados de la descomposición de la distribución de frecuencias de marcas en escama para embalse Florentino Ameghino
| Moda (mm) | Desv. Std. | N |
| 31,26 | 4,139 | 49 |
| 50,68 | 5,187 | 54 |
| 67,14 | 3,246 | 36 |
| 77,33 | 3,977 | 25 |
| 86,97 | 0,651 | 6 |
| 92,94 | 0,667 | 3 |
Tabla No 4b: Resultados de la descomposición de la distribución de frecuencias de tallas retrocalculadas para embalse Florentino Ameghino
| Moda (cm) | Desv. Std. | N |
| 11,60 | 1,173 | 42 |
| 16,32 | 1,952 | 46 |
| 21,65 | 1,700 | 49 |
| 26,42 | 1,547 | 32 |
Tabla No 5a: Resultados de la descomposición de la distribución de frecuencias de marcas en escama para Esquel
| Moda (mm) | Desv. Std. | N |
| 20,17 | 9,487 | 14 |
| 38,95 | 4,127 | 91 |
| 59,92 | 4,925 | 71 |
| 73,24 | 4,360 | 55 |
| 85,14 | 2,725 | 54 |
| 96,12 | 3,212 | 46 |
| 105,20 | 2,440 | 16 |
| 111,14 | 3,400 | 5 |
| 119,00 | 0,202 | 1 |
Tabla No 5b: Resultados de la descomposición de la distribución de frecuencias de tallas retrocalculadas para Esquel
| Moda (cm) | Desv. Std. | N |
| 7,23 | 1,228 | 10 |
| 14,78 | 1,811 | 98 |
| 22,52 | 1,869 | 75 |
| 26,92 | 1,286 | 41 |
| 30,91 | 1,169 | 61 |
| 34,97 | 1,121 | 50 |
| 38,22 | 1,145 | 18 |
Tabla No 6: Tallas medias retrocalculadas para cada ambiente, con sus respectivos desvíos standard y número de individuos.
| Musters | Colhué Huapí | Florentino Ameghino | Esquel | ||
| Edad 1 | Media | 99,15 | 111,93 | 115,03 | 148,72 |
| D. Std. | 17,585 | 20,629 | 10,506 | 16,276 | |
| N | 89 | 99 | 40 | 78 | |
| Edad 2 | Media | 175,71 | 179,98 | 168,60 | 223,74 |
| D. Std. | 20,617 | 19,212 | 18,573 | 20,882 | |
| N | 95 | 91 | 43 | 69 | |
| Edad 3 | Media | 248,59 | 232,83 | 216,57 | 276,04 |
| D. Std. | 21,271 | 20,776 | 16,459 | 28,229 | |
| N | 86 | 72 | 35 | 49 | |
| Edad 4 | Media | 311,05 | 286,82 | 250,00 | 314,30 |
| D. Std. | 20,565 | 23,560 | 15,593 | 29,020 | |
| N | 60 | 39 | 26 | 50 | |
| Edad 5 | Media | 360,48 | 334,05 | 273,10 | 340,98 |
| D. Std. | 18,247 | 17,927 | 12,819 | 22,201 | |
| N | 44 | 22 | 10 | 42 | |
| Edad 6 | Media | 403,62 | 369,54 | 295,00 | 365,73 |
| D. Std. | 21,026 | 20,533 | --- | 16,922 | |
| N | 26 | 13 | 1 | 15 | |
| Edad 7 | Media | 443,82 | 395,11 | --- | 374,43 |
| D. Std. | 17,696 | 21,700 | --- | 17,145 | |
| N | 11 | 9 | --- | 7 | |
| Edad 8 | Media | 504,00 | 413,00 | --- | 408,00 |
| D. Std. | --- | 21,680 | --- | --- | |
| N | 1 | 5 | --- | 1 | |
| Edad 9 | Media | 539,00 | 425,00 | --- | --- |
| D. Std. | --- | --- | --- | --- | |
| N | 1 | 1 | --- | --- |
Tabla No 7: Resultados de los ajustes a la curva de Von Bertalanffy.
| Muster | Colhué Huapí | Embalse Ameghino | Esquel | |
| L∞ | 721,4 | 580,2 | 370,2 | 414,9 |
| D. Std. L∞ | 36,39 | 29,12 | 27,71 | 11,24 |
| K | 0,137 | 0,155 | 0,249 | 0,325 |
| D. Std. K | 0,011 | 0,014 | 0,040 | 0,026 |
| to | -0,070 | -0,378 | -0,480 | -0,370 |
| D. Std. to | 0,047 | 0,067 | 0,132 | 0,083 |
Tabla No 8: Valores medios de los parámetros ambientales considerados, para los cuatro ambientes (ver abreviaturas y unidades en que están expresadas en el texto).
| ESQUEL | MUSTERS | COLHUE HUAPI | F. AMEGHINO | |
| A^ | 2,8 | 414 | 662 | 9,1 |
| z | 2,0 | 20,0 | 2,0 | 24,6 |
| LS | 3,1 | 1,1 | 0,1 | 1,3 |
| K20 | 186 | 418 | 1324 | 224 |
| PT | 53 | 28 | 592 | 51 |
| NOT | 652 | 429 | 1668 | 321 |
| pH | 7,8 | 8,1 | 8,6 | 7,7 |
| DQO | 20,3 | 16,9 | 83,0 | 9,7 |
| Chl eq | 3,7 | 5,6 | 16,3 | 2,8 |
 | 1232 | 860 | 2123 | 1439 |
| LP1 | 883 | 550 | 895 | 610 |
| BP1 | 900,5 | 34,7 | 138,6 | 13,9 |
| CPUE | 200,5 | 53,1 | 43,9 | 47,1 |
| %PBC | 78 | 82 | 59 | 19 |
| %PBG | 0 | 2 | 37 | 49 |
| %ATE | 0 | 3 | 4 | 26 |
| %TAI | 22 | 13 | 0 | 6 |
Tabla No 9: Valores de los coeficientes de correlación entre las variables ambientales y los parámetros de las curvas de Von Bertalanffy, para los datos sin transformar.
| L∞ | K | to | |
| z^ | 0,031 | -0,224 | 0,169 |
| LS | -0,512 | 0,875 | -0,114 |
| K20 | 0,416 | -0,623 | -0,027 |
| PT | 0,216 | -0,458 | -0,231 |
| NOT | 0,219 | -0,344 | -0,182 |
| pH | 0,625 | -0,720 | 0,229 |
| DQO | 0,281 | -0,441 | -0,143 |
| Chl eq | 0,417 | -0,584 | -0,015 |
 | 0,044 | -0,133 | 0,385 |
| LP1 | -0,282 | 0,357 | -0,449 |
| BP1 | -0,409 | 0,784 | -0,186 |
| CPUE | -0,419 | 0,817 | -0,130 |
| %PBC | 0,622 | -0,146 | 0,731 |
| %PBG | -0,407 | -0,128 | -0,692 |
| %ATE | -0,539 | 0,122 | -0,545 |
| %TAI | -0,146 | 0,623 | 0,274 |
Tabla No 10: Valores de los coeficientes de correlación entre las variables ambientales y los parámetros de las curvas de Von Bertalanffy, para los datos transformados según ln (x + 1).
| L∞ | K | to | |
| z^ | 0,038 | -0,265 | 0,181 |
| LS | -0,515 | 0,817 | -0,048 |
| K20 | 0,629 | -0,770 | -0,181 |
| PT | 0,166 | -0,397 | -0,316 |
| NOT | 0,303 | -0,257 | -0,058 |
| pH | 0,679 | -0,723 | 0,268 |
| DQO | 0,425 | -0,407 | -0,036 |
| Chl eq | 0,605 | -0,653 | 0,185 |
 | -0,290 | 0,010 | -0,699 |
| LP1 | -0,238 | 0,372 | -0,408 |
| BP1 | -0,101 | 0,495 | -0,016 |
| CPUE | -0,376 | 0,794 | -0,042 |
| %PBC | 0,657 | -0,203 | 0,735 |
| %PBG | -0,165 | -0,349 | -0,545 |
| %ATE | -0,239 | -0,256 | -0,402 |
| %TAI | -0,204 | 0,529 | 0,294 |

Figura 1: Gráfico de dispersión de los valores de la relación radio de escama (R) y largo total (L). (O) Musters (n = 115); (+) Colhué Huapí (n = 106); (□) embalse Florentino Ameghino (n = 50) y (Δ) Esquel (n = 99).
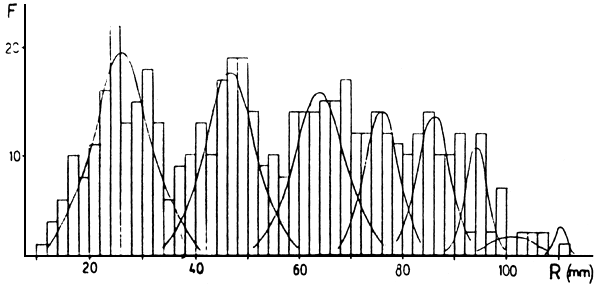
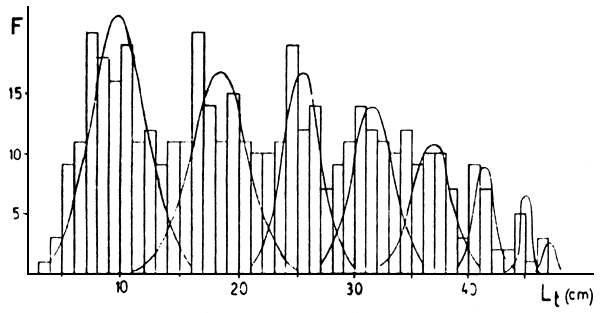
Figura 2: Descomposiciones de distribuciones de frecuencias de marcas en escama (R) (arriba) y de tallas retrocalculadas (Lt) (abajo) para Musters. Las frecuencias son absolutas.
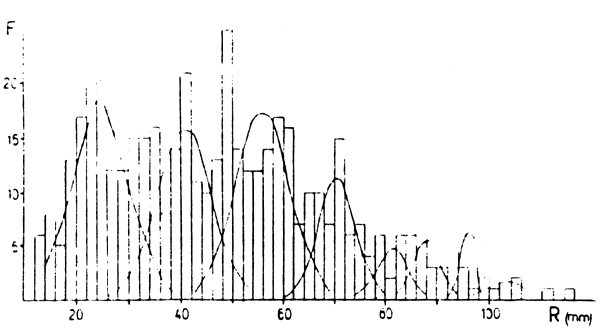

Figura 3: Descomposiciones de distribuciones de frecuencias de marcas en escama (R) (arriba) y de tallas retrocalculadas (Lt) (abajo) para Colhué Huapí. Las frecuencias son absolutas.


Figura 4: Descomposiciones de distribuciones de frecuencias de marcas en escama (R) (arriba) y de tallas retrocalculadas (Lt) (abajo) para embalse Florentino Ameghino. Las frecuencias son absolutas.

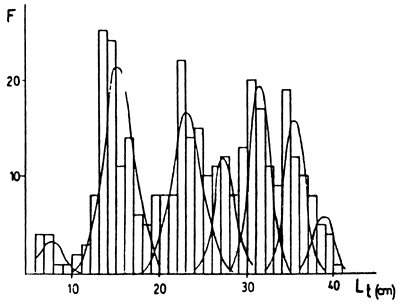
Figura 5: Descomposiciones de distribuciones de frecuencias de marcas en escama (R) (arriba) y de tallas retrocalculadas (Lt) (abajo) para Esquel. Las frecuencias son absolutas.

Figura 6: Tallas medias a cada edad, la barra representa dos desvíos standard. (■) Muster, (▲) Colhué Huapí, (X) embalse Florentino Ameghino y (•) Esquel.