4.1 Crecimiento
4.2 Crecimiento diferencial por sexos
4.3 Relación talla-peso
4.4 Razón de sexos
4.5 Mortalidades
4.6 Rendimiento por recluta
4.7 Modelos de producción
4.8 Autocorrelación en la serie de cpue
El cuadro 1 y las figuras 9, 10, 11 y 12 muestran las modas que se encontraron en cada campaña estudiada.
Un factor subjetivo influye decisivamente en este cuadro en su parte derecha. Hemos procurado, sin embargo, “adivinar” la posición de las modas en el cuadro a base de homogeneizar los valores de cada columna, reduciendo así las diferencias entre filas; de cualquier modo debemos insistir en que las dos ultimas modas de cada fila deberían ser acompañadas por interrogaciones, considerándose su valor, por el momento, como poco más que hipotético.
Suponiendo la existencia de dos máximos bien definidos cada año en la puesta, las campañas realizadas en julio-agosto deberían rendir una distribución de tallas muy similar a la realizada en enero-febrero de 1976, y ese es el caso. Es de notar que en la distribución de tallas de Cort y Pérez-Gándaras no aparece la primera moda de las demás distribuciones, alrededor de los 7-8 cm; la malla utilizada, sin embargo, en esa época y zona por la flota pesquera española era de 35 mm (Cort, com. pers.).
El acuerdo entre las primeras modas es muy grande. La segunda moda que aparece podría corresponder a los individuos de alrededor de un año de edad, cuyos huevos hicieron eclosión en agosto-septiembre. Esta moda se sitúa, en todos los casos, entre 11 y 12 cm (siempre nos referimos a la longitud del manto). La tercera, que correspondería a año y medio se situaría entre 14 y 15 cm, salvo para la campaña de 1978, donde tras la partición de la distribución de tallas no aparece ninguna moda en ese punto. De hecho, esta campaña resulto ser un tanto más difícil de analizar. Modas sucesivas aparecen a 18-19 cm, ésta con gran nitidez siempre, a 20-21 cm y una ultima, realmente dudosa por el escaso número de ejemplares capturados a estas tallas, a 24-25 cm.
Dado que Itami et al. encontraron que la talla media del pulpo a los 5 o 6 meses de la eclosión era de 5-6 cm de longitud del manto, podemos inferir que la segunda moda de las distribuciones de callas analizadas, salvo la de Cort y Pérez-Gándaras, que sería la primera presente, se corresponde efectivamente a individuos que se acercan al año de edad. La tercera moda correspondería a casi el año y medio, y la cuarta a casi los dos años. Recordemos que tanto la ecuación de crecimiento de Guerra como la de Hatanaka predicen, para pulpos de un año de edad, alrededor de 12 cm de talla media; la gran diferencia entre ambas ecuaciones surge a partir del segundo año; según la ecuación de Hatanaka, ejemplares de dos años medirían sobre 17 cm y de 3 años, 20,3 cm. Según la ecuación de Guerra, por el contrario, ejemplares de dos años medirían 26,8 cm, y de tres años, 36,8 cm.
La elección de un valor de K, que ha sido ensayada repetidamente es un intento que debería afrontarse con más cuidado del que se ha tenido hasta el momento, ya que, de no hacerlo así, serviría solo para crear confusión y pérdida de horas. Véamoslo con un ejemplo: nuestros datos parecen confirmar que, al año de edad, la talla modal serían de unos 12-13 cm, y a los dos años se encontraría sobre los 18-19 cm. Si consideramos una tercera moda anual a los 24 cm, obtendríamos simultáneamente K = 0,34 y L¥ = 36,21 cm, para valores de ll = 12 cm, l2 = 19 cm y 13 = 24 cm.
Bastaría que cambiásemos l1 = 12 cm por l1 = 13 cm para obtener valores de K = 0,18 y L¥ = 109,53 cm; si consideramos que los parámetros de crecimiento tienen un significado biológico, este segundo resultado debería ser rechazado como absurdo, debido al valor de L¥ obtenido. Cualquier intento de estimar el valor de K a partir de nuestros datos debería pasar, por tanto, por la restricción, a priori. o a posteriori, del valor de L¥; este valor acotado de L¥ acotará, a su vez, los valores posibles de K.
La sensibilidad de K y L¥ a cambios tan ligeros en las tallas modales - sensibilidad que depende, evidentemente, de las pocas modas utilizadas - debería llevarnos a ser prudentes a la hora de utilizar una ecuación de von Bertalanffy con fines de evaluación. Un hecho a tener en cuenta es que el valor elegido por Guerra de Loo es sin duda demasiado alto; probablemente, y tras lo que acabamos de exponer, sería más aconsejable acotar ya de principio el valor de L¥ entre 30 y 40 cm de longitud del manto, rechazando todas aquellas estimaciones que no dieran como resultado valores de Loo comprendidos en ese intervalo. Podríamos admitir como posibles, por tanto, valores de K = 0,34 y L¥ = 36,41, que ya hemos señalado; K = 0,29 y L¥ = 40 cm, o K = 0,36, L¥ = 35 cm, etc.
Tras de este acuerdo, ya no tiene mucha importancia la ecuación de crecimiento concreta que elijamos. Si consideramos tallas medias de edades sucesivas de 13, 19, 23 y 26 cm, surge una ecuación de crecimiento con K = 0,38 y L¥ = 32,15 cm. Dado que en este ensayo se hace un mejor aprovechamiento de los datos obtenidos por el análisis de las distribuciones de tallas y que su resultado se mantiene en los límites considerados como posibles, retendremos esta ecuación para los ensayos de rendimiento. La ecuación de von Bertalanffy toma la forma
lt = 32,15 (l - e-0,38((t + 0,36))
sin que esto quiera decir que descartemos cualquier otra solución que mantenga L¥ en un valor comprendido entre 30 y 40 cm, tal como hemos explicado.
Un segundo problema es el crecimiento diferencial por sexos. El trabajo de Cort y Pérez-Gándaras nos ha permitido separar los componentes normales de las distribuciones de tallas por sexos. Puede observarse una concordancia grande entre machos y hembras en las dos primeras modas, que corresponderían a la segunda y tercera moda de los demás autores. La tercera moda se marca en 19 cm para machos y 17 cm para hembras, la cuarta en 22 cm y 20 cm respectivamente y la quinta en 24-25 y 22 cm. Las distribuciones de tallas a que se hace referencia, aparecen en las figuras 13 y 14 para machos y hembras respectivamente.
Debe recordarse que, en la gama de tallas en que se observa un crecimiento diferencial por sexos, las hembras están sometidas a una fuerte mortalidad y este hecho podría sesgar mucho nuestras estimaciones de crecimiento si la mortalidad resultara ser específica de talla. Si este no fuera el caso, nos inclinaríamos a pensar en que un valor adecuado de K para hembras se encontraría alrededor de K = 0,5, con L¥ alrededor de 25 cm. Recuérdese que la hembra de mayor talla medida en la campana citada tenía una talla de manto de 24 cm, mientras que el mayor macho alcanzo 30 cm.
Una ecuación de von Bertalanffy posible para hembras sería entonces de
lt = 24,5 (1 - e-0,5(t + 0,32))
Dicha ecuación, junto con la general, se muestra en la figura 15.
Para propósitos de evaluación y por el momento, retendremos la ecuación general ya descrita, aunque para trabajos sucesivos sería mas exacto utilizar las ecuaciones diferenciales por sexos,
La ecuación “general” se conforma, en realidad, con el crecimiento de los machos dado que las modas que aparecían en las distribuciones de tallas generales coinciden con las modas que presentan los machos; este hecho se debe a la mortalidad de las hembras en la gama de tallas en que el crecimiento es diferencial, lo que hace que a la hora del ajuste tres de los cuatro puntos utilizados correspondan a tallas en que prácticamente solo se presentan machos,
Los datos de talla y peso de dos campanas realizadas por el equipo de pesca del Instituto Español de Oceanografía, Laboratorio de Canarias han servido para profundizar en el estudio de la relación talla-peso en el pulpo de estos stocks.
El cuadro 2 muestra el peso medio por talla para ejemplares eviscerados de pulpo de 11 cm a 19 cm recogidos en julio de 1978 y marzo de 1979 (campanas 7 807 y 7 905 respectivamente) . Puede observarse la gran diferencia existente entre ejemplares de la misma talla en cuanto al peso.
Aunque en principio, podríamos estar tentados a pensar que es el factor de condición el responsable de estas diferencias, la cosa no se presenta tan clara si observamos resultados de campanas anteriores. Así, por ejemplo, Cort y Pérez-Gándaras publican una relación talla-peso que predice pesos muy inferiores a los ya expuestos, a pesar de que su campana fue realizada en la misma época (julio-agosto) que la 7 807.
Volviendo al cuadro 2, podemos observar que el peso medio de una campana a otra varía en un factor de 1,2-1,3, y volviendo a multiplicar los pesos así obtenidos por un factor de 1,4-1,5, conseguimos “llegar” a los pesos de la campana 7 903.
El hecho de que podamos pasar de una a otra por medio de un factor prácticamente constante en la gama de tallas que se encuentra en la fase explotada hace que, para el propósito de evaluar rendimientos, pierda importancia el emplear una u otra relación, en cuanto a las variaciones interanuales. No pasa lo mismo, por desgracia, con la condición de una pesquería estacional como esta.
En todo caso, existe una necesidad urgente de investigar, tanto la condición estacional del pulpo como las variaciones geográficas y de ano en ano de la relación talla-peso.
Nosotros retendremos, mientras tanto, la relación obtenida en la campana 7 903 para pulpo eviscerado,
W = 1,27 L2,62
El cuadro 3 analiza la razón de sexos que se deriva de los datos presentados por Cort y Pérez-Gándaras (1973).
La figura 16 muestra la reducción que se va produciendo en la proporción de hembras en la captura; la curva que representa esa reducción ha sido trazada a mano.
El segmento A supone la sustitución de la curva por una desaparición masiva de las hembras “en filo de cuchillo”, que se produciría a una talla aproximada de 22,25 cm, correspondiente a una edad de 2,74 anos, según la ecuación de von Bertalanffy general retenida. Por ello, supondremos mas adelante, con propósito de evaluación, que se produce una mortalidad masiva de las hembras a los 2,75 anos de edad, quedando reducida en ese momento a la mitad la biomasa del stock.
La partición de los histogramas de tallas en componentes normales ha permitido un primer estudio de la mortalidad total por medio de curvas de captura (Ricker, 1958; 1975).
Las estimaciones de Z obtenidas deben considerarse solo como primeras y groseras aproximaciones a su valor real; no es muy lícito emplear curvas de captura en este caso, dado que se supone que cada punto aparecerá como reflejo de la abundancia de una cohorte; las cohortes están separadas por semestres y el esfuerzo (reflejo de la mortalidad) no se mantiene estable de un semestre a otro, al menos para la flota española.
Tampoco se dispone de ningún dato sobre la evolución de reclutamientos sucesivos, que, de presentar tendencia, podrían incidir sobre las estimaciones obtenidas; por ultimo, es casi evidente la existencia de diferencias en la mortalidad tanto de una cohorte a otra como de una clase de edad a la siguiente.
A pesar de ser conscientes de todos estos hechos, consideramos conveniente aprovechar al máximo la información de que disponemos, así que hemos analizado las curvas de captura con las distribuciones corregidas para selectividad, dado que esta cubre gran parte de la gama de tallas de la fase explotada.
El resultado se muestra en la figura 17. Las estimaciones de mortalidad corresponden a puntos separados por semestres y corresponden por tanto a tasas de mortalidad a dicha escala de tiempo.
Un dato importante es la semejanza de la pendiente de las curvas correspondientes a los anos 1972, 76 y 78 - 1,27, 1,09 y 1,10 respectivamente, promediando las diferencias de los neperianos consecutivos correspondientes a las abundancias de las cuatro primeras clases de edad obtenemos cifras de 1,49, 1,09 y 1,42 para las tres fechas citadas,
La imagen que obtenemos no contradice a la que se deduce de la serie histórica de esfuerzos publicada por el Grupo de Trabajo de CPACO, donde la pesquería ha pasado por dos etapas claramente diferenciadas: un período de mortalidad baja, en el que se encontrarla incluido el ano 1967, fecha de la campana descrita por Cabrera (1967), y otro de alta mortalidad, que comenzaría en el año 1971 y donde se encontrarían incluidas las otras tres campanas a que hacemos referencia.
Para el ano 1967, la mortalidad total hallada es de 0,75 sobre una base semestral. El valor de Z obtenido para el ano 1978 debe, de hecho, estar sobreestimado, ya que a partir del ano 1977 la flota española cambio de malla, por lo que en su abundancia se contabilizan los supervivientes no capturados, configurándose un período de fuerte transición.
Según el Grupo de Trabajo de CPACO (CECAF, 1968), el esfuerzo desarrollado en 1976 fue 2,22 veces mayor que el desarrollado en 1967 y el de 1972 2,16 veces mayor.
Utilizando las pendientes de las curvas de captura respectivas como estimaciones absolutas de la mortalidad total en cada ano, obtendríamos valores de M respectivos de 0,96 y 0,6 sobre una base anual, por medio de las relaciones
(Zi - M)/(Zj - M) = Fi/Fj = fi/fj
Para nuestros propósitos de evaluación retendremos, por tanto, un límite inferior del valor de M de 0,5 sobre una base anual y un límite superior de 1,0.
Examinando las distribuciones de tallas por sexos que figuran en el trabajo de Cort y Pérez-Gándaras, podemos observar la diferente mortalidad de machos y hembras, diferencia que va aumentando con la edad. Esa diferencia se hace especialmente grande a partir de la tercera clase de edad, ano y medio de vida de los ejemplares, como puede verse en la figura 18, que representa las curvas de captura de machos y hembras.
En todas las figuras de curvas de captura aparece una fuerte pendiente correspondiente a las primeras clases de edad, que disminuye a partir de la clase que hemos denominado IV y que correspondería a los dos anos de edad de los ejemplares. Este hecho parece demostrar que la pesca va dirigida preferentemente hacia los ejemplares jóvenes, o, lo que quizás sea mas correcto, que tal como se realiza la actividad pesquera, los ejemplares jóvenes quedan sometidos a una mayor mortalidad. Efectivamente, la mortalidad total disminuye a las edades altas, a pesar del aumento en la mortalidad natural de las hembras. Los valores obtenidos de mortalidad total a altas edades nos conducen a pensar en que el valor real de M debería encontrarse mas cercano al límite inferior que hemos elegido, M = 0,5 sobre una base anual, que al límite superior M = 1,0, hecho que deberíamos tener en cuenta en los capítulos de evaluaciones.
El calculo del rendimiento por recluta propuesto por Ricker (1958; 1975) es una buena herramienta para crear el marco de rendimientos obtenibles a reclutamiento constante en este o estos stocks.
Hemos utilizado en todos los casos el modelo lineal de Ricker, en la seguridad de que el modelo exponencial no nos conduciría a grandes diferencias.
La estrategia seguida fue la siguiente: se supuso la entrada en la pesquería de 1 000 kg de reclutas a la talla de 7 cm, supuesta talla de primera captura con malla de 40 mm. El primer intervalo acaba cuando el pulpo alcanza 10,16 cm de talla del manto, talla de primera captura correspondiente a la malla que permite la reglamentación CPACO.
Los siguientes intervalos acaban cuando el pulpo alcanza 1, 1,5, 2 y 2,75 anos de edad. En ese ultimo momento, se produce la mortalidad masiva de las hembras y la población se reduce a la mitad. Los siguientes intervalos acaban a los 3,5, 4,5 y 5,5 anos de edad, momento en que se supone que abandonan la pesquería.
Se ha utilizado la ecuación de von Bertalanffy ya citada,
lt = 32,15 (1 - e-0,38(t + 0,34))
y una relación talla-peso derivada de los datos de la ultima campana realizada por el personal del Instituto Español de Oceanografía, Laboratorio de Canarias, correspondiente a marzo de 1979.
W = 1.27L2,62
Se utilizaron valores de mortalidad natural M sobre una base anual de 0,5 y 1 (= uno), (M/K = 1,32 y 2,64 respectivamente) y valores de mortalidad por pesca F constante de 0,5, 1, 1,5 y 2 para malla de 40 mm; de 0,5, 0,75, 1,0, 1,25, 1,5 y 2 para malla de 60 mm y M= 0,5; y de 0,5, 0,75, 1, 1,25, 1,5, 1,75, 2 y 2,5 para malla de 60 mm y M = 1.
En unos ensayos, se suponía que la mortalidad por pesca comenzaba a actuar a partir de una talla de 7 cm y en otros a partir de 10,16, tallas de primera captura correspondientes a mallas de 40 y 60 mm, como ya hemos dicho. Por ultimo, se calculo el rendimiento por recluta para los vectores del cuadro 4, con F variable, vector que suponemos que reflejaba aproximadamente la situación real en 1976.
La figura 19 muestra la evolución de la biomasa de la cohorte no explotada para ambos valores de M.
Los resultados que se presentan en los cuadros 5 y 6 y en las figuras 20 y 21 muestran conclusiones muy interesantes; para ambos valores de M se producen aumentos importantes en los rendimientos cuando se cambia la malla a tasas altas de explotación. El cambio de malla bajo el esquema actual supondría, en particular, un aumento del 34 por ciento en los rendimientos por recluta para M = 0,5 y del 23 por ciento para M = 1.
Con M = 0,5, los rendimientos por recluta comenzarían a disminuir a partir de F = 1 para ambas mallas; con M = 1 y con malla de 40 mm, se produciría una reducción del rendimiento a partir de F = 1. Con malla de 60 mm, el rendimiento se estabilizaría a partir de F = 1,5. Todo hace pensar, por tanto, que cualquier aumento del esfuerzo pesquero sobre el del período 1972-1976 provocaría un descenso en los rendimientos, o, en el mejor de los casos, ninguna ganancia apreciable. Mas bien puede pensarse que nos encontramos ante una situación de sobrepesca de crecimiento, pudiendo obtenerse mayores capturas por medio de una reducción del esfuerzo. En el capítulo de conclusiones discutimos con mas amplitud este tema.
Con respecto a las fecundidades relativas, han sido calculadas como la relación a razón entre la biomasa media de las hembras de 1 a 2,75 años de edad, en cada esquema de explotación y la biomasa media de hembras fecundas en el stock virgen, como muestran los cuadros 7 y 8 y las figuras 22 y 23. Esta hipótesis equivale a suponer que las hembras presentan una fecundidad dependiente de su peso.
Puede comprobarse la gran reducción en la fecundidad por recluta a altas tasas de explotación. Al no conocer nada sobre la relación stock/reclutamiento, no podemos prever la importancia de este hecho para la regulación del stock. SÍ podemos decir que el cambio de malla debe haber provocado un aumento importante en la fecundidad, aunque esta se mantenga a valores muy bajos.
El Grupo de Trabajo CPACO ya citado (1978), realizo el ajuste de series estadísticas de captura/esfuerzo a modelos de producción de Schaefer (Schaefer; 1954; 1957; Beverton y Schaefer, 1963) y Fox (1970) con modelos de regresión funcional. Este grupo utilizo una unidad de esfuerzo arbitraria obtenida por combinación de datos españoles y japoneses.
Nosotros hemos juzgado con la misma serie de datos, introduciendo algunas variaciones en la elaboración de los modelos para conocer con mas rápida precisión su comportamiento. En todos ellos hemos resuelto el modelo de regresión predictivo, fácilmente transformable en regresión funcional si se recuerda que:
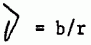
Los distintos modelos que ajustamos fueron los siguientes:
1) Con la cpue y el esfuerzo utilizado en el Grupo de Trabajo, se resolvió gráficamente el modelo de producción generalizado, con el objeto de visualizar la forma de la curva y orientarnos sobre el posible valor del parámetro m. Este modelo resuelto gráficamente se muestra en la figura 24. Su forma es muy parecida a la del modelo de Fox (1971), m tiende a 1, y solo ligeramente mas pesimista, por lo que podríamos prever un valor de m ligeramente superior al. El modelo de Fox, que se muestra superpuesto al generalizado en la figura 25, predice un RMS (Rendimiento Máximo Sostenible) de 110 000 t para un esfuerzo de 1 258 unidades del Grupo de Trabajo (r = -0,94; = 0,0008456).Los valores de los diferentes ensayos figuran para mas claridad en el cuadro 9.2) Ensayamos un modelo de producción con la serie de cpue española. La razón era la preponderancia de las capturas españolas en la zona norte, mientras que las capturas japonesas se repartían entre dos zonas donde habitan probablemente stocks diferentes desde el punto de vista de la dinámica (zonas de Cabo Garnett y Cabo Blanco), con un cambio importante en la proporción de las capturas de una zona a otra en los últimos anos.
El resultado fue un RMS de 136 000 t, correspondientes a un esfuerzo de 1 165·103 unidades españolas para el modelo de Schaefer y de un RMS de 124 000 t para un esfuerzo de 1 216 x 103 unidades según el modelo de Fox, que dio un ajuste de r = -0,98 (ajuste realizado sobre nueve pares de valores).
3) Dado el cambio en las estrategias de pesca a partir del ano 1976, decidimos realizar un nuevo modelo basado en los datos de captura y esfuerzo del Grupo de Trabajo de CPACO (1978), pero sin tener en cuenta los datos de 1976 y 1977.
El modelo de Fox dio como resultado un RMS de 111 000 t, correspondiente a un esfuerzo de 1 259 unidades del Grupo de Trabajo (r = -0,93). El modelo de Schaefer dio un RMS de 114 000 t, a esfuerzo de 1 127 unidades.
4) Se sometió a standardización la cpue española por una parte y la japonesa y coreana, supuestas homogéneas, por otra, dividiendo las series respectivas de cpue por su valor medio. El esfuerzo total se obtuvo tras obtener el esfuerzo conjunto de estos tres países y extrapolarlo al correspondiente a la captura total.
En este caso, el RMS predicho por el modelo de Fox fue de 105 000 t a esfuerzo standard de 135 unidades, mientras que el modelo de Schaefer predecía un RMS de 113 000 t a esfuerzo de 131 unidades.
5) El mismo proceso se repitió eliminando los anos 1976 y 1977, con RMS de unas 102 000 t para el modelo de Fox y unas 110 000 t para el de Schaefer.
Para clarificar un poco el panorama y construir un criterio que nos permitiera elegir los ensayos que con mayor probabilidad se ajustaran a la situación real, calculamos los coeficientes de correlación entre las distintas series de cpue. Los resultados fueron los siguientes:
a) Entre las series de cpue japonesa y española para el período 1969-1977, la correlación resulto ser de 0.0325, mientras que para el período 1969-1975 se elevaba a 0,92, confirmando el “ruido” introducido por estos dos últimos años en los análisis, con dos posibles causas principales: el cambio de estrategia ya mencionado de los arrastreros orientales y una interrupción en la serie de cpue española, que pasa a tener como base el esfuerzo de los arrastreros congeladores.Nuestra conclusión es que el caso (5) deberla ser considerado como el mas apto para reflejar la situación actual, de modo que el RMS se encontraría entre las 100 000 y las 110 000 t. El caso (3) también podría ser considerado aceptable, con valores para el RMS de entre 110 000 y 115 000 t. Las figuras 25 y 26 muestran la representación gráfica de estos modelos para regresiones predictivas.b) La correlación entre la serie de cpue japonesa y la del Grupo de Trabajo fue de 0,75.
c) La correlación entre la cpue española y la del Grupo de Trabajo fue de 0,96.
En análisis sucesivos debería tenerse muy en cuenta la falta de correlación surgida a partir de 1976 entre ambas series de cpue, japonesa y española, así como la posibilidad de manejar datos de esfuerzo coreanos.
Estas ultimas figuras que citamos muestran, en todo caso, el buen ajuste de las series de captura/esfuerzo a los modelos globales y particularmente al de Fox. Varios puntos a tener en cuenta surgen de estas figuras.
a) En el ano 1975, el stock fue sometido a una fuerte sobrepesca; no sabemos con seguridad si ese esfuerzo disminuyo en los anos 1976 y 1977, pues difiere aquí la medida del esfuerzo del Grupo de Trabajo de CPACO y del esfuerzo standardizado utilizado por nosotros en el presente trabajo.b) En todo caso, hubiera sido necesario reducir el esfuerzo de pesca generado en el ano 1975 en un 30 por ciento para encontrarnos alrededor del esfuerzo que provocaría capturas alrededor del RMS.
c) No parece oportuno pensar en una transición que durase mas de uno o dos años. Podemos observar sobre los modelos de producción realizados por el Grupo de Trabajo o los que figuran en este mismo trabajo, como las desviaciones del equilibrio no son grandes, a pesar de enormes variaciones del esfuerzo de un ano al siguiente. Por ello, no creemos que se debiera pensar en términos de cpue de años anteriores, tal como se hace en el informe del Grupo de Trabajo CPACO (cuadro 10), a la hora de pensar en cuotas de captura.
d) El Comité de CPACO ha aconsejado la utilización de una malla de 60 mm en lugar de la malla tradicional de 35 mm utilizada en esta zona (Recomendación CECAF/VI/2, 6a sesión, Agadir, diciembre 1979.
Este hecho debería hacer variar el modelo de producción, en el sentido de aumentar el RMS, al tiempo que debería variar la escala del eje de abscisas. La imagen actual, por tanto, es mas optimista de los que nos muestran las figuras presentadas.
e) El RMS que muestran las figuras es, por tanto, una subestimación del RMS real; dicha estimación podría servir como margen de seguridad a la hora de asignar cuotas de captura, por ejemplo.
f) La falta de correlación de las cpue japonesa y española en los anos 1976 y 1977 puede deberse a causas que ya hemos mencionado: cambio de zona de pesca de parte de la flota japonesa, su sustitución por la coreana y el cambio de la base de medida del esfuerzo por parte de la flota española.
Todos estos hechos permiten constatar la necesidad de un profundo estudio de esta pesquería en los próximos anos.
g) El que se haya producido una expansión gradual de la zona de pesca en el período histórico de la pesquería, puede estar mostrándonos una visión optimista, por el contrario, de su situación actual, que se concretaría en un valor de m estimado mas bajo del real. Nosotros creemos en la posibilidad de que en este stock, y por lo menos a niveles bajos de abundancia, los reclutamientos se redujeran casi proporcionalmente al aumento de la mortalidad por pesca, con fuerte caída en la rama derecha de las curvas de producción; es decir, si el modelo se ajustase mejor a una curva de Fox que a una de Schaefer, sería debido a que no habríamos tenido en cuenta en el la expansión citada de la zona de pesca.
h) Sería necesario aclarar a que se ha debido el aumento de la cpue de la flota japonesa, pues podría tener relación con un cambio de caladero. Si así fuese, sería necesario en el futuro estudiar mas a fondo la estructura del stock, desde un punto de vista de la dinámica.
La figura 27 muestra pares de valores de cpue del Grupo de Trabajo CPACO en anos sucesivos y en escala logarítmica.
La interpretación de esa figura no es sencilla, pues hay dos factores que deben influir grandemente en ella; por una parte, el esfuerzo ejercido, que hace surgir una correlación espúrea entre cpue (i) y la cpue (i + 1).
Efectivamente, las dos nubes de puntos que se observan corresponden a los dos grandes períodos de la pesquería; un período del 1964 al 1971 de bajo nivel de esfuerzo, y otro del 1972 al 1977 de alto nivel.
Pero en la figura tiene que influir otro factor, sin duda, que es el reclutamiento que se produce cada ano. Lo que vemos en ella es que las “oscilaciones” que se producen entre dos pares sucesivos de valores son pequeñas; digamos que la figura es demasiado regular para lo que solemos esperar; o, lo que es lo mismo, los nuevos reclutamientos no parecen influir demasiado en la regularidad de la figura.
Dado que no estamos en condiciones, por falta de datos, de definir una relación stock/reclutamiento, no seguiremos discutiendo este punto, pero debe recordarse que, por el crecimiento ya descrito del pulpo, se encuentran en la pesquería en numero importante, no mas de dos clases anuales. Si la afirmación anterior resultara cierta, sería necesario mantener una estricta vigilancia sobre el tamaño del stock reproductor como componente importante en la definición del reclutamiento sucesivo.