Ce modéle schématise les relations entre les captures, les cpue et l'effort de pêche. Il est trés connu et son utilisation a été généralisée dans le monde entier, en particulier dans les commissions des pêches. Bien que ce modéle soit également critiqué à l'heure actuelle (Larkin 1977, Sissenwine 1978), il restera encore pendant quelques années au moins un outil essentiel faute de mieux. Il est donc intéressant de se pencher sur les conséquences de l'instabilité des ressources sur la théorie classique.
Nous ne nous attarderons pas sur l'effet des variations de capturabilité (liées aux variations de biomasse) sur les modéles de production. Ces variations qui tendent à produire un modéle déformé, à une surestimation de l'effort correspondant au maximum de production et à une sous-estimation de l'augmentation de la mortalité par pêche et peuvent donc conduire à une sévére surexploitation, ont été étudiées par ailleurs (Fox, 1971).
Lorsque l'environnement affecte beaucoup la production, le modéle de production décrivant la réaction du stock à l'exploitation ne peut plus être envisagé comme une simple fonction déterministe (fig. 14A) mais comme une famille de courbes correspondant à des conditions ambiantes et des capacités biologiques du milieu différentes (fig. 14) ou comme un modéle multivariable :
Capture = f (effort, environnement)
La trajectoire de la pêcherie à travers cette famille de courbes devient complexe et non automatiquement réversible. Il n'existe plus un seul rendement maximal soutenu (RMS) mais plusieurs selon les conditions ambiantes, et la notion de RMS classique n'a plus de sens qu'à trés long terme. Il faut noter qu'il à été démontré que lorsque les variations sont importantes, la Prise Maximale Moyenne réellement obtenue (Maximum Average Yield, MAY) sera inférieure au RMS (Sissenwine, 1978).
Ce modéle largement utilisé (mais peu démontré) dans la littérature classique dépeint les relations quantitatives qui existent éventuellement entre la taille d'un stock reproducteur parental et l'importance de la progéniture (ou recrutement) qui en découle. Un exemple de relation classique (type Ricker) est donné sur la fig. 15A. L'impact de la variabilité naturelle sur ce modéle à été largement discuté par Garcia (1983). Au lieu d'un tel modéle déterministe, il est nécessaire de considérer un modéle multivariable ou une famille de courbes (fig. 15B) correspondant chacune à un ensemble de conditions ambiantes données. Dans ces conditions, il n'existe plus un seul et unique point d'équilibre (El, fig. 15A) pour la pêcherie à l'intersection entre la courbe S→R (relation intrinséque entre le stock et les recrues) et la courbe R→S (relation triviale entre les recrues et le stock qui en découle dont la pente est fonction de F, la mortalité par pêche) mais toute une série de points d'équilibre virtuels (El à E5 sur la fig. 15B) situés le long de la ligne OA. En d'autres termes, le stock variera d'une année à l'autre, de maniére auto-corrélée, à cause des changements dans le recrutement, même si l'effort reste inchangé et la notion d'équilibre devient purement statistique.
De la même maniére, on ne pourra plus considérer qu'il existe un niveau caractéristique de mortalité par pêche F (critique) pour lequel la fonction R→S occupe une position limite à laquelle le taux de remplacement du stock devient insuffisant et le stock s'effondre (fig. 15A). Il faut en revanche admettre que le risque “d'effondrement” existe toujours même pour un stock vierge comme le démontrent les observations relatives à la sardine de Californie dans le passé (Soutar et Isaacs, 1974) ainsi que les simulations de Laurec, Fonteneau et Champagnat, 1980). On pourra en revanche définir une zone à risque élevé (secteur hachuré dans la fig. 15B) dans laquelle l'administration des pêches pourra estimer que le risque bioéconomique devient insupportable.
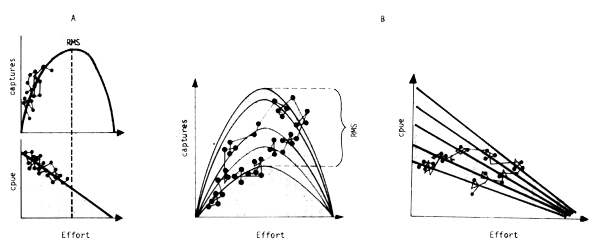
Fig. 14 - A : Modèle de production classique
B : Modèle de production affecté par une variable climatique
Les points représentent la trajectoire théorique d'une pêcherie. La figure 14 B illustre le fait que dans ce cas la trajectoire n'est plus forcément réversible.
Notons que lorsque la capturabilité q varie en fonction de la biomasse (et en particulier s'accroît quand la biomasse décroît), la droite de remplacement R→S (fig. 15B) évoluera vers la gauche à cause d'un accroissement de la mortalité par pêche F (non liée à une augmentation de l'effort de pêche) et tendra à se rapprocher de la zone de F critique, où les risques d'effondrement sont trés élevés. Les variations naturelles de biomasse, accompagnées de variations de q entraînent donc des variations importantes du risque d'effondrement même si l'effort de pêche n'augmente pas.
D'autre part, les variations “naturelles” de q et donc de F se traduiront également par des variations dans les captures totales même en l'absence de variations de l'effort nominal en raison de la relation entre F et les captures reconnues dans le modéle de production. Dans ce cas, il y a confusion entre les effets de l'environnement et ceux de la pêche.
Lorsque les variations “naturelles” du recrutement sont trés largement supérieures à celles produites par la pêche et par les changements de la taille du stock parental, la relation stock-recrue pourraît être simplement remplacée par un modéle R = f (environnement).
Ce modéle est en général considéré comme peu susceptible d'être affecté par des variations climatiques car il n'est pas affecté par les variations du recrutement. On a démontré cependant que les variations naturelles d'abondance s'accompagnent de variations de la croissance, de la mortalité naturelle, de la maturité, etc. On doit donc admettre que ce modéle sera affecté également, ce qui pourraît conduire à réviser les réglementations en matiére d'âge à la premiére capture par exemple.
La reconnaissance de l'instabilité d'une ressource naturelle importante pose aussitôt le probléme de son suivi continu, par des méthodes acoustiques par exemple. Elle pose également le probléme de la prédiction car il devient alors fondamental de prévoir à l'avance l'évolution de l'abondance pour pouvoir prendre à temps les mesures d'aménagement requises (prédiction de R, de la biomasse, des captures). Les modéles de prédiction peuvent être recherchés en utilisant les caractéristiques pertinentes de l'environnement comme variables prédictives (cf Garcia et LeReste, 1981; LeReste, 1982). Ils ne sont utiles cependant que si ils permettent réellement une prédiction avec un temps d'anticipation suffisamment long pour permettre à l'industrie et à l'administration des pêches de réagir, et si la précision des prédictions est suffisante.
Les conséquences décrites au paragraphe 3.1 concernant le modéle de production peuvent être élargies au modéle global économique, largement utilisé en économie de pêches. Le modéle classique (fig. 16A) suppose qu'il existe un point d'équilibre Z auquel le dévelopement de la pêcherie s'arrêtera, et où la rente économique sera nulle. L'existence de variations naturelles de l'abondance entraîne l'existence théorique d'une famille de modéles bioéconomiques (fig. 16B). Il n'existe donc plus un point mais une droite d'équilibre OA le long de laquelle la pêcherie tendra à se déplacer lorsque le stock passe de l'abondance correspondant à la courbe inférieure à celle correspondant à la courbe supérieure. La conséquence essentielle est l'existence de fluctuations importantes de la rente (fig. 17) et en particulier la possibilité d'accroissement exceptionnel de celle-ci même dans le cas d'une pêcherie surexploitée. Les fluctuations naturelles d'abondance (et en particulier les accroissements, périodiques ou non, de biomasse) seront donc des stimulis puissants pour l'exercice par les professionnels, de pressions très fortes sur les gouvernements pour obtenir les aides nécessaires à l'expansion et à la reconversion (du marché en frais à la farine par exemple). Elles seront finalement la source de surinvestissements atteignant des niveaux astronomiques et hors de proportion avec les niveaux de surinvestissement qu'une ressource plus constante est suceptible de générer dans une contexte de marché stable.
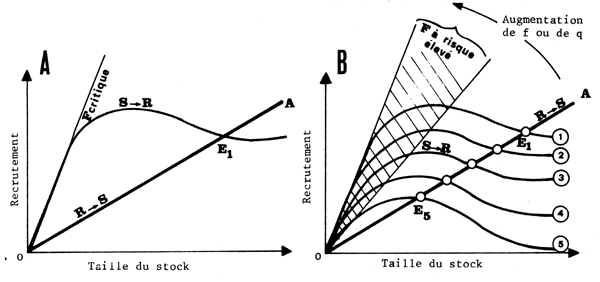
Fig. 15 - Relation stock-recruitment classique (A) et affectée par l'environnement (B)
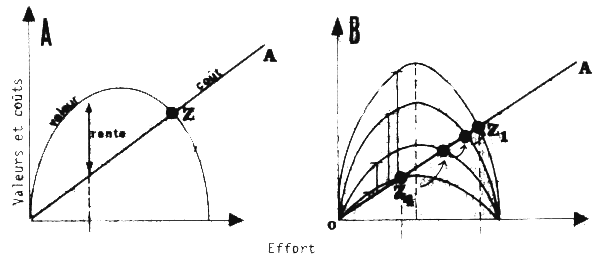
Fig. 16 - Modèle bioéconomique classique (A) et affecté par l'environment (B)