El marco teórico-analítico dirigido a proponer pautas para el manejo de recursos pesqueros ha sido tradicionalmente desarrollado, tanto en el aspecto biológico como en el económico, en base a modelos que consideran una sola especie. Se ha argumentado que las interacciones entre los componentes de una comunidad carecen de relevancia al evaluar el estado de un recurso y sugerir estrategias para su explotación, en particular cuando el esfuerzo pesquero es moderado y dirigido a la especie ecológicamente dominante. Sin embargo, en pesquerías de varias regiones del mundo se han detectado cambios agudos en la abundancia y composición relativa de las especies que constituyen una comunidad, generalmente asociados con una creciente intensidad de pesca (ver ejemplos en Mercer, 1982; May, 1984; Pauly & Murphy, 1982). Se han observado fenómenos de sobrepesca, en términos de una progresiva disminución de las especies más valiosas en el mercado, que en general corresponden a los eslabones más altos de la cadena trófica (Pauly, 1982; Bustamante & Castilla, 1987). Esto ha llevado a reconocer que en la práctica la explotación pesquera opera sobre un recurso multiespecífico (May et al., 1979), obtenido incidental o intencionalmente por una flota variable en sus características básicas, tales como tamaño, poder de pesca y tipo de arte empleado (Gulland & Garcia, 1984).
En las últimas dos décadas, el cuerpo teórico - práctico dirigido a manejar los recursos pesqueros ha intentado incluir las interdependencias ecológicas (e.g. competencia, relación depredador-presa) y la estabilidad de la comunidad asociada, es decir, su respuesta a perturbaciones diferenciales en cada uno de sus componentes, así como las interdependencias tecnológicas que resultan de la actividad extractiva de unidades pesqueras con características tecnológicas disímiles operando sobre diferentes componentes de una población o bien distintas especies objetivo (FAO, 1978; Huppert, 1979; May, 1984 y referencias contenidas en éstos).
No obstante tales esfuerzos, la transición desde el análisis y manejo de recursos uni a multiespecíficos requiere mucho más que la extensión de los modelos tradicionales. Se ha documentado que la adición de una especie a un modelo uniespecífico incrementa su complejidad (e.g. número de interacciones en un modelo compuesto por subsistemas multicompartimentalizados: Silvert, 1982). El elevado número de parámetros requeridos como entrada para diseñar un modelo multiespecífico, así como las diversas fuentes de error y variabilidad natural en las estimaciones -que frecuentemente inducen a que el modelo no sea validado- ha sido la razón por la cual la aproximación multiespecífica es raramente aplicada en la práctica o sus resultados son considerados poco creíbles (Larkin, 1982; Majkowski, 1982; Sugihara et al., 1984).
Si bien, a pesar de las dificultades, los conceptos anteriores denotan un creciente interés en el plano biológico de las implicaciones de manejo debidas a la explotación de recursos multiespecíficos, se ha dado poca importancia a la teoría económica aplicada a esta problemática (sin embargo, ver Mitchell, 1982; Clark, 1976; 1985; Heen, 1989; Anderson, 1986; May et al., 1979). Una de las razones principales de esto es la complacencia científica en cuanto a la aplicabilidad de los conceptos económicos desarrollados por Gordon (1953; 1954) para pesquerías uniespecíficas (ver Cap. 2) en un contexto multiespecífico, lo cual no siempre es válido (Mitchell, 1982; Ströbele & Wacker, 1991; Flaaten, 1991).
En este Capítulo se discute la extensión del modelo bioeconómico clásico para recursos multiespecíficos y se analizan las implicaciones bioeconómicas de las interdependencias ecológicas y tecnológicas que se suscitan en pesquerías. Se discute la aplicabilidad del modelo para diferentes tipos de recursos (e.g. pelágicos y bentónicos) en función de su biología, dinámica y estrategias de explotación. Finalmente, se sugieren futuros tópicos claves de investigación en el área.
Una interdependencia tecnológica ocurre cuando flotas de diferentes características, ya sea en su poder de pesca (e.g. flota artesanal y mecanizada) y/o tipos de artes empleados, operan sobre diferentes componentes de un stock (e.g. juveniles y adultos) o bien sobre distintas especies objetivo de un stock múltiple (“mixed stock”: Clark, 1985) y en consecuencia afectan su magnitud en forma diferencial (Fletcher et al., 1988). También ocurre en el caso de una flota que captura especies co-ocurrentes en el espacio, dependientes o no ecológicamente. El concepto de flota es aqui utilizado en un sentido amplio, incluyendo la recolección manual de organismos en pesquerías litorales artesanales de subsistencia.
Una interdependencia ecológica es definida cuando existe cierta relación entre dos stocks explotados (Anderson, 1975a, b; Mitchell, 1982) o bien entre diferentes componentes poblacionales de un mismo stock (e.g. reclutas y adultos). En base a ello se definen dos tipos de interacciones: competencia y depredación.
La competencia se define en base a los efectos negativos que un organismo ejerce sobre otro al consumir o interferir en el acceso a un recurso cuya disponibilidad (oferta) está limitada (Keddy, 1989). Esta interacción lleva a la reducción en la sobrevivencia, crecimiento y/o reproducción de los competidores, en especial el jerárquicamente subordinado (Giller, 1984; Begon et al., 1990). Es necesario discernir entre competencia interespecífica e intraespecífica, debido a que las consecuencias de estos procesos desde un punto de vista ecológico pueden ser muy diferentes. Los mecanismos por los cuales los competidores interactúan distinguen a la competencia por interferencia y por explotación (Schoener, 1983). Por medio de la dominancia competitiva una especie inhibe a otra en el uso de un recurso, ya sea a través de explotación o interferencia (Giller, 1984): el individuo competitivo dominante ósuperior disminuye la abundancia del recurso limitante al competitivo subordinado ó inferior y en casos de recursos sedentarios tiende a establecer la monopolización en el uso del sustrato primario y en consecuencia un monocultivo (sensu Paine, 1984). La visión diferencial de la competencia desde la perspectiva del dominante o subordinado (ver Goldberg & Fleetwood, 1987; Goldberg, 1987) tendrá relevancia en un contexto ecológico-pesquero, al evaluar los efectos bioeconómicos derivados de esta interdependencia ecológica.
La depredación es el consumo de un organismo (presa) por otro (depredador) a través de carnivoría, herbivoría u omnivoría (Begon et al., 1990). Un depredador puede ser clasificado de acuerdo a la amplitud de su dieta en monófago, oligófago y polífago, o también en especialista (monófagos y oligófagos) y generalistas (polífagos) según si reacciona o no a perfiles de abundancia de presas. Exhibe preferencia trófica por alguna presa cuando la proporción de ésta en su dieta alimentaria es mayor que la proporción en el ambiente (Begon et al., 1990). Estos conceptos serán tomados en cuenta al evaluar el significado de dicha interdependencia ecológica en pesquerías.
El marco teórico desarrollado en el Capitulo 2 suponía la explotación de un stock biológicamente independiente por parte de una flota homogénea. Las interdependencias ecológicas quedaban implícitamente consideradas en los parámetros K y r de la ecuación (2.1). En esta sección se expande el modelo a efecto de ilustrar las interdependencias ecológicas y tecnológicas relevantes en pesquerías multiespecíficas, manteniéndose los mismos supuestos que en el modelo uniespecífico.
En una pesquería se puede presentar heterogeneidad en el esfuerzo pesquero ejercido sobre una especie objetivo, generándose interdependencias de tipo tecnológico entre las flotas (o embarcaciones) con diferente poder de pesca y muchas ocasiones con costos unitarios heterogéneos del esfuerzo pesquero.
La captura sostenible de dos flotas con diferente poder de pesca (e.g. artesanal y mecanizada) puede representarse de la siguiente forma:
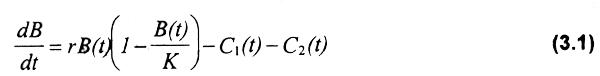
donde:
C1(t) = captura de la flota 1 en el tiempo t.
C2(t) = captura de la flota 2 en el tiempo t.
Análisis estático. Bajo condiciones de equilibrio biológico dB/dt=0, por lo que:
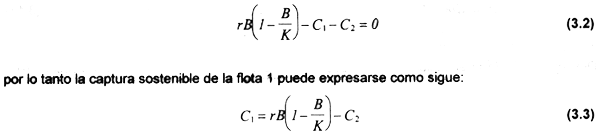
Por otra parte se sabe que:
Ct = qt ft B (3.4)
C2 = q2 f2 B (3.5)
Despejando B en la ecuación (3.2) y sustituyendo C1 y C2 por las expresiones (3.4) y (3.5) se obtiene:

Sustituyendo la ecuación (3.6) en las ecuaciones (3.4) y (3.5), la captura para cada una de las flotas será:
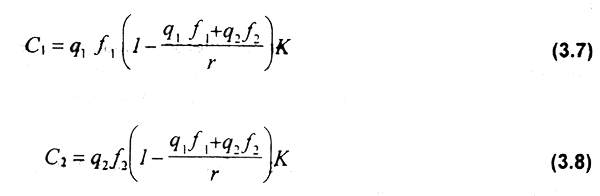
y la renta económica de cada flota:
π1 = pC1 - c1 f1 (3.9)
π2 = pC2 - c2 f2 (3.10)
Para obtener el equilibrio bioeconómico de las diferentes flotas, por ejemplo la flota 1, se hace π1 = 0 y se estima el correspondiente esfuerzo pesquero en equilibrio bioeconómico. En tal sentido, al sustituir la ecuación (3.7) en la (3.9) se obtiene:
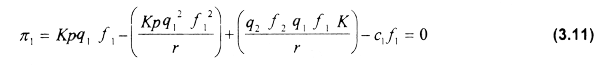
Despejando f1 de la ecuación 3.11 se obtiene el esfuerzo pesquero en equilibrio bioeconómico para la flota 1.

El MRE de la flota 1 se obtiene al igualar a cero la primera derivada de los ingresos netos, lo cual puede expresarse de la siguiente manera:

despejando f1 de la ecuación anterior se obtiene el esfuerzo de la flota 1 en máximo rendimiento económico:
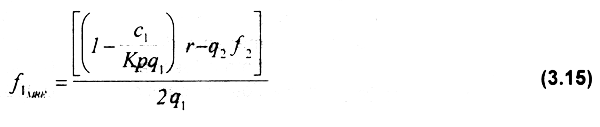
Comparando las ecuaciones 3.11 y 3.14 se puede observar que dado el esfuerzo de la flota 2 el esfuerzo pesquero en máximo rendimiento económico fMRE de la flota 1 es igual a la mitad del esfuerzo en equilibrio bioeconómico fEBE de esa misma flota.
De igual manera se obtiene el esfuerzo pesquero en MRE y en equilibrio bioeconómico para la flota 2.
Análisis dinámico. Para observar la trayectoria hacia el equilibrio bioeconómico o bien el comportamiento de la dinámica de la estructura de la población explotada y de la intensidad de pesca, es necesario resolver numéricamente dicho modelo construyendo programas de computación. En el siguiente ejemplo se analiza la evolución dinámica de dos flotas con diferente poder de pesca que inciden sobre el mismo recurso, suscitándose una interdependencia tecnológica.
Ejemplo. 3.1 Flotas con diferente poder de pesca
Dada una pesqueria de una especie pelágica cuyos parámetros aparecen en la Tabla 3.1, se analiza el comportamiento dinámico de la biomasa de la población, de las capturas y esfuerzo pesquero desplegado por dos flotas con diferente poder de pesca (mecanizada = industrial y artesanal), asi como los diferentes niveles de ingresos γ costos generados por ambas flotas.
| Parámetro/Variable | Valor | Unidad de medida |
|---|---|---|
| Tasa intrínseca de crecimiento | 0.36 | -- |
| Capacidad de soporte del ecosistema | 4000000 | ton |
| Coef. capturabilidad flota artesanal | 0.0002 | -- |
| Coef. capturabilidad flota mecanizada | 0.00035 | -- |
| Precio de la especie | 60 | US$/ton |
| Costo unitario esfuerzo artesanal | 15000 | US$/viaje |
| Costo unitario esfuerzo mecanizado | 45000 | US$/viaje |
| Parámetro de dinámica flota artesanal | 0.00001 | -- |
| Parámetro de dinámica flota mecanizada | 0.00001 | -- |
En la Figura 3.1 se pueden observar los resultados de la corrida de simulación a un horizonte de 50 años, con el correspondiente comportamiento dinámico de la biomasa del recurso, así como de las capturas de ambas flotas γ las rentas económicas generadas por la actividad, todas en función del esfuerzo pesquero de ambas flotas. Los costos unitarios del esfuerzo γlos coeficientes de capturabilidad relativos de ambas flotas determinan la expansión de la flota artesanal hasta llevar la biomasa a niveles inferiores de dos millones de toneladas con la consecuente eliminación de la renta de la flota industrial. Lo anterior motiva en consecuencia la salida de embarcaciones industriales liberando biomasa que es capturada posteriormente por la flota artesanal.
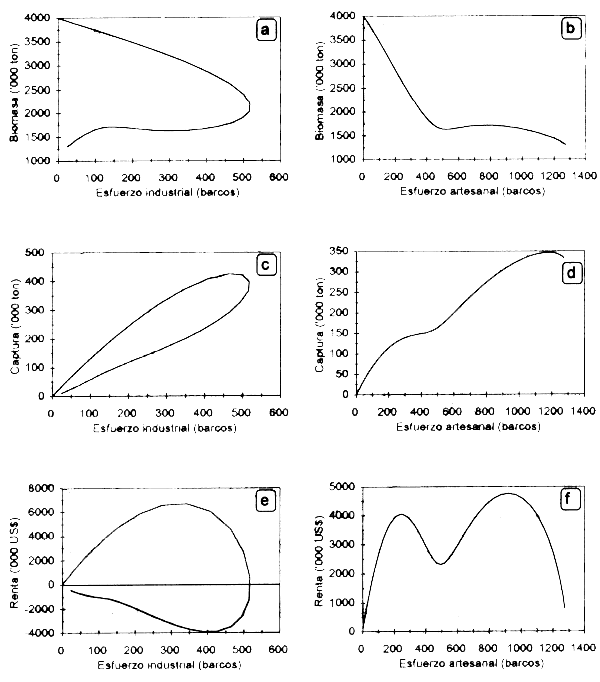
Figura 3.1 Comportamiento dinámico de la biomasa del recurso (a, b), las capturas por flota (c, d) así como la distribución de la renta económica (e, f) por tipo de flota, como resultado de las interdependencias tecnológicas entre ellas.
La Figura 3.2. muestra el comportamiento dinámico de la biomasa γ el esfuerzo pesquero aplicado por las flotas artesanal γ mecanizada. Se observa el brusco descenso de la biomasa poblacional durante los 10 primeros años de la pesquería, como consecuencia de un fuerte incremento del esfuerzo pesquero en la fase de desarrollo o expansión de la actividad. Esto resulta evidente en el caso de la flota artesanal, que con sus menores costos operativos e inversión posibilita un crecimiento más acelerado del número de barcos. La tendencia en el largo plazo de ambas variables es a presentar ciclos levemente desfasados en el tiempo (e.g. 5 años) como producto del retraso en la respuesta de la decisión de inversión por parte de los pescadores con respecto a variaciones en la abundancia del recurso (Fig. 3.2a). La amplitud de las oscilaciones de ambas variables disminuye en magnitud, hasta llegar en el largo plazo a un equilibrio en biomasa (1170000 ton) y en el número de barcos de la flota mecanizada (7) y artesanal (1275). En esa etapa los ingresos netos de ambas flotas tenderán a cero (ingresos totales = costos totales), y por tanto a un equilibrio bioeconómico donde no habrá incentivo para la entrada de nuevas unidades pesqueras. Es clara la tendencia de la flota artesanal a excluir a la mecanizada, debido a la ocurrencia de costos operativos mucho menores.
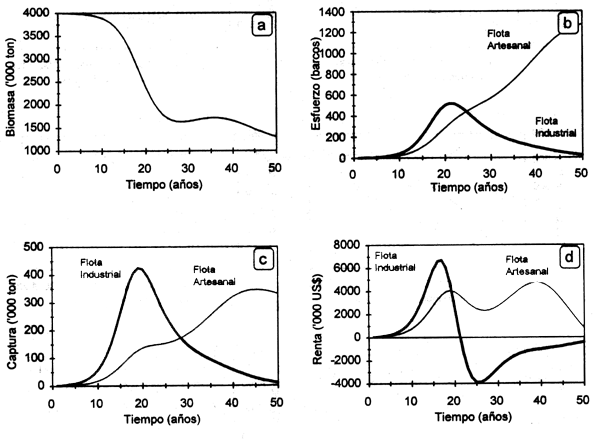
Figura 3.2 Trayectoria dinámica de la biomasa (a), el esfuerzo (b), la captura (c) γ la renta económica (d) obtenida por las flotas industrial γ artesanal.
Este caso pudiera ser considerado en el contexto de una pesquería secuencial (ver más abajo), sin embargo no considera la estructura por edades de la población y en consecuencia desconoce el efecto que cada flota pudiera tener en los diferentes componentes poblacionales. En efecto, es común encontrar que la pesquería artesanal tiende a afectar a organismos juveniles que se distribuyen en zonas costeras, mientras que la mecanizada tiende a hacer lo propio con los organismos adultos que se distribuyen hacia mayores profundidades (e.g. camarón: ver Willmann & Garcia, 1985). Este caso es desarrollado en la sección correspondiente a pesquerías secuenciales.
En este caso dos stocks sin ninguna interdependencia ecológica (e.g. nichos disjuntos, sensu Pianka, 1978) aparecen representados en las capturas realizadas por una flota con artes de pesca no discriminatorios. Cada unidad de esfuerzo afecta por igual a ambos stocks, por lo cual su representación relativa en las capturas dependerá del tamaño poblacional y magnitud de esfuerzo utilizado. A continuación se desarrolla la teoría aportada por Clark (1985) como fundamento para el análisis de este tipo de interdependencias.
Marco teórico (Clark, 1985). La ecuación básica del modelo de Schaefer para una población explotada (2.2) puede ser empleada para describir las tasas de cambio en biomasa de la especie X:

y en forma análoga para la especie Y
En condiciones de equilibrio dBΧ (t)/dt = dB,Υ(t)/dt = 0, por lo tanto:
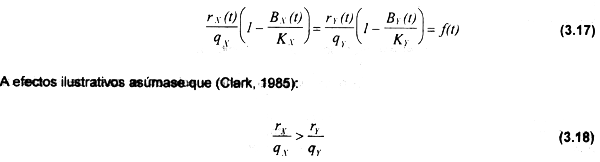
En ausencia de esfuerzo pesquero, la curva de equilibrio resultante de (3.17) se origina en el nivel de la capacidad de carga de ambas especies KΧ,KΥ.
Las especies decrecen en biomasa a medida que se intensifica el esfuerzo pesquero. La especie Y, con menor tasa de crecimiento según (3.18), se extinguirá en cierto nivel de esfuerzo P, mientras que X aún provee una captura sostenible. En el nivel de esfuerzo P, para la especie X se tendrá una biomasa (Bχρp) que puede estimarse de la siguiente forma:
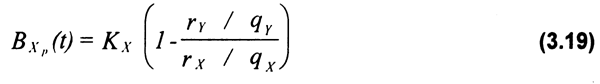
La especie γ será eliminada si:
F y = qy f (t) > ry (3.20)
o sea, la mortalidad por pesca FY de Y excede su tasa intrinseca de crecimiento. En el caso de X, la condición (3.18) garantiza que FX < rX, por lo cual la pesqueria persistirá como económicamente viable aún cuando Y no aparezca representada en las capturas.
De acuerdo al análisis anterior, la eliminación de especies con menor tasa intrínseca de crecimiento poblacional es factible en condiciones de acceso abierto en un contexto multiespecífico. Considerando la extensión de (2.20), los ingresos netos generados por una pesqueria serán:
π(t) = [P x q x Bx (t) + py qy By(t) -c ] f (t) (3.21)
En una pesquería de libre acceso Υ será eliminada si Bx<BXp, o sea:

La sobreexplotación γ probable extinción de una especie dependerá de su valor en el mercado, su posición γ papel funcional en la cadena trófica y aspectos inherentes a sus características biológicas γ poblacionales.
En este tipo de pesquerias, el esfuerzo pesquero es dirigido a dos o más stocks. Si bien las actividades pesqueras son mutuamente excluyentes (Huppert, 1979; Anderson, 1981, 1982a), es factible obtener captura incidental. Esto es particularmente viable en el caso de stocks de especies sedentarias con cierto grado de segregación espacial, lo cual permite direccionar el esfuerzo pesquero. En este tipo de recursos los pescadores perciben a la costa como una colección de áreas discretas que son objeto de rotación en función de la magnitud de aquellas agregaciones de individuos que optimizen la combinación adecuada de tallas de interés comercial (Caddy, 1975; Hall, 1983).
El “modelo de producción excedente en mosaico” (Munro, 1979; Polovina, 1989; Caddy & Garcia, 1983; Caddy, 1986) constituiria una buena aproximación uni ó multiespecifica al respecto: los datos colectados en diferentes zonas de pesca con cierta identidad geográfico-ambiental y diferentes intensidades de pesca, pueden ser empleados para definir estrategias óptimas de explotación γ rendimientos sostenibles por unidad de área. Considerando k áreas con una extensión Ak en el mismo ó en diferentes años t, la ecuación 2.14 del modelo de Schaefer es modificada como:

Esta aproximación, que supone equilibrio en el sistema (aproximación estática), implica un buen mapeo de cada zona de pesca, así como una idea previa de la productividad y características poblacionales de los stocks. Dado que se asume en este caso que las actividades pesqueras en cada stock son mutuamente excluyentes, es factible conjuntar los resultados de cada uno a posteriori y elaborar un “mapa de rendimiento bioeconómico”, en base a los ingresos netos (ec. 3.21) generados por cada stock.
Clark (1982) y Hilborn & Walters (1987) entre otros, han desarrollado modelos tendientes a simular la dinámica espacial de un recurso multiespecífico y del esfuerzo pesquero aplicado a éste. Parten de la ecuación (2.3) en una base multiespecífica:
Ctk = Bki f ki (t) q i (3.24)
aplicada a i especies en k zonas de pesca, estimando los ingresos netos por unidad de esfuerzo, zona de pesca y especie.
CASO 1: la flota 1 captura incidentalmente la especie objetivo de la flota 2. Considérense dos flotas: la flota 1, concentrada en la explotación de la especie X pero obteniendo incidentalmente cierto porcentaje de Y, la cual a su vez es objetivo de la flota 2. En la Tabla 3.2 se muestran los datos relevantes de ambas especies γ flotas, a efectos de su introducción en el análisis bioeconómico dinámico de la corrida de simulación.
| Parámetro/Variable | Valor | Unidad de medida |
|---|---|---|
| r especie χ | 0.36 | -- |
| r especie γ | 0.30 | -- |
| K especie χ (ton) | 4000000 | ton |
| K especie γ (ton) | 2000000 | ton |
| q especie χ flota 1 | 0.0004 | -- |
| q especie χ flota 2 | 0 | -- |
| q especie γ flota 1 | 0.00015 | -- |
| q especie γ flota 2 | 0.0025 | -- |
| Precio especie X | 60 | US$/ton |
| Precio especie Y | 45 | US$/ton |
| Costo unitario flota 1 | 60000 | US$/año |
| Costo unitario flota 2 | 15000 | US$/año |
| Parámetro de dinámica flota 1 | 0.00001 | -- |
| Parámetro de dinámica flota 2 | 0.000015 | -- |
La Figura 3.3 muestra los resultados del modelo bioeconómico dinámico que representa la interdependencia tecnológica. Las fluctuaciones en biomasa muestran un acentuado declive de ambas especies como resultado del desarrollo de la pesqueria (Fig. 3.3a). La flota 1, con mayor poder de pesca, realiza importantes capturas de χ en los primeros 20 años, lo cual determina una reducción de la abundancia a la mitad de su capacidad de carga durante el mismo período. La flota 2, cuyo objetivo es la especie Y, alcanza un máximo de sus capturas y desarrollo de la pesquería a los 8 años de haberse iniciado la misma (Fig. 3.3b). Sin embargo, el aumento de la captura incidental a partir de dicho lapso determina una reducción de sus rendimientos y una renta económica negativa en los años subsiguientes, en concordancia con un aumento sostenido de capturas, esfuerzo γ renta económica de la flota 1, la cual a su vez percibe ingresos adicionales derivados de la captura incidental de Y (Figs. 3.3c y 3.3d). En el largo plazo ambas flotas alcanzan el equilibrio bioeconómico a niveles de esfuerzo de 420 (flota 1) y 500 (flota 2) barcos. Sin embargo, la tendencia será a mostrar ciclos variables en amplitud de acuerdo a la presión pesquera ejercida por ambas flotas. En una situación ideal, el nivel de esfuerzo en 1 debería ser expandido hasta que el retorno marginal de la captura en ambas pesquerías iguale el costo marginal del esfuerzo pesquero en 1, mientras que para 2 es aplicable similar razonamiento.
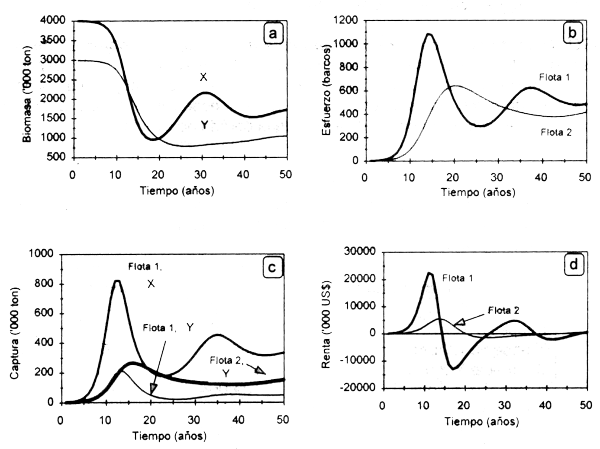
Figura 3.3. Modelo bioeconómico dinámico de interdependencias tecnológicas entre dos flotas: biomasa de la especie objetivo e incidental (a), esfuerzo pesquero (b), capturas de ambas especies (c) y renta económica generada (d).
CASO 2: las flotas 1 y 2 se afectan mutuamente. Esto se da cuando las dos flotas obtienen incidentalmente capturas del stock objetivo de la otra pesquería. El tamaño poblacional y rendimientos de los stocks χ e γ son función del nivel de esfuerzo en ambas pesquerías. Sin embargo, el retorno de una dependerá del nivel de esfuerzo generado por la otra. Para la pesquería 1 (especie objetivo X):
π1 (t) = p X Y X1 (f 1, f 2) + p Y Y Y1 (f 1, f 2) - c 1 f1 (3.25)
mientras que para la pesqueria 2 (especie objetivo Y):
π2 (t) = p Y Y Y2 (f 1, f 2) + p Y Y Y2 (f 1, f 2) - c 2 f2 (3.26)
A medida que una flota incrementa su esfuerzo, el rendimiento en equilibrio por parte de la otra flota decaerá γ en consecuencia su nivel de esfuerzo en acceso abierto.
Es el caso de dos o más flotas de diferentes características que explotan diferentes componentes poblacionales en el ciclo de vida de una especie (e.g. juveniles y adultos) generalmente segregados en el espacio. Es común en casos de pesca costera artesanal o deportiva y pesca mecanizada de altura, γ generalmente incluye conflictos producidos por competencia por el recurso entre los diferentes usuarios. Al respecto se han desarrollado modelos bioeconómicos estáticos γ dinámicos, a efectos de determinar la asignación óptima de capturas entre dos flotas que explotan un stock en forma secuencial (Geen & Nayar, 1988).
En este tipo de pesquerías se observa el efecto de mutua interacción entre dos flotas segregadas en el espacio (e.g. artesanal costera y mecanizada de altura) que afectan diferencialmente a distintos componentes del ciclo vital de las especies involucradas. Por tanto, si bien la especie en cuestión posee una única curva de población en equilibrio, existirán dos trayectorias diferentes en las capturas, así como dos estructuras relativas precio-costo e ingresos generados por las flotas involucradas. La exclusión o coexistencia competitiva de las flotas ocurrirá en condiciones de libre acceso, mientras que un óptimo balance en la asignación de capturas dependerá especialmente de los cocientes entre precios y costos de ambas flotas, conjuntamente con aquellos parámetros biológicos que determinan la estructura por edades, reclutamiento γ sobrevivencia del stock (Hoppensteadt & Sohn, 1981; Seijo et al., 1994b).
Debe recalcarse la importancia de considerar la estructura por edades de las poblaciones explotadas, así como el efecto diferencial que cada flota pudiera tener en los diferentes componentes poblacionales. El siguiente ejemplo se basa en un modelo bioeconómico multiespecífico de estructura por edades con interdependencias tecnológicas secuenciales (Seijo et al.,, 1996). Los valores de entrada de los parámetros al modelo se muestran en la Tabla 3.3.
En la Figura 3.4. se observan las fluctuaciones en el tiempo de los niveles de abundancia, captura, esfuerzo γ renta económica para las flotas mecanizada y artesanal que componen la pesquería secuencial multiespecífica. En el caso de la biomasa (Fig. 3.4a), se produce un pronunciado decremento de ambas especies durante los primeros años de desarrollo de la pesquería, como resultado de una franca expansión de la flota mecanizada. Las capturas de dicha flota alcanzan su máximo a los 20 años (Fig. 3.4b), coincidiendo con el máximo número de barcos (Fig. 3.4c); a partir de ese período, la flota comienza a decrecer en forma paulatina hasta el final del horizonte simulado (50 años). En contraste, la pesquería artesanal muestra una expansión no tan pronunciada pero constante de las capturas, como producto de un fuerte incremento del esfuerzo pesquero a partir del comienzo de la declinación de la flota mecanizada (20 años).
Ejemplo 3.3 Pesquería multiespecífica con interdependencias tecnológicas secuenciales.
| Parámetro/Variable | Valor | Unidad de medida |
|---|---|---|
| Edad máxima especie Χ | 20 | años |
| Edad máxima especie γ | 12 | años |
| Edad primera madurez Χ | 3 | años |
| Edad primera madurez γ | 2 | años |
| Proporción por sexos (ambas spp.) | 0.50 | -- |
| Reclutamiento máximo observado Χ | 50000000 | organismos |
| Reclutamiento máximo observado γ | 10000000 | organismos |
| Tasa mortalidad natural Χ | 0.4 | 1/año |
| Tasa mortalidad natural γ | 0.45 | 1/año |
| Fecundidad promedio de Χ | 1200000 | huevos |
| Fecundidad promedio de γ | 1500000 | huevos |
| Parámetro curvaturaΧ | 0.12 | 1/año |
| Parámetro curvaturaγ | 0.19 | 1/año |
| Parámetro de ajusteΧ | -0.55 | anual |
| Parámetro de ajusteγ | 0.50 | anual |
| Longitud asintóticaΧ | 920 | mm |
| Longitud asintóticaγ | 600 | mm |
| Peso asintóticoΧ | 12500 | g |
| Peso asintóticoγ | 2400 | g |
| Precio mínimoχ | 1500 | US$/ton |
| Precio mínimoγ | 1000 | US$/ton |
| Pendiente curva de preciosχ | 50 | -- |
| Pendiente curva de preciosγ | 5 | -- |
| Costo unitario flota 1 | 55000 | US$/barco/año |
| Costo unitario flota 2 | 5000 | US$/barco/año |
| Parámetro de dinámica flota 1 | 0.00001 | -- |
| Parámetro de dinámica flota 2 | 0.0001 | -- |
| Area barrida flota 1 | 2.50 | Km2 |
| Area barrida flota 2 | 0.18 | Km2 |
| Long. retención 50%γ75% sp.χflota 1 | 450;650 | mm |
| Long. retención 50%γ75% sp.χ flota 2 | 300;450 | mm |
| Long. retención 50%γ75% sp.γ flota 1 | 300;450 | mm |
| Long. retención 50%γ75% sp.γ flota 2 | 200;275 | mm |
| Area de distribución ambas spp. | 5000 | Km2 |
Los menores costos operativos de la flota artesanal tienden a inducir un aumento del número de barcos e indirectamente a excluir en el largo plazo a la flota mecanizada. Otro efecto del aumento del esfuerzo en la flota artesanal puede ser la sobrepesca en el reclutamiento, lo cual a su vez disminuye el potencial del stock a ser capturado por la flota mecanizada. En cuanto a la renta económica generada por la actividad pesquera, la sobreinversión como producto de amplios márgenes de ganancia en la flota mecanizada (entre los años 15 y 20) produce su sobredimensionamiento γ posteriores pérdidas a la flota (entre años 20 y 25), para luego tender al equilibrio bioeconómico. La flota artesanal, con pequeños valores de renta y siempre cercana a este equilibrio, presenta una leve tendencia creciente de su renta económica en el largo plazo (Fig. 3.4d).
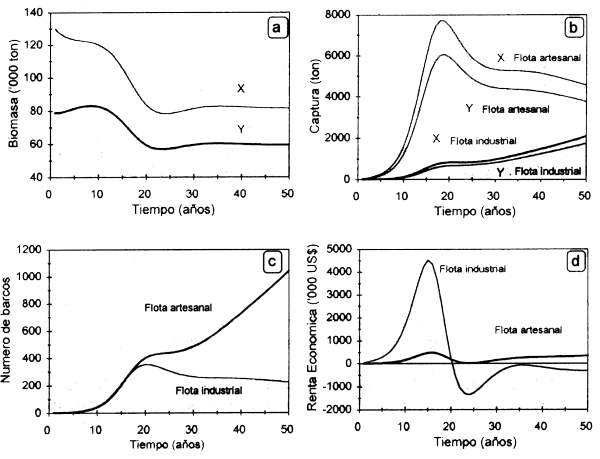
Figura 3.4 Interdependencias tecnológicas. Niveles de biomasa (a), esfuerzo (b), captura (c) y renta económica generada por las flotas industrial y artesanal (d).
Análisis gráficos alternativos son desarrollados por Anderson (1977; 1986). En ambos casos se presenta a una pesquería secuencial en un contexto estático.
El modelo básico empleado anteriormente asumia carencia de interacción entre las especies X e Y. En caso de especies ecológicamente interdependientes sujetas a explotación, un modelo general es descrito por el siguinte sistema de ecuaciones (Clark, 1985):
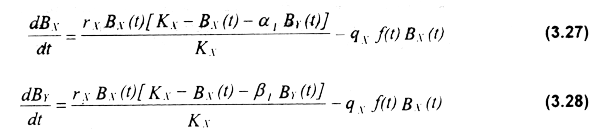
donde los términos β y β1 son comeficientes de competencia que miden el efecto per capita de una especie sobre otra (Begon et al.,1990); valores inferiores a 1 suponen un efecto inhibitorio interespecifico mayor que el intraespecífico.
Un sistema simple depredator (especie Y) - presa (especie X) en el cual ambas especies son explotadas, puede expresarse en base a las ecuaciones 3.29 y 3.30 (Clark, 1985):
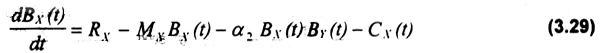
donde: μXes la tasa de mortalidad de X.
α2BXBγ(t) representa la tasa de consumo de X por Y.
RX es la tasa de reclutamiento de X(denso-independiente).
La ecuación (3.29) supone una distribución uniforme de la presa, lo cual impone limitaciones al modelo. Asimismo, el modelo supone que las capturas de cada especie son realizadas en forma independiente, e.g. no constituyen un stock múltiple. Formas alternativas de interacción depredador-presa, incluyendo agregacióde presas γ diferente comportamiento del depredador, han sido discutidas en el plano ecológico (Taylor, 1988; Comins & Hasell, 1979; Begon et al.,1990).
La otra ecuación que conforma el sistema es:
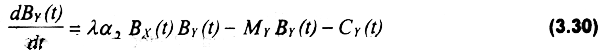
El término ΒX(t)ΒY(t) representa la tasa natural de crecimiento poblacional del depredador. γ es depredador especialista de X.μ es un parámetro adimensional que puede interpretarse como un indice de conversión alimenticia de X, a Y. En caso que el stock Y no sea explotado, existirá una biomasa critica de X, γxc, dada por:

de tal manera que habrá crecimiento poblacional en Y siempre que la biomasa de X supere a Βxc
La ecuación (3.29) asume asimismo que X (presa) posee una tasa de reclutamiento R constante, e.g denso-independiente. Se asume asimismo que Βxc menor a la capacidad de carga KXen ausencia de depredación Y explotación, dada por:
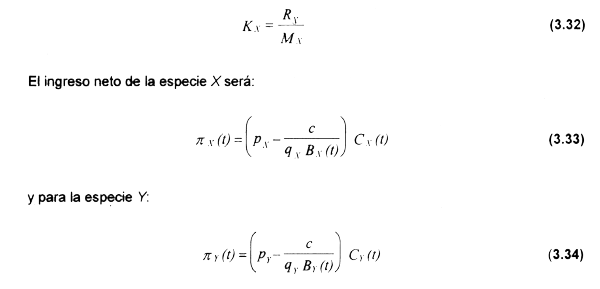
donde el término c/qB representa el costo de captura una unidad de biomasa cuando la biomasa total es Β (Clark, 1985), lo cual es fácilmente deducible a partir de la función de CT(t) definida en el Capítulo 2.
El equilibrio bioeconómico simultáneo se dará cuando πχ(t)=πY(t)=0. Una análisis completo sobre la construcción de curvas de rendimiento sostenible en pesquerías multiespecíficas es encontrado en Ströbele & Wacker (1991).
Este estudio pierde relevancia si no se especifican las caracteristicas trófico-conductuales del depredador (e.g. especialista ó generalista), así como la magnitud de las interacciones que unen a la presa X con otros competidores.
Exclusión competitiva. Este concepto es definido de acuerdo a la teoria de nicho (Hutchinson, 1958, 1959; Vandermeer, 1972). En ausencia de competidores, una especie ocupará su nicho fundamental, dado por la combinación óptima de condiciones y recursos que le permiten mantener cierto nivel poblacional. La presencia de competidores lo restringe a su nicho realizado, definido como el conjunto observado de condiciones en las cuales la especie existe normalmente. Las dimensiones estarán determinadas por la magnitud de las interacciones, γ en consecuencia el nicho realizado es menor o igual al fundamental (Giller, 1984; Begon et al., 1990). En este contexto, el Principio de Exclusión Competitiva (Gause, 1934) establece que si dos especies coexisten en un ambiente, lo harán como resultado de la diferenciación de sus nichos (e.g. coexitencia competitiva; nichos realizados). Si esta diferenciación denichos no es viable, el competidor superior excluirá al subordinado cuando su nicho realizado se superponga totalmente con el nicho fundamental del subordinado.
Pongamos por ejemplo dos recursos sedentarios, en los cuales la competencia interespecífica es generalmente muy intensa γ se relaciona con la disponibilidad de espacio. En organismos filtradores de este tipo dicho proceso trae como consecuencia que una especie domine la comunidad a través de la exclusión del competidor subordinado (Branch, 1984). Un ejemplo tipico lo constituye la interacción entre los bivalvos suspensivoros Mesodesma mactroides-Donax hanleyanus en el litoral Atlántico uruguayo (de Alava, 1993). En ausencia de impacto humano, M. mactroides es competidor dominante γ reduce a minimas densidades a D. hanleyanus. La explotación preferencial de la primera disminuye la magnitud de la interacción por un aumento del espacio disponible, en este caso el recurso limitante. De esta manera se suscita alternancia en la abundancia de dichos bivalvos, dependiendo de la magnitud del impacto humano (Fig. 3.5). Sin embargo, la caracteristica variabilidad en el reclutamiento de estos recursos que suponen en su mayoria ciclos de vida complejos (Roughgarden et al., 1988), unida a la inestabilidad de las comunidades relacionadas (Warwick, 1986; Menge & Sutherland, 1987) y el grado variable de impacto humano (Castilla, 1988), alteran constantemente la magnitud de las interacciones. En este contexto, fuentes importantes de variación son ocasionadas por la competencia intraespecifica por espacio y/o alimento, lo cual es analizado en numerales siguientes.
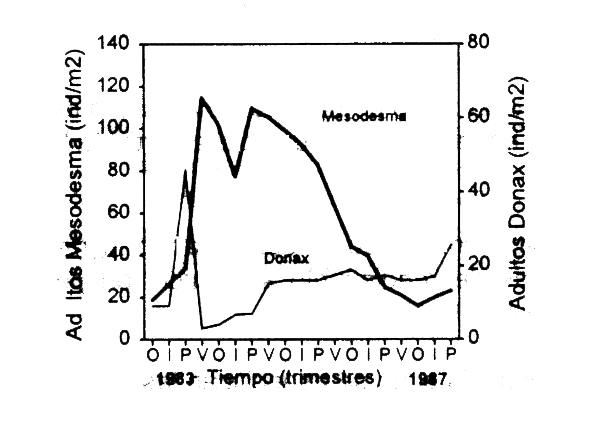
Figura 3.5 Varianción temporal en la abundancia de los bivalvos suspensivors Mesodesma mactroides y Donax hanleyanus de la costa atlántic uruguaya (de Alava, 1993).
Coexistencia competitiva. En el contexto del modelo de Gause (1934), la competencia interespecifica puede expresarse en base a las ecuaciones (3.35) y (3.36) en ausencia de explotación, o sea:

las cuales responden al modelo Lotka-Volterra (Volterra, 1926; Lotka, 1932).
Anderson (1986) desarrolla otra aproximación gráfica basada en un criterio estático, asumiendo equilibrio en las poblaciones: previo a la explotación pesquera, dos especies X e Y coexisten en forma estable (Keddy, 1989). X es competidor superior Y posee una población mayor; y es competidor inferior. Se asume que, si bien ambas especies son valoradas en el mercado, la explotación es dirigida a X en una primera instancia, y que hay cierta segregación espacial que permite una discriminación de las especies en la actividad extractiva. Asimismo, considérese que el espacio disponible para el asentamiento es el recurso limitante por el cual compiten las dos especies sedentarias. A medida que el esfuerzo f(t) aumenta sobre X, disminuye la magnitud de la interacción, hay liberación de espacio disponible para el asentamiento Y en consecuencia aumenta el tamaño poblacional de la especie competitiva inferior. Esta tendencia ocurre hasta cierto nivel de esfuerzo f1, donde X virtualmente desaparece e Y alcanza su máximo tamaño poblacional. La disminución de la especie competitiva superior produce un direccionamiento del esfuerzo pesquero a la explotación a Y en niveles de esfuerzo mayores a f1. La forma de las curvas de rendimiento sostenible Y de ingresos sostenibles y costos totales dependerán de la magnitud de las interacciones biológicas, capacidad de crecimiento poblacional, el valor relativo de las especies en el mercado Y los costos de extracción.
Es importante hacer notar que tal como lo establece Anderson (1986), en un escenario de competencia entre especies que son capturadas por una misma flota es de esperarse que ocurran equilibrios bioeconómicos tanto estables como inestables en el tiempo.
La relevancia de este análisis se ve minimizada por su naturaleza estática. Es común encontrar situaciones donde la especie competitiva subordinada tiene mucho mayor valor económico. Como resultado, la curva de ingresos totales es mayor que en el caso estático, al igual que su presión de explotación (Mitchell, 1979). Este análisis está limitado además desde un punto de vista ecológico. La sobreposición de nicho (Giller, 1984) entre dos especies con respecto a un recurso puede no ser un fiel indicador de la situación real, dado que el número potencial de competidores por otros recursos no tomados en consideración aumenta al examinar más ejes del nicho definidos por otras variables ambientales. Por tanto, si bien la sobreposición de nicho puede ser pequeña, el efecto acumulativo de esta competencia difusa (sensu Pianka, 1974) puede reducir severamente el tamaño del nicho realizado de una especie, lo cual a su vez repercutirá en el manejo del recurso en caso de ser explotado. Por ejemplo, los valores de MRS, MRE Y EBE podrían suceder a menores niveles de esfuerzo pesquero. Una vez más, la jerarquia competitiva de las especies explotadas, asi como la magnitud y número de los ligamientos tróficos horizontales (competencia) Γ verticales (depredación) determinarán los efectos bioeconómicos derivados de esta interdependencia.
Competencia intraespecifica. Si bien el Capítulo ha sido encarado bajo un marco multiespecífico, se considera de importancia mencionar a la competencia intraespecifica como una interdependencia ecológica relevante en poblaciones marinas.
La competencia intraespecifica se manifiesta de diversas formas (e.g. en organismos bentónicos se produce por limitación del espacio disponible para el asentamiento larval: Branch, 1984; Holm, 1990; Raimondi, 1990). La abundancia de un stock inducirá a fenómenos de denso-dependencia de intensidad variable en el crecimiento, mortalidad y reclutamiento, dependiendo de la estrategia de vida de la especie (Caddy & Sharp, 1986) y de la estructura por edades del stock. Continuando con el ejemplo de Mesodesma mactroides, se ha observado una relación stock-reclutamiento sujeta a procesos de sobrecompensación Y que por tanto se explica por el modelo stock-reclutamiento de Ricker (1975) (Defeo, 1993a). Dicha relación repercute directamente en el crecimiento del recurso (en longitud Y peso individual) Y por consiguiente en su biomasa disponible para explotación Y en los ingresos netos derivados de la actividad pesquera.
Esta interdependencia debe ser considerada en el manejo de un recurso pesquero, tomando en cuenta la variabilidad espacio-temporal de la magnitud del reclutamiento a diferentes niveles de stock y variables ambientales. La predicción de la magnitud del reclutamiento en función de la magnitud del stock tendrá un efecto bioeconómico sustancial en el manejo de un recurso explotado. Así por ejemplo, en el recurso sedentario de referencia, la adopción de medidas regulatorias podrían basarse en maximizar cierto nivel de stock que permita liberar el necesario espacio disponible para un asentamiento exitoso.
En este caso, dos stocks que constituyen pesquerías independientes tienen una relación de competencia o depredación, por lo cual se suscitarán efectos directos e indirectos que beneficiarán o perjudicarán a una u otra pesqueria. La magnitud de las interacciones entre especies en el caso de competencia,Y el grado de especificidad del depredador en su dieta alimentaria, determinarán la estrategia de uso óptimo de ambos stocks. Dependiendo de ello, el equilibrio bioeconómico en libre acceso de cada pesqueria estará supeditado al monto de esfuerzo producido en la otra.
CASO 1: Stocks sujetos a coexistencia competitiva. La Figura 3.6 muestra las trayectorias dinámicas de biomasa Y capturas por especie Y la renta económica generada por estos recursos a una flota que ejerce su esfuerzo con un arte de pesca no discriminatorio. Como puede observarse, en ausencia de esfuerzo de pesca la abundancia de la especie χ (competidor dominante) es mayor que la de la especie Y. Al irse incrementando el esfuerzo de pesca, la abundancia de la especie dominante comienza a decrecer liberando el recurso por el que se compite (hábitat YO alimento) en el ecosistema en cuestión. El incremento en la disponibilidad del recurso permite que la especie dominada incremente su abundancia en términos absolutos y relativos con respecto a la especie dominante, hasta un nivel de esfuerzo después del cual su abundancia comienza también a decrecer. Bajo condiciones de acceso abierto, la pesquería alcanza su nivel de equilibrio bioeconómico con un nivel de esfuerzo pesquero que resulta en niveles bajos de abundancia de la especie X, existiendo la posibilidad de que si el precio de la especie Y fuera lo suficientemente alto, la biomasa de la especie X podría alcanzar niveles cercanos al agotamiento. Las biomasas relativas y las capturas resultantes de ejercer un esfuerzo de pesca que tiende a maximizar la renta económica que genera la pesquería se obtienen con un nivel de esfuerzo en el orden de 300 barcos (Fig. 3.6).
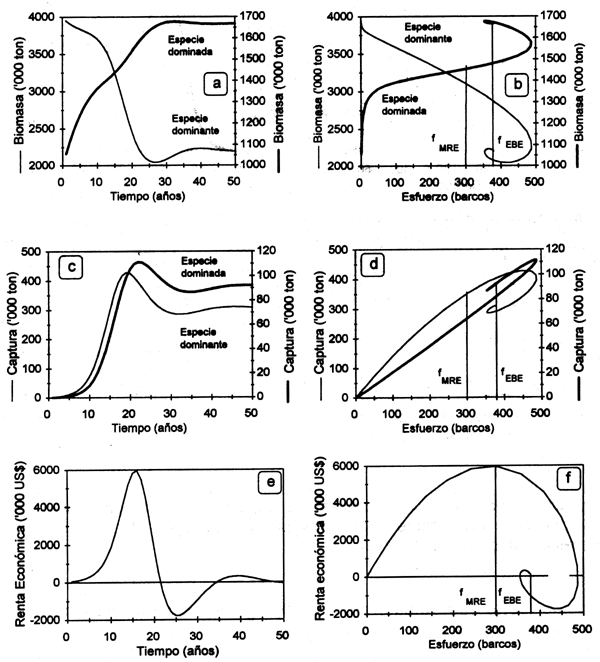
Figura 3.6 Trayectorias dinámicas de la biomasa (a,b), la captura por especie (c,d), así como la renta económica (e,f) generada por una flota con arte de pesca no discriminatorio.
CASO 2: stocks con relación depredador-presa. En este caso las curvas de equilibrio bioeconómico y de rendimiento óptimo en equilibrio para la pesquería 1, dirigida sobre el depredador, tendrán pendiente negativa relativa (Fig. 3.7), dado que un incremento en el esfuerzo pesquero dirigido sobre la presa disminuirá su abundancia y en consecuencia la magnitud de recurso disponible para el depredador en caso de ser éste especialista o bien oligófago. La tendencia inversa ocurrirá en el caso de la presa y las caracteristicas de sus curvas de equilibrio bioeconómico y rendimiento máximo dependerán de la magnitud del esfuerzo ejercido en la pesquería del depredador, así como en la conducta trófica de éste.
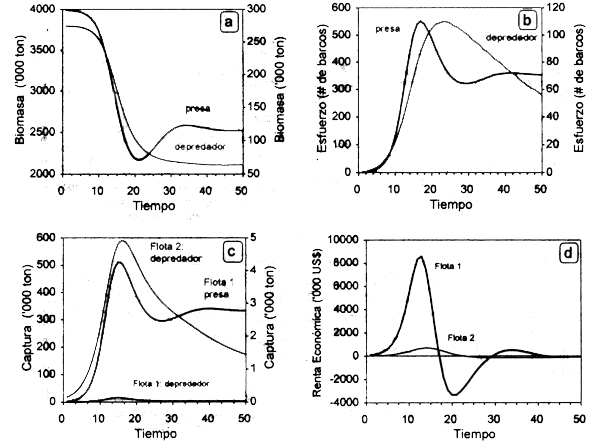
Figura 3.7 Trayectoria dinámica de las biomasas de especies con relación depredador-presa (a), el esfuerzo de dos flotas que inciden diferencialmente sobre ellas (b), las capturas correspondientes (c) y la renta económica estimada para cada flota (d).
Una variante del caso anterior seria la explotación de stocks ecológicamente interdependientes por parte de dos flotas sujetas a interdependencias tecnológicas, lo cual constituye una interdependencia tecno-ecológica. El análisis en este caso se dificulta por la naturaleza múltiple de la interacción. Sin embargo, se aportan aqui dos ejemplos basados en interdependencias de competencia y depredación.
CASO 1: stocks sujetos a interacción competitiva
Los modelos que analizan la relación de competencia entre dos especies están generalmente basados en el modelo Lotka-Volterra anteriormente desarrollado, así como en el modelo aportado por Gause & Witt (1935). En este caso, las ecuaciones diferenciales básicas involucradas son:
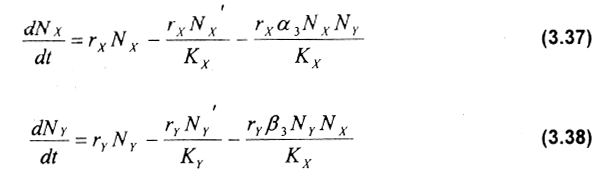
donde NX y NY es la abundancia poblacional de las especies X (dominante) e Y (subordinada) respectivamente, rX y rY son sus tasas intrínsecas de crecimiento, KX y KY son las capacidades de carga del ambiente cuando ambas especies crecen solas, α3 es una constante que considera el efecto de la especie X sobre la Y, y β3 es una constante que considera el efecto de la especie Y sobre la X. Básicamente, estas ecuaciones diferenciales expresan que el incremento en la densidad poblacional de una especie está limitado por efectos intra e interespecíficos, éstos dados por la naturaleza y magnitud de la interacción competitiva.
CASO 2: stocks con relación depredador-presa
En este caso el modelo depredador-presa utilizado para generar la interdependencia ecológica está basado en el sistema de ecuaciones logísticas aportadas por Leslie & Gower (1960):
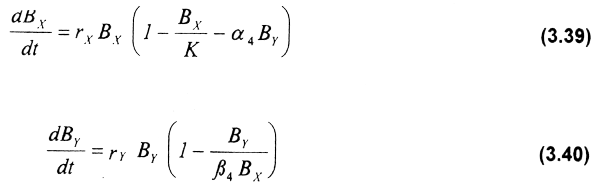
En estas ecuaciones, el crecimiento de la presa está limitado tanto por la capacidad de carga del sistema, K, como por el término de depredación, α.4 El crecimiento de los depredadores es función de su tasa intrínseca de crecimiento rY , y del número de presas. La constante β4 relaciona el número de presas con la biomasa máxima capaz de ser alcanzada por el depredador, en función de la capacidad de carga del sistema.
A continuación se brinda un ejemplo numérico y gráfico basado en un programa de computación (Seijo et al., 1996) que considera una interdependencia tecno-ecológica en conjunto con una interdependencia ecológica de depredación.
| Parámetro/Variable | Valor | Unidad de Medida |
|---|---|---|
| r especie X | 0.36 | -- |
| r especie Y | 0.15 | -- |
| K especie X | 4000000 | ton |
| K especie Y | 275000 | ton |
| q especie X flota 1 | 0.0004 | -- |
| q especie X flota 2 | 0.0 | -- |
| q especie Y flota 1 | 0.0002 | -- |
| q especie Y flota 2 | 0.0004 | -- |
| Precio especie X | 60 | US$/ton |
| Precio especie Y | 275 | US$/ton |
| Costa unitario flota 1 | 60000 | US$ |
| Costa unitario flota 2 | 9000 | US$ |
| Parámetro de dinámica flota 1 | 0.00001 | -- |
| Parámetro de dinámica flota 2 | 0.000015 | -- |
| α4 constante de depredación: especie X | 0.00000001 | -- |
| β4 constante de depredación: especie Y | 0.069 | -- |
En este caso las variaciones en el tiempo de las curvas de biomasa de la presa y el depredador no serán las clásicas encontradas en la literatura ecológica (Begon et al., 1990), sino que se ven afectadas por la magnitud diferencial de la interdependencia tecnológica (Fig. 3.8a). La disminución en la abundancia de ambas especies resulta del aumento del esfuerzo pesquero durante los primeros 15 años de la pesquería. El efecto de la flota 1, cuyo objetivo es la presa, también repercute en la biomasa y capturas efectuadas sobre el depredador durante ese lapso de expansión, para luego decaer paulatinamente (Fig. 3.8b). Dicho efecto puede observarse en la Figura 3.8c, donde el aumento de la flota 1 aparece como respuesta a los rendimientos logrados tanto en base a la especie objetivo (presa) como incidental (depredador). Ese incremento repercute en la renta económica generada por esa flota, mientras la flota 2, cuyo único objetivo es el depredador, no sufre variaciones substanciales en la renta sino que se presenta siempre cerca del equilibrio bioeconómico (Fig. 3.8d).
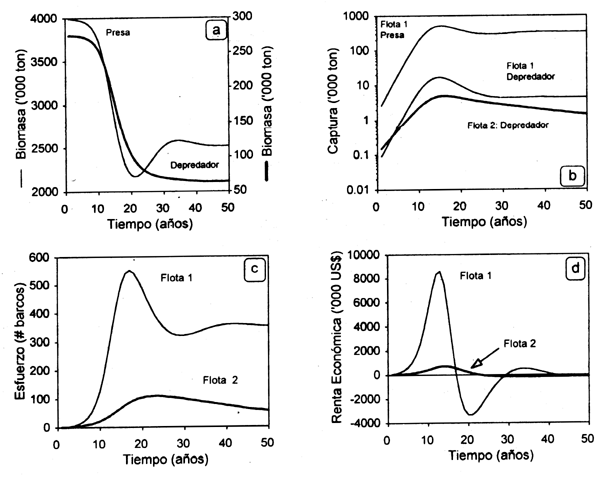
Figura 3.8 Interacción tecno-ecológica: stocks con interacción depredador-presa capturados por dos flotas tecnológicamente interdependientes.
Es obvia la correspondencia entre las abundancias de ambas especies, dado que un incremento en el esfuerzo pesquero dirigido sobre la presa disminuirá su abundancia y en consecuencia la magnitud de recurso disponible para el depredador en caso de ser éste especialista o bien oligófago. La tendencia inversa ocurrirá en el caso de la presa y las características de sus curvas de equilibrio bioeconómico y rendimiento máximo dependerán de la magnitud del esfuerzo ejercido en la pesquería del depredador, así como en la conducta trófica de éste.
La inclusión de la variabilidad espacio-temporal en la abundancia poblacional y en el ambiente, conjuntamente con la cuantificación de la magnitud de las interdependencias ecológicas a diferentes niveles de esfuerzo pesquero, debe ser el camino adecuado para el modelaje multiespecifico (Pauly, 1979; 1988; Pope, 1979; Sainsbury, 1988). Las propuestas deben contemplar asimismo la interacción larva-adulto como factor regulador de la abundancia, incluyendo mecanismos compensatorios y sobre-compensatorios (Sale, 1982; Menge & Sutherland, 1987, Fogarty et al., 1991). En un contexto pesquero, el conocimiento de estas interdependencias posibilitará la predicción de biomasa y por tanto los ingresos netos derivados de la actividad.
Teniendo en cuenta las observaciones realizadas en el numeral anterior, es importante discernir entre diferentes escalas espacio-temporales de análisis (Orensanz et al., 1991). Esto es relevante si se consideran las bruscas variaciones de abundancia observadas en las especies que poseen ciclos de vida complejos (e.g. fase larval plantónica γ vida adulta bentónica:ver Roughgarden et al., 1985; 1988). La estrategia de estudio a implementarse dependerá de la complejidad (sensu Cohen, 1978) de cada comunidad. Estudios experimentales recientes han demostrado que la estructura de una comunidad explotada difiere drásticamente de una prístina debido a que la explotación induce una modificación de la magnitud de las interdependencias ecológicas. En tal sentido, comunidades de macrofauna bentónica intermareal, protegidas o con menor interferencia antropogénica, han sido comparadas con aquéllas donde el hombre ha ejercido una persistente influencia en el sistema (Castilla & Durán, 1985; Hockey & Bosman, 1986; Moreno, 1986; Bosman et al.,1987; Castilla & Paine, 1987; Bustamante & Castilla, 1990; Hockey et al., 1988). Se ha podido demostrar que la influencia del hombre en comunidades marinas costeras ha repercutido fundamentalmente en las especies depredadas, pero también en forma indirecta en otros organismos. Se han determinado importantes efectos de cascada (Paine, 1984; Castilla, 1988; Estes & Palmisano, 1974; Moreno et al., 1984; 1986) debidos a la explotación de un depredador tope ó especie clave (“keystone species”, sensu Paine, 1980). Estos efectos indirectos son mayormente visibles cuando los ligamientos entre especies son muy fuertes (Moreno, 1986; Durán et al., 1987).
Como consecuencia de lo anterior, la respuesta de una comunidad a la presión pesquera dependerá de la magnitud de las interacciones entre las especies, así como del papel funcional de la especie objeto de explotación. En efecto, características del depredador, tales como su espectro trófico, selectividad (especialista ó generalista) y eficiencia de depredación, así como de las presas (si compiten ó no y si la competencia es simétrica o no) incidirán en la respuesta de la comunidad a la explotación y por tanto sus efectos tendrán muy disímiles consecuencias a nivel pesquero y ecológico. A modo de ejemplo, la depredación sobre un competidor dominante tenderá a incrementar la diversidad en una comunidad (Paine, 1966; Durán & Castilla, 1989), mientras que la explotación de especies claves puede conducir a una simplificación de la comunidad y disminución de la diversidad. Ambas situaciones muestran la existencia de múltiples estados de equilibrio en una comunidad (Sutherland, 1974; Connell & Sousa, 1983). De acuerdo a los niveles de explotación, la magnitud de las interdependencias pueden ser modificadas y el esquema de manejo y regulación de los recursos alterado (de Alava, 1993).
Teniendo en cuenta las características de estas interacciones, los ingresos netos derivados de la explotación pesquera podrán ser maximizados inclusive sobreexplotando deliberadamente algunas especies a efectos de producir el aumento de un recurso altamente valuado en el mercado, pero cuya disponibilidad es limitada como consecuencia de fuertes interdependencias ecológicas. La minimización de los impactos potenciales adversos derivados de la explotación multiespecifica puede alcanzarse asimismo durante períodos de máxima separación ó bien optimizando el nivel de esfuerzo en el momento de la co-ocurrencia espacial (Murawski & Finn, 1989). Es importante remarcar que investigaciones recientes no integran al hombre como depredador especialista eficiente sino que consideran una conducta generalista a medida que se van imponiendo vedas y cuotas sobre los recursos tradicionalmente explotados (Smith & McKelvey, 1986).
Se ha demostrado la dificultad de separar y cuantificar la importancia relativa de los diferentes agentes perturbadores de una comunidad (e.g. aspectos tecnológicos y ecológicos: ver Sainsbury, 1988; Deriso et al., 1986) lo cual a su vez dificulta el manejo de recursos desde una visión multiespecifica. Las aproximaciones holisticas (e.g. ECOPATH: Christensen & Pauly, 1990) pueden resultar útiles en casos en que la contribución de las especies (e.g. valor presente esperado, ver Sainsbury, 1988) a una pesqueria es similar, sin embargo la dinámica de la comunidad ante diferentes grados de perturbación es dificilmente estimable (Sainsbury, 1987). La agregación de especies a efectos de un análisis más simple requiere de supuestos o del conocimiento de la dinámica de los componentes de dichas agregaciones (Sugihara et al., 1984), lo cual limita el poder predictivo de dichas aproximaciones. Por tanto, la verificación de la ocurrencia de competencia y depredación, asi como la magnitud de las interacciones e incidencia de la pesca, requerirá necesarianmente de manipulación experimental en terreno (Cobb & Caddy, 1989; Defeo, en prensa), dado que las comunidades marinas sujetas a explotación no constituyen sistemas estables en equilibrio espacialmente homogéneos, tal cual asume la teoría (Larkin, 1978; Caddy, 1983; Beddington, 1984; Chesson & Case, 1986).
No obstante el importante desarrollo teórico (e.g. Pope, 1979; Clark, 1985; Saila & Erzini, 1987; Ströbele & Wacker, 1991), el estado actual del conocimiento permite afirmar que no existen a la fecha modelos multiespecificos capaces de generar resultados adecuados para llevar a cabo un manejo a largo plazo. Tal como lo expresa claramente Clark (1985), la pregunta actual no debe ser si los modelos multiespecificos pueden ser construidos, sino si éstos serán de algún valor a la hora de proponer pautas para el manejo de recursos. Esta inquietud surge como respuesta a la común observación que los modelos actuales han logrado un impacto relativo en el manejo de recursos pesqueros (Ursin, 1982; Larkin, 1982; Brander, 1988; Cobb & Caddy, 1989; Cobb et al., 1986).
Como resultado de la complejidad de la estructura de una comunidad, la predicción de los efectos de la explotación de una especie en la abundancia de otra ecológicamente interdependiente es dificil de determinar (Miller, 1985; Akenhead et al., 1982). Esto puede resultar de extrema gravedad si se considera que una severa sobrepesca en una especie puede ocasionar impactos de diferente magnitud en sistemas cuya estructura trófica, asi como la potencia relativa de las interrelaciones horizontales (e.g. competencia) y verticales (e.g. depredación) se desconoce (Paine, 1980; Sainsbury, 1982).
Al igual que en los modelos tradicionales, la incertidumbre y estocasticidad en los procesos de estructuración comunitaria deben ser incorporados en modelos holísticos deterministicos simples y de uso masivo (Arreguin-Sánchez et al., 1993). Modelos tales como el ECOPATH (Christensen & Pauly, 1990, 1993), podrian ser modificados a efectos de adecuar los principios generales de la bioeconomia de recursos, los cuales por el momento emergen en una forma más clara y definida a partir de los modelos analiticos simples (Clark, 1985). La dificultad de análisis de la composición de la dieta en especies que constituyen ensambles o comunidades bentónicas, en contraposición a las nectónicas, limitan un análisis estructural epifenoménico de las mismas, tales como las que pudieran derivarse de la aplicación de los modelos mencionados. Por tal razón se ha desarrollado una rutina complementaria a ECOPATH denominada ECOSIM (Walters et al., en prensa), mediante la cual se amplia la capacidad de efectuar predicciones que incluyan el efecto de la explotación pesquera. En este contexto, las ecuaciones lineales que describen los flujos tróficos bajo condiciones de equilibrio en ECOPATH se modifican para definir interacciones dinámicas que varian con cambios en la biomasa de los recursos y en el régimen de explotación. La incorporación de ECOSIM en ECOPATH permite conducir análisis de alternativas de manejo considerando explicitamente las interacciones tróficas dentro del sistema.
Los estudios biológicos básicos y experimentales, en diferentes escalas de espacio y tiempo, pueden proveer la única alternativa válida para predecir los efectos bioeconómicos derivados de posibles interdependencias ecológicas y tecnológicas. Es necesario el desarrollo de modelos que incluyan una correcta identificación del sistema, análisis de sensibilidad a modo de indices de desempeño del modelo e intervalos de confianza para las predicciones, asi como una cuidadosa estimación de los parámetros de entrada al mismo (Majkowski, 1982; Silvert, 1981; 1982; Walters, 1986; Seijo, 1986; Clark, 1989; Seijo et al., 1994a).
Tanto la pesqueria como las interacciones ecológicas, el ambiente fisico y el desarrollo dinámico del sector pesquero tienen efectos en el recurso, con un retraso diferencial en su impacto. En el estado actual del conocimiento, la alternativa más viable parece ser el manejo adaptativo (Walters, 1984; 1986; Hilborn & Walters, 1987), esto es, manejar a través de experimentación, cambiando deliberadamente los niveles de esfuerzo a efectos de entender la dinámica de la comunidad y la pesqueria. Esta estrategia permite la inclusión de mecanismos de control y regulación a corto plazo en respuesta a un flujo continuo de información sobre variaciones en el estado de un recurso. Tal como lo expresan Cobb & Caddy (1989):
“nuestra habilidad para modelar la dinámica de poblaciones explotadas ha sobrepasado nuestra habilidad para verificar el realismo de esos modelos… Es tiempo ya de elaborar hipótesis contrastables a través de experimentación en terreno y estudios comparativos”.
Los efectos de diferentes tipos de regulación, incluyendo asignación de cuotas de pesca, cuotas individuales transferibles, rotación de áreas de pesca, asi como la variabilidad en el descarte producida por la puesta en práctica de algún tipo de medida especie-dirigida, deberán ser considerados a través de modelos de optimización con criterios múltiples (Seijo, 1986; Charles, 1989). En caso contrario,
“el manejo de recursos multiespecificos permanecerá probablemente como un arte, más que una ciencia, y la asignación de altos presupuestos dirigidos a resolver problemas cientificos relacionados con el manejo de pesquerias multiespecificas será injustificado en términos de los beneficios potenciales que se lograrian” (Clark, 1985).