Las administraciones pesqueras tienen la necesidad de conocer, de manera sistemática, los posibles impactos bioeconómicos resultantes de estrategias alternativas para el manejo sostenible de recursos pesqueros. Se requiere determinar cuáles instrumentos de política pesquera deberían de utilizarse para satisfacer criterios biológicos y económicos. Entre los criterios que pudieran identificarse se encuentran los siguientes: nivel de biomasa de las especies objetivo e incidentales (incluyendo especies amenazadas), capturas por especie, flota y país, ingresos netos obtenidos por las flotas artesanales e industriales, empleos directos, generación de divisas y contribución a la producción alimentaria de la región. Es en este sentido que el flujo intertemporal de costos y beneficios de estrategias alternativas de manejo requiere estar sustentado en análisis robustos de la estructura dinámica de las poblaciones, tanto objetivo como incidentales. Asimismo, la preocupaci%on creciente de las administraciones pesqueras en el sentido de incorporar criterios no monetarios en el análisis, tales como conservación de la biodiversidad marina, protección de especies amenazadas que son capturadas incidentalmente, y otros valores sin precio (valor de existencia y valor de demanda opcional), necesitan enfoques novedosos para conciliar criterios económicos-ecológicos en muchas ocasiones conflictivos entre sí (Charles, 1989; Charles & Herrera, 1994). Se desea, por una parte, maximizar el valor presente de los beneficios netos recibidos por los diferentes usuarios de los recursos (e.g. pescadores artesanales y pescadores industriales), y por otra, que la abundancia de las especies objetivo e incidentalmente capturadas se mantengan en niveles que impidan su sobreexplotación o agotamiento. Es por esto que en el Capítulo 6 se presenta un enfoque de estudio que contempla la realización de diversos análisis bioeconómicos para el manejo de pesquerías con criterios múltiples.
Dadas las características inherentes de los recursos pesqueros discutidas en el Capítulo 1, el uso inteligente en el tiempo requiere de la elaboración de planes de manejo. En este Capítulo se mencionan y analizan en detalle las diferentes etapas necesarias para la ordenación de pesquerísa; se hace énfasis en el enfoque metodológico relacionado con la aplicación de ciencia de sistemas como una herramienta útil y robusta para analizar en forma sistemática las pesquerías. Finalmente se aporta un ejemplo ilustrativo derivado de dicha aplicación.
A continuación se presentan las etapas necesarias para realizar la ordenación y manejo sistemático de pesquerias (Anderson, 1981; Seijo et al., 1991a).
(i) Evaluar la pesquería desde los puntos de vista biológico, ecológico y económico, considrando el tamaño y dinámica de la estrucura de la población, de la floata y de la captura. Asimismo, esta evaluación deberá estimar los flujos de costos y beneficios en el tiempo de las flotas que inciden en la pesqueria, los empleos directos e indirectos y las divisas generadas.
(ii) Establecer claramente los objetivos y metas de manejo de la pesquería con base en la evaluación de la etapa(i). Estos objetivos deberán ser expresados cuantitativamente para poder evaluar posteriormente los resultados del plan.
(iii) Seleccionar la combinación apropiada de variables de desempeño tanto biológicas como económicas, y determinar las variables de control correspondientes que permitan lograr los niveles deseados en los criterios de desempeño de la pesquería.
(iv) Determinar las estrategias alternativas de manejo y su mecanismo de implementación, para hacer operativas las variables de control establecidas en la etapa (iii).
(v) Realizar un seguimiento de la pesquería para observar la dirección de los impactos del plan de manejo.
(vi) Determinar si los objetivos y metas de manejo están siendo logrados, tratando de identificar los posibles factores que podrían influir para que éstos no sean alcanzados.
(vii) Reevaluar periódicamente la pesquería y los objetivos y metas establecidos para su manejo.
Un enfoque que contribuye a la solución del problema antes mencionado consiste en la aplicación de ciencia de sistemas (Manetsch & Park, 1982; Seijo 1987, 1989; Seijo & Defeo, 1994b). Dicho enfoque comprende los siguientes pasos (Fig. 5.1):
(i) Definir claramente las necesidades de información de la pesquería.
(ii) Caracterizar la pesquería en términos de la dinámica del recurso, las posibles interdependencias ecológicas y tecnológicas, el esfuerzo pesquero que se ejerce y los instrumentos de manejo factibles de ser implementados exitosamente.
(iii) Modelar matemáticamente las interrelaciones entre los diferentes componentes de la pesqueria ya caracterizada.
(iv) Colectar datos de fuentes primarias y secundarias para estimar los para estimar los parámetros del modelo matemático.
(v) Desarrollar un modelo de computadora que resuelva numéricamente el modelo matemático correspondiente.
(vi) Realizar análisis de estabilidad y sensibilidad del modelo de computadora.
(vii) Validar el modelo, en especial en base a la comparación estadística de las observaciones y las predicciones generadas por aquél.
(viii) Evaluar el impacto bioeconómico de estrategias alternativas de manejo. En el caso que el problema de manejo lo requiera, integrar el modelo bioeconómico dinámico de la pesquería a un algoritmo de optimización (no-lineal o lineal) con criterios múltiples (o simples) para generar un vector de instrumentos de manejo que minimice la diferencia entre los niveles deseados por el administrador del recurso en las variables de desempeño y los generados por el modelo bioeconómico dinámico.
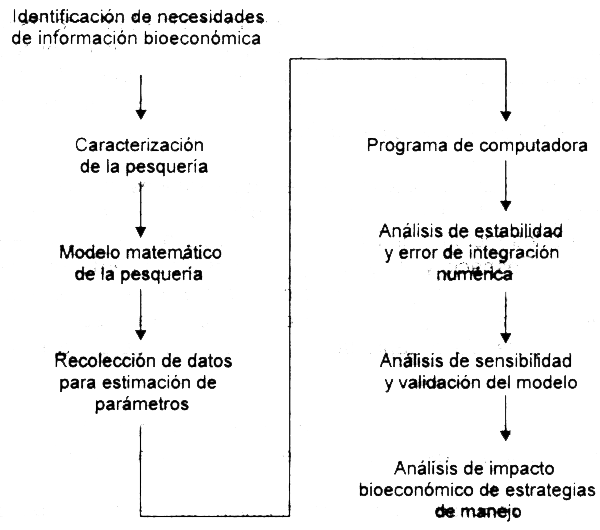
Figura 5.1. Enfoque de análisis y modelación bioeconómica de una pesquería (Seijo, 1989).
Con la participación de los administradores de la pesquería y los especialistas del recurso pesquero, se requiere definir claramente el problema de manejo en términos de (Ackoff, 1962; Seijo, en prensa):
a) La(s) persona(s) que tiene(n) el problem, e.g. el administrador de la pesquería, los pescadores (industriales y artesanales) o ambos.
b) Los objetivos cuantificables deseados por el administrador respecto a variables biológicas y económicas de la pesqueria.
c) Al menos dos alternativas de instrumentos de manejo cuya implementación, vigilancia y cumplimiento sea viable física, politica y económicamente.
d) Estado de duda sobre cual de las alternativas o combinaciones de diferentes niveles de éstas, es mejor para lograr los objetivos enunciados en el inciso (b).
e) Ambiente o contexto de manejo de la pesquería.
Esta importante etapa del proceso requiere de un cuidadoso análisis tanto de las caracteristicas y los factores que determinan el comportamiento dinámico del recurso (especies objetivo e incidentales) como del esfuerzo pesquero ejercido por los pescadores. En la Figura 5.2 se pueden observar las interdependencias existentes entre el recurso, sus usuarios directos (los pescadores) y los responsables de su manejo (administradores).
Subsistema “El recurso”. En la caracterización del recurso es necesario identificar: (1) aspectos de su ciclo de vida, incluyendo hábitat, biología reproductiva y dinámica del reclutamiento, crecimiento y mortalidad; (2) los factores ambientales que pudieran ser críticos en determinar su abundancia y distribución en el espacio y el tiempo; (3) las posibles interdependencias ecológicas (e.g. competencia, depredación) que pudieran existir entre la especie objetivo, aquellas capturadas incidentalmente y otras que pudieran ser objetivo de otra pesquería pero con las que se tienen relaciones de competencia o depredación; (4) la dinámica de la estructura espacio-temporal del recurso.
Caracterizado el recurso en su dinámica poblacional, hábitat e interdependencias ecológicas, se requiere caracterizar el esfuerzo pesquero que se ejerce sobre él.
Subsistema “Usuarios del recurso”. La especificación del esfuerzo pesquero requiere generalmente su desagregación por tipo de flotas con diferente poder de pesca, y/o que operan sobre diferentes componentes de la estructura de la población. Asimismo, se debe analizar la posible presencia de interdependencias tecnológicas tales como pesquerías secuenciales, aquellas que capturan múltiples especies y las tecnológicamente interdependientes. Como se expresó en el Cap. 3, estas últimas existen cuando la captura incidental de una flota pesquera constituye especie objetivo de otra flota.
En este subsistema es necesario contar con funciones de capturabilidad por especie, talla y tipo de flota, por lo que se requerirá estimar las curvas de selectividad correspondientes; asimismo, estimar los costos unitarios del esfuerzo pesquero por tipo de flota y especificar los precios de las especies objetivo e incidentales.
Una vez caracterizados el tipo de recurso y el esfuerzo pesquero, se procede a seleccionar los métodos apropiados para la estimación de parámetros y funciones que describen la dinámica poblacional del recurso y del esfuerzo pesquero. De no contar con la base de datos adecuada, se procederá a elaborar un diseño muestral para colectar la información biológica y económica de frecuencia de tallas de la captura comercial y del esfuerzo pesquero correspondiente. En esta colecta de información se deberá obtener los costos de operación por viaje de pesca o cualquier otro indicador nominal (e.g. dias de pesca) o efectivo (horas efectivas de pesca) del esfuerzo pesquero y los precios pagadas al pescador tanto por las especies objetivo como incidentales.
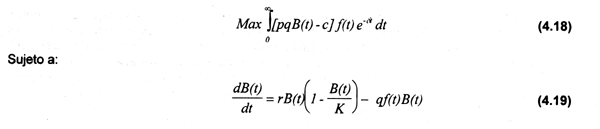
| ALIMi(t)= alimento consumo doméstico | Lij=longitud del organismo |
| Bijk(t)= bimasa | MNi= tasa de mortalidad natural |
| Cijkm(t)= capturas | Nijkm(t)=número de individuos |
| cm= costo unitario del esfuerzo | πm(t)= renta económica |
| cp= costos de procesamiento | qijm=capturabilidad |
| EMPm(t)=empleo generado | Rjk(t)=recultamiento |
| EXPm(t)=generació divisas, sector capturas | SELijm=selectividad del arte de pesca |
| EXPp(t)=generació divisas, sector procesamiento | Vim(t)=número de barcos Wij=peso del organismo |
| fijkm(t)= intensidad de pesca | wpi=precio de planta xpj=precio de playa |
| FRijk(t)= tasa de mortalidad por pesca |
done: i=especie; j=edad; k=sitio; m=flota; t=tiempo; P = procesamiento
Figura 5.2. Caracterixación de una pesquería.
Subsistema “Manejo del recurso”. Para lograr los objetivos y las metas establecidas en la etapa (iii) del plan de manejo, es necesario considerar las posibles formas de intervención del Estado en la pesqueria, los criterios de selección de medidas de manejo correspondientes y la forma de contender en situaciones de criterios múltiples en la combinación o selección de estrategias de manejo del recurso. Estos importantes aspectos serán discutidos con detalle en el Capítulo 6.
Para evaluar el impacto bioeconómico de diversas estrategias de manejo de un recurso, es necesario elaborar un modelo matemático dinámico de la pesquería que permita realizar experimentos de simulación. Este modelo matemático deberá contener entonces las relaciones causa-efecto especificadas para cada uno de los tres subsistemas antes mencionados, las cuales posibilitan la evaluación de los posibles efectos de cambios temporales en el esfuerzo pesquero ejercido sobre el recurso.
En esta etapa es importante hacer notar que las funciones que describen los procesos básicos que determinan la abundancia de una población en especies pelágicas han sido ampliamente reportadas en la literatura (Beverton & Holt, 1954; Ricker, 1975; Gulland, 1983; Sparre et al., 1989), donde se satisface el supuesto básico de agrupamiento dinámico de la población y de homogeneidad en la distribución espacial del recurso y del esfuerzo pesquero. Cuando dichos supuestos son violados por las características inherentes al comportamiento relativamente sedentario o bien sesil de especies bentónicas, tales como moluscos y arrecifes coralinos entre otros, se han reportado recientemente formas de modelar el comportamiento de agregación del recurso y del esfuerzo de pesca ejercido (Caddy, 1975; Sluczanowski, 1984; Orensanz, 1986; Defeo et al., 1991; Defeo, 1993a; Seijo & Defeo, 1994b; Seijo et al., 1994c). En este Capítulo se exponen modelos para representar pesquerías cuyo comportamiento satisface el supuesto de agregamiento dinámico de la población. En el Capítulo 6 se presentan modelos recientemente desarrollados para pesquerías de especies sedentarias donde la heterogeneidad en la distribución del recurso y la correspondiente intensidad de pesca se consideran en forma prioritaria.
Dinámica poblacional. La dinámica poblacional de un recurso puede ser modelada utilizando los principios básicos de las tablas de vida (Seijo, 1986; Begon et al., 1990). Este método se basa en la contabilidad dinámica de entradas y salidas de individuos a cada cohorte de la poblción. El número de organismos de la especie i de la edadj en el tiempo t+DT (Ni(t+DT)) se obtiene de la integración en el intervalo [t,t+DT] del número de individuos de la edad j-1 que sobreviven y se incorporan a la edad j en tiempo t (Si1 (t) Ni1(t)), menos la tasa de mortalidad total de la cohorte j en el tiempo t (Aij(t)Nij(t)), menos la tasa a la cual los organismos de la especie i, del grupo de edad j que sobreviven, se incorporan al cohorte j+1 en el tiempo t (SRij(t)Nij(t)). Como resultado, la estructura de la poblción es estimada en forma dinámica por la expresión (5.1):
Nij(t + DT) = Nij (t) + t + DT∫t(SRij-1τ)Nij-1(τ) - (SRij(τ) + Aij(τ)) Nij (τ)) dτ (5.1)
donde:
Nij (t) = numero de individuos de la especie i,edad j en el tiempo t. SRij(t)=tasa de supervivencia de individuos de la especie i, edad j en el tiempo t. Aij(t)= tasa de mortalidad total de individuos de la especie i, edad j en el tiempo t.
Integrando numéricamente la expresión (5.1) por el método de Euler (Chenney & Kincaid, 1985) y dado que por definición SRij (t)+Aij (t) = 1 (Gulland, 1983: p.83), se obtiene la expresión siguiente:
Nij(t + DT) = Nij (t) + DT (SRij-1(t) Nij-1(t) - Nij(t)) (5.2)
La tasa de supervivencia por edad en el tiempo t se obtiene al restarle a la unidad la tasa de mortalidad total de la edad j en el tiempo t.
Aij (t) es la suma de la tasas de mortalidad natural (MNi) y tasa de explotación por edades Frij (t) en el tiempo t (sensu Gulland, 1983). Esta última resulta de dividir la suma de las capturas por edades de los diferentes tipos de embarcación (m), (Cijm(t)), entre la biomasa por edades (Bij (t)) en el tiempo t.

La retroalimentación de la expresión (5.2) se genera por una expresión estocástica de reclutamiento, que en el caso de la función tipo Beverton & Holt (1957) se describe como:

donde Hmaxi representa el número máximo de huevos que puede generar el stock desovante de la especie i. Rmaxi es el reclutamiento máximo observado para la especie i, HSi(t) es el número de huevos que se estiman serán generados por el stock desovante de la especie i en el tiempo t RNi(t) es una variable aleatoria normalmente distribuida con media igual a cero y varianza observada que representa la variabilidad no explicada por las variables independientes de la ecuación (5.4).
Debe mencionarse que la función de reclutamiento antes mencionada puede ser reemplazada por una que describa mejor la especie que se esté estudiando (e.g. Ricker). Una variedad de opciones de curvas de reclutamiento y respectivas expresiones matemáticas son explicadas claramente por Hilborn & Walters (1992) y De Anda et al. (1994).
HSi(t) se estima para cada período de desove por medio de la expresión (5.5), la cual expresa que la población sexualmente madura en el tiempo t es multiplicada por la proporción de hembras (Hi) presentes en la estructura de la población y por la fecundidad promedio de las hembras de diferentes edades (FECij)
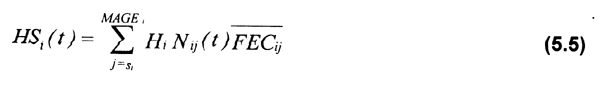
donde:
MAGEi = edad máxima de la especie i
si = edad de primera madurez sexual de la especie i.
La biomasa por especie i es estimada por la ecuación siguiente:

donde el peso promedio de organismos de la especie i (Wij), de la edad j, es estimada por la expresión Wij=aLijb (a y b son porámetros a estimarse). Lij es calculada por la bien conocida función de crecimiento individual de von Bertalanffy (1938):
Lij=L∞i(l-e(-kpi(j-toi))) (5.7)
donde:
Lij = longitud de la especie j a la edad j.
Lxi = longitud asintótica de la especie j.
kpi = parámetro de curvatura de la ecuación de crecimiento individual de la especie i.
toi = parámetro de ajuste al tiempo inicial para la ecuación de crecimiento de la especie j.
Debe mencionarse que se sugiere la utilización de funciones de crecimiento adecuadas para la especie sujeta de análisis. En crustáceos se ha encontrado que las funciones de unidad paso, representan con mayor precisión el crecimiento (Arce et al., 1991).
Los períodos de desove y eclosión pueden ser modelados utilizando el método de “retraso distribuido” (Manetsch, 1976, Seijo, 1986). Este modelo se basa en la función de densidad probabilistica Erlang o Gamma y puede ser descrito de la siguiente forma:
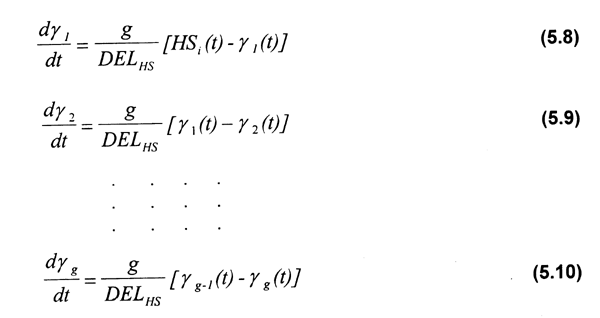
donde:
HSl(t) = entradas al proceso de retraso (número de huevos que son desovados en el tiempo t) γg(t) = salidas del proceso de retraso (número de huevos que eclosionan en el tiempo t). γ1(t), γ2(t), …, γyg-1(t)son las tasas intermedias del proceso de retraso. DELHS = valor esperado del tiempo maduración de huevos de la especie de interés. g = orden del proceso de retraso.
El parámetro g especifica al miembro (distribución) de la familia de funciones de densidad probabilistica Erlang que describe el tránsito de entidades en su paso por el proceso de retraso.
Dinámica de la flota. La variación del esfuerzo pesquero en el tiempo es modelada utilizando la ecuación de dinámica del esfuerzo desarrollada por Smith (1969):
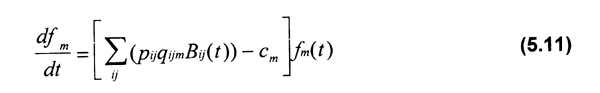
La dinámica estacional de la flota se puede modelar utilizando también el método de retraso distribuido para representar la incorporación de las unidades de pesca a la pesqueria a lo largo de la temporada de pesca.
La captura por especie y por tallas Cijm(t) generada por diferentes tipos de flotas m en el tiempo t, es calculada por la siguiente ecuación:
Cijm=qijmfm(t)Bij(t)+Rm(t) (5.12)
donde Rm(t) es una variable aleatoria de la captura exponencialmente autocorrelacionada.
Utilizando los conceptos básicos de Baranov (1918) para estimar la mortalidad por pesca con el método de área barrida, se calcula el coeficiente de capturabilidad para la correspondiente selectividad por tallas del arte de pesca empleado por tipo de flota (qijm):
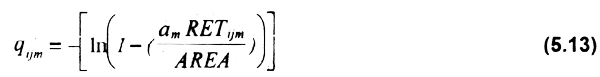
donde:
AREA = área ocupada por el stock
RETijm = retención por especie i por talla j del arte de pesca utilizado por el barco tipo m, definida por la ojiva de selectividad del arte de pesca.
am = área barrida por dia de pesca por el barco tipo m.
La retención por tallas del arte de pesca especifico, es estimada por la siguiente ecuación (Sparre et al., 1989):

donde los parámetros S1im and S2im son estimados por las ecuaciones (5.15) y (5.16) respectivamente:

donde:
L50%im = longitud de la especie i al 50 % de retención del arte de pesca utilizado por tipo de barco m.
L75%im = longitud de la especie i al 75 % de retención del arte de pesca utilizado por tipo de barco m.

Cabe mencionar que la función de capturabilidad descrita anteriormente no es válida para especies pelágicas como los clupeidos, ya que se ha demostrado que ésta se incrementa exponencialmente en la medida que la biomasa del stock disminuye (MacCall, 1976). Esta función de capturabilidad para pelágicos menores se explica por el comportamiento de agregación de este tipo de especies. Se recomienda utilizar la función de selectividad que mejor describa las condiciones especificas del arte de pesca y del tipo de especie sobre la cual se aplica el esfuerzo pesquero.
La incertidumbre inherente a la captura por viaje por tipo de embarcación, se representa en la expresión (5.12) a través de la generación de la variable aleatoria Rm(t), con varianza observada y una función de densidad probabilistica que mejor describa los residuos observados en los datos de captura.
La renta económica por tipo de embarcación (πm(t)) a lo largo de la temporada es estimada en la expresión (5.17), donde RTm(t) y CTm(t) son los ingresos y costos totales por tipo de embarcación en el tiempo t, respectivamente.
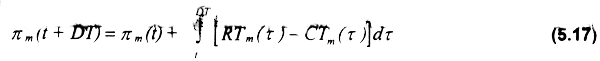
Los ingresos totales por tipo de embarcación deben ser estimados tomando en consideración los precios y cantidades de captura objetivo e incidental. Los costos totales se estiman considerando costos fijos, costos variables y costos de oportunidad de mano de obra y capital (ver Capitulo 2).
Los empleos directos generados por la pesqueria, (EMP(t+DT), son expresados por la ecuación (5.18) de la forma siguiente:
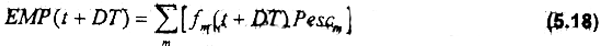
donde Pescm representa el número promedio de tripulantes por embarcación tipo m.
La contribucion de la pesqueria a la disponibilidad de alimentos en la zona costera a lo largo de la temporada (ALIMi(t+DT)), es estimada por la expresión (5.19):
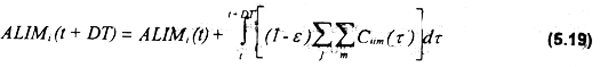
donde ε es la proporción de la captura de la especie i proveniente de las diferentes flotas, que se estima será destinada al mercado de exportación, y por tanto 1-ε es la proporción destinada al mercado doméstico.
Finalmente, la generación de divisas de la pesqueria a lo largo del año es estimada de la forma siguiente:
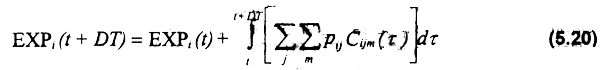
donde pij es el precio de exportación de la especie i con edad (talla) j.
Para conducir análisis bioeconómico de pesquerías es necesario recolectar información biológica y económica de las especies capturadas y del esfuerzo pesquero heterogéneo que se ejerce sobre ellas (Seijo et al., 1991b, c). A continuación se presenta un listado de información requerida para parametrizar el modelo matemático que se haya construido para la pesqueria en cuestión.
Información de parámetros biológico-pesqueros
· Estimaciones de la mortalidad natural.
· Estimaciones del coeficiente de capturabilidad del arte de pesca, método de captura, o tipo de embarcación. Seria deseable contar con estimaciones de este parámetro por tallas o edades.
· Estimaciones de la mortalidad por pesca por edad o talla.
· Función del crecimiento individual relación peso-longitud, general o para cada sexo.
· Composición por sexos de la población.
· Edad de primera madurez sexual.
· Fecundidad promedio de la población desovante, de ser factible por edades o tallas.
· Estimación de la estructura de la población.
Número de individuos por edad o talla.
Estimación del tamaño de la población.
Información de esfuerzo pesquero
· Tipo de embarcaciones.
· Tipo de motor.
· Arte de pesca en cada tipo de embarcación.
· Número promedio de pescadores por tipo de embarcación.
· Número de embarcaciones involucradas en la pesqueria de interés.
- Por puerto.
- Por temporada.
· Principales áreas de pesca para la captura de la especie objetivo.
· Número promedio de dias efectivos de pesca por viaje, por tipo de embarcación, por pesquería.
· Duración promedio del viaje de pesca.
· Tipo(s) de carnada utilizada (si se requiriere).
Información de la captura
· Puertos de desembarque de la especie objetivo.
· Captura total de las especies objetivo por año.
- Por tipo de embarcación.
- Por temporada.
- Por viaje.
- Por dia efectivo de pesca.
· Composición por tallas de la captura (especies objetivo).
· Si la pesquería involucra una población compartida, o bien si se otorgan licencias para ejercer esfuerzo pesquero en la ZEE del pais en cuestión, es necesario contar con información de la captura y el esfuerzo pesquero de las embarcaciones extranjeras.
Ingresos y costos por tipo de embarcación
· Ingresos por viaje de pesca
- Precio promedio de las especies objetivo.
- Precio promedio de las especies incidentales.
- Estimaciones de la captura objetivo e incidental a lo largo del año.
Si la captura de la flota en cuestión contribuye con un porcentaje significativo de la oferta global de la especie objetivo, entonces será necesario estimar la función de precios (ecuación de demanda) correspondiente.
· Costos del esfuerzo pesquero
Costos variables
Gasolina y aceite.
Hielo.
Carnada.
Reemplazo de artes de pesca dañadas.
Alimentos.
Mantenimiento del motor y la embarcación.
Costos fijos
Depreciación de la embarcación, del motor y de los equipos y artes de pesca.
Intereses sobre capital prestado.
Seguros y gastos de administración si los hubiere.
· Costos de oportunidad de capital y mano de obra
El costo de oportunidad del capital invertido en la pesqueria es lo que pudo haber generado este capital en la siguiente mejor alternativa de inversión. Para realizar las estimaciones de los costos de oportunidad de capital, intereses sobre capital prestado, y depreciaciones, es necesario contar con información de los costos de inversión correspondientes a la embarcación, el motor, las artes de pesca y otros equipos. Asimismo, es necesario especificar la tasa promedio de interés sobre préstamos de avío y refaccionarios para el sector pesquero del país en cuestión y la tasa de interés bancaria sobre depósitos a plazo fijo.
El costo de oportunidad de la mano de obra lo constituye el ingreso que podria haber obtenido dicha mano de obra en su siguiente mejor opción de empleo. Para estimar el costo de oportunidad de la mano de obra (horas pescador), se debe indicar la forma de pago a pescadores en la pesqueria especifica considerando, entre otras, las siguientes posibilidades: (i) pago a cada pescador como un porcentaje de la captura de la embarcación por viaje, (ii) pago a cada pescador como salario diario, y (iii) tasa salarial diaria en la siguiente mejor opción de empleo abierta al pescador promedio.
Otra información relevante
· Porcentaje de la captura anual que se queda dentro de la comunidad costera para propósitos de subsistencia.
· Porcentaje de la captura que va al mercado local y doméstico.
· Porcentaje de la captura que va a un procesamiento posterior.
· Porcentaje de la captura que va al mercado de exportación.
· Precio de las especies objetivo e incidentales en el mercado de exportación.
Una vez colectada la información antes mencionada, se procede a estimar los parámetros tanto biológicos como económicos para elaborar y/o aplicar el modelo bioeconómico de computadora basado en un modelo matemático como el especificado en el inciso anterior.
Programa de computadora para obtener una solución numérica
El programa de computadora puede ser desarrollado en cualquier lenguaje de programación estructurada (QuickBASIC, Visual BASIC, FORTRAN 77, C, etc.) para simular el estado de la pesqueria en el tiempo. La estructura general del programa incluye las siguientes etapas:
Fase de asignación de parámetros y valores iniciales
a. Asignación de valores a las constantes y parámetros del modelo.
b. Asignación de valores iniciales a variables de cambio y de estado.
c. Tiempo inicial: T=0.
Fase de especificación de la corrida de simulación
d. Periodo de simulación.
e. Incremento de tiempo.
f. Especificaciones para impresión de salidas.
Fase de ejecución
g. Actualización de la variable tiempo: T=T+DT.
h. Cómputo de variables de estado.
i. Cómputo de variables de cambio para el tiempo T.
j. Impresión de variables de estado y de cambio.
k. Retornar a (g) si la corrida de simulación no ha terminado.
En el análisis de estabilidad se determina el valor apropiado del incremento de tiempo DT para realizar simulaciones estables de ecuaciones diferenciales, tales como las incluidas en modelo de retraso distribuido. Si se utiliza el método de integración numérica de Euler para resolver las ecuaciones diferenciales del modelo, la condición necesaria de estabilidad involucra que DT esté dentro del intervalo siguiente:
2MIN[Dn]>DT>0 (5.20)
donde Dn =DEL/g y MIN [Dn] es la constante de retraso más pequeña del modelo (Manetsch y Park, 1982).
Dado que el modelo de simulación presentado anteriormente contiene procesos de retroalimentación en el componente de la estructura de la población, se requiere que:

donde: c = 1/Dn
Por tanto, el valor de DT requiere estar dentro del intervalo dado por: 1 > DT > 0. Con el objeto de reducir el error de integración numérica a niveles menores a 5 %, el valor del incremento de tiempo sugerido es: DT=.01
Es necesario además conducir un análisis de sensibilidad para verificar el comportamiento del modelo ante cambios marginales en sus parámetros y en las condiciones iniciales de operación. La biomasa inicial, el parámetro de supervivencia en la eclosión, tasa de mortalidad natural, y los niveles de esfuerzo pesquero, entre otros, deben ser modificados en incrementos y decrementos del 20% por ejemplo, a efectos de observar el comportamiento del modelo.
La validación de un modelo requiere que éste se comporte conforme al sistema mismo. Adicionalmente a pruebas estadisticas no-paramétricas (e.g. Kolmogorov-Smirnov) utilizadas para probar la hipótesis nula de igualdad de las distribuciones de las variables observadas y las generadas por el modelo matemático: ver Defeo et al., 1991), cuatro enfoques pueden ser utilizados para validar un modelo de simulación (Payne, 1982; Graybeal & Pooch, 1980):
a. Comparación de captura real y captura simulada por el modelo.
b. Comparación de la dinámica real y simulada de la flota durante la temporada de captura.
c. Consistencia con teorias aceptadas en la literatura de ciencia pesquera.
d. Análisis de los resultados del modelo de simulación con expertos del recurso.
Contando ya con un modelo dinámico, es relativamente sencillo realizar experimentos de simulación con diversas estrategias de administración del recurso para observar los impactos bioeconómicos en la pesqueria. A continuación se presentan, a manera de ilustración, 4 estrategias que pueden experimentarse: (i) incremento de 20% en el esfuerzo pesquero de las flotas artesanal e industrial; (ii) ampliación (o reducción) de un mes en el periodo de veda; (iii) aplicación de una talla minima de captura; (iv) incremento de 20% en el esfuerzo de las flotas artesanal e industrial y ampliación de 1 mes en el periodo de veda.
Se desea asesorar a la administración pesquera de un pais en su misión de manejar una pesqueria de camarón (e.g.Penaeus occidentalis) en la que participan dos tipos difernciables de flotas: embarcaciones artesanales que capturan juveniles y adultos jóvenes del stock, y embarcaciones industriales que esencialmente capturan organismos adultos. Se le ha solicitado al analista en bioeconomía que sugiera elementos para establecer individualmente o en combinaciones los siguientes instrumentos de manejo considerados como viables para ser vigilados efectivamente: talla minima de captura, duración de la temporada de captura y la especificación de los meses de veda correspondientes. Lo anterior es sobre la base de que se ha limitado el número de embarcaciones que pueden operar en esta pesqueria. En la determinación de la duración de la temporada asúmase que la flota industrial no es versátil y que por lo tanto se deberán cargar los costos fijos durante el tiempo que la flota esté inactiva. Ya que existen periodos ambientalmente favorables para reclutamientos arriba del promedio (20% de los años observados), el decisor está considerando la posibilidad de ampliar en 25% el número de licencias de ambos tipos de flotas para esta pesqueria. En la Tabla 5.1 se presentan los principales parámetros biológico-pesqueros y económicos de la pesquería.
Dinámica de corto y largo plazo
En el corto plazo el modelo antes descrito nos permite representar dinámicamente dos procesos bioeconómicos fundamentales: la distribución intra-anual del reclutamiento y del esfuerzo pesquero. En la Figura 5.3a se puede observar la ocurrencia y distribución temporal de los dos picos de reclutamiento especificados en la Table 5.1. De manera análoga, la dinámica de la flota a lo largo de la temporada de captura es ilustrada por el modelo (Fig.5.3b).
Al tenerse una temporada de captura de 10 meses iniciando en el mes 3, el efecto en el stock desovante se ve reflejado en la magnitud relativa de los dos reclutamientos. En el primer reclutamiento el número máximo de individuos es de 13.2 millones, mientras que en el segundo es de 7.8 milliones. Si la fecha de inicio de la temporada de captura cambiase, la distribución relativa de los reclutamientos podria afectarse. De manera análoga, la magnitud de ambos reclutamientos se veria afectada si la duración de la temporada se redujera o incrementara.
| Parámetro/variable | Valor | Unidad de medida |
|---|---|---|
| Edad máxima de la especie | 24 | meses |
| Edad de primera madurez sexual | 6 | meses |
| Edad de primera captura flota 1 | 3 | meses |
| Edad de primera captura flota 2 | 2 | meses |
| Fecundidad promedio | 1072000 | huevos |
| Parámetro de curvatura ec. de crec. | 0.27 | 1/mes |
| Parámetro t0 de ec. de crecimiento | -0.03 | 1/mes |
| Longitud asintótica | 245 | mm |
| Peso asintótica | 140 | g |
| Area barrida por dia flota 1 | 1.41 | Km2 |
| Area barrida por dia flota 2 | 0.25 | Km2 |
| Long. 50% retención del arte, flota 1 | 170 | mm |
| Long. 50% retención del arte, flota 2 | 150 | mm |
| Long. 75% retención del flota 1 | 175 | mm |
| Long. 75% retención del flota 2 | 170 | mm |
| Area total de distribución del recurso | 6405 | Km2 |
| Tipos de flotas | 2 | -- |
| Parámetro de dinámica de la flota 1 | 0.000001 | -- |
| Parámetro de dinámica de la flota 2 | 0.0000015 | -- |
| Máximo reclutamiento observado | 76900000 | organismos |
| Longitud de la estación de captura | 10 | meses |
| Mes de inicio de la temporada de captura | 3 | -- |
| Mes del primer reclutamiento | 4 | -- |
| Mes del segundo reclutamiento | 11 | -- |
| Longitud de la corrida de simulación | 3 | años |
| Orden del retraso distribuido | 2 | meses |
| Promedio de dias de pesca por mes flota 1 | 20 | -- |
| Promedio de dias de pesca por mes flota 2 | 12 | -- |
| Tiempo de retraso entrada a la pesqueria | 0 | días |
| Tiempo promedio de tránsito de reclutas | 2 | meses |
| Costo unitario del esfuerzo | 65000 | US$/barco/año |
| Costo unitario del esfuerzo | 3000 | US$/barco/año |
| Precio minimo (90–100/lb) | 1500 | US$/ton |
| Pendiente curva de precios por talla | 700 | US$ |
| Ingreso incidental ponderado | 318 | US$/ton |
Lo anterior permite explorar combinaciones de fechas de inicio y duración de la temporada de captura dados los picos de reclutamiento. Desde luego el propósito será mantener y de ser posible incrementar la renta económica que la pesqueria puede generar en el tiempo.
Las capturas por tipo de flota son presentadas en la Figura 5.3c y d. Se observa que las capturas son decrecientes para ambos tipos de flotas. Sin embargo, en el caso de flota artesanal, su relativamente bajo costo unitario del esfuerzo pesquero le permite continuar obteniendo renta económica del recurso tal como fuera mencionado anteriormente.
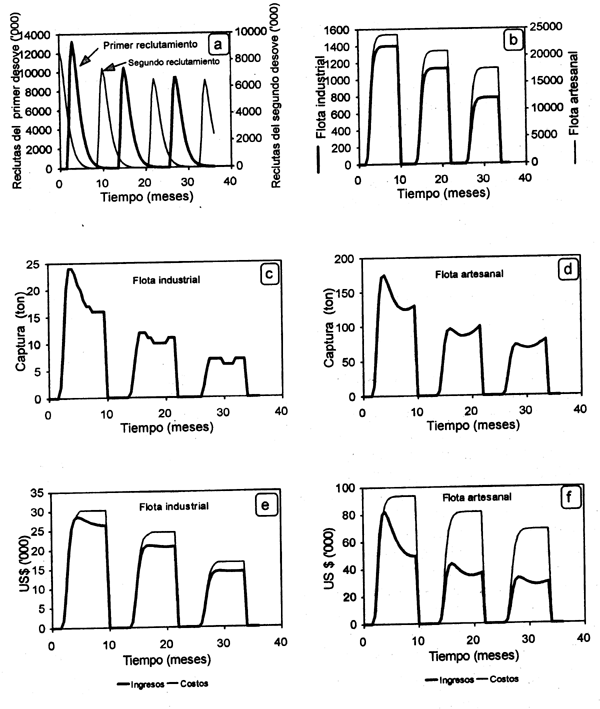
Figura 5.3 Dinámica en el corto y mediano plazo del reclutamiento (a), del esfuerzo (b), de las capturas (c, d) y de la renta y costos (e,f) para dos tipos de flotas en una pesquería hipotética de camarón.
En las Figuras 5.3e y f se observan las estimaciones de costos y beneficios percibidos por las flotas artesanal e industrial que ejercen su esfuerzo pesquero sobre el recurso camarón. La renta acumulada a lo largo de la temporada de captura determinará, bajo condiciones de acceso abierto, los posibles cambios en el número de embarcaciones que permanecerán en la pesquería en el largo plazo (dinámica interanual). Para la flota industrial, el número de embarcaciones comienza a decrecer desde el segundo año de la corrida de simulación como resultado de experimentar rentas negativas. La flota artesanal, de manera análoga, decrece moderadamente ya que continúa, aunque a una tasa decreciente, obteniendo renta negativa.