3.6 Responses to policies and market signals

3.6.1 Production response
3.6.2 Relevant exercises
3.6.3 Consumption response and market demand
3.6.4 Relevant exercises
3.6.5 Supply response
3.6.6 Relevant exercises

Different production systems will respond to government policy interventions according to their degree of market integration and factors which influence individual household goals and aspirations. This section analyses the effects of price policy on semi-subsistence and commercial production systems in terms of production, consumption and supply.

3.6.1 Production response

Types of price-production responses

When assessing production responses to price, bear in mind that the desire to increase cash income is not the only (and sometimes not even the most important) determinant of the pattern of production. A rise in the price of a product will not necessarily result in an expansion of production. Many food crops (and livestock products such as milk) are primarily produced for subsistence and are more or less independent of market prices. In these circumstances, prices may have a negligible effect on production decisions. In some cases, production for sale will be based on the need to meet fixed cash obligations (ceremonies, school fees, tax etc) or to fulfil particular aspirations (e.g. to purchase certain commodities). In other cases, sales will tend to be opportunistic in nature, occurring only when surpluses above subsistence needs are obtained. Sales will thus be either inversely related to prices (Figure 3.4a) or wholly independent of them.

However, inverse relationships between production and price are unlikely to persist over the long term as the transition towards greater integration in the economy occurs. As rural markets for goods and services develop, price increases usually begin to have a positive influence on production. In the following discussion, we will assume that price/production responses are positive, as shown in Figure 3.4b. A positive long-term production response does not, however, preclude a negative short-term market supply response. This will be discussed later with particular reference to the impact of prices on herd development.

Figure 3.4. Inverse and positive production responses.

a) Inverse production response

b) Positive production response

Adjustment mechanisms to increase production

In considering positive responses, profitability will be the driving force to increase the quantity of output or agricultural production. This can be achieved in three possible ways, namely:

· by utilising slack resources

· by substituting enterprises

· by intensifying production.

· Utilising slack resources. Land, labour or other resources available to a production unit may not be fully used. Utilising slack resources implies strategies such as expanding the area under cultivation, shortening fallow periods, building up herd numbers and working longer hours.
Such strategies for increasing production have been Africa's traditional response to the rising demand for food caused by population growth, but they are now putting severe pressure on the natural resource base.

· Substituting enterprises. Commodities produced on a farm compete for the use of resources such as land and labour. When the profitability of one commodity increases relative to another, resources can be shifted to it. Substitution is common between cropping enterprises but may also occur between crops and livestock or between different livestock species or products (e.g. cattle and smallstock, meat and milk).

· Intensifying production. Opportunities for intensifying production depend predominantly on the availability of external inputs and new technologies. Intensification means that producers respond to a rise in the price of a commodity by seeking to raise yields rather than by expanding the area cultivated or, in the case of livestock, the number of animals kept. It is difficult to begin intensifying highly extensive production systems such as pastoralism because the delivery of external inputs is hampered by the lack of infrastructure. Technologies are also less well developed for such systems.

The decision to substitute one enterprise for another depends on their relative profitability.
This, in turn, depends on the physical productivity of the inputs and resources used and on the relationship between input and output prices.

The gross margin of an enterprise is a measure of profitability which takes these factors into account. Gross margin also provides a basis for analysing the likely impact of a price change on production. It is defined as:

Gross margin = gross value of output - variable costs

Since purchased inputs are used in limited amounts in semi-subsistence systems, the gross margin for an enterprise in such systems is often closer to the gross value of its output than in more commercial systems, where substantial amounts of inputs may be used. In theory, comparisons between enterprises should be based on a calculation of gross margin per unit of the scarcest resource. In practice, however, several resources (e.g. both land and labour) may restrict the opportunities for substitution, and personal factors such as risk aversion will also play their part. For these reasons, a simple ranking of enterprises on the basis of gross margins per unit of land or labour used may not be sufficient. In such cases, more complex techniques such as linear programming will be needed, but these will not be discussed here. For our purposes, the essential principles of substitution can be demonstrated using a simple gross margin planning model as explained in Exercise 3.3.

The profitability of adopting intensified production methods, and the amounts produced by these methods, will depend on three main factors:

· The marginal physical productivity (MPP) of the inputs used (i.e. how much more output one gets per additional unit of input). In many cases, MPP declines per extra unit of input used, especially when not all the inputs can be increased simultaneously or to an equal extent.
For example, if we add more cows to the same farm size or more oil cake to the same cow, each extra unit of input is likely to bring about less extra output (milk) than the previous one.

· The marginal revenue (MR) generated by each extra unit of output. For the individual farmer, MR is usually identical to the producer or market price and usually the same per unit sold however many units are sold. Sometimes - for instance when a farmer is selling under a minimum or maximum quota system or to a customer who obtains reductions for additional purchases - market price will differ from MR, reflecting the new price level used when the extra unit is sold. The marginal value product (MVP) is obtained by multiplying MPP by
MR.

· The marginal factor cost (MFC) per extra unit of input used. For the individual farmer, MFC is usually identical to the purchase or market price, and is usually the same however many units of input are used. Sometimes, for instance when the input is difficult to obtain and can only be bought on the black market, the MFC will exceed the market price of the previous unit used. Or, for example, when discounts are offered for bulk purchases, it will be less.

As a general rule, a farmer wishing to maximise profits through intensification should use extra inputs to increase output so long as MVP exceeds MFC.

To give a simple example, a farmer has two half-bred cows and no capacity to keep any more. She can buy a special dairy mix feed at a special farmers' price of 105 cents/kg if she restricts her purchases to 1 kg/day, but she has to pay an unsubsidised price of 210 cents/kg if she exceeds this rate. She card sell up to 10 litres of milk a day locally (2 litres to each of five families) at 100 cents/litre, but has to sell amounts above this level to the government milk collection scheme which, because of limited market outlets, will only buy up to 6 litres/farmer at a price of 80 cents/litre. Thus, she has to make amounts of milk higher than 16 litres into butter, which she sells at a price equivalent to 40 cents/litre of milk.

Without being fed concentrates, our farmer's cows each give only three litres/day. This rises rapidly to five litres when they are fed 0.5 kg daily of dairy mix, but the yield response to feed levels higher than this is limited by the cow's low genetic potential. At a daily feed level of 3 kg of dairy mix, the cows will not yield more than 9.5 litres each.

Table 3.4 presents the effects of feeding different levels of dairy mix on milk output, revenue and cost. The table indicates that, given current government policy, our profit maximising farmer should feed 1 kg of dairy mix daily to each of her cows, giving a total milk output of 13 litres daily. A new policy intervention in the form of an initial 15% rise in the price of milk paid by the government collection scheme (from 80 to 92 cents/litre) should evoke a rise in feeding level to 1.5 kg and in milk output to 15.5 litres (a rise of 19%). A further milk price rise of 15% (to 106 cents/litre) should not evoke any more output unless it were accompanied by a lifting of the maximum supply quota of 6 litres/farmer. If this were relaxed, the feeding level should rise to 2 kg/cow per day and milk output to 17.5 litres (a rise of 13%).

Table 3.4. Feeding dairy mix to milking cows: Effects on productivity, revenue and cost, with and without policy interventions.

Productivity revenue and cost		Feed intake/cow (kg of dairy mix/day)
		0	0.5	1.0	1.5	2.0	2.5	3.0
Yield/cow (litres/day)		3.00	5.00	6.50	7.75	8.75	9.25	9.50
MPP of intake (litres/kg)		n.a.	4.00	3.0	2.5	2.0	1.0	0.5
MR (cents/litre)
	Pre - new policy	100	100	80	80	40	40	40
	Post- new policy	100	100	92	92	40	40	40
				106*	106*	106+	106+	106+
MVP of intake (cents/kg)
	Pre - new policy	n.a.	400	240	200	80	40	20
	Post - new policy	n.a.	400	276	230	80	40	20
				480*	265*	212+	106+	52+
MFC of intake (cents/kg)		n.a.	105	210	210	210	210	210

MPP = Marginal physical product.	n.a. = not applicable.
MR = Marginal revenue	* = further 15% price rise.
MVP = Marginal value product.	+ = maximum quota lifted.
MFC = Marginal factor cost.

We need to distinguish between the concepts of the marginal and the average. The marginal is the additional product/revenue/cost brought about by adding one more unit of input or output. The average is the total production/revenue/cost divided by all the units of input or output involved. For example, in Table 3.4, the marginal physical product of feeding an extra half kg of feed, raising feed intake from one half to one kg daily, is 1.5 kg of milk/half kg of feed. The average physical product of half a kg of feed at that feeding level is 3.25 kg of milk (i.e. 6.5 kg of milk divided by 2 half kg of feed; see third column of figures in Table 3.4). The total product per cow at that feed level is 6.5 kg of milk.

In summary, an increase in the price of a product will affect production through one or more of the adjustment mechanisms outlined above, such that:

Total production response = resource expansion effect + enterprise substitution effect + intensification effect

(Hint to instructors: Ask the participants what a person-day is. Does the concept provide a sensible basis for assessing labour requirements in African agriculture?)

3.6.2 Relevant exercises

Exercise 3.3: The effect of product and input price changes on farm production and income.

Example: Refer to the example given in Exercise 3.2. Excluding, for the moment, data on the cost of manure (a within-farm transfer), fixed costs and non-farm income, the original situation with regard to total gross margin is shown in the table below. The table also presents information on the constraints imposed on crop and livestock production by land availability.

Box 3.2: Short-term supply and long-term production responses The response to a price change in the short term may be quite different from that in the long term. This is particularly true of livestock production systems. Farmers' responses to price changes are not usually instantaneous but lagged in time. For instance, a maize producer may react to a past price increase by increasing output in the next production period. However, if the price in that period falls, the apparent response in the short term will be negative. That is, production will appear to have risen in response to a price drop. Lagged responses to price are most pronounced in cattle production, since gestation and maturation periods tend to be long. Producers may thus react to a price increase initially by reducing rather than increasing offtake, in order to increase herd numbers and hence herd value. Future offtake may increase as a result, but the time-lag before such an increase has any impact on the market may be three years or more. Thus, a serious imbalance between market prices and marketed output may occur in the short term. This imbalance feeds on itself. As a result of the shortfall in market supply, prices may be even further stimulated in the short term, further reinforcing the short-term negative supply response and the long-term positive production response. This scenario, known as cyclical over response, continues until market offtake starts to reduce prices again. Price cycles have a stronger influence on market supply in the developed world than they do in Africa, where drought and other factors also intervene. Figure 3.5 illustrates the price cycle. Herd size adjusts gradually to changes in price in such a way that movements in marketed output and herd size do not correspond. Exercise 3.4 contains a herd development model which again demonstrates this type of response. Figure 3.5. Lagged response of herd size and market output to a change in producer price. In conclusion, cattle production systems may be characterised by the following features: · relatively low or even negative price elasticities of supply in the short term · higher and positive price elasticities of both production and supply in the long term. Examples of these responses, expressed in terms of the price elasticity of supply, are shown in Table 3.9.

Activity	Minimum quantity constraint (kg)	Gross margin/ha ($)	Optimum plan		Total farm gross margin ($)
			(ha)	Quantity(kg)
Maize	³ 750	6.60	3.0	750	19.80
Beans	£ 100	13.20	0.5	100	6.60
Groundnuts	³ 75	3.00	0.5	75	1.50
Sorghum	£ 300	8.70	1.0	300	8.70
Livestock	n.a.	n.a.	-	-	30.00
Total			5.0		66.60

n.a = not applicable.

Now, let us assume a rise in the farm-gate price of sorghum and groundnuts to 6 and 14 cents/kg, respectively, and a fall in the price of beans from 12 to 7 cents/kg. All other prices and input costs remain unchanged. The table below shows the optimum farm plan and the total gross margin in this new situation:

Activity	Minimum quantity constraint (kg)	Gross margin/ha ($)	Optimum plan		Total farm gross margin ($)
			(ha)	Quantity(kg)
Maize	³ 750	6.60	3.0	750	19.80
Beans	£ 100	7.70	0.0	0.0	0.00
Groundnuts	³ 75	8.40	1.0	150	8.40
Sorghum	£ 300	17.40	1.0	300	17.40
Livestock	n.a.	n.a.	-	-	30.00
Total			5.0		75.60

n.a. = not applicable.

Exercise: (estimated time required: 2 hours).

Question 1. For the example above, comment on the changes which have occurred in the farm plan and the total farm gross margin. Estimate the percentage increase in total farm gross margin and total income, assuming that non-farm income and fixed costs remain constant (refer to Table 3.3, Exercise 3.2; continue to ignore manure cost and income).

Question 2. What would you expect to be the effects on farm output from an increase in meat and/or milk prices? Give a qualitative answer distinguishing between the short- and long-term effects of a price increase.

Question 3. For the small-scale dairy example (Exercises 3.1 and 3.2) assume the following:

Constraints on area cultivated:

Enterprise	ha
Maize	= 0. 5
Beans	> 0.1
Groundnuts	> 0.1
Coffee	= 0.2
Dairy	= 1.0
All enterprises	2.0

Price changes:

Maize:	3 cents/kg to 3.5 cents/kg
Groundnuts:	5 cents/kg to 14 cents/kg
Coffee:	15 cents/kg to 35 cents/kg

Using this information and the data in Exercises 3.1 and 3.2, tabulate your results to obtain the total farm gross margin for the original and new optimum farm plans. Estimate the percentage change in output resulting from the price changes for maize, beans, groundnuts and coffee. Summarise the data in a table, placing the percentage change in price for each enterprise against the corresponding percentage change in output. Discuss your results.

Question 4. List some of the factors you consider would influence the supply response to price for the commodities produced by the sample small-scale dairy unit. Explain why you think these factors would influence the response.

Question 5. Discuss qualitatively the possible effects of a significant decrease in the price of fertiliser or concentrate.

Exercise 3.4: Livestock production response: The use of cattle herd projection models.

Example: Herd projection models can be useful in understanding how producers are likely to respond to market signals over time. A pastoral model will be used to demonstrate changes in offtake rate, herd size and herd composition over 10 years. To do this, the following information on initial herd structure, expected performance parameters and offtake rates are needed:

Herd size and structure (years 1-5):

Stock category		Initial number	% total herd (after calving)
Calves:
	Males	(12)a	10.9
	Females	(12)a	10.9
1- to 2-year-old males		9	8.2
1- to 2-year-old females		9	8.2
2- to 3-year-old males		8	7.3
2- to 3-year-old females		8	7.3
Males >3 years old		12	10.9
Cows		40	36.3
Total		86	100.0

^a For simplicity, it is assumed that calves are born just after the start of the year.

Performance parameters (years 1-10):
Calving rate (%)		60.0
Mortality rates (%):
	Calves	25.0
	1- to 2-year-olds	10.0
	2- to 3-year-olds	10.0
	Cows	8.0
	Bulls or oxen	8.0

Offtake rates:

The overall offtake rate (expressed as a proportion of the initial total herd number) is:

Years 1-5:	11.0%
Years 6-8:	15.0%
Years 9-10:	11.0%

Cows are culled at an annual rate of 10% and mature males at 30%. Residual sales (required to obtain the offtake rate selected) are made up entirely of 2- to 3-year-old males.

Table 3.5 presents a simple herd projection model based on the information provided above. Note how the increase in offtake rate from year 6 progressively reduces herd size until the original rate is re-established in year 9. At this rate, herd size begins to grow again, but it will take five years to regain the level of years 1-5. We may assume that the reduction in net sales from year 9 onwards reflects a desire to prevent a further decline in herd size.

Exercise: (estimated time required: 1 hour).

Question 1. Using the same production parameters as in the example above, estimate total herd size and herd structure for years 11 and 12, assuming that the overall offtake rate remains at 11% from year 9 onwards.

Question 2. Compare your result with the original herd statistics.

3.6.3 Consumption response and market demand

Basic concepts guiding consumption response

In order to understand the factors affecting household consumption responses, it is first necessary to introduce a number of concepts from economic theory. Much of the economic theory of consumption is based on three key propositions. The first proposition is that the way in which people spend their incomes and consume commodities is not haphazard but has some underlying rationale which can be understood and predicted. We will deal with only one element of this proposition here - the relationship between the amount consumed and the satisfaction afforded. According to theory, for most commodities the amount of satisfaction per unit consumed diminishes with each additional unit. For example, one or two chocolates, mangoes or cigarettes are very enjoyable; above that number, each succeeding one gives less enjoyment.

Because the additional satisfaction a person gets with each unit tends to decline, he or she will be prepared to pay less in order to acquire the next unit, perhaps preferring to spend the money on some other commodity. For the first mango one will be prepared to pay 50 cents, for the second only 45 cents, for the third 40 cents and so on. If we aggregate all these preferences of individual consumers, we can construct a market demand schedule (market demand backed up by cash with which to pay). The imaginary schedule below shows how much of a commodity (say poultry) would be demanded at different prices, other things being equal:

Table 3.5. Projected herd numbers by category of stock: Pastoral example.

Year	Stock category1	Opening number	Births	Deaths	Net sales	Closing no. (year end)2	Opening no. (next year start)
1-5	0-1 y.o males		12	3		9
	0-1 y.o females		12	3		9
	1-2 y.o males	9		1		8	9
	1-2 y.o females	9		1		8	9
	2-3 y.o males	8		1	2	5	8
	2-3 y.o females	8		1		7	8
	>3 y.o males	12		1	4	7	12
	Cows	40		3	4	33	40
	Total	86	24	14	10	86	86
6	0-1 y.o males		12	3		9
	0-1 y.o females		12	3		9
	1-2 y.o males	9		1		8	9
	1-2 y.o females	9		1		8	9
	2-3 y.o males	8		1	5	2	8
	2-3 y.o females	8		1		7	8
	>3 y.o males	12		1	4	7	9
	Cows	40		3	4	33	40
	Total	86	24	14	13	83	83
7	0-1 y.o males		12	3		9
	0-1 y.o females		12	3		9
	1-2 y.o males	9		1		8	9
	1-2 y.o females	9		1		8	9
	2-3 y.o males	8		1	5	2	8
	2-3 y.o females	8		1		7	8
	>3 y.o males	9		1	3	5	7
	Cows	40		3	4	33	40
	Total	83	24	14	12	81	81
8	0-1 y.o males		12	3		9
	0-1 y.o females		12	3		9
	1-2 y.o males	9		1		8	9
	1-2 y.o females	9		1		8	9
	2-3 y.o males	8		1	6	1	8
	2-3 y.o females	8		1		7	8
	>3 y.o males	7		1	2	4	5
	Cows	40		3	4	33	40
	Total	81	24	14	12	79	79
9	0-1 y.o males		12	3		9
	0-1 y.o females		12	3		9
	1-2 y.o males	9		1		8	9
	1-2 y.o females	9		1		8	9
	2-3 y.o males	8		1	4	3	8
	2-3 y.o females	8	1		7	8
	>3 y.o males	5		1	1	4	7
	Cows	40		3	4	33	40
	Total	79	24	13	9	81	81
10	0-1 y.o males		12	3		9
	0-1 y.o females		12			9
	1-2 y.o males	9		1		8	9
	1-2 y.o females	9		1		8	9
	2-3 y.o males	8		1	3	4	8
	2-3 y.o females	8		1		7	8
	>3 y.o males	7		1	2	4	8
	Cows	40		3	4	33	40
	Total	81	24	14	9	82	82

¹ Herd projection models would normally exclude this column. It has been included to demonstrate the derivation of opening herd number statistics for each production year.

² y.o = year old.

Retail price	Quantity demanded
(cents/kg)	(t/year)
100	30,000
90	39,000
80	48,000
70	57,000
60	66,000
50	75,000
40	84,000

Such a relationship can be plotted graphically, and Figure 3.7 illustrates the general shape of the resulting demand curve. Market demand will be discussed further under the third key proposition.

The second proposition is that consumption patterns change in response to changes in income. These responses differ according to the nature of the goods in question and the income level of the consumer. As income rises, the rate of increase in demand for staple commodities tends to decline until a point of saturation is reached. When the consumption of a good increases at a rate below the rate of growth in income, that good is known as a relatively inferior good. If consumption declines in absolute terms as income increases, the commodity is known as an absolutely inferior good. This good is then replaced by others in the individual's budget. An example would be the replacement of maize or sorghum by wheat or wheat flour as incomes increase in urban areas. When the consumption of a good increases faster than the rate of income growth, that good is said to be a superior good. Examples in African urban areas include meat, milk and fish.

Two concepts are important to this discussion on the relationship between income and consumption: propensity to consume and income elasticity of demand. The average propensity to consume a commodity is the proportion of consumers' total incomes spent on that commodity. If total income is $ 1000, of which $ 500 is spent on grain, then the average propensity to consume grain is 0.5. A more useful term is the marginal propensity to consume (MPC). The MPC can be defined as the proportion of an additional dollar of income that is used to consume a given commodity.

Figure 3.6 illustrates the relationship between income, the consumption of food and non-food commodities, and savings. Up to the relatively low level of income indicated by point A, all income is spent on food. Both the average and the marginal propensity to consume are equal to 1. Between income levels A and B. MPC declines rapidly and an increasing proportion of income is spent on non-food commodities. At income levels above B. the MPC for food is practically zero and some income starts to be saved. However, the average propensity to consume food at income level B and above is still about 0.5.

Figure 3.6. The effect of income on consumption.

Table 3.6 presents empirical data from a rural household survey in Sierra Leone in 1977. The table shows typical shifts in the pattern of consumption associated with increases in rural income. Notice how the share of subsistence consumption declines as incomes increase. A higher proportion of income is allocated to urban-produced non-food goods within the higher income classes.

Table 3.6. Marginal propensities to consume by income class for commodities grouped by origin, Sierra Leone, 1977.

Origin classification	Marginal propensity to consume
	Income class
	Lowest decile	2nd & 3rd decile	4th & 5th deciles	6th & 7th deciles	8th & 9th deciles	Highest decile
Rural subsistence food products	0.684	0.588	0.49?	0.436	0.370	0.286
Rural purchased food products	0.153	0.178	0.201	0.218	0.235	0.257
All rural food products	0.837	0.765	0.698	0.654	0.605	0.543
Rural non-farm goods	0.013	0.012	0.011	0.011	0.010	0.009
Rural services and ceremonial	0.036	0.023	0.080	0.117	0.158	0.211
All rural products	0.814	0.801	0.789	0.782	0.773	0.763
Small urban products	0.034	0.043	0.061	0.066	0.062	0.069
Large urban products	0.019	0.019	0.020	0.020	0.021	0.021
Imported products	0.133	0.137	0.140	0.142	0.144	0.147
Total	1.000	1.000	1.000	1.000	1.000	1.000

Source: King and Byerlee (1977).

The second concept expressing the relationship between income and consumption (or demand) is the income elasticity of demand. This expresses the proportionate change in demand¹ in relation to a proportionate change in income, both changes expressed as percentages.

¹ Demand, defined as cash expenditure on a commodity, is easier to measure than physical consumption.

Thus:

An income elasticity of demand of 0.25 would mean that for every 1 % rise in income, demand for a given commodity would rise by 0.25%. Table 3.7 presents empirical data on the income elasticities of demand for livestock products and cereals in different parts of the world.

Table 3.7. Income elasticities of demand for livestock products and cereals, 1975.

Country group/Region	Meat	Milk	Eggs	Cereals
Developed economies1	0.25	-0.05	0.27	-0.22
Developing economies1	0.63	0.57	1.00	0.16
Africa	0.79	0.68	1.05	0.21
Asia and Far East	0.97	0.52	1.07	0.22
Near East	0.72	0.53	0.83	0.13
Latin America	0.37	0.49	0.60	0.16

Source: FAO (1978).

¹ Countries are grouped according to the classification system of the Food and Agriculture Organization of the United Nations.

The third key proposition is that consumption responds to changes in the price of a commodity. This response is measured by the price elasticity of demand, defined as follows:

For example, if the price of a product were to increase by 10%, resulting in a 1% decline in demand for it, the price elasticity of demand would be -0.1. Note that the sign is negative, indicating the normal inverse relationship between price and demand that exists for most products.

A price change will in fact have two separate effects on consumer demand for a product. These are known as the income effect and the substitution effect. The income effect of a price increase is to reduce the purchasing power of a given level of nominal income (all other things being equal). This means that, unless it is also a producing household, a consuming household will be unable to maintain previous consumption levels without sacrificing the consumption of other goods. The effect of a commodity price change on consumer's income will depend on the share of that commodity in total expenditure. Increases in the price of staple foods in third world countries will often have a significant effect by virtue of their high share in household expenditure (often greater than 60%). A change in the price of non-staple commodities such as beef and milk will have less effect.

A substitution effect occurs when a change in the price of a product alters the demand not only for that product but also for its substitute(s). An increase in the price of maize, for example, will tend to reduce the demand for maize and at the same time increase the demand for cassava and grain sorghum. Similar substitution effects occur in the livestock subsector, for instance between beef and other meat products. Under normal conditions, expenditures on most products accounts for only a small proportion of total income, so that substitution effects tend to outweigh income effects.

The demand response for the good in question is known as the own price effect, while that for its substitute(s) is called the cross price effect. These two effects are shown in Figure 3.7.

Consumption response of producing household

So far we have assumed that a household has a given income which is allocated between consumption and saving according to prevailing prices and individual preferences. This assumption does not apply to semi-subsistence households, where a portion of farm production is allocated to home consumption. In such cases, the producer price for a good moves with the consumer price, so that nominal total income is not predetermined (as consumption theory normally assumes). Rather, nominal income varies as producer prices vary.

Figure 3.7. Own and cross price effects on consumption response.

a) Own price effect

b) Cross price effect

For example, a rise in the consumer, and hence the producer, price of meat increases the value of meat output and therefore the value of total farm income. This increase may encourage the household to consume more meat, a response which could be called the producer income effect and which will normally be positively related to price changes. The household will also be aware that each unit of meat consumed has become more expensive - either, in the case of a surplus-producing household, because of the extra market income foregone or, in the case of a deficit household, because the costs of purchasing additional meat at market have gone up. In the latter case, the household is negatively affected by the price increase in the same way as the non-producing household.

Thus, for a subsistence commodity, the overall income effect of a price change (i.e. whether it is positive or negative) will depend on the commodity's share in the total value of farm output as well as its share in total consumption. When the share in total cash income is high, but the share in consumption is low (as is the case for beef in the typical agropastoral household), the positive effect of a price increase on producer income will often more than compensate for the negative effect on consumption.

The examples given in Exercises 3.5 and 3.6 show how to calculate income and price effects on consumption.

Consumption response of non-producing household

Two additional points need to be made with respect to the consumption response of non-producing households. Specifically:

· Increases in the price of food have a direct depressive effect on consumption in urban households because a decline in real income is not partially offset by an increase in producer income (the reverse is also true).

· In most African countries, inequalities of income are more pronounced in urban than in rural areas.

Box 3: Equity and the urban consumer. Increases in food prices have a serious impact on the urban poor. For example, a 10% increase in the price of food led to a 9% reduction in the real income of the lowest decile urban income group in Nigeria. For the highest decile group, however, the increase resulted in only a 5.7% decline in real income. The difference reflects the proportion of income allocated to food consumption within each group. In the former group, between 60 and 80% of total income was spent on food; in the latter group, the proportion was much smaller. The composition of commodities in the city dweller's "food basket" changes as income rises. Figure 3.8 depicts the typical pattern of change according to FAO data for a number of developing countries. The figure shows how the relative share of animal products increases rapidly as incomes increase. In other words, the income elasticity of demand for such products is high. Figure 3.8. The effect of income on diet schematised: Percentage of total calories derived from fats, carbohydrates and proteins, by annual per caput GNP. Note: The figure is drawn in semi-logarithmic scale. Source: Perisse et al (1969). While the response to a price change for livestock commodities is likely to be elastic, the effect of such a change on real income will tend to be small in most African countries, because the proportion of income devoted to livestock commodities is still low. In contrast, a change in consumer prices for staples will have a pronounced effect on income, particularly for the poor. This will often be an important consideration when evaluating the equity effects of a price policy.

3.6.4 Relevant exercises

Exercise 3.5: The effect of income changes on food consumption.

Example: Refer again to the agropastoral example given in Exercises 3.1 to 3.3. Assume this time that increases in crop and/or livestock production have resulted in a 10% increase in real income.

The income elasticities of demand for the various food items consumed by this household are:

Maize	+ 0.1
Beans	+ 0.4
Groundnuts	+ 0.4
Sorghum	+ 0.1
Milk	+ 1.0
Meat	+ 1.0

Income increases also affect demand for non-food items, but these will be ignored in this example.

The effect on the demand for food can be summarised as follows:

Commodity	Income elasticity of demand	% change in consumption	Original consumption level (kg)	Extra amount consumed (kg)	New consumption level kg
Maize	0.1	+1.0	1160	+11.60	1171.6
Beans	0.4	+4.0	90	+3.60	93.6
Groundnuts	0.4	+4.0	95	+ 3.80	98.8
Sorghum	0.1	+1.0	325	+3.25	328.3
Milk	1.0	+10.0	150	+ 15.00	165.0
Meat	1.0	+10.0	20	+ 2.00	22.0

Note: Consumer and producer prices used for the agropastoral example do not correspond.

Exercise: (estimated time required: 1 hour).

Question 1. Using the small-scale dairy farm model in Exercises 3.1 to 3.3 and assuming a 15% increase in real income resulting from improved productivity, calculate consumption changes for the following commodities consumed by the household:

Commodity	Income elasticity of demand
Maize	0.12
Beans	0.45
Groundnuts	0.45
Beef	1.20
Milk	1.10

Note: Use the estimates you obtained for consumption in Exercise 3.2 as the basis for calculating consumption changes.

Question 2. Rank the following consumer commodities according to their probable income elasticities of demand for a middle-income and a high-income rural household, respectively, in an African country of your choice (commodities may be grouped together if necessary). State the reasons for your ranking.

Maize	Eggs
Sorghum	Fish
Millet	Oils and fats
Rice	Hotel drinks
Pulses	Sugar
Meat	Clothing

Exercise 3.6: The effect of price changes on food consumption.

Example: Table 3.8 summarises cash expenditure for an urban middle-income household.

Table 3.8. Cash expenditure for a middle-income urban household.

Item/commodity		Amount consumed (kg)	Value of consumption ($)
Food expenditure
	Maize	1100	55.00
	Milk	400	24.00
	Meat (CDW1)	60	21.00
	Sugar	50	5.00
	Vegetables	200	20.00
	Beverages	n.a.	30.00
Total food expenditure		n.a.	155.00
Non-food expenditure		n.a.	250.00
Total consumption expenditure		n.a.	405.00
Total savings		n.a.	45.00
Total cash income		n.a.	450 00

¹ CDW = cold dressed weight (for the relationship between dressing out percentage, CDW and price, see box, Exercise 4.1).

n.a. = not applicable.

Holding total cash income and non-food prices constant, let us examine the impact of price changes for selected food commodities on total cash expenditure and total savings. Commodity price changes have occurred as shown in the following table:

Commodity	Original price (cents/kg)	New price (cents/kg)	Price change (%)	Price elasticity of demand
Maize	5.0	6.0	+20	-0.1
Milk	6.0	5.4	-10	-1.2
Meat1	35.0	38.5	+10	-1.2
Sugar	10.0	10.0	0	-0.2
Vegetables	10.0	13.0	+30	-0.5

¹ CDW.

Given the above data, changes in total cash expenditure on food, in total savings and in total income will be as follows:

Item/commodity		Original consumption level (kg)	% change in consumption	New consumption level (kg)	New value of consumption($)
Food expenditure
	Maize	1100	-2	1078.0	64.60
	Milk	400	+12	448.0	24.19
	Meat1	60	-12	52.0	20.33
	Sugar	50	0	50 0	5 00
	Vegetables	200	-15	170.0	22.10
	Beverages	n.a.	n.a.	n.a.	30.00
Total food expenditure					166.30
Non-food expenditure					250.00
Total consumption expenditure					416.30
Total savings					33.70
Total cash income					450.00

¹ CDW.
n.a. = not applicable.

Price increases for maize, meat and vegetables have resulted in a decline in their amounts consumed, accompanied by an increase in expenditure on maize and vegetables. A decline in the price of milk has resulted in an increase in the amount consumed and a marginal increase in cash expenditure for that commodity. Savings have declined by approximately 25% because of a 7% increase in the amount spent on food.

Note that this analysis has not taken into account the substitution effect. In this exercise, we are merely concerned with own price demand responses and have assumed a zero cross elasticity of demand between the goods consumed.

Exercise: (estimated time required: 1 hour).

The following table summarises data on cash expenditure, savings and total cash income for a low-income urban household:

Item/commodity		Amount consumed (kg)	Current value ($)
Food expenditure
	Maize	1300	65.00
	Milk	100	6.00
	Meat1	70	24.50
	Sugar	40	4 00
	Vegetables	200	20.00
	Beverages	n.a.	15.00
Total food expenditure		n.a.	134.50
Non-food expenditure		n.a.	150.00
Total consumption expenditure		n.a.	284.50
Total savings		n.a.	15.50
Total cash income		n.a.	300.00

¹ CDW.
n.a. = not applicable.

Question 1. Examine the impact on food consumption, cash expenditure and household savings (assuming that non-food expenditure and total cash income remain constant), given the following information:

Commodity	Original price (cents/kg)	New price (cents/kg)	Price elasticity of demand
Maize	5.0	7.0	-0.1
Milk	6.0	6.6	-1.4
Meat1	35.0	28.0	-1.3
Sugar	10.0	12.0	-0.6
Vegetables	10.0	15.0	-0.9
Beverages	no price change throughout

¹ CDW.

Question 2. Comment briefly on the results obtained. Pay particular attention to changes in the savings level.

3.6.5 Supply response

Individual supply response

Market supply response (as opposed to production response) can be considered as the residual of other responses to price changes. The response can be computed as follows: market supply response = production response - net stock increase - home consumption response

It is not possible to draw specific conclusions about the nature of supply response to price signals without reference to empirical data. However, as a general rule, the market supply response for most products is positively related to output prices and negatively related to input prices. Figure 3.9 provides an example from semi-subsistence agriculture. (The figure ignores changes in net stock levels). Production responds positively and consumption negatively to a price increase. Above the threshold price, where production equals consumption, this household produces a market surplus, i.e. net supply (production minus home consumption) is positive. Below the threshold price, the residual is negative, i.e. there is a household deficit or net market demand (shown on the left hand side of the figure).

Figure 3.9. Net supply/net demand function as a residual of production and consumption in a semi-subsistence household.¹

¹ For simplicity, it is assumed that consumer and producer prices are identical.

Returning to the agropastoral example, assume a case in which a portion of annual herd offtake is consumed at home and the remainder is sold. A relative decline in the price of beef might persuade the producer to increase offtake for sale (i.e. reduce herd size), in order both to increase average herd productivity so as to maintain revenue above cost, and to transfer resources into other enterprises. Beyond a certain point, however, further sales would force a decline in home consumption of beef. The retail price at market would now become the basis for valuing beef output. This change from farm gate to retail price might dissuade the producer from further reducing herd size.

Aggregate supply response

So far we have discussed how price changes influence individual farmers, but not how to assess their influence on production and supply as a whole. From a policy perspective, it is the aggregate rather than the individual supply response which is of concern. In practice it would be impossible to obtain the aggregate response at the national level by predicting and summing all individual responses. Instead, analysts tend to rely on sectoral statistics of market supplies to estimate supply responses. The data obtained can then be related to other time series or cross sectional data in order to establish explanatory relationships.

However, because the results of aggregate response estimates tend to be mathematically and practically unreliable, an understanding of how individual farmers are likely to respond is essential. Extrapolations from individual to aggregate responses form a useful comparison with aggregate responses derived from sectoral data.

When extrapolations of this kind are made, remember that not all producers will be able to respond as they wish to, so that aggregate response will always be less than the intended responses of all individuals summed. This is because increased competition for resources constrains individual responses, since input prices may rise and pasture, water or other resources may become scarce.

(Hint to instructors: When assessing aggregate response, be careful not to double count by attributing the same production gain to more than one stage in the production chain e.g. breeder, stock-feeder, fattener.)

The direction and intensity of an aggregate supply response is measured by the price elasticity of supply, calculated as follows:

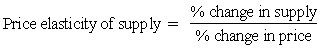
Empirical estimates of supply elasticity are rare for African livestock production systems, largely because of problems in data collection. Table 3.9 summarises data on livestock supply responses recorded in Africa and Latin America. The table demonstrates that while supply elasticities may be negative or very low in the short term, they tend to be both higher and positive in the longer run.

Table 3.9. Livestock supply elasticities: Country examples.

Product	Country	Price elasticity
		Short run	Long run
Beef	Latin America	-0.1 to -1.2	0.4 to 1.6
Beef stock	Botswana	0.3	2.6
Beef (commercial)	Zimbabwe	-0.5 to -0.6	2.6
Beef (communal)	Zimbabwe	-0.3	n.a.
Cattle	Swaziland	-1.1	n.a.
Cattle	Sudan	1.1	n.a.

Source: Rodriguez (1985; 1986).

Market equilibrium and market price

We have now examined the concepts of a supply curve, which relates the quantity of a commodity supplied to price, and a demand curve, which relates the quantity demanded to price. Neither of these curves tell us what a price will actually be. They are much like conditional sentences: "If the price is W then the amount supplied will be X."; "If the price is Y then the amount demanded will be Z." In this section we will discuss how market prices are determined by the relationship between the two curves, assuming an open economy as the basis for discussion.

The columns below set out demand and supply schedules for a given commodity, in this case poultry meat. These columns provide the raw material for our supply and demand curves.

Supply schedule		Demand schedule
Producer price (cents/kg)	Amount supplied (t)	Retail price (cents/kg)	Amount demanded (t)
80	75,000	100	30,000
70	69,000	90	39,000
60	63,000	80	48,000
50	57,000	70	57,000
40	51,000	60	66,000
30	45,000	50	75,000
20	39,000	40	84,000

The prices in these supply and demand schedules are recorded at different points of sale. It is the price paid to the producer at the point where he or she sells (the farm gate or primary market) that determines how much he or she will supply, and hence the supply schedule. It is the price paid by the consumer at the point where he or she buys (in the market place or the retail shop) that determines how much he or she will demand, and hence the demand schedule. Only rarely, in large modern economies, do farmers sell directly to the consumer, such that the price the consumer pays is the price the farmer receives. Normally, transport costs, taxes, traders' and butchers' costs and margins fill the gap between the producer price and the consumer (retail) price.

In order to relate the supply and demand schedules to each other, we need to use a common price. For simplicity, assume there is a uniform gap of 20 cents/kg between the producer and consumer prices in the schedules given above. We can either deduct this from consumer prices or add it to producer prices, obtaining either derived consumer prices or derived producer prices, respectively. Below are the poultry meat supply and demand schedules, harmonised at a common derived retail price.

Quantity supplied (t)	Derived retail price (cents/kg)	Quantity demanded (t)
75,000	100	30,000
69,000	90	39,000
63,000	80	48,000
57,000	70	57,000
51,000	60	66,000
45,000	50	75,000
39,000	40	84,000

What will the market retail price actually be? Assume that supply and demand can respond instantaneously to price. Suppose the price is 80 cents/kg. At that price, producers will be prepared to supply 63,000 t but consumers will only demand 48,000 t. The price would have to fall to about 60 cents/kg to persuade consumers to buy it all. But at 60 cents/kg, producers will be prepared to supply only 51,000 t, which will not be enough to meet demand. As a result, consumers will start competing with each other by offering a higher price. At 70 cents/kg, the amount supplied (57,000 t) will be equal to the amount demanded. That is the equilibrium price at which the market will settle; at all other prices, either producers or consumers will be dissatisfied and will adjust their supply or demand.

3.6.6 Relevant exercises

Exercise 3.7: Supply, demand and market equilibrium.

Example: Given below are (imaginary) supply and demand schedules for beef, unadjusted for derived prices:

Supply schedule		Demand schedule
Producer price (cents/kg)	Amount supplied (t)	Retail price (cents/kg)	Amount demanded (t)
35	50,000	45	17,000
30	45,000	40	23,000
25	40,000	35	29,000
20	35,000	30	35,000
15	30,000	25	41,000
10	25,000	20	47,000

Exercise: (estimated time required: 1.5 hours).

Question 1. Draw up the schedules again, using a marketing margin which is fixed at 10 cents/kg.

Question 2. Draw the supply and demand curves. Do they cross one another? If so, what price will the consumer actually pay at the point of intersection?

Question 3. In the text we assumed that supply and demand respond instantaneously to price changes. Now suppose that demand adjusts instantaneously but that it takes two years before producers can adjust their supply to each price change. What effect will this have on reaching market equilibrium?

Question 4. If a government controls retail prices at a level lower than equilibrium, what will this do to the quantities demanded and supplied? What is likely to happen as a result?

Important points (3.6) Production response The production response to price may be neutral, negative or positive. However, with increased integration to a market economy, positive responses are more common over the long term. · A long-term production response is, in some situations, associated with a negative short-term market supply response, · An increase in the price of a product will affect production through one or more of the following adjustment mechanisms: - utilising slack resources - substituting enterprises - intensifying production. · The decision to substitute one enterprise for another depends on their relative profitability measured in terms of the gross margin, expressed as: · Gross margin = gross value of output - variable costs · The profitability of adopting intensified methods will depend on three main factors: - The marginal physical productivity (MPP) of the inputs used, i.e. output per additional unit of input. - The marginal revenue (MR) generated by each extra unit of output. When MPP is multiplied by MR, we get the marginal value product (MVP). - The marginal factor cost (MFC) per unit of input used. · To maximise profits through intensification, one can use extra inputs so long as MVP exceeds MFC. Consumption response · Three key propositions of the economic theory of consumption are: - For most commodities, the amount of satisfaction per unit consumed diminishes with each additional unit. - Consumption patterns change in response to change in income. Consumption responses will differ according to the nature of the good in question and the income level of the consumer. - Consumption responds to changes in the price of the commodity. · Two important concepts to express the relationship between income and consumption - marginal propensity to consume - elasticity of demand. · The marginal propensity to consume is defined as the proportion of an additional dollar of income that is used to consume a given commodity. The income elasticity of demand expresses the proportional change in demand in relation to a proportional change in income, both changes being expressed as percentages. Thus: · The consumption response to change in commodity price is measured in terms of price elasticity of demand, defined as: · A change in the price of a commodity has two separate effects on consumer demand: income effects and substitution effects. · The income effect of a price rise is to reduce the purchasing power of a given level of income. A substitution effect occurs when a change in the price of a product alters the demand not only for that product but also for its substitute. · The demand response for the good in question is known as the own price effect, while that for its substitute(s) is called the cross price effect. · A rise in the price of a food commodity will have a direct depressive effect on its consumption in urban households. The effect of price rise on consumption in producing households will depend on the commodity's share in the total value of farm output as well as its share in total consumption. · Long-term market supply response for most products is directly related to output price and negatively related to input price. Supply response · Market supply response is the residual of the production and consumption. It expressed as: Market supply response = production response - net stock increase - home consumption response · From a policy perspective, it is the aggregate rather than the individual supply response which is of concern. The aggregate response is estimated on the basis of sectoral statistics on market supplies. · The direction and intensity of a given supply response is measured by its supply elasticity, calculated as: · The supply schedule of a product is related to producer price while the demand schedule is related to retail price. The difference between the two is called marketing margin. Common derived prices are used as the basis for relating supply with demand. · The market equilibrium price is that price at which the supply and demand curves intersect, It occurs at that price where quantity demanded is exactly equal to quantity supplied or, put another way, at that price at which consumers are willing to buy all the producer offers for sale.