La mayor parte de las magnitudes que aparecen en la investigación pesquera no pueden ser observadas o medidas directamente para el conjunto de la población; por ejemplo, es virtualmente imposible medir todos los peces capturados y, aún menos, todos los peces que existen en el mar. Se hace preciso, por tanto, examinar una parte o muestra de la población para deducir las características que la definen, por ejemplo, el porcentaje de peces maduros, o la talla media. Suponiendo que esta muestra viene a ser una representación del conjunto de la población, se puede hacer una estimación de los valores verdaderos en la población. Si se ha empleado un buen sistema de muestreo, entonces las estimaciones realizadas diferirán poco de los valores verdaderos. Precisamente, el propósito de este manual es exponer métodos para el desarrollo de sistemas adecuados de muestreo para la deducción de las magnitudes de mayor interés en la? investigaciones de biología pesquera.
Ejemplo 1.2.1
Ejemplo 1.2.2
Ejemplo 1.2.3
Ejemplo 1.2.4
Ejemplo 1.2.5
Ejemplo 1.2.6
Antes de entrar en la materia, es necesario describir algunos de los conceptos básicos de la teoría del muestreo. La estadística versa sobre las propiedades numéricas de los conjuntos (o poblaciones) de objetos. Tales poblaciones pueden ser realmente biológicas, como los Rastrelliger del océano Indico, o conjuntos de medidas concretas, como, por ejemplo, una serie de temperaturas, o las estimaciones posibles de una cantidad (por ejemplo, la longitud media de los peces) obtenidas a partir de un determinado sistema de muestreo. Así resulta que las medidas que se hacen sobre una población (longitudes de peces) pueden constituir por sí mismas a su vez otra población (cuando se calcula la longitud media). Cada miembro de una población (un pez) tiene un valor numérico (su longitud), que se llama la variable, y ha de pertenecer a un intervalo de valores posibles. De esta manera, una población puede ser descrita por la frecuencia con que cada valor posible aparece. A esta representación se le llama una distribución de frecuencias, que puede ser, o bien discontinua, cuando sólo son posibles ciertos valores, como los de 1, 2, 3, 4, 5, ó 6 que proporciona un dado, o bien continua, cuando, al menos dentro de un intervalo, pueden darse todos los valores; por ejemplo, las longitudes de los peces. A menudo, la distribución se representa gráficamente, ya sea por medio de un histograma o por un polígono de frecuencias, pero, a este efecto, los valores de las variables continuas se suelen agrupar. La altura de cada punto de un polígono de frecuencias vendrá determinada por la frecuencia; por ejemplo, el número de individuos de un cierto valor o que se producen en un determinado intervalo (en cuyo caso se toma el punto medio del intervalo); en el caso de un histograma, la frecuencia en el intervalo viene expresada por el área de cada sección, pudiéndose usar diferentes clases de intervalos, como, por ejemplo, de 1 cm para los peces pequeños, y de 5 cm para los grandes.
Para la distribución de frecuencias de longitudes del bacalao del Mar del Norte (tomado de Russell, 1922), colóquense los datos siguientes a modo de un polígono de frecuencias y de un histograma, primero tal como están dados los datos (en intervalos de 1 cm), y luego agrupados, por ejemplo, cada 2 cm, 3 cm, 5 cm, 10 cm y 20 cm.
|
Long. |
Frec. |
l |
n |
l |
n |
l |
n |
l |
n |
l |
n |
|
25 |
2 |
39 |
18 |
53 |
15 |
67 |
- |
81 |
- |
95 |
- |
|
26 |
7 |
40 |
15 |
54 |
8 |
68 |
- |
82 |
2 |
96 |
- |
|
27 |
8 |
41 |
13 |
55 |
6 |
69 |
- |
83 |
1 |
97 |
- |
|
28 |
9 |
42 |
13 |
56 |
11 |
70 |
1 |
84 |
- |
98 |
- |
|
29 |
13 |
43 |
19 |
57 |
7 |
71 |
1 |
85 |
- |
99 |
- |
|
30 |
12 |
44 |
19 |
58 |
4 |
72 |
- |
86 |
1 |
100 |
- |
|
31 |
9 |
45 |
21 |
59 |
5 |
73 |
1 |
87 |
1 |
101 |
- |
|
32 |
15 |
46 |
13 |
60 |
1 |
74 |
- |
88 |
- |
102 |
1 |
|
33 |
7 |
47 |
19 |
61 |
2 |
75 |
- |
89 |
- |
103 |
- |
|
34 |
7 |
48 |
21 |
62 |
1 |
76 |
- |
90 |
- |
104 |
- |
|
35 |
5 |
49 |
8 |
63 |
2 |
77 |
1 |
91 |
- |
105 |
- |
|
36 |
12 |
50 |
22 |
64 |
- |
78 |
1 |
92 |
1 |
|
|
|
37 |
13 |
51 |
18 |
65 |
- |
79 |
- |
93 |
- |
|
|
|
38 |
16 |
52 |
18 |
66 |
2 |
80 |
1 |
94 |
- |
TOTAL: 449 | |
Trácese también un histograma utilizando un agrupamiento menos sutil (por ejemplo, 10 cm contra 2 cm), para los peces de más de 60 cm.
Compárese el agrupamiento usando diferentes puntos para esta operación, por ejemplo, para un agrupamiento de 5 en 5 cm, los grupos 25-29, 30-34, etc., o bien 27-31, 32-36, etc.
El trazado de las gráficas debe hacerse a la misma escala efectiva; si se usan intervalos de 2 cm, las frecuencias para cada intervalo serán dobles que si son de 1 cm y, por lo tanto, la escala deberá ser la mitad; por ejemplo, si en el intervalo de 1 cm empleamos 10 unidades del papel para gráficas para significar la unidad de frecuencia, cuando usamos los intervalos de 2 cm esta misma frecuencia deberá estar representada por 5 unidades del papel. Es decir, la longitud de la escala deberá quedar inalterada. Colocando de esta manera varios polígonos e histogramas, resultarán casi idénticos.
Emplearemos el mismo ejemplo para considerar la elección correcta de la clase de intervalo. En este caso, el intervalo de 1 cm resulta ínfimo, y produce mucho trabajo en los cálculos, en la escritura, etc. Los valores que se dan son sólo una muestra de una cantidad mucho mayor de datos, por lo que fácilmente puede suponerse que las irregularidades que aparecen entre grupos contiguos son puramente casuales. Posiblemente una excepción sea el máximo en 50 cm y la baja frecuencia en 49 cm, lo que también aparece, aunque menos marcado, en la serie completa de datos. Este fenómeno bien puede ser debido a una tendencia inconsciente a redondear las medidas, de modo que varios peces que en realidad tenían 49 (o 51) cm fueron medidos como de 50 cm.
La mejor forma de agrupamiento - seguramente en el ejemplo de cada 3 ó 5 cm - dependerá de los mismos datos; cuanto mayor sea la cantidad de datos y más compleja la distribución de frecuencias tanto más numerosos y sutiles serán los intervalos. Una buena regla consiste en considerar que el número máximo normal de intervalos es de unos 20, y que, excepto para unos pocos intervalos de los extremos de la distribución, la cantidad en cada intervalo no debe ser mucho menor de 10.
En el siguiente cuadro (tomado de Fitch, 1958) se da la composición de tallas de la caballa del Pacífico capturada en aguas de California en los años 1956-57.
|
l = longitud, en cuartos de centímetro; n = número de peces | |||||||||
|
l |
n |
l |
n |
l |
n |
l |
n |
l |
n |
|
80 |
|
95 |
6 |
110 |
25 |
125 |
19 |
140 |
13 |
|
81 |
|
96 |
|
111 |
24 |
126 |
26 |
141 |
16 |
|
82 |
|
97 |
9 |
112 |
24 |
127 |
13 |
142 |
15 |
|
83 |
1 |
98 |
6 |
113 |
28 |
128 |
22 |
143 |
8 |
|
84 |
|
99 |
10 |
114 |
31 |
129 |
17 |
144 |
5 |
|
85 |
|
100 |
21 |
115 |
19 |
130 |
24 |
145 |
3 |
|
86 |
|
101 |
13 |
116 |
24 |
131 |
20 |
146 |
11 |
|
87 |
1 |
102 |
14 |
117 |
25 |
132 |
14 |
147 |
2 |
|
88 |
1 |
103 |
16 |
118 |
30 |
133 |
18 |
148 |
6 |
|
89 |
2 |
104 |
22 |
119 |
30 |
134 |
27 |
149 |
|
|
90 |
2 |
105 |
33 |
120 |
17 |
135 |
16 |
150 |
|
|
91 |
1 |
106 |
24 |
121 |
28 |
136 |
20 |
151 |
2 |
|
92 |
3 |
107 |
21 |
122 |
31 |
137 |
15 |
153 |
1 |
|
93 |
1 |
108 |
23 |
123 |
16 |
138 |
16 |
154 |
1 |
|
94 |
6 |
109 |
31 |
124 |
28 |
139 |
13 |
156 |
1 |
|
|
|
|
|
|
|
|
|
TOTAL 1011 | |
Colóquense estos datos en un histograma.
Repítase usando grupos de 1/2, 1 y 2 cm.
Muchas distribuciones de frecuencias, al ser representadas gráficamente, presentan máximos con oscilaciones más o menos amplias por encima o por debajo de estos máximos. La diferencia más esencial entre las distribuciones consiste en la diversa posición de dichos máximos (por ejemplo, el máximo en el Ejemplo 1.2.1 se encuentra entre 40 y 50 cm y en la parte que se extiende por encima y por debajo del máximo). Para determinar la posición de la distribución, se suelen emplear una o más de tres cantidades. La de uso general es la media aritmética, o simplemente la media, que generalmente se representa por una m.
Supongamos que han sido medidos 10 peces, de tallas 15, 19, 17, 22, 14, 13, 18, 17, 16 y 18 cm; entonces
Esto se puede escribir de una forma más general llamando x a la longitud del pez, y añadiendo un sufijo para denotar la longitud de peces determinados; en el ejemplo anterior x1 = 15, x2 = 19, etc., y entonces
Aún mejor, podemos representar por xi la longitud de un pez cualquiera, siendo i uno de los valores, 1, 2, 3,... 10 y m = 1/10 (Suma de los xi cuando i = 1, 2... 10). Matemáticamente esto puede abreviarse usando el símbolo S en vez de suma de, y poniendo los valores extremos de i arriba y abajo del símbolo S, tal como
De la misma manera que el símbolo Ö indica que debe tomarse la raíz cuadrada del número que sigue a continuación, el símbolo S se refiere a lo que debe hacerse con los números que, le siguen, esto es, sumarlos todos desde el término inicial al final, según se indica con los números colocados arriba y abajo del símbolo S.
Con frecuencia, esta expresión aún se abrevia más suprimiendo las i de los valores extremos, cuando, como ocurre corrientemente, es obvio que i toma los valores, en este ejemplo, de 1 a 10
o bien, más abreviada, cuando se sobreentienden fácilmente cuáles son estos límites
De la misma manera, si deseamos escribir una expresión de la media para un número indeterminado de términos, indicamos con n dicho número (en el ejemplo anterior n = 10), esto es
o
o
............................(1.1)
También se usa la moda, o el valor en el cual se produce uno (o varios) máximos de frecuencia, y la mediana, o punto del 50 por ciento, que es un valor tal que en la población hay igual número de individuos de los que valen más como de los que valen menos. En la mayor parte de las distribuciones, la mediana queda entre la moda y la media, algo más cerca de esta última (como sugiere la disposición de las palabras en un diccionario). La moda tiene sus mejores aplicaciones en las distribuciones complejas con varios máximos, por ejemplo, en la composición de longitudes de la captura de peces que pertenecen a varias clases anuales. En estos casos, la media aritmética puede tener mucha menos importancia que los valores de cada moda, que, por ejemplo, pueden representar las longitudes de cada clase anual. La forma más sencilla de determinar la moda o modas consiste en colocar los datos en forma de histogramas o de polígono de frecuencias, pudiendo leer los valores en la curva trazada. Las formas de estas distribuciones suelen quedar muy afectadas por las variaciones al azar de los datos, de modo que son precisas muestras muy numerosas para determinar las modas con alguna precisión.
La mediana queda menos afectada por los errores al azar que la moda, aunque más que la media, que es la que con mayor precisión da la medida de la posición de la distribución. Sin embargo, cuando los datos no han sido agrupados, o lo han sido de una manera sutil, la mediana puede ser calculada rápidamente. En el caso de que no hayan sido agrupados, la estimación de la mediana vendrá dada por el miembro central, si el número de la muestra es impar, o por valor intermedio entre los dos miembros centrales, si es par. Cuando los datos han sido agrupados, puede hacerse una estimación aproximada de la mediana tomando el punto medio del intervalo en que se encuentra el miembro central; más precisamente, está dado por una proporción dentro de este intervalo. Por ejemplo, en una muestra de 101 peces, 40 tienen una longitud inferior a 16 cm, 15 están entre 16/17 cm y 46 miden más de 17 cm. El miembro central estará en el grupo de los que miden 16/17 cm, y será el décimo empezando por los más pequeños, de modo que la estimación de la mediana será 16 + 10/15 = 16,7 cm
Estímense la media, la mediana y la moda de la distribución del Ejemplo 1.2.1. Compárese el tiempo requerido para estimar cada cantidad.
La mediana vendrá dada por el 225° pez, colocados éstos por orden ascendente o descendente de tamaños, y que, por consiguiente, pertenece al grupo de 44 cm. Si los peces han sido medidos agrupándolos en el centímetro más próximo, de modo que este grupo contiene peces que miden de 43,5 cm hasta 44,5 cm, una estimación más precisa de la mediana será
43,5 + 12/19 = 44,1 cm
(Obsérvese que la mediana puede ser estimada haciendo la proporción tanto a partir del pez más pequeño como del más grande, siendo conveniente confrontar ambas estimaciones.)
Existe una moda definida sobre el valor de 30 cm, y otras probables alrededor de 40 y 50 cm.
Repítase el Ejemplo 1.2.3, usando los datos del Ejemplo 1.2.2, tal como están dados, y en grupos de 1/2 y 1 cm. Compárese la estimación realizada de la posición de las modas con el hecho de que los datos originales proceden de peces pertenecientes a clases de 6 años, siendo aproximadamente las longitudes medias de las clases anuales de 21 cm (sólo cuatro peces), 27,5 cm, 31 cm, 33,5 cm y 38 cm (sólo tres peces).
La media (o la moda o la mediana) dicen cuál es la posición de la distribución - qué es el valor medio (o el más frecuente o central) de los individuos; por ejemplo, las longitudes del bacalao en el Ejemplo 1.2.1 están centradas alrededor de 50 cm. También se desea conocer cómo varían estas longitudes con respecto al valor central - si todas las longitudes de peces quedan entre 49 y 51 cm, o si, como en el ejemplo, varían entre 25 y 100 cm, o entre 5 y 150 cm. Si se toman las diferencias entre los valores individuales y la media, algunas serían positivas y otras negativas, y, por tanto, el promedio de todas será de aproximadamente cero. Por ello se suele tomar el cuadrado de la diferencia entre el valor individual y la media, y al valor medio de estos cuadrados se le llama variancia. Así, un grupo de 10 peces del Ejemplo 1.2.1 tiene las longitudes de
35, 38, 40, 44, 45, 47, 50, 52, 53 y 66 cm
La longitud media es de 47 cm; las diferencias individuales con respecto a la media son
-12, -9, -7, -3, -2, 0, +3, +5, +6 y +19 cm
de modo que la variancia de la población formada por las longitudes de este pequeño grupo de peces será
La raíz cuadrada de la variancia, que viene a ser un valor medio de las desviaciones con respecto a la media, se llama desviación típica. La desviación típica de la población anterior es 8,45 cm.
En términos matemáticos, la variancia se representa generalmente por S2, y la fórmula para la variancia es
.....................................(1.2)
donde M es la media de la población y N el número total en la población. Si se tiene una muestra de n individuos de una población, la estimación de la variancia será1
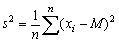
1 Es preciso señalar que, en la teoría estadística, es de importancia fundamental la distinción entre los valores de los parámetros (media, variancia, etc.) de las verdaderas poblaciones y los valores que resultan de las estimaciones realizadas a través de las muestras. En la mayor parte de los libros de texto, para distinguirlos, se usan letras griegas para los valores de la población, y latinas para las estimaciones. En aplicaciones sencillas se puede ignorar esta distinción, pero en este caso era preciso tenerla en cuenta.
Sin embargo, normalmente la verdadera media de la población, M, no es conocida, y se debe emplear la media m de la muestra. La estimación de la variancia será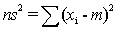 ; reescribiendo cada elemento de la suma en términos de M, se tiene
; reescribiendo cada elemento de la suma en términos de M, se tiene
Esta expresión es simplemente la suma de una serie de términos, que, agrupados en una forma ligeramente diferente, se transforma en esta otra
En el segundo término, el factor 2 (M - m) es común para todos los elementos de la suma, así que puede sacarse y, en el tercer término, todos los elementos son iguales, habiendo n de ellos, de modo que la expresión puede escribirse
y como (m - M)2, por ser un cuadrado, debe ser siempre positivo (o cero si m fuera exactamente igual a M), entonces 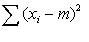 será siempre menor, o igual, que
será siempre menor, o igual, que 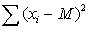 .Por tanto,
.Por tanto, 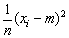 será menor que
será menor que 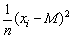 , y dará lugar a una estimación baja y sesgada de la variancia, que puede ser exactamente corregida dividiendo no por n, sino por n - 1, como puede demostrarse matemáticamente. Así pues, las estimaciones no sesgadas de la variancia se obtienen por medio de la fórmula
, y dará lugar a una estimación baja y sesgada de la variancia, que puede ser exactamente corregida dividiendo no por n, sino por n - 1, como puede demostrarse matemáticamente. Así pues, las estimaciones no sesgadas de la variancia se obtienen por medio de la fórmula
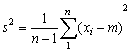 .......................................(1.3)
.......................................(1.3)
Las fórmulas de la media y de la variancia pueden ser escritas de varias maneras con objeto de simplificar las computaciones. Reescribiendo la fórmula de la variancia tenemos que
que también puede ser puesta como que
o
...............................(1.4)
La fórmula (1.4) es muy útil cuando se dispone de una máquina de calcular que permita cálculos rápidos de sumas de cuadrados. Si las computaciones se disponen de una manera adecuada, entonces llegan a ser en una gran extensión autocomprobantes. Primero debe calcularse S xi y la media. Luego colocar x1 en el registrador y elevarlo al cuadrado, de modo que en el resultado del registrador aparezca x12, y en el registrador del multiplicador x1. Sin borrar estas entradas, poner x2 y elevarlo al cuadrado, de modo que en los resultados del multiplicador aparezcan xi2 + x22 y xi + x2 respectivamente. Repitiéndose esto para los n números, se obtiene finalmente S xi2 y S xi debe comprobarse que S xi concuerda con el valor ya obtenido, lo que permitirá detectar la mayor parte de los errores pequeños, como, por ejemplo, la omisión o mala lectura de un valor de x.
Realizando una transformación adecuada de los datos originales, se pueden simplificar mucho los cálculos y reducir las ocasiones de error. Por ejemplo, supongamos que los desembarcos mensuales de peces durante seis meses fueran 75, 67, 82, 73, 69 y 71 toneladas; en lugar de calcular 752, etc., podemos tomar un origen arbitrario, pongamos 70, y computar la media y la variancia de 5, -3, 12, 3, -1 y 1 (2,83 y 28,17 respectivamente). Volviendo a la escala original, la media de la distribución será 2,83 + 70 = 72,83 toneladas. La variancia es siempre igual aunque cambie la escala, así que también para los datos originales es 28,17, y la desviación típica s = 5,31.
Las capturas anteriores pueden ser expresadas en una escala diferente, 75.000...71.000 kilogramos. Expresadas en toneladas, con un origen en 70 toneladas, obtendremos como antes una media de 2,83, una variancia de 28,17 y una desviación típica de 5,31. Para pasar a kilogramos, deberemos añadir 70 y multiplicar por 1.000, con lo que la media mensual de desembarcos será 72.833 kilogramos.
Así pues, en vez de calcular con los valores correspondientes a x, que pueden ser grandes, podemos usar otra serie de valores y, obtenidos de los x mediante una relación directa, y = f (x). La más sencilla de estas transformaciones consiste en un cambio de origen, de modo que
y = x - a (como en el primer ejemplo, donde a = 70)
Las medias y variancias, obtenidas por las ecuaciones (1.1) y (1.2), serán
media x = Mx = My + avariancia de x = Sx2 = Sy2
Otra transformación sencilla consiste en un cambio de escala
y = bx (como en el segundo ejemplo, donde b era igual a 1.000)
Entoces
Las dos transformaciones pueden ser combinadas, y = b (x - a)
Los pesos de los peces desembarcados en la isla de Rameswaram, India del sur, durante los 12 meses entre julio de 1953 y junio de 1954, fueron 205, 218, 150, 136, 89, 55, 112, 28, 93, 105, 186 y 253 toneladas (datos de Krishnamurthi, 1957).
Calcúlense el desembarco medio mensual, la variancia y la desviación típica; compruébese que la extensión (253 - 28 = 225 toneladas) es de 3,2 veces la desviación típica.
Cuando los datos están agrupados en intervalos de clases, tal como una composición de longitudes en la que se diera la frecuencia para cada centímetro, el cálculo de la media y de la variancia requieren una disposición ligeramente diferente. El valor de cada clase, esto es, su punto medio, debe ser tenido en cuenta f veces, donde f es la frecuencia de individuos en cada clase. De esta manera, las ecuaciones 1.1 y 1.4 deben ser reescritas como sigue
...............................(1.5)
.....................(1.6)
donde k es el número de clases
n = número de individuos = S fi,
En estos cálculos suele ser también de gran utilidad realizar cambios en el origen de la escala de los datos antes de empezar las computaciones; lo mejor será referirnos a un ejemplo, en el que se calculan la media y la variancia de la longitud de los Rastrelliger muestreados en el mercado de Bangkok en octubre de 1958. Como origen de trabajo se toma 17,5 cm, y como unidades de trabajo los medios centímetros.
|
Grupo de longitud (cm) |
Frecuencia |
Nueva escala |
|
|
|
xi |
fi |
yi |
fiyi |
fiyi2 |
|
15,5 |
8 |
-4 |
-32 |
128 |
|
16,0 |
7 |
-3 |
-21 |
63 |
|
16,5 |
4 |
-2 |
-8 |
16 |
|
17,0 |
2 |
-1 |
-2 |
2 |
|
17,5 |
8 |
0 |
S fiyi = -63 |
|
|
18,0 |
11 |
+1 |
11 |
11 |
|
18,5 |
2 |
+2 |
4 |
8 |
|
19,0 |
3 |
+3 |
9 |
27 |
|
19,5 |
1 |
+4 |
4 |
16 |
|
|
n = 46 |
|
|
S fiyi2 = 271 |
El origen ha sido escogido próximo a la media probable de la distribución, ya que una buena elección del origen reduce el trabajo de computaciones, sin que la diferencia de uno a tres grupos, ya sea en más o en menos, afecte mucho al trabajo. Los valores de fiyi se obtienen multiplicando los valores de la segunda columna por los de la tercera, y los de fiyi2 multiplicando de nuevo por yi sin que haya necesidad de computar los valores de yi2 como tales. Para calcular la media, se suman separadamente los valores positivos y negativos de fiyi entonces
Transformados los datos en la escala original, resultan ser, longitud media = 17,5 - 0,38 = 17,12 cm, variancia = 5,4/4 = 1,4 cm2, desviación típica = 1,2 cm.
En el caso de que los intervalos de clase no sean unidades, de suerte que las escalas de x e y puedan ser diferentes, como en el caso anterior, se ha de tener mucho cuidado al convertir los resultados de la media y la variancia en la escala apropiada.
Todos los resultados obtenidos por medio de estas computaciones deben ser comprobados para la necesaria exactitud y precisión en su aplicación. La repetición de las mismas computaciones, además de resultar tediosa, puede ser ineficaz, ya que con frecuencia se vuelve a incurrir en los mismos errores. Una buena comprobación, cuando lo que se exige es la exactitud, consiste en computar no solamente los valores de S x y S x2, sino también los de S (x + 1) y S (x + 1)2.
Así, tomando los datos del Ejemplo 1.2.1, se computaría
S x = 2 x 25 x7 x 26 + ... + 1 x 102 = A
y
S x2 = 2 x (25)2 x7 x (26)2 + ... + 1 x (102)2 = B
y también
S (x+1) = 2 x 26 x7 x 27 + ... + 1 x 103 = CS (x+1)2 = 2 x (26)2 x7 x (27)2 + ... + 1 x (103)2 = D
En C cada pez es 1 unidad más largo que en A, y como hay 499 peces, si A (e incidentalmente C) se ha calculado correctamente, A + 449 = C. Asimismo, D deberá ser mayor que B, pero por una cantidad equivalente al doble de la suma de los longitudes más el número de observaciones, es decir,
D = B + 2 × A + 449
Calcúlense con los datos del Ejemplo 1.2.1 las cantidades A, B, C y D citadas, y compruébese que:
(i) C = A + 449
(ii) D = B + 2A + 449
y asimismo, con los datos del Ejemplo 1.2.2, que se refieren a un total de 1.011 peces, calcúlese
S x, S (x + 1) y S x2 y S (x + 1)2,
comprobando que:
(i) S (x + 1) = S x + 1.011
y
(ii) S (x + 1)2 = S x2 +2x + 1.011
Las reglas generales que se seguirán, siempre que no se hayan cometido errores en los cálculos, serán:
(i) S (xi + 1) = S xi + n(ii) S (xi + 1)2 = S xi2 + 2S xi + n
donde n es el número de observaciones.
Una prueba sencilla de la exactitud (aunque no de la precisión), que siempre debería hacerse, consiste en valorar el rango (el valor mayor menos el menor) y dividirlo por la desviación típica. Normalmente, esta relación suele quedar entre 3 y 6, siendo mayor cuando aparece algún valor extremo aislado, y cuando el número de datos de la distribución es grande. Conviene no confundir la exactitud con la precisión. Por ejemplo, si la longitud media de un número de peces es 43,26 cm, una estimación de 43,18 es muy precisa y exacta, otra de 43 cm no es muy precisa pero es exacta; otra de 37,2 cm es precisa pero inexacta, y otra de 35 cm es imprecisa e inexacta. La precisión define la amplitud o estrechez del resultado; así una estimación de 37,2 se entiende que incluye todos los valores desde 37,15 hasta 37,25. La precisión, por tanto, está en relación con el número de cifras dadas en el resultado. La exactitud es el grado de acercamiento, o alejamiento, de la estimación con respecto al valor real.
PRECIO: $ 0,50
PM33271,11.66/S/1/1600