2.1 Introducción
2.2 Muestreo al azar
2.3 Muestreo estratificado
2.4 Submuestreo, o muestreo en dos etapas
Cada sistema de muestreo se usa para obtener estimaciones de ciertas propiedades de la población objeto de estudio, y será tanto más adecuado cuanto mejores sean las estimaciones que proporcione. Las estimaciones individuales pueden ser, por casualidad, muy aproximadas o diferir considerablemente del verdadero valor, dando una prueba deficiente de los méritos del sistema. Un mal sistema de muestreo puede dar a veces algunas estimaciones muy exactas, así como también un buen sistema dar alguna muy alejada del verdadero valor. La mejor manera de juzgar un sistema de muestreo consiste en observar la distribución de frecuencias de las estimaciones que se obtienen por muestreos repetidos. Un buen sistema proporciona estimaciones cuya distribución de frecuencias posee una pequeña variancia y su valor medio está muy próximo al valor verdadero. La diferencia entre la estimación media y el valor verdadero se denomina sesgo. (El término «sesgo» se usa también refiriéndose al proceso por el cual se producen las diferencias.) Las magnitudes del sesgo y la variancia de un sistema de muestreo son, en una gran extensión, independientes entre sí; un sistema puede dar estimaciones con una pequeña variancia, es decir, difiriendo poco entre ellas, pero con un gran sesgo, esto es, quedando todas las estimaciones muy lejos del valor verdadero. (Un ictiómetro con las cifras de la escala casi ilegibles introducirá cierta variancia extra; y un medidor con la escala desplazada producirá un sesgo.)
Dos observadores examinan el porcentaje en que aparece en capturas de peces una especie de Leiognathus en una mezcla con otras varias. El observador A trabaja rápidamente pero con poco cuidado, equivocándose en la identificación de algunos peces; el observador B trabaja mucho más lentamente pero con más cuidado. Según una serie de muestras, las estimaciones del porcentaje de presencia de Leiognathus splendens en las capturas fueron
|
A. |
4 |
4 |
3 |
5 |
4 |
|
|
3 |
5 |
4 |
6 |
4 |
|
|
6 |
3 |
4 |
3 |
5 |
|
|
4 |
5 |
4 |
4 |
6 |
|
|
5 |
3 |
5 |
4 |
5 |
|
B. |
9 |
7 |
11 |
4 |
8 |
|
|
4 |
10 |
8 |
9 |
12 |
|
|
8 |
3 |
6 |
10 |
15 |
|
|
11 |
12 |
7 |
13 |
11 |
|
|
10 |
5 |
8 |
9 |
12 |
Después de calculadas las medias y variancias de las anteriores distribuciones, resulta que: (a) las estimaciones obtenidas por A son más precisas (tienen una variancia menor) que las de B (0,89: 9,03); (b) sabiendo, por otras estimaciones, que el verdadero porcentaje es 9,1, resulta que A tiene un fuerte sesgo negativo; (c) si se admite que A omite la mitad de los peces, se puede obtener una estimación relativamente no sesgada y precisa duplicando las estimaciones obtenidas por A (media 8,64, sesgo [o sea, diferencia entre la media estimada y la real] - 0,46, variancia 3,6).
Se puede producir un sesgo como consecuencia de un método deficiente de análisis, pero con más frecuencia por una elección defectuosa de las muestras, o por el mismo método que se emplea para realizar las mediciones o al contar las muestras; por ejemplo, si los peces se clasifican por tamaños al ser desembarcados, y se toma una muestra de una partida de los grandes, se producirá una sobreestimación de la talla - un sesgo positivo en la talla media - o si se hacen caladas con una red clara para plancton, al escapar las diatomeas pequeñas, quedarán éstas subestimadas, mientras que las grandes resultarán sobreestimadas (sesgos negativo y positivo respectivamente en la proporción de diatomeas pequeñas y grandes). Es difícil librarse de los sesgos, especialmente si se toman muestras en ambientes marinos naturales, bien de diatomeas con una red de plancton, o peces con un arte de arrastre.
Por más que se aumente el tamaño de la muestra, o se combinen varias de ellas, el sesgo permanece inalterado, pero la variancia se reducirá de una manera inversamente proporcional al tamaño de la muestra, o al número de muestras combinadas. Esta doble manera de reducir la variancia está, a su vez, muy en relación con el problema del ahorro de trabajo y del costo de un programa de muestreo. Al menos en teoría, se puede obtener un grado de precisión1 determinado, tomando una muestra suficientemente grande. El objetivo de un buen muestreo es no sólo obtener un nivel de precisión (variancia pequeña), sino también hacerlo con el menor costo. El sesgo, por el contrario, no puede ser reducido aumentando el muestreo, y a menudo no se logra descubrir su presencia por un análisis de los datos (en el Ejemplo 2.1.1 no hay ningún indicio para que, por medio de los propios datos, podamos descubrir si las muestras A o B están sesgadas). Normalmente, el sesgo sólo podrá descubrirse y eliminarse nada más que a través de un examen cuidadoso del sistema de muestreo, desde el comienzo al fin. En la mayor parte de las situaciones, debe ponerse un gran cuidado para comprobar que han sido eliminadas todas las fuentes probables de sesgos. Sin embargo, hay casos en los que resulta muy fácil medir el sesgo y, por lo tanto, eliminarlo de los análisis posteriores (por ejemplo, las redes de enmalle son altamente selectivas del tamaño de los peces que capturan, y darán muestras sesgadas en la estimación de la talla media. Sin embargo, esta selectividad puede ser medida, y corregida, en los análisis posteriores). No obstante, en este caso, como en todos los demás, es preciso examinar todas las posibilidades de sesgos antes de proceder al muestreo y, si se reconoce la existencia de un sesgo, éste debe medirse cuidadosamente, independientemente del proceso del muestreo.
1 Conviene aquí seguir manteniendo la distinción entre precisión y exactitud, que se corresponde estrechamente con la distinción entre variancia y sesgo (o, más bien, sus recíprocos). Una cantidad precisa tendrá poca variancia y será dada con muchas cifras, pero puede estar alejada del valor verdadero. Siendo la talla real de un pez 17,638 cm, serán mediciones precisas de su longitud 17,64 cm, ó 18,32 cm, pero esta última será aproximadamente inexacta. Más exactas, pero menos precisas, serán las tallas de 17,6 ó 18 cm.
En el Ejemplo 2.1.1 puede considerarse que las muestras mayores están compuestas por otras cinco de las originales. Tomando la media de estas muestras menores, como una estimación de las grandes, aparece:
a) que las variancias de las dos series han sido reducidas (la de A de 0,89 a 0,52, y la de B de 9,03 a 1,29);b) que el valor del sesgo de las muestras de A no se modifica (la media queda inalterada).
Las condiciones anteriores (eliminación del sesgo, o al menos conocerlo y medirlo, y la reducción de la variancia a un mínimo, dada una cantidad de muestreo) determinarán el método de muestreo, pero la cantidad de muestras a tomar dependerá del grado de precisión que se requiera. Corrientemente, no es posible determinar la precisión deseada, pero si se pueden dar dos límites. En el límite más bajo la variancia será tan grande que la información que proporcionará la muestra no tendrá valor práctico, con lo que la muestra deberá hacerse mayor o abandonarse el método de muestreo. Las estimaciones obtenidas por medio de un plan de muestreo frecuentemente se completan con otros datos, que pueden proceder de otros planes de muestreo, y la mayoría de ellos con una variancia diferente. La variancia final dependerá de la variancia de todas las informaciones aportadas, pero sobre todo de las menos exactas, de la misma manera que la fortaleza de una cadena depende de los eslabones más delgados. Por ejemplo, la captura total de una flota puede estimarse multiplicando la captura media por el total de desembarques. Si la precisión con que se conoce el número de desembarques es del orden de ± 10 por ciento, aunque se conozca muy bien la captura media, la cantidad total desembarcada sólo será conocida, en el mejor de los casos, con una precisión de ± 10 por ciento. Una vez que en un plan único de muestreo se ha conseguido un cierto grado de precisión, las nuevas mejoras que se introduzcan no aumentarán la precisión de los resultados, por lo que será mejor dedicar el esfuerzo (tiempo, mano de obra, etc.) a incrementar la precisión de otros datos.
El concepto básico de todo muestreo es el de la muestra al azar. Una muestra de objetos de una población se llama al azar cuando todos los miembros de la población tienen igual oportunidad de aparecer en la muestra. Es muy importante insistir en que esto es igualmente válido para todos los miembros de la población, tanto para los raros como para los típicos. Por ejemplo, el plegonero (Merlangus merlangus) desembarcado por un solo barco en Lowestoft suele tener (aquí supondremos que siempre) una composición de longitudes suavemente unimodal, con la moda normalmente entre 28 y 30 cm, pero alguna vez, por ejemplo, una entre 30, llega a ser hasta de 35 cm. Por lo tanto, si tomamos una muestra al azar de plegonero de cada barco, una vez de cada 30, por término medio, tendrá una moda de 35 cm o más, aunque normalmente estará entre 28 y 30 cm. Si entonces un biólogo pesquero, apoyándose en una sola muestra, obtiene una moda de 35 cm, esta desviación de la media de 29 cm no significará necesariamente una muestra que no sea al azar, puesto que se puede dar este caso una vez de cada 30; pero se puede comprobar tomando más muestras, por ejemplo tres muestras, que sólo tendrán juntas una moda superior a 35 cm una vez entre 27.000.
Un procedimiento muy útil y de amplia aplicación para tomar muestras al azar consiste en utilizar números al azar, tal como se describe en la mayor parte de los libros de estadística. A cada individuo de la población de la cual se quiere extraer una muestra se le atribuye un número, y los que se tomen como muestra estarán determinados por la tabla de números al azar. Por ejemplo, si se quieren elegir 5 individuos entre 100, como una muestra, y los 5 primeros números de la tabla son 3, 47, 43, 73 y 86, se tomarán los individuos correspondientes a estos números. Cuando la cantidad de individuos no sea exactamente 100 (o 1.000, etc.) saldrán números que no correspondan a ningún individuo, y no se tendrán en cuenta. Esta pérdida de tiempo puede ser reducida atribuyendo a cada individuo dos o más números, con tal de que todos tengan igual cantidad de números. Supongamos, por ejemplo, que se quieren tomar 5 unidades de una población de 24; en este caso, a cada individuo se le adscriben cuatro números; así la primera unidad tendrá, por ejemplo, los números 01 al 04, etc., la 24 tendrá 93-96, con lo que quedarán sólo cuatro números, 97-100, sin utilizar. Los individuos sometidos al muestreo, que corresponden a la serie previa de 5 números al azar, serían entonces los números 1, 12, 11, 16 y 22 (si uno de los números al azar es 97 o más, se descarta y se toma otro). En lugar de escoger todas las unidades en la muestra individualmente de la tabla de números al azar, las unidades se pueden tomar a intervalos regulares, por ejemplo, cada 5 ó 100 individuos, y solamente el primero elegido utilizando los números al azar. En el primer ejemplo, la muestra era de 1/20 de la población, de modo que el intervalo de la muestra será 20 y como el primer número elegido al azar era el 3, los siguientes serían 23, 43, 63 y 83. Este sistema es peligroso si en la población hay una periodicidad natural equivalente al intervalo elegido; por ejemplo, en el caso de someter a muestreo los desembarcos totales en un puerto, no se debe anotar la captura cada 7 ó 14 días, puesto que pudiera haber grandes variaciones sistemáticas asociadas a los distintos días de la semana.
En un determinado lugar se efectúan los desembarcos de pesca durante todo el año. Se desea determinar la cantidad total anual desembarcada, mediante el muestreo de la captura en 30 días del año. Determínense los días en que se debe efectuar el muestreo por medio de números al azar:
a) directamente por medio de una serie de números al azar del 000 al 999, y numerando los días del año de 1 a 365;b) dando a cada día 2 números, desde el 1 y 2 al 729 y 730;
c) dando a cada día 27 números, de 1-27 a 9.829-9.855, y usando números al azar de 0000 a 9999;
d) haciendo un muestreo cada 12 días a partir de un día elegido al azar entre los 1-12 días primeros (algunas muestras podrán tener 31 días).
Si no se usan números al azar, o cualquier otro proceso similar, entonces lo más probable es que no todos los individuos de la población tengan igual oportunidad de salir en la muestra. Caso de haber alguna correlación entre la cantidad que se va a medir y la probabilidad de que aparezca en la muestra, el resultado podría estar sesgado, quizás demasiado. Por ejemplo, al hacer el muestreo de la captura procedente de un barco en una lonja abarrotada de peces, muchas veces se hace necesario trabajar con las cajas que se desembarcan primero. Dado que en éstas vendrán los peces últimamente capturados, si es que se pretende conocer la frescura media obtendremos una estimación muy sesgada; en cambio, lo más probable es que sus tamaños sean similares a los de los peces capturados anteriormente, de modo que la muestra dará estimaciones sin sesgo de la talla media. Nunca debe darse rápidamente por supuesto que no existen sesgos, y la posibilidad de su existencia debe investigarse cuidadosamente. En el ejemplo anterior existiría cierto sesgo si los barcos acostumbran hacer una última calada cerca ya del puerto, donde el tamaño medio de los peces se desvía del tamaño medio general. Estas y otras fuentes de posibles sesgos solamente pueden encontrarse y eliminarse si se tiene un completo conocimiento de la pesquería - cómo se capturan los peces, cómo se manipulan a bordo y qué distribución sufren en el mercado.
La precisión de las estimaciones que se obtienen por verdaderos muestreos al azar puede ser determinada rápidamente. Si se está efectuando el muestreo de una población para conocer alguna de sus características (como el número de vértebras), cuya media en la población es M y la variancia S2, y se toma al azar una muestra de n individuos, cuyos valores son xi...xn, la estimación de la media de la población será
.....................................(2.1)
y la media de 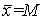 (si las estimaciones no están sesgadas) y la variancia de
(si las estimaciones no están sesgadas) y la variancia de 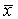 (o más brevemente var
(o más brevemente var 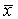 ) =
) = 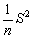 , si es que N, el número total en la población, es grande comparado con n.
, si es que N, el número total en la población, es grande comparado con n.
En caso contrario, la fórmula de la variancia se hace
a) Suponiendo que la media y la variancia de los datos en el Ejemplo 1.2.1 están próximos a los valores de la población, calcúlese la variancia en la estimación de la longitud media a partir de las muestras de 5, 20, y 100 peces;b) mediante el empleo de números al azar, o por cualquier otro método, tómense 20 muestras al azar de 5 peces de los 449 del Ejemplo 1.2.1. Calcúlese la longitud media de cada una de estas muestras; calcúlese la variancia de estos 20 valores, y compárese con la variancia esperada tal como se calculó en (a). (Nótese cómo la variancia calculada a partir de una serie de números no mayor de 20 está sujeta a cierta variabilidad);
c) si se necesita estimar la longitud media del bacalao del Mar del Norte con una precisión de ±5 cm, determínese el tamaño de la muestra al azar que es preciso tomar (para esto se requiere que el doble de la desviación típica de la longitud media estimada sea igual a 5).
Cuando se efectúa el muestreo de una población heterogénea, se puede incrementar la precisión, a veces de manera muy señalada, y reducir el riesgo de sesgos, dividiéndola en una serie de secciones, cada una de las cuales es relativamente homogénea, y haciendo el muestreo de cada sección (o estrato) por separado. Así, se hace una muestra de cada estrato independientemente, obteniéndose estimaciones para cada uno de ellos. Luego estas estimaciones pueden combinarse para dar la estimación del conjunto de la población. La variancia de esta estimación se obtendrá también combinando las variancias de las estimaciones hechas en cada estrato. Como las variancias de cada estrato tenderán a ser pequeñas, dado que los estratos son relativamente homogéneos, posiblemente mucho menores que la variancia en la población en conjunto, la variancia final de la estimación combinada será también pequeña.
En términos matemáticos, sea una población de N individuos, Ni en el estrato i°, de modo que N = S Ni, y una muestra ni del estrato i°, en la que los valores de la cantidad que hay que estimar (longitud del pez, peso capturado, etc.) es igual a yij = 1...ni; la estimación del valor medio 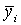 en el estrato será
en el estrato será
................... (2.2)
obteniéndose una estimación sin sesgo de la media de la población total como la media ponderada de las medias de los estratos, siendo el factor ponderador el número total en cada estrato, es decir:
Si la variancia en el estrato i° es Si2
y
.............................(2.3)
suponiendo que ni, sea pequeño comparado con Ni. En otro caso, la variancia será
Esta variancia puede compararse con la de la estimación obtenida por un muestreo al azar en el conjunto de la población, que será
si n no es pequeño comparado con N, y donde S2 es la variancia en el conjunto de la población.
La captura de eglefino de un barco de arrastre se desembarca en Aberdeen dividida en cuatro categorías de tamaños, que serán los cuatro estratos (datos tomados de Pope, 1956). Se hicieron muestras de cada categoría, y los resultados se pueden resumir del modo siguiente:
|
Categoría |
Ni |
ni |
S yij |
S y2ij |
|
Pequeño |
2 432 |
152 |
5 284 |
185 532 |
|
Pequeño-ediano |
1 656 |
92 |
3 817 |
158 953 |
|
Mediano |
2 268 |
63 |
3 033 |
146 357 |
|
Grande |
665 |
35 |
2 027 |
118 169 |
|
TOTAL |
7 021 |
342 |
14 161 |
609 011 |
donde y = longitud del pez en cm.
Partiendo de estos datos, se realizan estimaciones de Si2 por medio de
y se tiene:
|
Categoría |
|
|
Si2 |
Si2/ni |
Ni2Si2/ni |
|
Pequeño |
34 763 |
84 544 |
12,21 |
0,0803 |
474 900 |
|
Pequeño-mediano |
41 489 |
68 706 |
6,47 |
0,0703 |
192 800 |
|
Mediano |
48 143 |
109 188 |
5,48 |
0,0870 |
447 500 |
|
Grande |
57 914 |
38 513 |
22,85 |
0,6529 |
288 700 |
|
|
|
300 951 |
|
|
1 403 900 |
y de aquí
y desviación típica
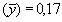
Los límites de seguridad del 95 por ciento para la longitud media verdadera de los peces capturados son, por tanto, 42,9 ± 2 × 0,17, es decir, 42,6 - 43,2 cm.
Los datos pueden usarse también para dar una medida aproximada de la variancia de la estimación obtenida de una muestra al azar de 342 del conjunto de la captura. En este caso tomaremos como una estimación de s2 la variancia del conjunto de la población,
por tanto, s2 = 66,4 (compárese con la mayor variancia obtenida dentro de un estrato, que fue 22,85).
y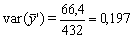
desviación típica
Aunque esta estimación de s2 no sea del todo correcta, puesto que la muestra estaba lejos de ser una verdadera muestra al azar, ya que los peces medianos no estaban completamente representados, no obstante, ha servido para poner de manifiesto la gran reducción de la variancia al usar un muestreo estratificado, que es del orden de 1/7, lo que equivaldría a haber aumentado siete veces la muestra.
Se pueden incrementar las ventajas de un muestreo estratificado si se efectúa un muestreo de cada estrato en la forma más conveniente. Los estratos conteniendo muchos individuos, o que sean muy variables, requerirán mayor muestreo que los poco numerosos o más homogéneos. La variancia será mínima para un cierto tamaño total de muestra, n, si
Ni x Si µ ni
o
Si µ ni/Ni
es decir, si la proporción bajo muestra es proporcional a la variancia del estrato. Si ni no es pequeña comparada con Ni, esta fórmula no es enteramente exacta, pero sirve para tener una buena idea sobre la mejor distribución de las muestras.
Determínese en el Ejemplo 2.3.1 la mejor distribución en cada estrato del número total de peces sometidos a muestreo (342) y, usando los valores de S2, calcúlese la variancia de la longitud media estimada por esta distribución de las muestras.
A lo largo de una costa, los peces se desembarcan en 100 lugares, que pueden clasificarse, grosso modo, en tres categorías, de acuerdo con el peso de los peces. En el transcurso de una semana, los pesos de los desembarcos fueron:
|
Lugares de grandes desembarcos: |
45 |
59 |
87 |
41 |
71 |
25 |
9 |
69 |
10 |
7 |
|
Medianos: |
17 |
13 |
19 |
26 |
1 |
8 |
27 |
11 |
12 |
26 |
|
|
5 |
8 |
10 |
16 |
16 |
4 |
16 |
16 |
13 |
29 |
|
|
14 |
25 |
29 |
27 |
20 |
25 |
2 |
7 |
3 |
12 |
|
Pequeños: |
2 |
6 |
7 |
0 |
1 |
2 |
1 |
5 |
4 |
7 |
|
|
8 |
9 |
3 |
2 |
5 |
4 |
2 |
0 |
2 |
8 |
|
|
5 |
3 |
8 |
9 |
8 |
9 |
1 |
6 |
5 |
3 |
|
|
3 |
4 |
7 |
5 |
5 |
3 |
2 |
4 |
6 |
1 |
|
|
6 |
2 |
5 |
1 |
0 |
3 |
8 |
0 |
4 |
3 |
|
|
3 |
5 |
5 |
0 |
7 |
0 |
9 |
7 |
9 |
0 |
Determínese, mediante el cálculo de la variancia en cada categoría y en el conjunto de la población, cuál es el mejor método de estimación de la captura semanal total en toda la costa, si es que sólo se puede registrar la captura en 20 lugares (uno de cada cinco, visitando los lugares de desembarco), cuál es la variancia de esta estimación, y compararla (a) con la obtenida de una sola muestra al azar del conjunto de la población, y (b) usando un muestreo estratificado, tomando una muestra que sea de 1/5 de cada categoría.
Cuando las poblaciones son muy extensas, o complejas, la simple toma de muestras al azar se transforma en un gran problema, que suele requerir mucho tiempo. El tiempo necesario para obtener una muestra de dimensiones determinadas puede ser muy abreviado mediante el empleo de un muestreo en dos etapas. En primer lugar, el conjunto de la población puede ser dividido en una serie de unidades primarias, o subpoblaciones, varias de las cuales se toman como muestra. Se toma una muestra secundaria, o submuestra, de cada una de estas subpoblaciones, que a su vez son muestras de la población total. Por ejemplo, para estimar la captura total a lo largo de una línea costera, se puede tomar como unidad básica cada desembarco. La medición de una serie de desembarcos tomados al azar a lo largo de la costa requeriría efectuar muchos viajes, imposibles de realizar; la solución consiste en seleccionar (por ejemplo, mediante números al azar) ciertos lugares de desembarco en determinados días, y en estos lugares seleccionar una serie de desembarcos.
Por supuesto, el submuestreo se puede realizar en más de dos etapas. En el ejemplo anterior, podría interesar algún dato, como el estado de madurez, para lo cual se tomaría una caja de pescado (o una parte de la misma), con lo que el muestreo se habría realizado en tres (o cuatro) etapas.
La desventaja de un submuestreo consiste, desde luego, en que los individuos de una misma unidad primaria son probablemente más parecidos entre sí que los del conjunto de la población. De esta manera, después de examinar un individuo de una unidad, tal como el peso de la captura de un barco en un lugar determinado, si se siguen examinando individuos de esa unidad, se obtendrá menos información del conjunto de la población (por ejemplo, la captura media por barco de todos los lugares de desembarco) que si se examinan individuos de otras unidades primarias. El problema consiste en deducir el número más conveniente de muestras que se debe tomar en un tiempo dado al emplear un muestreo en dos etapas. En términos generales, si los individuos dentro de una unidad primaria son muy variables, lo mejor será tomar muchas muestras dentro de cada unidad en, comparativamente, pocas unidades primarias. Por el contrario, si la variación de los individuos es pequeña dentro de cada unidad, pero hay diferencias considerables entre las unidades, entonces deberán someterse a muestreo muchas unidades primarias, con un pequeño número de individuos por muestra en cada una de ellas.
El método puede ser ilustrado en términos matemáticos: supóngase, para mayor sencillez, que la población puede dividirse en K unidades primarias, cada una de N individuos, y que están sometidas a muestreo k unidades primarias, tomándose una submuestra de n individuos en cada una.
Si M es la media de la población, y Mi la media de la ia unidad primaria, entonces la estimación de la media de una unidad primaria bajo muestreo será:
donde xij es el valor del j° individuo en la unidad ia y la estimación de la media de la población será
............................(2.4)
La variancia de mi en torno a Mi será 1/n × Sw2, en donde Sw2 es la variancia de los individuos de la ia unidad primaria en torno a la media de la unidad. La variancia de la media estimada para la población constará de dos partes: la variancia de las medias estimadas para las unidades en torno a las medias verdaderas de las unidades, y la variancia de estas últimas en torno a la media de la población; esto es
........................................(2.5)
donde SB2 es la variancia de las medias de las unidades en torno a la media de la población. Una estimación no sesgada de la variancia de m será
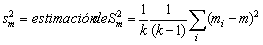
.............................(2.6)
(tomado de Pope, 1956)
Como muestra al azar del desembarco total de arenque en una semana, se toma una serie de desembarcos individuales, y de cada desembarco seleccionado una muestra de 50 arenques, y se miden. Se obtienen los siguientes datos:
|
Barco |
1 |
2 |
3 |
4 |
5 |
|
Suma |
1 244,3 |
1 324,2 |
1 335,4 |
1 299,7 |
1 270,5 |
|
Suma de cuadrados |
31 020,97 |
35 127,08 |
35 730,30 |
33 900,99 |
32 558,55 |
Estímese la longitud media del arenque en los desembarcos de la semana, y su error típico. Primero se obtendrá la media para cada barco, que son 24,9, 26,5, 26,7, 26,0 y 25,4. Por tanto, las estimaciones que se piden se obtendrán por
m2 = 1/5 (24,9 + ... + 25,4) = 25,9
sm=0,34
Las variancias entre y dentro de las unidades primarias pueden también estimarse separadamente. Dentro de cada unidad primaria, se tendrá una estimación de Sw2 por
Estas estimaciones por separado en las unidades primarias pueden combinarse por medio de
.............................(2.7)
Según las ecuaciones (2.5) y (2.6) la variancia entre las unidades puede deducirse de la ecuación
.............................(2.8)
Siendo dados los valores de Sw2 por la ecuación (2.7)
Calcúlese la variancia de la longitud del arenque dentro y entre los barcos, de acuerdo con los datos del Ejemplo 2.4.1. Como estimación de la variancia dentro de los barcos, se tiene que
5 x 49 x Sw2 = (31020,97 - 1/50 x 1244,32) + ... + ...
por tanto
245 Sw2 = 378,62Sw2 = 1,545
También
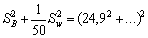
SB2 = 0,56 - 0,03 = 0,53
En los cálculos de los ejemplos 2.4.1 y 2.4.2 se ha podido ver que la mayor parte de Sm2, la variancia de la longitud media estimada de todos los peces desembarcados, se debe a SB2 la variancia entre los barcos. De la ecuación (2.5) se deduce que el efecto de esta variancia puede reducirse aumentando k, o sea, el número de unidades primarias bajo muestreo, pero no incrementando n, el número de individuos sometidos a muestreo en cada unidad primaria. Así pues, el tiempo empleado en el muestreo de los desembarcos de arenque podría aprovecharse más eficazmente reduciendo el número de individuos en las muestras y aumentando el número de barcos bajo muestra, por ejemplo, 6 muestras de 30 peces, con un total de 180 peces, en vez de 5 muestras de 50 peces, con un total de 250 peces. La mejor forma de utilizar el tiempo dependerá del que se emplee en cada etapa de muestreo y de la variancia contenida en ellas. El tiempo total empleado se puede dividir aproximadamente en tres partes:
a) el tiempo inicial; el tiempo que se emplea en la preparación, incluyendo el traslado desde el centro de trabajo al área de muestreo. Este tiempo es más o menos constante, independientemente del volumen del muestreo;b) el tiempo entre las unidades primarias; en el ejemplo anterior, el tiempo empleado en ir de un barco a otro, que será proporcional al número de unidades primarias;
c) el tiempo dentro de las unidades primarias; que es el tiempo que se emplea en examinar los individuos en cada unidad primaria. El tiempo total podra ser, por tanto, igual a
t = t0 + k tb + n k tw .............................. (2.9)t0 = tiempo inicial
tb = tiempo para ir de una unidad primaria a otra
tw = tiempo empleado en examinar un individuo.
La mejor forma de distribuir el tiempo de muestreo (es decir, la que da una variancia mínima), de acuerdo con un número determinado de individuos bajo muestreo en cada unidad primaria, viene dada por
............................(2.10)
Utilizando los datos de los ejemplos anteriores, y suponiendo que en un minuto se pueden medir 20 peces, y que el tiempo empleado para ir de un barco a otro es de 5 minutos, demuéstrese que la variancia mínima en la longitud media estimada y para una cantidad dada de muestreo es de 17 peces aproximadamente, resultado obtenido con muestras secundarias.
Hasta ahora, se había supuesto que todas las unidades primarias eran del mismo tamaño, pero esto no es lo corriente. Cuando sean desiguales, se hará preciso aplicar un factor de corrección para cada unidad. La ecuación (2.4) puede reescribirse como sigue
..........................(2.11)
donde Ni = número de individuos en la ia unidad primaria
N = S Ni = número total en todas las unidades primarias de muestreo
o como..................................(2.12)
donde ni es el número de individuos bajo muestra en la ia unidad primaria, que no tiene por qué ser igual en todas ellas. Si se toma ni en cada unidad de tal manera que en todas ellas la razón de muestreo ni/Ni sea la misma para todas las unidades, e igual a p, entonces (2.12) se reduce a
es decir
..........................................(2.13)
donde n es el número total de individuos de la muestra, siendo ésta, desde luego, la forma más conveniente de computación. La fórmula de la variancia (ecuación 2.5) puede también reescribirse así
donde
La fórmula (ecuación 2.10) sobre el mejor número de individuos por muestra en cada unidad no hay que aplicarla de manera estricta. Podría modificarse para que determinara con precisión la mejor muestra en cada unidad primaria. Sin embargo, esta fórmula sería más bien prolija, y necesitaría una información adicional sobre la variancia en cada unidad primaria (que puede no ser igual en todas las unidades). Tanto esfuerzo puede muy bien no merecer la pena, y ser más razonable utilizar la ecuación (2.10), modificada empíricamente, incrementando la muestra en las unidades más grandes o más variables.
Cuando el objetivo del muestreo sea medir alguna cantidad total, como el peso total desembarcado de cierta especie de peces, y no un valor medio, como la longitud media de los peces, el análisis de los resultados, como figura en las ecuaciones (2.11) - (2.13) deberá modificarse. El total en la ia unidad bajo muestreo será
donde Ni/ni es el factor elevador o de ponderación para la ia unidad primaria, y es igual al recíproco de la proporción tomada como muestra. El total en el conjunto de la población viene dado por
donde N = número total de individuos en la población. Si N no es conocido, como bien puede suceder, entonces en vez de N/Ni debe emplearse como factor aproximado elevador K/k, donde K es el número total de unidades primarias y k es el número total de unidades bajo muestreo (si el número de individuos de cada unidad primaria fuera el mismo, los dos factores coincidirían). Es absolutamente indispensable utilizar dos factores elevadores, uno para relacionar la muestra con el conjunto de la unidad primaria, y otro para relacionar las unidades primarias sometidas a muestreo con el conjunto de la población. El empleo de factores ponderadores equivocados puede ocasionar sesgos importantes, si es que hay grandes diferencias en la composición entre las unidades primarias, en especial si están correlacionadas con el número de individuos en la unidad primaria. Supóngase, por ejemplo, que se desea estimar la cantidad total desembarcada en un cierto lugar de una determinada especie de peces que viven predominantemente en fondos costeros. Como unidad primaria se puede tomar la captura de cada barco, utilizando como muestra una caja de pescado de cada barco seleccionado. Es muy probable que los barcos grandes pesquen en fondos más alejados de la costa, que consigan capturas mayores, y que haya en ellas una pequeña proporción de peces costeros. Si a las muestras de estos barcos grandes se les diera el mismo factor ponderador que a las de los más pequeños que actúan junto a la costa, la proporción de especies costeras podría muy bien ser sobreestimada.
Treinta barcos desembarcaron peces en un lugar determinado. Se tomaron como muestra 10 barcos, de cada uno de los cuales se sometió a muestreo una caja, determinándose el peso de dos de las especies, con los siguientes resultados:
|
Número del barco |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Número de cajas desembarcadas |
28 |
10 |
16 |
20 |
18 |
12 |
10 |
5 |
15 |
25 |
|
Peso de la especie A en 1 caja (kg) |
10 |
1 |
2 |
2 |
7 |
8 |
3 |
2 |
9 |
12 |
|
Peso de la especie B en 1 caja (kg) |
1 |
10 |
2 |
2 |
2 |
7 |
3 |
9 |
8 |
2 |
Calcúlese el peso total de los desembarcos de cada especie, (a) utilizando la información anterior, (b) utilizando la información adicional de que el total de desembarcos de todos los barcos fue de 450 cajas. Compárese la proporción de las dos especies en el total de desembarcos, con la proporción en las 10 cajas bajo muestreo (una caja equivale a 50 kg).