Population “saharienne” de sardine (Sardina pilchardusWalb., 1972).
par
N. Barkova
(Atlant NIRO, URSS)
La grande majorité des capturées était constituée d'individus mesurant de 18 à 20 cm (19 cm en moyenne, tab. 1). Les générations fécondes de 1985 ägées de 3 ans (33.6%) et celles de 1986 ägées de 4 ans (30.3%) prédominent. La génération à grand rendement de 1984 ägée de 5 ans constitue encore 14.5% (tab. 2). Les poids par ägesn'a pas changé.
| Age, ans | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Poids, kg | 0.031 | 0.057 | 0.075 | 0.085 | 0.103 | 0.120 | 0.131 |
1- L'evaluation du stock et du total admissible de captures
(TAC).
La biomasse de sardine pour 1980–1988 a été évaluée selon la méthode APV d'après la composition par âge des prises totales réalisées par toutes les firmes de pêche (“Zapryba”, “Sevryba”, “Aztcherryba”). La standardisation de l'effort a été effectuée selon le modèle multiplicatif de Gavaris et Robson (1983) au moyen de la méthode de Shimada-Shaeffer. Dans les deux cas en tant que standard il a été choisi le type du bateau RTMA comme celui qui pratique la pêche de l'espèce donnée de façon la plus stable. Lors de la standardisation selon la méthode multiplicative il a été analysé la prise par effort avec un mois standard différent pour chaque année. Les mois sans pêches n'ont pas été pris en considération pour l'estimation de valeurs moyennes. Il a été fait une analyse de coincidence de la prise par effort calculée pour un mois concret et de la prise réelle au cours de cette période. Le mois où la prise moyenne par effort était proche de la prise moyenne calculée, est pris pour un mois standard. L' effort sommaire standardisé de chaque année a été déterminé avec les différentes valeurs de la prise par effort (limite inférieure, valeur moyenne, limite supérieure de l'intervalle).
La capture moyenne par effort du mois standard a été prise en compte.
Il est à noter une tendance identique de variation de la prise par effort obtenue selon les deux méthodes suivant les années.
Le coefficient de mortalité naturelle “instantanée” a été autrefois déterminé selon les méthodes suivantes:
Selon la différence de logarithmes naturels d'abondance (en prenant pour le coefficient de mortalité naturelle la mortalité “instantanée” totale de la première année de pêche (1972) compte tenu du fait que la composition taille-âge au début de la pêche reflète l'état “primitif” des populations capturées).
Selon la méthode de Silliman (1943).
Selon la mortalité totale pour deux périodes de pêche (Beverton et Holt, 1958) caractérisées par la stabilisation de prise par effort avec les différents niveaux d'intensité de la pêche (Barkova, 1977; COPACE, 1979, 1980). Le coefficient de mortalité naturelle est de 0.6.
En vue de trouver le coefficient de départ de mortalité par pêche il a été appliqué les méthodes avancées par Pope et Shepherd (1983), ainsi que d'autres méthodes: celle de valeurs moyennes de plusieurs années (Babajan et al., 1984); équation de régression selon la dépendance entre l'effort de pêche et le coefficient de mortalité par pêche, de même que la méthode de Rivard (1983).
En tant que critère d'adéquation des méthodes il a été utilisé l'erreur moyenne quadratique d'approximation de la prise par effort à l'aide de l'équation de régression dont l'argument est la biomasse évaluée au moyen de l'APV (S), ainsi qu'en tant que critère supplémentaire —le coefficient de corrélation prévu par la méthode pour chaque groupe d'âge. Pour la méthode de calibration “Equation de régression” c'est le coefficient de corrélation entre la mortalité par pêche et l'effort de pêche, pour celle de Pope-Shepherd c'est le coefficient de corrélation entre le logarithme du coefficient de capturabilité et l'effort de pêche, etc.
Presque pour toutes les méthodes de “calibration” le coefficient de corrélation chez les principaux groupes d'âge n'est pas élevé.
| Méthode | Valeur |
|---|---|
| Equation de régression | 11.436 |
| moyenne de plusieures années | 11.876 |
| gamma-méthode | 11.182 |
| M. d'Armstrong | 11.417 |
| Saville | 12.363 |
| Highdoll-Jones | 12.363 |
| Laurec | 12.334 |
| moyenne pondérée | 11.774 |
Les erreurs les plus petites d'approximation permettent d'analyser de près la méthode d'Armstrong qui se base sur la détermination du coefficient de capturabilité selon les années de pêche en utilisant les valeurs préliminaires du coefficient de mortalité par pêche.
Nous utilisons la méthode de calibration de Rivard basée sur l'idée de l'existence d'une relation entre l'indice d'abondance caractérisant le stock (dans le cas donnée c'est la prise par effort) et la biomasse. En tant que critère de cette méthode il est appliqué le coefficient de corrélation entre l'indice et la biomasse évaluée à l'aide de l'APV. Le calcul selon cette méthode se fait avec des intervalles variés de centrage pour le groupe d'âge avancé et avec les centrages variés de années pour calculer le coefficient de recrutement partiel. Le coefficient de corrélation obtenu selon cette méthode est assez élevé: 0.64. En outre, l'erreur moyenne quadratique (7.69) s'est avérée la plus basse, ce qui a permis de préférer la méthode de Rivard (Waldron et Funning) dans les études ultérieures. En outre, cette méthode saisit bien la tendance de variations du stock, ce qui confirme sa convenance,
Les coefficients terminaux de mortalité par pêche obtenus selon la méthode d'Armstrong et Rivard sont résumés au Tableau 2.
| Age, ans | Ft | |
|---|---|---|
| Rivard | Armstrong | |
| 1 | 0.0100* | 0.0095 |
| 2 | 0.0660 | 0.0675 |
| 3 | 0.6825 | 0.2969 |
| 4 | 1.4120 | 0.5498 |
| 5 | 1.6662 | 0.8069 |
| 6 | 1.5034 | 1.3064 |
| 7 | 1.5034 | 1.5709 |
En outre, il a été fait une tentative d'utiliser la méthode de réglage pour la détermination des coefficients de mortalité pour l'ensemble de groupes d'âge. Bien que la matrice de corrélation nous a donné de l'espoir, car le coefficient de corrélation entre les groupes 1,2,3 est assez élevé: 0.5–0.9 et le processus d'itération coincide à la précision donnée, cependant le Ft pour le groupe d'âge 3 s'est avéré extrêmement élevé (II), ce qui nécessite une analyse ultérieure de la composition par âge relative à la période plus longue.
Le recrutement partiel obtenu selon la méthode de Rivard est donné au tableau 3.
| Age, ans | 1 | 2 | 3–7 |
|---|---|---|---|
| Recrutement | 0.0077 | 0.0734 | 1.0000 |
| partiel |
Recrutement. Pour mettre en évidence la dépendance entre le stock de parents et le recrutement les calculs ont été menés selon les modèles:
1. Dépendance linéaire; 2. Beverton; 3. Ricker; 4. Cushing; 5. Chapman.
En tant que critère d'adéquation de méthodes il a été utilisé une erreur d'approximation calculée d'après la formule (tabl. 4):
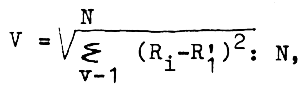
avec R — recrutement (abondance d'individus âgés d'un an);
R1 — valeur précalculée du recrutement;
N — volume d'échantillon pour déterminer le paramètre de dépendance.
| Méthode | V1 |
|---|---|
| Dépendance linéaire | 7718 |
| Beverton | 8209 |
| Ricker | 213430 |
| Cushing | 7863 |
| Chapman | 6749 |
En effet, l'application du modèle de Chapman est correcte. Ici l'équation qui relie le stock et le recrutement est la suivante:
R = AP 3/2 - BP2,
avec R — recrutement;
P — stock de parents;
A,B — const.
La précision d'estimations des paramètres de l'équation (A et B) se détermine au moyen de critère de Student avec une probabilité de confiance Δ = 0.95 et le nombre de degrés de liberté N = 2.
Sont obtenus les paramèrtes de dépendance:
| A = 0.03753; | B = 0.000194 |
Le recrutement et les précalculs selon la méthode de Champman sont présentés au tableau 5.
| Année | Données de départ | Recrutement précalculé | écarts R et R', % | |
|---|---|---|---|---|
| recrutement R (abondance du groupe d'âge I selon l'APV) | stock de parents E (abondance du groupe d'âge 2- 7 selon l'APV) | R' = A.E3/2-BE2 | ||
| 1981 | 26947.63 | 12522.07 | 22107.63 | 18.0 |
| 1982 | 34985.75 | 12894.88 | 22631.52 | 35.0 |
| 1983 | 30729.21 | 20719.29 | 28475.19 | 6.3 |
| 1984 | 22154.60 | 28930.56 | 21966.69 | 1.0 |
| 1985 | 16033.21 | 29524.21 | 20933.63 | 30.0 |
| 1986 | 28443.76 | 25628.75 | 26292.56 | 0.92 |
| 1987 | 26326.30 | 20021.09 | 28355.25 | 1.1 |
Le taux de recrutement pour 1989 calculé selon le modéle de Chapman représente 28 milliards d'exemplaires. Il est très proche au taux moyen de plusieures années (26533 millions d'ex.).
En tant que critère d'utilisation de ce modèle il a été déterminé le coefficient de corrélation entre le recrutement calculé selon l'APV et le recrutment précalculé selon le modèle. Il est de 0.76. Le coefficient assez élevé de corrélation confirme l'utilisation correcte de cette dépendance. A l'heure actuelle on sait que ce sont les conditions thermiques et l'intensité de l'upwelling qui constituent un des facteures essentiels du milieu faisant leur effet sur l'apparition de générations fécondes de sardine. Dans les années où ont apparu les générations fécondes (1981, 1982) il a été observé un maximum bien prononcé de température en période précédant la ponte. La ponte commençait impétueusement en novembre—décembre et se passait très vite. Son pic d'hiver dépasse de beaucoup celui de printemps. Ensuite la température baissait vers le minimum d'hiver, la diminution étant de 3.8–6.0°. La période la plus froide était assez courte, l'élévation de température au printemps et en été était énergique. Dans les années “maigres” (1983–1984) la période de baisse de température en automne- hivers est étendue, les gradients de température ne sont pas hauts, le rechauffement de printemps est tardif et se passe lentement jusqu'au mois de juillet. L'amplitude annuelle de température est plus étroite et, ce qui est l'essentiel, la période froide est plus longue. Cela pourra avoir un effet négatif sur les jeunes poissons Les conditions de la saison de ponte 1987/88 (XI.87-IY.88): l'upwelling faible modéré (inférieur à la norme), l'alizé faible — permettent de supposer que la génération de 1988 sera aussi soit au niveau moyen de les dernièrs années, soit au niveau plus élevé.
La répartition de prises commerciales, de coefficient de mortalité par pêche, la biomasse et l'abondance sont présentés à tab. 3, 4, 5, 6.
| Longueur, cm | I984 | I985 | I986 | I987 | I988X |
|---|---|---|---|---|---|
| 8 | 0,0I | ||||
| 9 | 0,05 | 0,0I | |||
| I0 | + | 0,04 | 0,03 | ||
| II | 0,I | 0,0I | 0,03 | 0,08 | 0,03 |
| I2 | 0,5 | 0,04 | 0,4 | 0,4 | 0,03 |
| I3 | I,6 | 0,I | I,0 | I,3 | 0,2 |
| I4 | 2,I | 0,5 | I,I | 3,5 | I,I |
| I5 | I,3 | I,4 | 0,9 | 4,6 | 3,I |
| I6 | I,0 | I,4 | 0,6 | 2,7 | 5,I |
| I7 | 5,7 | 7,9 | I,7 | 2,4 | 6,0 |
| I8 | 27,8 | 37,0 | 9,0 | 7,8 | I5,3 |
| I9 | 39,0 | 39,95 | 3I,8 | 25,3 | 30,3 |
| 20 | I7,0 | I0,3 | 30,0 | 24,4 | 23;5 |
| 2I | 3,7 | I,3 | I6,7 | 24,4 | I0,6 |
| 22 | 0,2 | 0,I | 5,9 | 2,8 | 3,9 |
| 23 | + | 0,8 | 0,3 | 0,6 | |
| 24 | + | 0,06 | 0,02 | - | |
| 25 | + | 0,0I | |||
| Longueur moyenne (cm) | I9,09 | I9,02 | 20,07 | I9,69 | I9,5I |
| Poids moyen (Kg) | 0,074 | 0,073 | 0,09I | 0,097 | 0,085 |
| Effectif | I27780 | 7643 | 28633 | 69I02 | 38668 |
| Age (ans) | I984 | I985 | I986 | I987 | I988X |
|---|---|---|---|---|---|
| I | 3,6 | I,9 | 4,0 | 6,2 | 3,9 |
| 2 | I9,0 | 20,2 | I9,9 | II,3 | I4,7 |
| 3 | 46,2 | 55,0 | 35,2 | 26,7 | 33,6 |
| 4 | 25,3 | 2I,6 | 25,4 | 3I,5 | 30,3 |
| 5 | 5,8 | I,2 | 9,8 | I9,3 | I4,5 |
| 6 | 0,08 | 0,07 | 5,0 | 4,9 | 2,9 |
| 7 | 0,02 | 0,03 | 0,7 | 0,I | 0,I |
| Age moyen (ans) | 3,I | 3,0 | 3,3 | 3,6 | 3,5 |
| Age(ans) | 1982 | 1983 | 1984 | 1985 | 1986 | 1987 | 1988 |
|---|---|---|---|---|---|---|---|
| I | 0,0002 | 0,0027 | 0,0070 | 0,0043 | 0,0I27 | 0,0I25 | 0,0I00X |
| 2 | 0,0286 | 0,0369 | 0,06I0 | 0,0624 | 0,0864 | 0,0770 | 0,0660 |
| 3 | 0,2482 | 0,377I | 0,4249 | 0,3224 | 0,2279 | 0,2837 | 0,6825 |
| 4 | 0,9II8 | 0,6953 | 2,2920 | 0,4755 | 0,3865 | 0,62I8 | I,4220 |
| 5 | I,586I | I,0721 | I,3497 | I,I330 | 0,6937 | I,2368 | I,6662 |
| 6 | I,9I20 | 0,2I42 | 0,0927 | 0,0578 | 3,I658 | 2,885I | I,5034 |
| 7 | I,9I2I | 0,2I43 | 0,0927 | 0,0578 | 3,I657 | 2,8850 | I,5034 |
* valeur corrigée
| Classe d'âge | Coefficient de mortalité naturelle | I982 | I983 | I984 | I985 | I986 | I987* | I988X |
|---|---|---|---|---|---|---|---|---|
| I | 0,600 | 3,28 | 7I,26 | I62,00 | 7I,9I | I52,08 | 266,50 | I97,08 |
| 2 | 0,600 | I60,92 | 403,07 | 855,00 | 764,55 | 756,60 | 485,80 | 742,83 |
| 3 | 0,600 | 627,25 | 972,49 | 2079,00 | 208I,7I | I338,3I | II47,80 | I697,90 |
| 4 | 0,600 | 6I0,82 | 625,76 | II38,50 | 8I7,54 | 965,7I | I354,20 | I53I,I4 |
| 5 | 0,600 | I74,05 | I49,20 | 26I,00 | 45,40 | 372,60 | 829,70 | 732,72 |
| 6 | 0,600 | 39,4I | 4,45 | 3,60 | 2,65 | I90,I0 | 2I0,70 | I46,55 |
| 7 | 0,600 | 26,27 | 0,60 | 0,90 | I,I4 | 26,6I | 4,30 | 5,05 |
| Total | I642,0 | 2226,9 | 4500,0 | 3784,9 | 3802,0 | 4299,0 | 5053,3 |
| Age,(ans) | I982 | I983 | I984 | I985 | I986 | I987 | I988X |
|---|---|---|---|---|---|---|---|
| I | 26947,63 | 34985,75 | 30729,2I | 22I54,60 | I6033,2I | 28443,76 | 26326,30 |
| 2 | 7576,2I | I4786,77 | I9I48,57 | I6746,36 | I2I06,22 | 8688,29 | I54I5,89 |
| 3 | 3749,II | 4040,64 | 782I,52 | 9886,84 | 8634,34 | 6094,2I | 44I5,04 |
| 4 | I299,30 | I605,36 | I520,88 | 2806,66 | 3930,74 | 3772,85 | 25I8,55 |
| 5 | 270,25 | 286,52 | 439,59 | 84,35 | 957,46 | I465,74 | IIII,88 |
| 6 | 56,35 | 30,36 | 53,82 | 62,56 | 23I,49 | 262,57 | 233,54 |
| 7 | 37,56 | 4,57 | I3,45 | 26,92 | 32,40 | 5,36 | 8,05 |
| Total | 39936,4 | 55739,9 | 59727,I | 5I768,3 | 4I925,9 | 48732,7 | 50029,2 |
| Age (ans) | I982 | I983 | I984 | I985 | I986 | I987 | I988X |
|---|---|---|---|---|---|---|---|
| I | 835,38 | I084,56 | 952,6I | 686,79 | 497,03 | 88I,76 | 8I6,I2 |
| 2 | 43I,84 | 842,85 | I09I,47 | 954,54 | 690,05 | 495,23 | 878,7I |
| 3 | 28I,I8 | 303,05 | 586,6I | 74I,5I | 647,57 | 457,07 | 33I,I3 |
| 4 | II0,44 | I36,46 | I29,27 | 238,57 | 334,II | 320,69 | 2I4,08 |
| 5 | 27,84 | 29,5I | 45,28 | 48,69 | 98,62 | I50,97 | II4,52 |
| 6 | 6,76 | 3,64 | 6,46 | 7,5I | 27,78 | 3I,5I | 28,02 |
| 7 | 4,92 | 0,60 | I,76 | 3,53 | 4,24 | 0,70 | I.05 |
| Total | I698,4 | 2400,6 | 28I3,4 | 268I,I4 | 2299,4 | 2337,9 | 2383,6 |
* Données préliminaires
| I979 | I980 | I98I | I982 | I983 | I984 | I985 | I986 | I987 | I988 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | ||||||||||
| 6 | ||||||||||
| 7 | ||||||||||
| 8 | 0,I | 0,0I | ||||||||
| 9 | 0,3 | 0,I | 0,05 | 0.01 | ||||||
| I0 | 0,9 | 0,I | 0,04 | 0.03 | ||||||
| II | I,0 | 0,7 | 0,I | 0,0I | 0,03 | 0,08 | 0.03 | |||
| I2 | 0,5 | I,0 | 0,2 | I,I | 0,5 | 0,04 | 0,4 | 0,4 | 0.03 | |
| I3 | I,6 | 0,4 | 0,4 | 0,07 | 0,5 | I,6 | 0,I | I,0 | I,3 | 0.2 |
| I4 | 3,7 | 0,3 | I,2 | 0,05 | 0,2 | 2,I | 0,5 | I,I | 3,5 | 1.1 |
| I5 | 4,9 | 0,3 | I,3 | 0,08 | 0,7 | I,3 | I,4 | 0,9 | 4,6 | 3.1 |
| I6 | I,6 | 0,6 | I,5 | 0,3 | I,8 | I,0 | I,4 | 0,6 | 2,7 | 5.1 |
| I7 | 0,3 | 4,5 | 4,4 | 2,9 | 7,4 | 5,7 | 7,9 | I,7 | 2,4 | 6.0 |
| I8 | I,I | I5,4 | I4,5 | I4,9 | 24,I | 27,8 | 37,0 | 9,0 | 7,8 | 15.3 |
| I9 | I7,2 | 28,2 | 33,7 | 22,2 | 32,8 | 39,0 | 40,0 | 3I,8 | 25,3 | 30.3 |
| 20 | 42,3 | 29,2 | 30,2 | I8,3 | 22,7 | I7,0 | I0,3 | 30,0 | 24,4 | 23.5 |
| 2I | 23,0 | I3,5 | I0,2 | 2I,8 | 6,6 | 3,7 | I,3 | I6,7 | 24,4 | 10.6 |
| 22 | 3,3 | 3,4 | 2,I | I4,2 | I,0 | 0,2 | 0,I | 5,9 | 2,8 | 3.9 |
| 23 | 0,5 | 0,8 | 0,3 | 4,3 | 0,I | 0,8 | 0,3 | 0.6 | ||
| 24 | 0,I | 0,9 | 0,06 | 0,02 | ||||||
| 25 | 0,0I | |||||||||
| 26 | ||||||||||
| 27 | ||||||||||
| 28 | ||||||||||
| Nbre d'ex. | 2408 | 689I4 | 42246 | I4635 | 4948I | I27780 | 7643 | 28633 | 69I02 | 38668 |
| Long. moy.,cm | I8,97 | I9,67 | I9,70 | 20,59 | I9,28 | I9,08 | I9,02 | 20,07 | I9,69 | 19.51 |
| Poids moy.,kg | 0,090 | 0,094 | 0,095 | 0,I05 | 0,090 | 0,087 | 0,073 | 0,09I | 0,097 | 0.085 |
| Longueur,cm | Mois | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IY | Y | YI | YII | YIII | IX | X | XI | XII | |
| 8 | 0,I | |||||||||||
| 9 | - | 0,0I | ||||||||||
| I0 | 0,5 | 0,09 | ||||||||||
| II | 0,I | 0,I | 0,I | 0,3 | 0,2 | |||||||
| I2 | I,0 | 0,0I | I,5 | 0,2 | I,0 | 0,3 | ||||||
| I3 | 4,6 | 0,0I | 0,05 | 8,6 | I,2 | I,9 | I,I | |||||
| I4 | 8,0 | 0,09 | 0,I | 30,5 | I4,7 | I,7 | 2,3 | |||||
| I5 | 7,4 | 0,5 | 0,4 | 3I,2 | 26,7 | 2,7 | 2,7 | |||||
| I6 | 4,9 | I,8 | 4,4 | I2,5 | I3,2 | 2,3 | 3,6 | |||||
| I7 | 0,I | 6,9 | 2,5 | I4,8 | 0,I | 3,8 | 5,2 | 2,8 | 4,3 | |||
| I8 | 7,9 | 20,2 | 7,7 | 43,7 | I0,7 | I,I | I,0 | 4,0 | 6,6 | 23,6 | ||
| I9 | 38,5 | 27,7 | 29,8 | 26,0 | 44,3 | 0,7 | I4,4 | I2,0 | 24,3 | 35,6 | ||
| 20 | 40,3 | I6,5 | 39,0 | 8,7 | 34,5 | 2,4 | 27,9 | I3,2 | 27,3 | I9,9 | ||
| 2I | II,I | 2,2 | I5,5 | I,7 | 9,4 | 2,I | 29,9 | 6,7 | 2I,I | 5,2 | ||
| 22 | 2,0 | 0,4 | 2,9 | 0,I | 0,9 | 3,2 | 22,I | 2,I | 7,3 | I,0 | ||
| 23 | 0,I | 0,I | 0,2 | 0,04 | 0,I | 2,0 | 4,4 | 0,I | 0,7 | 0,I | ||
| Total | I3472 | 9848 | I7764 | 2I200 | 3300 | 952 | 3300 | 725 | 926 | I5803 | ||
| Mois | Longueur, cm | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 | I0 | II | I2 | I3 | I4 | I5 | I6 | I7 | I8 | I9 | 20 | 2I | 22 | 23 | 24 | Total | |
| I | 0,02 | 0,08 | 0,I | 0,I | 0,7 | 2,5 | 2,7 | 2,4 | 3,5 | I9,I | 36,0 | 2I,9 | 8,5 | 2,3 | 0,I | =24285 | |
| II | 0,3 | 2,4 | 4,0 | 7,5 | 7,3 | 6,7 | 8,6 | 20,5 | 22,I | I3,4 | 4,4 | 2,2 | 0,6 | =8069 | |||
| III | I,0 | 7,7 | I0,5 | 6,7 | II,5 | 38,6 | 20,0 | 3,4 | 0,6 | =I2383 | |||||||
| IY | 0,2 | I,8 | 6,5 | I0,5 | I7,7 | 3I,0 | 24,3 | 6,I | I,7 | 0,2 | =6936 | ||||||
| Y | 0,2 | 2,2 | 4,0 | 5,2 | I5,2 | 33,7 | 26,3 | II,2 | I,4 | =I960 | |||||||
| YI | 0,7 | 4,3 | I3,6 | 36,5 | 30,5 | I3,0 | I,4 | =384 | |||||||||
| YII | 0,3 | 0,3 | 32,2 | I7,2 | 25,4 | I8,9 | 4,8 | 0,9 | =I286 | ||||||||
| YIII | 0,6 | 3,0 | 30,I | 3I,4 | 2I,4 | I2,2 | I,3 | =760 | |||||||||
| IX | |||||||||||||||||
| X | 0,08 | I,4 | 7,6 | 6,9 | 5,8 | 5,9 | 3,0 | 6,3 | I3,8 | 23,6 | I4,3 | 8,6 | 2,7 | 0,02 | =I0I9 | ||
| XI | 0,7 | 6,4 | I9,5 | 40,0 | 26,3 | 6,6 | 0,5 | =I370 | |||||||||
| XII | I0,7 | 43,0 | 29,3 | II,7 | 4,3 | 0,7 | 0,3 | =900 | |||||||||
| I | II | III | IY | Y | YI | YII | YIII | IX | X | XI | XII | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| II | 0,03 | |||||||||||
| I2 | 0,I | 0,03 | ||||||||||
| I3 | 0,4 | 0,6 | ||||||||||
| I4 | 0,9 | I,5 | ||||||||||
| I5 | 0,05 | 0,0I | 0,7 | I,0 | ||||||||
| I6 | 0,I | 0,2 | 0,2 | 0,3 | 0,5 | |||||||
| I7 | 3,0 | 3,4 | I,2 | 0,I | I,0 | |||||||
| I8 | IO,9 | I7,9 | I0,4 | 0,6 | I,5 | I0,7 | ||||||
| I9 | 44,6 | 50,8 | 22,0 | I,9 | I7,I | 40,I | ||||||
| 20 | 27,8 | 2I,5 | 24,4 | I7,8 | 35,9 | 33,6 | ||||||
| 2I | I2,I | 5,4 | 26,7 | 38,9 | 29,3 | 8,5 | ||||||
| 22 | I,4 | 0,7 | II,9 | 33,7 | I3,0 | 2,I | ||||||
| 23 | 0,05 | 3,0 | 4,5 | 2,6 | 0,3 | |||||||
| 24 | 0,2 | 0,I | 0,6 | 0,03 | ||||||||
| 25 | 0,0I | |||||||||||
| Total | 59I6 | 44I8 | 330I | 3000 | 3500 | 8498 |