3. MEASURING HORIZONTAL ANGLES
3.0 Introduction
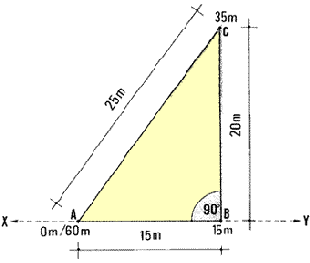
|
What is a horizontal angle?
|
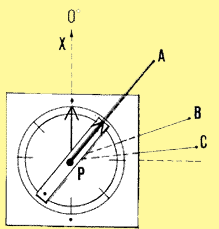
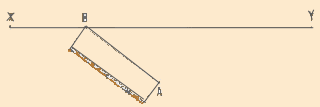
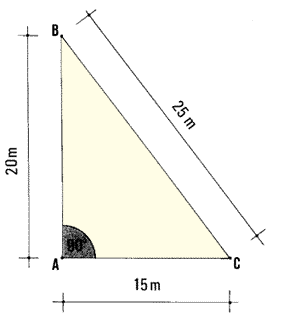
| 1. In topography, the angle made by two ground lines is measured
horizontally, and is called a horizontal angle. You
may replace these ground lines by two lines of sight AB and AC.
These lines of sight are directed from your eyes, which form the summit
A of the angle BAC, towards permanent landmarks such as
a rock, a tree, a termite mound, a telephone pole or the corner of a building.
|
|
 The lines of sight in angle BAC
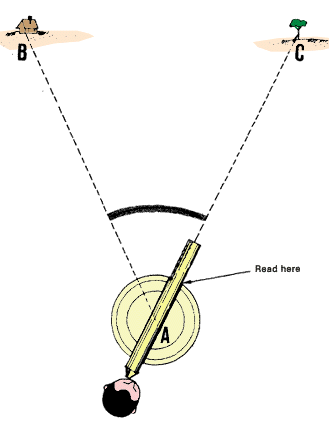
The lines of sight in angle BAC |
| |
|
|
Expressing horizontal angles
|
|
|
|
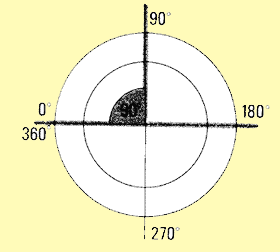
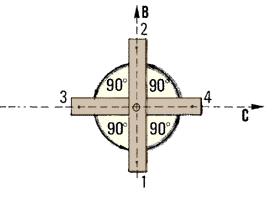
2. Horizontal angles are usually expressed in degrees. A full
circle is divided into 360 degrees, abbreviated as 360�.
Note from the figure these two particular values:
- a 90� angle, called a right angle, is made of two perpendicular
lines. The corners of a square are all right angles;
- a 180� angle is made by prolonging a line. In
fact, it is the same as a line.
3. Each degree is divided into smaller units:
- 1 degree = 60 minutes (60');
- 1 minute = 60 seconds (60").
These smaller units, however, can only be measured with high-precision
instruments.
|
|
 Horizontal angle BAC
Horizontal angle BAC |
| |
|
| |
 A circle has 360 degrees
A circle has 360 degrees |
Some general rules about angles
|
|
4. A rectangular or a square shape has four straight sides and four interior
90� angles. The sum of these four interior angles is equal to 360�.
5. The sum of the four interior angles of any four-sided shape is also
equal to 360�, even if they are not right angles.
6. lt will be useful for you to remember the general rule that the
sum of the interior angles of any polygon (a shape with several
sides) is equal to 180� times the number of sides, (N), minus 2,
or:
|
Sum angles = (N - 2) x 180�
|
|
|
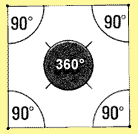 90� + 90� + 90� + 90� = 360� 4 sides = 360�
90� + 90� + 90� + 90� = 360� 4 sides = 360� |
| |
|
|
|
Examples
(a) A piece of land has five sides. The sum of its interior angles
equals (5-2) x 180� = 540�.
(b) A piece of land has eight sides. The sum of its interior angles
equals (8-2) x 180� = 1080�.
|
|
 90� + 90� + 90� + 90� = 360� 4 sides = 360�
90� + 90� + 90� + 90� = 360� 4 sides = 360� |
| |
|
|
 60� + 110� + 150� + 40� = 360�
4 sides = 360�
60� + 110� + 150� + 40� = 360�
4 sides = 360� |
|
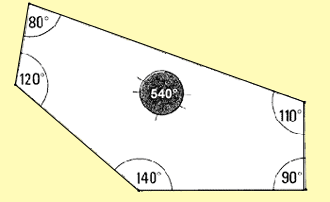 120� + 80� + 110� + 90� + 140� = 540�
5 sides = 540�
120� + 80� + 110� + 90� + 140� = 540�
5 sides = 540� |
| 7. When you measure angles in a field, you
can check on the accuracy of your measurements by applying this basic rule.
Remember that the sum of the interior angles of any triangle equals
(3-2) x 180� = 180�. |
|
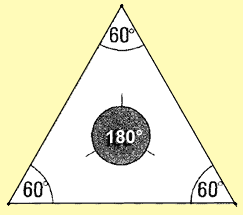 Triangle with equal sides: 60� + 60� + 60� = 180�
Triangle with equal sides: 60� + 60� + 60� = 180�
|
| |
|
|
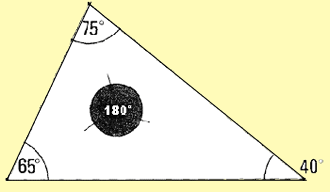 Any triangle: 65� + 75� + 40� = 180�
Any triangle: 65� + 75� + 40� = 180� |
|
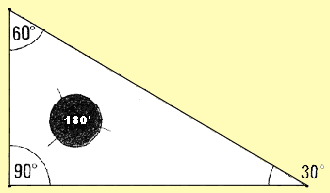 Right triangle: 90� + 60� + 30� = 180�
Right triangle: 90� + 60� + 30� = 180� |
Choosing the most suitable method
8. There are only a few ways to measure horizontal angles in
the field. The method you use will depend on how accurate a result you need,
and on the equipment available. Table 2 compares various methods
and will help you to select the one best suited to your needs.
Note:because 90� angles are very important in topographical surveys,
the measurement of these angles (used for laying out perpendicular lines) will
be discussed in detail.
|
TABLE 2
Horizontal angle measurement methods
| Section1 |
Method
|
Horizontal angle
|
Accuracy
|
Remarks
|
Equipment2
|
| 3.1* |
Home-made graphometer
|
Medium to large
|
Low
|
Best for 40-80 m
For angles greater than 10�
|
Graphometer
|
| 3.2** |
Magnetic compass
|
Medium to large
|
Medium
|
Best for 40-100 m
For angles greater than 10�
No magnetic disturbance
|
Compass
|
| 3.3* |
Compass or protractor
|
All sizes
|
Low to medium
|
Dry weather only
|
Simple compass, protractor, drawing sheet
|
| 3.3** |
Plane-table
|
All sizes
|
Low to medium
|
Dry weather only
|
Plane-table drawing paper
|
| 3.4* |
Right-angle method
|
Small
|
Medium to high
|
Perpendicular to be set out
|
Measuring line
|
| 3.5*** |
Theodolite or transit
|
All sizes
|
High
|
Useful on long distances
|
Transit level with graduated horizontal circle
|
| 3.6 |
Miscellaneous
|
Right-angle only
|
Medium to high
|
Adapt method to length of perpendicular
|
Various
|
1*Simple **More difficult
***Most difficult
2 In italics, equipment you can make yourself
from instructions in this book.
|
3.1 How to use the graphometer
|
|
1. A graphometer is a topographical instrument used to
measure horizontal angles. It is made up of a circle graduated in 360�
degrees. Around the centre of this circle, a sighting device can turn
freely. This device, called an alidade, makes it possible
to create a line of sight that starts from your eyes, passes through
the centre of the graduated circle, and ends at the selected landmark
or ranging pole. When in use, the graphometer is rested horizontally
on a stand.
2. You can build your own graphometer by following the instructions
below. It might be a good idea to ask a carpenter to help you.
|
|
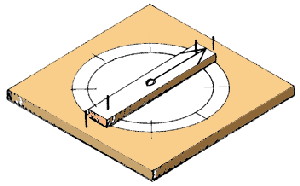 A graphometer
A graphometer
|
| |
|
|
Building your own graphometer
|
| 3. Begin building your graphometer with the graduated
circle given in Figure 1. You can make an enlarged
copy of it, or you can draw a copy of it using tracing paper. |
|
 Materials to build a graphometer
Materials to build a graphometer |
| |
|
|
|
4. Get a wooden board, 1 cm thick and 21 cm square.
5. Find its centre by drawing two diagonal lines on this board, from
opposite corners. The point where the lines cross is the exact
centre of the board.
6. Obtain one nut and bolt, about 1.5 cm long. At the centre of
the board, drill a hole into which the bolt will fit tightly.
On the bottom side of the board, drill the outside of the hole slightly
larger to fit the nut.
|
|
 Find the centre of the board and drill a hole there
Find the centre of the board and drill a hole there |
| |
|
|
| 7. Cut a hole of about the same size exactly at the centre
of the graduated circle (Figure 1). Glue this sheet of paper on to the wooden
board. Carefully align the central holes in the board and the circle,
and make sure the four sides of the sheet are parallel to the sides of
the board. You can do this easily by matching the two diagonal axes you
have drawn on the board with the circle graduations 45�, 135�, 225� and
315�, respectively. |
|
 Glue Figure 1 to the board
Glue Figure 1 to the board |
| |
|
|
| 8. If possible, protect the sheet of paper. To do this,
get a piece of transparent plastic sheet bigger
than the board, and stretch it over the front side of the board. Attach
it at the back with several thumbtacks. |
|
 Protect the paper with a sheet of plastic
Protect the paper with a sheet of plastic |
|
FIGURE 1
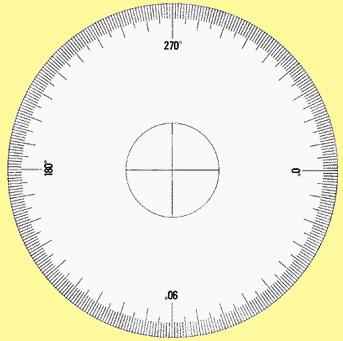 |
| 9. Now build the sighting device, called the mobile alidade.
Get a thin wooden ruler, 16 cm long and 3.5 cm wide. Find its centre, as
you did on the board, by drawing on it two diagonal lines from opposite
corners. Draw a line through this centre point parallel to the long sides
of the ruler. At the same point, drill a hole just a little larger than
the diameter of the bolt. Exactly on the central line
you have drawn, near each of its ends, drive a thin, headless
nail 4 to 5 cm long into the ruler. Be careful not to let the nails break
through to the other side of the ruler, and make sure you drive them in
vertically. Your alidade is now ready. |
|
 Find the centre of the ruler and drill a hole there
Find the centre of the ruler and drill a hole there |
| |
|
|
|
10. To attach the alidade to the base, place a thin washer
over the hole in the board you have prepared. Align the central hole of
the alidade over the washer. Add a washer above the alidade and one below
the wooden board, aligned with the central holes. Push the bolt through
all the washers and holes and tighten the nut, so that the alidade will
turn around under slight pressure.

Drive the sighting nails into the ruler along the centre line
|
|
 Bolt your alidade to the base
Bolt your alidade to the base |
| |
|
|
| 11. On the board, along the 0� to 180� line, but outside the
graduated circle, drive in two headless nails like the ones placed in the
alidade. These will form a second line of sight. Clearly mark the top half
of this line of sight with an arrow pointing exactly at the 0� graduation.
12. On one end of the alidade, draw an arrow from the centre-bolt, along
the median line, and through the nail at the end. The tip of the arrow
should point exactly to the end of the median line above this nail. This
arrow will help you to determine the graduation when you need to read
it.
|
|
 Mark your sighting line with nails and arrows
Mark your sighting line with nails and arrows |
| |
|
|
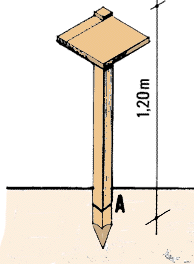
| 13. To make your measurements more accurate, get a stake about
1.20 m high, and sharpen one end into a point. Drive this end into the ground
and rest your graphometer on the other end as you measure. |
|
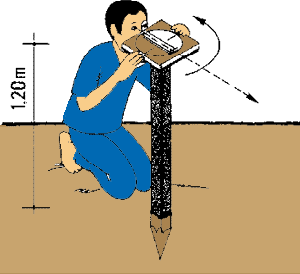 Using the graphometer with a stake to steady it
Using the graphometer with a stake to steady it |
Using the home-made graphometer to measure horizontal angles
|
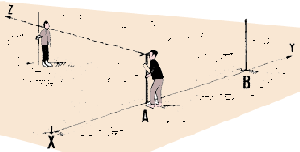
| 14. Orient the graphometer with its 0� to
180� sighting line on the left side AB of the angle you need to measure.
Position the graphometer so that its centre, the bolt, is exactly
above point A on the ground, the station, from which you will
measure horizontal angle BAC. For more accuracy, you can use
a plumb-line (see Section 4.8). If you have attached your
graphometer by its centre to a stake, drive the pointed end of the stake
vertically into the ground at the angle's summit A.
15. Check that the graphometer is as horizontal as possible. To do this,
place a round pencil on the board. If the pencil does not roll off, turn
it 90� degrees and check again. When the pencil does not roll off in either
direction, the graphometer is horizontal.
|
|
 Angle BAC
Angle BAC |
| |
 When the pencil does not roll off in either
When the pencil does not roll off in either
direction, the graphometer is horizontal |
16. Check again that the 0� to 180� sighting line is aligned well
with the left side AB of the angle you need to measure. Adjust it if necessary,
making sure not to disturb either the position of the station or the horizontality
of the graphometer.
 Sight from A to B
Sight from A to B |
|
 Make sure the 0�-180� line is on line AB
Make sure the 0�-180� line is on line AB |
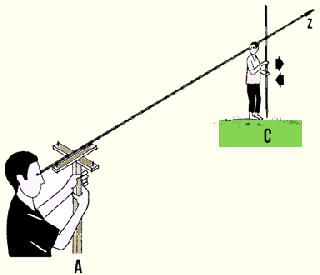
17. Move the mobile alidade around to the right until its sighting
line lines up with the right side AC of the angle BAC.
18. Read the graduation above the arrow on the central line of the mobile alidade.
This is the value of angle BAC in degrees.
 Now sight from A to C, moving the alidade
Now sight from A to C, moving the alidade
but not the graphometer |
|
|
Note: it is easier to position the graphometer above
the station on the ground and make it horizontal without sighting with the 0�
to 180� line. Just make sure that the left side AB of the angle is to the
right of this 0� to 180� line. Then take two readings, using the mobile
alidade for both the left side AB and the right side AC of the angle. The value
of the angle equals the difference between these two readings.
Example
-
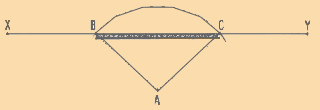
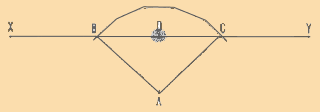
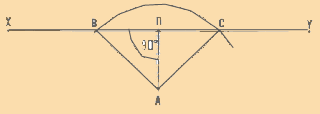
Two lines, X and Y, form an angle XAY at station A.
-
Clearly define lines X and Y by placing ranging poles at B
and C, for example.
-
Position the graphometer at station A, with its 0�-180� sighting
line oriented to the left of AB.
-
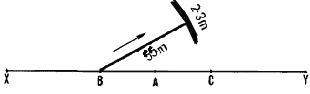
With the mobile alidade, sight at ranging pole B and read
the graduation, AB = 23�.
-
Turn the mobile alidade to sight at ranging pole C and read
the graduation, AC = 75�.
-
The angle BAC equals 75� - 23� = 52�.
|
|
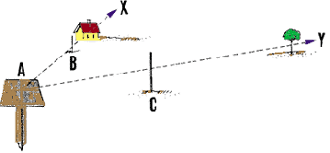 Set the graphometer at point A
Set the graphometer at point A |
| |
|
|
| |
|
 Take the readings of lines AB and AC
Take the readings of lines AB and AC |
| |
|
|
| |
|
|
Measuring an angle with an inaccessible summit
|
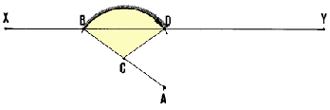
| 19. To use the preceding method, you must be
able to reach the summit A of the angle. When you cannot reach the summit,
you have a choice of two methods. |
|
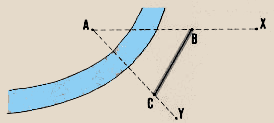 Measure angles CBA and BCA to calculate angle BAC
Measure angles CBA and BCA to calculate angle BAC |
| |
|
|
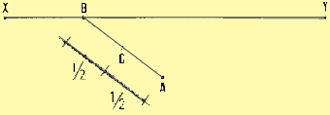
20. You can set out a line CB from any point on
one of the angle's sides to any point on its other side, making a triangle
within the angle. Measure the two angles made by this new line and the angle's
sides. The angle at the inaccessible summit of the triangle you have made
equals the difference between 180� and the sum of the other two angles.
|
|
 Summit A is across a river
Summit A is across a river |
| |
|
|
|
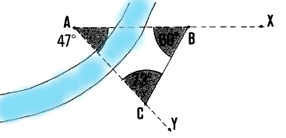
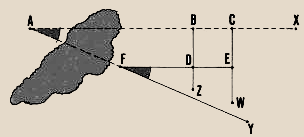
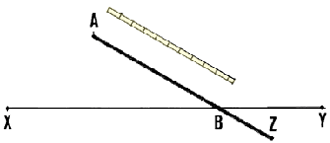
Example
You cannot reach summit A to measure angle XAY. From point B on
line AX, set out Iine BC, where point C is on line AY. At station B, measure
angle CBA = 60�; at station C, measure angle BCA = 73�. Calculate angle
XAY = 180� - (60� + 73�) = 47�.
Set out line BC
|
|
 Angle BAC = angle XAY
Angle BAC = angle XAY |
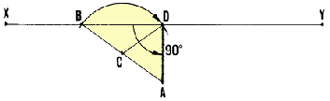
| 21. Or you can lay out
two perpendicular lines (see Section 3.6) from two points
on one of the angle's sides. On each of these new lines, measure an equal
distance. Join these two points with a line, which will be parallel to one
of the angle's sides. Prolong the line until it intersects the other side
of the original angle. At the intersection point, measure the new angle
which is equal to the summit angle. |
|
 Summit A lies behind an obstacle
Summit A lies behind an obstacle |
| |
|
|
|
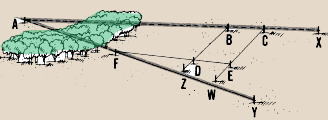
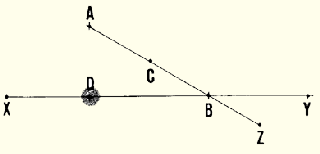
Example
You cannot reach summit A to measure angle XAY. On line AX, mark
two points B and C. From these points, lay out perpendiculars BZ and CW.
On these perpendiculars, measure segments of equal length from line AX,
calling them segments BD and CE. Connect points E and D to form a line,
which is parallel to AX. Then extend line ED until it intersects line
AY at point F. From a station at point F, measure angle EFY. Its measurement
will be the same as that of angle XAY.
|
|
 Set out perpendiculars BZ and CW
Set out perpendiculars BZ and CW |
| |
|
|
 Find line ED, and prolong it to F
Find line ED, and prolong it to F |
|
|
| |
|
|
 Measure angle EFY
Measure angle EFY |
|
 Angle EFY = angle XAY
Angle EFY = angle XAY |
Measuring consecutive angles
|
|
22. At one station, you may have to measure several angles formed by
a series of lines which meet at one point, called converging lines.
The angles they form are called consecutive angles.
23. To measure consecutive angles from one station, first measure all
the angles by using the line furthest left as the reference line.
Then, by simple substraction, you can calculate the individual angles.
|
|
 XPA, APB and BPC are consecutive angles
XPA, APB and BPC are consecutive angles |
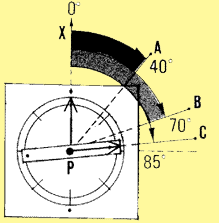
Example
At station P, you have to measure three consecutive angles, XPA, APB and
BPC. Take PX (furthest to the left) as the reference line and align the 0� graduation
of the graphometer with it. Keeping the graphometer fixed in that position,
move the mobile alidade around and measure each angle in turn (in this case,
angles XPA = 40�, XPB = 70� and XPC = 85�). Calculate the consecutive angles
as follows: XPA = 40�, as directly measured;
APB =XPB -XPA = 70� - 40� = 30�; BPC = XPC - XPB = 85� - 70�= 15�.
 Measure each angle from the 0� line...
Measure each angle from the 0� line... |
|
 ... then calculate the individual values
... then calculate the individual values |
3.2 How to use the magnetic compass
|
What is a magnetic compass?
|
|
1. A simple magnetic compass is usually a magnetic needle
which swings freely on a pivot at the centre of a graduated ring.
The magnetic needle orients itself towards the magnetic north*.
The needle is enclosed in a case with a transparent cover to protect it.
2. Orientation compasses are often mounted on a
small rectangular piece of hard transparent plastic. They have a sighting
line in the middle of a movable mirror. If you tilt this mirror, you can
see both the compass and the ground line.
|
|
 A simple compass
A simple compass |
| |
|
|
 An orientation compass
An orientation compass |
|
 A prismatic compass
A prismatic compass |
| |
|
|
| 3. Prismatic compasses give more accurate readings.
To use one, hold it in front of your eyes so that you can read its scale.
You can see the scale through a lens by means of a prism. Then
turn the compass horizontally until the cross-hair is aligned with the ground
mark (an optical illusion makes the hairline appear to continue above the
instrument's frame). At the same time, the reading is shown on the compass-graduated
circle behind the actual hairline. Since the graduated ring automatically
orients itself, the reading directly gives the measure of the angle
between magnetic north* and the line of sight (see also next paragraphs). |
|
|
| |
|
|
| 4. A magnetic needle always points in the same
direction - the magnetic north. This is why compasses are often
used for orientation in the field and for mapping surveys (see, for example,
Section 7.1 of this manual). The part of the compass needle pointing to
the magnetic north is clearly marked, usually in red or a dark colour.
5. The outside ring of a compass is usually graduated in 360�.
The 0� or 360� graduation is marked N, which means north.
In most compasses, the graduation increases clockwise
and the following letters can be read on the circle:
- at 90�, E for east;
- at 180�, S for south;
- at 270�, W for west.
Intermediate orientations, such as NE, SE, SW and NW, are also shown
sometimes.
|
|
|
Using the compass to measure horizontal angles
|
| 6. You have learned that the needle of a compass always points
in the same direction - the magnetic north. To use this direction
as a reference, you need to make sure that the 0� graduation lines
up with it. If the 0� graduation of your compass does not line up
exactly with the magnetic north, turn the external ring until it does. Only
then can you use your compass as described below. |
|
|
| |
|
|
|
7. At any station, the angle formed by the magnetic
north and a straight line is called the azimuth of that line.
This magnetic azimuth from north, called azimuth or Az, is
always measured clockwise, from the magnetic north to the line.
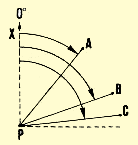
Example
Azimuth OA = 37�;
Az OB = 118�; Az OC = 230�; Az OD = 340�.
|
|
|
Measuring the azimuth of a line
|
|
8. To measure the azimuth of a line, take a position at any point on
the line. Holding your compass horizontally, sight at another point on
the line, such as a ranging pole. To do this, align the sighting marks
of the compass with this point. If necessary (as with some orientation
compasses), first align the 0� graduation N exactly with the northern
point of the magnetic needle. At the intersection of the sighting line
and the graduated ring, read the azimuth of the line from the point of
observation. The reading will be most accurate if you limit the length
of the sighting line to 40 to 120 m. Place more ranging poles on
the line as you need them.
Note: to check the value of an azimuth, turn around and look
in the opposite direction at another point on the same line. Read the
measurement of this azimuth, which should differ by 180�. Usually,
the difference will not be exactly 180�. If the difference is small enough,
you can ignore it, or correct it by averaging the two readings. If it
is large, you have made an error which you should correct.
|
|
 Check the azimuth in both directions
Check the azimuth in both directions |
| |
|
|
| |
|
|
| |
|
|
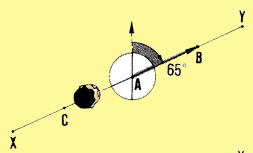
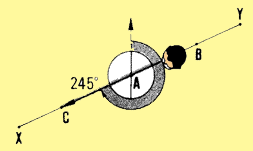
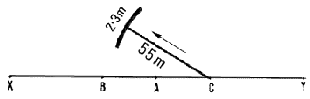
| Example
To determine the azimuth of line XY, marked by ranging poles B and
C. stand with the compass at station A in the middle of the line. Sight
forward with the compass at ranging pole B and read azimuth AB = 65�.
This is the forward azimuth. Check this value by turning around, sight
backward with the compass at ranging pole C and read the rear azimuth,
AC = 245�. The difference between the two azimuths is 245� - 65� = 180�,
which means that the measurements are accurate.
|
|
|
| |
|
|
| |
|
|
| |
|
|
 Forward azimuth = 65�
Forward azimuth = 65� |
|
 Rear azimuth = 245�
Rear azimuth = 245� |
Measuring
a horizontal angle
|
|
9. To measure a horizontal angle, stand at the angle's summit and measure
the azimuth of each of its sides; calculate the value of the angle as
follows.
10. If the magnetic north falls outside the angle, calculate the value
of the angle between the two lines of sight as equal to the difference
between their azimuths. Always subtract the smaller number from
the larger one, no matter which azimuth you read first. Just be sure that
the magnetic north is not inside the angle.
Example
(a) Angle BAC; Az AB = 25�; Az AC = 64�;
BAC = 64�- 25� = 39�
|
Angle XAY = Az. YA - Az. XA
|
|
|
|
| |
|
|
| (b) You have to measure angle XAY; measure the azimuth
of AX = 265�; measure the azimuth of AY = 302�; the angle XAY measures 302�
- 265� = 37�. |
|
|
| |
|
|
| 11. If the magnetic north falls inside the angle, the angle
between the two lines of sight is equal to 360� minus the difference
between their azimuths. To calculate the angle, first find the difference
as you did in step 10, above, then subtract this number from 360�.
Example
You have to measure angle EAF; measure the azimuth of AE = 23�;
measure the azimuth of AF = 310�; angle EAF measures 360� - (310�- 23�)
= 73�.
|
Angle EAF = 360� - (Az. AF- Az. AE)
|
Note: to check on your measurements and to improve their accuracy,
you should repeat each measurement three times from the same station.
These measurements should give similar results.
|
|
|
| |
|
|
|
12. If you cannot reach the summit of the angle, separately measure the
azimuth of each line from another point situated on it (see step 8, above)
and calculate the angle as in step 9, above.
Example
You have to measure angle BAC, but the summit A is not accessible;
at point X on AB, measure azimuth XB = 39�; at point Y on AC, measure
azimuth
YC = 142�. Since the magnetic north falls outside angle BAC, calculate
its measurement as 142�- 39� = 103�.
|
Angle BAC = Az. YC - Az - XB
|
|
|
|
Surveying a polygonal site
|
|
13. When you must survey a polygonal* site, measure the azimuth
of two sides from each of the summits. For each side of the polygon,
you will thus determine one forward and one rear azimuth. You
can then check on the accuracy of the two azimuths, which should differ
by 180�. If they do not, subtract 180� from the greatest azimuth and calculate
the average between this value and the smallest azimuth. To do this, add
the two numbers and divide by two. From averages like this for the other
pairs of azimuths, you can calculate the interior angles of the polygon,
as explained above.
Note: to make a final check, add all the interior
angles. This sum should equal (N - 2) x 180�, N being the
number of sides of the polygon (see Section 3.0, step 6).
|
|
|
| |
|
|
| Example
You have to survey polygon ABCDEA. From summit A measure forward
Az AB = 40� and rear Az AE = 120�. Move clockwise to summit B and measure
rear Az BA = 222� and forward Az BC = 110�. Proceed in the same way from
the other three summits C, D and E. In total, you get ten measurements.
Mark them down in your notebook. (See columns 1 and 2 where the order
of measurements is shown in parentheses.)
Calculate the values of column (3) by subtracting 180� from the
largest azimuth measured at each summit. This gives you values which should
be equal to the smallest observed azimuths, written either in column 1
or in column 2, according to the position of the summit.
|
|
|
| |
|
|
- When the values are equal to the smaller observed azimuths (summits
C,E), transfer these measurements to columns 4 or 5, according to the
type of azimuth they represent.
- When they are not equal (summits A, B, D):
- Use columns 1 or 2 and column 3 to calculate the average smallest
azimuth. To do this, add the measurement of the smallest Az from column
1 or 2 to the number in column 3. Divide the total by 2 to find the
average. For example at summit A, forward Az AB = (42 + 40) � 2 =
41�. At summit D, rear Az ED = (66 + 68) � 2 = 67�. Enter a forward
Az in column 4 and a rear Az in column 5.
- Add 180� to the smallest calculated azimuths to calculate the
remaining azimuths. For example, at summit A, rear Az BA = 41 + 180
= 221� and at summit D, forward Az DE = 67 + 180 = 247�. As before,
enter a forward Az in column (4) and a rear Az in column (5).
|
|
|
| |
|
|
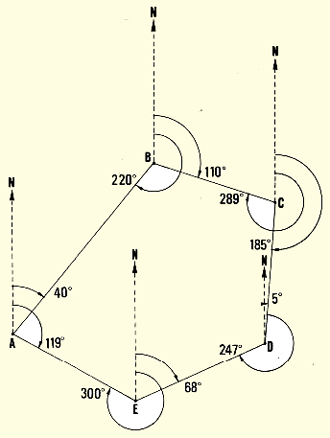 The observed forward and rear azimuths of polygon ABCDE, in a table
and in a sketch
The observed forward and rear azimuths of polygon ABCDE, in a table
and in a sketch |
|
Summit of polygon
|
Observed Azimuths
|
Largest Azimuth - 180�
|
Calculated Azimuths
|
|
Forward Az
|
Rear Az
|
Forward Az
|
Rear Az
|
|
Column
|
1
|
2
|
3
|
4
|
5
|
|
A
|
(1) AB = 40
|
(4) BA = 222
|
42
|
AB = 41
|
BA = 221
|
|
B
|
(3) BC = 110
|
(6) CB = 288
|
108
|
BC = 109
|
CB = 289
|
|
C
|
(5) CD = 185
|
(8) DC = 5
|
5
|
CD = 185
|
DC = 5
|
|
D
|
(7) DE = 246
|
(10) ED = 68
|
66
|
DE = 247
|
ED = 67
|
|
E
|
(9) EA. = 300
|
( 2) AE = 120
|
120
|
EA = 300
|
AE = 120
|
|
Calculate interior angles, combining the calculated azimuths (columns
4 and 5) two by two as follows, with the help of a little sketch:
- angle EAB = Az AE - Az AB = 120� - 41� = 79�
|
|
|
| |
|
|
- angle ABC = Az BA - Az BC = 221� - 109� = 112�
|
|
|
| |
|
|
- angle BCD = Az CB - Az CD = 289� - 185� = 104�
|
|
|
| |
|
|
- angle CDE = 360� - (Az DE- Az DC)= 360� - (247� - 5�) = 118�
|
|
|
| |
|
|
- angle DEA = 360�- (Az EA - Az ED) = 360� - (300� - 67�) = 127�
|
|
|
14. If you have
to measure consecutive angles, proceed as described earlier (see end of Section 3.1).
Checking when using a compass
When using a magnetic compass to
measure horizontal angles, you should carefully check the following points:
15. The magnetic needle must swing freely on its pivot. Keep the compass horizontal
in one hand and, with the other hand, bring an iron object close to the magnetized
needle's point. Make the needle move to the left with the iron; when you move
the iron away, the needle should swing quickly and smoothly to its original
position. Repeat the movement in the opposite direction
to double check
Put the iron near the compass to attract the needle

|
|
... then pull it away. The needle should swing
back into place
|
| |
|
|
| 16. The magnetic needle must be horizontal when the compass
is horizontal. Lay the compass on a horizontal wooden surface (such as a
table) and check that the needle remains horizontal. If it does not, you
will have to open the case of the compass and add a light weight to the
needle. To do this, you can wind some cotton sewing thread around the part
of the needle that is highest, and move the thread back and forth until
the needle is balanced and horizontal. |
|
If the needle is not horizontal

|
| |
|
|
... wrap some thread around it for balance
|
|
|
17. Do not keep iron objects close to the compass. Iron will attract
the magnetic needle, and your measurements will be wrong. Distance measuring
lines made of metal, such as steel bands, steel
tapes and chains, as well as metal ranging poles and marking pins, should
be kept 4 to 5 m away from the compass when you are measuring angles.
If you wear eyeglasses with metal frames, you will
also have to keep them away from the compass. Remember that concrete
structures (towers, bridges, etc.) are built with iron bars which may
also cause the compass needle to move.
18. Do not use a compass when there is thunder. It affects
the needle.
19. Do not use a compass near an electric power line.
20. Keep the compass horizontal while you are measuring with it.
|
Metal and electricity can affect your compass
|
|
|
|
|
Note: because the magnetic needle of the
compass is always affected by the presence of iron
nearby, checking the measured azimuths (as explained
earlier) is extremely important. If your results do not agree after
repeated measurements, local magnetic disturbances
caused by the presence of iron in the ground may be responsible for
the errors. You should then use another method of measurement.
3.3 Graphic methods for measuring horizontal angles
To use the graphic methods for measuring horizontal angles, you need
to draw the angle on paper first. Then you will measure the angle with
a protractor (see step 11, below). As you have seen
with other methods, you can obtain more accurate results if you repeat
the procedure at least twice to discover possible errors.
Using a simple compass and a protractor in the field
1. With this method, you can use a simple magnetic compass (see Section 3.2.).
The only purpose of this compass is to show the direction of the magnetic
north*.
|
|
|
|
| |
|
|
| 2. Get a 30 x 30 cm piece of stiff cardboard or thin wooden
board, and several sheets of square-ruled paper (such as millimetric
paper). Lightly glue each sheet, at its four corners, to the board, one
on top of the other.
3. On the upper left-hand corner of the top sheet, attach the compass,
for example with a string or rubber band or within a small wooden frame,
so that its 0� to 180� reference line is parallel to one of
the rules on the paper. With a pencil, draw an arrow straight up toward
the top of the sheet, and mark it North.
|
|
|
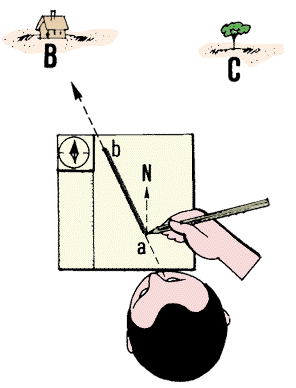
4. To draw the horizontal angle BAC you need to measure, stand at the
angle's summit A and look at aground line AB which
forms one of the sides of the angle.
5. Keeping your board horizontal on the palm of one hand held in front
of you, turn it slowly around until the northern point of the
compass needle reaches the 0�-graduation Your sheet of paper
is now oriented, with its arrow facing north.
Note: it will be easier if you rest the board on a stable
support, such as a wooden pole driven into the ground.
Line up your board so the compass points
to magnetic
north 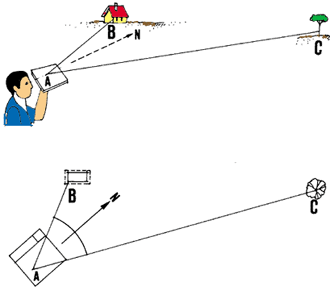
|
|
Rest the board on a support for stability
|
6. Without moving the
board any more, trace on the paper in pencil, with your free hand, a line ab going
straight ahead in the direction of the ground line AB.
7. Repeat the procedure described in steps 5 and 6 above, looking at the ground
line AC which forms the other side of the angle and drawing line ac.
Sight and draw line ab
|
|
Then sight and draw line ac
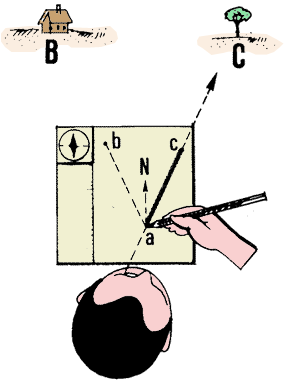
|
8. Using a protractor (see steps 15 to 17 below), measure the azimuths of the
lines you have traced as the angles formed by them with any of the paper
rules running parallel to the north. Remember to measure the angle clockwise
from the north to the pencil line (see Section 3.2).
Note: you only need to measure angles smaller
than 90�, since the square-ruled paper shows the 90�, 180� and 270�
directions.
9. Take the azimuths of the two sides of the horizontal angle, and calculate
the value of the angle as described in Section 3.2.
Using
a plane-table and a protractor
10. If you have a plane-table (see Section 7.5),
you can use it to draw the angles on paper while you are in the field. Then
it is easy to measure them with a protractor (see steps 15 to 17, below).
Measure the azimuths with a protractor

|
|
|
What is a protractor?
11. A protractor is a small instrument used in drawing. It is graduated
in degrees or fractions of degrees. The semicircular protractor
is the most common type, but a full-circle protractor may
be best for measuring angles greater than 180�. Protractors are usually made
of plastic or even paper. You can buy one cheaply in stores that sell school
supplies. Or you can use the one provided in Figure 2. Either
make a copy of it, or copy it on to transparent tracing paper. Note that the
arrow points at the exact position of the protractor's centre.
FIGURE
2
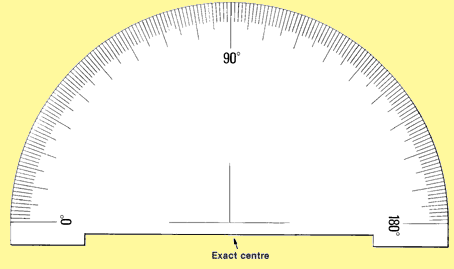
|
Making your own protractor
|
| 12. Cut the drawing of the protractor in Figure
2, exactly along its curved outer edge. |
|
13. Glue this paper protractor onto a slightly larger piece
of stiff cardboard. |
| |
|
|
|
|
|
|
| |
|
|
| 14. Cut the cardboard, exactly following the shape of the
protractor. |
|
|
Using the protractor to measure an angle you have drawn
|
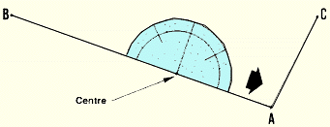
| 15. AIign the 0� to 180� straight edge of the protractor with
one of the angle's sides AB. |
|
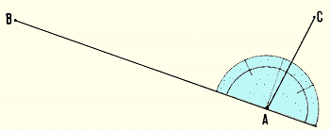
16. Move the protractor so that its centre is positioned exactly
on the summit A of the angle, keeping the 0� to 180� straight edge on the
angle's side AB. |
| |
|
|
Line up the protractor
|
|
Centre it at the angle's summit
|
| |
|
|
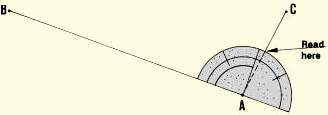
| 17. Look for the point where the angle's other side AC intersects
the graduation on the round edge of the protractor. Read the value of the
angle from this graduation. This value may be expressed in degrees and minutes
(remember that half of 1 degree equals 30 minutes). |
|
Note: if the sides of the angle are
not long enough to intersect the edge of the protractor, lengthen them before
you begin measuring. |
| |
|
|
Read the graduation
|
|
Prolong lines if necessary
|
3.4 How to measure horizontal angles by the right-angle
method
|
| 1. The right-angle method is best for measuring angles
smaller than 10 degrees in the field, since the preceding
methods do not give accurate results. The right-angle method is based on
the geometrical properties of right- angled triangles
(see Section 3.0, step 7). |
|
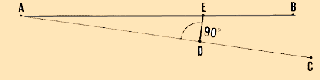
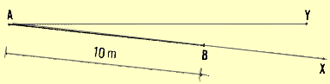
2. From the angle's summit A, measure 10 m along
one of the sides AC of the angle. Clearly mark this point D, with a ranging
pole for example. |
| |
|
|
|
|
|
Measure 10m

|
| |
|
|
| 3. From point D, lay out a perpendicular
line and prolong it until it intersects the second side of the angle.
Clearly mark this intersection point E. |
|
4. Accurately measure the length, in metres, of this perpendicular
line DE. |
| |
|
|
Lay out a perpendicular
|
|
Calculate the value
|
5. Divide this length by 10 to obtain the tangent* of the angle.
6. Look for this value in Table 3 and find the measurement of the angle BAC
in degrees and minutes.
Example
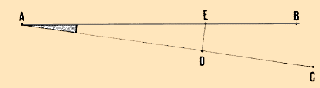
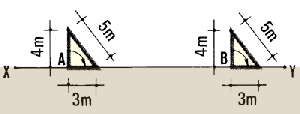
You have to measure the small angle XAY:
- from summit A measure 10 m on line XA and mark point B;
|
|
|
Measure 10 m to point B
|
| |
|
|
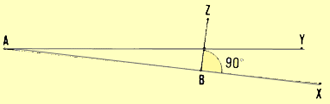
- from B trace perpendicular line BZ which intersects line YA at point
C;
|
|
- exactly measure distance BC = 1.12 m;
- dividing this value by 10, you obtain the tangent of angle XAY, 0.112;
|
| |
|
|
Lay out perpendicular BZ
|
|
From distance BC = 1.12 m, calculate the value
XAY = 6�20'

|
- look for 0.112 in Table 3. The closest value you find is 0.1110. Based
on this value, angle XAY = 6� 20'.
TABLE 3
Tangents and values of angles
(Tan = angles expressed in degrees d and minutes m)
|
Tan
|
d
|
m
|
Tan
|
d
|
m
|
Tan
|
d
|
m
|
Tan
|
d
|
m
|
Tan
|
d
|
m
|
Tan
|
d
|
m
|
Tan
|
d
|
m
|
|
0
|
0
|
0
|
0.0875
|
5
|
0
|
0.1763
|
10
|
0
|
0.2679
|
15
|
0
|
0.3640
|
20
|
0
|
0.4663
|
25
|
0
|
0.5774
|
30
|
0
|
|
0.0029
|
|
10
|
0.0904
|
|
10
|
0.1793
|
|
10
|
0.2711
|
|
10
|
0.3673
|
|
10
|
0.4699
|
|
10
|
0.5812
|
|
10
|
|
0.0058
|
|
20
|
0.0934
|
|
20
|
0.1823
|
|
20
|
0.2742
|
|
20
|
0.3706
|
|
20
|
0.4734
|
|
20
|
0.5851
|
|
20
|
|
0.0087
|
|
30
|
0.0963
|
|
30
|
0.1853
|
|
30
|
0.2773
|
|
30
|
0.3739
|
|
30
|
0.4770
|
|
30
|
0.5890
|
|
30
|
|
0.0116
|
|
40
|
0.0992
|
|
40
|
0.1883
|
|
40
|
0.2805
|
|
40
|
0.3772
|
|
40
|
0.4806
|
|
40
|
0.5930
|
|
40
|
|
0.0145
|
|
50
|
0.1022
|
|
50
|
0.1914
|
|
50
|
0.2836
|
|
50
|
0.3805
|
|
50
|
0.4841
|
|
50
|
0.5969
|
|
50
|
|
0.0175
|
1
|
0
|
0.1051
|
6
|
0
|
0.1944
|
11
|
0
|
0.2867
|
16
|
0
|
0.3839
|
21
|
0
|
0.4877
|
26
|
0
|
0.6009
|
31
|
0
|
|
0.0204
|
|
10
|
0.1080
|
|
10
|
0.1974
|
|
10
|
0.2899
|
|
10
|
0.3872
|
|
10
|
0.4913
|
|
10
|
0.6048
|
|
10
|
|
0.0233
|
|
20
|
0.1110
|
|
20
|
0.2004
|
|
20
|
0.2931
|
|
20
|
0.3906
|
|
20
|
0.4950
|
|
20
|
0.6088
|
|
20
|
|
0.0262
|
|
30
|
0.1139
|
|
30
|
0.2035
|
|
30
|
0.2962
|
|
30
|
0.3939
|
|
30
|
0.4986
|
|
30
|
0.6128
|
|
30
|
|
0.0291
|
|
40
|
0.1169
|
|
40
|
0.2065
|
|
40
|
0.2994
|
|
40
|
0.3973
|
|
40
|
0.5022
|
|
40
|
0.6168
|
|
40
|
|
0.0320
|
|
50
|
0.1198
|
|
50
|
0.2095
|
|
50
|
0.3026
|
|
50
|
0.4006
|
|
50
|
0.5059
|
|
50
|
0.6208
|
|
50
|
|
0.0349
|
2
|
0
|
0.1228
|
7
|
0
|
0.2126
|
12
|
0
|
0.3057
|
17
|
0
|
0.4040
|
22
|
0
|
0.5095
|
27
|
0
|
0.6249
|
32
|
0
|
|
0.0378
|
|
10
|
0.1257
|
|
10
|
0.2156
|
|
10
|
0.3089
|
|
10
|
0.4074
|
|
10
|
0.5132
|
|
10
|
0.6289
|
|
10
|
|
0.0407
|
|
20
|
0.1287
|
|
20
|
0.2186
|
|
20
|
0.3121
|
|
20
|
0.4108
|
|
20
|
0.5169
|
|
20
|
0.6330
|
|
20
|
|
0.0437
|
|
30
|
0.1317
|
|
30
|
0.2217
|
|
30
|
0.3153
|
|
30
|
0.4142
|
|
30
|
0.5206
|
|
30
|
0.6371
|
|
30
|
|
0.0466
|
|
40
|
0.1346
|
|
40
|
0.2247
|
|
40
|
0.3185
|
|
40
|
0.4176
|
|
40
|
0.5234
|
|
40
|
0.6412
|
|
40
|
|
0.0495
|
|
50
|
0.1376
|
|
50
|
0.2278
|
|
50
|
0.3217
|
|
50
|
0.4210
|
|
50
|
0.5280
|
|
50
|
0.6453
|
|
50
|
|
0.0524
|
3
|
0
|
0.1405
|
8
|
0
|
0.2309
|
13
|
0
|
0.3249
|
18
|
0
|
0.4245
|
23
|
0
|
0.5317
|
28
|
0
|
0.6494
|
33
|
0
|
|
0.0553
|
|
10
|
0.1435
|
|
10
|
0.2339
|
|
10
|
0.3281
|
|
10
|
0.4279
|
|
10
|
0.5354
|
|
10
|
0.6536
|
|
10
|
|
0.0582
|
|
20
|
0.1465
|
|
20
|
0.2370
|
|
20
|
0.3314
|
|
20
|
0.4314
|
|
20
|
0.5392
|
|
20
|
0.6577
|
|
20
|
|
0.0612
|
|
30
|
0.1495
|
|
30
|
0.2401
|
|
30
|
0.3346
|
|
30
|
0.4348
|
|
30
|
0.5430
|
|
30
|
0.6619
|
|
30
|
|
0.0641
|
|
40
|
0.1524
|
|
40
|
0.2432
|
|
40
|
0.3378
|
|
40
|
0.4383
|
|
40
|
0.5467
|
|
40
|
0.6661
|
|
40
|
|
0.0670
|
|
50
|
0.1554
|
|
50
|
0.2462
|
|
50
|
0.3411
|
|
50
|
0.4417
|
|
50
|
0.5505
|
|
50
|
0.6703
|
|
50
|
|
0.0699
|
4
|
0
|
0.1584
|
9
|
0
|
0.2493
|
14
|
0
|
0.3443
|
19
|
0
|
0.4452
|
24
|
0
|
0.5543
|
29
|
0
|
0.6745
|
34
|
0
|
|
0.0729
|
|
10
|
0.1614
|
|
10
|
0.2524
|
|
10
|
0.3476
|
|
10
|
0.4487
|
|
10
|
0.5581
|
|
10
|
0.6787
|
|
10
|
|
0.0758
|
|
20
|
0.1644
|
|
20
|
0.2555
|
|
20
|
0.3508
|
|
20
|
0.4522
|
|
20
|
0.5619
|
|
20
|
0.6830
|
|
20
|
|
0.0787
|
|
30
|
0.1673
|
|
30
|
0.2586
|
|
30
|
0.3541
|
|
30
|
0.4557
|
|
30
|
0.5658
|
|
30
|
0.6873
|
|
30
|
|
0.0816
|
|
40
|
0.1703
|
|
40
|
0.2617
|
|
40
|
0.3574
|
|
40
|
0.4592
|
|
40
|
0.5696
|
|
40
|
0.6916
|
|
40
|
|
0.0846
|
|
50
|
0.1733
|
|
50
|
0.2648
|
|
50
|
0.3607
|
|
50
|
0.4628
|
|
50
|
0.5735
|
|
50
|
0.6959
|
|
50
|
|
3.5 How to measure horizontal angles with a theodolite
|
What is a theodolite?
|
|
1. A theodolite, sometimes called a transit, is
an expensive instrument which surveyors use to measure horizontal angles
precisely. It is like a graphometer, but more complicated
(see Section 3.1). Most theodolites are designed to measure vertical angles
as well. The theodolite's basic features for measuring horizontal angles
are:
- a horizontal circle, graduated in degrees, which may be
rotated and then clamped in any position;
- a circular plate which may be rotated inside this circle,
and which shows additional graduations for reading the graduations on
the circle with greater precision;
- a telescope which is attached to this circular plate and
turns with it, and which can also be turned up and down in the vertical
plane.
- a tripod (three-legged support) on which to place the theodolite
when measuring.
|
|
|
Using the theodolite to measure a horizontal angle
2. If you want to measure angle BAC, place the theodolite horizontally on its
tripod at summit A. Set the index on the horizontal graduated circle at zero
and take a sighting to B. Clamp the circle in position. Turn the telescope and
its circular plate to take a sighting to C, while rotating through the angle
BAC. You may read the angle measurement directly from the circular plate index.
Sight at the points...

|
|
... and read the measurements
|
What are the main problems you will face?
2. There are two main problems
to be solved:
Dropping a perpendicular from point A to line
XY


|
|
Laying out a perpendicular from point X on line
AB

|
|
7. Measure on XY the distance BC between these two marked
points.
8. Divide this distance by 2 and measure this new distance from point
B. Mark this point D - it will be exactly in the middle of BC.
|
|
Measure distance BC
|
| |
|
|
| 9. Connect point D and the original point A to form a new
line AD perpendicular to XY. |
|
Divide by 2 to find mid-point D
|
| |
|
|
Connect points D and A to form the perpendicular
|
|
|
Dropping a perpendicular by the half-circle method
Set out line XY and point A as
described above. Prepare a measuring line a little longer than half the distance from
point A to the line XY on which you will drop the perpendicular.
10. From any point B on line XY,
measure distance AB to point A.
11. Divide this distance AB by 2
and mark the centre point C.
12. Attach one end of your measuring line to point C as in step 4, above.
Mark point A

|
|
Measure distance AB
|
| |
|
|
Divide by 2 to find mid-point C
|
|
|
13. Walk with the other end of your line to point B on XY, and clearly
mark this distance CB on the measuring line.
14. Trace an arc on the ground
with the line length CB. To do this, swing the line in a curve to the right until you
intersect XY again. Mark this point D.
15. Join D to the original point A to form a new line AD perpendicular
to XY.
Find length CB on your rope

|
|
Trace an arc on the ground to find point D
|
| |
|
|
Connect point A and D to form the perpendicular
|
|
|
|
Setting out a perpendicular by the mid-point method
|
| 16. The easiest way of setting out a perpendicular from a
fixed point A on line XY is to use a simple line clearly marked at
its mid-point with, for example, a knot. This line can be a liana,
a rope or a string or you may use a measuring tape, whose graduations will
help you to locate the exact mid-point. For good results, the line
should be at least 8 m long. A longer line will make your measurements
even more accurate. If you are working alone, make a small loop at each
end of the line. |
|
|
| |
|
|
|
|
17. Set out line XY and mark point A from which you will set out the perpendicular.
On either side of point A and along line XY, measure the equal distances
AB = AC of about 2 m. You can use part of the measuring line
to do this. Mark points B and C with stakes.
18. Loop one end of the line over stake B and the other
end over stake C.
Setting out a perpendicular by the intersection method
20. To set out a perpendicular
by the intersection method, you can use a simple line again. The method you use will
depend on the length of the line. Remember that:
- if the perpendicular is to be
short, it is best to use the first method (steps 21-29);
- if the perpendicular is to be
long, it is best to use the second method (steps 30-38).
Using the short-line intersection method
|
|
21. To use this method, you will need a simple measuring line
such as a liana or a rope 5 to 6 m long, a short pointed stick
or thin piece of metal (such as a big nail) and five marking stakes.
22. Set out line XY. On this line, choose point A, from which you will
set out the perpendicular, and mark it clearly with a stake.
23. With part of your measuring line, measure a 2 to 3 m distance
to the left of point A on XY. Mark this point B with a stake.
24. Measure the same distance on XY to the right of point
A. Mark this point C with a stake.
|
|
Mark point A

|
| |
|
| |
With the rope find point B

|
| |
|
| |
... and, by making an arc, point C

|
| |
|
| |
|
| 25. Make a fixed loop at one end of your line,
and securely attach the pointed stick or piece
of metal to the other end.
26. Place this loop around marking stake B. Then, keeping the line
well-stretched, trace a large arc on the ground with the other end
of the line. This arc should extend beyond point A, and a long way on
either side of XY.
27. Take up the loop from stake B and place it around stake C. Trace
another arc on the ground which should intersect the first arc
at two points, D and E.
28. Clearly mark these two points D and E with stakes.
|
|
|
| |
|
|
Do the same from point C - the arcs intersect
at points D and E

|
|
From point B, trace a large arc on both sides of
line XY

|
| |
|
|
|
29. Taking up the loop from stake C, place it around stake D; holding
the other end of the line, walk to stake E and attach it there; check
to see if the line touches the central stake A (remember that the perpendicular
was originally to be set out from point A); if it does, line DE forms
this perpendicular on the ground.
|
|
Attach the line at point D and walk to point E

|
| |
|
|
The stretched line forms perpendicular DAE

|
|


|
Using the long-line intersection method
|
|
30. To use this method, you will need a simple line about 55 m
long, a short pointed stick or thin piece of metal
and four marking stakes.
31. Clearly mark point A on line XY with a stake. You will set out
the perpendicular from this point.
32. Measure 25 to 30 m to the left of point A
on line XY, using part of your measuring line; mark this point B with
a stake.
33. Measure the same distance on XY to the right of A; mark this point
C with a stake.
34. Make a fixed loop at one end of your line. Securely
attach the pointed stick or piece of metal to the other end
of the line (as in step 25, above).
|
|
Mark point A

|
| |
|
| |
Use the line to find point B...

|
| |
|
| |
... and point C

|
|
35. Place the loop around marking stake B and, with the
other end of the line in one hand, walk diagonally away from line XY.
When you reach a point above A where the line is well stretched,
trace an arc 2 to 3 m long on the ground with the end of your line.
36. Repeat the last step from the second stake C. The arc you mark
on the ground from this point should intersect the first arc at point
D.
37. At this intersection point D, drive a marking stake into the ground.
38. The line AD joining D with the original point A is perpendicular
to XY.
Note: you can only use the intersection method
on ground that is clear of large rocks and high vegetation, because
you must be able to mark and see the arcs easily. If necessary, you
can clear the ground as you work.
|
|
From point B, trace an arc above point A
|
| |
|
| |
Do the same from point C - the arcs intersect
at point D
|
| |
|
|
Connect points D and A to form the perpendicular
|
|
|
Setting out a perpendicular by the 3:4:5 rule method
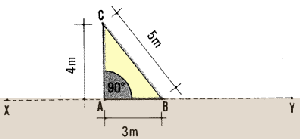
39. The 3:4:5 rule is that any triangle with sides in the proportion
3:4:5 has a right angle opposite the longest side. The method
is based on this rule.
The length of the simple line you use for measuring will
depend on the length of the perpendicular you are setting out. The longer the
perpendicular, the longer your measuring line must be.
Examples
- Very short line: about 1.5 m long, a little longer than 0.3 m + 0.4
m + 0.5 m = 1.2 m;
- Short line: about 13 m long, a little longer than 3 m + 4 m + 5 m =
12 m;
- Medium line: about 38 m long, a little longer than 9 m + 12 m + 15
m = 36 m;
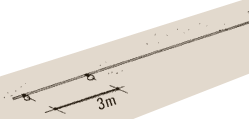
- Long line: about 65 m long, a little longer than 15 m + 20 m + 25 m
= 60 m.
40. To make your simple line, get a rope 1-1.5 cm thick; it is best
if made from natural fibres which will stretch or shrink very little. A piece
of used sisal rope will stretch or shrink less than a new one. You
can also use a measuring tape.
41. There are several ways of using the 3:4:5 rule method,
depending on the type of measuring line you use and the number of people
who can work together with you. When using medium or long lines, it
is best to work in a team of three people. When using a short or very
short line, you can work by yourself.
Making your own 3:4:5 measuring line
|
|
42. You can easily make a simple line to use with the 3:4:5
rule method. This line is sometimes known as a ratio rope.
The following shows one way of making a short line about 13 m long, but
you can make shorter or longer lines in the same way.
43. Take a piece of rope about 13 m long. A few centimetres from one
end, tie a metal ring to it securely with heavy string.
|
|
|
| |
|
|
|
44. Measure a length of 3 m along the rope from this ring, and attach
a second ring to the rope.
45. Using a measuring tape, check that the distance from the first to
the second ring is exactly 3 m. If it is not, adjust it.
|
|
Tie the ring on securely
|
| |
|
|
Measure again when the ring is in place
|
|
Attach the second ring 3 m down
|
|
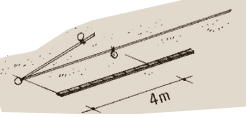
46. Measure a length of 4 m from the second ring and attach a third ring.
With a measuring tape, check that the distance is exactly 4 m. Adjust
it if necessary.
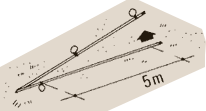
47. Measure a length of 5 m from the third ring. Attach this end point
of the rope to the first ring. Check the length with a measuring tape
and adjust if necessary.
|
|
Attach the third ring 4 m down and
check the measurement
|
| |
|
|
| |
|
5 m from the third ring...
|
| |
|
|
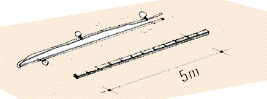
Check the final measurements
|
|
... attach the rope to the first ring

|
| 51. Hold the ring between the 4 m and 5 m segments, and pull
the ratio rope into the shape of a triangle, making sure that the 4 m and
5 m segments are tightly stretched. Using this ring, stake the
rope at C.
52. The angle which has been formed at A between the 3 m and 4 m segments
of the ratio rope is a right angle.
|
|
With the third ring, walk away from line XY

|
| |
|
|
When the rope is stretched tight, mark point C
to form the right angle
|
|
|
Note: you can also use a 3:4:5 ratio rope with much shorter segments.
A 30 cm: 40 cm: 50 cm line, for example, is ideal for measuring angles
of smaller areas, which can be used for laying out a V-knotch weir, for
example (see Vol.4, Water, Section 3.6).
Using the medium 3:4:5 line to set out a right angle
|
|
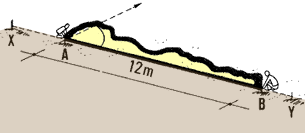
53. Use a line about 36 m long, prepared like the short line,
except that the sections should be 9 m, 12 m and 15 m long. Starting at
point A, where the right angle has to be set out, stretch the 12 m segment
along line XY; at this point attach the ring on the line to stake B.
54. With the 15 m segment, walk away from B while your assistant returns
to the original point A with the 9 m segment of the line.
55. When these last two sides of the triangle are fully stretched,
mark the point C which connects the 9 m and 15 m lengths. This point forms
perpendicular AC at A.
|
|
|
| |
|
|
With a longer line, use an assistant
|
|
|
Using the long 3:4:5 line to set out a right angle
|
|
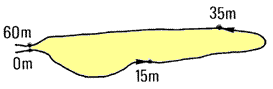
56. On a rope about 65 m long, clearly mark the
0 m, 15 m, 35 m and 60 m lengths. You should work in a team of three people
when using this line.
57. The first person holds the rope at the 15 m mark at point
B on line XY, from which the perpendicular is to be set out.
58. The second person holds the 0 m and 60 m marks
together at point A along XY.
|
|
|
| |
|
|
|
|
|
Keep the 0 m and 60 m marks together at point A
|
| |
|
|
| |
|
At point B, the second person holds the 15 m mark

|
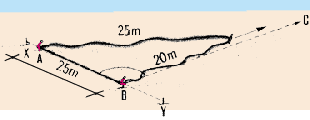
| 59. The third person takes the rope
at the 35 m mark and walks away from XY. He or she adjusts his or her position
until the two sides of the triangle are stretched. When this is done, the
position point C is marked. Joined to point B, this forms perpendicular
BC to XY.
Note: you should always double-check distances
to make sure that no errors have been made.
|
|
The third person walks away, holding the 35 m mark
|
| |
|
|
| |
|
When the rope is stretched tight, mark point C
to make the right angle
|
Using a measuring tape to set out a right angle
You need to set out the centre-line WZ of a dike perpendicular to the centre-line
XY of another dike, for example. Using a measuring tape at least 80 m long
and working in a team of three, proceed as follows:
60. From the intersection point A of the two dike centre-lines, measure 40
m along XY, the known centre-line. Mark this point B.
Setting out a perpendicular with a cross-staff
|
|
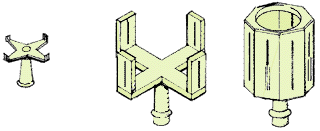
63. A cross-staff is an inexpensive sighting instrument which
is very useful for setting out right angles. There are several models,
such as the octagonal brass cross-staff, which has sighting
slits cut at right angles to each other, and the foresight/backsight
model. In use, cross-staffs must be firmly fastened to a support,
usually a stake driven vertically into the ground. Their useful range
does not extend beyond 30 to 40 m. You might be able to borrow a cross-staff
from a surveyor's office, or you can build your own as described below.
Note: the octagonal cross-staff also
has additional sighting slits cut at 45�, and is useful for
setting out 45-degree angles (see, for example, Section 2.9, step 7).
|
|
Professional cross-staffs
|
| |
|
|
Sighting with a home-made cross-staff
|
|
|
Making your own cross-staff
|
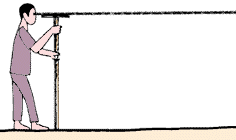
| 64. Get two metal or wooden strips 2 to 3 cm wide and 20 to
25 cm long. Find the centres of the strips at the intersection of two diagonal
lines, as you found the centre of your alidade in step 9. Drill a small
hole exactly at this centre point you have found on each strip. These are
the cross-pieces. |
|
|
| |
|
|
| 65. Provide a sighting line on each cross-piece.
To do this on wooden strips, drive in one small headless nail, centred,
near each end of each strip. On metal strips, you can weld or glue small
nails or metal points near the ends of the strips |
|
|
| |
|
|
|
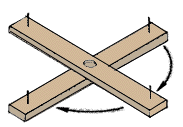
66. Place the cross-pieces approximately at right angles and, with a
screw, attach them loosely in that position to the top of a 1.50 m vertical
stake. If you use washers between the wooden cross-pieces and the stake,
it will be easier to tighten the strips securely later.
|
|
|
Adjusting the home-made cross-staff
|
|
67. Lay out a right angle on the ground using
a long 3:4:5 ratio rope (see steps 56 to 59, this section). The sides
of the triangle will be next 15 m, 20 m and 25 m long.
68. Put a short stake at point A, the corner of the right angle, between
the 15 m and 20 m sides. Then put ranging poles at points B and C to mark
the sides of the angle.
69. Position the cross-staff and its vertical support at point A.
70. Align one cross-piece alongside AB and sight
towards point E.
71. Without moving the vertical support, align the second cross-piece
along the other side AC of the angle, and sight towards point C. Tighten
the screws a little to keep the cross-pieces in place.
|
|
Lay out a right triangle
|
| |
|
|
Sight point B with one cross-piece
|
|
Sight at point C with the other one
and tighten the screw
|
72. Rotate the vertical support 90� to check that the cross-pieces
are truly at a right angle. Sight at points B and C again and correct the position
of the cross-pieces if necessary.
73. Repeat this process until you are sure that each cross-piece
is aligned with one side of the right angle, that is, that
they are at 90� angles from each other.
74. When both cross-pieces are properly aligned, firmly tighten
the screw holding them to the vertical support.
75. Check both sighting lines
again after tightening the screw to make sure that the cross-pieces have not slipped.
76. To help you adjust the cross-pieces later, cut or engrave (with
a large nail) marks in the wood or metal of the bottom cross-piece
when the top piece is in position.
Rotate the cross-staff to check its accuracy
|
|
|
| |
|
|
| |
|
Mark the lower cross-piece for reference
|
Using the cross-staff to set out a right angle
77. To use the cross-staff, you will need an assistant.
78. Lay out straight line XY on which you need to construct the right angle
at point A.
79. Place the support of the
cross-staff in a vertical position at point A.
80. Ask your assistant to hold a
ranging pole in a vertical position at point B, near the end of XY.
81. Sight along one of the
cross-pieces and rotate the vertical support until the sighting line is aligned on B.
82. Without moving the cross-staff and its vertical support, sight along the
other cross-piece. At the same time, direct your assistant to stand with a ranging
pole as near to this sighting line as possible.
Sight along XY to align the cross-staff
|
|
Sight along the other cross-piece to
find the perpendicular
|
| |
|
|
|
|
|
|
83. Tell your assistant to hold the ranging pole in front of him or her and
move to the right or left until the pole is exactly on the sighting line AZ.
84. When you are sure he or she
is on line AZ, tell him or her to mark his position with stake C.
85. The angle BAC you have determined at point A, where the cross-staff is
placed, is a 90� angle.
Place the ranging pole at point C on line AZ
|
|
BAC is a right angle

|
Note: with the help of a cross-staff you
can easily determine the rectangular areas which you need for a fish-
pond lay out. You can also build a grid of squares by determining intermediate
angles along your straight lines. This is a method used in estimating
reservoir volumes, for example (Volume 4, Water, Section
4.2).
3.7 How to set out parallel lines
What are parallel lines?
1. Parallel lines, also called parallels, are lines equally distant from
each other at every point. Parallel lines run side by side
and will never cross. They are very important in fish culture and
are often used in designing fish- farms (for example, for parallel dikes and
ponds), in building dams and in setting out water canals. Parallels are also
useful when laying out lines under difficult conditions (see
Section 1.7).
Setting out parallels by the 3:4:5 rule
|
|
One way to set out a parallel line uses the 3:4:5 rule. It works like
this:
2. On given line XY, select two points A and B which are fairly
distant from each other (for example, 20 to 30 m apart), and mark them
with pegs.
3. From each of these points, set out a perpendicular
using the 3:4:5 rule method. Remember that the length of the
line you will use depends on the length of the perpendicular you are setting
out (see Section 3.6, step 35).
4. Prolong these two perpendiculars as required. Then, measure an
equal distance from the given line XY on each of them;
mark these two points C and D.
5. Through these two points, set out a line WZ. This line will be parallel
to XY.
|
|
Set out two perpendiculars...

|
| |
|
|
Prolong each one equally

|
|
Connect the points to form the parallel.
|
Setting out parallels with the crossing-lines method
|
|
To use the crossing-lines method, you do not need to set out perpendiculars;
you will only measure distances. However, this method cannot be used when
you need to measure the exact position of the parallel you
need to set out. It is useful when the distance of the parallel is not
important, such as when you are prolonging
a line over an obstacle (see Section 1.7). Proceed as follows:
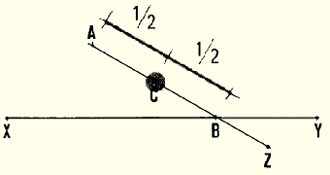
6. Lay out line XY. Select any point A which will belong to the
parallel line you need to set out. Clearly mark point A with a peg.
|
|
Choose point A

|
| |
|
|
|
7. From point A, set out an oblique line AZ. Mark point B
where AZ intersects the original line XY.
Note: an oblique line is neither parallel, nor
perpendicular.
8. Measure the length of the oblique line AB.
9. Divide this length by 2, measure this distance from point A, and mark
this central point C.
|
|
Divide AB by 2 to find point C
|
| |
|
|
Choose point D
|
|
Lay out AZ, find point B, measure distance AB
|
|
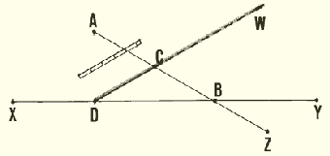
10. On the original line XY, select point D, which should lie as nearly
opposite point A as possible.
11. From point D, set out a straight line DW passing through point
C.
|
|
Set out line DW
|
| |
|
|
|
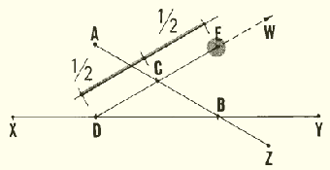
12. Measure distance DC.
13. From point C on line DW, measure a distance equal to distance DC.
Mark the end of the segment point E.
14. Connect points E and A with a line KL. This line is
parallel to line XY.
|
|
Find point E
|
| |
|
|
|
Connect the points A and E to form the parallel
|
|
|
Setting out a series of rectangular areas
15. When you build a fish-farm, you will often need to set out a series of
rectangular plots on the ground. These plots are the future sites of ponds or
other constructions, (see the next manual in this series, Constructions
for Freshwater Fish Culture).
|
|
|
|
| |
|
|
| 16. First select the direction of the main dike's centre-line
XY, and set it out on the ground with ranging poles. Using the measurements
along this line, you will be able to mark the points A, B and C where you
will set out the centre-lines of the secondary dikes. To do this, proceed
as follows: |
|
Set out the centre line of the main dike and the
points
where the other dikes will cross it
|
| |
|
|
| 17. Set out a few perpendiculars*
on XY, using one of the methods given in Section 3.6, for example, from
two extreme points A and B (near the end-points of XY) and from
one intermediate point C. |
|
Lay out perpendiculars from these points
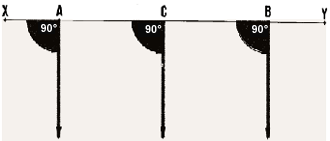
|
| |
|
|
| 18. Starting from points A and B, measure equal distances
AF and BG along their perpendiculars; these distances should be equal to
the selected distance between the main dike centre-line XY and the centre-line
of the opposite dikes. Mark the two points on the perpendiculars, F and
G, with ranging poles. |
|
Measure equal distances along the perpendiculars
|
| 19. Clearly set out line WZ through points F and G using
ranging poles.
20. Starting from point B on line XY, measure intermediate distances
BE, EC and CD. Then move back to line WZ; starting from point G, measure
intermediate distances GH, HI and IJ equal to BE, EC and
CD, respectively. Mark points H, I and J with pegs.
21. While you are doing this, check that point I falls exactly
on the intermediate perpendicular set out from C. If
there is a small difference, adjust the positions of the perpendicular
and point I. If there is a large difference, check your previous work
for errors.
22. As a final check, be sure that the last measurement JF lines up
with point F.
|
|
Set out parallel WZ

|
| |
|
|
|
|
|
Set out and check intermediate distances

|
